Cox Proportional Hazards Regression for Interval-Censored Data with an Application to College Entrance and Parental Job Loss
Abstract
1. Introduction
2. Theoretical Background
2.1. A Relationship between Parental Unemployment and College Entrance
2.2. Characteristics of Time to Admission as Survival Data
3. Data and Methodology
3.1. Cox Proportional Hazards Regression
3.2. Multiple Imputation for Interval-Censored Time
- In the i-th iteration, the estimates for the regression coefficient and the baseline survival function are denoted by and . Note that the starting value is . After assuming a uniform distribution for and in the m sets, the failure time is randomly generated and designated as an imputed value. This is expressed as and . The baseline survival probability is the Breslow estimate of the baseline survival probability for the k-th replaced data set.
- We generate m sets of imputed data which are possibly right-censored as follows. For each observation , , m sets created as right-censored data by replacing interval-censored time is empirically appropriate, and in the second step is discrete assumed as follows:Each object has and , if . Samples are from the distribution, under the condition that , let , and . In the case of , and .is interval-censored time and the i-th base survival function is following the probability mass function at . Here, the failure time is randomly proportional to the probability at with the probability mass function value .
- Since all the interval-censored values are imputed, the Cox proportional hazard model can be employed. Through this, the regression coefficient estimate can be considered as being and the covariance estimate can be considered as being .
- denotes the k-th right-censored data of m sets obtained through the imputation of the interval-censored data. denotes the regression coefficients obtained by fitting a Cox proportional hazard model. The Breslow estimate for the basis survival function is calculated based on and .
- In the i-th iteration, the of m sets is summed and divided by m, which is denoted by . In this way, the basis survival function is also obtained. The covariance is the sum of the intragroup and intergroup imputation variances. This can be expressed as an equation as follows.Finally, it repeats from the first until the converges.
4. Simulation Study
4.1. Simulation Settings
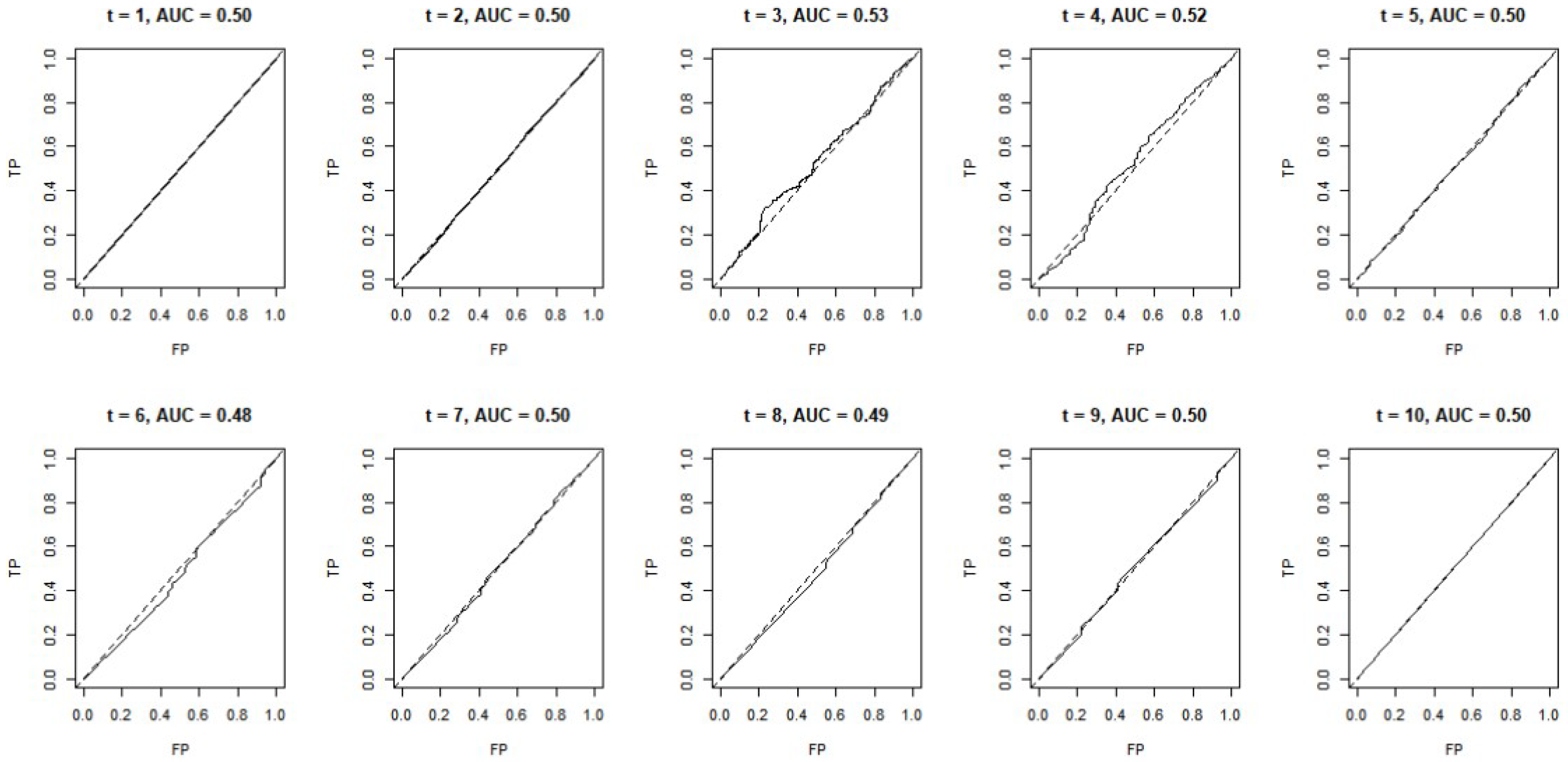
4.2. Simulation Results
5. Data Analysis
5.1. Data
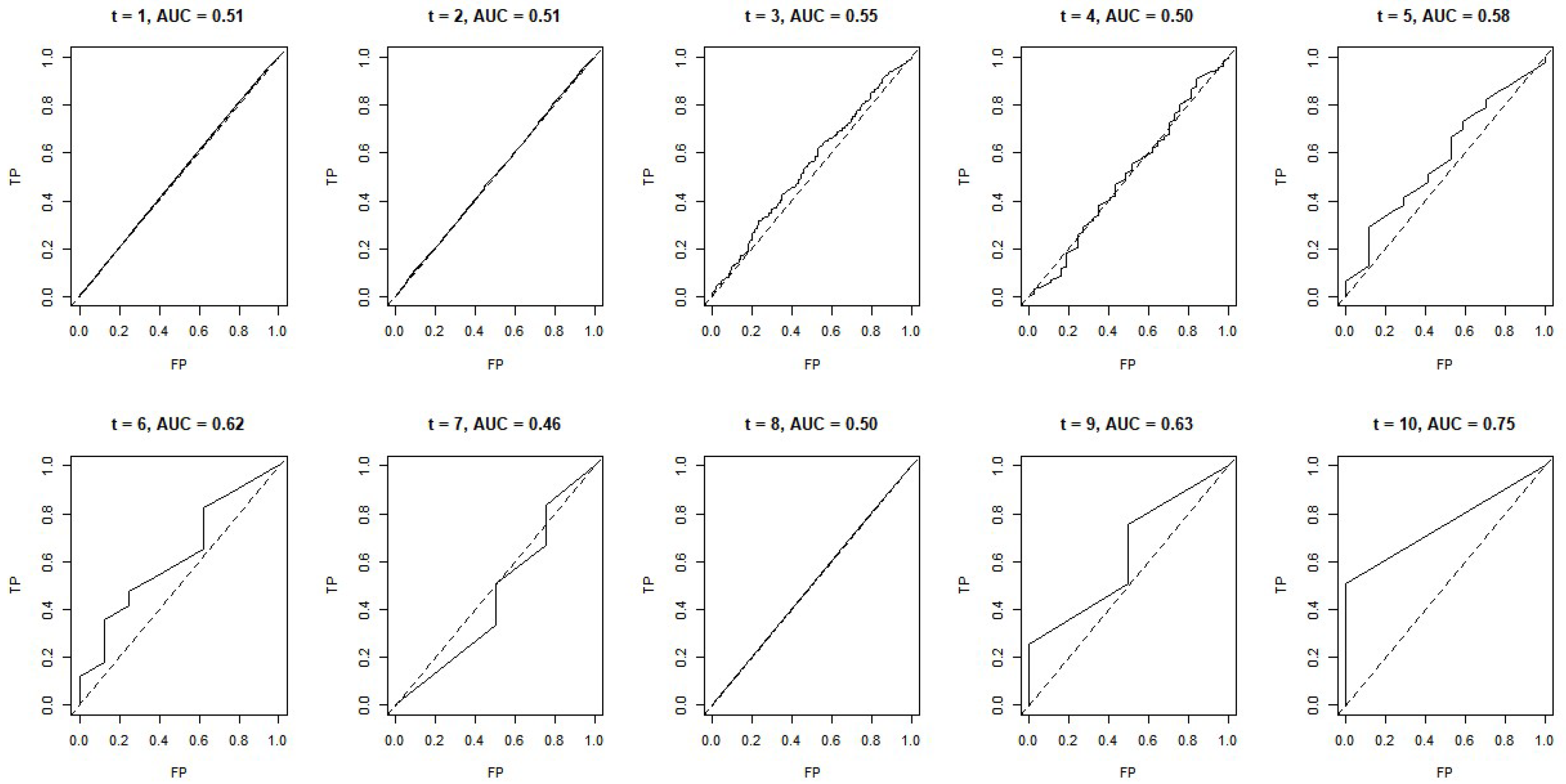
5.2. Analysis Results
5.3. Comparison of Predictive Performance According to the Imputation Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| right censoring | 20% | ||||||||
| sample size | 100 | 300 | 1000 | ||||||
| interval censoring | 15% | 30% | 45% | 15% | 30% | 45% | 15% | 30% | 45% |
| omission | 0.905 | 0.495 | 0.552 | 0.207 | 0.141 | 0.149 | 0.061 | 0.058 | 0.072 |
| midpoint imputation | 0.857 | 0.397 | 0.448 | 0.192 | 0.137 | 0.133 | 0.059 | 0.053 | 0.062 |
| multiple imputation | 0.775 | 0.392 | 0.441 | 0.200 | 0.144 | 0.140 | 0.064 | 0.060 | 0.065 |
| IntCens | 2.887 | 0.723 | 1.144 | 0.485 | 0.292 | 0.363 | 0.174 | 0.189 | 0.167 |
| right censoring | 20% | ||||||||
| sample size | 100 | 300 | 1000 | ||||||
| interval censoring | 15% | 30% | 45% | 15% | 30% | 45% | 15% | 30% | 45% |
| omission | 0.619 | 0.327 | 0.980 | 0.127 | 0.198 | 0.221 | 0.049 | 0.054 | 0.067 |
| midpoint imputation | 0.468 | 0.314 | 0.686 | 0.122 | 0.163 | 0.188 | 0.045 | 0.045 | 0.055 |
| multiple imputation | 0.486 | 0.344 | 0.688 | 0.116 | 0.166 | 0.187 | 0.049 | 0.048 | 0.060 |
| IntCens | 0.818 | 0.946 | 1.495 | 0.330 | 0.444 | 0.434 | 0.155 | 0.169 | 0.167 |
| right censoring | 20% | ||||||||
| sample size | 100 | 300 | 1000 | ||||||
| interval censoring | 15% | 30% | 45% | 15% | 30% | 45% | 15% | 30% | 45% |
| omission | 0.502 | 0.708 | 1.172 | 0.197 | 0.250 | 0.217 | 0.040 | 0.054 | 0.071 |
| midpoint imputation | 0.484 | 0.530 | 0.643 | 0.163 | 0.128 | 0.150 | 0.035 | 0.038 | 0.051 |
| multiple imputation | 0.490 | 0.485 | 0.605 | 0.163 | 0.109 | 0.133 | 0.036 | 0.034 | 0.051 |
| IntCens | 1.156 | 1.092 | 1.481 | 0.470 | 0.456 | 0.555 | 0.255 | 0.203 | 0.177 |
References
- Baum, Charles L., II. 2003. Does early maternal employment harm child development? An analysis of the potential benefits of leave taking. Journal of Labor Economics 21: 409–48. [Google Scholar]
- Becker, Gary S. 2009. Human Capital: A Theoretical and Empirical Analysis, with Special Reference to Education. Chicago: University of Chicago Press. [Google Scholar]
- Becker, Gary S., and Nigel Tomes. 1986. Human capital and the rise and fall of families. Journal of Labor Economics 4: S1–S39. [Google Scholar] [CrossRef]
- Berger, Lawrence M., Christina Paxson, and Jane Waldfogel. 2009. Income and child development. Children and Youth Services Review 31: 978–89. [Google Scholar] [CrossRef]
- Blau, David M. 1999. The effect of income on child development. Review of Economics and Statistics 81: 261–76. [Google Scholar] [CrossRef]
- Brand, Jennie E. 2015. The far-reaching impact of job loss and unemployment. Annual Review of Sociology 41: 359. [Google Scholar] [CrossRef]
- Breen, Richard, and John H. Goldthorpe. 1997. Explaining educational differentials: Towards a formal rational action theory. Rationality and Society 9: 275–305. [Google Scholar] [CrossRef]
- Charles, Kerwin Kofi, and Melvin Stephens, Jr. 2004. Job displacement, disability, and divorce. Journal of Labor Economics 22: 489–522. [Google Scholar] [CrossRef]
- Codjoe, Henry M. 2007. The importance of home environment and parental encouragement in the academic achievement of african-canadian youth. Canadian Journal of Education 30: 137–56. [Google Scholar] [CrossRef]
- Coelli, Michael B. 2011. Parental job loss and the education enrollment of youth. Labour Economics 18: 25–35. [Google Scholar] [CrossRef]
- Cox, David R. 1972. Regression models and life-tables. Journal of the Royal Statistical Society: Series B (Methodological) 34: 187–202. [Google Scholar]
- Delord, Marc, and Emmanuelle Génin. 2015. Multiple imputation for competing risks regression with interval-censored data. Algorithms 11: 22. [Google Scholar] [CrossRef]
- DiPrete, Thomas A., and Patricia A. McManus. 2000. Family change, employment transitions, and the welfare state: Household income dynamics in the united states and germany. American Sociological Review 65: 343–70. [Google Scholar] [CrossRef]
- Finkelstein, Dianne M. 1986. A proportional hazards model for interval-censored failure time data. Biometrics 42: 845–54. [Google Scholar] [CrossRef] [PubMed]
- Gangl, Markus. 2006. Scar effects of unemployment: An assessment of institutional complementarities. American Sociological Review 71: 986–1013. [Google Scholar] [CrossRef]
- Goldthorpe, John H. 1996. Class analysis and the reorientation of class theory: The case of persisting differentials in educational attainment. British Journal of Sociology 47: 481–505. [Google Scholar] [CrossRef]
- Groeneboom, Piet, and Jon A. Wellner. 1992. Information Bounds and Nonparametric Maximum Likelihood Estimation. Berlin: Springer Science & Business Media, vol. 19. [Google Scholar]
- Jahoda, Marie, Paul F. Lazarsfeld, Hans Zeisel, and Christian Fleck. 2017. Marienthal: The Sociography of an Unemployed Community. London: Routledge. [Google Scholar]
- Johnson, Rucker C., Ariel Kalil, and Rachel E. Dunifon. 2012. Employment patterns of less-skilled workers: Links to children’s behavior and academic progress. Demography 49: 747–72. [Google Scholar] [CrossRef][Green Version]
- Kalil, Ariel, and Patrick Wightman. 2011. Parental job loss and children’s educational attainment in black and white middle-class families. Social Science Quarterly 92: 57–78. [Google Scholar] [CrossRef] [PubMed]
- Kim, Eun-jung. 2007. A study on the social economic status of the family, extra tutoring fee, parent-child relationship and children’s educational achievement. Korean Journal of Sociology 41: 134–62. [Google Scholar]
- Kopycka, Katarzyna. 2021. Higher education expansion, system transformation, and social inequality. social origin effects on tertiary education attainment in poland for birth cohorts 1960 to 1988. Higher Education 81: 643–64. [Google Scholar] [CrossRef]
- Ku, In-Hoe. 2003a. The effect of economic loss and income levels on adolescents’ educational attainment. Korean Journal of Social Welfare 53: 7–30. [Google Scholar]
- Ku, In Hoe. 2003b. The effect of family background on adolescents educational attainment. Korean Journal of Social Welfare Studies 22: 5–32. [Google Scholar]
- Lim, Yong Bin. 2020. Labor market and economic activity of dual-income households. Labor Review 180: 79–94. [Google Scholar]
- Lindemann, Kristina, and Markus Gangl. 2019. The intergenerational effects of unemployment: How parental unemployment affects educational transitions in germany. Research in Social Stratification and Mobility 62: 100410. [Google Scholar] [CrossRef]
- Mörk, Eva, Anna Sjögren, and Helena Svaleryd. 2020. Consequences of parental job loss on the family environment and on human capital formation-evidence from workplace closures. Labour Economics 67: 101911. [Google Scholar] [CrossRef]
- Muola, James Muthee. 2010. A study of the relationship between academic achievement motivation and home environment among standard eight pupils. Educational Research and Reviews 5: 213–217. [Google Scholar]
- Nielsen, François, and J. Micah Roos. 2015. Genetics of educational attainment and the persistence of privilege at the turn of the 21st century. Social Forces 94: 535–61. [Google Scholar] [CrossRef]
- OECD. 2020. Population with Tertiary Education. Paris: OECD. [Google Scholar]
- Pan, Wei. 2000. A multiple imputation approach to cox regression with interval-censored data. Biometrics 56: 199–203. [Google Scholar] [CrossRef]
- Pan, Weixiang, and Ben Ost. 2014. The impact of parental layoff on higher education investment. Economics of Education Review 42: 53–63. [Google Scholar] [CrossRef]
- Parveen, Azra. 2007. Effect of Home Environment on Personality and Academic Achievement of Students of Grade 12 in Rawalpindi Division. Ph.D. thesis, National University of Modern Languages, Islamabad, Pakistan. [Google Scholar]
- Rege, Mari, Kjetil Telle, and Mark Votruba. 2011. Parental job loss and children’s school performance. The Review of Economic Studies 78: 1462–89. [Google Scholar] [CrossRef]
- Rubin, Donald B. 1987. Multiple Imputation for Nonresponse in Surveys. Wiley Series in Probability and Statistics; New York: Wiley. [Google Scholar]
- Shin, Myung-Ho. 2010. The academic performance gap between social classes and parenting practices. Korean Journal of Social Welfare Studies 41: 217–45. [Google Scholar]
- Turnbull, Bruce W. 1976. The empirical distribution function with arbitrarily grouped, censored and truncated data. Journal of the Royal Statistical Society: Series B (Methodological) 38: 290–95. [Google Scholar] [CrossRef]
- Van de Werfhorst, Herman G., Alice Sullivan, and Sin Yi Cheung. 2003. Social class, ability and choice of subject in secondary and tertiary education in britain. British Educational Research Journal 29: 41–62. [Google Scholar] [CrossRef]
- Wei, Greg C. G., and Martin A. Tanner. 1991. Applications of multiple imputation to the analysis of censored regression data. Biometrics 47: 1297–1309. [Google Scholar] [CrossRef]
- Wellner, Jon A., and Yihui Zhan. 1997. A hybrid algorithm for computation of the nonparametric maximum likelihood estimator from censored data. Journal of the American Statistical Association 92: 945–59. [Google Scholar] [CrossRef]
- Wightman, Patrick. 2012. Parental Job Loss, Parental Ability and Children’s Educational Attainment. Population Studies Center. Available online: http://www.psc.isr.umich.edu/pubs/abs/7648 (accessed on 1 March 2022).
- Yang, Kyung-Eun. 2016. Revisiting the effect of parents’ socioeconomic status on students’ academic performance in relation to welfare state regimes. Journal of Critical Social Welfare, 146–74. [Google Scholar]
- Yoo, Jin Seong. 2021. Analysis of the current status of educational indicators in korea and the impact of private education. KERI Insight 2021: 1–32. [Google Scholar]
- Zeng, Donglin, Lu Mao, and D. Y. Lin. 2016. Maximum likelihood estimation for semiparametric transformation models with interval-censored data. Biometrika 103: 253–71. [Google Scholar] [CrossRef]
| right censoring | 20% | ||||||||
| sample size | 100 | 300 | 1000 | ||||||
| interval censoring | 15% | 30% | 45% | 15% | 30% | 45% | 15% | 30% | 45% |
| omission | 0.444 | 0.432 | 0.473 | 0.195 | 0.216 | 0.190 | 0.088 | 0.095 | 0.105 |
| midpoint imputation | 0.337 | 0.309 | 0.317 | 0.184 | 0.191 | 0.157 | 0.080 | 0.080 | 0.080 |
| multiple imputation | 0.333 | 0.305 | 0.305 | 0.188 | 0.187 | 0.154 | 0.080 | 0.080 | 0.080 |
| right censoring | 20% | ||||||||
| sample size | 100 | 300 | 1000 | ||||||
| interval censoring | 15% | 30% | 45% | 15% | 30% | 45% | 15% | 30% | 45% |
| omission | 0.323 | 0.341 | 0.359 | 0.223 | 0.234 | 0.239 | 0.075 | 0.081 | 0.090 |
| midpoint imputation | 0.293 | 0.283 | 0.278 | 0.221 | 0.225 | 0.218 | 0.071 | 0.071 | 0.070 |
| multiple imputation | 0.295 | 0.283 | 0.276 | 0.218 | 0.222 | 0.216 | 0.071 | 0.071 | 0.071 |
| right censoring | 20% | ||||||||
| sample size | 100 | 300 | 1000 | ||||||
| interval censoring | 15% | 30% | 45% | 15% | 30% | 45% | 15% | 30% | 45% |
| omission | 0.740 | 0.775 | 0.952 | 0.249 | 0.313 | 0.406 | 0.061 | 0.075 | 0.090 |
| median imputation | 0.694 | 0.710 | 0.788 | 0.233 | 0.212 | 0.220 | 0.056 | 0.055 | 0.057 |
| multiple imputation | 0.689 | 0.683 | 0.726 | 0.231 | 0.212 | 0.216 | 0.056 | 0.055 | 0.055 |
| Frequency | Proportion (%) | ||
|---|---|---|---|
| education level of householder | middle school graduation or less (1) | 153 | 15.5% |
| high school graduation or less (2) | 458 | 46.3% | |
| college graduation or more (3) | 378 | 38.2% | |
| sex of the first child | male (0) | 500 | 50.6% |
| female (1) | 489 | 49.4% | |
| poverty | no (0) | 926 | 93.6% |
| yes (1) | 63 | 6.4% | |
| whether parents are unemployed | no (0) | 963 | 97.4% |
| yes (1) | 26 | 2.6% | |
| double income | no (0) | 109 | 11.0% |
| yes (1) | 880 | 89.0% | |
| the number of household members | 2 | 19 | 1.9% |
| 3 | 130 | 13.1% | |
| 4 | 635 | 64.2% | |
| 5 | 173 | 17.5% | |
| 6 | 32 | 3.2% | |
| censoring | right censoring | 58 | 5.9% |
| interval censoring | 79 | 7.9% | |
| no censoring | 852 | 86.2% | |
| Total | 989 | 100% | |
| High School Graduation or Less | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Omission | Midpoint Imputation | Multiple Imputation | ||||||||||
| n = 576; Number of Events = 524 | n = 610; Number of Events = 558 | n = 610; Number of Events = 558 | ||||||||||
| se() | p-Value | p-Value | se() | se() | p-Value | |||||||
| sex | 0.108 | 1.114 | 0.108 | 0.316 | 0.074 | 1.077 | 0.086 | 0.349 | 0.055 | 1.056 | 0.113 | 0.628 |
| double income | 0.285 | 1.330 | 0.186 | 0.125 | 0.138 | 1.148 | 0.148 | 0.370 | 0.068 | 1.071 | 0.195 | 0.727 |
| whether parents are unemployed | −0.787 | 0.455 | 0.384 | 0.040 ** | 0.186 | 1.204 | 0.254 | 0.330 | −0.877 | 0.416 | 0.391 | 0.025 ** |
| the number of household members | −0.091 | 0.913 | 0.085 | 0.283 | −0.043 | 0.958 | 0.063 | 0.409 | −0.059 | 0.943 | 0.088 | 0.502 |
| College Graduation or More | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Omission | Midpoint Imputation | Multiple Imputation | ||||||||||
| n = 333; Number of Events = 315 | n = 376; Number of Events = 357 | n = 376; Number of Events = 357 | ||||||||||
| se() | p-Value | p-Value | se() | se() | p-Value | |||||||
| sex | 0.114 | 1.120 | 0.108 | 0.292 | 0.108 | 1.114 | 0.108 | 0.316 | 0.070 | 1.073 | 0.112 | 0.530 |
| double income | 0.381 | 1.464 | 0.188 | 0.043 ** | 0.285 | 1.330 | 0.186 | 0.125 | 0.031 | 1.032 | 0.213 | 0.883 |
| whether parents are unemployed | −0.753 | 0.471 | 0.383 | 0.049 ** | −0.787 | 0.455 | 0.384 | 0.040 ** | −0.857 | 0.425 | 0.388 | 0.027 ** |
| the number of household members | −0.119 | 0.888 | 0.888 | 0.176 | −0.091 | 0.913 | 0.085 | 0.283 | −0.040 | 0.961 | 0.088 | 0.649 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kim, S.; Lee, E. Cox Proportional Hazards Regression for Interval-Censored Data with an Application to College Entrance and Parental Job Loss. Economies 2022, 10, 218. https://doi.org/10.3390/economies10090218
Kim H, Kim S, Lee E. Cox Proportional Hazards Regression for Interval-Censored Data with an Application to College Entrance and Parental Job Loss. Economies. 2022; 10(9):218. https://doi.org/10.3390/economies10090218
Chicago/Turabian StyleKim, HeeJin, Sunghun Kim, and Eunjee Lee. 2022. "Cox Proportional Hazards Regression for Interval-Censored Data with an Application to College Entrance and Parental Job Loss" Economies 10, no. 9: 218. https://doi.org/10.3390/economies10090218
APA StyleKim, H., Kim, S., & Lee, E. (2022). Cox Proportional Hazards Regression for Interval-Censored Data with an Application to College Entrance and Parental Job Loss. Economies, 10(9), 218. https://doi.org/10.3390/economies10090218





