1. Introduction
The effect of economic development on income inequality has been a debated subject for the past decades. To date, there have been controversies in both the theoretical predictions and empirical literature in identifying the role played by economic development in income inequality. Theories, such as the Kuznets hypothesis, postulate that there is nonlinearity between economic development and income inequality, stating that inequality tends to escalate during the early phase of development, as labour migrates from the low-paying sector, agriculture, to the high-paying sector, urban and non-agricultural economic activities (
Kuznets 1955). The Kaldor theory states that, if capitalists save more than workers, fast rates of growth are associated with a higher share of the profits (
Kaldor 1955).
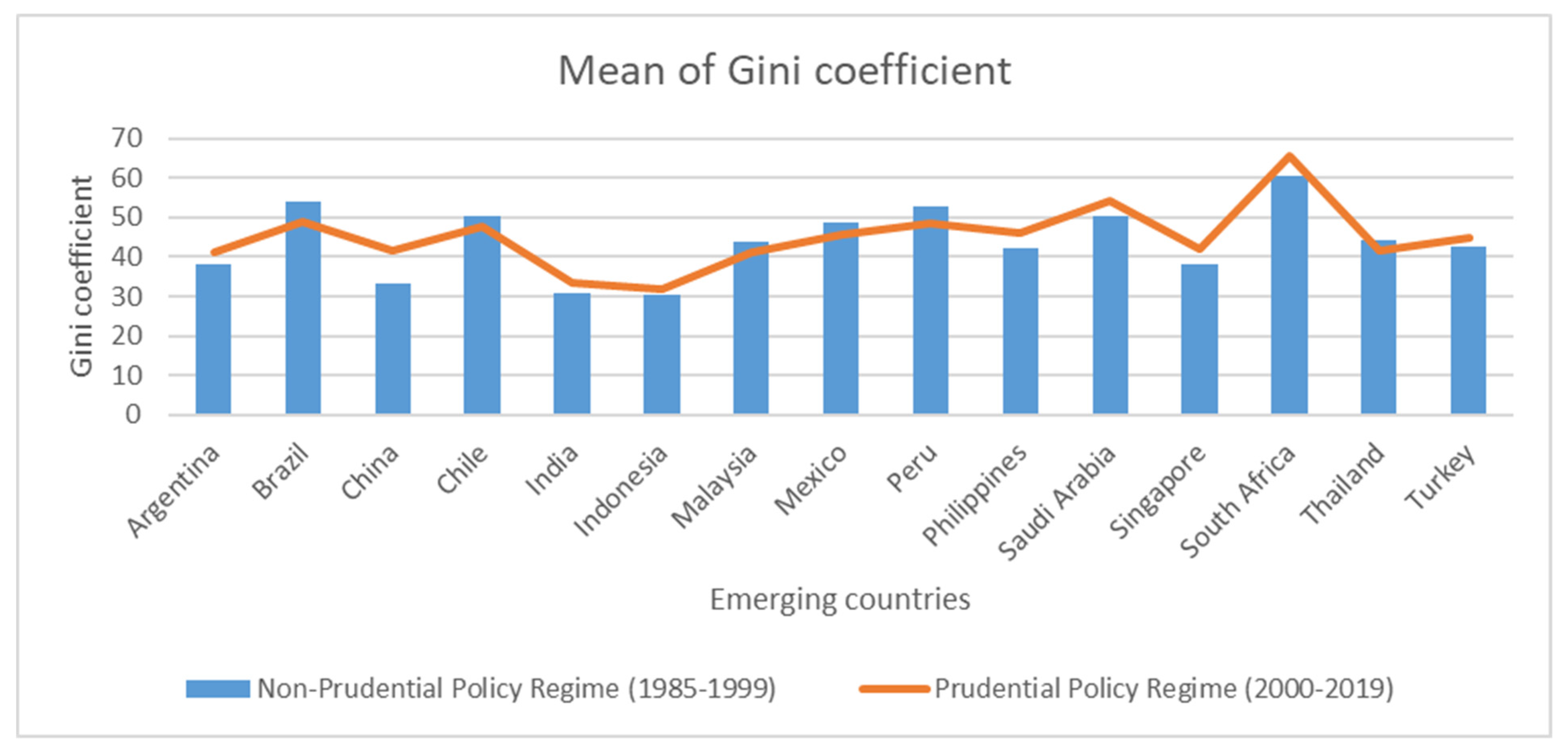
Figure 1 graphically demonstrates the mean Gini coefficient for both the prudential (1985–1999) and non-prudential policy regimes (2000–2019).
The insight gained from these two regimes (prudential and non-prudential policy regimes) demonstrates that during the non-prudential policy regime, about four countries, namely, Brazil, Chile, Malaysia, Mexico, Thailand, and Peru, experienced high income inequality as the Gini coefficient is above that of the prudential policy regime.
The remaining nine countries that are included in the sample are experiencing the challenge of high income inequality during the prudential policy regime, as the mean Gini coefficient is above the mean reported during the non-prudential policy regime.
The extant literature on the relationship between economic development and income inequality is vast and has capitulated extensive conflicting outcomes. Some authors found non-linearity, claiming that the relationship between economic development and income inequality is explained by the Kuznets inverted U-shape (
Paukert 1973;
Papanek and Kyn 1986;
Jha 1996;
Tirado et al. 2016), and others the U-shape (
Savvides and Stengos 2000;
Angeles 2010;
Zungu et al. 2021). There are also authors who fail to support the Kuznets curve hypothesis (
Robinson 1976;
Anand and Kanbur 1993;
Ram 1997;
Deininger and Squire 1998;
Tribble 1999;
Theyson and Heller 2015;
Kavya and Shijin 2020), while others find it inconclusive (
Barro 2000), or a mixed relationship (
Shahbaz 2010). The contradiction in these results may be due, but not limited to, the feasible explanation that the divergent results in the existing literature lie in the different model specifications, data sets, and estimation techniques, or the level of the economy being studied, when examining the development-inequality relationship.
This study extends the existing literature on this subject matter, following the seminal work of
Kavya and Shijin (
2020), who supported the Kuznets view by using panel GMM estimation tools on an unbalanced panel of 85 countries. In their analysis, they captured economic development, using the GDP per capita constant in 2010, while the Gini coefficient was used to capture income inequality. Their study controls for urban populations, inflation, trade, and government spending. Our study seeks to extend the existing debate on this subject matter, with roots back to the seminal work by Kuznets and many others on the so-called inverted U-shaped relationship, and then to add a twist by introducing a distinction between a prudential and a non-prudential regime, referring to the periods 1992–2005 and 2006–2019, respectively. Furthermore, we seek to include major monetary policy variables, known as macroprudential monetary policy instruments (such as borrower-related and capital-related instruments) that were adopted by federal banks in va- rious countries during the financial crisis of 2007. In a nutshell, we aim to examine how the adopted macroprudential policies during the financial crisis triggered the development-inequality relationship in emerging countries.
After reviewing the existing literature on the monetary policy side of the argument, these policies are argued to have a direct or indirect impact on inequality, which was not captured in the
Kavya and Shijin (
2020) model. We further believe that the correlation between the two variables might differ as countries switch from the non-prudential policy regime to a prudential policy regime. Furthermore, their study did not provide the threshold point above which economic development reduces inequality. Besides that, their ana-lysis was based on a group of countries with different levels of economic development.
It is because of these inconclusive and sometimes conflicting views that we seek to fill the gap in the literature by incorporating and examining the impact of economic development and those monetary policy variables and their effects on inequality in a group of emerging markets that most of the existing studies have not given attention to, and also by providing the threshold level of economic development that adversely affects inequality. This will provide new evidence in an emerging literature. We constructed a balanced panel of 15 emerging markets covering the period 1985–2019. Due to data availability, the non-prudential policy regime covers the period from 1985–1999, while the prudential regime starts with the period from 2000–2019. The 15 emerging countries are Singapore, Saudi Arabia, Chile, Turkey, Brazil, Mexico, Argentina, Malaysia, South Africa, Thailand, Peru, China, Indonesia, the Philippines, and India.
Specifically, this study proposes to clarify this debate by analysing the non-linear effects of economic development on inequality, employing the Panel Smooth Transition Regression (PSTR) model as well as the panel Generalized Method of Moments (GMM) and fixed-effect estimators. Furthermore, the PSTR model has never been applied to investigate this topic, despite the fact that it appears to be immensely relevant. This model definitely allows for an examination of the impact of economic development as shown by its various phases. The PSTR model could provide new insights, since this model endogenously identifies different regimes that correspond with distinct equations as well as the optimal degree of economic development, i.e., (id est/that is) the threshold value with respect to which the sign of the relationship could be different. Furthermore, the originality of the PSTR model consists of the fact that individuals can shift between groups and over time, as based on changes in the threshold variable. Because parameters fluctuate smoothly as functions of a threshold variable, the PSTR model also gives a parametric solution to the cross-country variability and time instability of the democracy-development coefficients. These features cannot be accounted for by dynamic or static panel techniques, nor by interaction effects. In addition, the time coverage of our panel data sets, compared to those in previous studies, makes our empirical model robust and useful for policy decision-making. Lastly, the inspiration for this study emanated not only from a lack of studies examining the non-linear effect of economic development on inequality in emerging economies, but more generally from the fact that this relationship may differ from the one that exists in the literature, due to the difference in the smoothness and implementation of their policies as well as the macro-economic policies that were adopted. Actually, our findings support the Kuznets inverted U-curve in both non-prudential and prudential policy regimes. However, what is interesting is that, during the adoption of these policies, they triggered the development-inequality relationship in emerging markets.
The remaining portion of the paper is organized as follows.
Section 2 briefly surveys the related literature.
Section 3 presents an overview of the model.
Section 4 discusses the results of the PSTR, GMM, and FE models.
Section 5 provides concluding remarks and discusses policy implications.
3. Research Methods and Data Adopted for This Study
This study adopted data covering the period from 1985 to 2019. However, as the study aimed to investigate the non-linear dynamics of development inequality in a prudential policy regime in emerging markets, a non-prudential policy regime (1985–1999) and a prudential policy regime (2000–2019) were adopted. The time span of our study is divided following the Cerutti data (
Cerutti et al. 2017). The Cerutti data included dummy-type variables for the implementation of various macroprudential instruments. We define the period of the prudential policy regime starting from 2000 onwards due to the availability of data starting from 2000 onwards, while from 1999 backwards is classified as the period of the non-prudential policy regime. Variables that were suggested in the literature as explaining the relationship between economic development and income inequality were utilized. The Gini coefficient was used as a proxy for income inequality (Gini) and GDP per capita in constant prices (US
$) (ED) as a proxy for economic development. We then controlled for borrower-related (BOR) and capital-related instruments (CCC), government expenditure (GE), investments (INV), and house prices (HP).
In our model, we adopted borrower-related and capital instruments, where the borrower-related instrument is calculated by summing the loan-to-value ratio with the debt-to-income ratio, while for capital instruments we used the general counter-cyclical capital buffer requirement (CTC) as a measure. A simulation of the countercyclical capital buffer designed in the Basel III package could impact bank lending as the buffer could help to reduce credit growth during booms and attenuate the credit contraction once it is released. This would help to dampen procyclicality, in addition to the beneficial effects of higher capital levels in terms of higher banking sector resilience to shocks. Then, this might have a direct or indirect impact on income inequality. Following
Acharya et al. (
2020), who argued that the borrower-related macroprudential instruments make the wealthy group wealthier, thus increasing income and wealth inequality, we then wanted to empirically test whether the borrower-related instrument has a direct or indirect impact on the development-inequality relationship.
The aim was to capture the impact of these instruments on income inequality while government expenditure was adopted, given the fact that the government is used as a tool to trigger output, which then leads to high growth and high employment while simultaneously decreasing inequality. Based on the argument of production, investment is included because increased capital investment requires some goods to be produced that are not immediately consumed, but instead are used to produce other goods, such as capital goods that lead to an increase in economic growth, which will then decrease inequality. Lastly, house prices were adopted for two reasons: (1) the existing literature studied the impact of house prices on income inequality, documenting that increasing house prices resulted in a housing affordability crisis in various countries, and (2) house prices at the same time increased homeowners’ wealth.
For the robustness model, we adopted the Gini coefficient from WIIDv2c to measure income inequality. However, the data from WIIDv2c had the problem of missing values. We then applied the data interpolation system using Eviews9 to fill the missing gaps. The variables were extracted from SWIID (
Solt 2020),
WDI (
2021) and Cerutti data (
Cerutti et al. 2017).
Panel Smooth Transition Regression Model
To evaluate the non-linear dynamic effect of the development-inequality relationship, the PSTR model developed by
González et al. (
2017) was used. The simplest case of the PSTR model, with two extreme regimes in a single transition function for illustrating the threshold effect of economic development (
) on income inequality (
is the following: Please unify the format. (Gini)
where
indicate a cross-section and the time dimensions of the panel, respectively. Whereas,
and
imply the fixed individual and time effects, correspondingly,
is the vector of control variables, and the errors term are denoted by
. Following
Granger and Teräsvirta (
1993) and
González et al. (
2017), the transition function in the logistic form
is a continuous function of the transition variable
bounded between 0 and 1 and defined as:
In (3)
)’ is an
dimensional vector of threshold parameters, where the slope parameter denoted by
controls the smoothness of the transitions. Moreover,
are restrictions imposed for identification purposes. In practice, for
, there are one or two thresholds of economic development around which their impact on income inequality is nonlinear
1, respectively. This nonlinear impact is represented by a continuum of parameters between the extreme regimes. For
, the transition function has a minimum of (
c1 +
c2)/2 and reaches a value of 1 for both low and high values of
. Therefore, if
tends towards infinity, the model becomes a three-regime threshold model. However, it is reduced to a homogenous or linear fixed-effects panel regression when the transition function becomes constant, i.e., when
tends towards 0.
Before estimating Equation (2),
González et al. (
2005) emphasized the need for a homogeneity or specification test. This test will determine whether the PSTR model is appropriate for assessing the impact of economic development on income inequality. To be more explicit, it allows the researcher to choose between using a linear model and a non-linear model to estimate Equation (2). Finally, we evaluate the correlation between economic development and income inequality using the Difference Generalized Method of Moments (Difference GMM) (
Arellano and Bond 1991;
Blundell and Bond 1998) and fixed-effect models (FE). We adopted the Difference GMM because we wanted to remove the problem of the individual effect. In these techniques, we generated the squared term of economic development to capture the non-linear form of development inequality in emerging economies. The dependent variable is further included in the GMM estimator as a lagged explanatory variable. This estimation approach is utilized since the economic development variable has an endogeneity problem, as the expansion of income inequality may have an effect on the level of development. Furthermore, for some of our control variables, the idea of double causation cannot be ruled out. Finally, the GMM estimator has two types of instruments: the external instrument and the internal instrument. It has been argued in the literature that internal instruments are recommended for the GMM system, compared to external instruments. This is because choosing an external instrument for the GMM is the most difficult part of the estimation. The internal instruments are instruments for the data the researcher is working with, such as the lagged values of the regressors. We took advantage of the ability to build instruments internally for the current study. Endogenous variables were, therefore, instrumented by their lagged values. In a nutshell, this means that the instrument of this analysis must come from within.
We also estimated Equation (4), which, in order to account for nonlinearity, includes interaction terms:
Equation (4) incorporates an interaction with a quadratic component to evaluate the non-linear influence of the transition variable, which is economic development. With the addition of an interaction term, it is possible to see if the marginal effect of economic development differs at greater levels of this variable. The other variables of Equation (4) are defined as in Equation (2). The Hausman test was used in order to decide between FE and random effects (RE) estimates under the full set of random effects assumptions. The results from the test suggest that the RE assumption is rejected; therefore, the FE estimates were used.
We extended Equation (4) into a dynamic model by introducing a lagged term of income inequality based on the static model to avoid biased estimates due to the omission of other important explanatory variables, as shown in Equation (5). In this study, the dynamic panel models are estimated using differential GMM:
4. Empirical Analysis of the Study
The descriptive statistics of the different variables are reported in
Appendix A (
Table A1). As described previously, the PSTR model contained three stages, which included finding the appropriate transition variable among all the candidate variables, testing for linearity, and finding the sequence for selecting the order
of the transition function using the LM-type test, with the proposed wild-cluster bootstrap (WCB) and wild bootstrap (WB) serving as robustness checks, before estimating the PSTR model. The results of the three stages are presented separately in the sections that follow.
4.1. The Results of the Transition Variable, Homogeneity Test and Selection of the Order m of the PSTR
Following
González et al. (
2017), we included all variables (ED, BRO, CCC, GE, HP and INV) as candidates for identifying the appropriate transition variable.
Table 1 presents the results of all the stages of the PSTR. The first column of
Table 1 shows the results of the appropriate transition in the panel regression of economic development and income inequality. The results show that both the
p-values of the
test (0.00) and
test (0.00009) signify ED as the most suitable choice of transition variable for this study, as the
p-values are smaller compared to other included variables as candidates.
The results of the homogeneity test are then reported in the second column of
Table 1. We generated the F-statistics and
p-values of both
(0.00) and
(0.00) to test the null hypothesis of linearity, while the proposed WCB (0.00) and WB (0.00) are robustness checks. Both the
p-values of
and
indicate the rejection of the null hypothesis of linearity, confirming that there is indeed nonlinearity between economic development and income inequality in emerging countries. This was further supported by WB and WCB, signifying that nonlinearity remains between the two variables. The homogeneity results are in line with studies by
Paukert (
1973);
Tribble (
1999);
Barro (
2000);
Huang et al. (
2012);
Theyson and Heller (
2015); and
Kavya and Shijin (
2020).
Lastly, the third column of
Table 1 reports the results of the sequence for choosing order
in PSTR
2. The results reject
in both the
and
when
, signifying that, when ED was selected as best transition variable, our model had one regime which separated the low level from the high level of economic development. Similar conclusions were documented by
Savvides and Stengos (
2000) using all countries in the Deininger–Squire data set. However, the results of the
and
were evaluated using the WCB and WB, following
Teräsvirta (
1994).
4.2. Model Evaluation and the Estimated Threshold of the PSTR Model
This section reports the results of the model evaluation and the estimated threshold of the PSTR. After estimating the PSTR model, following
Eitrheim and Teräsvirta (
1996), we first evaluated the reliability of selecting the order
as the best transition variable for our model, using two classes of the misspecification tests: parameter constancy (PC) and no remaining non-linearity (NRN) (
González et al. 2017).
Table 2 presents the results of the PC, NRN, and the estimated threshold. The first section of
Table 2 reports the results of the PC. The
p-value of the
and
for parameter constancy show that the parameters are constant, while the second section of
Table 2 shows the results of the WB and WCB tests that take both heteroskedasticity and possible within-cluster dependence into account, suggesting that the estimated model with one transition is adequate. Lastly, the third section of
Table 2 contains the results of the estimated threshold for our baseline model and robustness model.
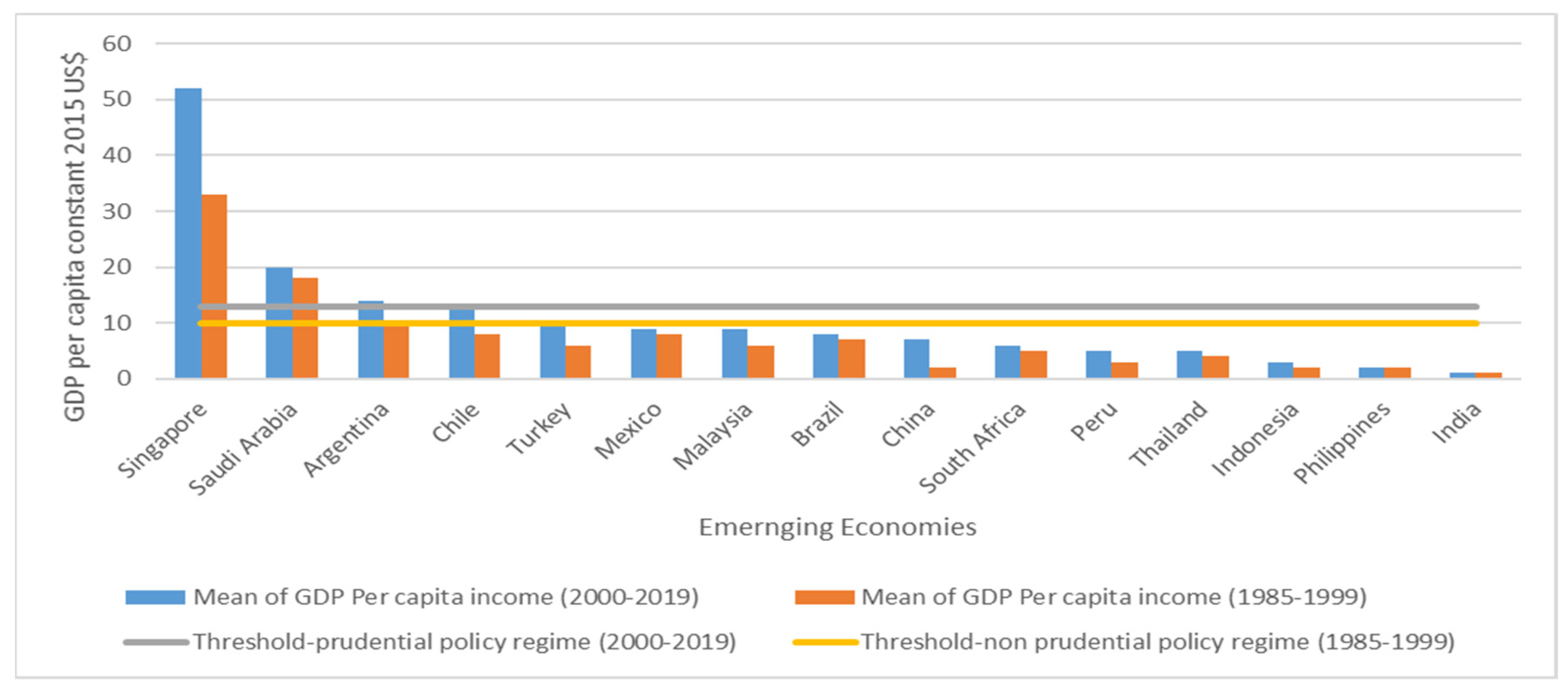
The results show that the estimated economic development threshold is US$13,800. Hence, the first regime, i.e., when the level of economic development is below the value of US$13,800, tends to benefit few people in the economy, which then increases income inequality. This demonstrates that, during low-phase economic development and high inequality, increasing inequality may lower the professional prospects accessible to society’s most disadvantaged groups, reducing social mobility and decreasing the economy’s growth potential. However, when the level of development is above the threshold of US$13,800, high economic development means an improvement in human resources, i.e., skills, education and training, and further improved investment in physical capital, i.e., machinery, factories, and roadways. This will lead to a decrease in income inequality.
These findings may be explained as follows: Firstly, countries below the threshold value are autocratic countries or democratic transition ones. As demonstrated in
Figure 2, all the selected emerging countries are at the lower end of economic development, except for Singapore and Saudi Arabia, with mean GDPs per capita of US
$38,699 and US
$19,381, respectively. According to the World Bank, these countries have a GDP per capita estimated at US
$59,500 and US
$23,762 in 2021, respectively. Therefore, it is not surprising to find the mean to be way above the estimated threshold. Some of these countries are even worse: below US
$5000 (Indonesia, the Philippines, and India).
There are various dynamics that might lead to these countries being at the lower/high end of the Kuznets curve, such as the high population levels and the policies adopted in these countries. For instance, countries like China are among the most developed countries in the world, with a very high population estimated at 1.398 billion (2019) and an unemployment rate below 4%, followed by India, with a population estimated at 1.366 billion and an unemployment rate below 6%. Indonesia and the Philippines are countries with a high population level, 270.6 million and 108.1 million, respectively, while their unemployment rates remain at 6% for both countries. Another possible factor might be the policies adopted that do not benefit the people in improving their standards of living. Therefore, policies that aim to attract investment, which will then create job opportunities and foster an improvement in the standard of living, are significant for countries below the threshold. For countries above the threshold, we noticed that they have a population estimate of 5.70 million for Singapore and 34.24 million for Saudi Arabia. This lends credence to the argument that countries with a high population density are more likely to suffer from low living standards (GDP per capita) and high inequality.
4.3. Empirical Results of the PSTR, GMM and FE Models
The results of the estimation relying on the PSTR, which is a lag of a two-regimes model as well as the GMM and fixed-effect models in supporting the PSTR, are presented in
Table 3. For our Difference GMM, we set the number of lags to one for yearly differences in our yearly data, and we further cut our time period for the prudential policy regime to start from 2005–2019 in order to comply with the conditions of the GMM that
should not be greater than
. First, in both prudential policy regimes, i.e., macroprudential and non-prudential regimes, the results of the PSTR model indicate that the direct economic development effect on income inequality, as measured by
, is positive and significant across all the specifications. As reported in
Table 1, the results confirm the homogeneity test: the effects of economic development on income inequality seem to be strongly non-linear. In fact, the coefficient of the non-linear component of the model,
, is negative and highly significant.
Consequently, the impact of economic development on income inequality is conditional on the development level. This result implies that changes in income inequality with regard to economic development range from , as the economic development variable varies from low to high. The shift between these extreme regimes occurs around the associated endogenous location parameter . Comparing the prudential policy regime to the non-prudential policy regime across all the estimation tools, we discover that, as much as the impact is similar, the magnitude of the coefficient for ED in the prudential policy regime, when the economy starts to develop, has a massive impact compared to its impact in a non-prudential policy regime. On the other hand, when the economic development is high above the threshold, the ED has a massive impact on the common man in the prudential policy regime, compared to the non-prudential policy regime. Focusing on our model of interest, the magnitude below the threshold is 6.82 and 2.32, while it is 2.89 and 0.47 above the threshold, respectively. The results make a very significant contribution towards understanding the non-linear dynamic impact of development on inequality in economies that adopt macroprudential policies, as it shows that adopting these policies at a low level of economic development might trigger the level of income inequality to increase by a very high magnitude. When the level of development is high above a certain threshold, these policies are helpful in reducing inequality; however, the magnitude of the coefficient is small in the high regime. The transmission mechanism of our results is based on the magnitude of impact economic development had before and after the adoption of these policies. Furthermore, it demonstrates that, depending on the regime of economic development, those policies play a critical role in both reducing and promoting income inequality. As explained above, in the low regime, the adoption of these policies strongly affects income inequality compared to its effect in the non-prudential policy regime and even in the high regime.
This finding is consistent with previous empirical studies that demonstrated a substantial positive and negative effect of economic development on income inequality, such as
Andries and Melnic (
2019). They found that macroprudential policies make an impact on income inequality with regard to the level of economic development. The current study further documents that there is evidence of an inverted U-shape relationship between economic development and income inequality, which further supports studies by
Paukert (
1973);
Onur (
2019); and
Kavya and Shijin (
2020). We compare our results with the findings documented by
Chiu and Lee (
2019), who classified 59 countries into 32 high-income countries and 27 low-income countries for the period 1985–2015. When we look closer at the countries classified as low-income countries in their study, most of them are the ones we classified as emerging economies in our study. Their findings confirmed the evidence of the Kuznets hypothesis to hold for low-income countries, while for high-income countries it does not hold. Comparing their findings with our results reveals the evidence that more work needs to be done in implementing policies that will foster the equal distribution of income for these countries and push the level of GDP per capita to be above the estimated threshold.
The possible logic behind the inverted U-shape in these economies could be that income growth generates inequality in a regime of low development, while an increase in economic development decreases inequality amongst the people in a regime of high development. This might be due to the fact that policy intervention in the two regimes (low and high) tends to favour different groups. For instance, during a recession period, government intervention through spending may boost household consumption, while in the upper regime it may be beneficial to investors.
A borrower-related instrument (BOR) has a statistically positive impact on income inequality in the low regime of development, while in the high regime it has a negative impact. This shows that a tightening in loan-to-debt and debt-to-income ratios is bad for income inequality during the low level of development, while at the high level of deve-lopment it is beneficial to inequality. Our results support the finding documented by
Frost and van Stralen (
2018) for a panel of 69 countries (
Arregui et al. 2013). Borrower-related macroprudential instruments increase inequality at introduction, as these instruments can have a direct redistributive effect by keeping low-income households out of the mortgage market, and then they can dampen the increase in inequality under adverse macroeconomic conditions, as they raise inequality by smoothing the credit cycle, and lessening the likelihood and conditional effect of a financial crisis. A capital-related instrument (CCC) has a statistically negative impact on income inequality in the low regime of development, while in the high regime it is positive and statistically insignificant. The results are supported by
Frost and van Stralen (
2018).
GE has a statistically negative impact on income inequality in the low regime of development, while in the high regime it has a positive impact. This empirical finding is in line with the results reported by
Zungu et al. (
2020) in the SADC region. In their paper, they further stress that there is a serious argument behind whether government expenditure plays a major role in declining/increasing income inequality: as they point out, the study by
Tanzi (
1974) argues that government expenditure not only may do nothing towards reducing income inequality but may even worsen it (
Zungu and Greyling 2021). HP has a positive and statistically significant effect on income inequality in both regimes. Our results document that rising house prices paved the way to a housing affordability crisis, but at the same time increased homeowners’ wealth. This supports the findings reported by
Gibson et al. (
2011) and
Filandri and Olagnero (
2014).
Finally, INV has a negative and statistically significant impact on income inequality in both regimes, but beyond the threshold it becomes statistically insignificant. However, during the non-prudential policy regime, investment has a negative impact on income inequality above the threshold, while below the threshold it becomes statistically insigni-ficant. The results confirmed the findings documented by
Blonigen and Slaughter (
2001) for the US and
Figini and Görg (
2011) for 100 developing and developed countries. Theoretically, the argument behind the negative impact of investment on income inequality is the fact that production due to increased capital investment causes some goods to be produced that are not immediately consumed, but are used to produce other goods as capital goods instead, which leads to an increase in economic growth and, subsequently, a decrease in inequality (
Bhandari 2007).
4.4. Sensitivity Analysis and Robustness Checks
The results we have obtained prove that the effect of economic development on income inequality is indeed non-linear in emerging countries, regardless of the variable used to measure income inequality. We adopted the pre-tax national income top 10% from the World Inequality Database to measure income inequality. The variables have the same definition as defined in the baseline methodology. For our Difference GMM, we set the number of lags to one for yearly differences in our yearly data, and we further cut our time period for the prudential policy regime to start from 2005–2019 in order to comply with the conditions in the GMM that should not be greater than. In this section, we offer further evidence of the robustness of these results. The results of the robustness checks are reported in
Table 4 for all the adopted models in the main methodology. Again, all the testing procedures for these models were followed.
We also checked the sensitivity of our findings to the inclusion of additional control variables. Given the adverse effect of inflation, especially in emerging markets, we also controlled for inflation by using the logarithm of inflation. This was to help us find out whether the results reported in the baseline methodology were sensitive to the variables adopted as control variables. The estimation results demonstrated that the non-linear effect of economic development on income inequality was not sensitive to the inequality-measurement and control variables used. Indeed, the findings were very similar to those initially obtained.
5. Conclusions and Policy Recommendations
The theoretical and empirical literature is marked by a controversy surrounding the relationship between economic development and income inequality. This paper aims to overcome these inconclusive results by examining this subject, focusing on the prudential policy period and comparing it with the non-prudential policy regime—in a nutshell, by examining how the adopted macroprudential policies during the financial crisis triggered the development-inequality relationship in emerging countries. Based on the estimation of panel data using smooth transition regression, dynamic GMM, and fixed-effect models, this study investigates the impact of economic development on income inequality in the case of emerging economies.
The estimation results strongly support the presence of non-linearities in the relationship between economic development and income inequality in emerging economies. Our findings show that, in the case of emerging economies, there are two extreme regimes where economic development has a different impact on income inequality, depending on the level of economic development. First, below the threshold of US$13,800, a low level of economic development benefits only a minority of people in the economy, which then increases income inequality. In this case, more policies aimed at ensuring that professional prospects are accessible to society’s most disadvantaged groups and increasing social mobility and investment are significant. Second, above the threshold, the high level of economic development is found to reduce income inequality. More specifically, after passing the threshold of US$13,800, being more developmental, it increases investments and employment, which then stimulate growth and reduce income inequality. These findings were found to be not sensitive to the methodology used and control variables adopted, as we obtained the same results using the GMM and fixed-effect estimator methods, even if we included inflation in the system. Adopting macroprudential policies, such as borrower-related (loan-to-value and debt-to-income ratio) and capital-related (countercyclical capital requirement) policies, was found to improve inequality in the lower regime, while reducing it in the higher regime, except for capital-related instruments which were found to be insignificant. We further document that a surge in house prices increases the level of income inequality in both policy regimes (the prudential and non-prudential policy regimes), showing that income differences and high house prices limit access to decent and affordable housing for low-income renters and owners. Government expenditure supports the BARS hypothesis, while investment was found to have a detrimental effect on income inequality above the threshold.
From a policy perspective, our findings may have various policy implications. First, the presence of an economic development threshold challenges the effectiveness of distribution policies and GDP per capita as regards its impact on reducing inequality. Second, countries that are situated just below the threshold value are encouraged to work towards formulating policies that aim to attract investment, which will then create job opportunities and foster an improvement in the standard of living, triggering an increase in the level of GDP per capita. Thirdly, our findings may help policymakers in African emerging economies to develop policies that will foster house prices to be accommodative, which would be significant for these countries. We suggest that future research should focus on a comparative study where African emerging countries are compared to European or other countries. Conducting a panel smooth transition vector error correction model (VECM) will be a measurable contribution. However, this can only be conducted in a bivariate setting. The interesting feature of the latter methodology is a Granger causality test that is conducted in a non-linear framework. Further study will also require using a different variable to measure income inequality, as will including more macroprudential policy variables in the development-inequality relationship in tracing how it is triggered by the other variables that are not controlled for in this study. Including variables that aim to control government effectiveness will be crucial for new studies.