Effect of the Complexity of the Customs Tax System on the Tax Effort
Abstract
:1. Introduction
2. Definitions: Tax Effort, Revenue Potential, and Tax Complexity
3. Literature Review
- Construction of the Stochastic Tax Frontier
- I represents the number of observations;
- t is a time period;
- is the actual revenue collected by the Customs Administration (i) in year (t);
- corresponds to the set of variables that explain the potential revenue of i in year (t);
- is a constant;
- represents the input parameters of the production function;
- is a random error and an independent and identically distributed stochastic component with a mean of zero and a constant variance N (0, that represents any exogenous factor that cannot be controlled by the Customs Administration, e.g., a tax exemption that affects revenue collection. It may also refer to measurement errors. may take a positive or negative value;
- is a random stochastic component of the technical inefficiency and a non-negative term that is assumed to be independently distributed. In this context, the inefficiency represents the inability to achieve the maximum amount of revenue collection. The components and are assumed to be independent of each other and the estimators.
- Factors influencing the Tax Effort
- is the set of exogenous variables that would explain the inefficiency in tax collection;
- is a vector of coefficients to be estimated; and
- is a random variable defined as a truncated normal distribution with mean of zero and a constant variance. The point of truncation is , so that .
4. Methodology and Data
- Estimate the tax capacity or potential tax revenues, in which the maximum level of tax revenue considered is influenced by the socio-economic characteristics of the country; and
- Decompose the error term into two components (random noise and the tax effort), so it is possible to model the tax effort through a set of variables. For example, we can determine whether the complexity of the customs tax system has any influence on the revenue collection efficiency.
4.1. Model Specification
4.2. Data Description
- Ri2 is the share of customs tax i in the total revenue, squared; and
- n is the total number of customs taxes.
5. Results and Discussion
6. Conclusions
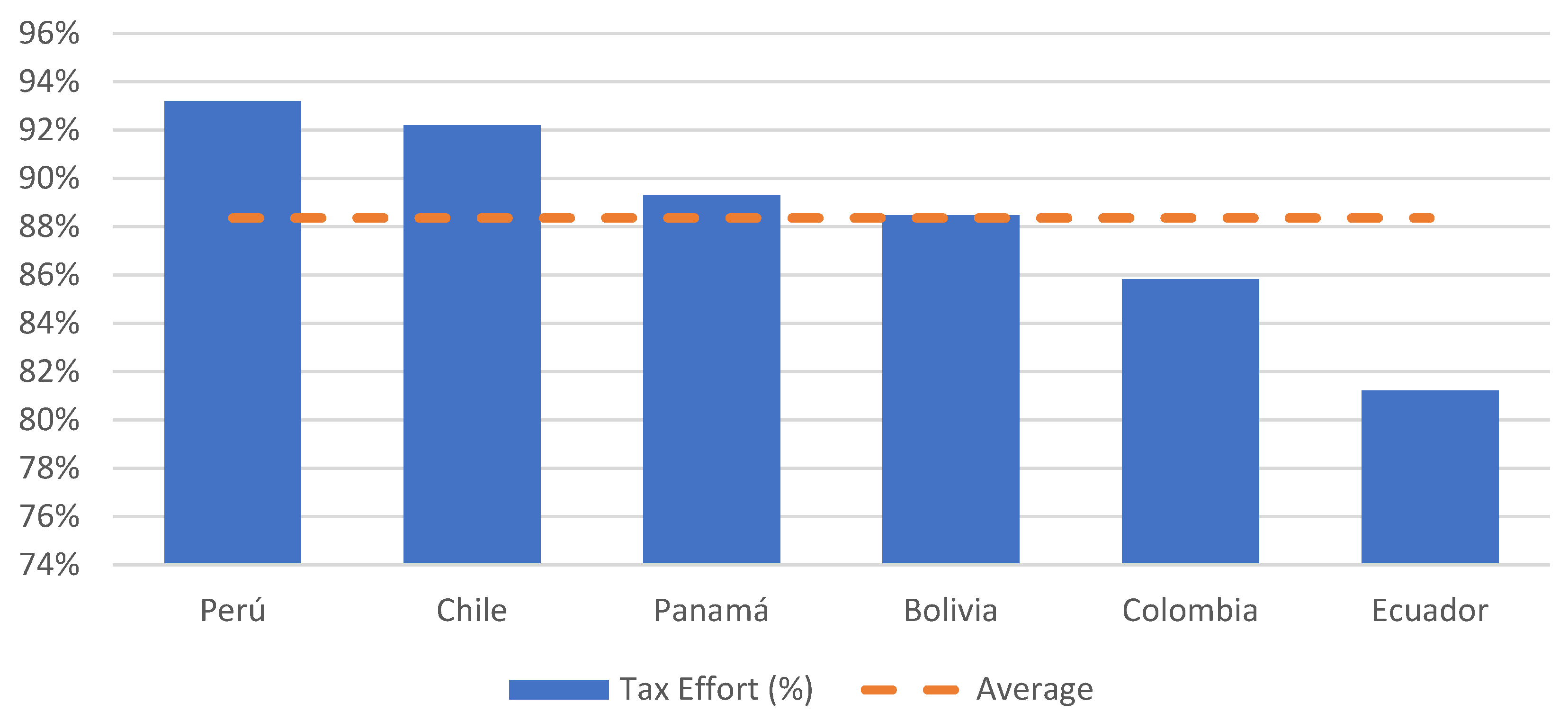
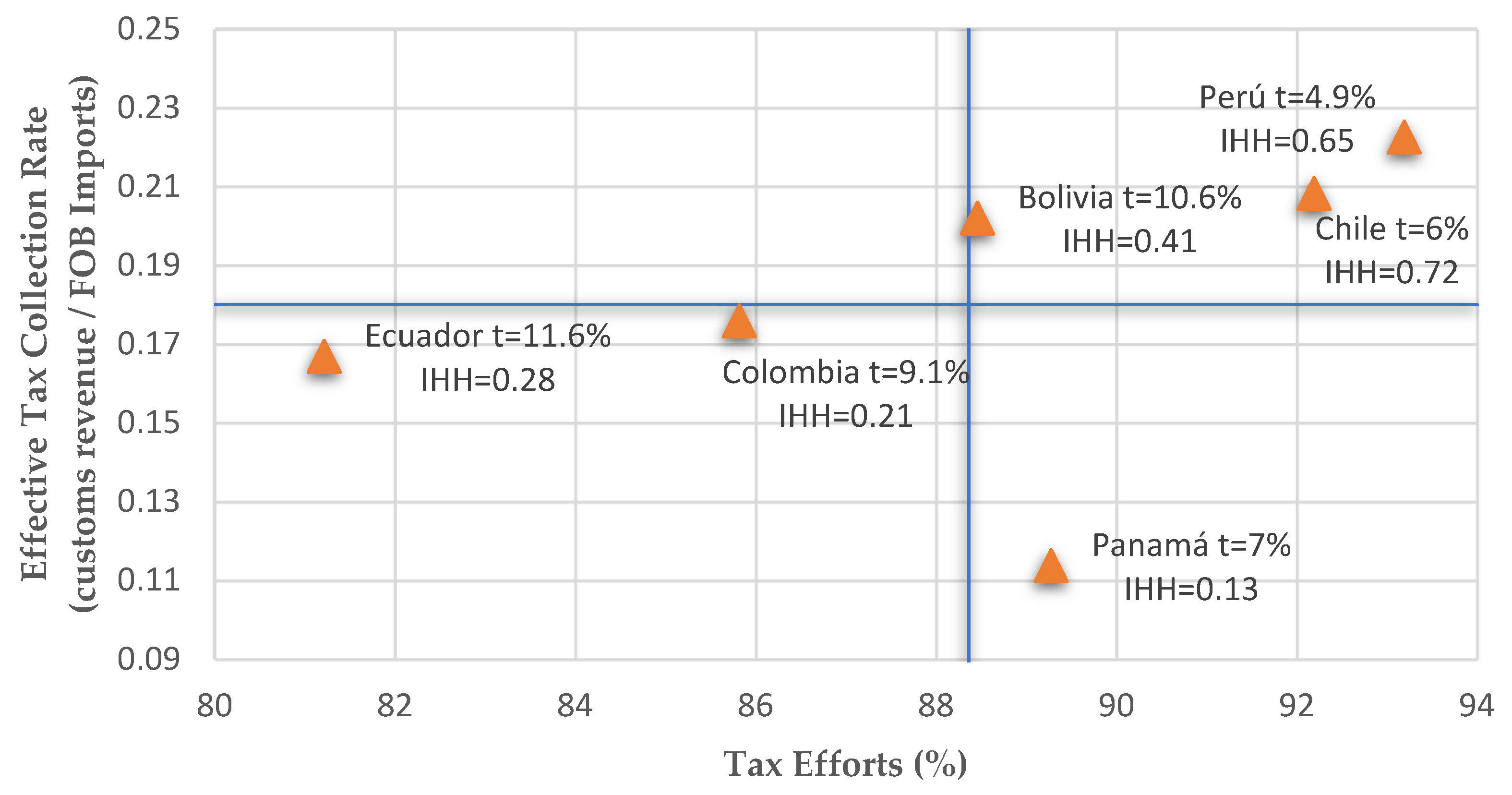
- The countries whose customs tax system has a lower degree of complexity have a better level of collection and tax effort (Peru, Chile, and Bolivia). Therefore, the greatest possible degree of simplicity in the design of the tax system is desirable.
- Panama’s potential customs revenue collection is very close to its actual customs revenue collection, but its actual revenue collection is low compared with the other countries in the sample. Therefore, work could be carried out on aspects that help to reduce the shadow economy in order to improve tax revenues.
- An improvement in the quality and dissemination of statistical data helps to improve transparency and the possibility of questioning government decision-making, which contributes to improving the tax effort. Notably, labor efficiency levels tend to increase when there are means to audit through tangible results.
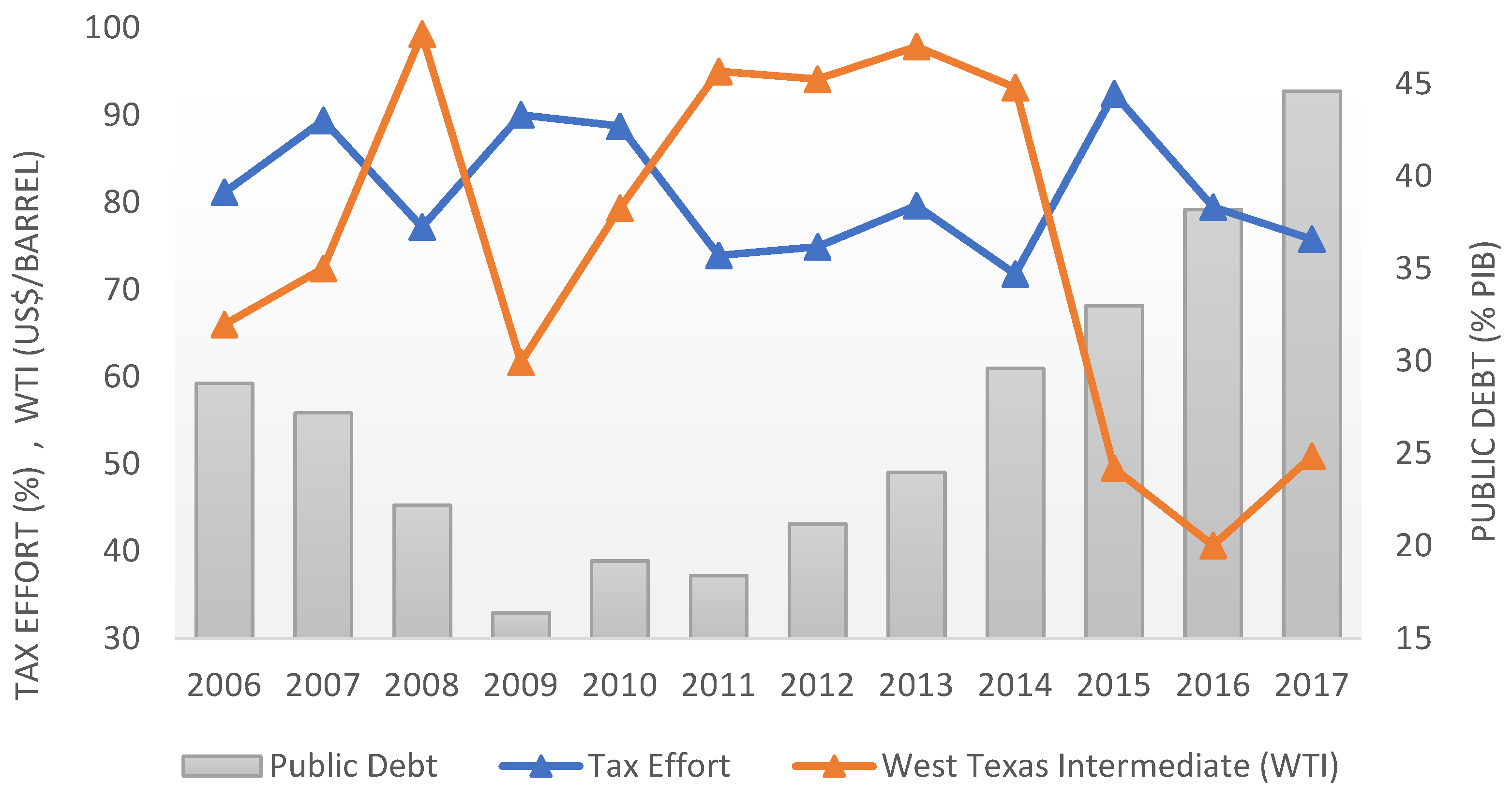
- When revenue levels from non-renewable natural resources such as minerals and oil increase, the tax effort shows a downward trend. In the case of Ecuador, a certain degree of laziness in tax control was observed during the years when the WTI crude oil price increased that did not justify the increase in the level of debt. In contrast, a greater tax effort could have been made to increase customs revenues, for example through a reduction in the complexities of the customs tax system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Aigner, Dennis, C. A. Knox Lovell, and Peter Schmidt. 1977. Formulation and estimation of stochastic frontier production function models. Journal of Econometrics 6: 21–37. [Google Scholar] [CrossRef]
- Alfirman, Luky. 2003. Estimating Stochastic Frontier Tax Potential: Can Indonesian Local Governments Increase Tax Revenues under Decentralization? Boulder: Centre for Economic Analysis, pp. 3–19. [Google Scholar]
- Battese, George Edward, and Tim J. Coelli. 1988. Prediction of Grm-level technical efficiencies: With a generalized frontier production function and panel data. Journal of Econometrics 38: 387–99. [Google Scholar] [CrossRef]
- Battese, George Edward, and Tim J. Coelli. 1992. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. Journal of Productivity Analysis 3: 153–69. [Google Scholar] [CrossRef]
- Battese, George Edward, and Tim J. Coelli. 1995. A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empirical Economics 20: 325–32. [Google Scholar] [CrossRef] [Green Version]
- Beccaria, Luis. 2017. Capacidad Estadística: Una Propuesta Para su Medición. IDB-TN-1274. Washington, DC: Nota técnica del BID (Banco Interamericano de Desarrollo). [Google Scholar]
- Budak, Tamer, and Simon James. 2018. The level of tax complexity: A comparative analysis between the UK and Turkey based on the OTS index. International Tax Journal 44: 27–40. [Google Scholar]
- Carroll, Deborah. 2009. Diversifying municipal government revenue structures: Fiscal illusion or instability? Public Budgeting and Finance 1: 27–48. [Google Scholar] [CrossRef]
- Cyan, Musharraf, Jorge Martinez-Vazquez, and Violeta Vulovic. 2013. Measuring Tax Effort: Does the Estimation Approach Matter and Should Effort Be Linked to Expenditure Goals? International Center for Public Policy Working Paper Series 39; Atlanta: Georgia State University. [Google Scholar]
- Esteller, Alejandro. 2003. La eficiencia en la administración de los tributos cedidos: Un análisis explicativo. Papeles de Economía Española 95: 320–34. [Google Scholar]
- Frank, Henry J. 1959. Measuring State Tax Burdens. National Tax Journal 12: 179–85. [Google Scholar] [CrossRef]
- Hsiao, Cheng. 1986. Analysis of Panel Data. Econometric Society Monographs. New York: Cambridge University Press, vol. 11. [Google Scholar]
- Jha, Raghbendra, Madhusudan S. Mohanty, Somnath Chatterjee, and Puneet Chitkara. 1999. Tax efficiency in selected Indian States. Empirical Economics 24: 641–54. [Google Scholar] [CrossRef]
- Jondrow, James, C. A. Knox Lovell, Ivan S. Materov, and Peter Schmidt. 1982. On The Estimation of Technical Inefficiency in The Stochastic Frontier Production Function Model. Journal of Econometrics 19: 233–38. [Google Scholar] [CrossRef] [Green Version]
- Jorratt, Michael. 1996. Evaluación de la capacidad recaudatoria del sistema tributario y de la evasión tributaria. In Conferencia Técnica del CIAT. Viterbo: Centro Interamericano de Administradores Tributarios-CIAT. [Google Scholar]
- Khwaja, Munawer Sultan, and Indira Iyer. 2014. Revenue Potential, Tax Space, and Tax Gap: A Comparative Analysis Policy Research. Working Paper No. 6868. Washington, DC: World Bank. [Google Scholar]
- Maekawa, Satoko, and Naosumi Atoda. 2001. Technical inefficiency in Japanese tax administration. In 57th Congress of the International Institute of Public Finance. Linz: Institute of Public Finance. [Google Scholar]
- Meeusen, Wim, and Julien van Den Broeck. 1977. Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error. International Economic Review 18: 435–44. [Google Scholar] [CrossRef]
- Minh Le, Tuan, Blanca Moreno-Dodson, and Nihal Bayraktar. 2012. Tax Capacity and Tax Effort: Extended Cross-Country Analysis from 1994 to 2009. Policy Research Working Paper 6252. Washington, DC: World Bank. [Google Scholar]
- Pessino, Carola, and Ricardo Fenochietto. 2010. Determining countries tax effort. Economía Pública 4: 65–87. [Google Scholar]
- Pessino, Carola, and Ricardo Fenochietto. 2013. Understanding Countries Tax Effort. Working Paper Fiscal Affairs Department, IMF WP/13/244. Washington, DC: International Monetary Fund. [Google Scholar]
- Sachs, Jeffrey D., and Andrew Warner. 1997. Natural Resource Abundance and Economic Growth. NBER Working Paper 5398. Cambridge: Harvard Institute for International Development. [Google Scholar]
- Schneider, Friedrich. 2012. The Shadow Economy and Work in the Shadow: What Do We (Not) Know? IZA Discussion Paper No. 6423. Bonn: Institute of Labor Economics-IZA. [Google Scholar]
- Schneider, Friedrich, and Leandro Medina. 2018. Shadow Economies Around the World: What Did We Learn Over the Last 20 Years? IMF Working Paper No. 18/17. Washington, DC: International Monetary Fund. [Google Scholar]
- Shah, Anwar. 1996. A Fiscal Need Approach to Equalization. Canadian Public Policy 2: 99–115. [Google Scholar] [CrossRef]
- Smith, Adam. 1776. An Inquiry into the Nature and Causes of the Wealth of Nations. Londres: W. Strahan & T. Cadell. [Google Scholar]
- Thuronyi, Victor. 1996. Drafting Tax Legislation. In Tax Law Design and Drafting. Edited by V. Thuronyi. Washington, DC: International Monetary Fund, vol. 1, Retrieved 28 September 2017. Available online: http://www.imf.org/external/pubs/nft/1998/tlaw/eng/ (accessed on 28 September 2017).
- Tran-Nam, Binh. 2004. Assessing the Tax Simplification Impact of Tax Reform: Research Methodology and Empirical Evidence from Australia. Sydney: National Tax Association, pp. 376–82. [Google Scholar]
- Wagner, Richard E. 1976. Revenue structure, fiscal illusion and budgetary choice. Public Choice 1: 45–61. [Google Scholar] [CrossRef]
- Weingast, Barry. 2006. Second Generation Fiscal Federalism: Implications for Decentralized Democratic Governance and Economic Development. Social Science Research Network (SSRN). Available online: https://ssrn.com/abstract=1153440 (accessed on 1 February 2019).
- World Bank. 2019. Tariff Rate, Applied, Weighted Mean, All Products (%). Retrieved from The World Bank. Available online: https://tcdata360.worldbank.org (accessed on 19 October 2019).
- World Trade Organizations (WTO). 2019. Trade Policy Review Report: Ecuador. Geneva: WTO. [Google Scholar]
| Variable | Description |
|---|---|
| Stochastic Tax Frontier | |
| i | Country of Customs Administration |
| t | Year t (t = 2006… 2017) |
| Constant | |
| Coefficients of elasticities measuring the percentage change in the dependent variable with respect to the unit percentage change in the independent variable | |
| Logarithm of customs revenue as a proportion of the gross domestic product (GDP) of country i in year t | |
| Logarithm of the gross domestic product per capita by purchasing power parity (constant 2011 international dollars) for country i in year t | |
| Ln (PIB pc) squared | |
| Logarithm of merchandise trade as a proportion of the GDP for country i in year t | |
| Logarithm of the Gini coefficient | |
| Logarithm of government expenditure on education as a percentage of the GDP for country i in year t | |
| Logarithm of the shadow economy as a proportion of the GDP for country i in year t | |
| Assumed to be error terms independent of | |
| The term of inefficiency for country i in year t. It is a non-negative disturbance term and is assumed to be . We assumed a half-normal distribution and estimated this term following the procedure suggested by Battese and Coelli (1988), which the SAS software identifies as TE1. | |
| The effects of inefficiency | |
| Constant | |
| Elasticity coefficients measuring the percentage change in the dependent variable with respect to the unit percentage change in the tax effort | |
| Hirschman–Herfindah concentration index used as a proxy for the degree of complexity of the customs tax system for country i in year t | |
| Mineral rents as a percentage of the GDP for country i in year t | |
| Oil rents as a percentage of the GDP for country i in year t | |
| Statistical capacity indicator for country i in year t | |
| Public expenditure as a percentage of the GDP | |
| Dummy variable for the time period (1 = 2006… 12 = 2017) | |
| Variable | Unit/Range | Arithmetic Mean | Standard Deviation | Extreme Values | |
|---|---|---|---|---|---|
| Minimum | Minimum | ||||
| R_PIB | % del PIB | 4.20541 | 1.21971 | 2.26546 | 6.84701 |
| PIBpc | GDP (constant 2011 USD) | 12,689.10 | 5250.76 | 4778.72 | 22,331.23 |
| C_PIB | % of PIB | 54.8901137 | 19.9516675 | 26.9274299 | 105.0440641 |
| Gini | 0–100 | 49.0513889 | 3.4076547 | 43.2 | 56.7 |
| E_sum_pib | % of PIB | 37.47328 | 15.60411 | 12.64000 | 61.77000 |
| Edu_PIB | % of PIB | 3.8975423 | 0.9708080 | 2.3256992 | 6.2673162 |
| IHH | 0–1 | 0.3992382 | 0.2276815 | 0.0820689 | 0.7476185 |
| Min_pib | % of PIB | 4.751 | 5.919 | 0 | 20.917 |
| Oil_pib | % of PIB | 3.460 | 4.700 | 0 | 18.477 |
| Stat | 0–100 | 81.20371 | 9.11059 | 66.66667 | 98.88889 |
| GP_PIB | % of PIB | 29.9565 | 9.5988 | 17.1190 | 54.8 |
| Yeardum | annual | 6.5 | 3.4762778 | 1 | 12 |
| Variable | Mean | Standard Error | Type | ||
| Ln_R_PIB | 1.392752 | 0.302494 | Frontier (Prod) Half-Normal | ||
| Model Fit Summary | |||||
| Number of Endogenous Variables | 1 | ||||
| Endogenous Variable | Ln_R_PIB | ||||
| Number of Observations | 72 | ||||
| Log Likelihood | 57.48817 | ||||
| Maximum Absolute Gradient | 0.00549 | ||||
| Number of Iterations | 32 | ||||
| Optimization Method | Quasi-Newton | ||||
| AIC | −96.97634 | ||||
| Schwarz Criterion | −76.48635 | ||||
| Sigma | 0.16979 | ||||
| Lambda | 2.73209 | ||||
| Parameter Estimates | |||||
| Parameter | DF | Estimate | Standard Error | t Value | Approx.Pr > |t| |
| Dependent variable Ln_R_PIB, assuming a half-normal distribution for μit | |||||
| Intercept | 1 | 56.220266 | 8.878678 | 6.33 | <0.0001 |
| Ln_PIBpp | 1 | −9.447874 | 1.861098 | −5.08 | <0.0001 |
| Ln_PIBpp2 | 1 | 0.473165 | 0.100365 | 4.71 | <0.0001 |
| Ln_c_pib | 1 | 0.557979 | 0.048773 | 11.44 | <0.0001 |
| Ln_gini | 1 | −2.033298 | 0.175228 | −11.60 | <0.0001 |
| Ln_e_sum_pib | 1 | −0.447409 | 0.042602 | −10.50 | <0.0001 |
| Ln_edu_PIB | 1 | −0.394444 | 0.083245 | −4.74 | <0.0001 |
| _Sigma_v | 1 | 0.058359 | 0.020406 | 2.86 | 0.0042 |
| _Sigma_u | 1 | 0.159442 | 0.031864 | 5.00 | <0.0001 |
| Summary Statistics of Continuous Response | |||||
| Variable | Mean | Standard Error | Type | Lower Limit | Upper Limit |
| TE1 | 0.883614 | 0.070368 | Truncated | 0 | 1 |
| Model Fit Summary | |||||
| Number of Endogenous Variables | 1 | ||||
| Endogenous Variable | TE1 | ||||
| Number of Observations | 72 | ||||
| Log Likelihood | 118.47527 | ||||
| Maximum Absolute Gradient | 0.0000243 | ||||
| Number of Iterations | 14 | ||||
| Optimization Method | Quasi-Newton | ||||
| AIC | −220.95055 | ||||
| Schwarz Criterion | −202.73722 | ||||
| Parameter Estimates | |||||
| Dependent variable tax effort, assuming a truncated distribution for μit | |||||
| Intercept | 1 | 0.648964 | 0.119214 | 5.44 | <0.0001 |
| IHH | 1 | 0.137516 | 0.073344 | 1.87 | 0.0608 |
| Yeardum | 1 | −0.013865 | 0.002727 | −5.09 | <0.0001 |
| Min_pib | 1 | −0.007127 | 0.00329 | −2.17 | 0.0303 |
| Oil_pib | 1 | −0.012981 | 0.00216 | −6.01 | <0.0001 |
| Stat | 1 | 0.003632 | 0.001333 | 2.72 | 0.0065 |
| Gp_pib | 1 | 0.00203 | 0.001155 | 1.76 | 0.0789 |
| _Sigma | 1 | 0.054205 | 0.005719 | 9.48 | <0.0001 |
| Country | Bolivia | Chile | Colombia | Ecuador | Panama | Peru | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | TE1 | TE2 | TE1 | TE2 | TE1 | TE2 | TE1 | TE2 | TE1 | TE2 | TE1 | TE2 |
| 2006 | 0.92229 | 0.92130 | 0.82023 | 0.81900 | 0.95765 | 0.95713 | 0.81178 | 0.81056 | 0.89813 | 0.89697 | 0.95589 | 0.95534 |
| 2007 | 0.92997 | 0.92906 | 0.88098 | 0.87975 | 0.95739 | 0.95686 | 0.89420 | 0.89302 | 0.93254 | 0.93166 | 0.96334 | 0.96291 |
| 2008 | 0.84175 | 0.84049 | 0.97212 | 0.97183 | 0.95420 | 0.95363 | 0.77177 | 0.77061 | 0.95310 | 0.95251 | 0.97104 | 0.97074 |
| 2009 | 0.85336 | 0.85210 | 0.93443 | 0.93358 | 0.91821 | 0.91718 | 0.90055 | 0.89940 | 0.89809 | 0.89692 | 0.93215 | 0.93127 |
| 2010 | 0.87608 | 0.87483 | 0.94575 | 0.94505 | 0.95857 | 0.95807 | 0.88759 | 0.88638 | 0.94393 | 0.94320 | 0.91729 | 0.91625 |
| 2011 | 0.77658 | 0.77541 | 0.91308 | 0.91201 | 0.86756 | 0.86631 | 0.73935 | 0.73824 | 0.91282 | 0.91175 | 0.83511 | 0.83387 |
| 2012 | 0.78662 | 0.78544 | 0.93900 | 0.93821 | 0.81844 | 0.81722 | 0.74912 | 0.74800 | 0.89051 | 0.88931 | 0.87856 | 0.87733 |
| 2013 | 0.87873 | 0.87749 | 0.94077 | 0.93999 | 0.77392 | 0.77275 | 0.79639 | 0.79520 | 0.87244 | 0.87119 | 0.93274 | 0.93187 |
| 2014 | 0.95511 | 0.95455 | 0.92857 | 0.92765 | 0.79335 | 0.79216 | 0.71800 | 0.71692 | 0.83401 | 0.83277 | 0.95085 | 0.95022 |
| 2015 | 0.97886 | 0.97868 | 0.95031 | 0.94967 | 0.81109 | 0.80987 | 0.92473 | 0.92377 | 0.89501 | 0.89383 | 0.96063 | 0.96016 |
| 2016 | 0.91535 | 0.91430 | 0.92759 | 0.92665 | 0.75642 | 0.75528 | 0.79470 | 0.79351 | 0.86754 | 0.86629 | 0.95085 | 0.95023 |
| 2017 | 0.90063 | 0.89948 | 0.91041 | 0.90931 | 0.73180 | 0.73070 | 0.75795 | 0.75681 | 0.81544 | 0.81422 | 0.93490 | 0.93405 |
| Mean | 0.88461 | 0.88359 | 0.92194 | 0.92106 | 0.85822 | 0.85726 | 0.81218 | 0.81104 | 0.89280 | 0.89172 | 0.93195 | 0.93119 |
| Pearson Correlation Coefficient, N = 72 | ||||||
|---|---|---|---|---|---|---|
| Prob > |r| Assuming H0: Rho = 0 | ||||||
| Ln_PIBpp | Ln_PIBpp2 | Ln_C_PIB | Ln_Gini | Ln_E_sum_pib | Ln_Edu_PIB | |
| Ln_PIBpp | 1 | |||||
| Ln_PIBpp2 | 0.99967 | 1 | ||||
| (<0.0001) | ||||||
| Ln_C_PIB | 0.11184 | 0.12283 | 1 | |||
| (0.3496) | (0.304) | |||||
| Ln_Gini | 0.00814 | 0.01018 | 0.07302 | 1 | ||
| (0.9459) | (0.9324) | (0.5421) | ||||
| Ln_E_sum_pib | −0.50701 | −0.50768 | 0.31014 | 0.16473 | 1 | |
| (<0.0001) | (<0.0001) | (0.008) | (0.1667) | |||
| Ln_Edu_PIB | −0.4005 | −0.38583 | 0.18416 | −0.21645 | 0.00286 | 1 |
| (0.0005) | (0.0008) | (0.1215 | (0.0678) | (0.981) | ||
| Pearson Correlation Coefficient, N = 72 | |||||
|---|---|---|---|---|---|
| Prob > |r| Assuming H0: Rho = 0 | |||||
| IHH | Min_pib | Oil_pib | Stat | Gp_pib | |
| IHH | 1 | ||||
| Min_pib | 0.84589 (<0.0001) | 1 | |||
| Oil_pib | −0.25482 (0.0308) | −0.43442 (0.0001) | 1 | ||
| Stat | 0.57777 (<0.0001) | 0.59179 (<0.0001) | −0.21168 (0.0743) | 1 | |
| Gp_pib | −0.26038 (0.0272) | −0.44105 (0.0001) | 0.37837 (0.001) | −0.63918 (<0.0001) | 1 |
| Variable: Resid_Ln_R_PIB (Ln_R_PIB Residual) | ||||
|---|---|---|---|---|
| Test | Statistical | p Value | ||
| Shapiro–Wilk | W | 0.971471 | Pr < W | 0.1009 |
| Kolmogorov–Smirnov | D | 0.082440 | Pr > D | >0.1500 |
| Variable: Resid_TE1 (TE1 Residual) | ||||
|---|---|---|---|---|
| Test | Statistical | p Value | ||
| Shapiro–Wilk | W | 0.973903 | Pr < W | 0.1396 |
| Kolmogorov–Smirnov | D | 0.094733 | Pr > D | >0.1075 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González Aguirre, J.; Del Villar, A. Effect of the Complexity of the Customs Tax System on the Tax Effort. Economies 2022, 10, 55. https://doi.org/10.3390/economies10030055
González Aguirre J, Del Villar A. Effect of the Complexity of the Customs Tax System on the Tax Effort. Economies. 2022; 10(3):55. https://doi.org/10.3390/economies10030055
Chicago/Turabian StyleGonzález Aguirre, Jazmín, and Alberto Del Villar. 2022. "Effect of the Complexity of the Customs Tax System on the Tax Effort" Economies 10, no. 3: 55. https://doi.org/10.3390/economies10030055
APA StyleGonzález Aguirre, J., & Del Villar, A. (2022). Effect of the Complexity of the Customs Tax System on the Tax Effort. Economies, 10(3), 55. https://doi.org/10.3390/economies10030055





