Technical Efficiency and Productivity Growth of Crude Palm Oil: Variation across Years, Locations, and Firm Sizes in Indonesia

Abstract

Crude palm oil (CPO) is a valuable commodity for Indonesia’s economy as the country has become the world’s biggest producer and exporter. Therefore, maintaining productivity in the CPO industry is crucial to ensure that the global demand is met. This study aims to examine Indonesian CPO productivity and its components using total factor productivity growth (TFPg) with stochastic frontier analysis. This study analyzes the variation in the TFPg across years, locations, and firm sizes. The first two analyses imply that, on average, the CPO industry’s productivity declines annually, with firms in 20 provinces experiencing negative TFPg. Regarding size, the analysis demonstrates that the technical efficiency change (TEC) and technical change (TC) have regressed the TFPg in all scale firms. However, medium firms saw a smaller decline in comparison to large firms. Conversely, large firms possess slightly better scale efficiency change (SEC) than medium firms, although both types attain a negative SEC. The findings also show that the main factor contributing to the gain or decline in productivity is TC, which suggests the urgency of innovative technology in the CPO industry.

1. Introduction

Palm oil has been a valuable commodity for Indonesia’s economic growth for decades. In 1990, palm oil consumption reached 1.3 million tons, which tripled to approximately 4.87 million tons by 2007 (Rifin 2010). Over three decades, in 2019, consumption grew by about 1188 percent, reaching more than 16.75 million tons (Yuniartha 2021). This remarkable growth is in line with its upstream sector, i.e., crude palm oil (CPO), which has contributed to approximately 58.3% of the global CPO production, making Indonesia the largest CPO producer and exporter.

The rapid growth of the Indonesian CPO industry can be associated with its role in the local economy (Rifin 2010). Palm oil is essential in Indonesian households. Data from the Indonesian Palm Oil Association (2022) show that cooking oil consumption is 8 million tons annually. Another utilization includes biodiesel, which has been growing since the government stipulated a mix of 30% biodiesel (B30) in diesel engine fuel. Second, the CPO industry is labor-intensive, with more than 16.2 million workers employed (Earthworm 2020). The increasing number of laborers is in line with the growth of the number of plants from 695 units with 37,213 tons of fresh fruit bunches (FFB) per hour in 2012 to 713 units with 34,628 tons of FFB per hour (Rifin 2017).

However, there is a trade-off between expanding CPO production, which often translates into economic growth and environmental degradation. The question is whether the world’s demands for CPO commodities can be met without degrading the environment and sustaining its output growth. In this regard, strategic policies must be formulated to boost CPO production. Rifin (2017) argued that CPO production could be boosted by increasing the number of plants or improving efficiency. The first aims to increase the FFB yield from the land and process it directly after being harvested (Nasution et al. 2015). The immediate processing is necessary because the FFB quality may decline over time, leading to a lower return on investment.

Improving efficiency includes the technical and cost aspects. Technical efficiency means utilizing production factors to generate a maximum volume of outputs. Meanwhile, cost efficiency means the optimal use of resources for plants to produce the best yield (Sari et al. 2016). The efficiency approach embraces plants’ heterogeneous productivity and attributes the levels of production to the levels of managerial expertise across firms. This is arguably more accurate in approximating the CPO industry in Indonesia.

Literature on the measurement of manufacturing firms’ performance has been growing. For example, a study by Esquivias and Harianto (2020) identifies the factors of technical efficiency from the perspective of market competition and foreign direct investment in Indonesian manufacturing firms between 2010–2014. They found that less competitive sectors show higher technical efficiency. Meanwhile, technical efficiency tends to be higher with foreign capital, export-import activities, and larger firm size. In China, Hu and Yin (2022) examined how intellectual property rights can protect and encourage firms’ productivity. They suggested that protected intellectual property rights enable firms in China to achieve more TFP growth in the presence of trade liberalization. In identifying firm performance, a study by Suyanto et al. (2021) clustered productivity into nine groups to accommodate the high heterogeneity. The findings reveal that the impacts of foreign capital vary across clusters but unanimously affect productivity positively. The study also suggests the importance of technical efficiency estimation in a homogeneous industrial group to estimate productivity gains more precisely.

In manufacturing firms, estimating technical efficiency is important because it captures the optimal level where inputs can generate maximum output. Empirical studies in Indonesia have estimated the technical efficiency of all subsectors of the manufacturing industry (Yasin 2021; Ikhsan 2007; Margono and Sharma 2006; Setiawan and Sule 2020). However, none of the studies has specifically identified the technical efficiency of crude palm oil plants in Indonesia. Moreover, studies estimating the technical efficiency of CPO plants have only measured the efficiency scores (Anam and Suhartini 2020; Suroso et al. 2020; Rifin 2017). Consequently, those studies cannot identify the contribution of efficiency to the dynamic indicator, such as the total factor productivity (TFP) growth. Unlike the usual productivity measurement, TFP not only compares the total outputs relative to the total inputs used in production but also reveals the compound effect of other factors, including new technologies, efficiency gains, economies of scale, managerial skills, and changes in the production organization. In this regard, estimating a firm’s performance using technical efficiency and TFP growth is essential to extend the body of knowledge in the industrial organization.

This study aims to investigate the efficiency performance of CPO firms in Indonesia and contributes to the literature in three ways. First, this study employs a parametric approach of stochastic frontier analysis (SFA), widely used in previous studies to estimate TFP growth with three decompositions. Since initiated in 1977 by Aigner et al. (1977), various SFA models have been developed to accommodate data characteristics, e.g., Battese and Coelli (1988, 1995), Lee and Schmidt (1993), and Greene (2005a, 2005b). Therefore, this study employs these models to ensure the estimation using SFA represents the crude palm oil companies in Indonesia adequately. Second, this study decomposes the components of total factor productivity growth of the Indonesian CPO companies into three components: changes in technical efficiency, technical change, and scale efficiency. This decomposition enables comparison between technical efficiency and other components, which can provide more accurate information for strategic policy-making. Meanwhile, scale efficiency captures the dynamic performance of managerial expertise at the plantations in producing outputs and allocating production costs, and technical change captures technological progress in each plantation. Third, this study analyzes the TFP growth and the components, i.e., years, locations, and firm sizes. In sum, this study offers a wider scope of analysis regarding the changes in TFP and its components.

2. Methodology

2.1. Material

The data were collected from the annual survey of medium and large manufacturing firms conducted by Statistics Indonesia (BPS). Medium and large firms are defined as those employing at least 20 workers annually. This study uses unbalanced panel data from two ISIC codes, 10,431 for the crude palm oil industry and 10,432 for the palm cooking oil industry. The study period was from 2010 to 2014. Due to the subsector shifting or business closing, the number of observations varies each year. The lowest number of establishments was 457 firms (in 2010), while the highest was 654 firms (in 2014).

The production function consists of output and input variables. The output variable is measured by the total value output produced by a firm in a given year. The inputs are capital, labor, material, and energy1. The capital is proxied by the estimated value of fixed assets, i.e., lands and buildings, vehicles, machinery, and other capital goods. This estimate takes significant repairs, depreciation, sale, addition, reduction, and purchase values into account. Due to a lack of data, the perpetual inventory approach could not be applied in this study. However, the same capital data is also being used in other studies (see Margono and Sharma 2006; Amin 2010; Sari et al. 2016). Due to the unavailability of data, labor is defined as the number of employees working in the firm. Material input is calculated using the total cost of materials required in the production process, sourced domestically or imported. Energy is the expenditure on gasoline, diesel fuel, kerosene, public gas, lubricant, and electricity. Output and capital, material, and energy variables are measured in deflated monetary values. The deflation uses a wholesale price index (WPI) at a constant price of 2010. The descriptive statistics of the output and input variables are listed in

Table 1. The Descriptive Statistics of Output and Input Variables.

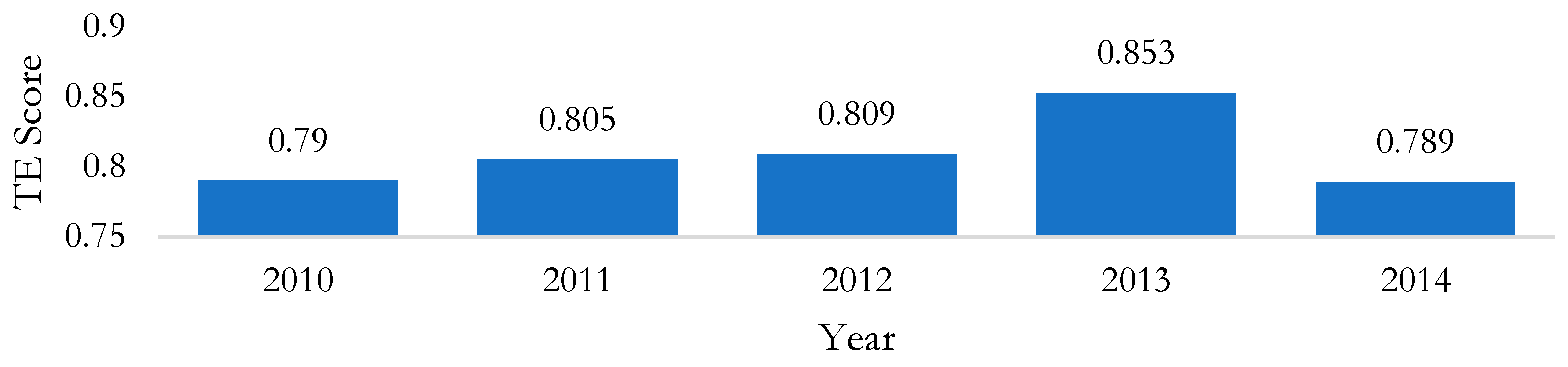
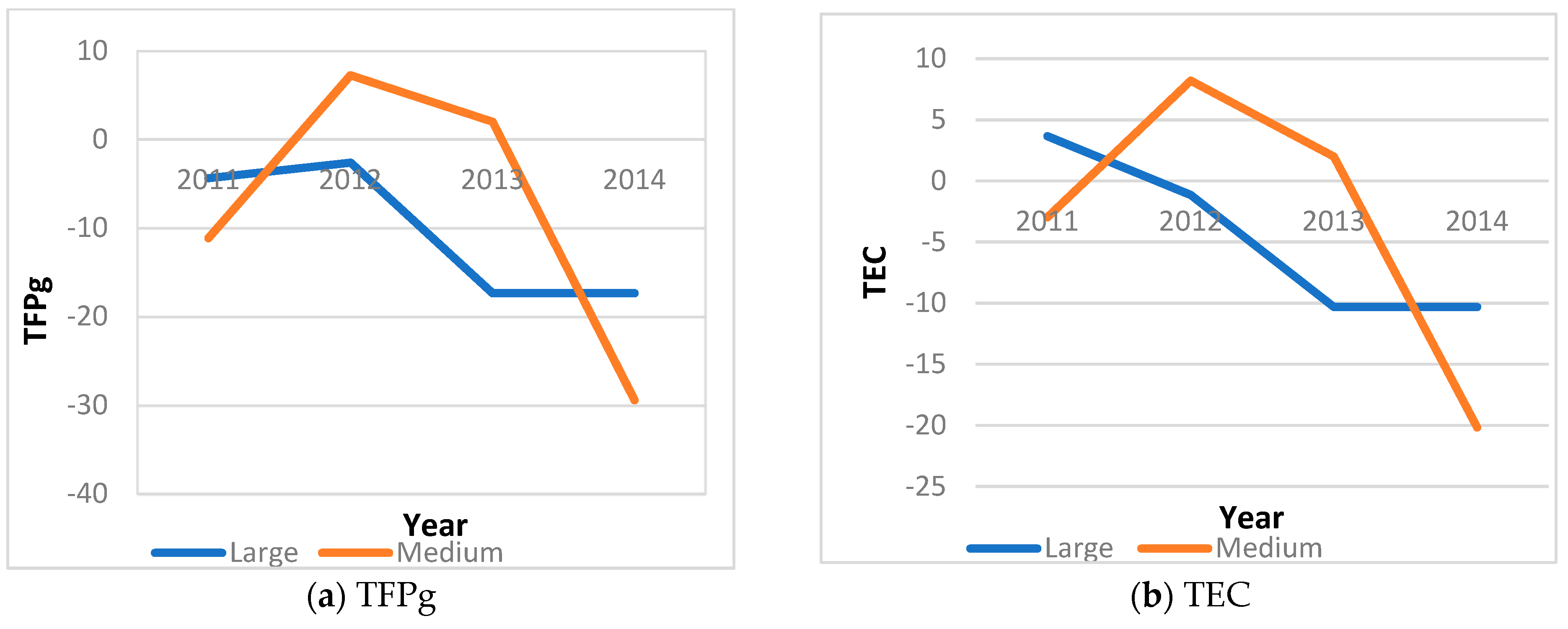
Variable	Unit		2010	2011	2012	2013	2014
Output (Y)	Billion Rupiah	Mean	488.968	719.184	700.218	790.220	580.551
		Std. Dev	977.892	1511.323	1435.908	3014.861	2850.227
Capital (K)	Billion Rupiah	Mean	9.574	14.287	15.389	19.088	136.997
		Std. Dev	23.309	35.104	44.763	97.881	1069.036
Labor (L)	Workers	Mean	291.867	303.700	310.874	297.007	299.249
		Std. Dev	457.494	630.855	656.225	549.791	663.593
Material (M)	Billion Rupiah	Mean	310.906	496.481	478.865	554.444	333.426
		Std. Dev	530.538	1042.153	965.570	2588.200	1183.289
Energy (E)	Billion Rupiah	Mean	21.730	31.243	30.823	28.140	21.917
		Std. Dev	63.746	84.170	91.291	77.992	119.710

Note: The mean is referred to as the arithmetic mean, while Std. Dev stands for the standard deviation.

.

2.2. Methodology

This study uses stochastic frontier analysis (SFA), which was proposed by Aigner et al. (1977) and Meeusen and Broeck (1977), and has been used widely to estimate technical efficiency. Instead of using non-parametric forms like data envelopment analysis (DEA) in estimating production function, SFA demonstrates the effect of inputs on the outputs in various parameter validities. Past studies have developed parametric forms and assumptions of the stochastic frontier model. For instance, Kumbhakar (1987), Pitt and Lee (1981), and Schmidt and Sickles (1984) treated inefficiency as time-invariant. Their models may not know whether heterogeneity or inefficiency results from the systematic time-invariant differences in output. Meanwhile, the models developed by Battese and Coelli (1992) and Kumbhakar (1990) defined inefficiency as a function of time and an individual-specific effect. The variants allow inefficiency to change over time without considering the firm’s effects. The time-variant inefficiency of each firm is the same in these models, which makes inefficiency and individual heterogeneity interchangeable. Battese and Coelli’s (1995) model allows the inefficiency to rely on exogenous variables so the determinants of inefficiency can be estimated.

The conventional panel stochastic models are not designed to distinguish unobserved individual heterogeneity from inefficiency. In this regard, the models inadvertently add time-invariant heterogeneity to the estimated inefficiency (Wang and Ho 2010). Therefore, it may create a bias in the measurement of inefficiency. Greene (2005a) proposes a true fixed effect stochastic model to address this problem, formulated as follows:

$$y_{it}^{\ast }=\alpha +{\beta }^{\prime }{x}_{it}+{\tau }^{\prime }{z}_i+v_{it}$$

(1)

where $y_{it}^{\ast }$ is the output of firm i at year t; $x_{it}$ refers to the vector of inputs; $z_i$ indicates a vector of firm-specific characteristics; $\alpha$ and $\beta$ are the parameters to be estimated while $v_{it}$ denotes the random error. This model includes the time-invariant terms, ${\tau }^{\prime }{z}_i$, in ${\beta }^{\prime }{x}_{it}$ and the model becomes:

$$y_{it}=\alpha +{\beta }^{\prime }{x}_{it}+v_{it}-u_{it}$$

(2)

where $u_{it}$ is the inefficiency term. The efficiency estimation by using this framework begins by estimating the technology parameters ($\alpha ,\beta , {\sigma }_u \mathrm{and} {\sigma }_v$) so the composed deviation can be measured, formulated as follows:

$${\epsilon }_{it}=v_{it}-u_{it}=y_{it}-\alpha -{\beta }^{\prime }{x}_{it}$$

(3)

However, the purposes of the studies are mainly to estimate inefficiency term (u_it), and not the firm-specific heterogeneity (${\epsilon }_{it})$. The measurement of inefficiency in this study applies the measurement of inefficiency done by Jondrow et al. (1982) (JLMS), formulated as follows:

$$E\left[u_{it}|{\epsilon }_{it}\right]=\frac{\sigma \lambda }{1+{\lambda }^2}\left[\frac{\varphi \left(a_{it}\right)}{1-\mathsf{\Phi }\left(a_{it}\right)}-a_{it}\right]$$

(4)

where $\sigma =\left[{\sigma }_{v^2}+{\sigma }_{u^2}\right]/2,\lambda ={\sigma }_u/{\sigma }_v, a_{it}=\pm ({\epsilon }_{it}\lambda )/\sigma$; and $\varphi \left(a_{it}\right)$ captures the standard normal density; $\mathsf{\Phi }\left(a_{it}\right)$ refers to the cumulative distribution function evaluated at $\left(a_{it}\right)$. SFA requires the selection of the best-fitted production function model. Therefore, the flexible functional form of a production function, namely the translog model, will be tested against the sub-translog models. As such, the risk of error in terms of model specification could be reduced. The translog production function model is adapted from Equation (2) and formulated as follows:

$$\begin{array}{cc}\hfill ln{y}_{it}={\alpha }_0+& {\beta }_{1}ln{K}_{it}+{\beta }_{2}ln{L}_{it}+{\beta }_{3}ln{E}_{it}+{\beta }_{4}ln{M}_{it}+\frac{1}{2}{\beta }_5{\left(ln{K}_{it}\right)}^2\hfill \\ & \hspace{1em}+\frac{1}{2}{\beta }_6{\left(ln{L}_{it}\right)}^2+\frac{1}{2}{\beta }_7{\left(ln{E}_{it}\right)}^2+\frac{1}{2}{\beta }_8{\left(ln{M}_{it}\right)}^2+{\beta }_{9}ln{K}_{it}\ast ln{L}_{it}\hfill \\ & \hspace{1em}+{\beta }_{10}ln{K}_{it}\ast ln{E}_{it}+{\beta }_{11}ln{K}_{it}\ast ln{M}_{it}+{\beta }_{12}ln{L}_{it}\ast ln{E}_{it}\hfill \\ & \hspace{1em}+{\beta }_{13}ln{L}_{it}\ast ln{M}_{it}+{\beta }_{14}ln{E}_{it}\ast ln{M}_{it}+{\beta }_{15}t+\frac{1}{2}{\beta }_{16}{t}^2\hfill \\ & \hspace{1em}+{\beta }_{17}ln{K}_{it}t+{\beta }_{18}ln{L}_{it}t+{\beta }_{19}ln{E}_{it}t+{\beta }_{20}ln{M}_{it}t+v_{it}-u_{it}\hfill \end{array}$$

(5)

where $y$ is the total output, while the independent variables K (firm capital value), L (labor), $M$ (Material), and E (Energy) are used in the inputs production process. $v_{it}$ represents the random error while $u_{it}$ is the technical inefficiency. The subscript i and t denote the i-th firm and t-th year, respectively. The $\beta$ implies the estimated coefficient. In this study, the output and input variables are transformed into natural logarithms, and each observation’s deviation from the geometric mean is calculated. For instance, the geometric mean of capital ($K_{it}$) is $\overline{K}$, which is transformed into a natural logarithm (ln($\overline{K}$)). Each observation in a capital variable is transformed into a natural logarithm $\ln (K_{it})$ before being subtracted from the geometric mean. The formula is as follows:

$$k_{it}=\ln \left(K_{it}\right)-\ln \left(\overline{K}\right)$$

(6)

Generally, the sub-translog production function models consist of Hicks-neutral, no technological progress, and the Cobb–Douglas model. Each of these models is tested, and the best-fitted model is used as the production function model in this analysis. At first, the hypothesis testing is done by the test between Hicks-neutral (H₀) and translog (H₁). The hicks-neutral model is defined by dismissing the input and time parameter interaction $({\beta }_{nt}=0)$ in Equation (5). The next is the test between the no technological progress (H₀) and translog (H₁). The no technological model assumes that the time coefficients are excluded (${\beta }_t={\beta }_{tt}={\beta }_{nt}=0)$ from the translog model. The third test is Cobb-Douglas (H₀) against the translog (H₁) production function. The null hypothesis consists of the parameter of inputs $\left({\beta }_{nm}={\beta }_{nt}={\beta }_t={\beta }_{tt}=0\right)$. These hypotheses testing is consistently estimated using generalized likelihood ratio statistics by the following formula:

$$\lambda =-2\left[l\left(H_0\right)-l\left(H_1\right)\right]$$

(7)

The $l(H_0)$ represents the log-likelihood estimated value of the restricted frontier model, while $l\left(H_1\right)$ represents the log-likelihood estimated value of the translog model. If the $\lambda$ calculation is less than the critical value of χ² distribution, the null hypothesis is accepted.

The estimation results of the inputs in the production function from Equation (5) are calculated into elasticity output concerning each input. The calculation of the elasticity is as follows:

$${\epsilon }_{nit}=\partial y_{it}/\partial x{n}_{it}={{\beta }^{\prime }}_n+\frac{1}{2}{\displaystyle \sum }_{n=1}^4{\displaystyle \sum }_{m=1}^4{{\beta }^{\prime }}_{nm}x{m}_{it}+{{\beta }^{\prime }}_{nt}t$$

(8)

The elasticity output with respect to each input in each year is summed up and accounted into total elasticity, formulated as follows:

$${\epsilon }_{Tit}={\displaystyle \sum }_{n=1}^N{\epsilon }_{nit}$$

(9)

This study analyzes total factor productivity (TFP), defined as the proportion of output not explained by the inputs used in the production but by the efficiency and intensity of input usage in the production process (Comin 2010). TFP is calculated by summing up its components, namely technical efficiency change (TEC), scale efficiency change (SEC), and technological change (TC). The formula for TFP growth is as follows:

$$TFP{g}_{it,t-1}=TE{C}_{it,t-1}+SE{C}_{it,t-1}+T{C}_{it,t-1}$$

(10)

where:

$$TE{C}_{it,t-1}=\ln \left(\frac{T{E}_{it}}{T{E}_{it,t-1}}\right)\times 100$$

(11)

$$SE{C}_{it,t-1}=\frac{1}{2}{\displaystyle \sum }_{n=1}^N[(\frac{{\epsilon }_{Tit}-1}{{\epsilon }_{Tit}}\epsilon n_{it}+\frac{{\epsilon }_{Tit-1}-1}{{\epsilon }_{Tit-1}}\epsilon n_{it-1})\left(x{n}_{it}-x{n}_{it-1}\right)]\times 100$$

(12)

$$T{C}_{it,t-1}=0.5\left[\left(\frac{\partial y_{it-1}}{\partial t}\right)+\left(\frac{\partial y_{it}}{\partial t}\right)\right]\times 100$$

(13)

$T{E}_{it}$ is technical efficiency and ${\epsilon }_{Tit}$ is the total elasticity of output with regard to inputs. $\epsilon n_{it}$ refers to the elasticity of output concerning each input. $y_{it }$ is the output and $x{n}_{it}$ is the input used in the production function. The subscript of i and t are the index of firm and time, respectively. TEC denotes managerial improvement. SEC reflects the movement towards the most optimum production scale. TC represents the shift of the production frontier because of the usage of sophisticated technology (Arora and Lohani 2017).

3. Results

The analysis starts with selecting the most suitable production function. This study relies on the utilization of the translog production function, so testing is essential to identify whether translog is the most suitable method. The test is conducted using a Log-likelihood Ratio based on a formula in Equation (7). The results are reported in

Table 2. Likelihood Ratio Test.

	Hicks-Neutral (df = 4)	No Technological Progress (df = 6)	Cobb Douglas (df = 17)	Decision
Translog (Baseline)	143.9	143.2	1148.0	Translog
${\mathit{\chi }}^{\mathbf{2}}$	13.2	31.9	6.4

, which shows that translog is the most suitable function with $\lambda >{\chi }^2$, not the technological progress or Cobb-Douglas model.

Table 3. Estimation Using Stochastic Frontier Analysis.

Variable	Translog	Hicks-Neutral	No Technological Progress	Cobb Douglas
$k$	0.0972 ***	0.0510 ***	0.0501 ***	0.0493 ***
	(0.0000235)	(0.000225)	(0.0000461)	(0.00000754)
$l$	0.0768 ***	0.0859 ***	0.0833 ***	0.0859 ***
	(0.0000227)	(0.0000352)	(0.0000322)	(0.0000168)
$e$	0.179 ***	0.188 ***	0.189 ***	0.206 ***
	(0.0000302)	(0.000109)	(0.0000690)	(0.00000901)
$r$	0.527 ***	0.564 ***	0.560 ***	0.447 ***
	(0.0000282)	(0.000236)	(0.0000740)	(0.0000146)
$k^2$	0.0448 ***	−0.0000645	−0.000528 ***
	(0.0000192)	(0.000145)	(0.0000244)
$l^2$	−0.00472 ***	−0.0118 ***	−0.00903 ***
	(0.0000201)	(0.0000347)	(0.0000252)
$e^2$	0.201 ***	0.185 ***	0.183 ***
	(0.0000480)	(0.000157)	(0.0000738)
$r^2$	0.421 ***	0.408 ***	0.405 ***
	(0.0000360)	(0.000153)	(0.0000661)
$k\times l$	0.0174 ***	0.0128 ***	0.0132 ***
	(0.0000191)	(0.0000499)	(0.0000258)
$k\times e$	0.0428 ***	0.0486 ***	0.0526 ***
	(0.0000212)	(0.000104)	(0.0000272)
$k\times r$	−0.102 ***	−0.0611 ***	−0.0669 ***
	(0.0000160)	(0.000140)	(0.0000224)
$l\times e$	0.0150 ***	0.0115 ***	0.0121 ***
	(0.0000172)	(0.0000546)	(0.0000251)
$l\times r$	−0.0123 ***	−0.0208 ***	−0.0157 ***
	(0.0000157)	(0.0000380)	(0.0000324)
$e\times r$	−0.287 ***	−0.283 ***	−0.281 ***
	(0.0000291)	(0.000108)	(0.0000648)
$t$	−0.0288 ***	−0.00222 ***
	(0.0000244)	(0.0000948)
$t^2$	−0.0204 ***
	(0.0000360)
$t\times k$	−0.0299 ***
	(0.0000141)
$t\times l$	−0.00624 ***
	(0.0000116)
$t\times e$	−0.00265 ***
	(0.0000164)
$t\times r$	0.0441 ***
	(0.0000130)
${\sigma }_u$
$Constant$	−2.827 ***	−2.773 ***	−2.773 ***	−2.396 ***
	(0.0387)	(0.0387)	(0.0387)	(0.0387)
${\sigma }_v$
$Constant$	−32.15	−29.41 ***	−31.57 **	−35.85
	(26.58)	(8.955)	(12.28)	(69.25)
Log-likelihood Ratio	1101.5	1029.58	1029.9	527.5

Note: The standard errors are in parentheses. ***, **, and * denote significance at alpha 1%, 5%, and 10% respectively.

reports the estimation results using SFA from four different production functions. According to Table 3, the coefficients across production functions tend to show similar magnitude and sign. In this regard, the estimation using the translog production function is robust. In terms of the coefficient’s magnitude, the variable of raw material reveals the largest magnitude, supporting prior studies discussing the Indonesian manufacturing industry (for some early examples, see Suyanto et al. 2021; Sari 2019; Esquivias and Harianto 2020; Yasin 2021).

The coefficient from the translog specification cannot be directly interpreted. Hence, a post-estimation regularity check of the coefficient is required. By referring to Equation (8), this study uses the elasticity approach to examine the monotonicity condition to prove that an increase in the input results in an increase in the related output (Yasin 2021). The result is reported in

Table 4. Output Elasticity.

Year	${\mathit{\epsilon }}_{\mathit{k}}$	${\mathit{\epsilon }}_{\mathit{l}}$	${\mathit{\epsilon }}_{\mathit{e}}$	${\mathit{\epsilon }}_{\mathit{r}}$	${\mathit{\epsilon }}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}$
2010	0.141	0.081	0.181	0.467	0.870
2011	0.108	0.079	0.163	0.526	0.875
2012	0.072	0.072	0.153	0.583	0.880
2013	0.049	0.065	0.167	0.604	0.885
2014	0.073	0.077	0.218	0.527	0.895
2010–2014	0.085	0.074	0.177	0.544	0.882

Note: ${\epsilon }_k$ denotes elasticity of capital, ${\epsilon }_l$ denotes elasticity of labor, ${\epsilon }_e$ denotes elasticity of energy, ${\epsilon }_r$ denotes elasticity of raw material, and ${\epsilon }_{total}$ denotes total elasticity.

, showing that the total elasticity’s magnitude is less than unity, indicating a decreasing return to scale of the productivity in the crude palm oil industry. The elasticity of output for all years is mainly attributable to raw materials. Banda and Verdugo (2011) argue that the FFB is insufficient to fulfill the production capacity. This shortage poses a challenge for firms in optimizing their profits. In other words, one of the main challenges in the crude palm industry is maintaining the supply of raw materials.

4. Discussion

This study examines technical efficiency and total factor productivity growth and the decompositions. The first analysis looks at the technical efficiency score of the firms in the CPO industry. The result is illustrated in Figure 1, showing that the average score of technical efficiency (TE) of the CPO industry in 2010–2014 ranged between 0.789–0.853. This result implies that the CPO industry remains technically inefficient for an average of about 14.7–21.1% over the five years. The low technical efficiency score might be sourced from the small number of trained laborers and the slight improvement of research and development in crucial aspects, such as process and product technologies. The technical efficiency result is similar to prior studies on the CPO industry (see Rifin 2017; Anam and Suhartini 2020). Rifin (2017) examined the year 2013 and revealed that the average technical efficiency score of the CPO industry was mainly less than 20%. In fact, there were merely 18 firms with TE score ranges between 61–99%. This significant magnitude may stem from the approach used by Rifin (2017), which employed non-parametric data envelopment analysis. Meanwhile, Anam and Suhartini’s (2020) study looked at 2015 using an approach similar to Rifin’s (2017) approach. However, Anam and Suhartini (2020) revealed that the technical efficiency score of the CPO industry in 2015 was an average of 98.5%, a magnitude that is nearer to the current study’s result.

The following analysis is to calculate TFP growth with its three decompositions: technical efficiency change (TEC), technical progress/technical change (TC), and scale efficiency change (SEC). The decomposition reveals how much each component contributes to the TFP growth magnitude. In this study, the analyzes of TFPg and its components are classified by year, region, and firm size.

Table 5. Year-wise Comparison of Total Factor Productivity Growth and Its Components.

Year	TFPg	TEC	TC	SEC
2010–2011	−5.097	3.176	−3.231	−5.041
2011–2012	−0.877	0.736	−1.156	−0.458
2012–2013	3.853	3.767	−1.495	1.581
2013–2014	−16.860	−9.285	−8.032	0.457
2010–2014	−5.191	−0.831	−3.664	−0.696

Note: TFPg, TEC, TC, and SEC represent the average in percentage.

shows the calculation of TFP growth and the decompositions annually. The CPO industry experiences negative TFP growth, or the average TFP score of the current period degrades from the average score in the prior period. The TFP growth for the average years of 2010–2014 was −5.191%, with the largest adverse impact from negative technical change by −3.66%. The negative TC implies that the CPO industry performs technological regress over 2010–2014. Likewise, other components (TEC and SEC) also experience negative magnitude, although those do not exceed 1%. These results are in accordance with the findings by Sari et al. (2021), which suggest the improvement of technological progress and optimization of production scale in the Indonesian crude palm oil industry. The years from 2012–2013, or TFP growth in 2013, is the only period with a positive score, contributed mostly by the solid magnitude of technical efficiency change (TEC) at 3.76%. In this period, TC remained negative, strengthening the arguments that the CPO industry faced technological regress. The industry could achieve technological progress by investing in research and development because the funding could be used to upgrade the machinery. This could result in the more efficient and sophisticated use of technology. In contrast, the data from World Bank (2020) show that the percentage of research and development to GDP in Indonesia was low (around 2%) from 1996 to 2018. This evidence indicates that Indonesia still lacks research and development funding.

Table 6. Region-wise Comparison of Total Factor Productivity Growth and Its Components.

No	Province	Number of Observation	TFP	TEC	TC	SEC
1	Naggroe Aceh Darussalam	60	−5.54	−1.40	−3.44	−0.70
2	North Sumatera	488	−5.40	−1.23	−3.41	−0.75
3	West Sumatra	76	−5.24	−1.17	−3.27	−0.81
4	Riau	476	−5.19	−1.12	−3.26	−0.81
5	Jambi	96	−5.17	−1.15	−3.25	−0.77
6	South Sumatra	52	−5.19	−1.22	−3.24	−0.73
7	Bengkulu	16	−5.09	−1.03	−3.23	−0.83
8	Lampung	36	−5.13	−1.07	−3.23	−0.84
9	Bangka Belitung Island	40	−4.23	−0.36	−2.94	−0.93
10	Riau Island	8	−24.93	−18.93	−5.96	−0.04
11	DKI Jakarta	16	−1.89	3.27	−4.13	−1.04
12	West Java	24	1.18	2.33	−3.38	2.22
13	Central Java	4	−2.73	−5.50	−4.12	6.88
14	East Java	24	−3.51	−3.44	−3.84	3.76
15	Banten	8	−16.55	−11.68	−5.11	0.24
16	West Kalimantan	60	−5.80	−0.73	−4.64	−0.43
17	Central Kalimantan	108	−4.66	−0.30	−3.64	−0.72
18	South Kalimantan	40	−4.46	−1.58	−3.85	0.97
19	East Kalimantan	32	−7.72	−1.54	−4.64	−1.55
20	Central Sulawesi	12	4.56	9.81	−5.70	0.45
21	South Sulawesi	8	9.07	19.85	−6.07	−4.71
22	West Sulawesi	20	−2.36	1.37	−3.14	−0.59
23	West Papua	8	10.50	19.09	−2.93	−5.66
24	Papua	12	−6.92	−2.29	−4.83	0.21
Total		1724	−5.51	−1.29	−3.42	−0.81

informs the average of TFP change and the decomposition by province. Based on the region, most crude palm oil firms are located in North Sumatra (28.31%) and Riau (27.61%). However, both provinces experience a regress in productivity. The TFP of 20 out of 24 provinces was negative, and six provinces’ TFP scores were below the total average. Among these underperforming firms, the degression in productivity was mainly driven by technological regress. This indicates that most firms need innovation in technology utilized in production. The other components of TFP, such as technical efficiency change, also showed negative scores. Meanwhile, the average scale efficiency change improved. On the other hand, West Java (1.18), West Papua (10.5), Central (4.56), and South Sulawesi (9.07) provinces displayed positive productivity. This productivity improvement can be attributed to technical efficiency change. Meanwhile, the rest of the total factor productivity components show negative magnitudes. From these four provinces, the scale efficiency change, West Papua (−5.66) and South Sulawesi (−4.71), scored the lowest and the second lowest, respectively. Anam and Suhartini (2020) study using data from 2015 found that the scale efficiency scores in both provinces were lower than others. The regulation might affect the firms’ productivity and influence the firm’s ability to adjust to economic and technological conditions. Therefore, an efficient scale of operation could not be achieved.

Figure 2 shows the variation of TFPg based on the firm size, divided into medium and large firms. The former employs 20 to 99 workers, and the latter employs more than 99 workers in a given year. The TFPg of large firms constantly exhibited a decline over the period, while the medium firms showed positive productivity for two consecutive years (2012–2013). On average, both firm sizes show a negative trend in productivity, but the decline in medium firms was smaller than in large firms. This result is consistent with the study by Halkos and Tzeremes (2007), stating that firm size is a crucial determinant of productivity. Their finding showed that the TFP of small firms in the Greek manufacturing industry performed better than the large firms. Likewise, Yeo and Park (2022) showed that the TFP and its components across different firm sizes in Korea also varied. However, Dhawan (2001) analyzed the US industry and found that small firms performed better. This is supported by Dvouletý and Blažková (2021), who found evidence that the more employees, the less productive the firm is. The sources of productivity changes in both firm sizes were TEC and TC.

On average, the decline of technical efficiency change is smaller in medium firms, indicating that these firms can use resources more efficiently, improve managerial expertise more significantly, and adjust to an external shock better than large firms. This result is supported by the argument by Utterback (1994), stating that due to a better strategy for managing change in the environment using greater organizational responsiveness, small firms outperformed large firms. The results of TC indicate that medium firms performed better than large firms, in line with the study by Halkos and Tzeremes (2007). Similarly, Nieto and Santamaria (2010) and Scherer (1991) clarify that small firms tend to adopt innovations more than larger firms, resulting in better technical change. In terms of scale efficiency change, although both firm sizes saw negative growths, large forms showed slightly better scale efficiency change than medium firms.

5. Conclusions

This study examines the TFP growth and decompositions of the crude palm oil industry through stochastic frontier analysis (SFA). The data were sourced from the annual survey of medium and large manufacturing establishments conducted by Statistics Indonesia from 2010 to 2014. The calculation result of elasticity of output for all years is mainly contributed to by raw materials. The total elasticity reveals that the magnitude is less than unity, indicating a decreasing return to productivity scale in the crude palm oil industry.

This study focuses the analyses on productivity growths by year, location, and firm size. Regarding the year, although the CPO industry’s productivity progressed positively from 2012 to 2013, the average productivity was negative and mainly attributed to the technical regress. Region-wise, the comparison shows that most provinces saw declining productivity. However, four provinces saw a rise in productivity: West Java, West Papua, Central, and South Sulawesi. On average, total factor productivity growths from the region-wise analysis could be attributed to the technical change. In terms of size, the technical efficiency change and technical change regressed the TFPg in all firm sizes, but medium firms declined less significantly than large firms. This indicates that medium firms can use resources and technology more efficiently, improve managerial expertise more effectively, and adjust an external shock better than large firms. Conversely, large firms showed a slightly higher scale efficiency than medium firms, although both types saw a negative scale efficiency change.

From all the analyses (year, location, and firm size), the main factor contributing to productivity gain or decline was technical change. This indicates that technology innovation is the most urgent driver in the crude palm oil industry. Therefore, the government needs to strengthen economic policies by supporting technological advancement, such as the research and development of technology in production processes.

6. Limitation and Future Research

A limitation of this study is related to data availability. To calculate firm productivity, the firm’s id is needed. However, the firm’s id in the annual survey of medium and large manufacturing firms over 2014 cannot be used to calculate productivity. Future research should improve the current work by using the newest data.