Appendix A
This appendix provides an explanation of the notation along with the list of definitions and related formulas of several statistical measures used throughout the paper.
Notation: We use the notation included in this section to formulate the problem of predicting recidivism with a single sensitive attribute of race. We need to find the model that helps predict with high accuracy and lowest bias possible amongst the given models, each one of which is developed with the rolling sum of prior individual crimes from N prior arrest records.
: quantified features of each elemnt in the dataset.
: Race-based binary sensitive attribute (African American, Caucasian)
: predicted variable (not reconvicted/reconvicted)
: target variable (will not reoffend/will reoffend).
Assumption: (X, A, Y) are generated from a distribution d denoted as
measure(A′): value of a metric for subpopulation with A = 0.
measure(A) : value of a metric for subpopulation with A = 1.
TP: True-Positive (TP) is a correct positive prediction. In our paper it means that a future recidivist was correctly forecasted to recidivate.
TN: True-Negative (TN) is a correct negative prediction. In our paper it means that a future non-recidivist was correctly forecasted to not recidivate.
FP: False-Positive (FP) is an incorrect positive prediction, when a future nonrecidivist was falsely forecasted to recidivate.
FN: False-Negatives (FN) is an incorrect negative prediction. In our paper it means that a future recidivist was erroneously labeled as nonrecidivist.
Positive Predictive Value: PPV, also referred to as Precision, is the total number of true-positive cases divided by a total of all predicted positive cases. The best possible value of PPV is 1 and is achieved when FP becomes zero, i.e., when none of the future non-recidivists are wrongly accused of being a recidivist. The worst value of PPV is 0 and happens when none of the individuals predicted to recidivate are actually recidivists, i.e., when TP is zero. Therefore, it is desirable to have PPV as close to 1 as possible. PPV also refers to the probability of an offender to truly belong to the positive class,
and
. PPV parity [
14] is achieved when
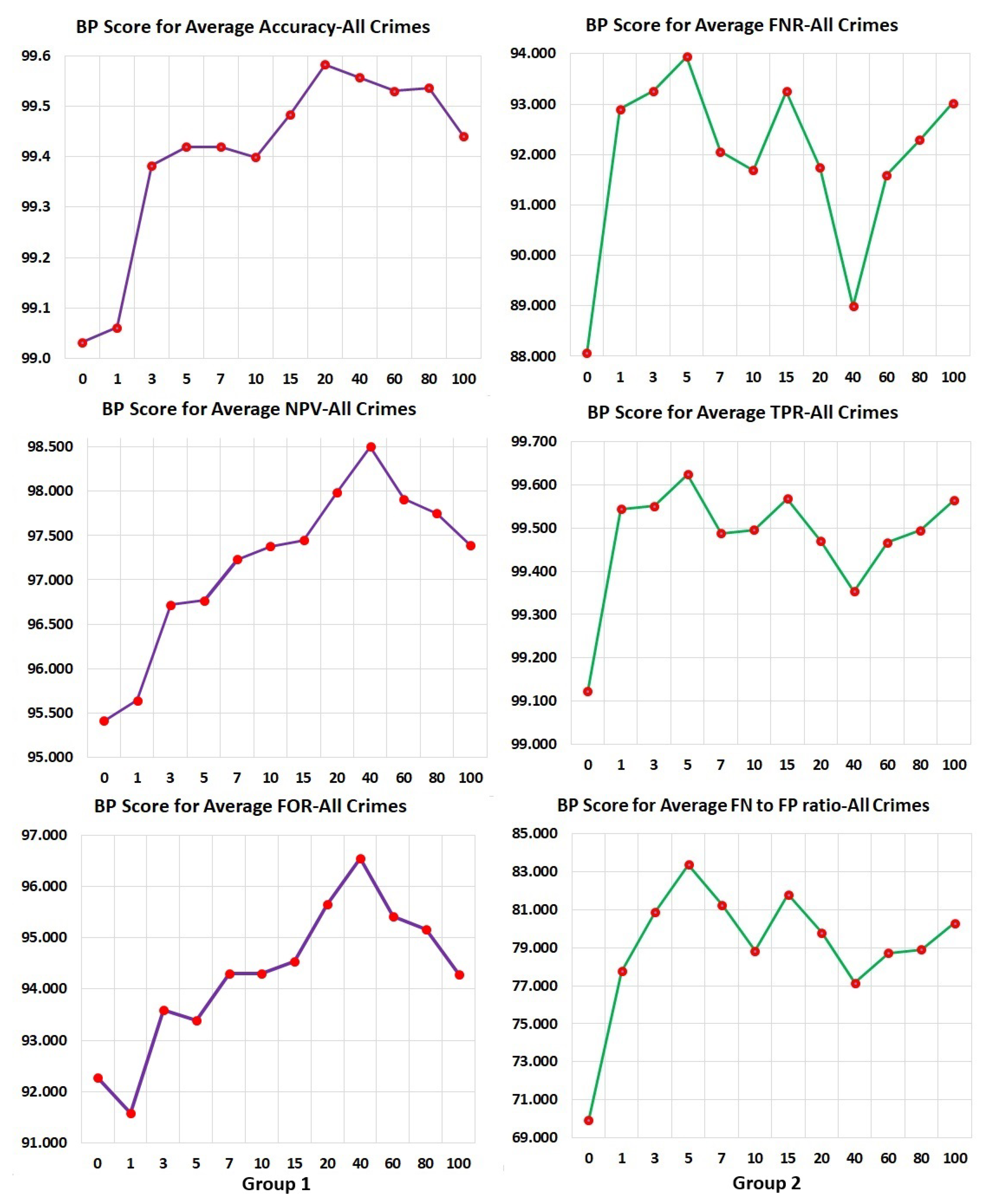
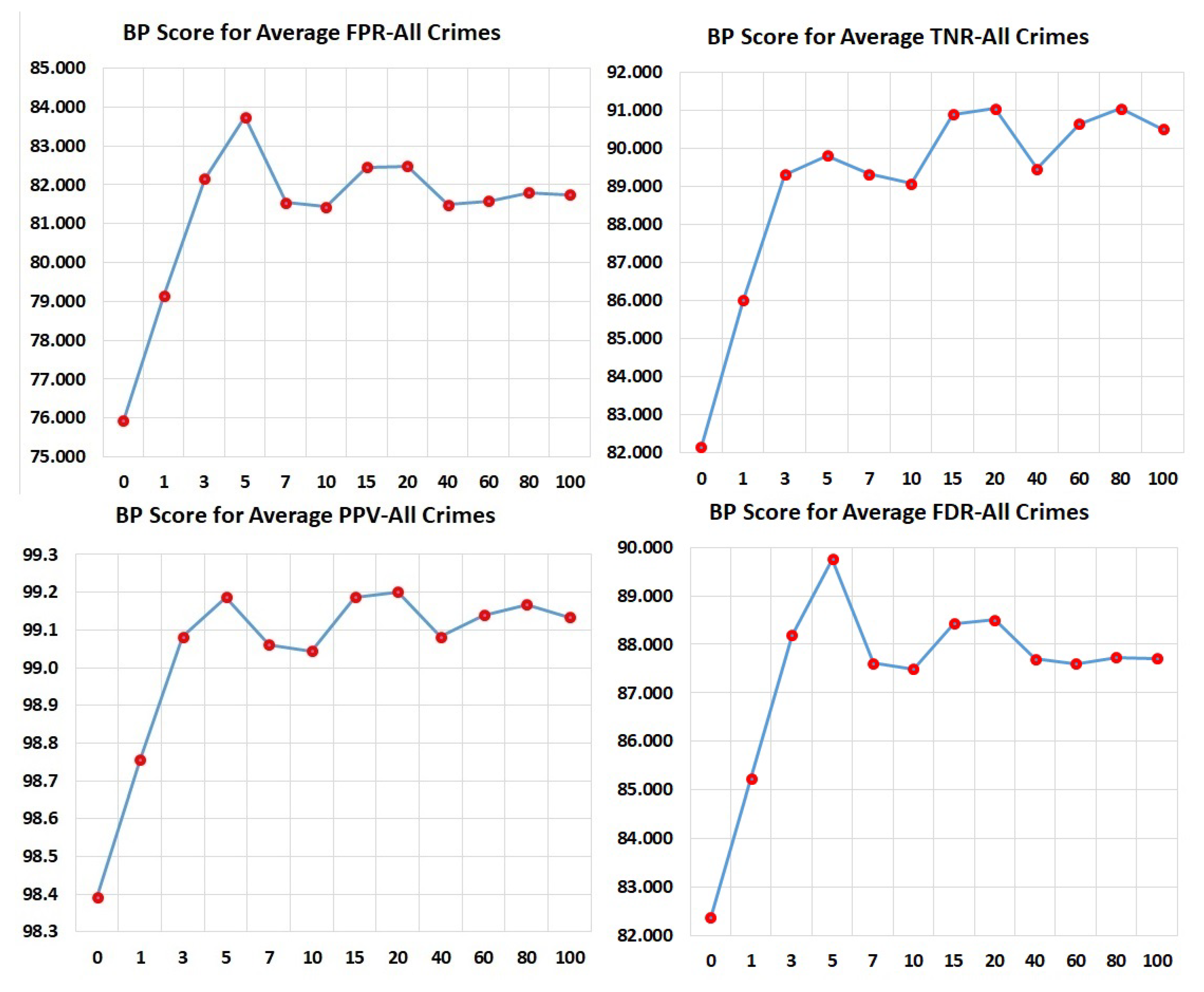
. Average PPV and BPS for the model with 5 past arrest cycles and all race data were 0.853 and 97.9, respectively.
False-Positive Rate: FPR is the total number of incorrect positive predictions divided by a total of all the non-recidivists (FP + TN) in the dataset. The best possible value of FPR is 0 and is achieved when FP becomes zero, i.e., none of the future non-recidivists are wrongly accused of being a recidivist. The worst value of FPR is 1 and happens when all future non-recidivists are falsely labeled as recidivists such that TN becomes 0. Therefore, it is desirable to have FPR as close to 0 as possible. FPR is represented as and .
FPR parity or false-positive error rate balance [
14] or predictive equality [
40] is achieved when
. Average FPR and BPS for the model with 5 past arrest cycles and all race data were 0.378 and 83.7, respectively.
False-Negative Rate: FNR is the total number of incorrect negative predictions divided by a total of all the recidivists (FN + TP) in the dataset. The best possible value of FNR is 0 and is achieved when FN becomes zero, i.e., none of the future recidivists are erroneously labeled as a non-recidivist. The worst value of FNR is 1 and happens when all future recidivists are falsely labeled as non-recidivists such that TP becomes 0. FNR is represented as
and
FNR parity is achieved when
. Average FNR and BPS for the model with 5 past arrest cycles and all race data were 0.056 and 93.9, respectively.
It is desirable to have both FPR and FNR as close to 0 as possible. A high FPR represents many future non-recidivists wasting behind bars while a high FNR means many future recidivists let lose to commit many needless crimes in the world. Both FPR and FNR mean different types of error and associated cost to society. Both higher FPR and higher FNR cause a decrease in the predictive accuracy.
False Discovery Rate: FDR is the total number of incorrect positive predictions (FP) divided by a total of all positive predictions (TP + FP). The best possible value of FDR is 0 and is achieved when FP becomes zero, i.e., none of the future non-recidivists are mislabeled as recidivist. The worst value of FOR is 1 and happens when all future recidivists are falsely labeled as non-recidivists such that TP becomes 0. Therefore, it is desirable to have FDR as close to 0 as possible. FDR refers to the probability of a positively labeled individual to actually belong to the negative class,
, or the probability of a person kept incarcerated to be a non-recidivist.
and
. FDR parity is achieved when
Average FDR and BPS for the model with 5 past arrest cycles and all race data were 0.071 and 89.8, respectively.
False Omission Rate: FOR is the total number of incorrect negative predictions (FN) divided by a total of all predicted non-recidivists (TN + FN). The best possible value of FOR is 0 and is achieved when FN becomes zero, i.e., none of the future recidivists are mislabeled as non-recidivist and let go. The worst value of FOR is 1 and happens when all future non-recidivists are falsely labeled as recidivists such that TN becomes 0. Therefore, it is desirable to have FOR as close to 0 as possible. FOR refers to the probability of a positive class to be labeled negatively, (P(Y = 1 |C = 0), or the probability of a someone who is let go to be a recidivist.
. FOR parity is achieved when
Average FOR and BPS for the model with 5 past arrest cycles and all race data were 0.323 and 93.4, respectively.
Negative Predictive Value: NPV is the total number of true-negatives divided by the total number of negative predictions. The best possible value of NPV is 1. The worst value of NPV is 0 when all negative class are predicted to be positive class such that FN =0. NPV refers to the probability of a negative prediction to truly belong to the negative class,
, or the probability of someone predicted to be a non-recidivist to actually be a non-recidivist.
and
. NPV parity is achieved when
. Average NPV and BPS for the model with 5 past arrest cycles and all race data were 0.677 and 96.8, respectively.
True-Positive Rate: TPR is the total number of true-positive cases identified divided by the total number of positive cases. The best possible value of TPR is 1 and is achieved when FN is equal to 0. TPR, also known as sensitivity or recall, is the probability of the positive class to be labeled as positive,
or the probability of a recidivist to be labeled as one.
and
. TPR parity is achieved when
. Average TPR and BPS for the model with 5 past arrest cycles and all race data were 0.944 and 99.6, respectively.
True-Negative Rate: TNR is the total number of correctly labeled negative predictions divided by all the negative cases. The best possible value of TNR is 1 and is achieved when FP is 0. TNR refers to the probability of a negative class being labeled negative,
This in our predictions is the probability of non-recidivists being labeled a non-recidivist.
and
. TNR parity is achieved when
. Average TNR and BPS for the model with 5 past arrest cycles and all race data were 0.622 and 89.8, respectively.
Accuracy: Accuracy is the total number of appropriately labeled predictions divided by the number of all the cases. The best possible value of Accuracy is 1 and is achieved when both FP and FN are 0. Accuracy refers to the probability of accurate labeling for both positive and negative classes, P(C = Y). This in our predictions is the probability of being correctly labeled as a recidivist or non-recidivist as the case is.
and
. Accuracy parity is achieved when
. Average Accuracy and BPS for the model with 5 past arrest cycles and all race data were 0.892 and 99.4 respectively.
Statistical Parity or Group Fairness or Demographical Parity [
15] or Equal Acceptance Rate [
41] is the property that the demographics of those labeled with a positive (or negative) classifications is the same as the demographics of the population as a whole [
15]. In other words, this is true if all subgroups have equal probability to be labeled as the positive class
[
12].
and
and and the condition
is satisfied. The fraction of all positive predicted cases from all cases and BPS (statistical parity) for the model with 5 past arrest cycles and all race data were 0.854 and 97.9, respectively.
The situation may be unfair for an individual even as statistical parity is accomplished. As per Dwork et al. [
15], this can provide fair affirmative action but may be insufficient in other situations, e.g., if one subgroup has in fact more members with positive class than the other group or when more unqualified members are chosen to fulfill the condition [
15]. In our dataset, it is used to give members of different races a possibility of parole but this may not be fair if one group reoffends more.
Treatment Equality [
13] or false-negative-to-false-positive ratio is achieved when the ratio of errors, i.e., false-negatives and false-positives for the subpopulations are equal, such that
and
and the condition
is satisfied. In our dataset this means that for both African-Americans and Caucasians, the ratio of recidivists labeled as non-recidivists (FN) to non-recidivists labeled as recidivists should be the same. The average fraction of all false-negative cases to false-positive cases from all cases and BPS (Treatment Equality) for the model with five past arrest cycles and all race data were 0.798 and 83.8, respectively.