Abstract
Transdermal optical wireless (TOW) communication links have recently gained particular research and commercial attention as a viable alternative for establishing high speed and effective implantable data transmissions, which is vital for a variety of neuroprosthetic and other medical applications. However, the development of this optical telemetry modality with medical implanted devices (IMDs) is adversely affected by skin-induced photon absorption, scattering and pointing errors effects. Thus, in this work a minimum mean-square error (MMSE) criterion is proposed for the estimation of the optical signal intensity in a typical TOW link of varying path loss and misalignment-induced fading characteristics. In this context, the stochastic nature of the transmitter–receiver misalignment has been considered and jointly modeled with transdermal path loss. Additionally, the link is assumed to employ the suitable On–Off Keying (OOK) with intensity modulation and direct detection scheme as well as a PIN photodiode at the receiver side for signal detection. Under these assumptions the results demonstrate that the stochastic amount of pointing mismatch strongly affects the received irradiance estimation.
1. Introduction
Transdermal optical wireless communication refers to the point-to-point data transfer via light between an in-body and an out-of-body device. As is the case with the well-known fiber-optic and free-air optical communication systems, the use of modulated light waves as information bit carriers leads to greatly increased high data rates along with low power consumption and extremely high immunity to electromagnetic interference (EMI) [1,2,3,4]. Consequently, transdermal optical wireless (TOW) biotelemetry is a very promising alternative to its radiofrequency (RF) and inductive coupling counterparts which are currently used in most implantable communication systems [5,6,7,8]. In this regard, TOW technology is a prime candidate especially for bandwidth-hungry medical applications which require high speed and secure transdermal data transfer, including mainly communication with cochlear implants, visual prostheses, recording of neural signal and cortical signal processing [6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Specifically, authors in [9] proposed a compact photocoupler-like TOW system which makes it possible to control prostheses by use of biopotentials inside the body. For advanced neuroprosthetic applications requiring very high speed and real-time data transmissions in order to achieve natural-feeling prosthetic control, i.e., complex and precise movement control that involves real-time neural sensing on cortical tissues or peripheral nerves, authors in [5] established a robust TOW telemetric link capable of transmitting up to 16 Mb/s through a skin sample of 4 mm while consuming a maximum power of 10 mW. Additionally, for neural cortical signal recording, authors in [6,7,8] presented a 50-Mbps TOW link through 4-mm porcine skin tissue where up to 100 channels can be simultaneously recorded and a TOW telemetric link operating as the interface between an implanted cortical array and an out-of-body receiver achieving 100 Mb/s through a 2.5-mm-thick perfused tissue in vivo on an anesthetized sheep, while requiring 4.1 mW and 2.1 mW of electrical power, respectively. In fact, the feasibility of TOW communication has been experimentally validated in [1,4,5,6,7,8,14]. What these papers have in common is the operation with appropriate wavelengths within the optical tissue window, i.e., between 600 and 1300nm, as an attempt to minimize photon absorption inside skin [6,15], as well as the use of On–Off Keying (OOK) modulation formats, while pointing errors have been considered either as a deterministic effect or as a negligible one. Lately, authors in [16,17,18,19] and more recently authors in [20,21,22] evaluated the stochastic nature of pointing errors which arise from the realistic relative motion between the transmitter and the receiver terminals along with the transdermal path loss. Their results demonstrate that pointing errors can significantly aggravate the already important TOW performance degradation due to skin-induced attenuation, even within the optical tissue window [13,14]. Moreover, while OOK with intensity modulation/direct detection (IM/DD) is the most feasible modulation scheme mainly due to its simplicity, it requires the detector threshold estimation and adjustment according to each of the respective varying fading channel states [21,23,24,25].
Under these circumstances, it becomes evident that in order to achieve optimum signal detection, a priori knowledge of signal intensity is required and hence, the need of signal estimation. Thus, it is wise to estimate the received signal intensity which attenuates traversing the skin-channel and randomly fluctuates due to misalignment-induced fading. To the best of the authors’ knowledge, although signal estimation has been reported in the traditional literature of free-air communication [26,27,28,29,30,31], there isnot any relative work for the emerging TOW communications [26]. Motivated by the latter and the above, the minimum mean-square error (MMSE) principle is proposed for the estimation of optical signal intensity in typical direct TOW communication links impaired by stochastic misalignment-induced fading.
2. Estimator and Channel Model
At the transmitter’s side, the out-of-body unit is assumed to consist of a data capturing unit which converts external stimulations into electrical signals followed by a digital signal processing (DSP) unit which digitizes and compresses data into OOK-modulated signals through an optical laser source. After traversing the skin channel, these data modulated with OOK light signals are collected through a PIN photodiode at the implanted receiver’s side which comprises, in turn, a DSP and a stimulation unit (STM) which generate the appropriate nerve stimulations [16,17,18,19,20,21]. Considering thus a direct-detection receiver along with shot noise-limited conditions, the optimum receiver architecture for detection of modulated signals is based on photon counting process to render a proper decision concerning the transmitted data symbols [26]. The block diagram of the whole TOW system appears in Figure 1.
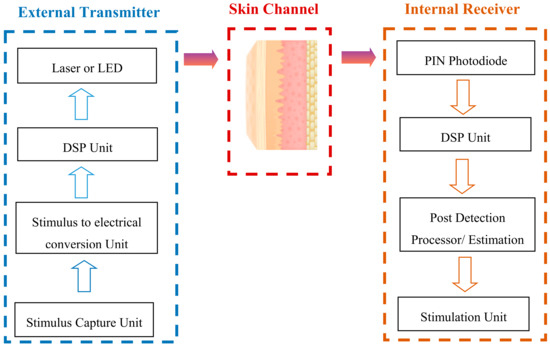
Figure 1.
Block diagram of the investigated transdermal optical wireless (TOW) system.
Under these conditions, a slow-varying skin channel is assumed, where the optical signal intensity is considered to be constant for a large number of data symbols. Specifically, the observation interval for estimating the signal intensity is l symbol interval long and consequently, the signal intensity is considered to remain constant over l symbol intervals.
Additionally, it is well known that MMSE estimation minimizes the MSE which is a common metric of estimator quality [31]. The MMSE estimator of signal intensity based on random variable is the conditional where is the signal intensity of the field in photons which is directly proportional to the optical signal intensity arriving at the receiver side and n is the signal photon count at the receiver side over a symbol interval [26]. In this respect, when is the observable vector of signal photon counts, observed over l symbol intervals, the estimator is with the probability density function (PDF) of the random variable conditioned on being [23,26]:
where is the product of independent densities which can be expressed as [23,26]:
with the above individual densities, , being Poisson distributed for deterministic signal intensity [23,26]:
For the TOW link under consideration we obtain [16,17,18,19,20,21]:
where is the deterministic channel coefficient due to skin-induced attenuation and denotes the stochastic process that models the geometric spread due to pointing errors [16,17,18,19,20,21].
With regard to pointing errors, by assuming that the elevation and the horizontal displacement follow independent and identical Gaussian distributions [32,33], the radial displacement at the receiver side should follow a Rayleigh distribution. Consequently, the PDF of the random variable can be expressed as [17,22,34]:
where describes pointing errors strength with denoting the equivalent beam radius in the internal detector aperture and representing the corresponding pointing error displacement, i.e., spatial jitter. Generally, larger parameter values correspond to stronger misalignment-induced fading [20,34]. Additionally, , where erf(.) denotes the error function (Equation (8.250.1) in Ref. [35]), and with being the radius of the circular receiver aperture and being the fraction of the collected power at = 0, respectively [20,34]. Moreover, which is obtained as [18]
represents the beam waist on the receiver plane at a propagating transdermal distance , which practically corresponds to skin thickness, considering the transmitter divergence angle [16].
Therefore, by using Equations (4) and (5) and the standard technique of random variables (RV) transformation [36], the PDF of the signal intensity is obtained:
Here, it should be recalled that where is the wavelength-dependent skin attenuation coefficient [17,19].
According to MMSE criterion, the above signal intensity can be estimated as below:
where the PDF of random process is expressed as:
Therefore, by substituting Equation (9) into (8), the latter can be written as:
Next, by substituting (3) and (7) into (10) and after some algebraic manipulations we get:
Assuming one observation, i.e., by setting l = 1, the latter expression (11), reduces to:
By expressing the exponential terms in (12) in form of Meijer’s G-function (Equation (8.4.3/1) in Ref. [37]), i.e.,, we get:
Then, by using (Equation (07.34.21.0009.01) in Ref. [38]), in order to calculate the integrals above and after some algebra, we conclude that:
where denotes the gamma function (Equation (8.310.1) in Ref. [35]).
By extending the approach above, the estimated signal intensity for l observations can be correspondingly obtained as
where . Note that when = 1, we observe that (15) reduces to (14) as it should.
3. Analytical Results
In this section we evaluate the received signal intensity through the proposed MMSE estimator via Equations (14) and (15) over a wide area of typical signal photon count values along with negligible-to-very-strong stochastic pointing errors. Without loss of generality, it is initially assumed that the estimated signal intensity is extracted for one observation, i.e., = 1. The photon count values as well as pointing errors strength are determined by skin channels’ and other links’ characteristics. Specifically, the divergence angle, , is fixed at 20°, while the link is assumed to operate with optical wavelength, , equal to 1100 nm. It should be noted that this selected wavelength value has been proven to be in [17,18] the optimal transmission wavelength within the medical optical window, i.e., between 700 and 1300 nm, where the highest tissue transmittance for the propagating light can be achieved [5,6]. Thus, the optical wavelength of 1100 nm has been selected on purpose, in an attempt to collect the maximum feasible number of transmitted photons at the receiver side. Moreover, transmitter and receiver apertures, r, are assumed to be equal to 0.5 mm. Additionally, the skin thickness, , of the TOW channel is set to be equal to 4 mm, 5 mm or 6 mm. In both cases, the corresponding beam waist, , can be calculated through Equation (6). Consequently, pointing errors effects can be evaluated by assuming varying spatial jitter values. According to , higher values of correspond to lower values of which, as mentioned above, indicate stronger pointing errors. In this context, when , pointing error effect can be considered as strong as possible, which implies that the beam center cannot coincide at all with the center of the implanted PIN receiver aperture.
Figure 2 illustrates the estimated signal intensity evolution via MMSE criterion from negligible to strong amounts of pointing mismatch between external transmitter and implanted receiver terminals when the TOW link length is assumed to be equal to 5 mm. It is revealed that stochastic pointing error strength increments significantly degrade the estimated signal intensity arriving at the receiver side. Additionally, as it was expected, the estimated signal intensity is enhanced as the number of propagating photons increases at the receiver side. Specifically, the optimum case in Figure 2 is for , i.e., when jitter variance at the internal receiver is getting its lower value. Furthermore, since corresponds to a very strong realistic jitter value, it comes closest to the curve with the maximum theoretical jitter value, i.e., . The latter demonstrates that the proposed MMSE estimator is suitable for the estimation of the intensity of the signal arriving at the non-perfectly aligned receiver terminal after traversing the skin channel. In this respect, MMSE estimator could be useful to estimate and correct misalignment-induced fading in a typical TOW link.
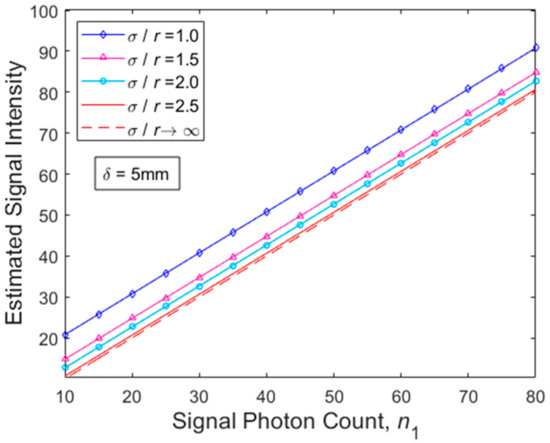
Figure 2.
Estimated signal intensity in case of weak, moderate and strong stochastic pointing errors for dermis thickness δ = 5 mm.
Figure 3 depicts quantitatively similar behavior to Figure 2, although it provides improved corresponding signal intensity results compared to Figure 2. This is because, in the case of Figure 3, the examined TOW link is assumed to be greater than 1mm in length, i.e., equal to 6 mm. Specifically, according to Equation (6), by increasing the transdermal propagating distance, , we obtain an increased beam waist on the receiver plane for a fixed transmitter divergence angle, which according to , in turn, translates into a weaker amount of pointing mismatch for the same jitter variance values. Indeed, the optimum case in Figure 3 outperforms its corresponding case in Figure 2 since, as mentioned above, the latter describes the scenario for , while Figure 3 describes the case of where the impact of pointing errors is practically getting weaker due to the increased geometric spread of the optical beam inside the skin. The latter behavior of pointing errors for different transdermal distances is consistent with findings in [16,17,18,19]. Additionally, it is highlighted that the variation just of 1 mm between TOW link lengths can be a critical issue for the total TOW performance and availability. This is also consistent with findings in many previous works including [5,7,12,13]. Therefore, the proposed MMSE estimator seems to be helpful for the design of typical TOW links.
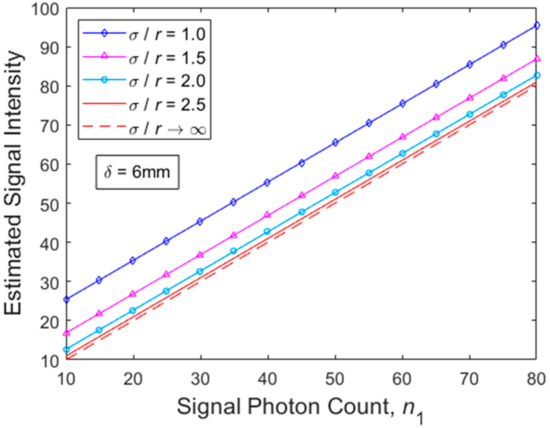
Figure 3.
Estimated signal intensity in case of negligible, weak, moderate and strong stochastic pointing errors for dermis thickness δ = 6 mm.
Figure 4 illustrates the estimated signal intensity evolution when multiple observations have been performed over a wide range of pointing-errors effect strengths. The transdermal link distance is equal to 4 mm, while the operating optical wavelength and the number of photos is fixed at 1100 nm and 60, respectively. As it was expected, we can observe increased estimated values as the observation interval is limited to fewer symbols and pointing errors are getting weaker. The latter behavior is quantitatively in a good agreement with findings in Refs. [26,27,28] which refer, however, to free-air links.
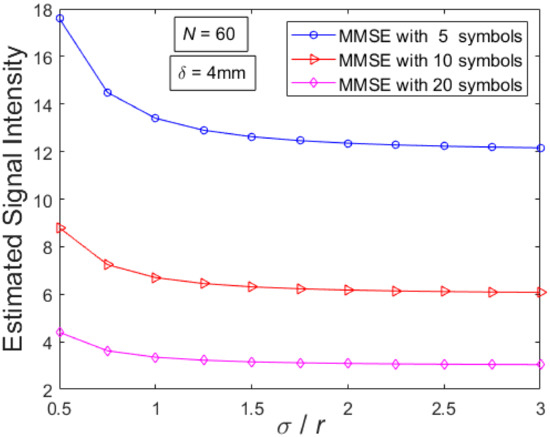
Figure 4.
Estimated signal intensity in case of weak-to-strong stochastic pointing errors for dermis thickness δ = 4 mm, N = 60, and l = 5, 10 or 20 symbols.
4. Discussion
TOW communication links for telemetry with medical implants are necessary for numerous crucial medical applications. However, apart from the deterministic impact of transdermal path loss, the stochastic misalignment-induced fading can also significantly degrade TOW performance and availability. Thus, the stochastic impact of pointing errors should be estimated in order to be counterbalanced. Bearing in mind that although the feasibility of TOW links with OOK has been demonstrated, (e.g., in [1,6] there is not any kind of TOW signal estimation which has been reported so far and little attention has been paid to the stochastic pointing error impact) in this work an estimator based on MMSE principle has been proposed for the estimation of the in-body received signal intensity for typical TOW link configurations with OOK, PIN-based optical receiver, under the presence of weak-to-extremely-strong stochastic pointing errors. Our findings demonstrate that the significant impact of stochastic pointing errors on the received signal intensity can be estimated through the relatively low computational complexity of the analysis proposed. In this context, the compact mathematical expressions derived along with the proper analytical results presented, reveal that our suggestion can be a useful tool for the estimation of stochastic pointing errors impact on the received signal intensity and thus, for the design and the establishment of typical TOW communication links for telemetry with medical implants. The analytical results presented demonstrate acceptable signal intensity estimated values for the proper operation of the examined TOW link configurations over a wide range of stochastic pointing errors strength. In fact, for typical skin thicknesses, the obtained analytical results are significantly improved as the number of photons arriving at the receiver side increases and as pointing error effects are getting weaker. Moreover, the provided analytical results are consistent with the expected fact that pointing error effects of up to 6mm skin thicknesses dominate skin-induced attenuation and thus, by increasing the transdermal distance within this typical skin thickness range, we obtain enhanced signal intensity estimated values since the beam footprint at the receiver aperture plane is getting larger, i.e., pointing errors are getting weaker. It is important to note, however, that the proposed MMSE estimator needs the knowledge of the joint statistical distribution including pointing errors. Thus, further future studies should focus on more sophisticated criteria.
5. Conclusions
In this work, we have first introduced a signal estimator motivated by MMSE principle for a PIN-based in-body receiver TOW link configuration operating with an IM/DD OOK signaling technique along with the presence of transdermal path losses and stochastic pointing errors. Bearing in mind that for optimal OOK demodulation, which is so far the only commercially viable signaling technique in the new emerging field of TOW communications mainly due to its simplicity, the receiver requires the knowledge of the instantaneous channel state; it becomes evident that the estimation of the corresponding irradiance of the signal arriving at the receiver side is a critical step for the design and the deployment of TOW communication links. In this context, compact mathematical expressions have been extracted for the estimation of the received irradiance under weak-to-strong misalignment-induced fading modeled through the suitable Rayleigh distribution. Their analytical results mainly demonstrate that the significant impact of stochastic pointing errors can be revealed and estimated through the proposed MMSE estimator over a wide misalignment-induced fading range and typical skin-channel thicknesses.
The main advantage of this method is its simplicity in comparison with other methods, such as quantifying the signal-to-noise ratio (SNR). Thus, especially when the received intensity threshold, i.e., sensitivity limit, is known, by using the proposed method we do not need to resort to more complex and cumbersome estimations. Nevertheless, based on the proposed estimator, it is a good idea for the future work to extend the signal estimation in terms of other significant performance metrics such as the SNR or the bit error rate (BER).
Author Contributions
Conceptualization, G.K.V., H.E.N., and K.A.; methodology, G.K.V., H.E.N., and K.A.; software, G.K.V.; validation, G.K.V., H.E.N., K.A., F.J., and K.K.M.R.; investigation, G.K.V., H.E.N., K.A., F.J., and K.K.M.R.; resources, G.K.V., H.E.N., K.A., F.J., and K.K.M.R.; writing—original draft preparation, G.K.V.; writing—review and editing, G.K.V. and H.E.N.; supervision, G.K.V., H.E.N., and K.A.; funding acquisition, H.E.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ajman University, grant number 2019-IDG-A-ENIT-3.
Acknowledgments
G.K.V., H.E.N., K.A., F.J., and K.K.M.R. acknowledge funding from the Ajman University under grant agreement 2019-IDG-A-ENIT-3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gil, Y.; Rotter, N.; Arnon, S. Feasibility of retroreflective transdermal optical wireless communication. Appl. Opt. 2012, 51, 4232–4239. [Google Scholar] [CrossRef] [PubMed]
- Guillory, K.S.; Misener, A.K.; Pungor, A. Hybrid RF/IR transcutaneous telemetry for power and high-bandwidth data. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 4338–4340. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Tombras, G.S. SIMO Optical Wireless Links with Nonzero Boresight Pointing Errors over M modeled Turbulence Channels. Elsevier Opt. Commun. 2017, 403, 391–400. [Google Scholar] [CrossRef]
- Abualhoul, M.Y.; Svenmarker, P.; Wang, Q.; Andersson, J.Y.; Johansson, A.J. Free space optical link for biomedical applications. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1667–1670. [Google Scholar]
- Parmentier, S.; Fontaine, R.; Roy, Y. Laser diode used in 16 Mb/s, 10 mW optical transcutaneous telemetry system. In Proceedings of the Biomedical Circuits and Systems Conference, BioCAS, Baltimore, MD, USA, 20–22 November 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 377–380. [Google Scholar]
- Liu, T.; Bihr, U.; Anis, S.M.; Ortmanns, M. Optical transcutaneous link for low power, high data rate telemetry. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), San Diego, CA, USA, 28 August–1 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3535–3538. [Google Scholar]
- Liu, T.; Anders, J.; Ortmanns, M. System level model for transcutaneous optical telemetric link. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 865–868. [Google Scholar]
- Liu, T.; Bihr, U.; Becker, J.; Anders, J.; Ortmanns, M. In vivo verification of a 100 Mbps transcutaneous optical telemetric link. In Proceedings of the Biomedical Circuits and Systems Conference (BioCAS), Lausanne, Switzerland, 22–24 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 580–583. [Google Scholar]
- Goto, K.; Nakagawa, T.; Nakamura, O.; Kawata, S. Transcutaneous photocoupler for transmission of biological signals. Opt. Lett. 2002, 27, 1797–1799. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.M.; Tillery, S.I.H.; Schwartz, A.B. Direct cortical control of 3D neuroprosthetic devices. Science 2002, 296, 1829–1832. [Google Scholar] [CrossRef] [PubMed]
- Chae, M.; Liu, W.; Yang, Z.; Chen, T.; Kim, J.; Sivaprakasam, M.; Yuce, M. A 128-channel 6mw wireless neural recording ic with on-the-fly spike sorting and uwbtansmitter. In Proceedings of the2008 IEEE International Solid-State Circuits Conference-Digest of Technical Papers, San Francisco, CA, USA, 3–7 February 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 146–603. [Google Scholar]
- Ackermann, D.M.; Smith, B.; Kilgore, K.L.; Peckham, P.H. Design of a high speed transcutaneous optical telemetry link. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 2932–2935. [Google Scholar]
- Ackermann, D.M.; Smith, B.; Wang, X.F.; Kilgore, K.L.; Peckham, P.H. Designing the optical interface of a transcutaneous optical telemetry link. IEEE Trans. Biomed. Eng. 2008, 55, 1365–1373. [Google Scholar] [CrossRef] [PubMed]
- Abita, J.L.; Schneider, W. Transdermal Optical Communications; John Hopkins APL Tech: Laurel, MD, USA, 2004; Volume 25, pp. 261–268. [Google Scholar]
- Ritter, R.; Handwerker, J.; Liu, T.; Ortmanns, M. Telemetry for implantable medical devices: Part 1-media properties and standards. IEEE Solid-State Circuits Mag. 2014, 6, 47–51. [Google Scholar]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Karagiannidis, G.K. On the impact of misalignment fading in transdermal optical wireless communications. In Proceedings of the 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Karagiannidis, G.K. Outage Performance of Transdermal Optical Wireless Links in the Presence of Pointing Errors. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Trevlakis, S.; Boulogeorgos, A.A.; Karagiannidis, G. Signal Quality Assessment for Transdermal Optical Wireless Communications under Pointing Errors. Technologies 2018, 6, 109. [Google Scholar] [CrossRef]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K. Optical wireless cochlear implants. Biomed. Opt. Express 2019, 10, 707–730. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, G.K.; Nistazakis, H.E.; Tombras, G.S.; Aidinis, K.; Jaber, F.; Rahman, M. On the use of diversity in transdermal optical wireless links with nonzero boresight pointing errors for outage performance estimation. In Proceedings of the 2018 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Rahman, K.K. Transdermal Optical Wireless Links with Multiple Receivers in the Presence of Skin-Induced Attenuation and Pointing Errors. Computation 2019, 7, 33. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Roumelas, G.D.; Jaber, F.; Rahman, K.K.M. Modulated Retro-ReflectorTransdermal Optical Wireless Communication Systems with Wavelength Diversity over Skin-Induced Attenuation and Pointing Errors. In Proceedings of the2019 IEEE International Symposium on Signal Processing and Information Technology(ISSPIT), Ajman, UAE, 10–12 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Varotsos, G.K.; Stassinakis, A.N.; Nistazakis, H.E.; Tsigopoulos, A.D.; Peppas, K.P.; Aidinis, C.J.; Tombras, G.S. Probability of fade estimation for FSO links with time dispersion and turbulence modeled with the gamma–gamma or the IK distribution. Opt. Int. J. Light Electron. Opt. 2014, 125, 7191–7197. [Google Scholar] [CrossRef]
- Manea, V.; Dragomir, R.; Puscoci, S. OOK and PPM modulations effects on bit error rate in terrestrial laser transmissions. Telecomunicat II Anul. LIV 2011, 2, 55–61. [Google Scholar]
- Elganimi, T.Y. Performance comparison between OOK, PPM and pam modulation schemes for free space optical (FSO) communication systems: Analytical study. Int. J. Comput. Appl. 2013, 79, 22–27. [Google Scholar]
- Cole, M.; Kiasaleh, K. Signal intensity estimators for free-space optical communications through turbulent atmosphere. IEEE Photonics Technol. Lett. 2004, 16, 2395–2397. [Google Scholar] [CrossRef]
- Cole, M.; Kiasaleh, K. Signal estimators for pin and APD-based free-space optical communication systems. In Proceedings of theIEEE Global Telecommunications Conference (GLOBECOM’04), Dallas, TX, USA, 29 November–3 December 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 1221–1224. [Google Scholar]
- Cole, M.; Kiasaleh, K. Signal intensity estimators for free-space optical communication with array detectors. IEEE Trans. Commun. 2007, 55, 2341–2350. [Google Scholar] [CrossRef]
- Muhammad, S.S.; Rashid, B.; Raza, A.D. Signal estimation for the gamma–gamma turbulence model. Opt. Eng. 2013, 52, 120501. [Google Scholar] [CrossRef]
- Khatoon, A.; Cowley, W.G.; Letzepis, N. Channel measurement and estimation for free space optical communications. In Proceedings of the2011 Australian Communications Theory Workshop, Melbourne, VIC, Australia, 31 January–3 February 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 112–117. [Google Scholar]
- Dabiri, M.T.; Sadough, S.M.S.; Khalighi, M.A. FSO channel estimation for OOK modulation with APD receiver over atmospheric turbulence and pointing errors. Opt. Commun. 2017, 402, 577–584. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging optical wireless communications-advances and challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Arnon, S. Effects of atmospheric turbulence and building sway on optical wireless-communication systems. Opt. Lett. 2003, 28, 129–131. [Google Scholar] [CrossRef] [PubMed]
- Farid, A.A.; Hranilovic, S. Outage capacity optimization for free space optical links with pointing errors. IEEE/OSA J. Lightwave Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 6th ed.; Academic: New York, NY, USA, 2000. [Google Scholar]
- Yang, F.; Cheng, J.; Tsiftsis, T.A. Free-space optical communication with nonzero boresight pointing errors. IEEE Trans. Commun. 2014, 62, 713–725. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Volume 3: More Special Functions; Gordon & Breach: New York, NY, USA, 1990. [Google Scholar]
- The Wolfram Functions Site. 2008. Available online: http://functions.wolfram.com (accessed on 15 June 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).