Waiter Robots Conveying Drinks
Abstract
1. Introduction
1.1. Waiter Robots in Food and Beverage (F&B) Industry
1.2. Robot Motion
2. Analyzing the Root Problem
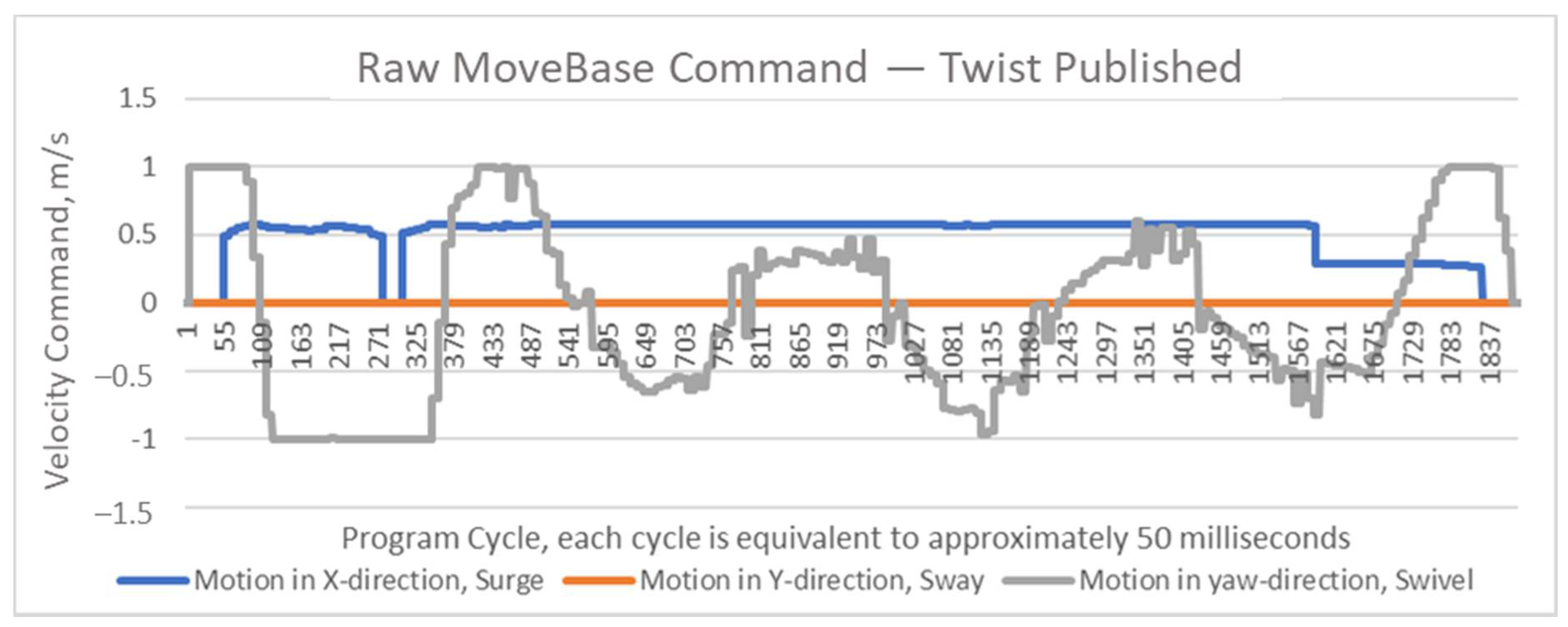
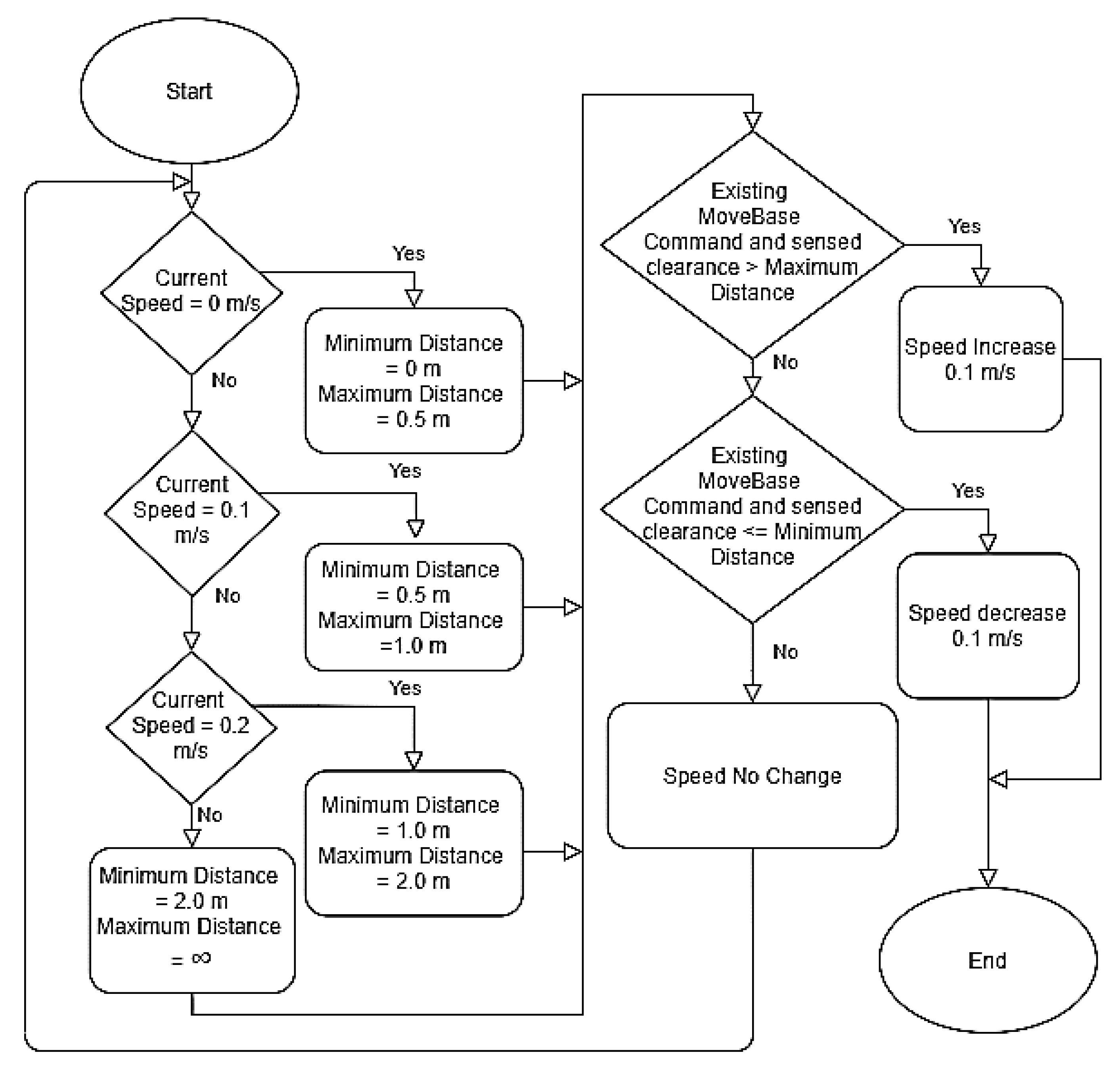
2.1. Velocity from ROS Navigation Package
2.2. Stability Versus Docking
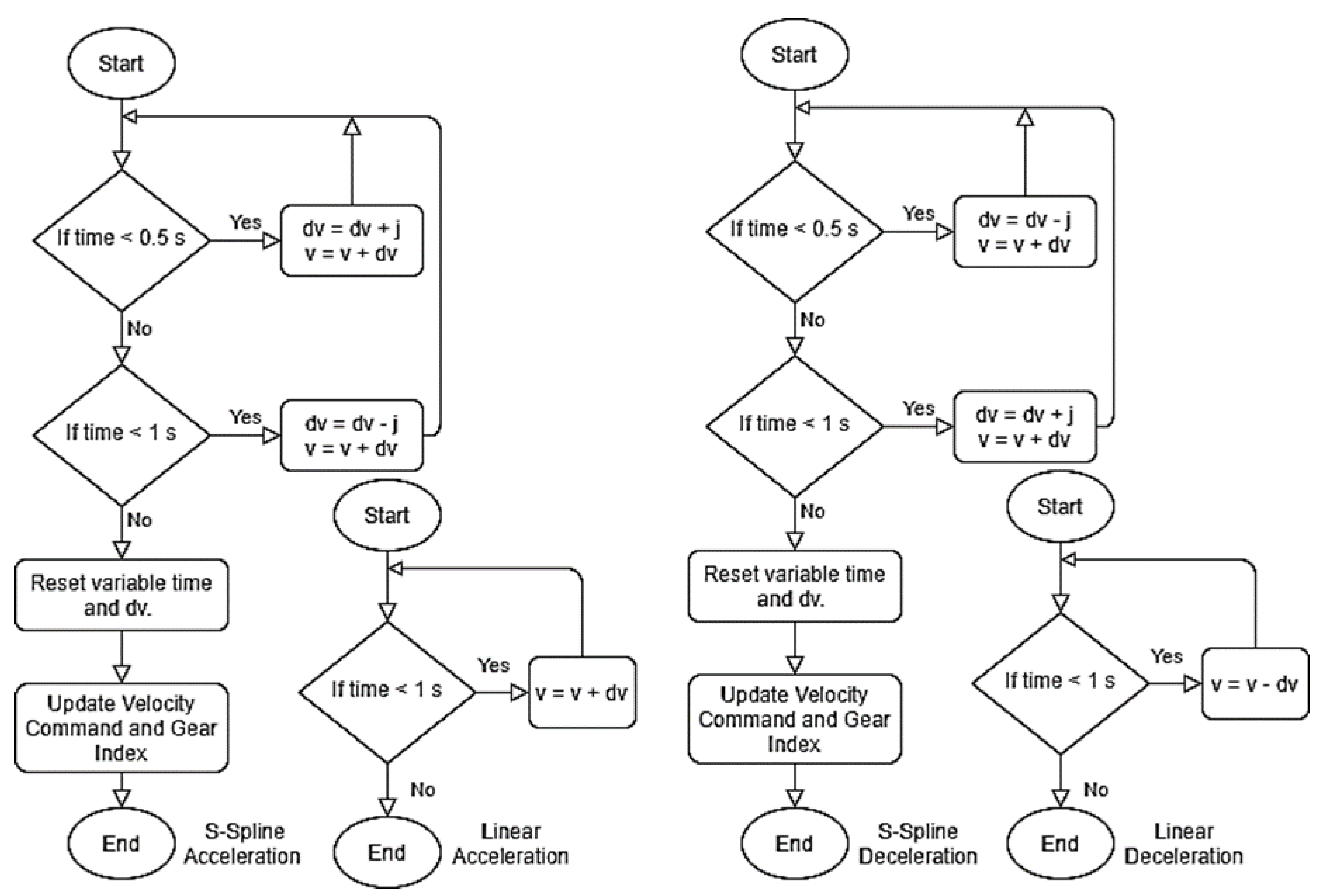
2.3. The S-Velocity Profile
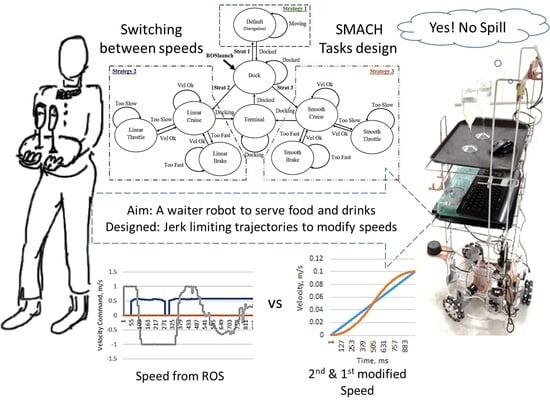
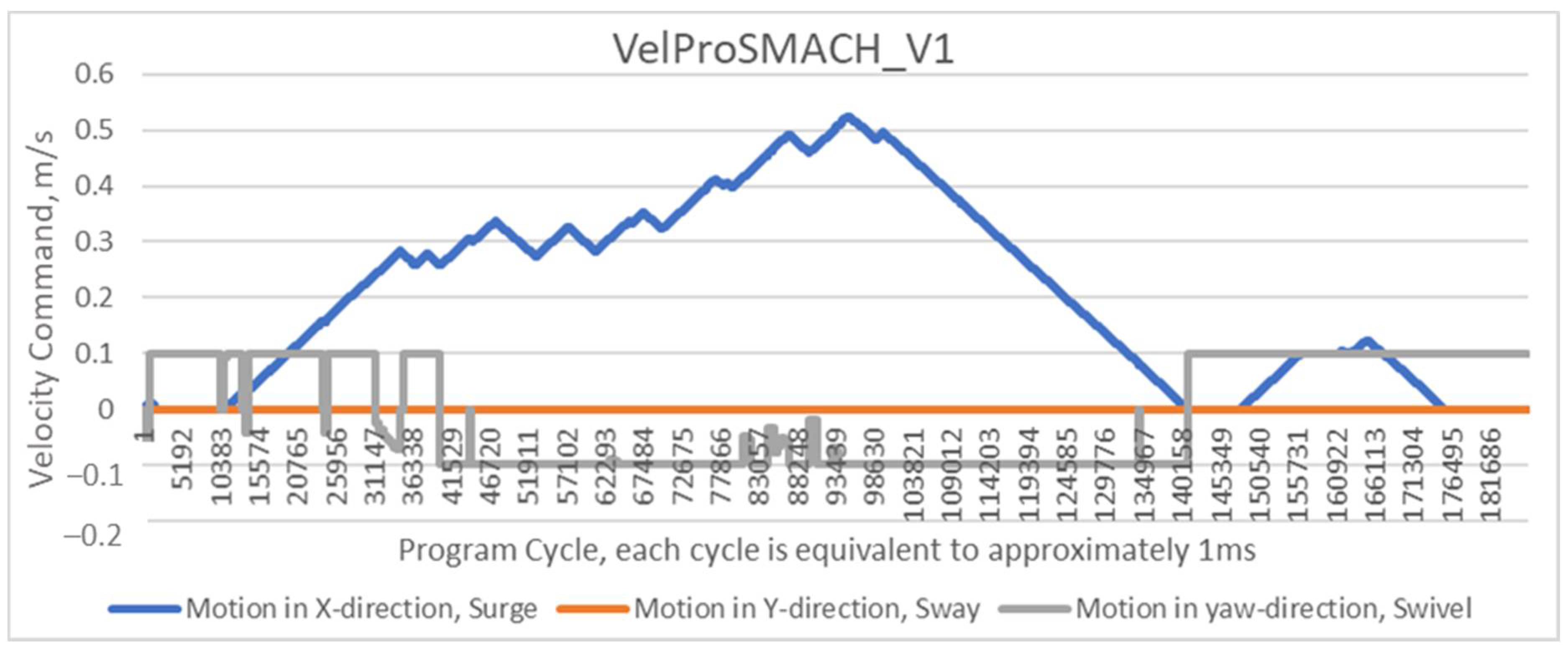
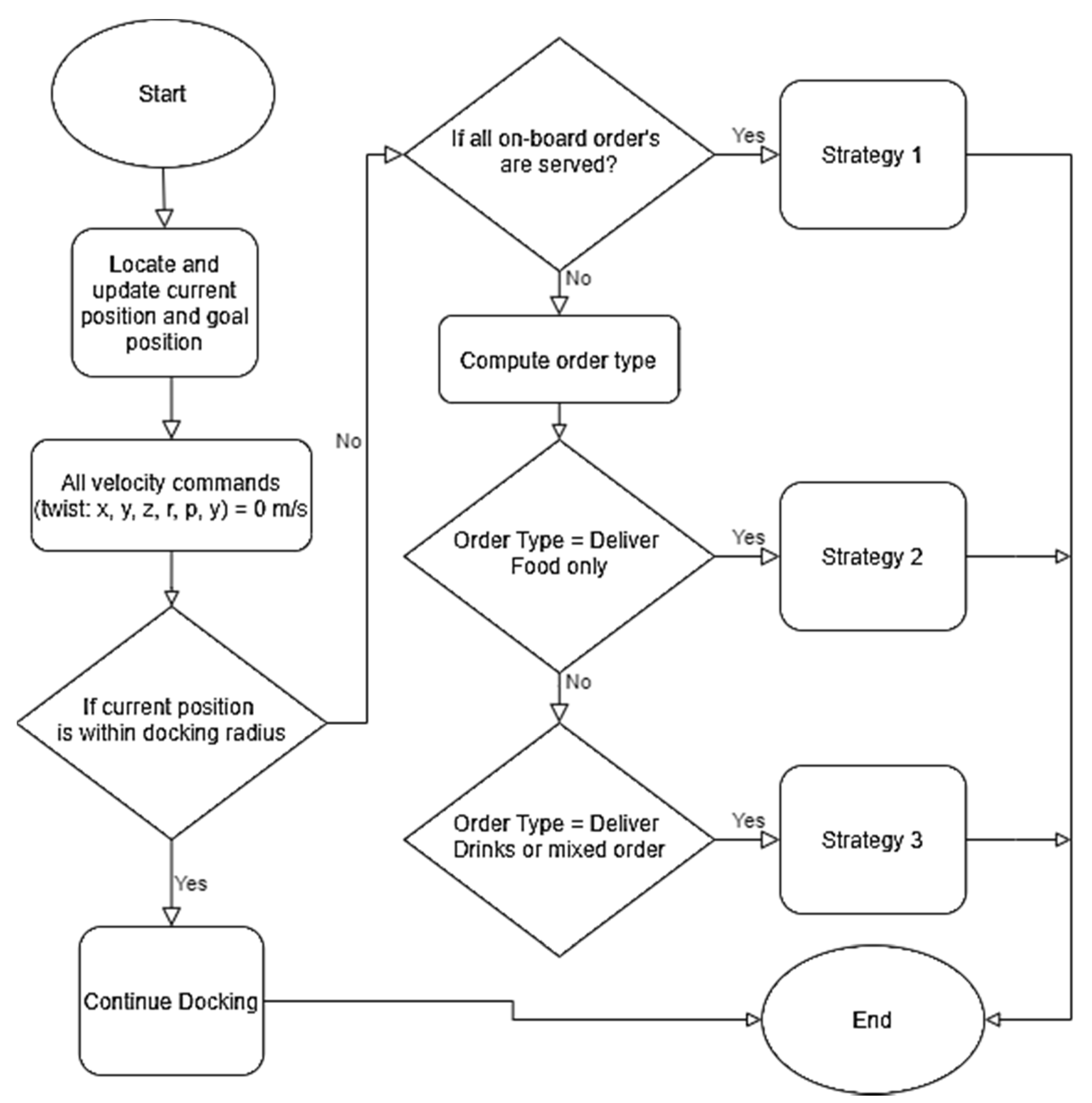
3. Designing the Waiter Robot Motion Behaviors—VelProSMACH_V2.py
3.1. Motion Behavioral Strategies
3.2. Reactive and Non-Reactive States for a Multispeed Design
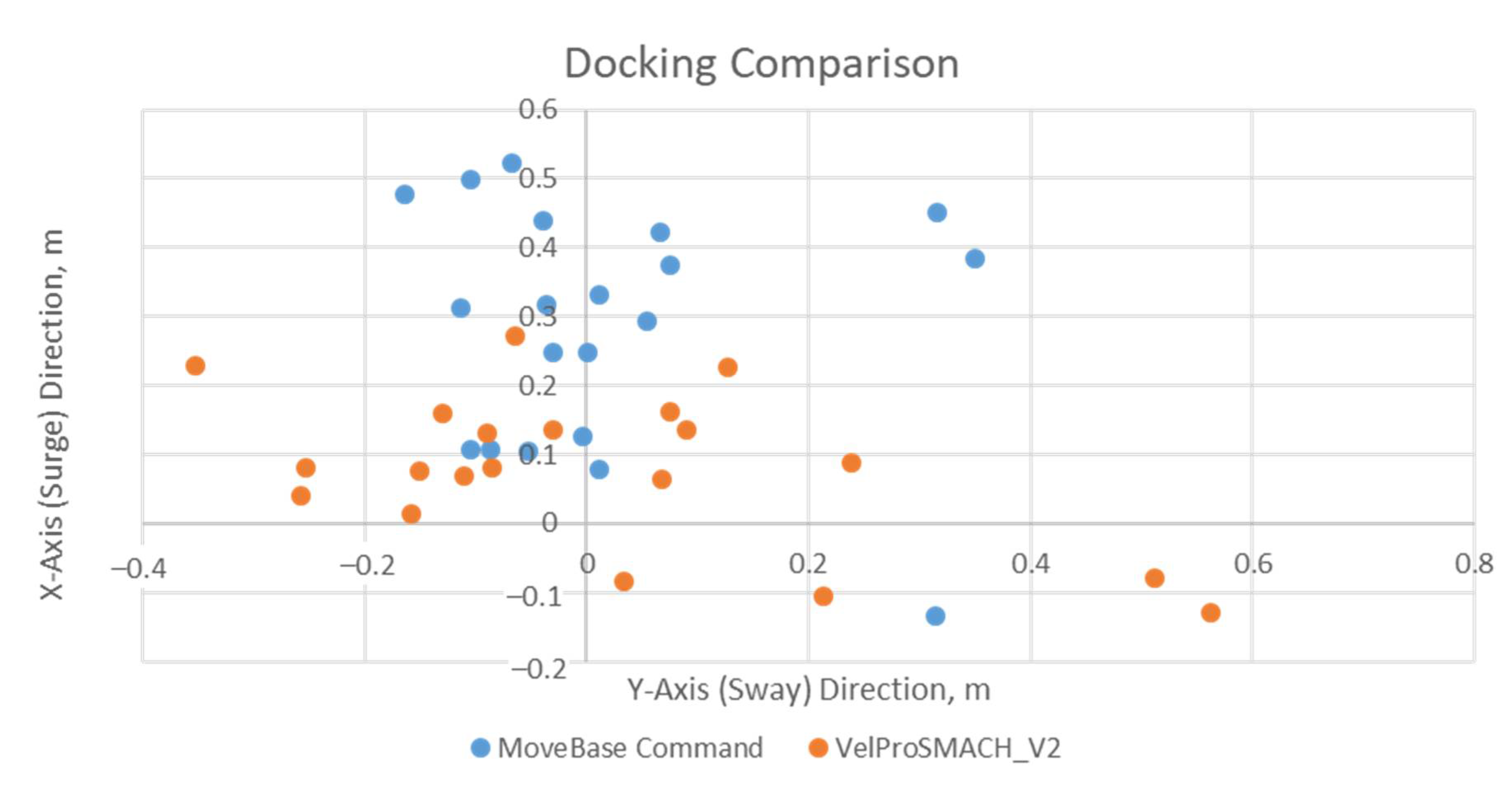
4. Comparing ROS Step-Velocity and S-Velocity
Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- MarketWatch. Service Robotics Market US $7.9 Billion Size Expected to Grow at 7% CAGR Forecast Till 2023. 2018. Available online: https://www.marketwatch.com/press-release/service-robotics-market-us-79-billion-size-expected-to-grow-at-7-cagr-forecast-till-2023-supplydemandmarketresearchcom-2019-02-01 (accessed on 22 February 2019).
- AFP/asiaone. Robots Replace Waiters in China Restaurant. 2018. Available online: https://www.asiaone.com/china/robots-replace-waiters-china-restaurant (accessed on 6 August 2018).
- Jen/shanghaiist. Guangzhou Restaurant Fires Its Robot Staff for Their Incompetence. 2018. Available online: https://shanghaiist.com/2016/04/06/restaurant_fires_incompetent_robot_staff/ (accessed on 5 May 2018).
- Lim, K. Meet Robot Waiters Le Le and Xiao Jin at Hot Pot Restaurant Pin Xian Lou. 2017. Available online: https://www.straitstimes.com/lifestyle/food/adding-byte-to-your-appetite (accessed on 8 January 2017).
- The Economic Times. Science City’s Robotic Gallery to soon Serve Food through Robots. 2018. Available online: https://economictimes.indiatimes.com/tech/science-citys-robotic-gallery-to-soon-serve-food-through-robots/robot-waiters/slideshow/66749025.cms (accessed on 22 February 2019).
- Robot Waiters will Serve You at This Restaurant in Coimbatore. 2018, p. 1. Available online: https://www.youtube.com/watch?v=PGYGUUsvtos (accessed on 22 February 2019).
- Lawson, H.; Fenyo, R.K.; Macdonald, L. Robots Serve up Food and Fun in Budapest Café. 2019. Available online: https://www.reuters.com/article/us-hungary-robotcafe/robots-serve-up-food-and-fun-in-budapest-cafe-idUSKCN1PJ1EJ (accessed on 22 February 2019).
- AFP. Nepal’s First Robot Waiter is Ready for Orders. 2018. Available online: https://phys.org/news/2018-11-nepal-robot-waiter-ready.html (accessed on 22 February 2019).
- Marder-Eppstein, E.A. Navigation. 2019. Available online: http://wiki.ros.org/navigation#Overview (accessed on 28 October 2019).
- Simon, J.S.G. Yocs_Velocity_Smoother. 2018. Available online: http://wiki.ros.org/yocs_velocity_smoother (accessed on 28 October 2019).
- ROS webpage. Available online: http://wiki.ros.org/joint_trajectory_generator (accessed on 28 October 2019).
- Eager, D.; Pendrill, A.; Reistad, N. Beyond velocity and acceleration: Jerk, snap and higher derivatives. Eur. J. Phys. 2016, 37, 065008. [Google Scholar] [CrossRef]
- Macfarlane, S.; Croft, E.A. Jerk-Bounded Manipulator Trajectory Planning: Design for Real-Time Applications. IEEE Trans. Robtics Autom. 2003, 19, 42–52. [Google Scholar] [CrossRef]
- Vass, G.; Lantosm, B.; Payandeh, S. Real-Time Optimized Robot Trajectory Planning with Jerk. In Proceedings of the IFAC Robot Control, Wroclaw, Poland, 1–3 September 2003; pp. 265–270. [Google Scholar]
- Huang, P.; Xu, Y.; Liang, B. Global Minimum-Jerk Trajectory Planning of Space Manipulator. Int. J. Control. Autom. Syst. 2006, 4, 405–413. [Google Scholar]
- Pattacini, U.; Nori, F.; Natale, L.; Metta, G.; Sandini, G. An experimental evaluation of a novel minimum-jerk cartesian controller for humanoid robots. IEEE/RSJ Int. Conf. Intell. Robot. Syst. 2010, 1668–1674. [Google Scholar] [CrossRef]
- Lin, H.I. A Fast and Unified Method to Find a Minimum-Jerk Robot Joint Trajectory Using Particle Swarm Optimization. J. Intell. Robot. Syst. 2014, 75, 379–392. [Google Scholar] [CrossRef]
- Zhao, R.; Sidobre, D. Trajectory Smoothing using jerk bounded shortcuts for service manipulator robots. IEEE/RSJ Int. Conf. Intell. Robot. Syst. 2015, 4929–4934. [Google Scholar] [CrossRef]
- Park, J.J.; Kuipers, B. A Smooth Control Law for Graceful Motion of Differential Wheeled Mobile Robots in 2D Environment. In Proceedings of the 1985 International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4896–4902. [Google Scholar]
- Korayem, M.H.; Nazemizadeh, M.; Nohooji, H.R. Smooth Jerk-Bounded Optimal Path Planning of Tricycle Wheeled Mobile Manipulators in the Presence of Environmental Obstacles. Int. J. Adv. Robot. 2012, 9, 105. [Google Scholar] [CrossRef]
- Wu, W.; Chen, H.; Woo, P. Time Optimal Path Planning for a Wheeled Mobile Robot. J. Robot. Syst. 2000, 17, 585–591. [Google Scholar] [CrossRef]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. In Proceedings of the 1985 International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 500–505. [Google Scholar]
- Wan, A.Y.S.; Foo, E.; Lai, Z.Y.; Chen, H.H.; Lau, W.S.M. Waiter Bots for Casual Restaurants. Int. J. Robot. Eng. 2019, 4, 018. [Google Scholar] [CrossRef]
- Bohren, J. Smach. 2018. Available online: http://wiki.ros.org/smach (accessed on 28 October 2019).
- Ben-Ari, M.; Mondada, F. Elements of Robotics; Springer Nature: Cham, Switzerland, 2017. [Google Scholar]
- Cheong, A.; Lau, M.W.S.; Foo, E.; Hedley, J.; Bo, J.W. Development of a Robotic Waiter System. IFAC Pap. Online 2016, 49, 681–686. [Google Scholar] [CrossRef]




| S\N | Performance Outcome (Y/N) | Moving Time (Min: Sec) | ||
|---|---|---|---|---|
| Spill? | Docked? | Crashed? | ||
| 1 | N | N | N | 2:18.06 |
| 2 | N | N | N | 3:52.85 |
| 3 | N | N | Y | 0:12.73 |
| 4 | N | N | N | Over 5 min |
| 5 | N | N | N | 02:58.61 |
| 6 | N | N | Y | 0:19.02 |
| 7 | N | N | Y | 0:50.97 |
| 8 | N | N | Y | 0:17.05 |
| 9 | N | N | N | 1:33.24 |
| 10 | N | N | Y | 0:43.26 |
| S\N | Performance Outcome (Y/N) | Docked Pose Wrt Goal Pose (mm) | Moving Time (s) | ||||
|---|---|---|---|---|---|---|---|
| Spill? | Docked? | Crashed? | X | Y | R | ||
| 1 | Y | Y | N | 0.523 | −0.068 | 0.527 | 24.5 |
| 2 | Y | Y | N | 0.105 | −0.053 | 0.118 | 22.7 |
| 3 | Y | Y | N | 0.318 | −0.036 | 0.320 | 22.8 |
| 4 | Y | Y | N | 0.247 | 0.001 | 0.247 | 22.8 |
| 5 | Y | Y | N | 0.106 | −0.087 | 0.137 | 22.3 |
| 6 | Y | Y | N | 0.478 | −0.164 | 0.505 | 22.7 |
| 7 | Y | Y | N | 0.078 | 0.012 | 0.079 | 27.0 |
| 8 | Y | Y | N | 0.294 | 0.054 | 0.299 | 30.7 |
| 9 | Y | Y | N | 0.331 | 0.012 | 0.331 | 22.7 |
| 10 | Y | Y | N | 0.438 | −0.039 | 0.440 | 22.5 |
| 11 | Y | Y | N | 0.374 | 0.075 | 0.382 | 29.8 |
| 12 | Y | Y | N | 0.499 | −0.105 | 0.510 | 20.9 |
| 13 | Y | Y | N | 0.249 | −0.030 | 0.251 | 21.8 |
| 14 | Y | Y | N | 0.312 | −0.113 | 0.332 | 28.3 |
| 15 | Y | Y | N | 0.423 | 0.067 | 0.428 | 31.6 |
| 16 | Y | Y | N | −0.133 | 0.314 | 0.340 | 22.1 |
| 17 | Y | Y | N | 0.384 | 0.350 | 0.519 | 33.7 |
| 18 | Y | Y | N | 0.106 | −0.104 | 0.148 | 21.2 |
| 19 | Y | Y | N | 0.450 | 0.316 | 0.550 | 22.8 |
| 20 | Y | Y | N | 0.125 | −0.004 | 0.125 | 22.2 |
| S\N | Performance Outcome | Docked Pose Wrt Goal Pose (mm) | Moving Time (s) | ||||
|---|---|---|---|---|---|---|---|
| Spill? | Docked? | Crashed? | X | Y | R | ||
| 1 | N | Y | N | 0.127 | 0.227 | 0.261 | 54.5 |
| 2 | N | Y | N | 0.563 | −0.129 | 0.578 | 51.4 |
| 3 | N | Y | N | −0.085 | 0.080 | 0.117 | 37.6 |
| 4 | N | Y | N | −0.110 | 0.070 | 0.130 | 37.7 |
| 5 | N | Y | N | 0.512 | −0.080 | 0.518 | 41.3 |
| 6 | N | Y | N | −0.253 | 0.082 | 0.266 | 30.2 |
| 7 | N | Y | N | 0.239 | 0.087 | 0.255 | 35.0 |
| 8 | N | Y | N | −0.065 | 0.273 | 0.280 | 39.0 |
| 9 | N | Y | N | −0.150 | 0.075 | 0.168 | 34.8 |
| 10 | N | Y | N | −0.090 | 0.130 | 0.158 | 29.9 |
| 11 | N | Y | N | 0.090 | 0.135 | 0.162 | 30.1 |
| 12 | N | Y | N | −0.130 | 0.160 | 0.206 | 36.6 |
| 13 | N | Y | N | 0.075 | 0.162 | 0.179 | 32.7 |
| 14 | N | Y | N | 0.214 | −0.106 | 0.239 | 42.4 |
| 15 | N | Y | N | −0.158 | 0.014 | 0.159 | 56.9 |
| 16 | N | Y | N | −0.353 | 0.228 | 0.421 | 37.0 |
| 17 | N | Y | N | 0.068 | 0.063 | 0.093 | 30.9 |
| 18 | N | Y | N | 0.033 | −0.083 | 0.089 | 32.4 |
| 19 | N | Y | N | −0.258 | 0.040 | 0.261 | 28.3 |
| 20 | N | Y | N | −0.030 | 0.135 | 0.138 | 30.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, A.Y.S.; Soong, Y.D.; Foo, E.; Wong, W.L.E.; Lau, W.S.M. Waiter Robots Conveying Drinks. Technologies 2020, 8, 44. https://doi.org/10.3390/technologies8030044
Wan AYS, Soong YD, Foo E, Wong WLE, Lau WSM. Waiter Robots Conveying Drinks. Technologies. 2020; 8(3):44. https://doi.org/10.3390/technologies8030044
Chicago/Turabian StyleWan, Ash Yaw Sang, Yi De Soong, Edwin Foo, Wai Leong Eugene Wong, and Wai Shing Michael Lau. 2020. "Waiter Robots Conveying Drinks" Technologies 8, no. 3: 44. https://doi.org/10.3390/technologies8030044
APA StyleWan, A. Y. S., Soong, Y. D., Foo, E., Wong, W. L. E., & Lau, W. S. M. (2020). Waiter Robots Conveying Drinks. Technologies, 8(3), 44. https://doi.org/10.3390/technologies8030044