An Improved Calculation Model for the Prediction of the Wear of Coated Electrical Contacts
Abstract
1. Introduction
- Micro deformation: the surface is plastically deformed in the form of grooves and scratches.
- Micro ploughing: the surface is plowed by hard particles due to such as the oxides of metal wear debris or the contaminants from the environment.
- Micro cutting: the adhesive junctions are broken down between the surfaces thereby resulting in mechanical failure of the contacting asperities.
- Micro cracking: the nucleation and propagation of the surface cracks and voids generate the particles between the surfaces.
2. Materials and Methods
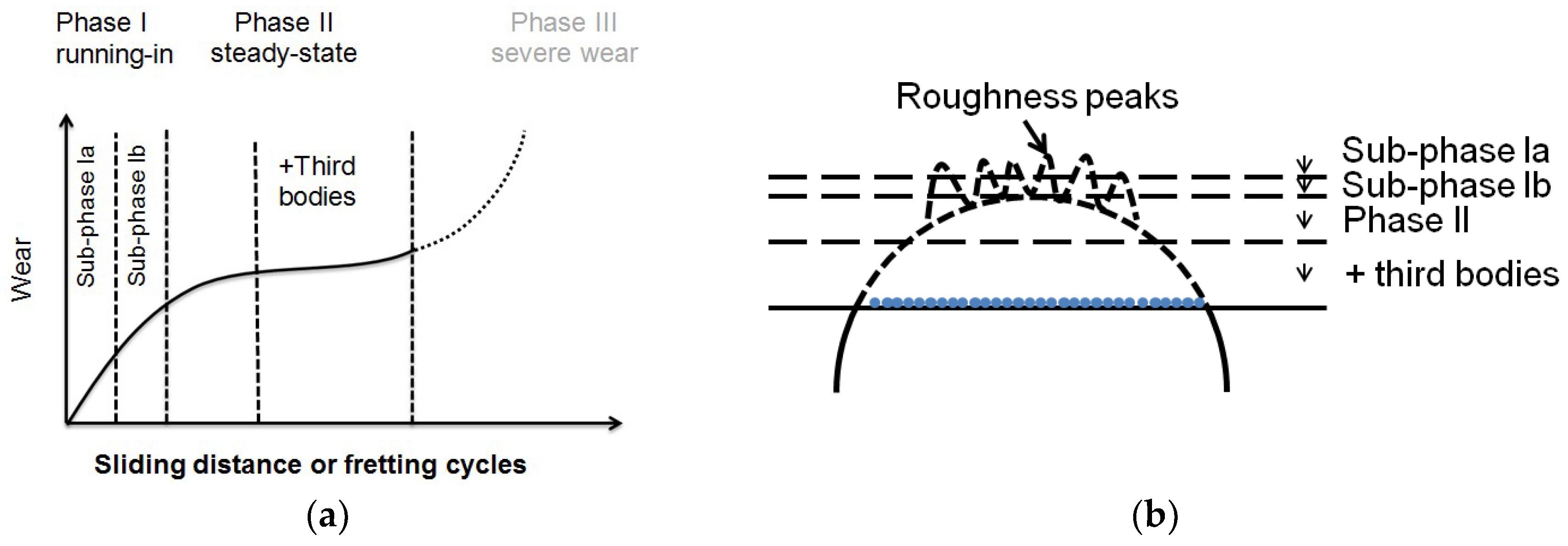
- Calculation of the deformation after the contact of the two contact parts considering the surface roughness with assistance of finite element analysis (FEA), involving the elastic-plastic material behavior and the surface roughness. The geometry is drawn corresponding to the real samples. The roughness is defined on the flat part according to the roughness measured with a confocal microscope μsurf explorer from Nanofocus AG, Germany. According to [16], the roughness structure for the tested samples can be simplified as triangular prisms. The boundary conditions are set based on the condition in the test.
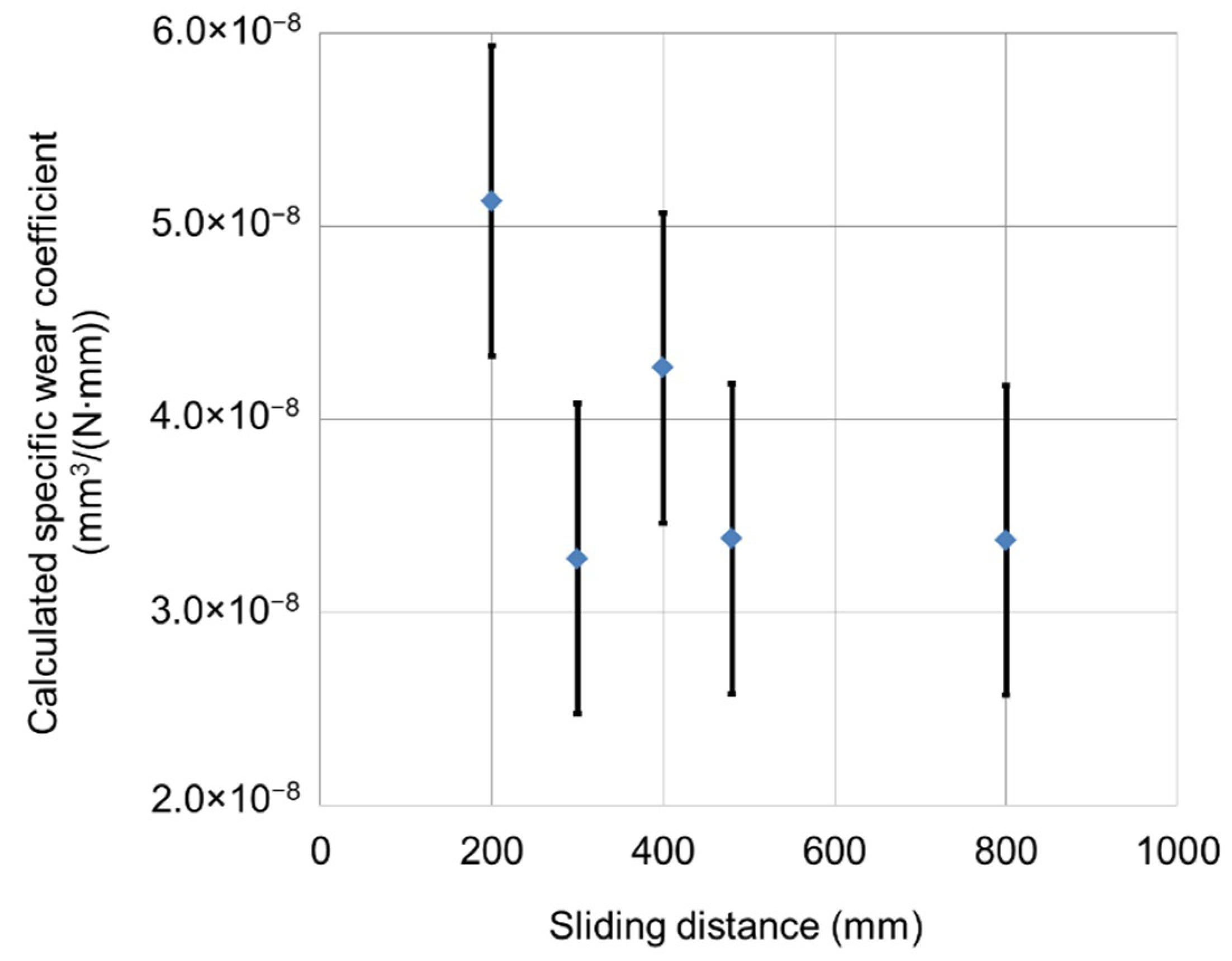
- Calculation of specific wear coefficient using data in phase I. For this purpose, more wear and fretting corrosion tests are conducted with the critical arrangement for different predefined fretting cycles in the running-in phase. The thickness reduction is measured after the tests. According to [16], the specific wear coefficient kcal, using the data in Phase I and considering the topography of the surface and its change due to the plastic deformation, can be calculated as following:where h1 is the wear depth in Phase I based on an assumption that every triangular prism experiences the same wear depth in the wear process, m is the number of triangular prisms involved in contact area, s1 is the sliding distance in Phase I, Rsm is the measured average groove width, Rk is the measured core roughness depth, h0,i is the reduction of coating thickness parallel to the normal force simulated by FEA, D0,i is the length of the deformed triangular prism simulated by FEA.
- Modification of the calculated specific wear coefficient according to the topography: simplification of the roughness on the flat part and the gaps on the roughness ribs following Equation (4):where, according to [16], αsimplification and αgap are 0.5 and 0.9, respectively.
- Involving the influence of the third bodies after a long-term sliding:
- Prediction of the wear curve:
3. Results
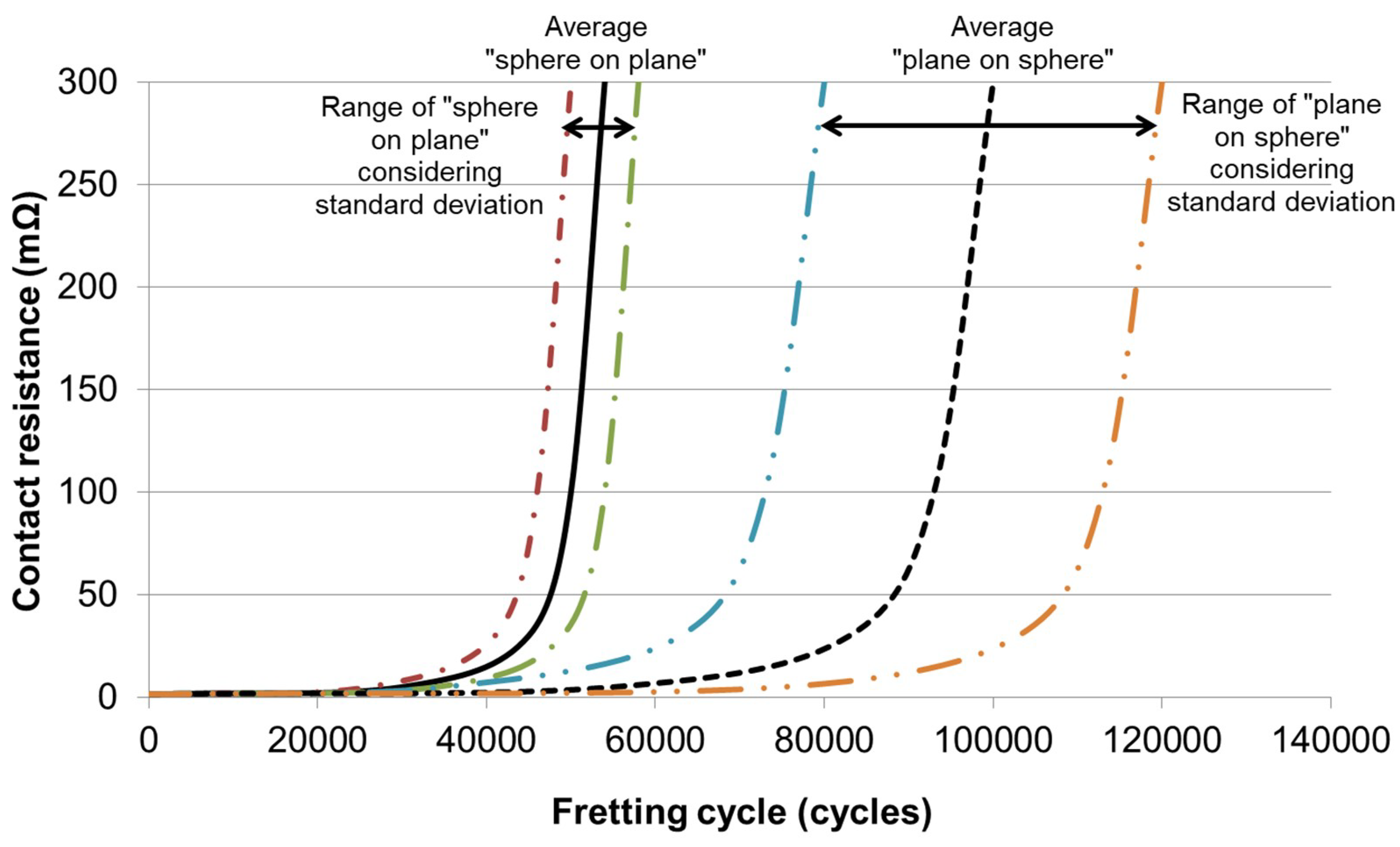
3.1. Lifetime of Electrical Contacts Tested with Different Sample Arrangements
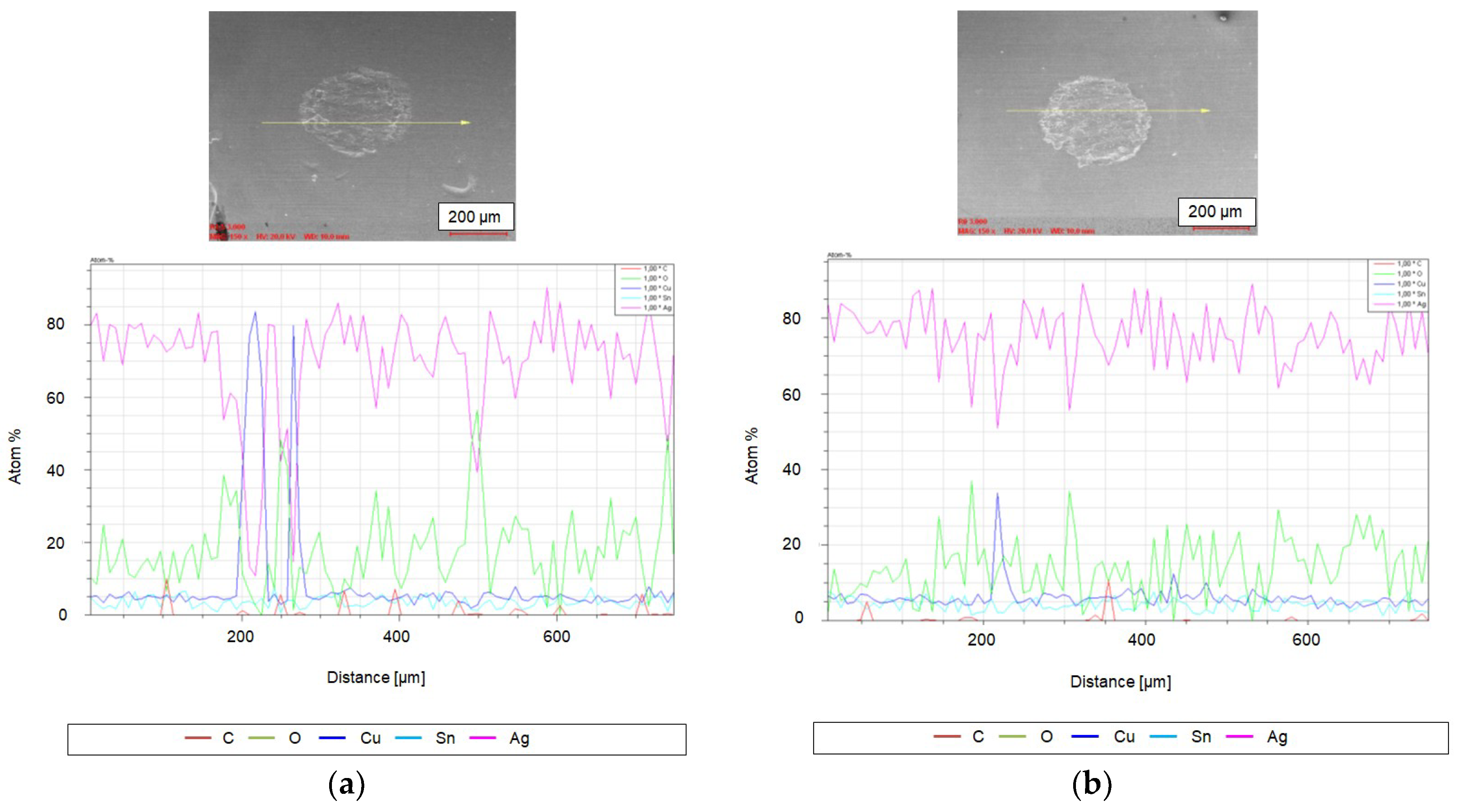
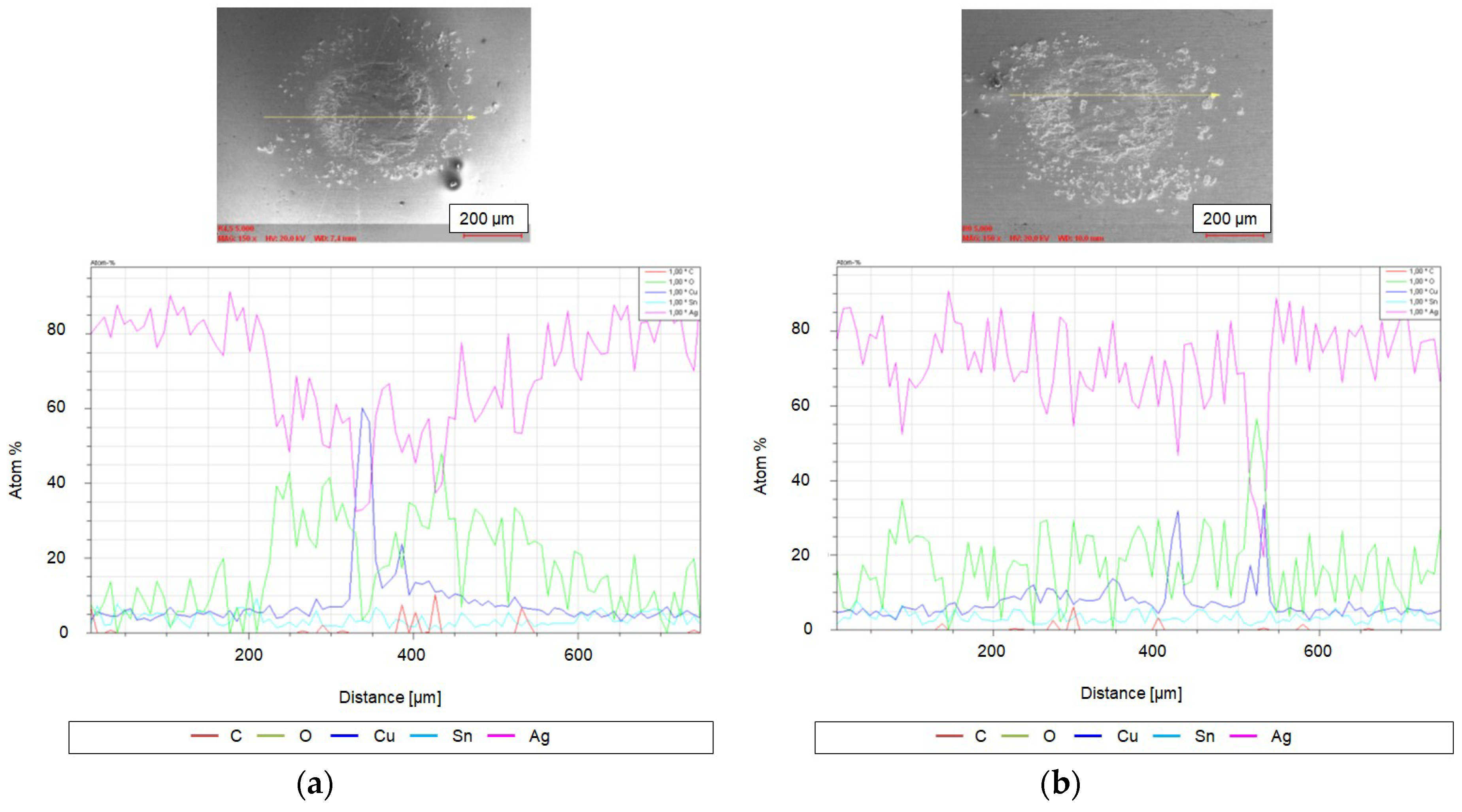
3.2. Element Content in Contact Area of Samples with Critical Sample Arrangement
3.3. Distribution of Wear Debris after the Wear and Fretting Corrosion Test
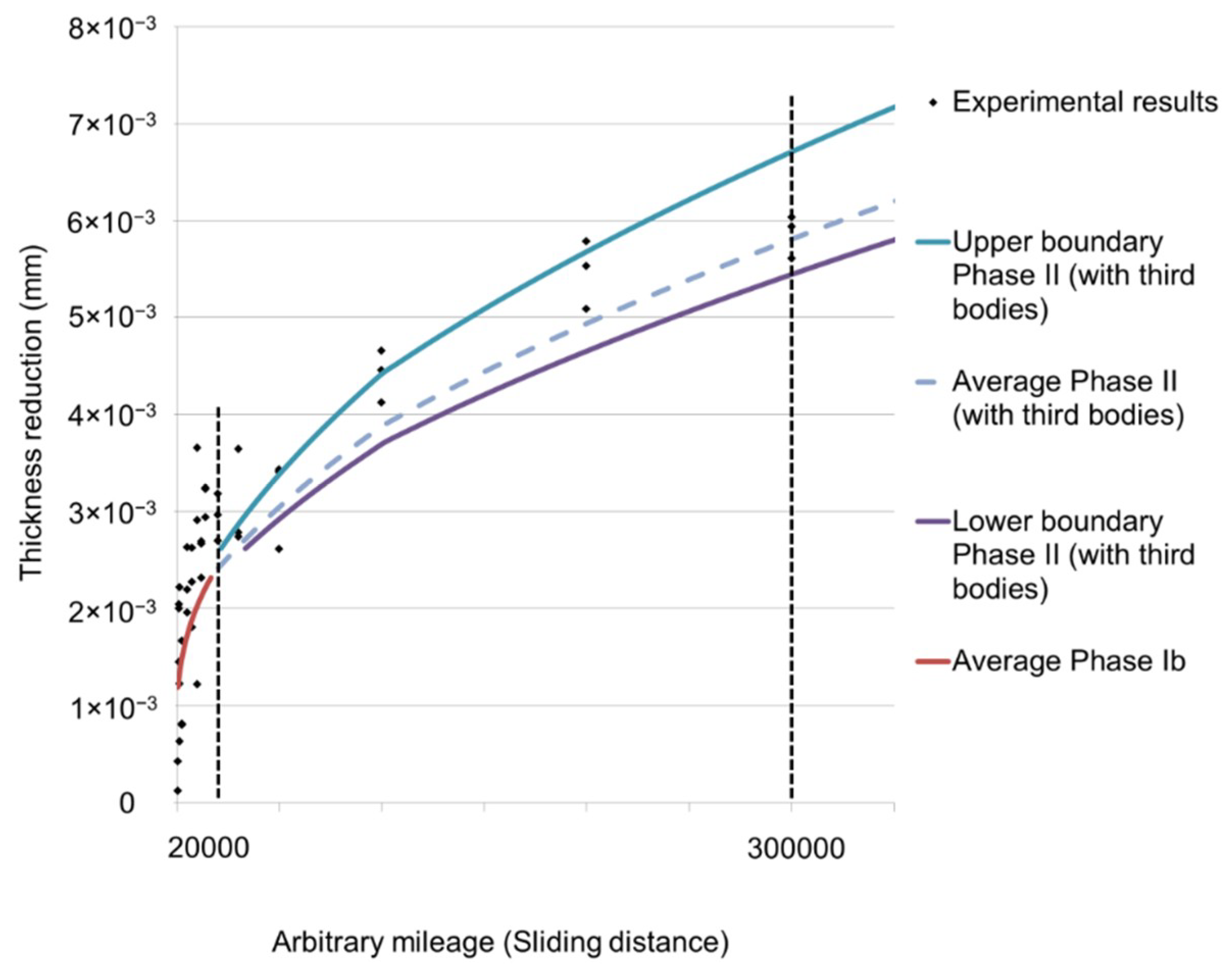
3.4. Thickness Reduction of the Samples with Critical Arrangement
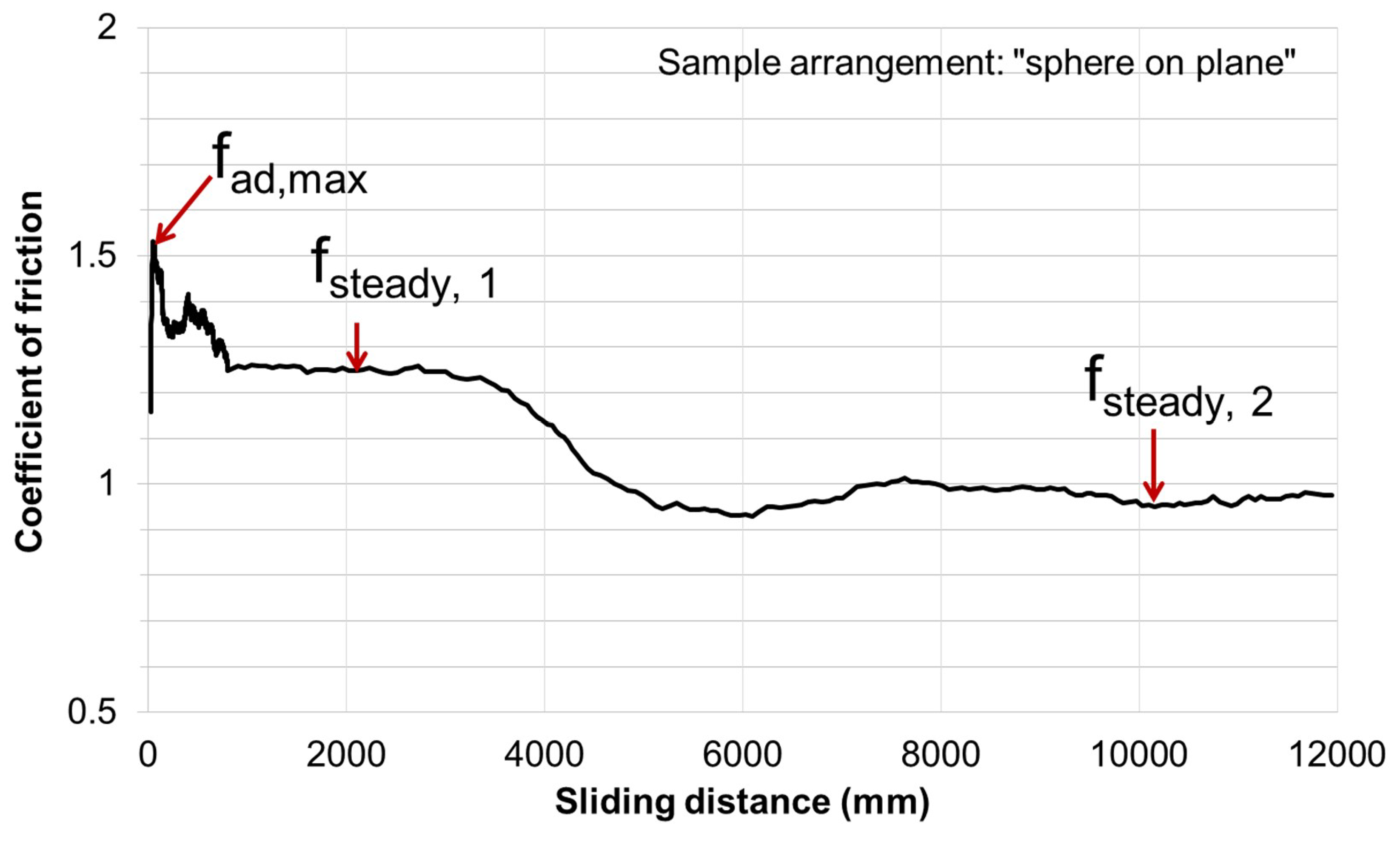
3.5. Coefficient of Friction of Samples with Critical Arrangement
4. Discussion
4.1. Calculation and Modification of Specific Wear Coefficient
4.2. Wear Curves
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zmitrowicz, A. Wear debris: a review of properties and constitutive models. J. Theor. Appl. Mech. 2005, 43, 3–35. [Google Scholar]
- Suh, N.P.; Sin, H.-C. On the genesis of friction and its effect on wear. In Solid Contact and Lubrication; Cheng, H.S., Keer, L.M., Eds.; American Society of Mechanical Engineers: New York, NY, USA, 1980; Volume 39, pp. 167–183. [Google Scholar]
- Song, J.; Schinow, V. Correlation between friction and wear properties and electrical performance of silver coated electrical connectors. Wear 2015, 330–331, 400–405. [Google Scholar] [CrossRef]
- Zum Gahr, K.H. Abrasiver Verschleiß metallischer Werkstoffe; VDI-Verlag: Düsseldorf, Germany, 1981. [Google Scholar]
- Zanoria, E.S.; Danyluk, S.; Mcnallan, M.J. Formation of cylindrical sliding-wear debris on silicon in humid conditions and elevated temperatures. Tribol. Trans. 1995, 38, 721–727. [Google Scholar] [CrossRef]
- Hintikka, J.; Lehtovaara, A.; Mäntylä, A. Third particle ejection effects on wear with quenched and tempered steel fretting contact. Tribol. Trans. 2016, 60, 70–78. [Google Scholar] [CrossRef]
- Niccolini, E.; Berthier, Y. Wheel–rail adhesion: laboratory study of “natural” third body role on locomotives wheels and rails. Wear 2005, 258, 1172–1178. [Google Scholar] [CrossRef]
- Fouvry, S.; Liskiewicz, T.; Kapsa, Ph.; Hannel, S.; Sauger, E. An energy description of wear mechanisms and its applications to oscillating sliding contacts. Wear 2003, 255, 287–298. [Google Scholar] [CrossRef]
- Fouvry, S.; Laporte, J.; Perrinet, O.; Jedrzejczyk, P.; Graton, O.; Alquier, O.; Sautel, J. Fretting Wear of Low Current Electrical Contacts: Quantification of Electrical Endurance. In Proceedings of the 63rd IEEE Holm Conference on Electrical Contacts, Denver, CO, USA, 10–13 September 2017; pp. 1–11. [Google Scholar] [CrossRef]
- Arnaud, P.; Fouvry, S.; Garcin, S. A numerical simulation of fretting wear profile taking account of the evolution of third body layer. Wear 2017, 376–377, 1475–1488. [Google Scholar] [CrossRef]
- Terwey, J.T.; Poll, G. Energy based modelling of adhesive wear in the mixed lubrication regime. In Proceedings of the 60th German Tribology Conference 2019 (60. Tribologie-Fachtagung 2019), Göttingen, Germany, 23–25 September 2018. Presentation No. 61. [Google Scholar]
- Fleischer, G.; Wolmirstedt, H.G.; Thum, H. Verschleiß und Zuverlässigkeit; VEB Verlag Technik: Berlin, Germany, 1980. [Google Scholar]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Foko Foko, F.; Heimes, J.; Magyar, B.; Sauer, B. Reibenergiebasierte Verschleißsimulation für Radialwellendichtringe. In Proceedings of the 60th German Tribology Conference 2019 (60. Tribologie-Fachtagung 2019), Göttingen, Germany, 23–25 September 2018. Presentation No. 47. [Google Scholar]
- Yuan, H.; Song, J.; Schinow, V. A Modification of the Calculation Model for the Prediction of the Wear of Silver-Coated Electrical Contacts with Consideration of Third Bodies. In Proceedings of the 64th IEEE Holm Conference on Electrical Contacts, Albuquerque, NM, USA, 14–18 October 2018; pp. 310–316. [Google Scholar] [CrossRef]
- Yuan, H.; Song, J.; Schinow, V. Simulation methodology for prediction of the wear on silver-coated electrical contacts with a sphere/flat configuration. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 364–374. [Google Scholar] [CrossRef]
- Song, J.; Schinow, V.; Yuan, H. Third bodies in electrical contacts — Wear and electrical performance. In Proceedings of the 63rd IEEE Holm Conference on Electrical Contacts, Denver, CO, USA, 10–13 September 2017; pp. 117–124. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Amplitude peak-peak | 200 µm |
| Normal force | 3 N |
| Temperature | ambient temperature (20 °C~23 °C) |
| Fretting frequency | 1 Hz |
| Relative humidity | 35~45% |
| Arrangement | ||
|---|---|---|
| Sphere on Plane | Plane on Sphere | |
| Lifetime (cycles) | 5.4 × 104 | 1.3 × 105 |
| 5.1 × 104 | 5.9 × 104 | |
| 5.0 × 104 | 1.0 × 105 | |
| 5.5 × 104 | 1.0 × 105 | |
| 5.2 × 104 | 1.2 × 105 | |
| 6.2 × 104 | 9.8 × 104 | |
| Average lifetime (cycles) | 5.4 × 104 | 1.0 × 105 |
| Standard deviation (cycles) | 4 × 103 | 2 × 104 |
| fad,max | fsteady,1 | αthird-body,1 | Average αthird-body,1 | fsteady,2 | αthird-body,2 | Average αthird-body,2 |
|---|---|---|---|---|---|---|
| 1.5 | 1.25 | 0.83 | 0.81 | 0.95 | 0.63 | 0.64 |
| 1.7 | 1.35 | 0.79 | 1.1 | 0.65 | ||
| 1.6 | 1.30 | 0.81 | 1.0 | 0.62 |
| Maximum | 2.3 × 10−8 | 1.9 × 10−8 | 1.5 × 10−8 |
| Minimum | 1.5 × 10−8 | 1.2 × 10−8 | 9.4 × 10−9 |
| Average | 1.8 × 10−8 | 1.4 × 10−8 | 1.1 × 10−8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Song, J. An Improved Calculation Model for the Prediction of the Wear of Coated Electrical Contacts. Technologies 2019, 7, 77. https://doi.org/10.3390/technologies7040077
Yuan H, Song J. An Improved Calculation Model for the Prediction of the Wear of Coated Electrical Contacts. Technologies. 2019; 7(4):77. https://doi.org/10.3390/technologies7040077
Chicago/Turabian StyleYuan, Haomiao, and Jian Song. 2019. "An Improved Calculation Model for the Prediction of the Wear of Coated Electrical Contacts" Technologies 7, no. 4: 77. https://doi.org/10.3390/technologies7040077
APA StyleYuan, H., & Song, J. (2019). An Improved Calculation Model for the Prediction of the Wear of Coated Electrical Contacts. Technologies, 7(4), 77. https://doi.org/10.3390/technologies7040077





