Abstract
The convention for the safeguarding of Intangible Cultural Heritage (ICH) by UNESCO highlights the equal importance of intangible elements of cultural heritage to tangible ones. One of the most important domains of ICH is folkloric dances. A dance choreography is a time-varying 3D process (4D modelling), which includes dynamic co-interactions among different actors, emotional and style attributes, and supplementary elements, such as music tempo and costumes. Presently, research focuses on the use of depth acquisition sensors, to handle kinesiology issues. The extraction of skeleton data, in real time, contains a significant amount of information (data and metadata), allowing for various choreography-based analytics. In this paper, a trajectory interpretation method for Greek folkloric dances is presented. We focus on matching trajectories’ patterns, existing in a choreographic database, to new ones originating from different sensor types such as VICON and Kinect II. Then, a Dynamic Time Warping (DTW) algorithm is proposed to find out similarities/dissimilarities among the choreographic trajectories. The goal is to evaluate the performance of the low-cost Kinect II sensor for dance choreography compared to the accurate but of high-cost VICON-based choreographies. Experimental results on real-life dances are carried out to show the effectiveness of the proposed DTW methodology and the ability of Kinect II to localize dances in 3D space.
1. Introduction
Intangible Cultural Heritage (ICH) is a prominent element of people’s cultural identity as well as a significant aspect for growth and sustainability [1]. The expression of identity through Intangible Cultural Heritage takes many forms, among which folkloric dances hold a central position [2]. It is reasonable to consider that analyzing choreographic sequences is essentially a multidimensional modelling problem, given that both temporal and spatial factors should be taken into account. Research has been published in the literature pertaining to ICH preservation which focuses on the time element [3,4,5,6]. Typical preservation acts include digitization, modelling, and documentation.
Another important factor in preserving any type of performing arts, would be the development of an interactive framework that enhances the learning procedure of folklore dances. The recent advances in depth sensors, which have concluded to the development of low-cost 3D capturing systems, such as Microsoft Kinect [7] or Intel RealSense [8], permit easy capturing of human skeleton joints, in 3D space, which are then properly analyzed to extract dance kinematics [9]. The preservation of folk dances can be facilitated by modern Information and Communication Technologies by leveraging recent developments in a variety of areas, such as storage, image and video processing, machine learning, cloud computing, crowdsourcing, and automatic semantic annotation, to name a few [10].
Nevertheless, the digitization and the modelling of the information remains the most valuable task. Due to the tremendous growth of the motion-capturing systems, depth cameras are a popular solution employed in many cases, because of their reliability, cost-effectiveness, and usability and despite their limited range. Kinect is one of the most recognizable sensors in this category and in the choreography context can be used for recording sequences of points in 3D space for body joints at certain moments in time. Several recent research papers in the literature make use of such sensors for dance analysis, for example educational dance applications using sensors and gaming technologies [11], trajectory interpretation [12], advanced skeletal joints tracking [13], action or activity recognition [14,15,16,17,18,19,20], key pose identification [21] and key pose analysis [22]. Apart from Kinect, another popular alternative motion capture system is VICON which is significantly more sophisticated and accurate [9,23,24].
In [25], a comparison between abilities of the Kinect and VICON for gait analysis is introduced in the orthopedic and neurologic field. In [26], the authors focus on the precision of the Kinect and the VICON motion-capturing systems creating an application for rehabilitation treatments. In [27], the authors propose that the Kinect was able to accurately measure timing of clinically relevant movements in people with Parkinson disease. Contrary to the linear regression-based approaches that have been carried out in the bio-medical field [25,26,27] regarding the similarities/dissimilarities and the precision of the adopted motion-capturing system, in this work we follow a Dynamic Time Warping (DTW) approach in the kinesiology field. Moreover, the aforementioned approaches pertain to simple movement sequences, i.e., knee flexion and extension, hip flexion and extension instead of our proposed choreographic dataset which includes more complex movements that combine several joints variations (see Table 1).

Table 1.
Greek folklore dances and the main choreographic steps.
In [28], the authors introduce a motion classification framework using DTW. The aforementioned work uses DTW algorithm to classify motion sequences using the minimum set of bones (7 body joints). On contrary, our proposed framework uses 25 body joints analyzing the motion sequences using the DTW and Move-Split-Merge algorithms, respectively. In [29], the authors propose an algorithm for 3D motion recognition which allows extensions of DTW with multiple sensors (view-point-weighted, fully weighted and motion-weighted) and can be employed in a variety of settings. DTW algorithm has also adopted to extract the kinesiology details from video sequences. In [30], the authors propose a video human motion recognition approach, which uses DTW to match motion projections in non-linear manifold space. In [31], the authors present a technique for motion pattern and action recognition, which employs DTW to match motion projections in Isomap non-linear manifold space.
Our proposed framework focuses on the similarity assessment of folkloric dances, using data from heterogeneous sources; i.e., data from high-cost devices such as VICON and low-cost devices such as Kinect II using predefined choreographic sequences. Research outcomes target on the underlying relationships among dances captured using the VICON and Kinect systems (see Table 2).

Table 2.
Summary of VICON and Kinect II sensing.
VICON is a high-cost, motion-capturing system, which exploits markers attached on dancers’ joints to extract motion variations and the trajectory of a choreography. The VICON motion-capturing system requires i) a properly equipped room of cameras and trackers, ii) experienced staff to manage the VICON devices, iii) a pre-capturing procedure, which is obligatory to calibrate the whole system. On the other hand, Kinect II is a low-cost depth sensor, which requires no markers to extract the depth and humans’ skeleton joints. This makes Kinect II applicable to non-professional users (everybody) from any environment (everywhere) and at any time. However, the captured trajectories are not as accurate as the ones extracted by the VICON system.
Consequently, the Kinect II device can be used as an in-home learning tool for most of dance choreographies by simple (non-experienced) users. This paper relates dance motion trajectories captured by the accurate VICON and the non-accurate Kinect II system. A Dynamic Time Warping (DTW) methodology is adopted to find out similarities/dissimilarities between the two devices, considering as accurate reference dance motion trajectory the one derived from the VICON system. DTW algorithm can localize dance steps patterns which cannot be accurately represented by the Kinect system and patterns that Kinect can be sufficiently described.
The contribution of this work can be summarized in the following: First, we present a comparative study on trajectory similarity estimation approaches, on data obtained by two types of sensors, using a complex dataset with challenging choreographic sequences, where joint movements are often varied and unstructured. Furthermore, the conducted experiments indicate that if significant levels of precision are ensured during initial data collection, design, development, and fine-tuning of the system, then low-cost and widely popular motion-capturing sensors, such as Kinect II, suffice to provide a smooth and integrated experience on the user end, which would allow for relevant educational or entertainment applications to be adopted at scale.
2. The Proposed Methodology
In this work we investigate the possibility of using skeleton data points as reference points, for the identification of dance choreographies. Data originates from professional motion capture equipment. These instances are used against corresponding skeletal data, recorded using low-cost sensors. The proposed approach consists of the following steps: (a)data capturing using high-end motion capture system, (b) feature extraction, (c) descriptive frames selection, for the database creation, (d) data capturing using low-cost sensors, (e) extraction of corresponding body joints and (f) similarity assessment among the dance patterns between high-end and low-cost sensors.
The idea of spatial-temporal information management [24,32] is applied, so that recorded dance sequences are summarized to a sequence of keyframes. This is achieved by employing an iterative clustering scheme, imposing time constraints. The proposed data managing scheme reduces the dance sequence to a few keyframes, which are selected using density-based clustering, in predefined time related subsets. It is important to note that noise or tempo variations do not affect the proposed approach. Given as set of keyframe sequences, for different dances, a comparison is performed among them. The sequences are signals containing information over dancer’s joints’ position and rotation. Signal similarity, employing the correlation measure is performed. Consequently, variations of the same dance should be easily identified, due to high similarity scores. Figure 1 depicts a block diagram of the proposed methodology.
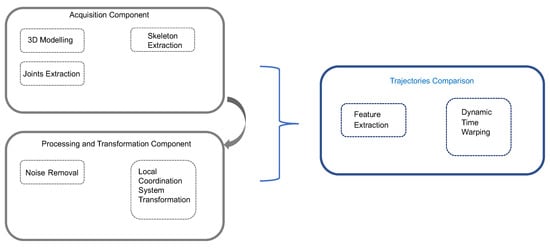
Figure 1.
A block diagram of our proposed methodology.
2.1. Data Capturing
Two type of sensors are used for the feature extraction: Kinect II and VICON. Despite their differences both sensors provide similar information for many of the body joints. Therefore, any comparisons based on leg joints as knees, angles, and hips are feasible with minor prepossessing steps, e.g., the frame rate reduction. Table 2 summarizes different aspects between VICON and Kinect II sensors. As we can observe, Kinect II is of low cost but also of low accuracy. On the other hand, VICON is of high accuracy but it yields a high-cost sensing. For this reason, VICON is used as a reference trajectory in our case.
Figure 2 shows a snapshot of the proposed Kinect II architecture while Figure 3 depicts the architecture of the VICON components. These shots have been obtained at one of our experiments conducted at the premises of Sports Science department of the Aristotle University of Thessaloniki. In these premises, different dances have been recorded as described in Section 4. Figure 4 shows a snapshot of the conducted dance experiment.

Figure 2.
Kinect workstation.

Figure 3.
Pictures of VICON components (https://www.vicon.com/products/vicon-devices/).

Figure 4.
A snapshot from the experiments conducted at the Aristotle University of Thessaloniki for capturing the folklore dances.
2.1.1. Kinect Sensor
In this work, a subset of human joints is considered for the dance analysis. Figure 5 depicts every frame as obtained by Kinect. Kinect permits capturing human motion variation as 3D data [15,32], combining the skeletal tracking data of multiple sensors to address the issue of occlusions [33] hence making skeletal tracking more robust. Kinect II sensor by Microsoft includes: (a) a depth sensor, (b) an RGB camera and (c) a four-microphone array that can deliver a full body 3D motion capture [7].
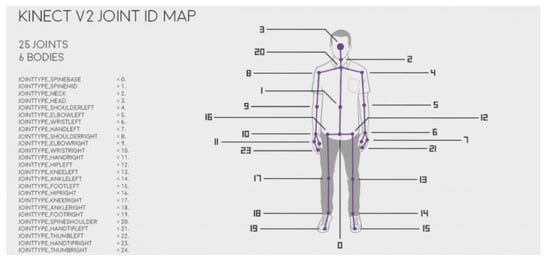
Figure 5.
A list of body joints captured by Kinect. For each joint, position and rotation values are stored in XML format (source: https://vvvv.org/documentation/kinect).
At first the positions and rotation values for each frame, , of a dance are extracted. Each choreographic sequence is represented by a matrix of size , where b is the number of body joints (i.e., 6, namely ) k is the number of feature vectors values (i.e., 3), and t is the sequence length. Please note that for every joint we have the following feature values: three coordinates and four rotations, and additionally two binary indicators, denoting whether values derive from measurement or estimation.
2.1.2. VICON Motion-Capturing System
The motion capture area of VICON is surrounded by several high-resolution cameras with LED strobe light rings (see Figure 4). A setup of VICON workstation is illustrated in Figure 3. Reflective markers facilitate the recording of the moving subject by the cameras (Figure 6a), while signal collection is controlled by Data station controls (Figure 3b). Signals are then passed to the VICON workstation (Figure 3b), equipped with a specialized software for collection, filtering, and processing of raw data. Two-dimensional data from cameras are processed and combined for the three-dimensional motion to be reconstructed.
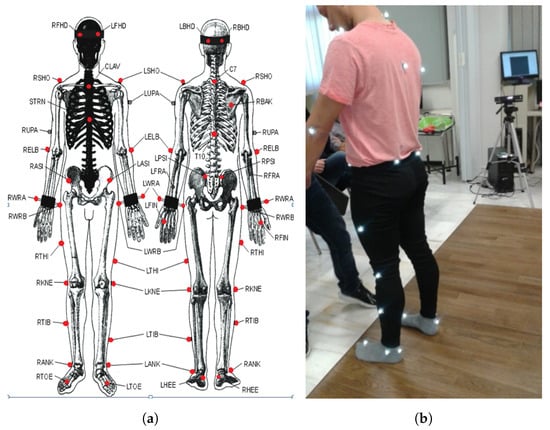
Figure 6.
(a) VICON body joints capturing capabilities. (b) Placement of markers to the Dancer.
2.2. Database Creation
Table 1 shows the dance recorded in our experiments along with a short description of them. As you can see from Table 1 six different Greek folkloric dances have been recorded, each of different beat duration and characteristics. Each dance was executed by different dancers including men and women so that we can evaluate different properties and characteristics of each dance. Table 3 depicts the different duration of these dances across three different dancers.

Table 3.
The considered dances and their variations along with the length of each sequence for each of the three dancers. These dances were recorded using Kinect II.
We assume here that any dance can be represented by a subset of frames, namely keyframes [34]. The keyframes are the most representative postures of each dance. Random sampling over k-means clusters [21] is an improvement of random selection with similar instances being likely to be clustered together. In this way, a random sampling from each cluster could be considered to give adequate information regarding the data set. The final dataset is a cell array, which contains all the recorded dances for each of the dancers.
3. Dynamic Time Warping for Evaluating the Kinect II Performance
3.1. Dynamic Time Warping
Dynamic Time Warping [35] calculates an optimal match between two temporal sequences. DTW generated matching path is based on linear matching, but has specific conditions that need to be satisfied, in particular the conditions pertaining to continuity, boundary condition, and monotonicity. In the following a brief description on matching between curve points is provided. If and are the number of points in two curves, then i-th point of curve 1 and the j-th point of curve 2 match if:
It should be mentioned that each point can match with maximum one point of the other curve. The boundary condition forces a match between the first points of the curve and a match between the last points of the curve. The continuity condition decides how much the matching can differ from the linear matching. The aforementioned condition is the heart of DTW. We formulate the aforementioned assumption as follows:
In the case that during the process of matching it is concluded that the i-th point of the first curve should match with the j-th point of the second curve, it is not possible: (i) that any point of the former with an index greater than i matches with a point of the latter with an index smaller than j, and (ii) that any point of the former with an index smaller than i matches with a point on the latter with index greater than j.
3.2. Kinect II Evaluation Using DTW
In our proposed methodology, we denote as reference sequences those are derived by the VICON motion-capturing system. In addition, each choreographic sequence obtained by the low-cost sensor Kinect II is contrasted to the VICON sequence. Our scope is to define the similarities/dissimilarities comparing the choreographic sequence for each dance using the DTW algorithm [35]. Furthermore, each choreographic sequence is depicted as a curve with different characteristics (e.g., duration, length). Our proposed framework is to define the similarities/dissimilarities between the curves of the heterogeneous motion-capturing systems. Every index of the choreographic sequence is matched with one (or more) indices of the other sequence for each dance. Figure 7 depicts time alignment between two independent signals, in our framework the signals are obtained by the motion-capturing systems. Let us denote, as the sequences of the Kinect sensor and the sequences of the VICON accordingly. The and enclosure the kinesiology features (body joints variations) for each dancer creating a motion database for the heterogeneous capturing system. To compare each feature, we define a local cost measure describing the similarity/dissimilarity of each feature. The cost matrix is defined as P∈ = . An (N,M) dynamic warping path p = (,⋯,) determines an alignment between the and vectors by assigning the element of to the element of . The vectors and are denoted as follows:
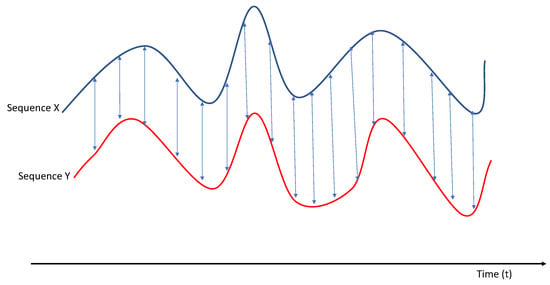
Figure 7.
Time alignment of two choreographic sequences. Aligned points are depicted by the arrows.
In the following, we create a space defined by F. Then , ∈F for n∈ [1:N] and m∈ [1:M]. In our framework, we define as and the features which are obtained by the motion-capturing system indicating every joint of the dancer’s body. Due to the heterogeneous motion-capturing system, we should define the local coordination system. Figure 8 depicts the transformation from the global coordination system to a local system for each motion-capturing system, which is simultaneously a type of range fix that takes into consideration body parameters such as limb length. Inevitably, for the aforementioned constraints we denote as the k-th joint out of the M = 35 acquired by VICON system and the l-th out of the L = 25 obtained by the Kinect II sensor respectively. Variables , and indicate the coordinates of the respective i-th joint with regard to a reference point setting VICON architecture (in our case the center of the square surface). We have acquired the aforementioned joints after applying a density-based filtering on the entirety of the detected joints to eliminate noise introduced during the acquisition procedure. The main difficulty in directly processing the extracted joints , k = 1,2,…,M is the coordinates system. Thus, we need to transform the from the VICON coordinate system to a local coordinate system, the center of which is the center of mass of the dancer. We follow the same procedure for the Kinect II architecture. This is obtained through the application of Equation (5) on the joint’s coordinates ,
where denotes the dancer’s center of mass regarding the coordination system expressed as:
and we recall that M, L refers to the total number of joints extracted by the VICON and Kinect capturing system, respectively.
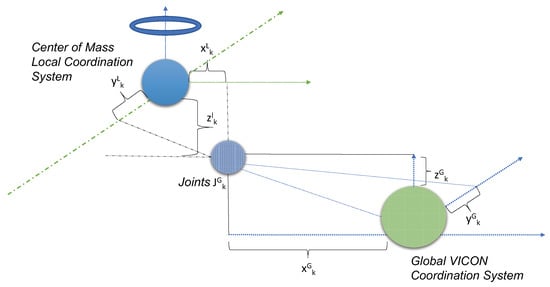
Figure 8.
VICON global coordination system being transformed to a local coordination system. Its center is the center of mass of the dancer [21]. This allows for compensation of the dancer spatial positioning.
Let us denote as cost matrix = the total cost of a warping path p between and .
The DTW distance between the and is defined as follows:
3.3. Kinect II Evaluation Using Move-Split-Merge
Motivated by the superiority of DTW for motion analysis shown in previous works e.g., against SVM [30], or approaches based on Locally Linear Embedding (LLE), Locality Preserving Projections (LPP) and LLP-HMM [31] we adopt DTW as our main reference algorithm. Moreover, we conduct further comparative experiments to also evaluate against a recent technique called Move-Split-Merge [36]. The Move-Split-Merge distance algorithm provides a means of measurement that resembles other distance-based approaches, where similarities/dissimilarities are computed by employing a series of operations for the transformation of a series “source” into a series “target”. Move-Split-Merge algorithm uses as building blocks three fundamental operators. The move operation is equivalent with a replacement operation, in which one value substitutes another. Split inserts an identical copy of a value immediately after its first instance, while Merge erases a value if it directly follows an identical value. Let us assume = as a finite motion sequence of real numbers . The move operation and the cost operation are defined as follows:
4. Experimental Results
In our study, for capturing of the dancers’ movement variations, we employ a multi-faceted motion capture system including one Kinect II depth sensor, the i-Treasures Game Design module (ITGD) module created in the context of i-Treasures project [1] and VICON motion-capturing system. The ITGD module gives the possibility of recording and annotating mocap data acquired by a Kinect sensor. The employed algorithms were implemented in MATLAB. A variety of Greek folk dances with varying levels of complexity have been obtained. Three dancers (two men and one woman) each performed every dance twice: Once in a straight line and once in a semi-circular curved line. Figure 9 and Figure 10 depict the most representative postures of the Syrtos at 2 beats and Enteka dance, respectively. Figure 11 depicts the main choreographic steps of Enteka dances and Figure 12 of Syrtos dance at 3 beats. Figure 13 depicts the most representative postures of the Syrtos at 3 beats dance. Each choreographic posture is illustrated with different color indicating the most representative frames that summarize the whole choreographic sequence providing the kinesiology patterns.

Figure 9.
Illustration of Syrtos dance (2 beats, circular trajectory).

Figure 10.
Illustration of Enteka dance performed by dancer 3.

Figure 11.
Illustration of Enteka dance.

Figure 12.
An instance that illustrates seven frames from the Syrtos at 3 beats dance.

Figure 13.
The most representative postures of the Syrtos at 3 beats dance. Each posture is depicted with different color indicating the keyframes of the folklore dance. These postures summarize the whole choreographic sequence.
4.1. Dataset Description
The dataset comprises six different folklore dances. For the Kinect capturing process, we use a single Kinect II sensors placed in the front. Every dance is described by a set of consecutive image frames. Every frame , has a corresponding extensible mark-up language (XML) file with positions, rotations and confidence scores for 25 joints on the body (see Figure 5) addition to timestamps. In Table 1, a brief description of the dances is provided [24]. After a series of processing steps, a skeleton from the VICON system is represented as shown in Figure 6a. In the discussed setting, ten Bonita B3 cameras were used. The capturing space was a square of 6.75 m width, and the square’s center constitutes the origin of the VICON coordinate system. We used a calibration wand with markers to optimize the calibration procedure. The dancers’ movements were captured using 35 markers at fixed positions on their bodies.
4.2. Similarity Analysis
Similarity analysis entails to a dance matching problem. Specifically, given a set of frames, from multiple body joints, captured using the Kinect, we try to identify the most closely related trajectories from the choreographic database. Assume that we have n experienced dancers in the database. Then each time a new user performs a dance, the algorithm calculates the similarity scores among the newly recorded dance and the existing dances in the DB. Then, for each of the n experienced dancers, we get the top 3 closest trajectories, given a distance metric. Thus, we have a total of n times 3 dance suggestions. In this study, we have 3 experienced dancers. Thus, we had 9 dance suggestions every time. The similarity score (i.e., DTW or MSM) is then used to rank the results. Performance analysis focuses on how accurate the system is in matching correctly the recorded dance.
At first, we asked the dancer to execute a specific choreography. Since, VICON’s frame rate is 4 times greater than Kinect, we have considered a sub-sample approach in a ratio 1 to 4; that way the frame rate matches the Kinect. Then, we exploit the similarity tests with existing entries in the database. Despite the variations in the trajectories, we expect that the movement itself will be similar among dancers. Thus, the similarity analysis has a solid base. Figure 14 and Figure 15 illustrate the left foot joint movement on the floor for two different dancers. As we observe, the choreographic pattern of each dance is extracted indicating not only the kinesiology variation of the dancers’ joints but also the music tempo. The main patterns appear the same, despite the variations in descriptive characteristics (e.g., length and height).
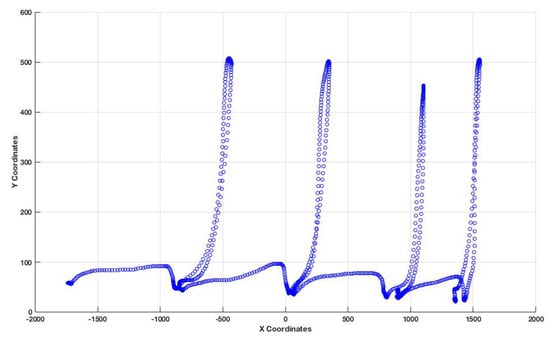
Figure 14.
The coordinates of the trajectory of the left foot joint, which shows the rhythm of the dance performed by dancer 1.
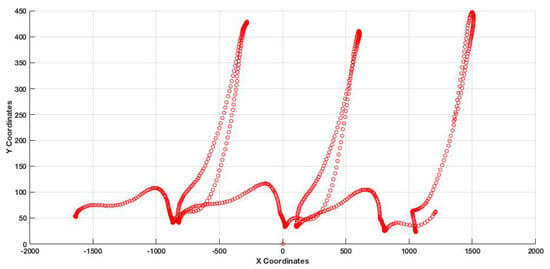
Figure 15.
The coordinates of the trajectory of the left foot joint, which shows the rhythm of the dance performed by dancer 2.
Proposed approach’s matching performance is displayed in Figure 16. Results illustrate the number of matches, for a specific recorded dance, to the existing dances in data base. There are three performance classes, denoted as Top3, Top6, and Top 9. Numbers 3, 6, and 9 indicate the number of the closest matched dances (from the database to the one currently performed). Recall that we have three professional dancers and each of them performed the same six dances. Thus, the highest possible score in category TopX is 3. Results indicate that the suggested methodology managed to match correctly at least once all the investigated dances, despite their complexity, as explained in [37].
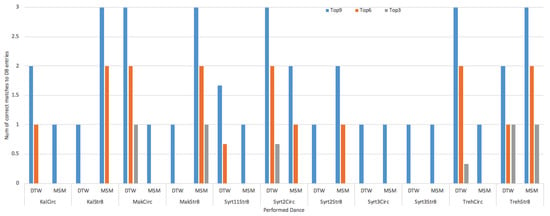
Figure 16.
Performance illustration for the matching process.
Figure 16 provides further insights to the similarity between the VICON and the Kinect II sensors. The x axis depicts the name of each the dance (see Table 3) and the y axis the number of the matches according to the choreographic database. For example, Makedonikos in circular trajectory (MakCirc) Top9 score indicates that among the nine closest trajectory patterns, we have 3 matches with the Makedonikos dance captured by Kinect II, one per dancer in the choreographic database. Consequently, Makedonikos dance captured by VICON system was matched to Makedonikos dance captured by Kinect II; to an extent, most of the choreographies were successfully matched, by defining a score using the DTW or MSM algorithms, despite the differences in employed motion capture technologies.
5. Conclusions
In this paper, we explore the feasibility of pattern matching between heterogeneous motion-capturing systems. The case study emphasizes on northern Greek folklore dances, which although complex and with several variations and particularities in their pattern, are characterized by elements of structure, contrary to chaotic versions of movement trajectories (e.g., [38]) in which similar explorations are far more difficult to perform. In this work, a two-step process is adopted. The first step uses Kinect II sensors, which provide dancer’s skeleton feature values and a database is created. The second step involves the comparison of the trajectories in the database with a second database, created using VICON. The employed algorithms calculate similarity scores. According to these scores the algorithm provides a similar dance suggestion, for each of the dancers, in the choreographic database. The obtained results suggest that low-cost sensors such as Kinect II can be used in the context of dance-related educational or entertainment applications, at least as part of the end-user side. Such a setup would however require the employment of a detailed and highly accurate dataset for training and development of the system, captured by a high precision system such as VICON. The conducted experiments indicate that if significant levels of precision are ensured during initial data collection, design, development, and fine-tuning of the system, then low-cost and widely popular motion-capturing sensors suffice to provide a smooth and integrated experience on the user end, which would allow for relevant educational or entertainment applications to be adopted at scale. Nevertheless, the proposed approach would not be appropriate for tasks that require great precision and accuracy in measurement of movement and positioning of individual joints, such as medical or rehabilitation applications.
Author Contributions
Conceptualization, E.P., A.V. and N.D.; Formal analysis, E.P. and A.V.; Funding acquisition, N.D. and A.D.; Investigation, G.B.; Methodology, E.P. and A.V.; Resources, N.D.; Software, I.R. and E.P.; Supervision, A.V., N.D. and A.D.; Validation, A.D. and G.B.; Visualization, I.R.; Writing—original draft, I.R. and E.P.; Writing—review & editing, A.V., A.D. and G.B.
Funding
This work is supported by the European Union project TERPSICHORE Transforming Intangible Folkloric Performing Arts into Tangible Choreographic Digital Objects funded under the grant agreement 691218.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ICH | Intangible Cultural Heritage |
| DTW | Dynamic Time Warping |
| ITGD | i-Treasures Game Design module |
| MSM | Move-Split-Merge |
References
- Dimitropoulos, K.; Manitsaris, S.; Tsalakanidou, F.; Nikolopoulos, S.; Denby, B.; Kork, S.; Crevier-Buchman, L.; Pillot-Loiseau, C.; Adda-Decker, M.; Dupont, S.; et al. Capturing the intangible: An introduction to the i-treasures project. In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP), Lisbon, Portugal, 5–8 January 2014; pp. 773–781. [Google Scholar]
- Shay, A.; Sellers-Young, B. Dance and Ethnicity. In The Oxford Handbook of Dance and Ethnicity; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Ioannides, M.; Hadjiprocopi, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E.; Makantasis, K.; Santos, P.; Fellner, D.; Stork, A.; Balet, O.; et al. Online 4D reconstruction using multi-images available under Open Access. ISPRS Ann. Photogr. Remote Sens. Sapt. Inf. Sci. 2013, 2, 169–174. [Google Scholar] [CrossRef]
- Kyriakaki, G.; Doulamis, A.; Doulamis, N.; Ioannides, M.; Makantasis, K.; Protopapadakis, E.; Hadjiprocopis, A.; Wenzel, K.; Fritsch, D.; Klein, M.; et al. 4D reconstruction of tangible cultural heritage objects from web-retrieved images. Int. J. Heri. Digit. Era 2014, 3, 431–451. [Google Scholar] [CrossRef]
- Doulamis, A.D.; Doulamis, N.D.; Makantasis, K.; Klein, M. A 4D Virtual/Augmented Reality Viewer Exploiting Unstructured Web-based Image Data. In Proceedings of the 10th International Conference on Computer Vision Theory and Applications, Berlin, Germeny, 11–14 March 2015; pp. 631–639. [Google Scholar]
- Voulodimos, A.; Doulamis, N.; Fritsch, D.; Makantasis, K.; Doulamis, A.; Klein, M. Four-dimensional reconstruction of cultural heritage sites based on photogrammetry and clustering. J. Electron. Imaging 2016, 26, 011013. [Google Scholar] [CrossRef]
- Zhang, Z. Microsoft kinect sensor and its effect. IEEE Multimed. 2012, 19, 4–10. [Google Scholar] [CrossRef]
- Keselman, L.; Woodfill, J.I.; Grunnet-Jepsen, A.; Bhowmik, A. Intel realsense stereoscopic depth cameras. arXiv 2017, arXiv:1705.05548. [Google Scholar]
- Voulodimos, A.; Rallis, I.; Doulamis, N. Physics-based keyframe selection for human motion summarization. Multimed. Tools Appl. 2018, 1–17. [Google Scholar] [CrossRef]
- Doulamis, N.; Doulamis, A.; Ioannidis, C.; Klein, M.; Ioannides, M. Modelling of static and moving objects: Digitizing tangible and intangible cultural heritage. In Mixed Reality and Gamification for Cultural Heritage; Loannides, M., Magnenat-Thalmann, N., Papagiannakis, G., Eds.; Springer: Cham, Switzerland, 2017; pp. 567–589. [Google Scholar]
- Kitsikidis, A.; Dimitropoulos, K.; Yilmaz, E.; Douka, S.; Grammalidis, N. Multi-sensor technology and fuzzy logic for dancer’s motion analysis and performance evaluation within a 3D virtual environment. In Proceedings of the International Conference on Universal Access in Human-Computer Interaction, Heraklion, Greece, 22–27 June 2014; pp. 379–390. [Google Scholar]
- Laggis, A.; Doulamis, N.; Protopapadakis, E.; Georgopoulos, A. A low-cost markerless tracking system for trajectory interpretation. In Proceedings of the ISPRS International Workshop of 3D Virtual Reconstruction and Visualization of Complex Arhitectures, Nafplio, Greece, 1–3 March 2017; pp. 413–418. [Google Scholar]
- Kitsikidis, A.; Dimitropoulos, K.; Douka, S.; Grammalidis, N. Dance analysis using multiple kinect sensors. In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP), Lisbon, Portugal, 5–8 January 2014; pp. 789–795. [Google Scholar]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Rallis, I. Kinematics-based Extraction of Salient 3D Human Motion Data for Summarization of Choreographic Sequences. In Proceedings of the 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 3013–3018. [Google Scholar]
- Rallis, I.; Langis, A.; Georgoulas, I.; Voulodimos, A.; Doulamis, N.; Doulamis, A. An Embodied Learning Game Using Kinect and Labanotation for Analysis and Visualization of Dance Kinesiology. In Proceedings of the 10th International Conference on Virtual Worlds and Games for Serious Applications (VS-Games), Wurzburg, Germany, 5–7 September 2018; pp. 1–8. [Google Scholar]
- Voulodimos, A.; Kosmopoulos, D.; Veres, G.; Grabner, H.; Gool, L.V.; Varvarigou, T. Online classification of visual tasks for industrial workflow monitoring. Neural Netw. 2011, 24, 852–860. [Google Scholar] [CrossRef] [PubMed]
- Kosmopoulos, D.I.; Voulodimos, A.S.; Varvarigou, T.A. Robust Human Behavior Modeling from Multiple Cameras. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 3575–3578. [Google Scholar]
- Doulamis, N.; Voulodimos, A. FAST-MDL: Fast Adaptive Supervised Training of multi-layered deep learning models for consistent object tracking and classification. In Proceedings of the 2016 IEEE International Conference on Imaging Systems and Techniques (IST), Chania, Greece, 4–6 October 2016; pp. 318–323. [Google Scholar] [CrossRef]
- Doulamis, N.D.; Voulodimos, A.S.; Kosmopoulos, D.I.; Varvarigou, T.A. Enhanced Human Behavior Recognition Using HMM and Evaluative Rectification. In Proceedings of the First ACM International Workshop on Analysis and Retrieval of Tracked Events and Motion in Imagery Streams, New York, NY, USA, 29 October 2010; pp. 39–44. [Google Scholar] [CrossRef]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018, 13. [Google Scholar] [CrossRef] [PubMed]
- Rallis, I.; Georgoulas, I.; Doulamis, N.; Voulodimos, A.; Terzopoulos, P. Extraction of key postures from 3D human motion data for choreography summarization. In Proceedings of the 9th International Conference on Virtual Worlds and Games for Serious Applications (VS-Games), Athens, Greece, 6–8 September 2017; pp. 94–101. [Google Scholar]
- Protopapadakis, E.; Grammatikopoulou, A.; Doulamis, A.; Grammalidis, N. Folk Dance Pattern Recognition Over Depth Images Acquired via Kinect Sensor. In Proceedings of the 3D ARCH-3D Virtual Reconstruction and Visualization of Complex Architectures, Nafplio, Greece, 1–3 March 2017; pp. 587–593. [Google Scholar]
- Rallis, I.; Doulamis, N.; Doulamis, A.; Voulodimos, A.; Vescoukis, V. Spatio-temporal summarization of dance choreographies. Comput. Graph. 2018, 73, 88–101. [Google Scholar] [CrossRef]
- Rallis, I.; Doulamis, N.; Voulodimos, A.; Doulamis, A. Hierarchical Sparse Modeling for Representative Selection in Choreographic Time Series. In Proceedings of the 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1023–1027. [Google Scholar]
- Pfister, A.; West, A.M.; Bronner, S.; Noah, J.A. Comparative abilities of Microsoft Kinect and Vicon 3D motion capture for gait analysis. J. Med. Eng. Technol. 2014, 38, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Fern’ndez-Baena, A.; Susín, A.; Lligadas, X. Biomechanical validation of upper-body and lower-body joint movements of kinect motion capture data for rehabilitation treatments. In Proceedings of the 4th International Conference on Intelligent Networking and Collaborative Systems, Bucharest, Romania, 19–21 September 2012; pp. 656–661. [Google Scholar]
- Galna, B.; Barry, G.; Jackson, D.; Mhiripiri, D.; Olivier, P.; Rochester, L. Accuracy of the Microsoft Kinect sensor for measuring movement in people with Parkinson’s disease. Gait Post. 2014, 39, 1062–1068. [Google Scholar] [CrossRef] [PubMed]
- Adistambha, K.; Ritz, C.H.; Burnett, I.S. Motion classification using Dynamic Time Warping. In Proceedings of the 2008 IEEE 10th Workshop on Multimedia Signal Processing, Cairns, Qld, Australia, 8–10 October 2008; pp. 622–627. [Google Scholar] [CrossRef]
- Choi, H.R.; Kim, T. Combined dynamic time warping with multiple sensors for 3D gesture recognition. Sensors 2017, 17, 1893. [Google Scholar] [CrossRef] [PubMed]
- Ikizler, N.; Duygulu, P. Human action recognition using distribution of oriented rectangular patches. In Human Motion—Understanding, Modeling, Capture and Animation; Elgammal, A., Rosenhahn, B., Klette, R., Eds.; Springer: Berlin, Germany, 2007; pp. 271–284. [Google Scholar]
- Blackburn, J.; Ribeiro, E. Human motion recognition using isomap and dynamic time warping. In Human Motion—Understanding, Modeling, Capture and Animation; Elgammal, A., Rosenhahn, B., Klette, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 285–298. [Google Scholar]
- Doulamis, A.; Doulamis, N.; Ioannidis, C.; Chrysouli, C.; Grammalidis, N.; Dimitropoulos, K.; Potsiou, C.; Stathopoulou, E.K.; Ioannides, M. 5D modelling: An efficient approach for creating spationtemporal predictive 3D maps of large-scale cultural resources. In Proceedings of the ISPRS Annals of Photogrammetry, Remote Sensing & Spatial Information Sciences, Taipei, Taiwan, 31 August–4 September 2015; pp. 61–68. [Google Scholar]
- Lalos, C.; Voulodimos, A.; Doulamis, A.; Varvarigou, T. Efficient tracking using a robust motion estimation technique. Multimed. Tools Appl. 2014, 69, 277–292. [Google Scholar] [CrossRef]
- Doulamis, A.; Soile, S.; Doulamis, N.; Chrisouli, C.; Grammalidis, N.; Dimitropoulos, K.; Manesis, C.; Potsiou, C.; Ioannidis, C. Selective 4D modelling framework for spatial-temporal land information management system. In Proceedings of the Third International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2015), Paphos, Cyprus, 16–19 March 2015; Volume 9535, p. 953506. [Google Scholar]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the 12th International Conference on Artificial Intelligence, Seattle, WA, USA, 31 July–4 August 1994; Volume 10, pp. 359–370. [Google Scholar]
- Stefan, A.; Athitsos, V.; Das, G. The Move-Split-Merge Metric for Time Series. IEEE Trans. Knowl. Data Eng. 2013, 25, 1425–1438. [Google Scholar] [CrossRef]
- Protopapadakis, E.; Voulodimos, A.; Doulamis, N. Multidimensional trajectory similarity estimation via spatial-temporal keyframe selection and signal correlation analysis. In Proceedings of the 11th PErvasive Technologies Related to Assistive Environments Conference, Corfu, Greece, 25–29 June 2018; pp. 91–97. [Google Scholar]
- Fortuna, L.; Frasca, M.; Camerano, C. Strange attractors, kinematic trajectories and synchronization. Int. J. Bifurcat. Chaos 2008, 18, 3703–3718. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).