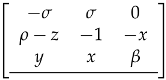Optimizing the Kaplan–Yorke Dimension of Chaotic Oscillators Applying DE and PSO

Abstract

When a new chaotic oscillator is introduced, it must accomplish characteristics like guaranteeing the existence of a positive Lyapunov exponent and a high Kaplan–Yorke dimension. In some cases, the coefficients of a mathematical model can be varied to increase the values of those characteristics but it is not a trivial task because a very huge number of combinations arise and the required computing time can be unreachable. In this manner, we introduced the optimization of the Kaplan–Yorke dimension of chaotic oscillators by applying metaheuristics, e.g., differential evolution (DE) and particle swarm optimization (PSO) algorithms. We showed the equilibrium points and eigenvalues of three chaotic oscillators that are simulated applying ODE45, and the Kaplan–Yorke dimension was evaluated by Wolf’s method. The chaotic time series of the state variables associated to the highest Kaplan–Yorke dimension provided by DE and PSO are used to encrypt a color image to demonstrate that they are useful in implementing a secure chaotic communication system. Finally, the very low correlation between the chaotic channel and the original color image confirmed the usefulness of optimizing Kaplan–Yorke dimension for cryptographic applications.

1. Introduction

Chaotic systems are a hot topic of interest for researchers in a wide variety of fields. In the case of optimization and applications, one is interested in finding appropriate design parameters that provide better characteristics like a high positive Lyapunov exponent (LE+) and a high Kaplan–Yorke dimension $D_{KY}$, and guaranteeing chaotic behavior for long-times. This task can be performed by varying the coefficients of a mathematical model under ranges that can be established from the evaluation of the bifurcation diagram. However, this requires extensive computing time and is more complex when the values of the coefficients have more fractional values. For example: The Lorenz chaotic oscillator has three design parameters: $\sigma ,\rho$, and $\beta$. They can have integer values and also fractional ones. If one chose varying them using two integer (${10}^2$) and four fractional numbers (${10}^4$), then the number of combinations becomes ${10}^6\times {10}^6\times {10}^6={10}^{18}$. Simulating this number of cases can be unreachable in a couple of years and not all cases will generate chaotic behavior. In this manner, metaheuristics can be applied to search for the best coefficient values that provide high LE+ and high $D_{KY}$.

Among all the different kinds of chaotic systems, the case studies of this work are three dimensional autonomous chaotic oscillators, and the analysis to determine their equilibrium points and eigenvalues are shown. The numerical simulation is performed by applying ODE45 to generate chaotic time series that are used to evaluate both LE+ and $D_{KY}$ by applying Wolf’s method [1]. In fact, chaotic flow is interesting for systems that have high complexity that can be quantified by evaluating the attractor dimension, which is associated to $D_{KY}$. For instance, the authors in [2] introduced a flexible chaotic system through applying modification in a recent rare chaotic flow which has adjustable $D_{KY}$, and it is used in a practical application showing a relation between $D_{KY}$ and the ability of the chaotic system to generate random numbers. The authors in [3] published a review paper of fully analog realizations of chaotic dynamics that can be considered canonical (minimum number of the circuit elements), robust (exhibit structurally stable strange attractors), and novel. The short term unpredictability of the chaotic flow is demonstrated via the calculation of $D_{KY}$ that is high, so that the generated chaotic waveforms can find interesting applications in the fields of chaotic masking, modulation, or chaos-based cryptography. Another new chaotic oscillator is proposed in [4], where the authors present a systematic study including phase portraits, dissipativity, stability, $D_{KY}$, etc. In the same line of research, the authors in [5] analyze a chaotic satellite system using dissipativity, equilibrium points, bifurcation diagrams, Poincaré section maps, and $D_{KY}$ to ensure the strange behavior of the chaotic system. As one can infer, $D_{KY}$ is quite useful to characterize a chaotic dynamical system that can be implemented with electronics for engineering applications like secure chaotic communication systems and it can also be useful to model natural dynamics like the predator-prey system given in [6]. In this manner, we show the application of two metaheuristics, namely: Differential evolution (DE) and particle swarm optimization (PSO) algorithms, in order to maximize $D_{KY}$ of three chaotic oscillators. The state variables of each chaotic oscillator with the highest $D_{KY}$ are used to encrypt a color image to demonstrate their usefulness in implementing a chaotic secure communication system.

The rest of the manuscript is organized as follows: Section 2 describes the three chaotic oscillators that are used to maximize $D_{KY}$. They are a chaotic system with infinite equilibria points [7], Rössler [8], and Lorenz [9] systems. Section 3 details the DE and PSO algorithms that are used to maximize $D_{KY}$. Section 4 details the maximization of $D_{KY}$ for the three chaotic oscillators and shows statistical results of 10 runs applying DE and PSO. Section 5 shows the chaotic time series with the highest $D_{KY}$ that are used to encrypt a color image. Finally, the conclusions are given in Section 6.

2. Chaotic Systems

This section describes three autonomous chaotic oscillators that are used as case studies to optimize their $D_{KY}$ by applying DE and PSO algorithms. The first chaotic system has infinite equilibria points and was introduced in [7]. Its mathematical model is described by (1), where it can be appreciated that the non-linearity is provided by the exponential function and has a single parameter, a. This attractor is simulated with a step size of 0.3 and its phase portrait is shown in Figure 1. The attractor is generated when the design parameter $a=0.1$ and provides an LE+ = 0.17 and $D_{KY}$ = 2.0791, as shown in Table 1.

$$\begin{array}{ccc}\dot{x}\hfill & =& -z\hfill \\ \dot{y}\hfill & =& x{z}^2\hfill \\ \dot{z}\hfill & =& x-a{e}^y+z(y^2-z^2)\hfill \end{array}$$

(1)

Figure 1. Phase portraits of Equations (1)–(3) with the parameters listed in Table 1, and simulated with a time-step: (a) $h=0.3$; (b) $h=0.0038$; and (c) $h=0.008$.

Table 1. LE${}_{+}$ and D${}_{ky}$ of Equations (1)–(3) reported in the literature.

System	Parameters	LE${}_{+}$	D${}_{\mathit{K}\mathit{Y}}$
Infinite equilibria [7]	$a\approx 0.1$	∼0.17	2.0791
Rössler [8]	$a=0.15$; $b=0.20$; $c=10.0$	0.1300	2.0100
Lorenz [9]	$\sigma =0.16$; $\rho =45.92$; $\beta =4.0$;	2.1600	2.0700

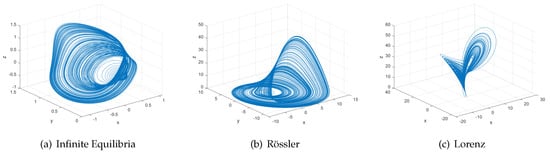
Other kinds of chaotic oscillators have nonlinearities that are associated to the multiplication of their state variables. This is the case of the Rössler system [8], which is described by (2). It consists of three design parameters shown in Table 1, $a=0.15$, $b=0.20$, and $c=10$, which are used to provide LE+ = 0.13 and $D_{KY}$ = 2.01, and its phase portrait is shown in Figure 1.

$$\begin{array}{ccc}\dot{x}\hfill & =& -y-z\hfill \\ \dot{y}\hfill & =& x+ay\hfill \\ \dot{z}\hfill & =& b+z(x-c)\hfill \end{array}$$

(2)

The third chaotic oscillator used in this article is the Lorenz chaotic system [9], which is described by (3), and its design parameters are $\sigma =0.16$, $\rho =45.92$, and $\beta =4$. Its numerical simulation provides LE+ = 2.16 and $D_{KY}$ = 2.07, as listed in Table 1, and its phase portrait is shown in Figure 1.

$$\begin{array}{ccc}\dot{x}\hfill & =& \sigma (x-y)\hfill \\ \dot{y}\hfill & =& x(\rho -z)-y\hfill \\ \dot{z}\hfill & =& xy-\beta z\hfill \end{array}$$

(3)

3. Differential Evolution and Particle Swarm Optimization Algorithms

As mentioned above, chaotic systems can be optimized in order to provide better characteristics like high LE+ and high $D_{KY}$ [10]. We show the application of metaheuristics because the design variables have large search spaces and thus require extensive computing time. A clear example is when trying to optimize the Lorenz chaotic oscillator, which has three design parameters: $\sigma$, $\rho$, and $\beta$, which can have fractional values. Therefore, if the design parameters are varied using two integer (${10}^2$) and four fractional numbers (${10}^4$), then the number of combinations becomes ${10}^6\times {10}^6\times {10}^6={10}^{18}$. As one can see, simulating this number of cases can be unreachable in a couple of years and the most important thing is that not all the combination cases will generate chaotic behavior. Another justification of applying metaheuristics is that an algorithm is used to evaluate $D_{KY}$, which is not based on derivatives.

The $D_{KY}$ requires evaluating the Lyapunov exponents of a chaotic oscillator, for which several methods has been published [11,12,13]. In this work we perform numerical simulations by applying ODE45 to generate chaotic time series that are used to evaluate both LE${}_{+}$ and $D_{KY}$ by applying Wolf’s method [1]. This process is performed within the optimization loops of the DE and PSO algorithms.

3.1. Differential Evolution Algorithm

This algorithm belongs to the focused-evolutionary family to solve optimization problems. DE is an algorithm that begins from generating D-dimensional vectors randomly as in a population: $x_{i,G}$ with $i=\{1,2,3,\dots ,N_p\}$, where G is the maximum number of generations and $N_p$ is the number of vectors in the population. As the generations run, new vectors are generated by performing mutation (4) and crossover (5) operations [14].

$$v_i^{g+1}\leftarrow x_c^g+F(x_a^g-x_b^g)$$

(4)

$$u_{ij}^{g+1}\leftarrow \left\{\begin{array}{c}{v}_{ij}^{g+1}if[U(0,1)\le CR]orrnbr\left(i\right)=j\hfill \\ x_{ij}^{g+1}if[U(0,1)>CR]andrnbr\left(i\right)\ne j\hfill \end{array}\right.$$

(5)

In Equation (4), a, b, and c are different vectors randomly selected, g is the current generation, and $F\in [0,2]$ is a mutant constant. In Equation (5), $j=\{1,2,\dots ,D\}$, $U(0,1)$ is a function that returns a real number with uniform distribution and within the range $[0,1)$, $CR\in [0,1]$ is a crossover coefficient selected by the user, and $rnbr\left(i\right)\in [0,1]$ is an index generated randomly. During the evaluation process, several operations are performed as follows: When evaluating the new generated vector ($u_{ij}^{g+1}$), if it is better than the previous vector ($x_{ij}^{g+1}$), then the new vector replaces the previous one and it will be part of the new population ($g+1$), otherwise, the new vector will be discarded. The DE algorithm stops when the maximum number of generations is reached (or other stop criterion is applied) and the values of optimization are retrieved. Algorithm 1 shows the pseudo-code of the DE algorithm that is detailed in [14].

Algorithm 1 Differential Evolution

Require:D, G, $N_p$, $CR$, F, and $func(•)$. 1: Initialize the population randomly (x)   2: Evaluate the population with your function [$func\left(x\right)$] 3: Save the evaluation results in $score$ 4: for ($counter=1;counter\le G;counter$++) do 5:   for ($i=1;i\le N_p;i$++) do 6:    Select three different indexes randomly (a, b, and c)   7:    for ($j=1;j\le D;j$++) do 8:     if $U(0,1)<CR\left|\right|j=D$ then 9:      $tria{l}_j\leftarrow x_{aj}+F(x_{bj}-x_{cj})$ 10:     else 11:      $tria{l}_j\leftarrow x_{ij}$ 12:     end if  13:    end for  14:    $fx\leftarrow func\left(trial\right)$   15:    if$fx$ is better than $scor{e}_i$ then 16:     $scor{e}_i\leftarrow fx$   17:     $x_i\leftarrow trial$   18:    end if  19:   end for  20: end for  21: returnx and $score$

3.2. Particle Swarm Optimization Algorithm

The PSO algorithm avoids performing a selection process as the evolutionary algorithms do. In PSO, all the population members survive in the whole optimization process. Basically, it updates the position and the velocity of the particles that follow the particle with the best result. The particles are associated to $x_i\in {\mathbb{R}}^J$ vectors, which are randomly initialized. The vectors are viewed as particles in the space, and their behaviors are defined by two formulas associated to their velocity (6) and position (7).

$$v_{ij}^{t+1}\leftarrow \alpha v_{ij}^t+U(0,\beta )\left(p_{ij}-x_{ij}^t\right)+U(0,\beta )\left(g_j-x_{ij}^t\right)$$

(6)

$$x_{ij}^{t+1}\leftarrow x_{ij}^t+v_{ij}^{t+1}$$

(7)

In Equations (6) and (7), i is the index of the particle, j is the dimension, $p_i$ is the best position finding in i, and $p_g$ is the best position obtained during the optimization. $\alpha \in \mathbb{R}$ is named inertial weight, $\beta \in \mathbb{R}$ is named acceleration constant, and $U(•)$ is a generator of random numbers uniformly distributed.

PSO is based on evaluating a $f\left(x_i\right)$ function and comparing the results. If the last result is better than the i-th results registered, this will be the new vector $p_i$. The global best value (g) is also compared, and if the last value is better than this, this is also replaced. This process is accomplished until it reaches the stop criterion. A feature of PSO is that during its execution, each particle moves around a centroid region determined by $p_i$ and g, so that the particles pursue new positions to reach the best solution. Algorithm 2 shows the pseudo-code of PSO algorithm, which is detailed in [15].

Algorithm 2 Particle Swarm Optimization

Require:D, G, $N_p$, $\alpha$, $\beta$, and $func(•)$. 1: Initialize the position of the particles randomly (x)   2: Initialize the velocity of the particles (v)   3: Evaluate the position of the particles with your function [$func\left(x\right)$]   4: Save the evaluation results in $score$ and $p\leftarrow x$   5: Find the best value from p and save it in g   6: for ($counter=1;counter\le G;counter$++) do 7:   for ($i=1;i\le N_p;i$++) do 8:    for ($j=1;j\le D;j$++) do 9:     $v_{ij}\leftarrow \alpha v_{ij}+U(0,\beta )\left(p_{ij}-x_{ij}\right)+U(0,\beta )\left(g_j-x_{ij}\right)$   10:     $x_{ij}\leftarrow x_{ij}+v_{ij}$   11:    end for  12:    $f_x\leftarrow func\left(x_i\right)$   13:    if $f_x$ is better than $scor{e}_i$ then 14:     $scor{e}_i\leftarrow f_x$   15:     $p_i\leftarrow x_i$   16:     if $p_i$ is better than g then 17:      $g\leftarrow p_i$   18:     end if  19:    end if  20:   end for  21: end for  22: returnx, p, g, and $score$

4. Maximizing D${}_{\mathit{KY}}$

The Lyapunov exponents give the most characteristic description of the presence of a deterministic non-periodic flow. Therefore, Lyapunov exponents are asymptotic measures characterizing the average rate of growth (or shrinkage) of small perturbations to the solutions of a dynamical system [16]. Lyapunov exponents provide quantitative measures of response sensitivity of a dynamical system to small changes in initial conditions [17]. The number of Lyapunov exponents equals the number of state variables, and if at least one is positive, this is an indication of chaos [18]. That way, the three chaotic oscillators given by Equations (1)–(3) have 3 Lyapunov exponents: One is positive LE+, one is zero (or very close to zero), and one is negative. The three Lyapunov exponents are used to evaluate the Kaplan–Yorke dimension, which can be obtained by Equation (8), where k is an integer such that the sum of the Lyapunov exponents (${\lambda }_i$) is non-negative. If chaotic behavior is guaranteed in Equations (1)–(3), then k = 2, so that ${\lambda }_{k+1}$ is the third Lyapunov exponent, and the dimension $D_{KY}$ is higher than 2.

$$D_{KY}=k+\frac{{\sum }_{i=1}^k{\lambda }_i}{{\lambda }_{k+1}}$$

(8)

In chaotic oscillators, an analysis of their eigenvalues is performed to determine unstable regions. The eigenvalues are determined from the evaluation of the equilibrium points. In this manner, the chaotic oscillator described by Equation (1), has the characteristic equation given by $s[s^2-{\left(y^{*}\right)}^{2}s+1]=0$, where $y^{*}$ includes the equilibrium points in y (that are infinite). In this case one eigenvalue is $s_1=0$ and the remainders $s_{2,3}$ are determined from $s^2-{\left(y^{*}\right)}^{2}s+1=0$. As already shown in [7], the unstable region is determined in $y^{*}\ne 0$, but following the eigenvalues criterion, this also must accomplish $\Delta <0$. If $\Delta ={\left(y^{*}\right)}^4-4$, the unstable region is in $-\sqrt[4]{4}<y^{*}<\sqrt[4]{4}$. Otherwise, the remainder eigenvalues are not complex.

The equilibrium points of Equations (1)–(3), and their associated Jacobians are shown in Table 2, where $\frac{\partial f_0}{\partial x}$ can take the values from evaluating Equation (9), so that each chaotic oscillator has three eigenvalues for each equilibrium point. For complex systems the eigenvalues can be calculated by applying Cardano’s method [19].

$$\frac{\partial f_0}{\partial x}=\left\{\begin{array}{cc}k,\hfill & if\left|x\right|\le 1\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

(9)

Table 2. Jacobian and equilibrium points of the chaotic systems given in Equations (1)–(3).

System	Jacobian	Equilibrium Points
Infinite Equilibria	$\left[\begin{array}{ccc}0& 0& -1\\ z^2& 0& 2xz\\ 1& a{e}^{y^{*}}& {\left(y^{*}\right)}^2-3z^2\end{array}\right]$	$(a{e}^{y^{*}},y^{*},0)$
Rössler	$\left[\begin{array}{ccc}0& -1& -1\\ 1& a& 0\\ z& 0& x-c\end{array}\right]$	$\left(\frac{c\pm \sqrt{c^2-4ab}}{2},-\frac{c\pm \sqrt{c^2-4ab}}{2a},\frac{c\pm \sqrt{c^2-4ab}}{2a}\right)$
Lorenz		$\left(\pm \sqrt{\beta (\rho -1)},\pm \sqrt{\beta (\rho -1)},\rho -1\right)$

The Lyapunov exponents of the three chaotic oscillators were obtained by applying Wolf’s method [1]. The initial conditions $(x_0,y_0,z_0)$ matters to reduce computing time in computing Lyapunov exponents and $D_{KY}$. In this manner, the appropriate initial conditions are: $(a{e}^{0.5},0.5,0.75)$ for the chaotic oscillator with infinite equilibria (1), $(0.5,0.5,0.5)$ for Rössler (2), and $(0.1,0.1,0.1)$ for Lorenz (3).

The DE and PSO algorithms were executed with the same conditions for the three chaotic oscillators, i.e., the same number of populations (P) and maximum generations (G). The numerical simulations were performed for 10,000 iterations, discarding the first 1000 iterations as they include the transient behavior. In this manner, the optimization was run to maximize $D_{KY}$ with the following conditions in both DE and PSO: $G=20$, $P=30$, and the search space $0.001\le a\le 1$ for the system with infinite equilibria; $G=20$, $P=30$, and the search spaces $0.001\le a\le 10$, $0.001\le b\le 10$, $0.001\le c\le 30$ for Rössler; and $G=20$, $P=30$, and the search spaces $0.001\le \sigma \le 60;0.001\le \rho \le 180;0.001\le \beta \le 30$ for Lorenz. The results are given in Table 3, where it can be appreciated that $D_{KY}>2$ in all cases and the maximum variation is approximately $\pm 0.05$, which demonstrates the usefulness of applying metaheuristics like DE and PSO algorithms.

Table 3. Results of 10 runs performed by differential evolution (DE) and particle swarm optimization (PSO) for the three chaotic oscillators.

Oscillator	Runs	DE			PSO
		Max D${}_{\mathit{KY}}$	Mean	$\mathit{\sigma }$	Max D${}_{\mathit{KY}}$	Mean	$\mathit{\sigma }$
Infinite Equilibria	1	2.0781	2.0789	0.02080	2.0764	2.0753	0.02059
	2	2.0791	2.0788	0.02079	2.0767	2.0753	0.02036
	3	2.0781	2.0787	0.02071	2.0767	2.0759	0.02036
	4	2.0788	2.0787	0.02075	2.0716	2.0765	0.02073
	5	2.0785	2.0787	0.02063	2.0740	2.0738	0.02077
	6	2.0786	2.0785	0.02026	2.0766	2.0715	0.02039
	7	2.0781	2.0788	0.02043	2.0766	2.0734	0.02077
	8	2.0782	2.0788	0.02031	2.0754	2.0751	0.02031
	9	2.0786	2.0789	0.02051	2.0754	2.0752	0.02054
	10	2.0789	2.0787	0.02070	2.0737	2.0736	0.02045
Rössler	1	2.0250	2.0395	0.02036	2.0235	2.0230	0.03285
	2	2.0350	2.0377	0.02043	2.0225	2.0224	0.03286
	3	2.0510	2.0364	0.02046	2.0270	2.0210	0.03286
	4	2.0300	2.0374	0.02048	2.0229	2.0240	0.03289
	5	2.0500	2.0381	0.02038	2.0198	2.0220	0.03285
	6	2.0203	2.0383	0.02039	2.0269	2.0240	0.03288
	7	2.0203	2.0363	0.02028	2.0233	2.0230	0.03288
	8	2.0204	2.0373	0.02044	2.0170	2.0240	0.03287
	9	2.0204	2.0405	0.02026	2.0254	2.0230	0.03285
	10	2.0055	2.0414	0.02039	2.0265	2.0220	0.03287
Lorenz	1	2.0754	2.0773	0.01486	2.0719	2.0713	0.00969
	2	2.0730	2.0732	0.01481	2.0718	2.0712	0.00969
	3	2.0843	2.0783	0.01466	2.0706	2.0703	0.00969
	4	2.0791	2.0775	0.01478	2.0712	2.0705	0.00969
	5	2.0785	2.0772	0.01474	2.0712	2.0702	0.00969
	6	2.0839	2.0770	0.01486	2.0662	2.0710	0.00969
	7	2.0796	2.0752	0.01487	2.0690	2.0702	0.00969
	8	2.0739	2.0738	0.01479	2.0684	2.0708	0.00969
	9	2.0733	2.0733	0.01451	2.0692	2.0703	0.00969
	10	2.0741	2.0740	0.01431	2.0714	2.0744	0.00969

Table 3 summarizes the feasible optimized results provided by DE and PSO algorithms for the three chaotic oscillators (1), (2), and (3). The highest values of D${}_{KY}$ are given in Table 4, where one can see the values of the design parameters associated to the best five values of $D_{KY}$ provided by DE and PSO, and it also shows their associated LE+.

Table 4. Design parameters of the five highest values of D${}_{KY}$ from Table 3, for each metaheuristic and chaotic oscillator, and their corresponding value of LE+.

Oscillator	DE			PSO
	Design Parameters	LE${}_{+}$	D${}_{\mathit{KY}}$	Design Parameters	LE${}_{+}$	D${}_{\mathit{KY}}$
Infinite Equilibria	a = 0.1006	0.0753	2.0791	a = 0.0937	0.0753	2.079
	a = 0.0938	0.0730	2.0789	a = 0.1007	0.0788	2.0789
	a = 0.0939	0.0726	2.0786	a = 0.1028	0.0796	2.0796
	a = 0.0935	0.0726	2.0785	a = 0.0935	0.0726	2.0785
	a = 0.1007	0.0747	2.0788	a = 0.1007	0.0787	2.0791
Rössler	a = 0.3609 b = 0.1000 c = 11.3470	0.2711	2.07890	a = 0.3609 b = 0.1000 c = 11.3470	0.2711	2.02700
	a = 0.3947 b = 0.5490 c = 9.12060	0.2600	2.07140	a = 0.3947 b = 0.5490 c = 9.12060	0.2600	2.02690
	a = 0.3720 b = 0.2055 c = 12.0147	0.2710	2.07870	a = 0.3947 b = 0.2055 c = 9.12060	0.2600	2.02650
	a = 0.3930 b = 0.8505 c = 13.0501	0.2645	2.07810	a = 0.3930 b = 0.8505 c = 13.0501	0.2645	2.02350
	a = 0.3643 b = 0.1537 c = 12.7643	0.2764	2.07880	a = 0.3643 b = 0.1537 c = 12.7643	0.2764	2.02330
Lorenz	$\sigma =29.9226$$\rho =89.8095$$\beta =13.9727$	3.3129	2.08430	$\sigma =30.0000$$\rho =90$$\beta =12.3872$	3.3129	2.07230
	$\sigma =29.9388$$\rho =89.8923$$\beta =14.1895$	3.3122	2.08390	$\sigma =29.8297$$\rho =90$$\beta =13.7954$	3.3122	2.07290
	$\sigma =29.7786$$\rho =89.7268$$\beta =13.4876$	3.3168	2.07960	$\sigma =29.9966$$\rho =90$$\beta =13.4876$	3.3168	2.07190
	$\sigma =29.9222$$\rho =89.9781$$\beta =14.1956$	3.3149	2.07910	$\sigma =30.0000$$\rho =90$$\beta =14.1956$	3.3149	2.07197
	$\sigma =29.7066$$\rho =89.8899$$\beta =13.7180$	3.3199	2.07410	$\sigma =29.8375$$\rho =90$$\beta =13.8036$	3.3199	2.07179

5. Encrypting Color Images Using State Variables with High D${}_{\mathit{KY}}$ and LE+

Chaotic masking has been performed for color images using chaotic oscillators that are synchronized by applying different techniques, as already shown in [20], where one can see details on the hardware implementation of a chaotic secure communication system using field-programmable gate arrays (FPGAs).

Figure 2 sketches the chaotic encryption of a color image, which basically consists of a transmitter and receiver blocks that communicate through a chaotic channel. The transmitter has a master chaotic oscillator that generates signals $E_D$ that contaminate the original image with data $E_M$, this masking process produces the chaotic channel containing data $E_T=E_D+E_M$ that is the input of the receiver system. The information is recovered when the chaotic oscillator in the receiver produces data $E_R=E_D$ because both oscillator are synchronized [20]. Therefore, the recovered image is saved into data $E_M^{\prime }=E_T-E_R$.

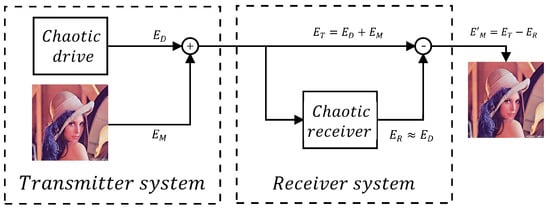
Figure 2. Encryption process adding chaos to an original image and recovering it through synchronizing two chaotic oscillators, as already shown in [20].

The chaotic encryption is applied herein to an RGB image of size 512 × 512 pixels. The chaotic data is generated by the chaotic oscillators with the best two $D_{KY}$ values from Table 4. In this manner, each state variable of each chaotic oscillator was selected to generate the chaotic data and then the correlation analysis between the original image and the chaotic channel as shown in Table 5.

Table 5. Correlation between the original image and the chaotic channel using each state variable of the two highest $D_{KY}$ of each chaotic oscillator.

Oscillator	D${}_{\mathit{KY}}$	State Variables	Correlation
Infinite Equilibria	2.0791	x	0.0332
		y	0.0589
		z	0.0371
	2.0789	x	0.0447
		y	0.2961
		z	0.0423
Rössler	2.0789	x	0.1144
		y	0.0075
		z	0.0112
	2.0788	x	0.0084
		y	0.0038
		z	0.0034
Lorenz	2.0843	x	0.0173
		y	0.0152
		z	0.0025
	2.0839	x	0.0009688
		y	0.0029
		z	0.0010

The experiments show that the best chaotic oscillator is Lorenz because it provides the lowest correlation. In this manner, Figure 3 shows the encryption of an RGB image using the state variable x of the Lorenz chaotic oscillator for the case $\mathit{D}{}_{\mathit{KY}}$ = 0.0009688. This confirms that the chaotic encryption is much better if one maximizes $D_{KY}$, as showed herein by applying DE and PSO.

Figure 3. Original image on the left, encrypted image in the chaotic channel in the center, and the recovered image on the right.

6. Conclusions

This article showed that the chaotic encryption of an image can be enhanced when using chaotic data from an oscillator that has a high Kaplan–Yorke dimension $D_{KY}$. However, maximizing $D_{KY}$ of a chaotic oscillator is not a trivial task because the design parameters or coefficients of the mathematical model can have huge search spaces, as shown by the three case studies documented herein.

We showed that metaheuristics like DE and PSO algorithms are quite suitable to maximize $D_{KY}$, both algorithms were run with the same conditions to find feasible solutions. The two highest values of $D_{KY}$ of each chaotic oscillator were selected to encrypt an RGB image and a correlation analysis was performed between the original image and the chaotic channel to identify the best masking. In this manner, after testing each state variable of each chaotic oscillator, the lowest correlation was provided by Lorenz, as showed in Table 5. This confirms that the best chaotic encryption can be performed if one maximizes $D_{KY}$, as shown herein applying DE and PSO.

References