Towards Analyzing the Complexity Landscape of Solidity Based Ethereum Smart Contracts

Abstract

Blockchain-based decentralized cryptocurrency platforms are currently one of the hottest topics in technology. Although most of the interest is generated by cryptocurrency related activities, it is becoming apparent that a much wider spectrum of applications can leverage the blockchain technology. The primary concepts enabling such general use of the blockchain are the so-called smart contracts, which are special programs that run on the blockchain. One of the most popular blockchain platforms that supports smart contracts is Ethereum. As smart contracts typically handle money, ensuring their low number of faults and vulnerabilities are essential. To aid smart contract developers and help to mature the technology, we need analysis tools and studies for smart contracts. As an initiative for this, we propose the adoption of some well-known OO metrics for Solidity smart contracts. Furthermore, we analyze more than 40 thousand Solidity source files with our prototype tool. The results suggest that smart contract programs are short, neither overly complex nor coupled too much, do not rely heavily on inheritance, and either quite well-commented or not commented at all. Moreover, smart contracts could benefit from an external library and dependency management mechanism, as more than 85% of the defined libraries in Solidity files code the same functionalities.

1. Introduction

Decentralized cryptocurrencies have gained considerable interest and adoption since Bitcoin was introduced in 2009 [1]. Users in a cryptocurrency network run a consensus protocol to maintain and secure a shared ledger of data (the blockchain). This means that cryptocurrencies are administered publicly by users in the network without relying on any trusted third parties. Blockchains were initially introduced for peer-to-peer payments, but since then it have become clear that blockchain technology can be used for much more than that. One such new use of blockchains is the execution of so-called smart contracts. A smart contract is a program that runs on the blockchain and has its correct execution enforced by the consensus protocol [2].

In this paper, we focus on the static analysis of smart contracts on the Ethereum network [3,4]. Ethereum is much more than a cryptocurrency blockchain and protocol. It defines a Turing-complete programming platform and a run-time environment called EVM (Ethereum Virtual Machine). EVM can run the bytecodes of smart contracts. Smart contracts can be written in several programming languages, but Solidity [5], a contract-oriented language is by far the most popular one.

At the end of 2018, 5–10% of the jobs advertised on one of the biggest freelancer site (https://www.guru.com, searched on 4 December 2018) was related to smart contracts and blockchain. There are also some undergraduate courses appearing to teach smart contract programming, for example at the University of Maryland [6]. Therefore, the growing importance and need for blockchain-related programming is becoming more and more obvious. Countries like the USA and China are heading the run to exploit all blockchain potential. These novelties call for specific tools, paradigms, principles, approaches, and research to deal with it and for a specific Blockchain Oriented Software Engineering (BO SE) [7].

As metrics for other languages play a very important role in various QA (i.e., quality assurance) activities, we anticipate that the same would be true for Solidity smart contracts. Given the nature of the blockchain-based programs, namely that once deployed they cannot be altered anymore, makes it even more crucial to be able to check and validate the code beforehand. TheDAO (i.e., Decentralized Autonomous Organization) smart contract is a classic example of how big damage can be caused by a smart contract with critical vulnerabilities. An exploit of a bug [8] in this contract led to a 60 million US dollar loss in June 2016.

If we think of the advanced usage of source code metrics in bug/vulnerability prediction, code review and refactoring or anti-pattern detection in classic OO (i.e., object-oriented) languages, it is clear that smart contract programming would also benefit from such easy to calculate static source code metrics. As the structure of the Solidity language is quite similar to that of the OO languages, the classic Chidamber & Kemerer [9] metrics can be defined for smart contracts in a quite straightforward manner.

Given such metrics for smart contracts, we can leverage the massive body of work existing in the OO metrics literature. There are numerous studies what concerns the relationship among software metrics and software quality, maintainability, reliability, performance defectiveness and so on. One of the first works dealing with OO software metrics and their measurement is the one by Chidamber and Kemerer (C&K), who introduced the popular C&K metrics suite for OO software systems [9]. Based on this work, many empirical studies showed significant correlations between some of C&K metrics and bug-proneness [10,11,12,13]. Product metrics, extracted by analyzing the static code of software, have been used to build models that relate these metrics to failure-proneness [10,11,12,14].

There are various static analysis tools targeting smart contracts specifically. Such tools are the Manticore [15] symbolic EVM byte code execution tool, security checker tools like Mythril [16] or Oyente [17,18], the solidity-coverage test coverage tool [19], or Solcheck [20] and Solint [21] linter tools.

In this paper, we propose some well-known static source code metrics for measuring smart contracts’ size, complexity, coupling, and inheritance-related attributes. We implemented a prototype tool called SolMet [22] that is able to parse Solidity smart contracts and calculate these metrics on them. To analyze the typical metric landscape of the smart contracts deployed on the Ethereum network, we collected 40,352 smart contracts with validated Solidity source code.

2. Smart Contract Analysis Approach and Study

2.1. The Solidity Language

Solidity is a contract-oriented, high-level language for implementing smart contracts. It was influenced by C++, Python, and JavaScript and is designed to target the Ethereum Virtual Machine (EVM). Solidity is statically typed, supports inheritance, libraries and complex user-defined types among other features. Using Solidity, it is possible to create contracts for voting, crowdfunding, blind auctions, multi-signature wallets and more.

2.2. Calculating Metrics for Solidity Programs

A contract in the sense of Solidity is a collection of code (its functions) and data (its state) that resides at a specific address on the Ethereum blockchain. Contracts also support constructors, special functions that are run during the creation of the contract and cannot be called afterward. Given the obvious similarities in structure, it is easy to map contracts to classes, states to attributes, and functions to member operations in the OO world and interpret classic OO metrics for Solidity-based smart contracts.

To calculate these metrics, we implemented a prototype tool called SolMet in Java. For parsing the Solidity source code, we used a generated parser based on a slightly modified version of an existing antlr4 grammar [23]. We made only a few adjustments (i.e., added proper handling of the underscore operator and language version identifiers) in the antlr grammar to be able to parse older and newer versions of the Solidity language as well. The calculation of metrics was performed either on the Solidity source code directly or by implementing visitors to collect the necessary information from the parser built abstract syntax-tree (AST). The source code and usage instructions of the SolMet tool is available on GitHub [22]. The tool is able to calculate the source code metrics listed in

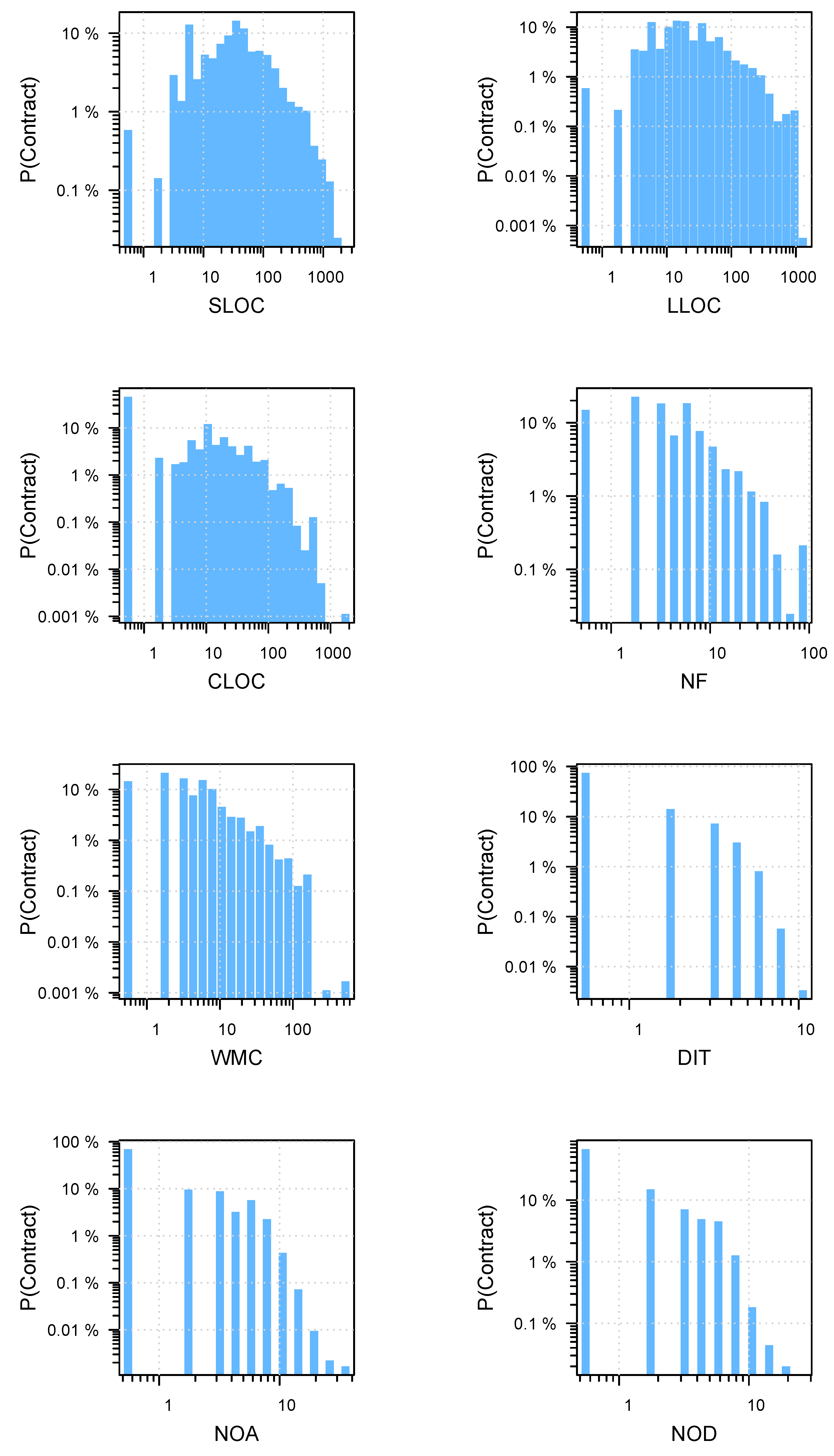
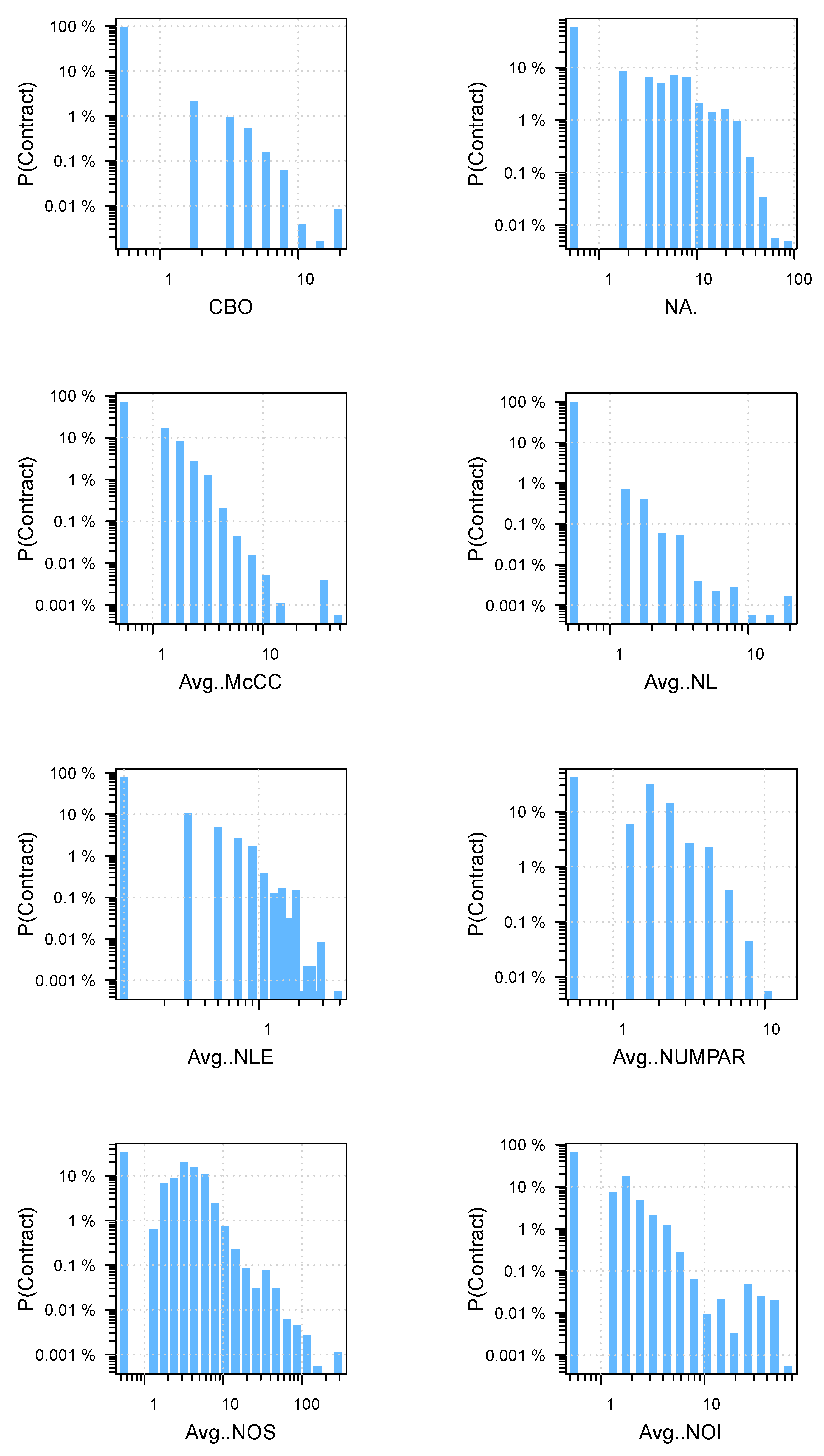
Table 1. Implemented source code metrics for smart contracts.

Metric	Description
SLOC	Source lines of code
LLOC	Logical lines of code
CLOC	Comment lines of code
NF	Number of functions
McCC	McCabe’s cyclomatic complexity
WMC	Weighted method complexity
NL	Nesting level
NLE	Nesting level else-if
NUMPAR	Number of parameters
NOS	Number of statements
DIT	Depth of inheritance tree
NOA	Number of ancestors
NOD	Number of descendants
CBO	Coupling between object classes
NA	Number of attributes (i.e., states)
NOI	Number of outgoing invocations (i.e., fan-out)

.

SLOC. The source lines of code metric denotes the number of source code lines of the contract, library or interface. It is calculated based on the starting and ending line number of the contracts, libraries, and interfaces provided by the parser.

LLOC. The number of logical lines of code metric counts the non-empty and non-comment lines of the contract, library or interface (i.e., only those lines are counted that contain actual statements). It is calculated based on the Solidity source code of the given contract, library or interface. We scan the source code line by line and filter out all the empty and comment lines to get the LLOC metric. We consider all lines to be comment only lines if they start with “/*”, “*”, “//” or end with “*/”.

CLOC. The comment lines of code metric is the number of comment lines of the contract, library or interface. It is calculated from the Solidity source file with the heuristic described above at LLOC metric.

NF. The number of functions in the contract, library or interface. It is calculated based on the function nodes in the AST, a simple visitor calculates how many function nodes are encountered during the traversal of the parse tree.

McCC. McCC is the McCabe’s cyclomatic complexity [14] (the number of branching statements + 1) of the functions. We calculate the McCabe complexity by traversing and counting all the branching statements (if, for, while, do-while) within a function (i.e., in the sub-tree of the AST under the appropriate function node). To represent the McCC value for contracts, we calculate the average of McCC values for all the functions within a contract.

WMC. The weighted method complexity metric is the weighted complexity of functions in a contract, library or interface. For weights, we use the McCC complexity metric of the functions. Therefore, WMC is the sum of the McCC values of the functions within a contract, library or interface.

NL. The nesting level metric denotes the sum of the deepest nesting level of the control structures within the functions of a contract, library or interface. The nesting levels of the individual functions are calculated by visiting all the statements in the sub-tree rooted by the function in question and counting the number of branching statements on the path from the statement to the function definition traversing the parent nodes. The final NL value of a function is the maximum of such nesting level values calculated for the statements within the function. The lowest possible NL value (i.e., where there are no embeddings within a function) is 0. To represent the NL value for contracts, we calculate the average of NL values for all the functions within a contract.

NLE. The nesting level without else-if metric is a variant of the NL metric described above. The only difference in the calculation is that if statements do not add to the nesting level count if they appear in an else-if structure. To represent the NLE value for contracts, we calculate the average of NLE values for all the functions within a contract.

NUMPAR. The number of parameters metric simply counts how many parameters a function has. The calculation of this metric is based on a visitor visiting the function nodes in the AST. To represent the NUMPAR value for contracts, we calculate the average of NUMPAR values for all the functions within a contract.

NOS. The number of statements metric is again a simple size metric that counts how many statements there are in a contract, library or interface. The calculation of this metric is based on a visitor visiting the statement nodes in the AST. To represent the NOS value for contracts, we calculate the average of NOS values for all the functions within a contract.

DIT. The depth of inheritance metric measures how deep a contract, library or interface is in the inheritance tree. We calculate this metric with a recursive algorithm that assigns a DIT value to each contract, library or interface that is the maximal DIT measure of its parents plus 1. Since Solidity supports multiple inheritance, we always take the deepest path through the inheritance tree. The DIT values of parent nodes are calculated recursively until we reach a node that has no parents, hence gets a DIT value of 0.

NOA. The number of ancestors metric counts all the different direct or transitive ancestors of a contract, library or interface. This measure tells us how many different contracts one inherits information from. The metric is calculated by traversing the parse tree through the inheritance relations and counting all the different contracts, libraries or interfaces encountered on the path.

NOD. The number of descendants metric measures how many different direct or transitive descendants a contract, library or interface has. It is measured with a recursive algorithm similar to that of DIT. The NOD value of each node in the inheritance list is incremented by one if the visited contract, library or interface derives from that node.

CBO. The coupling between object classes metric in the OO paradigm measures the number of classes that the actual class is connected to (by using the class as an attribute type, method parameter or return value, etc.). We abstracted this concept here to reflect how the contracts are connected to each other, namely how many other types of contracts are used by a particular contract (as state variable type, local variable type, function parameter, etc.). The metric is calculated by visiting and counting the user-defined type name nodes in the AST, which are the usage points of the other user-defined types (i.e., contracts, libraries or interfaces) within a contract.

NA. The number of attributes metric is adapted to Solidity to count the number of state variables. This metric counts all the state variable declaration nodes in the AST belonging to a contract, library or interface.

NOI. The number of outgoing invocations metric measures how many different functions are called from a function in a contract or library. This metric is meant to measure coupling through function calls. We consider only the calls to user-defined functions, and not to built-in functions, but we include modifier and event calls as well. The metric is calculated by visiting the call nodes in the AST. To represent the NOI value for contracts, we calculate the average of NOI values for all the functions within a contract.

2.3. Collecting Ethereum Smart Contracts

To use SolMet, we collected 40,352 Solidity source code files containing 208,639 contracts, libraries and interfaces altogether. We chose not to mine GitHub for smart contract codes, as we wanted to get a picture of smart contracts already deployed on the Ethereum network. For this, we downloaded the validated source code of deployed smart contracts monitored by the Etherscan [24] Ethereum blockchain explorer site. Validated source code means that the functionality of the Solidity source code and the deployed EVM bytecode (the Ethereum network stores only the latter one) is manually compared and validated. Thus, we can be sure that the code we analyze is actually the same as the contract being deployed on the network. We ran SolMet on each Solidity file and collected the calculated source code metrics into a comma-separated file. All the analyzed contract source code (.sol files), as well as the metric results, are publicly available on GitHub [25].

3. Analysis Results

Table 2. Statistics of the analyzed contracts.

	Total	Avg./sol File
Contract	178,987	4.44
Library	22,920	0.13
Interface	6732	0.04

summarizes the number of analyzed Ethereum smart contracts, libraries, and interfaces. In 40,352 Solidity source code files, we analyzed 178,987 contracts, 22,920 libraries, and 6732 interfaces (i.e., 208,639 elements altogether). The average number of contracts, libraries, and interfaces are shown in the second column.

On average, each Solidity source file contains 4.44 contracts and approximately every eighth file defines a library. An interesting note is that above 85% of these libraries are connected to the same functionality, namely, they define safe mathematic operations (e.g., division by zero and overflow checks). Interfaces are very rare; roughly, every 25th Solidity source code contains one.

Table 3. Descriptive statistics of the calculated metric values.

Metric	Min	Max	Avg.	Q1	Median (Q2)	Q3	Std.dev.
SLOC	1	1985	57.67	12	29	53	106.36
LLOC	1	1388	36.43	10	19	36	68.40
CLOC	0	1783	13.30	0	2	14	32.03
NF	0	127	4.94	2	3	5	6.44
WMC	0	522	6.66	2	4	6	12.44
DIT	0	11	0.82	0	0	1	1.12
NOA	0	30	1.17	0	0	2	1.86
NOD	0	22	1.17	0	1	2	1.64
CBO	0	17	0.20	0	0	0	0.63
NA	0	99	2.47	0	1	3	4.44
Avg. McCC	0	43	1.15	1	1	1.20	0.57
Avg. NL	0	17.86	0.14	0	0	0.20	0.31
Avg. NLE	0	4.5	0.13	0	0	0.20	0.27
Avg. NUMPAR	0	12	1.50	1	1.50	2	0.96
Avg. NOS	0	273	2.64	0	2.67	4	2.92
Avg. NOI	0	58	0.89	0	0.75	1.33	1.30

displays the descriptive statistics of the calculated source code metrics for all the contracts, libraries and interfaces altogether. Although the standard deviations are quite significant, we can draw some general conclusions.

On average, contracts are short (not considering empty and comment lines). They are actually either quite well-commented or not commented at all. Comment lines to logical lines ratio is high on average, but we can see that the median value of comment lines is only 2, thus there are many contracts with less than or equal to 2 comment lines.

On average, each contract defines approximately 5 functions, but the average weighted complexity is only 6.66. This low complexity is also observable on the average McCabe’s cyclomatic complexity values over all the functions, which is 1.15. It means that most of the functions use sequential control flows without too much complexity. This finding is strengthened by the average nesting level (Avg. NL and NLE) values, as the average of average deepest nesting in control structures is only 0.14 and 0.13, respectively. There are very few deeply nested control structures in smart contracts.

The coupling metric (CBO) measures how much contracts depend on each other. As even the third quartile of CBO values is 0 and the average is only 0.2, we can conclude that it is very rare that one contract uses another in any form. The average of the number of outgoing invocations (NOI) metric is also low, 0.89. This supports the fact that contracts are very loosely coupled and most of their functions are called by the users of the contract and not by other contract functions.

Inheritance features are seldom used. The depth of inheritance metric average is 0.82, its third quartile is only 1. More than half of the contracts have zero ancestors (NOA), meaning that inheritance is not used at all in these cases. However, the average NOA value is 1.17, so a smaller fraction of contracts do have ancestors and they have more than one of them. The average number of descendants (NOD) is also 1.17, but its distribution is more even, meaning that fewer contracts have zero descendants and the deviation of the values is lower compared to NOA.

Regarding the state variables, we can say that they are moderately used. The average of the NA metric value is 2.47, meaning that a contract defines and uses approximately 2.5 state variables on average.

3.1. Metrics Distributions

We plotted the frequencies of the individual metric values calculated for contracts, libraries, and interfaces in Figure 1 and  Figure 2. The x-axis denotes the metric values, while the y-axis shows the proportion of analyzed contracts with that particular value. All the charts are plotted on a log-log scale, meaning that values on both axes increase exponentially as large values are very rare.

The SLOC and LLOC charts in Figure 1 for example, show the source and logical code lines metric frequences. For the majority of the contracts, both types of source code line measures vary between 10 and 100. Values below 10 are not rare either, however, values above 1000 appear only in a very small fraction of the contracts. The largest SLOC and LLOC values belong to the same smart contract, UberDelta (Ethereum address is 0xd546551924a883b604d4127b0af309c95ba9ba6d). Even though the contract is very long, none of its other metrics are as extreme. For example, its WMC is only 77, where the maximum of WMC values among the contracts is 522. Its average number of statements and nesting level is low as well. Therefore, this contract provides many small functions, but in overall, its implementation is pretty straightforward.

The number of statements (NOS) is another size metric, the function wise average NOS values vary between 0 and 10, and values above 10 are uncommon. The largest Avg. NOS value is 273 in the Data contract (Ethereum address is 0xc244d24a3293150709913ce8377dc2854a3ec4a1). This contract contains only a constructor, in which a mapping is being initialized statically with predefined values (see sample in Listing 1).

Listing 1. A small excerpt from the Data contract.

Regarding the comment lines, more than 40% of the contracts contain no comments at all. Even the median of CLOC is only 2. In the rest of the smart contracts, CLOC is distributed around the value of 10. CLOC values above 100 are very rare. The maximum value of 1783 comment lines belongs to the contract genEOS (Ethereum address is 0xbfa82fbe0e66d8e2b7dcc16328db9ecd70533d13). The really interesting thing is that its LLOC metric (i.e., lines containing actual statements) is only 67. The reason is that the functions of this contract are separated with long blocks of unintelligible comments, like the one shown in Listing 2.

Listing 2. A small excerpt from the genEOS contract.

Regarding the number of functions (Figure 1, NF), the maximum is 127; the quartiles are only 2, 3, and 5. Interestingly, more than 10% of the contracts contain no functions at all. These contracts typically contain enums, structs or events and are used as parents of other contracts. The majority of contracts contain 1 to 10 functions and NF values above 30 are very rare. The maximal NF value, 127 appears in a library called CryptoUtils. Strangely enough, this library is present in eight entirely different Solidity files in the exact same form.

As for the complexity measures, Figure 1 shows the weighted complexity of the functions (WMC) and Figure 2 displays the average cyclomatic complexity and nesting level histograms (Avg. McCC, Avg. NL and Avg. NLE). WMC values between 1 and 10 are very frequent, contracts with WMC between 10 and 100 appear but much less common. WMC above 100 is very rare, however, the maximum is 522, but quartiles are only 2, 4, and 7, respectively. The contract called GeneScience has WMC of 522 in three different versions of the MonsterCore Solidity file (Ethereum address is 0x5dbd2e33f4aceeefba9d7d542913ba3e82216b7b). Nonetheless, most of the complexity comes from quite simple mapping statements achieved by sequential if constructs, like the one displayed in Listing 3.

Listing 3. A small excerpt from the GeneScience contract.

In line with this, the average nesting level metrics (NL and NLE) are around 0.5, which indicates that the control structures are indeed not nested deeply into each other. Therefore, this high WMC value is still manageable and reflects a somewhat special case.

The same tendency can be observed for nesting level in the context of all smart contracts. The vast majority of the contracts have an average nesting level between 0 and 1, indicating that deeply nesting control structures are something that is very uncommon in Solidity smart contracts. Considering this, the maximum value of Avg. NL (17.86) is a very outlying value. NL metric counts each else-if statement as an additional depth and the contract in question, WinMatrix (Ethereum address is 0xda16251b2977f86cb8d4c3318e9c6f92d7fc1a8f) contains a function with a huge if-else-if structure (see Listing 4).

Listing 4. A small excerpt from the WinMatrix contract.

The NLE metric is similar to NL, but without counting the else-if statements, thus the Avg. NLE metric for the very same contract is only 0.57. Avg. NLE is small in general, its maximum is only 4.5. This indicates that deep nesting is only induced by large if-else-if structures, but they are similar to switch-case statements, which argued to be easy to understand, thus not affecting complexity too much. However, Solidity does not support the switch statement, thus using if-else-if is the only possible way of expressing such case selections.

On average, functions have a small number of parameters (Avg. NUMPAR). Figure 2 shows that most of the contracts have average parameter numbers in the range of 0 to 3. The maximum value of 12 is in the BuilderCrowdfunding contract (Ethereum address is 0x113058c101b2d78e001d4a7d2174a66b5ff3a4a7). Function create takes 12 parameters (see Listing 5).

Listing 5. A small excerpt from the BuilderCrowdfunding contract.

Coupling is very limited among smart contracts. The majority of contracts, libraries, and interfaces have a CBO value of 0. However, contract DaiFab (this contract appears in 15 different Solidity files that seem to be identical) has a CBO of 17. However, that property is exceptional, as CBO values above 5 are extremely rare. Most of the contracts define a self-contained programming unit without any connection to other contracts. What is more, even the functions of a contract tend not to call any other functions within the same Solidity file. Avg. NOI values are mostly in the range of 0 to 2. The maximum of 58 is calculated for the contract InnovationAndCryptoVentures2018FinalProjects (Ethereum address is 0xb8d740574a9d31d55af5d78bdedac96cd7b33f7f), but all of the calls are event emission calls and not real function calls (see Listing 6).

Listing 6. A small excerpt from the InnovationAndCryptoVentures2018FinalProjects contract.

Solidity supports inheritance among the contracts. The majority of the contracts have a depth of inheritance (DIT) metric of 0 (see Figure 1). The rest of the contracts have a DIT between 1 and 6, higher DIT values are extreme and rare. The contract EtherbotsCore (Ethereum address is 0xd2f81cd7a20d60c0d558496c7169a20968389b40) has the maximum DIT value of 11 in the following inheritance chain.

$$Ownable\to Pausable\to EtherbotsPrivileges\to EtherbotsBase\to EtherbotsNFT$$

$$\to PerkTree\to EtherbotsAuction\to PerksRewards\to Mint\to EtherbotsMigrations$$

$$\to EtherbotsBattle\to EtherbotsCore$$

Regarding the NOA and NOD inheritance metrics, a large amount of contracts have no ancestors and/or descendants at all. Values between 1 and 10 are also frequent for both metrics, but more than 10 ancestors and/or descendants are very rare.

The number of state variables (NA metric) is 2.47 on average. The majority of contracts use between 0 and 10 state variables, however, the maximum is 99 for the CryptoUtils library. This is the library having the largest NF value as well. It defines many state variables as constants and uses them in simple functions to perform some bit manipulations on the input. A code snippet in Listing 7 demonstrates it.

Listing 7. A small excerpt from the CryptoUtils library.

All the detailed numbers and charts of the presented results are available online as well [25].

3.2. Discussion

Table 4. Descriptive statistics of the calculated metric values.

Metric	Most Typical Values	Level Compared to OO Programs
SLOC	10–100	Low
LLOC	10–100	Low
CLOC	0 and 10–100	Similar
NF	1–10	Very Low
WMC	1–50	Low
DIT	1–5	Similar
NOA	1–10	Low
NOD	1–10	Low
CBO	0–5	Very Low
NA	0–10	Similar
Avg. McCC	1–5	Very Low
Avg. NL	0–2	Very Low
Avg. NLE	0–1	Very Low
Avg. NUMPAR	0–3	Low
Avg. NOS	0–10	Very Low
Avg. NOI	0–2	Very Low

summarizes our findings and their comparison with typical OO metric values (Very Low, Low, or Similar). What we can observe is that except several extreme high values for each metrics, most of the smart contracts share some common properties. Most of them are short, defines only a few functions with few input parameters and sequential control structures. There is no common trend in using comments; the contracts are either well-commented or not commented at all.

Coupling is very low among the contracts, very few of the contracts use other contracts directly. Inheritance features are seldom used, more than half of the contracts have no ancestors. Regarding the state variables, we can say that they are moderately used.

We can see that almost all typical metrics have lower values compared to OO programs. Comments, the depth of inheritance and number of attributes metrics are those that show a similar level of values than that of the OO programs.

The fact that above 85% of the defined libraries implement similar safe mathematical operations cries for a better solution at the level of Solidity language. Some kind of common dependencies management system would be desirable.

From practical point of view, the results suggest that the real challenge in smart contract development is not the maintenance and handling the complexity of DApps, rather the secure design and error-free implementation of the program logic with limited language support. However, we believe that having a set of objective measures to assess and monitor the quality of smart contracts can definitely help developers to achieve these objectives.

4. Related Work

Some general works related to blockchain fundamentals are presented in [26,27,28,29,30]. Veranken [26], Giungato et al. [27], and Stuermer et al. [28] focus particularly on the sustainability of blockchain-based solutions. In his work, Lee [29] introduces blockchain technology, standardization, and its relationship with cloud computing. The paper also provides the considerations for blockchain as a service as a new standard. Palos-Sanchez et al. [30] overview the Location Based Services (LBS), which is a current trend for cryptocurrency and blockchain and proof on location for smart contracts.

As smart contracts provide an entirely new platform and paradigm for programmers, new tools helping them in code analysis and validation has already started to roll out. However, due to its recent creation, scientific literature in this area is quite limited.

The work of Tonelli et al. [31] is the closest to our current paper. The authors defined various metrics similar to those of C&K metrics in the OO world and compared their distributions with the metrics extracted from more traditional software projects on more than twelve thousands smart contracts written in Solidity and uploaded on the Ethereum blockchain. Their results show that generally smart contracts metrics have ranges more restricted than the corresponding metrics in traditional software systems. We also defined and implemented C&K style software metrics and analyzed their distributions. However, we worked on four times as many smart contracts and in contrast to Tonelli et al. we analyzed not just size and complexity, but other types of metrics as well, like coupling (CBO) or inheritance (NOA, NOD, DIT).

Numerous papers deal with fuzz testing of smart contracts [32,33,34]. In these works, the authors try to generate test inputs (i.e., transactions) for smart contracts based on various fuzzing techniques to detect possible security vulnerabilities.

There are works addressing vulnerability detection in smart contracts with other strategies as well [35,36,37]. Liu et al. proposed a novel semantic-aware security auditing technique called S-gram for Ethereum [35]. Their key insight is a combination of N-gram language modeling and lightweight static semantic labeling, which can learn statistical regularities of contract tokens and capture high-level semantics as well (e.g., flow sensitivity of a transaction). They implemented S-gram for Solidity smart contracts in Ethereum that can be used to predict potential vulnerabilities by identifying irregular token sequences and optimize existing in-depth analyzers (e.g., symbolic execution engines, or fuzzers).

Kolluri et al. investigate a family of bugs in blockchain-based smart contracts, which they call event-ordering (or EO) bugs [36]. These bugs are intimately related to the dynamic ordering of contract events, i.e., calls of its functions on the blockchain. The authors build an automatic tool called ETHRACER that requires no hints from users and runs directly on Ethereum bytecode. It flags smart contracts providing compact event traces that human analysts can run as witnesses. They found that half of the flagged contracts have subtle EO bugs.

Chang et al. propose an alternative approach to automatically identify critical program paths (with multiple function calls including inter-contract function calls) in a smart contract, rank the paths according to their criticalness, discard them if they are infeasible or otherwise present them with user-friendly warnings for user inspection [37]. Their approach has been implemented in a tool called sCompile. The authors show that many known vulnerabilities can be captured if the user inspects as few as 10 program paths generated by sCompile.

Other papers provide smart contract vulnerability categorization and taxonomies [38,39]. Atzei et al. analyze the security vulnerabilities of Ethereum smart contracts [39], providing a taxonomy of common programming pitfalls which may lead to vulnerabilities. They show a series of attacks which exploit these vulnerabilities, allowing an adversary to steal money or cause other damage.

The “Smart Contract Weakness Classification and Test Cases” website [38] provides a registry of smart contract vulnerabilities mapped to the CWE [40] entries widely used to classify security threats. It not only lists the various vulnerability types but provides real-world smart contracts as test cases for such vulnerabilities.

In contrast to these papers, our purpose is not to detect or categorize concrete vulnerabilities in smart contracts, but to be able to characterize them in terms of software metrics. Nonetheless, upon finding an appropriate set of metrics, we plan to use them for building vulnerability prediction models as well and provide yet another technique to achieve vulnerability detection in smart contracts.

Bartoletti and Pompianu analyzed the most common programming patterns in Ethereum [41]. They identified 9 typical design patterns, Token, Authorization, Oracle, Randomness, Poll, Time constraint, Termination, Math, and Fork check and quantified their usage in various contracts.

Mavridou and Laszka introduce FSolidM, a framework rooted in rigorous semantics for designing contracts as Finite State Machines (FSM). They present a tool for creating FSM on an easy-to-use graphical interface and for automatically generating Ethereum contracts. Furthermore, the authors introduce a set of design patterns, which they implement as plugins that developers can easily add to their contracts to enhance security and functionality.

We do not focus on typical design patterns in smart contracts, rather aim to find an objective set of measures for Solidity programs. However, given a set of well-defined and objective metrics, we can study design and anti-patterns from another perspective.

5. Conclusions and Future Work

In this paper, we proposed the use of well-known static OO metrics to the smart contracts written in the Solidity contract-oriented language. To the best of our knowledge, there are no tools for calculating such metrics. Given the fact that these metrics developed together with the programming languages themselves and many papers showed their efficient applications in QA activities, we believe that the new era of blockchain programming could benefit from them as well.

We implemented several size, complexity, coupling, and inheritance metrics in our SolMet tool and calculated them for 208,639 contracts, libraries, and interfaces from 40,352 Solidity smart contract source code files. We were able to get a quick overview of the typical structure of smart contracts in terms of their sizes, complexity, coupling and inheritance properties. Nonetheless, our tool is still in a development phase, thus all the presented results should be handled with appropriate care.

We continuously add new metrics to SolMet and expect them to provide even more thoughtful insights into smart contract structures. Once a proper metric suite is defined and implemented, we can start using them in various forms that worked very well for other languages, for example, to build bug or vulnerability prediction models, to aid code review and guide refactoring activities or detect common anti-patterns in the code before being deployed and becoming permanent.