Dynamic Evaluation on the Traffic State of an Urban Gated Community by Opening the Micro-Inter-Road Network
Abstract
:1. Introduction
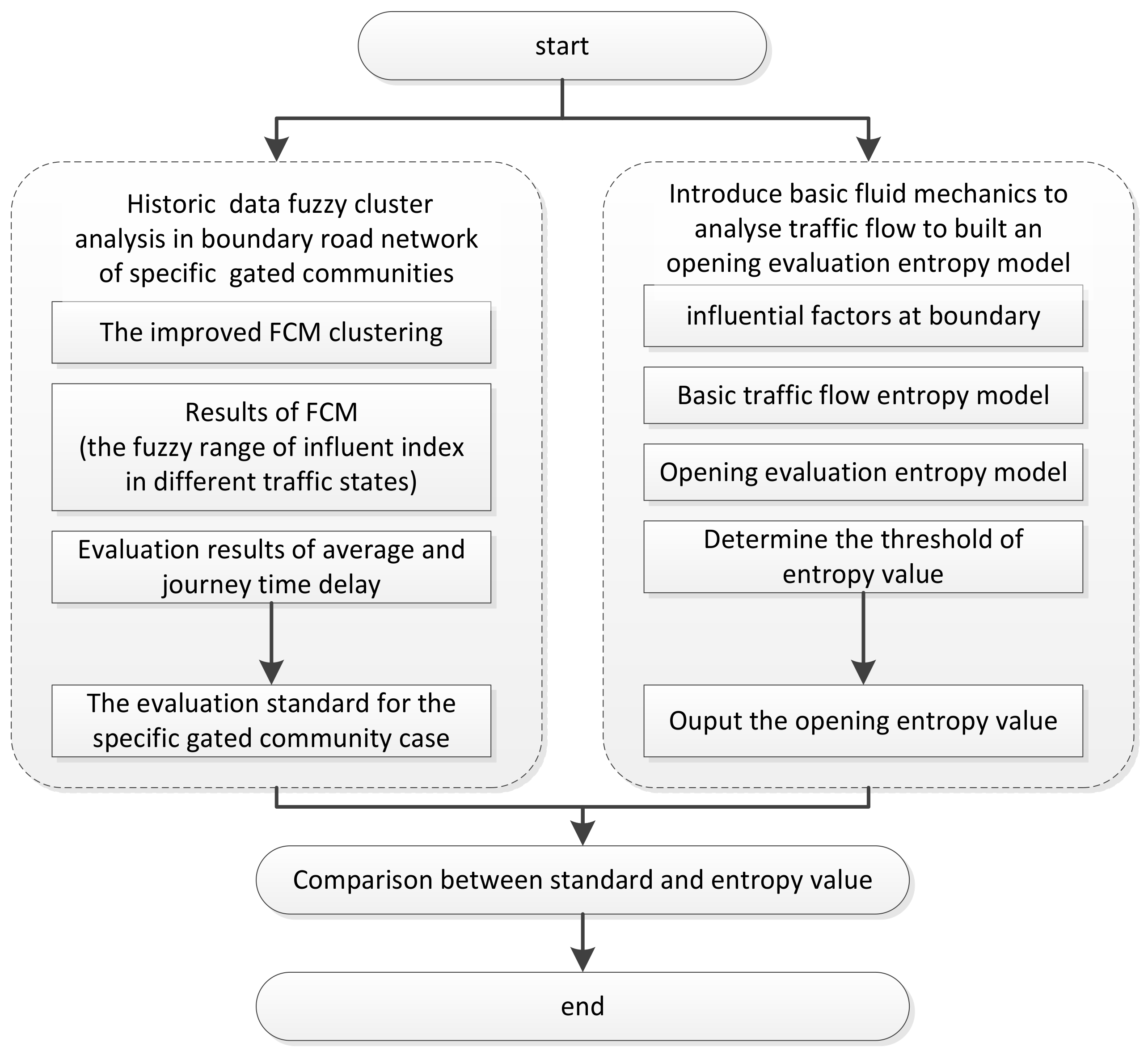
2. Proposed Framework and Process of Comprehensive Opening Evaluation Model
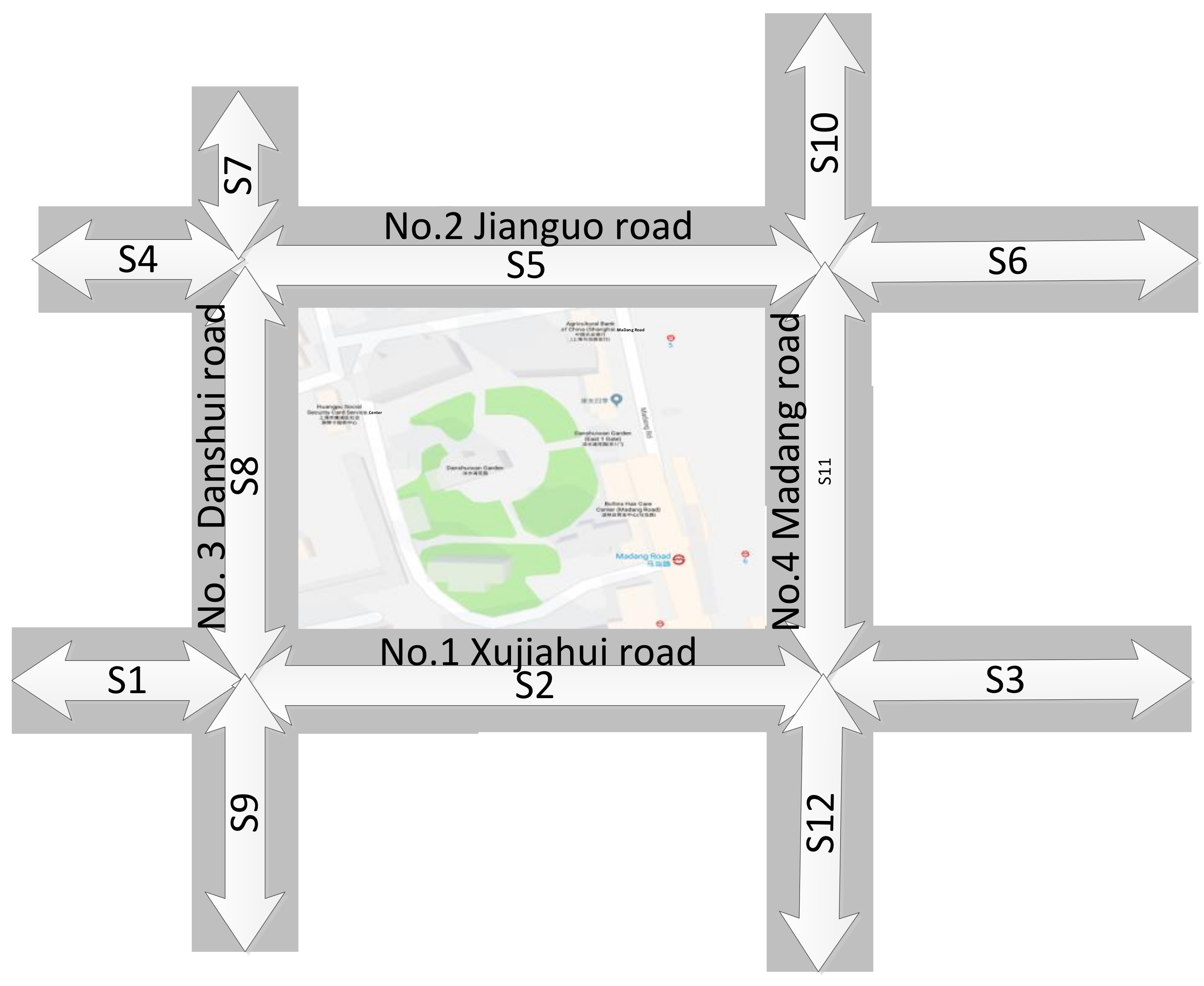
3. Evaluation of the Opening System at the Boundary Road Network
3.1. Variables of Interest at the Boundary Road Network
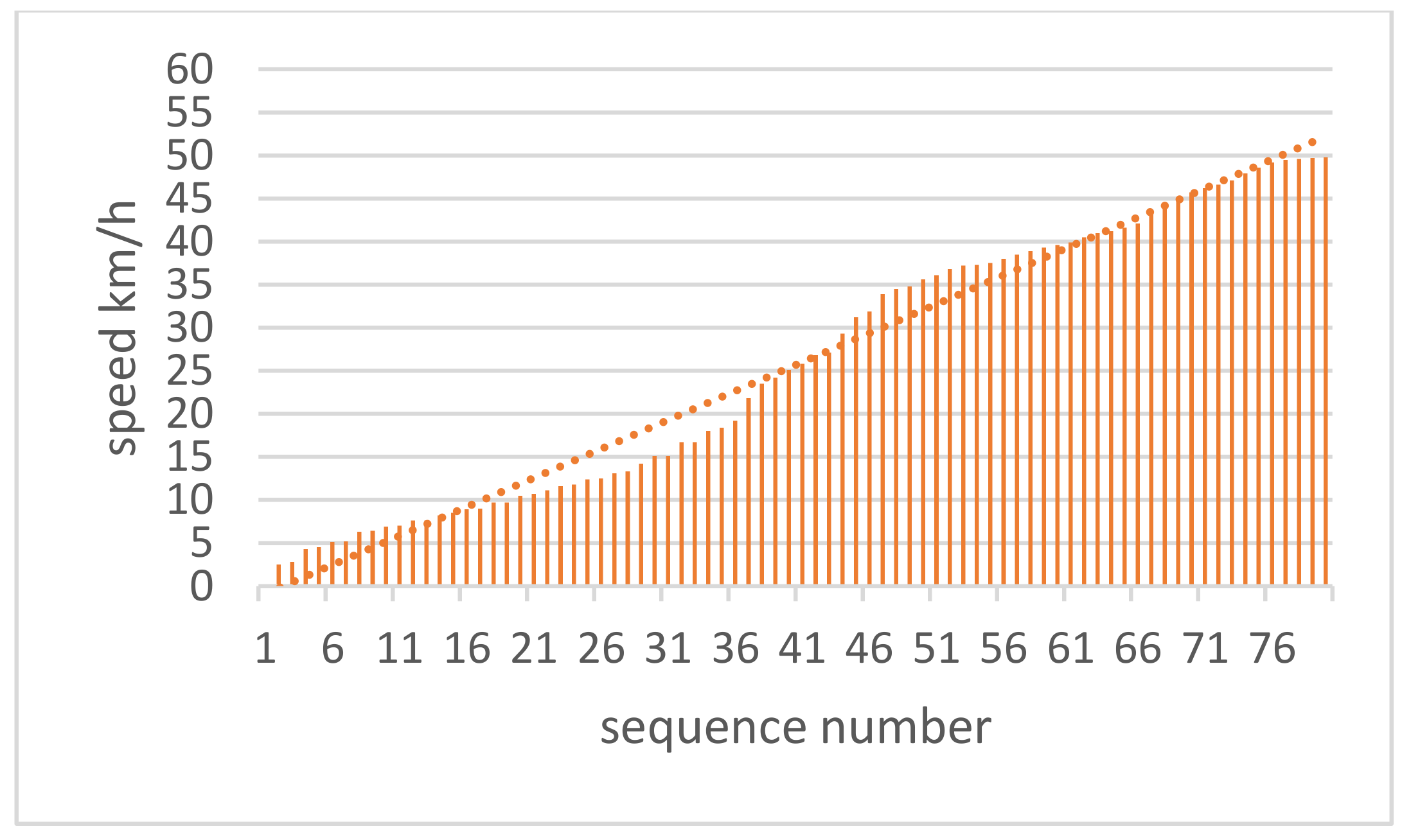
3.1.1. Free Flow Speed (uf)
3.1.2. Critical Speed (um)
3.1.3. Jam Density (kj)
3.2. Basic Traffic Flow Entropy Model at the Boundary Road Network
- 1.
- Steady Traffic Flow State
- 2.
- Unsteady Traffic Flow State
3.3. Opening Evaluation Entropy Model
3.4. FCM Clustering Analysis of Opening Traffic Data at Boundary
- Step 1.
- Set initialization parameters. In this paper, the opening state data was classified into five different states: the smooth-close state (A), the stable-ready close state (B), the slow-open state(C), the congested-open state (D), and the very congested-open state (E). The cluster number was set to c = 5, the iterative stopping threshold was set to , and the exponential weight was set to t = 2.5. Choose the initial cluster centers , andomly from the . The iteration number was set to r = 0. Here, xij is the j-th sample, Ki is the i-th cluster center, and n is the number of evaluation indices.
- Step 2.
- The membership matrix (U(r)) was computed or updated. We setas the distance between the i-th cluster center (Ki) for the j-th sample. The matrix (U(r)) was expressed by the following:where is the membership degree of the j-th sample belonging to the i-th cluster.
- Step 3.
- The new cluster centers (K(r+1)) were updated as follows:
- Step 4.
- We set . If , in which the iterative stopping threshold , the algorithm was deemed to be finished, and the membership matrix (U) and the clustering center (K) were output. If , , we returned to Step 2.
4. Results and Discussion
4.1. Environment of Simulation Gated Community
4.2. Opening Evaluation Results of Boundary Network
4.3. Clustering Analysis of the Fuzzy Standard Ranges
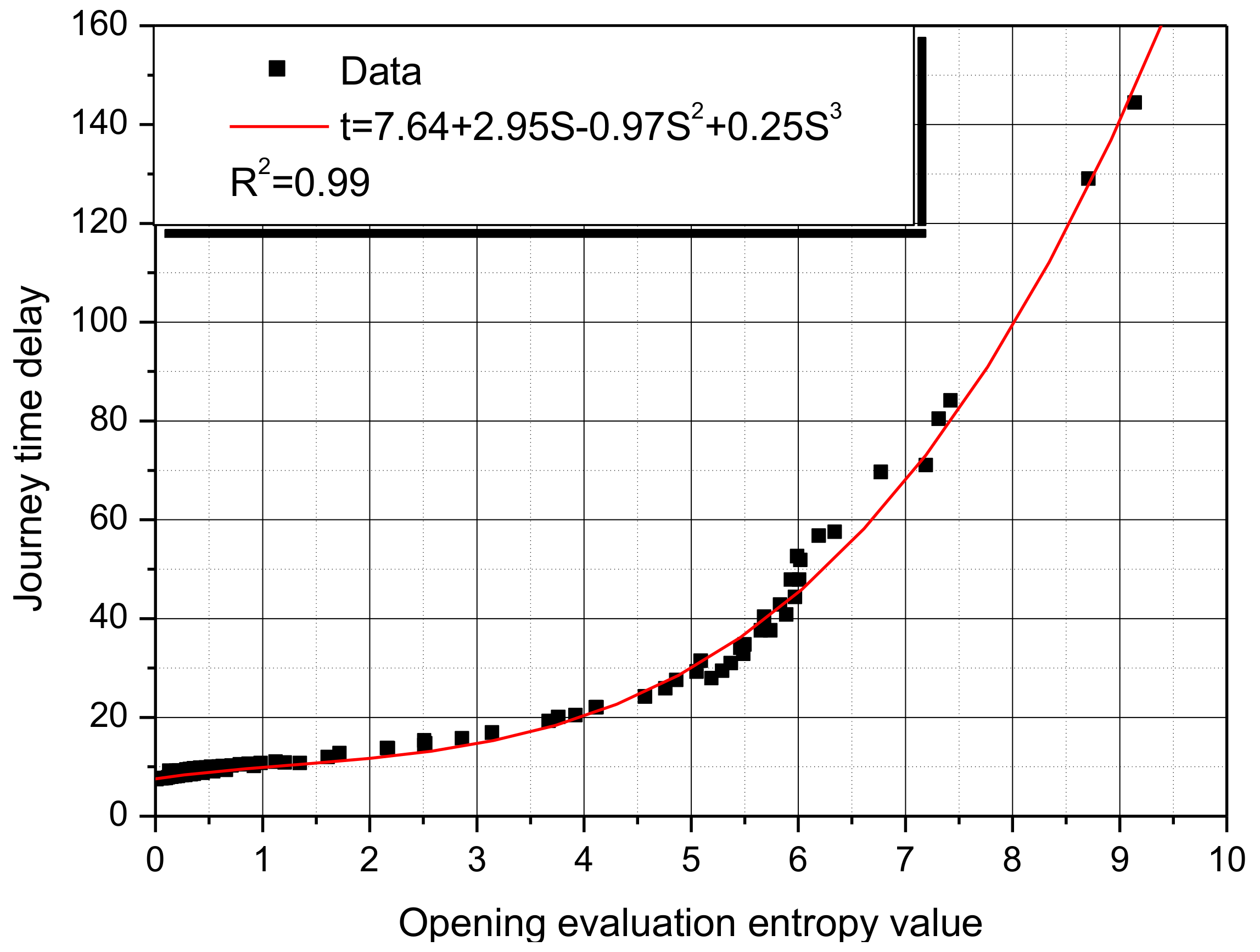
4.4. Comparison between Entropy Value and Journey Delay Time
5. Conclusions
- 1.
- The micro-inter-road network of the gated community should be opened as the entropy value reaches 2.5.
- 2.
- As the travel time becomes less than 20 s, the correlation between the opening entropy value and the journey delay time exhibits a good linear correlation which indicates smooth traffic flow.
Author Contributions
Funding
Conflicts of Interest
References
- Bar-Gera, H. Evaluation of a cellular phone-based system for measurements of traffic speeds and travel times: A case study from Israel. Transp. Res. C Emerg. Technol. 2007, 15, 380–391. [Google Scholar] [CrossRef]
- Transportation Research Board. Highway Capacity Manual; TRB, National Research Council: Washington, DC, USA, 2000.
- Shao, Y.; Cheng, L.; Wang, W. Application of Entropy-maximizing (EM) Model in Traffic Distribution Forecast. J. Transp. Syst. Eng. Inf. Technol. 2005, 5, 83–87. [Google Scholar]
- Guo, Y.-M.; Zhao, Y.; Zhou, Y.-M.; Xiao, Z.-B.; Yang, X.J. On the local fractional LWR model in fractal traffic flows in the entropy condition. Math. Methods Appl. Sci. 2017, 40, 6127–6132. [Google Scholar] [CrossRef]
- Lozano, A.; Manfredi, G.; Nieddu, L. An algorithm for the recognition of levels of congestion in road traffic problems. Math. Comput. Simul. 2009, 79, 1926–1934. [Google Scholar] [CrossRef]
- Sun, X.L. Urban Road Traffic State Evaluation and Prediction: A New Scheme with Applications. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2013. [Google Scholar]
- Antoniou, C.; Koutsopoulos, H.N.; Yannis, G. Dynamic data-driven local traffic state estimation and prediction. Transp. Res. Part C Emerg. Technol. 2013, 34, 89–107. [Google Scholar] [CrossRef]
- Feng, K.Y. Entropy and Component Properties of Mixed Traffie. J. Funan Univ. 1992, 19, 10–16. [Google Scholar]
- Jie, Q. Research on Traffic State Discrimination of Urban Trunk Road Based on Entropy and Hydrodynamics. Master’s Thesis, Northeast Forestry University, Harbin, China, 2010. [Google Scholar]
- Mao, X. Microcirculation: A Case Study of Donghu District in Nanchang. J. Landsc. Res. 2017, 9, 1–3. [Google Scholar]
- Yao, Y.; Ye, H.; Wu, D.; Zhang, Y.; Guan, Q. Estimating the effects of “community opening” policy on alleviating traffic congestion in large Chinese cities by integrating ant colony optimization and complex network analyses. Comput. Environ. Urban Syst. 2018, 70, 163–174. [Google Scholar] [CrossRef]
- Min, W.; Wynter, L. Real-time road traffic prediction with spatio-temporal correlations. Transp. Res. C Emerg. Technol. 2011, 19, 606–616. [Google Scholar] [CrossRef]
- Yuan, J.; Mills, K.A. A cross-correlation-based method for spatial–temporal traffic analysis. Perform. Eval. 2005, 61, 163–180. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Bhatnagar, V. Fuzzy data mining: a literature survey and classification framework. Int. J. Netw. Virtual Organ. 2012, 11, 382–408. [Google Scholar] [CrossRef]
- Wright, M.; Horowitz, R. Fusing loop and GPS probe measurements to estimate freeway density. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3577–3590. [Google Scholar] [CrossRef]
- Lo, C.-C.; Kuo, Y.-H. Traffic-aware routing protocol with cooperative coverage-oriented information collection method for VANET. IET Commun. 2017, 11, 444–450. [Google Scholar] [CrossRef]




| Factor | Average Speed (Vs) | Journey Time Delay (JTD) | |
|---|---|---|---|
| State | |||
| Smooth | 44~ | 50~16.8 | |
| Stable | 30~44 | 11.4~12.6 | |
| Slow (open) | 26~30 | 12.6~14.2 | |
| Congested (open) | 17~26 | 1.42~16.8 | |
| Very congested (open) | 0~17 | 16.8~ | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Rinoshika, A.; Tang, Z. Dynamic Evaluation on the Traffic State of an Urban Gated Community by Opening the Micro-Inter-Road Network. Technologies 2018, 6, 71. https://doi.org/10.3390/technologies6030071
Dong L, Rinoshika A, Tang Z. Dynamic Evaluation on the Traffic State of an Urban Gated Community by Opening the Micro-Inter-Road Network. Technologies. 2018; 6(3):71. https://doi.org/10.3390/technologies6030071
Chicago/Turabian StyleDong, Lin, Akira Rinoshika, and Zhixian Tang. 2018. "Dynamic Evaluation on the Traffic State of an Urban Gated Community by Opening the Micro-Inter-Road Network" Technologies 6, no. 3: 71. https://doi.org/10.3390/technologies6030071
APA StyleDong, L., Rinoshika, A., & Tang, Z. (2018). Dynamic Evaluation on the Traffic State of an Urban Gated Community by Opening the Micro-Inter-Road Network. Technologies, 6(3), 71. https://doi.org/10.3390/technologies6030071




