DC Model Cable under Polarity Inversion and Thermal Gradient: Build-Up of Design-Related Space Charge
Abstract
:1. Introduction
- The development of materials with improved performances regarding targeted applications, notably decrease the propensity to store space charge and manage field grading properties;
- The development of physical models for the material behavior: how charges are generated, stored and transported;
- The development of techniques, particularly charge distribution measurement techniques, relevant to the geometry and to the thermal and electrical stresses that are encountered;
- The proposal for materials assessment methodologies for the application: This means that relevant quantities have to be measured and figures of merit for materials provided in order to make systems more safe;
- The implementation of engineering models for stress distribution estimation.
2. Challenges and Opportunities for Developing HVDC Cables
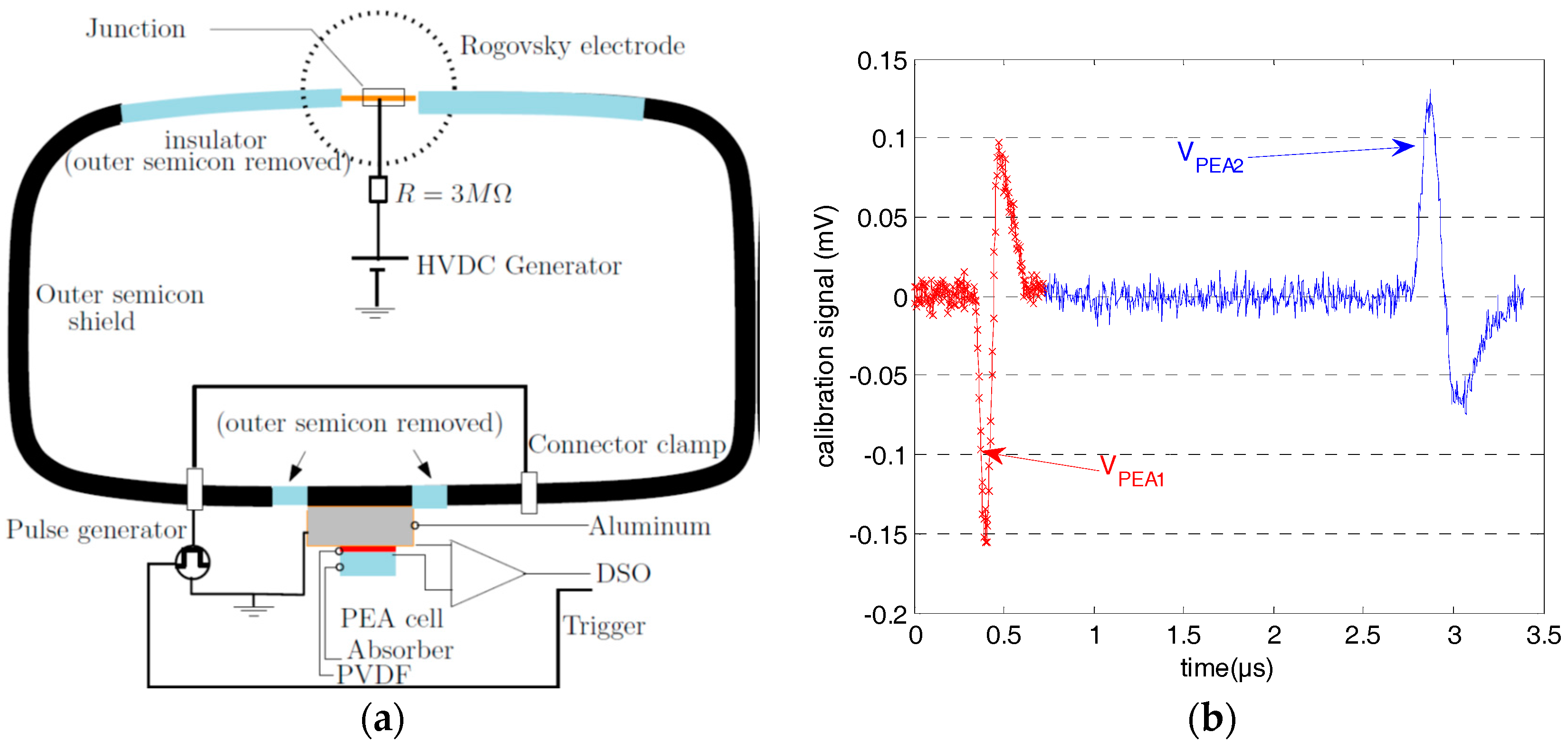
2.1. Techniques and Methodologies for Space Charge Assessment
2.2. Challenges Regarding Materials for HVDC Cables
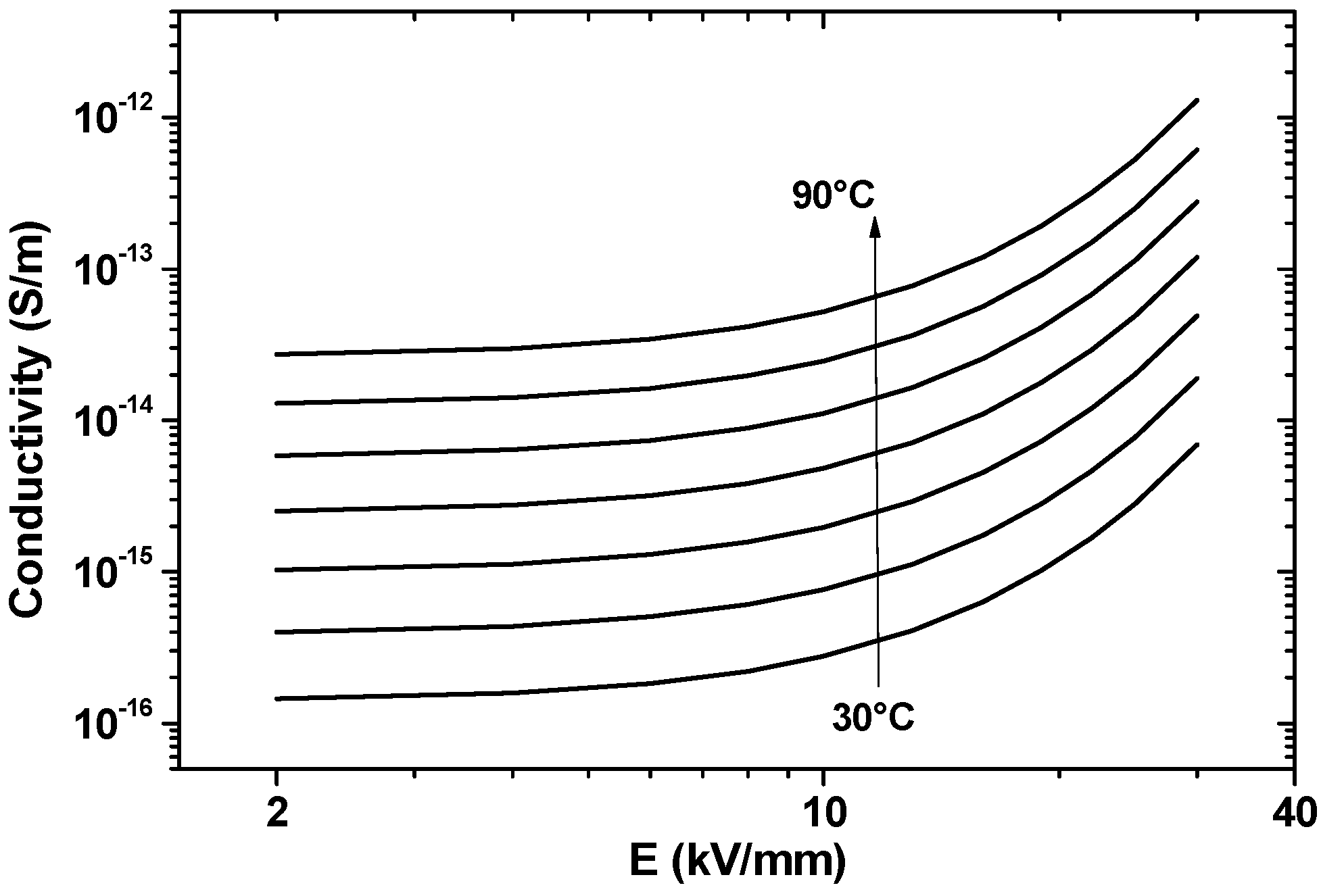
2.3. Conductivity Models
3. Design-Related Space Charge in Model Cables
3.1. Constitutive Equations for the Space Charge
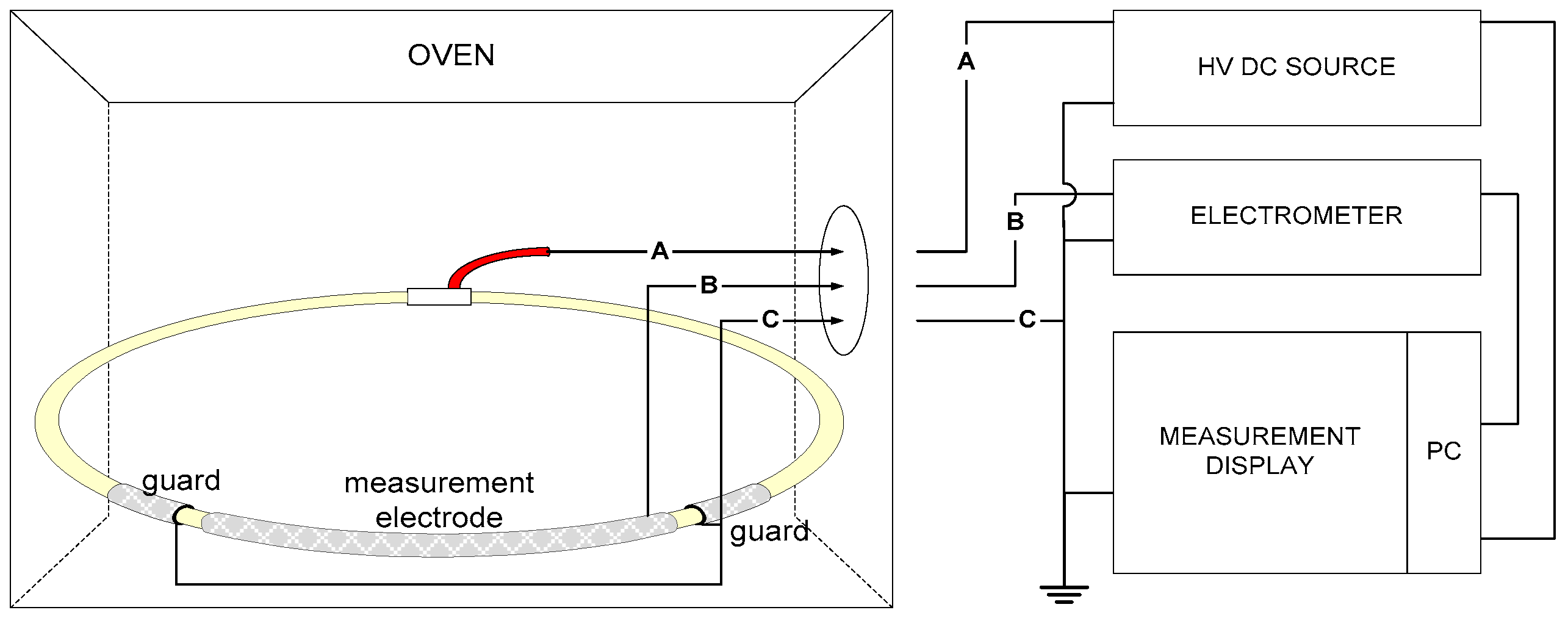
3.2. Test Conditions for Conductivity Measurements
3.3. Results for Conductivity
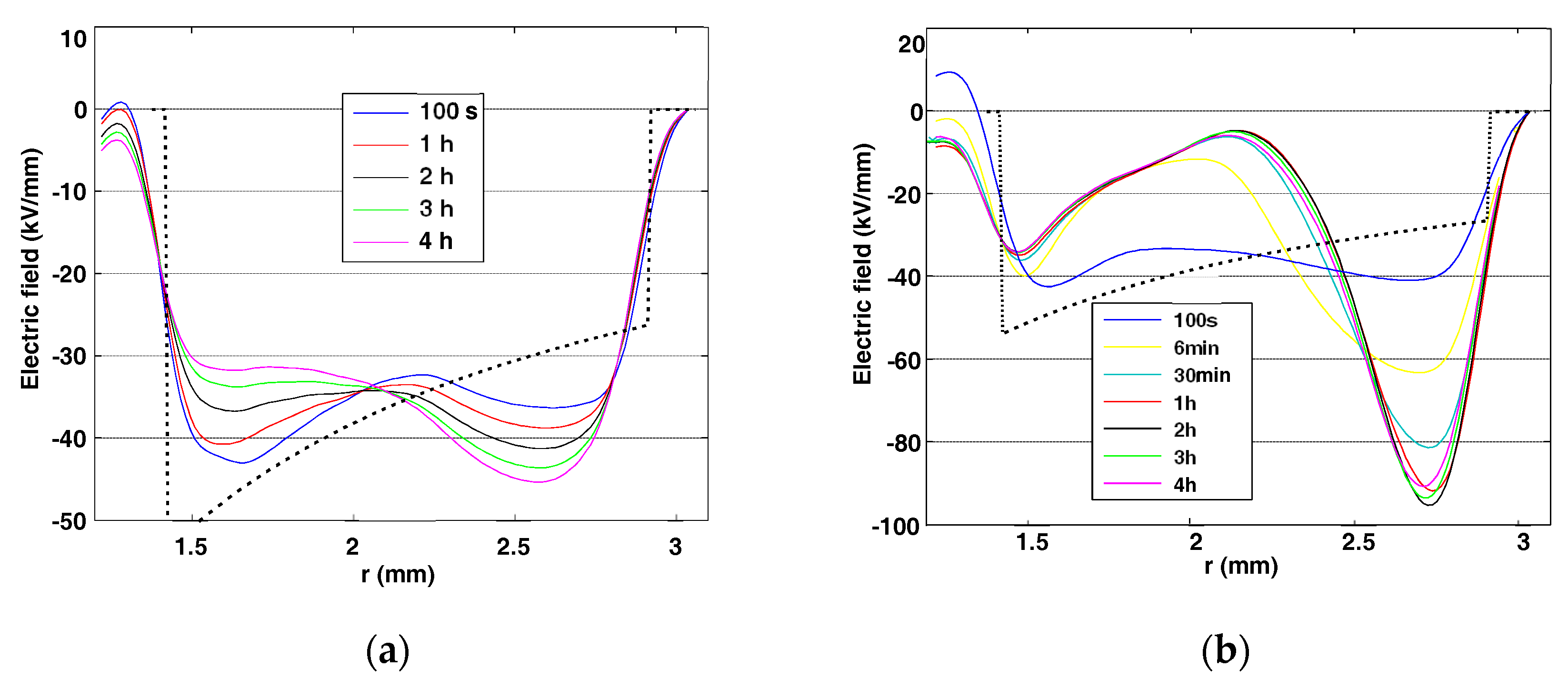
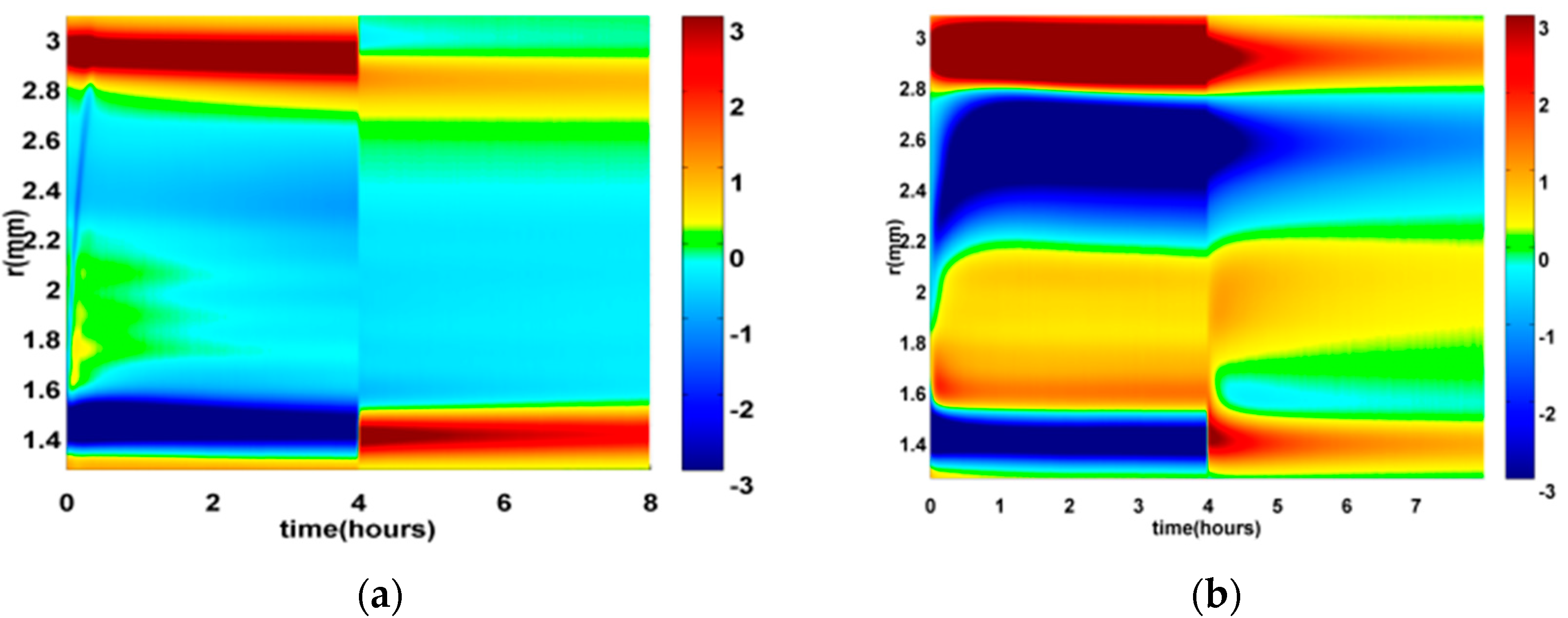
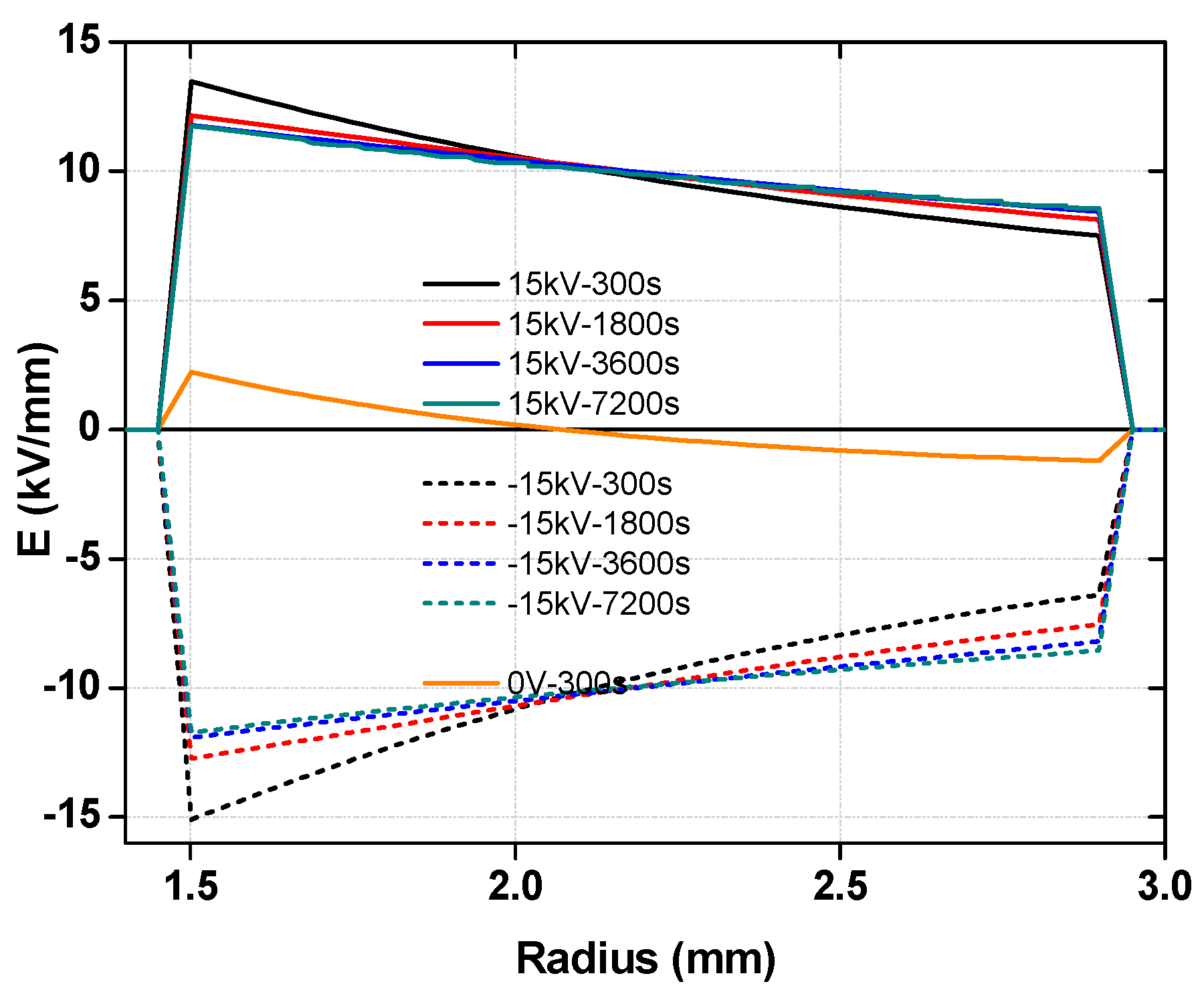
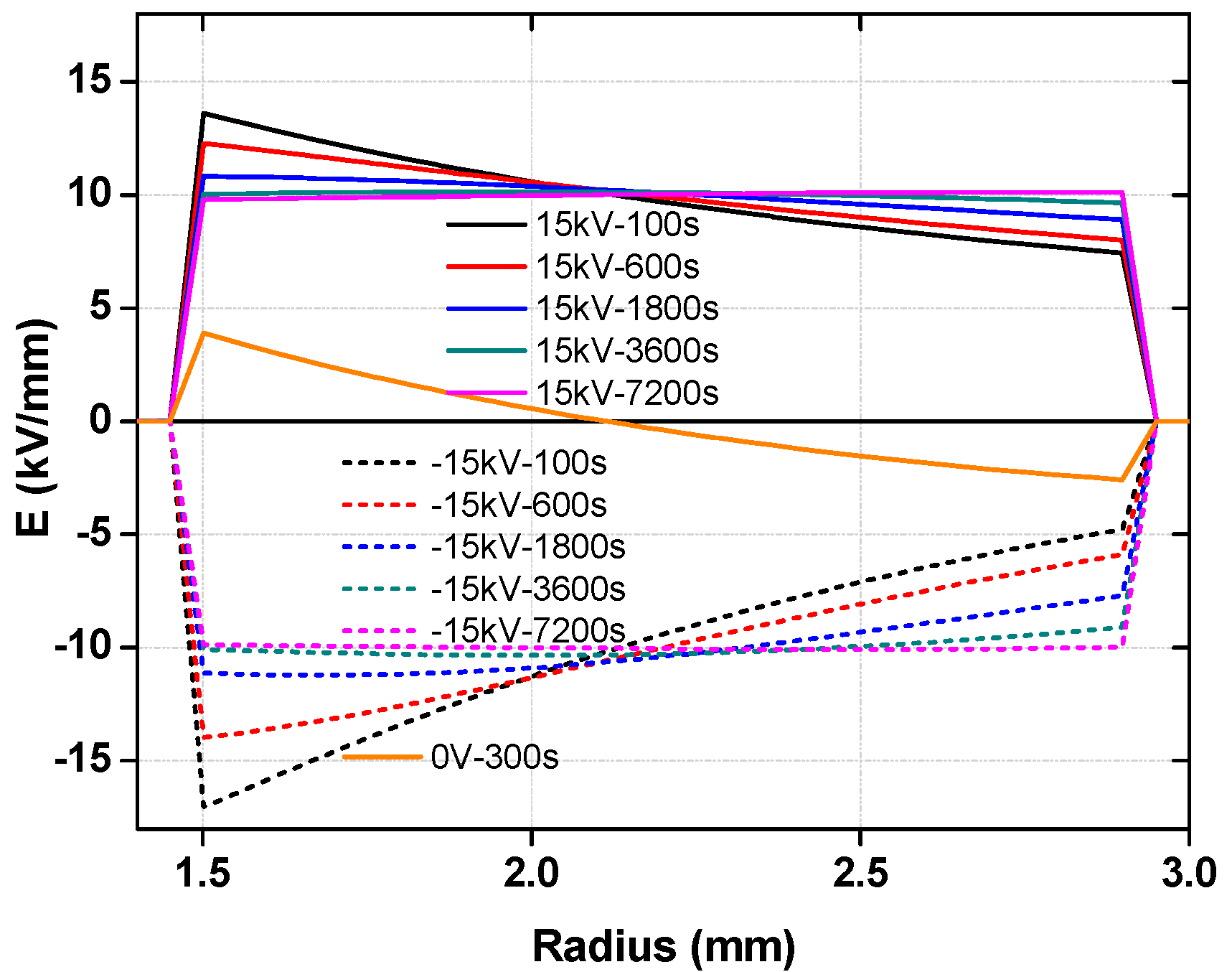
3.4. Electric Field Simulation Based on Conductivity Data
3.5. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DSO | Digital Signal Oscilloscope |
| HVAC | High-Voltage Alternate Current |
| HVDC | High-Voltage Direct Current |
| LCC | Line Commutated Converter |
| LDPE | Low Density Polyethylene |
| PEA | Pulsed Electroacoustic |
| PPLP | Polypropylene Laminated Paper |
| VSC | Voltage Source Converter |
| XLPE | Crosslinked Polyethylene |
References
- Mazzanti, G.; Marzinotto, M. Extruded Cables for High-Voltage Direct-Current Transmission; Wiley-IEEE Press: Hoboken, NJ, USA, 2013. [Google Scholar]
- Fabiani, D.; Montanari, G.C.; Laurent, C.; Teyssedre, G.; Morshuis, P.H.F.; Bodega, R.; Dissado, L.A. HVDC cable design and space charge accumulation. Part 3: Effect of temperature gradient. IEEE Electr. Insul. Mag. 2008, 24, 5–14. [Google Scholar] [CrossRef]
- Montanari, G.C. The electrical degradation threshold of polyethylene investigated by space charge and conduction current measurements. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 309–315. [Google Scholar] [CrossRef]
- Dissado, L.A.; Laurent, C.; Montanari, G.C.; Morshuis, P.H.F. Demonstrating a threshold for trapped space charge accumulation in solid dielectrics under DC field. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 612–620. [Google Scholar] [CrossRef]
- Holé, S.; Ditchi, T.; Lewiner, J. Non-destructive methods for space charge distribution measurements: What are the differences? IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 670–677. [Google Scholar] [CrossRef]
- Fukunaga, K. Progress and prospects in PEA space charge measurement techniques. IEEE Electr. Insul. Mag. 2008, 24, 26–37. [Google Scholar] [CrossRef]
- Notingher, P.; Holé, S.; Berquez, L.; Teyssedre, G. An insight into space charge measurements. Int. J. Plasma Environ. Sci. Technol. 2017, 11, 26–37. [Google Scholar]
- Hozumi, N.; Takeda, T.; Suzuki, H.; Okamoto, T. Space charge behavior in XLPE cable insulation under 0.2–1.2 MV/cm dc fields. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 82–90. [Google Scholar] [CrossRef]
- Castellon, J.; Notingher, P.; Agnel, S.; Toureille, A.; Matallana, J.; Janah, H.; Mirebeau, P.; Sy, D. Industrial installation for voltage-on space charge measurements in HVDC cable. In Proceedings of the Industry Applications Conference, Hong Kong, China, 2–6 October 2005; pp. 1112–1118. [Google Scholar]
- Hozumi, N.; Hori, M. Measuring space-charge in HVDC cables. Energize 2017, 2, 35–38. [Google Scholar]
- Mazzanti, G.; Chen, G.; Fothergill, J.C.; Hozumi, N.; Li, J.; Marzinotto, M.; Mauseth, F.; Morshuis, P.; Reed, C.; Tzimas, A.; et al. A protocol for space charge measurements in full-size HVDC extruded cables. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 21–34. [Google Scholar] [CrossRef]
- Tzimas, A.; Boyer, L.; Mirebeau, P.; Dodd, S.; Castellon, J.; Notingher, P. Qualitative analysis of PEA and TSM techniques on a 200kV extruded cable during a VSC ageing program. In Proceedings of the IEEE International Conference on Dielectrics (ICD), Montpellier, France, 3–7 July 2016; pp. 49–52. [Google Scholar]
- Maeno, T.; Kushiba, H.; Takada, T.; Cooke, C.M. Pulsed electro-acoustic method for the measurement of volume charge in e-beam irradiated PMMA. In Proceedings of the IEEE Electrical Insulation & Dielectric Phenomena, Amherst, NY, USA, 20–24 October 1985; pp. 389–397. [Google Scholar]
- Vissouvanadin, B.; Vu, T.T.N.; Berquez, L.; Le Roy, S.; Teyssèdre, G.; Laurent, C. Deconvolution techniques for space charge recovery using pulsed electroacoustic method in coaxial geometry. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 821–828. [Google Scholar] [CrossRef]
- Vu, T.T.N.; Teyssedre, G.; Vissouvanadin, B.; Le Roy, S.; Laurent, C. Correlating conductivity and space charge measurements in multi-dielectrics under various electrical and thermal stresses. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 117–127. [Google Scholar] [CrossRef]
- Meunier, M.; Quirke, N.; Aslanides, A. Molecular modeling of electron traps in polymer insulators: Chemical defects and impurities. J. Chem. Phys. 2001, 115, 2876–2881. [Google Scholar] [CrossRef]
- Teyssedre, G.; Vu, T.T.N.; Laurent, C. Negative differential mobility for negative carriers as revealed by space charge measurements on crosslinked polyethylene insulated model cables. Appl. Phys. Lett. 2015, 107, 252901. [Google Scholar] [CrossRef]
- Hjertberg, T.; Englund, V.; Hagstrand, P.O.; Loyens, W.; Nilsson, U.; Smedberg, A. Materials for HVDC cables. Revue Electricite Electronique 2014, 4, XI–XV. [Google Scholar]
- Gard, J.C.; Denizet, I.; Mammeri, M. Development of a XLPE insulating with low peroxide by-products. In Proceedings of the 9th International Conference on Insulated Power Cables, Versailles, France, 21–25 June 2015; pp. 1–5. [Google Scholar]
- Vu, T.T.N.; Teyssedre, G.; Le Roy, S.; Laurent, C. Space charge criteria in the assessment of insulation materials for HVDC. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1405–1415. [Google Scholar] [CrossRef]
- Tanaka, T.; Kindersberger, J.; Frechette, M.; Gubanski, S.; Vaughan, A.S.; Sutton, S.; Morshuis, P.; Mattmann, J.P.; Montanari, G.C.; Reed, C.; et al. Polymer Nanocomposites—Fundamentals and Possible Applications to Power Sector; CIGRE: Paris, France, 2011. [Google Scholar]
- Pourrahimi, A.M.; Hoang, T.A.; Liu, D.; Pallon, L.K.H.; Gubanski, S.; Olsson, R.T.; Gedde, U.W.; Hedenqvist, M.S. Highly efficient interfaces in nanocomposites based on polyethylene and ZnO nano/hierarchical particles: A novel approach toward ultralow electrical conductivity insulations. Adv. Mater. 2016, 28, 8651–8657. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Imai, T. Advances in nanodielectric materials over the past 50 years. IEEE Electr. Insul. Mag. 2013, 29, 10–23. [Google Scholar] [CrossRef]
- Huang, X.Y.; Jiang, P.K.; Yin, Y. Nanoparticle surface modification induced space charge suppression in linear low density polyethylene. Appl. Phys. Lett. 2009, 95, 242905. [Google Scholar] [CrossRef]
- Murakami, Y.; Nemoto, M.; Okuzumi, S.; Masuda, S.; Nagao, M.; Hozumi, N.; Sekiguchi, Y.; Murata, Y. DC conduction and electrical breakdown of MgO/LDPE nanocomposite. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 33–39. [Google Scholar] [CrossRef]
- Nelson, J.K. Nanodielectrics—The first decade and beyond. In Proceedings of the Electrical Insulating Materials (ISEIM), Niigata, Japan, 1–5 June 2014; pp. 1–11. [Google Scholar]
- Chen, G.; Hao, M.; Xu, Z.Q.; Vaughan, A.; Cao, J.Z.; Wang, H.T. Review of high voltage direct current cables. CSEE J. Power Energy Systems 2015, 1, 9–21. [Google Scholar] [CrossRef]
- Eoll, C.K. Theory of stress distribution in insulation of High-Voltage DC cables: Part I. IEEE Trans. Electr. Insul. 1975, 10, 27–35. [Google Scholar] [CrossRef]
- Boggs, S.; Dwight, H.; Hjerrild, J.; Holbol, J.T.; Henriksen, M. Effect of insulation properties on the field grading of solid dielectric DC cable. IEEE Trans. Power Deliv. 2001, 16, 456–462. [Google Scholar] [CrossRef]
- Choo, W.; Chen, G.; Swingler, S.G. Electric field in polymeric cable due to space charge accumulation under DC and temperature gradient. IEEE Electr. Insul. Mag. 2011, 25, 596–606. [Google Scholar] [CrossRef]
- Qin, S.; Boggs, S. Design considerations for High Voltage DC components. IEEE Electr. Insul. Mag. 2012, 28, 36–44. [Google Scholar] [CrossRef]
- Teyssedre, G.; Laurent, C. Charge transport modeling in insulating polymers: From molecular to macroscopic scale. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 857–875. [Google Scholar] [CrossRef]
- Alison, J.M.; Hill, R.M. A model for bipolar charge transport, trapping and recombination in degassed crosslinked polyethene. J. Phys. D Appl. Phys. 1994, 27, 1291–1299. [Google Scholar] [CrossRef]
- Le Roy, S.; Teyssedre, G.; Laurent, C.; Montanari, G.C.; Palmieri, F. Description of charge transport in polyethylene using a fluid model with a constant mobility: fitting model and experiments. J. Phys. D Appl. Phys. 2006, 39, 1427–1436. [Google Scholar] [CrossRef]
- Le Roy, S.; Segur, P.; Laurent, C.; Teyssedre, G. Description of bipolar charge transport in polyethylene using a fluid model with a constant mobility: model prediction. J. Phys. D Appl. Phys. 2004, 37, 298–305. [Google Scholar] [CrossRef]
- Le Roy, S.; Teyssèdre, G.; Laurent, C. Modelling space charge in a cable geometry. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2361–2367. [Google Scholar] [CrossRef]
- Li, S.; Zhu, Y.; Min, D.; Chen, G. Space charge modulated electrical breakdown. Sci. Rep. 2016, 6, 32588. [Google Scholar] [CrossRef] [PubMed]
- Le Roy, S.; Teyssedre, G. Ion generation and transport under electric stress in a low density polyethylene matrix. In Proceedings of the IEEE Annual Report Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 18–21 October 2015; pp. 63–66. [Google Scholar]
- Morshuis, P.; Jeroense, M. Space charge in HVDC cable insulation. In Proceedings of the IEEE Annual Report Conference on Electr. Insul. Dielectr. Phenom. (CEIDP), Minneapolis, MN, USA, 9–22 October 1997; pp. 28–31. [Google Scholar]
- McAllister, I.W.; Crichton, G.C.; Pedersen, A. Charge accumulation in DC cables: A macroscopic approach. In Proceedings of the IEEE International Symposium on Electrical Insulation, Pittsburgh, PA, USA, 5–8 June 1994; pp. 212–216. [Google Scholar]
- Delpino, S.; Fabiani, D.; Montanari, G.C.; Laurent, C.; Teyssedre, G.; Morshuis, P.H.F.; Bodega, R.; Dissado, L.A. Polymeric HVDC cable design and space charge accumulation. Part 2: Insulation interfaces. IEEE Electr. Insul. Mag. 2008, 24, 14–24. [Google Scholar] [CrossRef]
- Vu, T.T.N.; Teyssèdre, G.; Vissouvanadin, B.; Le Roy, S.; Laurent, C.; Mammeri, M.; Denizet, I. Field distribution in polymeric MV-HVDC model cable under temperature gradient : Simulation and space charge measurements. Eur. J. Electr. Engg. 2014, 17, 307–325. [Google Scholar]
- Vu, T.T.N.; Teyssedre, G.; Vissouvanadin, B.; Steven, J.Y.; Laurent, C. Transient space charge phenomena in HVDC model cables. In Proceedings of the 9th International Conference on Insulated Power Cables (JiCable), Versailles, France, 21–25 June 2015; pp. 1–6. [Google Scholar]
- Shao, S.J.; Agelidis, V.G. Review of DC system technologies for large scale integration of wind energy systems with electricity grids. Energies 2010, 3, 1303–1319. [Google Scholar] [CrossRef]
- Bresesti, P.; Kling, W.L.; Hendriks, R.L.; Vailati, R. HVDC connection of offshore wind farms to the transmission system. IEEE Trans. Energy Convers. 2007, 22, 37–43. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Longo, M.; Zaninelli, D. Improvement of wind energy production through HVDC systems. Energies 2017, 10, 157. [Google Scholar] [CrossRef]
- Jardini, J.A.; Vasquez-Arnez, R.L.; Bassini, M.T.; Horita, M.A.B.; Saiki, G.Y.; Cavalheiro, M.R. Overvoltage assessment of point-to-point VSC-based HVDC systems. Przegląd Elektrotechniczny 2015, 8, 105–122. [Google Scholar] [CrossRef]
- Vu, T.T.N.; Teyssedre, G.; Le Roy, S.; Laurent, C. Maxwell-Wagner effect in multi-layered dielectrics: Interfacial charge measurement and modelling. Technologies 2017, 5, 27. [Google Scholar] [CrossRef]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adi, N.; Vu, T.T.N.; Teyssèdre, G.; Baudoin, F.; Sinisuka, N. DC Model Cable under Polarity Inversion and Thermal Gradient: Build-Up of Design-Related Space Charge. Technologies 2017, 5, 46. https://doi.org/10.3390/technologies5030046
Adi N, Vu TTN, Teyssèdre G, Baudoin F, Sinisuka N. DC Model Cable under Polarity Inversion and Thermal Gradient: Build-Up of Design-Related Space Charge. Technologies. 2017; 5(3):46. https://doi.org/10.3390/technologies5030046
Chicago/Turabian StyleAdi, Nugroho, Thi Thu Nga Vu, Gilbert Teyssèdre, Fulbert Baudoin, and Ngapuli Sinisuka. 2017. "DC Model Cable under Polarity Inversion and Thermal Gradient: Build-Up of Design-Related Space Charge" Technologies 5, no. 3: 46. https://doi.org/10.3390/technologies5030046
APA StyleAdi, N., Vu, T. T. N., Teyssèdre, G., Baudoin, F., & Sinisuka, N. (2017). DC Model Cable under Polarity Inversion and Thermal Gradient: Build-Up of Design-Related Space Charge. Technologies, 5(3), 46. https://doi.org/10.3390/technologies5030046




