Cuff-Less and Continuous Blood Pressure Monitoring: A Methodological Review
Abstract
:1. Introduction
2. Cardiovascular System and the Electrical-Mechanical Coupling of the Heart
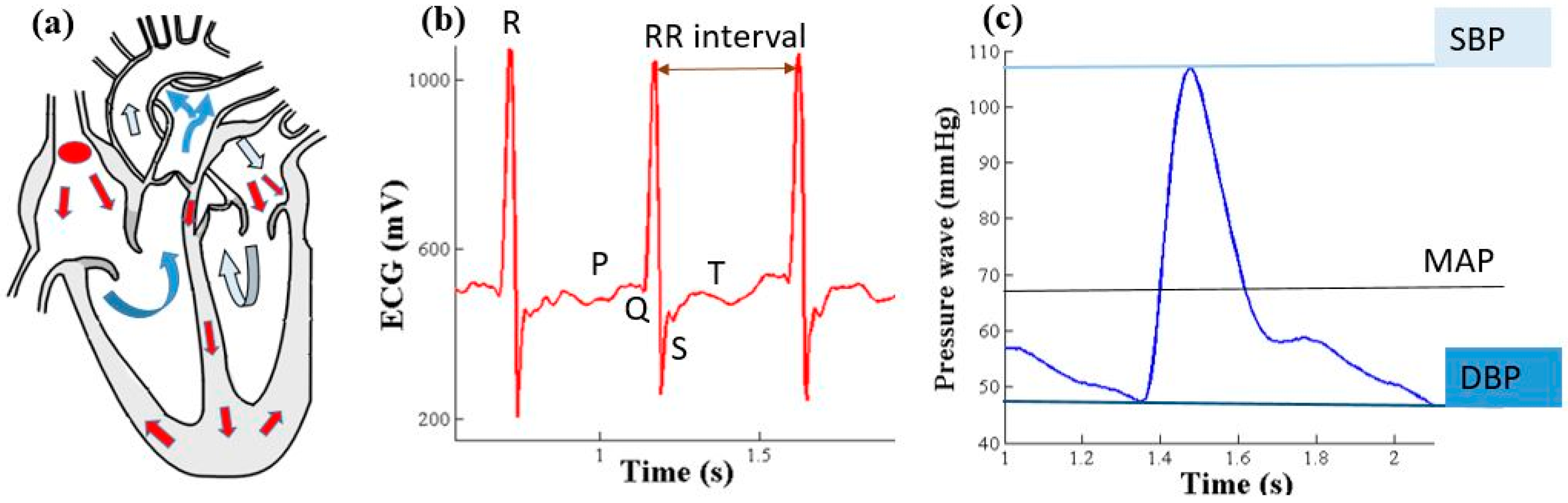
2.1. Electro-Mechanical Cardiac Signals
2.2. Relationship between BP, Pressure Wave Velocity (PWV) and Time Period
2.3. Determination of the “Time Delay”
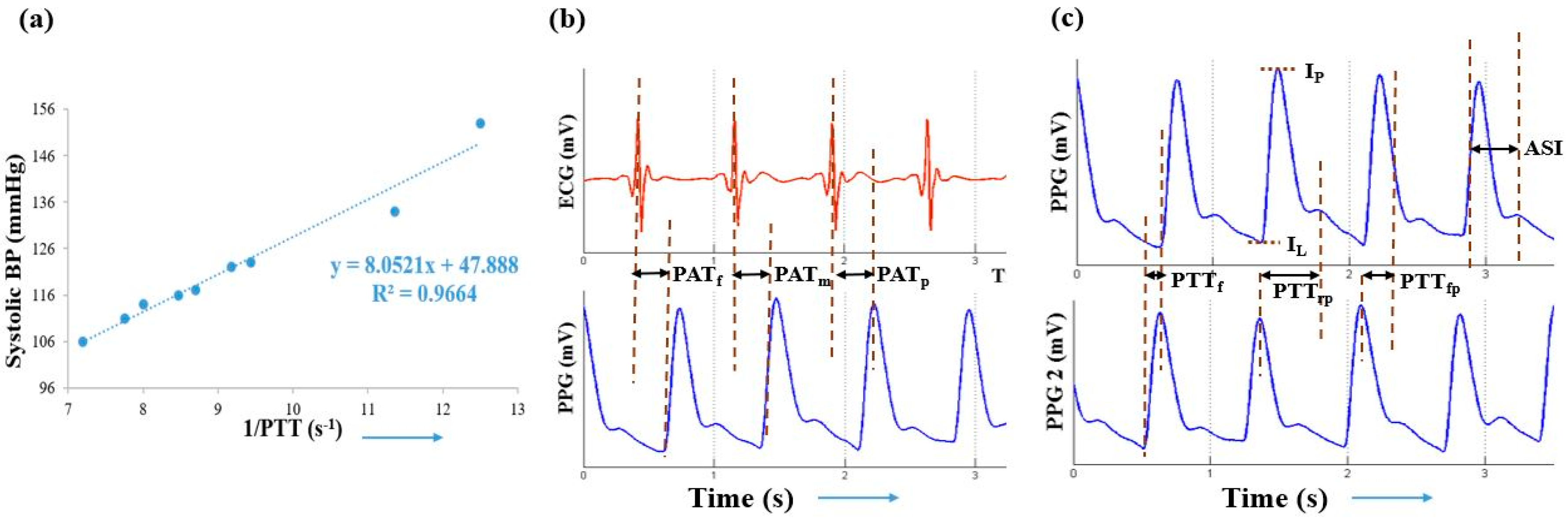
2.3.1. Pulse Transit Time (PTT)
2.3.2. Pulse Arrival Time (PAT)
3. Mathematical Models
3.1. Logarithmic Model
3.2. Proportional (Linear) Model
3.3. Inverse Square Model
3.4. Inverse Model
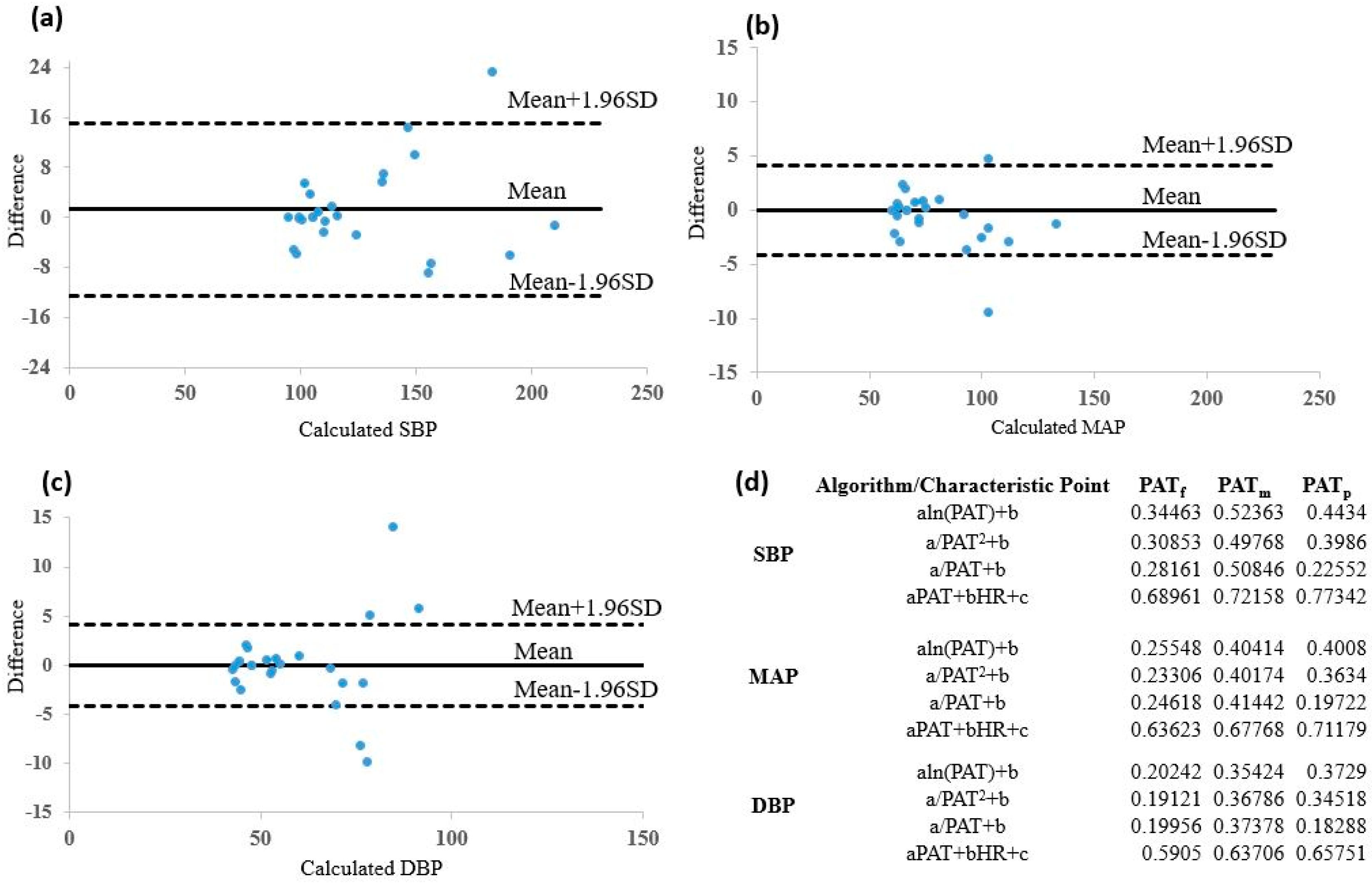
3.5. Comparison between Models
4. Discussion
5. Conclusions
Acknowledgment
Author Contributions
Conflicts of Interest
References
- Laflamme, M.A.; Murry, C.E. Heart regeneration. Nature 2011, 473, 326–335. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Kang, B.J.; Lee, C.-A.; Shung, K.K.; Hsiai, T.K. Electrical and mechanical strategies to enable cardiac repair and regeneration. IEEE Rev. Biomed. Eng. 2015, 8, 114–124. [Google Scholar] [CrossRef] [PubMed]
- Centers of Disease Control and Prevention. Vital signs: Awareness and treatment of uncontrolled hypertension among adults—United States, 2003–2010. Morb. Mortal. Wkly. Rep. 2012, 61, 703–709. [Google Scholar]
- Ubolsakka-Jones, C.; Sangthong, B.; Aueyingsak, S.; Jones, D.A. Older Women with Controlled Isolated Systolic Hypertension: Exercise and Blood Pressure. Med. Sci. Sports Exerc. 2016, 48, 983–989. [Google Scholar] [CrossRef] [PubMed]
- Moroz, L.A.; Simpson, L.L.; Rochelson, B. Management of severe hypertension in pregnancy. Semin. Perinatol. 2016, 40, 112–118. [Google Scholar] [CrossRef] [PubMed]
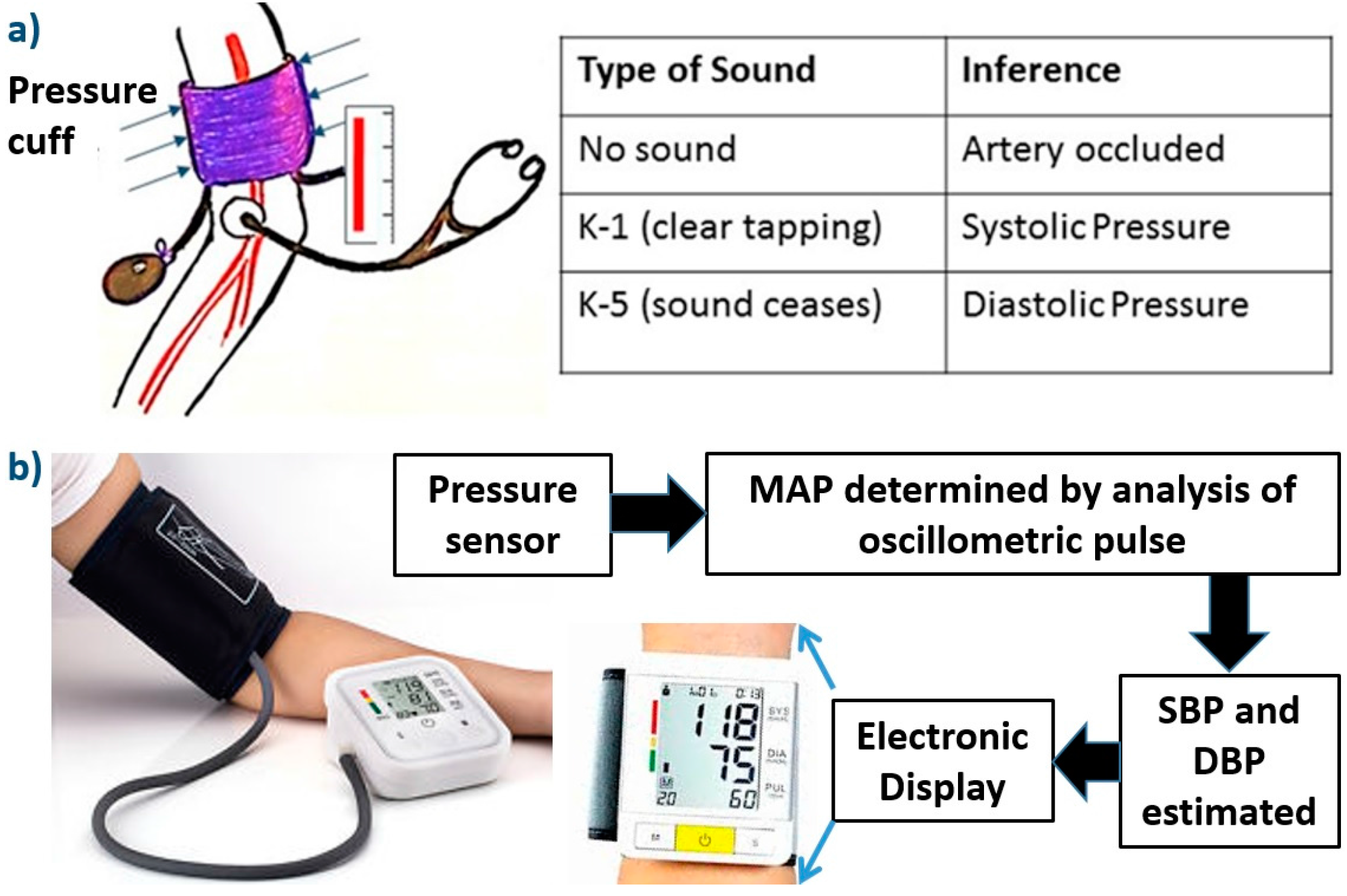
- Booth, J. A short history of blood pressure measurement. Proc. R. Soc. Med. 1977, 70, 793–799. [Google Scholar] [PubMed]
- Rocci, S.R. The technique of sphygmomanometry. Gazz. Med. Torino 1897, 10, 981–1017. [Google Scholar]
- Korotkoff, N. On methods of studying blood pressure. Bull. Imp. Mil. Med. Acad. 1905, 11, 365–367. [Google Scholar]
- Perloff, D.; Grim, C.; Flack, J.; Frohlich, E.D.; Hill, M.; McDonald, M.; Morgenstern, B.Z. Human blood pressure determination by sphygmomanometry. Circulation 1993, 88, 2460–2470. [Google Scholar] [CrossRef] [PubMed]
- Rivarocci, S. Un nuovo sfigmomanometro. Gazz. Med. Torino 1896, 47, 981–1017. [Google Scholar]
- O’Brien, E.; Atkins, N. Accuracy of an oscillometric automatic blood pressure device: The Omron HEM403C. J. Hum. Hypertens. 1995, 9, 169–174. [Google Scholar]
- O’Brien, E.; Waeber, B.; Parati, G.; Staessen, J. Blood pressure measuring devices: recommendations of the European Society of Hypertension. Br. Med. J. 2001, 322, 531–536. [Google Scholar] [CrossRef]
- Leung, A.A.; Nerenberg, K.; Daskalopoulou, S.S.; McBrien, K.; Zarnke, K.B.; Dasgupta, K.; Cloutier, L.; Gelfer, M.; Lamarre-Cliché, M.; Milot, A.; et al. Hypertension Canada’s 2016 Canadian Hypertension Education Program Guidelines for blood pressure measurement, diagnosis, assessment of risk, prevention, and treatment of hypertension. Can. J. Cardiol. 2016, 32, 569–588. [Google Scholar] [CrossRef] [PubMed]
- JCS Joint Working Group. Guidelines for the clinical use of 24 h ambulatory blood pressure monitoring (ABPM) (JCS 2010). Circ. J. 2012, 76, 508–519. [Google Scholar]
- Porter, K.B.; O’Brien, W.F.; Kiefert, V.; Knuppel, R.A. Flnapres: A Noninvasive Device To Monitor Blood Pressure. Obstet. Gynecol. 1991, 78, 430–433. [Google Scholar] [PubMed]
- Kermode, J.; Davis, N.; Thompson, W. Comparison of the Finapres blood pressure monitor with intra-arterial manometry during induction of anaesthesia. Anaesth. Intensive Care 1989, 17, 470–475. [Google Scholar] [PubMed]
- Thomas, S.S.; Nathan, V.; Zong, C.; Akinbola, E.; Aroul, A.L.P.; Philipose, L.; Soundarapandian, K.; Shi, X.; Jafari, R. BioWatch—A wrist watch based signal acquisition system for physiological signals including blood pressure. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 2286–2289. [Google Scholar]
- Kim, J.; Park, J.; Kim, K.; Chee, Y.; Lim, Y.; Park, K. Development of a nonintrusive blood pressure estimation system for computer users. Telemed. E-Health 2007, 13, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Chee, Y.J.; Park, J.W.; Choi, J.W.; Park, K.S. A new approach for non-intrusive monitoring of blood pressure on a toilet seat. Physiol. Meas. 2006, 27, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Baek, H.J.; Lee, H.B.; Kim, J.S.; Choi, J.M.; Kim, K.K.; Park, K.S. Nonintrusive biological signal monitoring in a car to evaluate a driver’s stress and health state. Telemed. E-Health 2009, 15, 182–189. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Poon, C.; Leung, H.; Sy, M.; Wong, M.; Zhang, Y. A novel method for the contactless and continuous measurement of arterial blood pressure on a sleeping bed. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society(EMBC), Minneapolis, MN, USA, 3–6 September 2009; pp. 6084–6086. [Google Scholar]
- Nye, E. The effect of blood pressure alteration on the pulse wave velocity. Br. Heart J. 1964, 26, 261–265. [Google Scholar] [CrossRef] [PubMed]
- Gribbin, B.; Steptoe, A.; Sleight, P. Pulse wave velocity as a measure of blood pressure change. Psychophysiology 1976, 13, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Chen, S.; Soueidan, K.; Batkin, I.; Bolic, M.; Dajani, H.; Groza, V. Electrocardiogram-assisted blood pressure estimation. IEEE Trans. Biomed. Eng. 2012, 59, 608–618. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Zhang, Q.; Ko, S. Noninvasive cuffless blood pressure estimation using pulse transit time and Hilbert–Huang transform. Comput. Electr. Eng. 2013, 39, 103–111. [Google Scholar] [CrossRef]
- Jeong, I.C.; Wood, J.; Finkelstein, J. Using individualized pulse transit time calibration to monitor blood pressure during exercise. Inf. Manag. Technol. Healthc. 2013, 190, 39–41. [Google Scholar]
- Yoon, Y.; Cho, J.H.; Yoon, G. Non-constrained blood pressure monitoring using ECG and PPG for personal healthcare. J. Med. Syst. 2009, 33, 261–266. [Google Scholar] [CrossRef] [PubMed]
- Špulák, D.; Čmejla, R.; Fabián, V. Parameters for mean blood pressure estimation based on electrocardiography and photoplethysmography. In Proceedings of the 2011 International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 7–8 September 2011; pp. 1–4. [Google Scholar]
- Lass, J.; Meigas, I.; Karai, D.; Kattai, R.; Kaik, J.; Rossmann, M. Continuous blood pressure monitoring during exercise using pulse wave transit time measurement. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEMBS 2004), San Francisco, CA, USA, 1–4 September 2004; pp. 2239–2242. [Google Scholar]
- Poon, C.; Zhang, Y. Cuff-less and noninvasive measurements of arterial blood pressure by pulse transit time. In Proceedings of the 27th Annual International Conference of the Engineering in Medicine and Biology Society (EMBS 2005), Shanghai, China, 1–4 September 2005; pp. 5877–5880. [Google Scholar]
- Lobodzinski, S.S.; Laks, M.M. New devices for very long-term ECG monitoring. Cardiol. J. 2012, 19, 210–214. [Google Scholar] [CrossRef] [PubMed]
- Cattivelli, F.S.; Garudadri, H. Noninvasive cuffless estimation of blood pressure from pulse arrival time and heart rate with adaptive calibration. In Proceedings of the 2009 Sixth International Workshop on Wearable and Implantable Body Sensor Networks, Berkeley, CA, USA, 3–5 June 2009; pp. 114–119. [Google Scholar]
- McCarthy, B.; O’Flynn, B.; Mathewson, A. An investigation of pulse transit time as a non-invasive blood pressure measurement method. J. Phys. Conf. Ser. 2011, 307, 012060. [Google Scholar] [CrossRef]
- Singh, R.B.; Cornélissen, G.; Weydahl, A.; Schwartzkopff, O.; Katinas, G.; Otsuka, K.; Watanabe, Y.; Yano, S.; Mori, H.; Ichimaru, Y.; et al. Circadian heart rate and blood pressure variability considered for research and patient care. Int. J. Cardiol. 2003, 87, 9–28. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, B.P.; Yu, C.-M.; Zhang, Y.-T.; Poon, C.C. Attenuation of systolic blood pressure and pulse transit time hysteresis during exercise and recovery in cardiovascular patients. IEEE Trans. Biomed. Eng. 2014, 61, 346–352. [Google Scholar] [PubMed]
- Wong, Y.; Zhang, Y. The effects of exercises on the relationship between pulse transit time and arterial blood pressure. In Proceedings of the 27th Annual International Conference of the Engineering in Medicine and Biology Society (EMBS 2005), Shanghai, China, 1–4 September 2005; pp. 5576–5578. [Google Scholar]
- Wong, M.Y.-M.; Pickwell-MacPherson, E.; Zhang, Y.-T. The acute effects of running on blood pressure estimation using pulse transit time in normotensive subjects. Eur. J. Appl. Physiol. 2009, 107, 169–175. [Google Scholar] [CrossRef] [PubMed]
- Griggs, D.; Sharma, M.; Naghibi, A.; Wallin, C.; Ho, V.; Barbosa, K.; Ghirmai, T.; Cao, H.; Krishnan, S.K. Design and development of continuous cuff-less blood pressure monitoring devices. In Proceedings of the 2016 IEEE Sensors, Orlando, FL, USA, 30 October–2 November 2016; pp. 1–3. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. Physiobank, physiotoolkit, and physionet components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Fye, W.B. A history of the origin, evolution, and impact of electrocardiography. Am. J. Cardiol. 1994, 73, 937–949. [Google Scholar] [CrossRef]
- Sundnes, J.; Lines, G.T.; Cai, X.; Nielsen, B.F.; Mardal, K.-A.; Tveito, A. Computing the Electrical Activity in the Heart; Springer Science & Business Media: Berlin, Germany, 2007; Volume 1. [Google Scholar]
- Braunwald, E.; Isselbacher, K.J.; Wilson, J.D.; Martin, J.B.; Kasper, D.; Hauser, S.L.; Longo, D.L. Harrison’s Principles of Internal Medicine, 14th ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Alastruey, J.; Parker, K.H.; Sherwin, S.J. Arterial pulse wave haemodynamics. In Proceedings of the 11th International Conference on Pressure Surges, Lisbon, Portugal, 24–26 October 2012; pp. 401–442. [Google Scholar]
- Nichols, W.W.; O’Rourke, M.F.; Kenney, W.L. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles, 3rd ed. J. Cardiopulm. Rehabil. Prev. 1991, 11, 407. [Google Scholar] [CrossRef]
- Penaz, J. Photoelectric measurement of blood pressure, volume and flow in the finger. In Digest of the 10th International Conference on Medical and Biological Engineering; The Conference Committee: Dresden, Germany, 1973. [Google Scholar]
- Wagenseil, J.E.; Mecham, R.P. Elastin in large artery stiffness and hypertension. J. Cardiovasc. Transl. Res. 2012, 5, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Geddes, L.A. Handbook of Blood Pressure Measurement; Springer Science & Business Media: Berlin, Germany, 1991. [Google Scholar]
- Peter, L.; Noury, N.; Cerny, M. A review of methods for non-invasive and continuous blood pressure monitoring: Pulse transit time method is promising? IRBM 2014, 35, 271–282. [Google Scholar] [CrossRef]
- Hughes, D.; Babbs, C.; Geddes, L.; Bourland, J. Measurements of Young’s modulus of elasticity of the canine aorta with ultrasound. Ultrason. Imaging 1979, 1, 356–367. [Google Scholar] [CrossRef] [PubMed]
- Harkness, M.L.; Harkness, R.; McDonald, D. The collagen and elastin content of the arterial wall in the dog. Proc. R. Soc. Lond. B Biol. Sci. 1957, 146, 541–551. [Google Scholar] [CrossRef] [PubMed]
- Burton, A.C. Relation of structure to function of the tissues of the wall of blood vessels. Physiol. Rev. 1954, 34, 619–642. [Google Scholar] [PubMed]
- Ferrari, A.U.; Radaelli, A.; Centola, M. Invited review: aging and the cardiovascular system. J. Appl. Physiol. 2003, 95, 2591–2597. [Google Scholar] [CrossRef] [PubMed]
- O’rourke, M.F.; Hashimoto, J. Mechanical factors in arterial aging: A clinical perspective. J. Am. Coll. Cardiol. 2007, 50, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Mukkamala, R.; Hahn, J.-O.; Inan, O.T.; Mestha, L.K.; Kim, C.-S.; Töreyin, H.; Kyal, S. Toward ubiquitous blood pressure monitoring via pulse transit time: Theory and practice. IEEE Trans. Biomed. Eng. 2015, 62, 1879–1901. [Google Scholar] [CrossRef] [PubMed]
- Cox, R.H. Regional variation of series elasticity in canine arterial smooth muscles. Am. J. Physiol. Heart Circ. Physiol. 1978, 234, H542–H551. [Google Scholar]
- Moens, A.I. Die Pulskurve; EJ Brill: Leiden, The Netherlands, 1878. [Google Scholar]
- Kanda, T.; Nakamura, E.; Moritani, T.; Yamori, Y. Arterial pulse wave velocity and risk factors for peripheral vascular disease. Eur. J. Appl. Physiol. 2000, 82, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.P.; Argod, J.; Pépin, J.-L.; Lévy, P.A. Pulse transit time: an appraisal of potential clinical applications. Thorax 1999, 54, 452–457. [Google Scholar] [CrossRef] [PubMed]
- Loukogeorgakis, S.; Dawson, R.; Phillips, N.; Martyn, C.N.; Greenwald, S.E. Validation of a device to measure arterial pulse wave velocity by a photoplethysmographic method. Physiol. Meas. 2002, 23, 581. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.; Murray, A. Age-related changes in peripheral pulse timing characteristics at the ears, fingers and toes. J. Hum. Hypertens. 2002, 16, 711–717. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wen, C.; Tao, G.; Bi, M.; Li, G. Continuous and noninvasive blood pressure measurement: A novel modeling methodology of the relationship between blood pressure and pulse wave velocity. Ann. Biomed. Eng. 2009, 37, 2222–2233. [Google Scholar] [CrossRef] [PubMed]
- Nitzan, M.; Khanokh, B.; Slovik, Y. The difference in pulse transit time to the toe and finger measured by photoplethysmography. Physiol. Meas. 2001, 23, 85–93. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, C.; Tao, G.; Bi, M. Continuous and noninvasive measurement of systolic and diastolic blood pressure by one mathematical model with the same model parameters and two separate pulse wave velocities. Ann. Biomed. Eng. 2012, 40, 871–882. [Google Scholar] [CrossRef] [PubMed]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.W.; Kobayashi, T.; Ichikawa, S.; Takeuchi, Y.; Togawa, T. Continuous estimation of systolic blood pressure using the pulse arrival time and intermittent calibration. Med. Biol. Eng. Comput. 2000, 38, 569–574. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Poon, C.C.; Zhang, Y.-T. Investigation of temporal relationship between cardiovascular variables for cuffless blood pressure estimation. In Proceedings of the 2012 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Hong Kong, China, 5–7 January 2012; pp. 644–646. [Google Scholar]
- Ma, T.; Zhang, Y. A correlation study on the variabilities in pulse transit time, blood pressure, and heart rate recorded simultaneously from healthy subjects. In Proceedings of the 27th Annual International Conference of the Engineering in Medicine and Biology Society (EMBS 2005), Shanghai, China, 1–4 September 2005; pp. 996–999. [Google Scholar]
- Schneider, J.A.; Davidson, D.M.; Winchester, M.A.; Taylor, C.B. The covariation of blood pressure and pulse transit time in hypertensive patients. Psychophysiology 1981, 18, 301–306. [Google Scholar]
- Ma, H.T. A blood pressure monitoring method for stroke management. Biomed. Res. Int. 2014, 2014, 571623. [Google Scholar] [CrossRef] [PubMed]
- García, M.T.G.; Acevedo, M.F.T.; Guzmán, M.R.; de Montaner, R.A.; Fernández, B.F.; del Río Camacho, G.; González-Mangado, N. Puede ser el tiempo de tránsito de pulso útil para detectar hipertensión arterial en pacientes remitidos a la unidad de sueño? Arch. Bronconeumol. 2014, 50, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Forouzanfar, M.; Ahmad, S.; Batkin, I.; Dajani, H.R.; Groza, V.Z.; Bolic, M. Model-based mean arterial pressure estimation using simultaneous electrocardiogram and oscillometric blood pressure measurements. IEEE Trans. Instrum. Meas. 2015, 64, 2443–2452. [Google Scholar] [CrossRef]
- Li, Q.; Belz, G. Systolic time intervals in clinical pharmacology. Eur. J. Clin. Pharmacol. 1993, 44, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Fung, P.; Dumont, G.; Ries, C.; Mott, C.; Ansermino, M. Continuous noninvasive blood pressure measurement by pulse transit time. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2004, 1, 738–741. [Google Scholar] [PubMed]
- Ochiai, R.; Takeda, J.; Hosaka, H.; Sugo, Y.; Tanaka, R.; Soma, T. The relationship between modified pulse wave transit time and cardiovascular changes in isoflurane anesthetized dogs. J. Clin. Monit. Comput. 1999, 15, 493–501. [Google Scholar] [CrossRef] [PubMed]
- Solà, J.; Rimoldi, S.F.; Allemann, Y. Ambulatory Monitoring of the Cardiovascular System: The Role of Pulse Wave Velocity; INTECH Open Access Publisher: Rijeka, Croatia, 2010. [Google Scholar]
- Naschitz, J.E.; Bezobchuk, S.; Mussafia-Priselac, R.; Sundick, S.; Dreyfuss, D.; Khorshidi, I.; Karidis, A.; Manor, H.; Nagar, M.; Peck, E.R.; et al. Pulse transit time by R-wave-gated infrared photoplethysmography: Review of the literature and personal experience. J. Clin. Monit. Comput. 2004, 18, 333–342. [Google Scholar] [CrossRef] [PubMed]
- Payne, R.; Symeonides, C.; Webb, D.; Maxwell, S. Pulse transit time measured from the ECG: An unreliable marker of beat-to-beat blood pressure. J. Appl. Physiol. 2006, 100, 136–141. [Google Scholar] [CrossRef] [PubMed]
- Young, C.C.; Mark, J.B.; White, W.; DeBree, A.; Vender, J.S.; Fleming, A. Clinical evaluation of continuous noninvasive blood pressure monitoring: accuracy and tracking capabilities. J. Clin. Monit. 1995, 11, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Gao, M.; Xu, D.; Olivier, N.B.; Mukkamala, R. Pulse arrival time is not an adequate surrogate for pulse transit time as a marker of blood pressure. J. Appl. Physiol. 2011, 111, 1681–1686. [Google Scholar] [CrossRef] [PubMed]
- Noordergraaf, A. Circulatory System Dynamics; Elsevier: Amsterdam, The Netherlands, 2012; Volume 1. [Google Scholar]
- Marie, G.V.; Lo, C.; van Jones, J.; Johnston, D.W. The relationship between arterial blood pressure and pulse transit time during dynamic and static exercise. Psychophysiology 1984, 21, 521–527. [Google Scholar] [CrossRef] [PubMed]
- Proença, J.; Muehlsteff, J.; Aubert, X.; Carvalho, P. Is pulse transit time a good indicator of blood pressure changes during short physical exercise in a young population? In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology (EMBC), Buenos Aires, Argentina, 31 August–4 September 2010; pp. 598–601. [Google Scholar]
- Wong, M.Y.-M.; Poon, C.C.-Y.; Zhang, Y.-T. An evaluation of the cuffless blood pressure estimation based on pulse transit time technique: A half year study on normotensive subjects. Cardiovasc. Eng. 2009, 9, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Baek, H.J.; Kim, K.K.; Kim, J.S.; Lee, B.; Park, K.S. Enhancing the estimation of blood pressure using pulse arrival time and two confounding factors. Physiol. Meas. 2009, 31, 145–157. [Google Scholar] [CrossRef] [PubMed]
- Wibmer, T.; Doering, K.; Kropf-Sanchen, C.; Rüdiger, S.; Blanta, I.; Stoiber, K.; Rottbauer, W.; Schumann, C. Pulse transit time and blood pressure during cardiopulmonary exercise tests. Physiol. Res. 2014, 63, 287–296. [Google Scholar] [PubMed]
- Masè, M.; Mattei, W.; Cucino, R.; Faes, L.; Nollo, G. Feasibility of cuff-free measurement of systolic and diastolic arterial blood pressure. J. Electrocardiol. 2011, 44, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Marcinkevics, Z.; Greve, M.; Aivars, J.I.; Erts, R.; Zehtabi, A.H. Relationship between arterial pressure and pulse wave velocity using photoplethysmography during the post-exercise recovery period. Acta Univ. Latv. Biol. 2009, 753, 59–68. [Google Scholar]
- Jadooei, A.; Zaderykhin, O.; Shulgin, V. Adaptive algorithm for continuous monitoring of blood pressure using a pulse transit time. In Proceedings of the 2013 IEEE XXXIII International Scientific Conference Electronics and Nanotechnology (ELNANO), Kiev, Ukraine, 16–19 April 2013; pp. 297–301. [Google Scholar]
- Gesche, H.; Grosskurth, D.; Küchler, G.; Patzak, A. Continuous blood pressure measurement by using the pulse transit time: comparison to a cuff-based method. Eur. J. Appl. Physiol. 2012, 112, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.-R.; Zhang, Y.-T.; Liu, J.; Dai, W.-X.; Tsang, H.K. Continuous cuffless blood pressure estimation using pulse transit time and photoplethysmogram intensity ratio. IEEE Trans. Biomed. Eng. 2016, 63, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Association for the Advancement of Medical Instrumentatio. American National Standard: Electronic or Automated Sphygmomanometers; AAMI: Washington, DC, USA, 1987. [Google Scholar]
- Baldridge, B.R.; Burgess, D.E.; Zimmerman, E.E.; Carroll, J.J.; Sprinkle, A.G.; Speakman, R.O.; Li, S.-G.; Brown, D.R.; Taylor, R.F.; Dworkin, S.; et al. Heart rate-arterial blood pressure relationship in conscious rat before vs. after spinal cord transection. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2002, 283, R748–R756. [Google Scholar] [CrossRef] [PubMed]
- Griggs, M.S.D.; Naghibi, A.; Barbosa, K.; Ho, V.; Wallin, C.; Ghirmai, T.; Krishnan, S.; Cao, H. Design and Development of Continuous Cuff-Less Blood Pressure Monitoring Devices. In Proceedings of the 2016 IEEE Sensors, Orlando, FL, USA, 30 October–2 November 2016. [Google Scholar]
- Saeed, M.; Villarroel, M.; Reisner, A.T.; Clifford, G.; Lehman, L.-W.; Moody, G.; Heldt, T.; Kyaw, T.H.; Moody, B.; Mark, R.G. Multiparameter Intelligent Monitoring in Intensive Care II (MIMIC-II): A public-access intensive care unit database. Crit. Care Med. 2011, 39, 952–960. [Google Scholar] [CrossRef] [PubMed]
- Tomson, J.; Lip, G.Y. Blood pressure demographics: nature or nurture...... genes or environment? BMC Med. 2005, 3, 3. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Bunce, C. Correlation, agreement, and Bland-Altman analysis: Statistical analysis of method comparison studies. Am. J. Ophthalmol. 2009, 148, 4–6. [Google Scholar] [CrossRef] [PubMed]
- Fagard, R.H. Exercise characteristics and the blood pressure response to dynamic physical training. Med. Sci. Sports Exerc. 2001, 33, S484–S492. [Google Scholar] [CrossRef] [PubMed]
- Longo, A.; Geiser, M.H.; Riva, C.E. Posture changes and subfoveal choroidal blood flow. Investig. Ophthalmol. Vis. Sci. 2004, 45, 546–551. [Google Scholar] [CrossRef]
- Parati, G.; Casadei, R.; Groppelli, A.; di Rienzo, M.; Mancia, G. Comparison of finger and intra-arterial blood pressure monitoring at rest and during laboratory testing. Hypertension 1989, 13, 647–655. [Google Scholar] [CrossRef] [PubMed]
- Ohlsson, O.; Henningsen, N. Blood pressure, cardiac output and systemic vascular resistance during rest, muscle work, cold pressure test and psychological stress. Acta Med. Scand. 1982, 212, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Peckerman, A.; Saab, P.G.; McCabe, P.M.; Skyler, J.S.; Winters, R.W.; Llabre, M.M.; Schneiderman, N. Blood pressure reactivity and perception of pain during the forehead cold pressor test. Psychophysiology 1991, 28, 485–495. [Google Scholar] [CrossRef] [PubMed]
- Al’Absi, M.; Bongard, S.; Buchanan, T.; Pincomb, G.A.; Licinio, J.; Lovallo, W.R. Cardiovascular and neuroendocrine adjustment to public speaking and mental arithmetic stressors. Psychophysiology 1997, 34, 266–275. [Google Scholar] [CrossRef] [PubMed]
- Agras, S.W.; Horne, M.; Taylor, B.C. Expectation and the blood-pressure-lowering effects of relaxation. Psychosom. Med. 1982, 44, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Davis, W.B.; Thaut, M.H. The influence of preferred relaxing music on measures of state anxiety, relaxation, and physiological responses. J. Music Ther. 1989, 26, 168–187. [Google Scholar] [CrossRef]
- Steptoe, A.; Smulyan, H.; Gribbin, B. Pulse wave velocity and blood pressure change: Calibration and applications. Psychophysiology 1976, 13, 488–493. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, K.; Miura, K.; Takata, Y.; Kurokawa, H.; Kajiyama, M.; Abe, I.; Fujishima, M. Changes in blood pressure and heart rate variability during dental surgery. Am. J. Hypertens. 1998, 11, 1376–1380. [Google Scholar] [CrossRef]
- Wiley, R.L.; Dunn, C.L.; Cox, R.H.; Hueppchen, N.A.; Scott, M.S. Isometric exercise training lowers resting blood pressure. Med. Sci. Sports Exerc. 1992, 24, 749–754. [Google Scholar] [CrossRef] [PubMed]
- Petrofsky, J.S.; Lind, A.R. Aging, isometric strength and endurance, and cardiovascular responses to static effort. J. Appl. Physiol. 1975, 38, 91–95. [Google Scholar] [PubMed]
- Petrofsky, J.S.; Burse, R.L.; Lind, A. Comparison of physiological responses of women and men to isometric exercise. J. Appl. Physiol. 1975, 38, 863–868. [Google Scholar] [PubMed]
- McCarthy, B.; Vaughan, C.; O’Flynn, B.; Mathewson, A.; Mathúna, C.Ó. An examination of calibration intervals required for accurately tracking blood pressure using pulse transit time algorithms. J. Hum. Hypertens. 2013, 27, 744–750. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.-R.; Zhang, Y.-T. Photoplethysmogram intensity ratio: A potential indicator for improving the accuracy of PTT-based cuffless blood pressure estimation. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 398–401. [Google Scholar]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuff-Less Blood Pressure Estimation Algorithms for Continuous Health-Care Monitoring. IEEE Trans. Biomed. Eng. 2017, 64, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Kim, K.K.; Baek, H.J.; Park, K.S. Effect of confounding factors on blood pressure estimation using pulse arrival time. Physiol. Meas. 2008, 29, 615. [Google Scholar] [CrossRef] [PubMed]
- Drinnan, M.J.; Allen, J.; Murray, A. Relation between heart rate and pulse transit time during paced respiration. Physiol. Meas. 2001, 22, 425–432. [Google Scholar] [CrossRef] [PubMed]
- di Rienzo, M.; Parati, G.; Radaelli, A.; Castiglioni, P. Baroreflex contribution to blood pressure and heart rate oscillations: Time scales, time-variant characteristics and nonlinearities. Philos. Trans. R. S. Lond. A Math. Phys. Eng. Sci. 2009, 367, 1301–1318. [Google Scholar] [CrossRef] [PubMed]
- Nichols, W.; O’Rourke, M. McDonald’s Blood Flow in Arteries, 4th ed.; Edward Arnold: London, UK, 1998. [Google Scholar]
- Shaltis, P.; Reisner, A.; Asada, H. A hydrostatic pressure approach to cuffless blood pressure monitoring. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–4 September 2004; pp. 2173–2176. [Google Scholar]
- Gaddum, N.; Alastruey, J.; Beerbaum, P.; Chowienczyk, P.; Schaeffter, T. A technical assessment of pulse wave velocity algorithms applied to non-invasive arterial waveforms. Ann. Biomed. Eng. 2013, 41, 2617–2629. [Google Scholar] [CrossRef] [PubMed]
- Gaballa, M.A.; Jacob, C.T.; Raya, T.E.; Liu, J.; Simon, B.; Goldman, S. Large Artery Remodeling During Aging Biaxial Passive and Active Stiffness. Hypertension 1998, 32, 437–443. [Google Scholar] [CrossRef] [PubMed]
- Mayor, S. Doctors are urged to measure blood pressure in both arms. BMJ 2016, 353, i2577. [Google Scholar] [CrossRef] [PubMed]
- Eşer, İ.; Khorshid, L.; Güneş, Ü.Y.; Demir, Y. The effect of different body positions on blood pressure. J. Clin. Nurs. 2007, 16, 137–140. [Google Scholar] [CrossRef] [PubMed]
- Ng, K.-G. Review of measurement methods and clinical validation studies of noninvasive blood pressure monitors: Accuracy requirements and protocol considerations for devices that require patient-specific calibration by a secondary method or device before use. Blood Press. Monit. 2011, 16, 291–303. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Kim, M.-J.; Kim, J. Development of real-time motion artifact reduction algorithm for a wearable photoplethysmography. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 23–26 August 2007; pp. 1538–1541. [Google Scholar]
- Poh, M.-Z.; Swenson, N.C.; Picard, R.W. Motion-tolerant magnetic earring sensor and wireless earpiece for wearable photoplethysmography. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 786–794. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Lee, J.; Jung, W.; Lee, G.-K. The periodic moving average filter for removing motion artifacts from PPG signals. Int. J. Control Autom. Syst. 2007, 5, 701–706. [Google Scholar]
- Solà, J.; Proença, M.; Ferrario, D.; Porchet, J.-A.; Falhi, A.; Grossenbacher, O.; Allemann, Y.; Rimoldi, S.F.; Sartori, C. Noninvasive and nonocclusive blood pressure estimation via a chest sensor. IEEE Trans. Biomed. Eng. 2013, 60, 3505–3513. [Google Scholar] [CrossRef] [PubMed]
- Teng, X.; Zhang, Y. The effect of applied sensor contact force on pulse transit time. Physiol. Meas. 2006, 27, 675–684. [Google Scholar] [CrossRef] [PubMed]
- Teng, X.-F.; Zhang, Y.-T. Theoretical study on the effect of sensor contact force on pulse transit time. IEEE Trans. Biomed. Eng. 2007, 54, 1490–1498. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Liu, Z.; McKenna, T.; Reisner, A.T.; Reifman, J. A method for automatic identification of reliable heart rates calculated from ECG and PPG waveforms. J. Am. Med. Inf. Associ. 2006, 13, 309–320. [Google Scholar] [CrossRef] [PubMed]
- Foo, J.Y.A. Use of independent component analysis to reduce motion artifact in pulse transit time measurement. IEEE Signal Proc. Lett. 2008, 15, 124–126. [Google Scholar] [CrossRef]
- Shin, H.S.; Lee, C.; Lee, M. Adaptive threshold method for the peak detection of photoplethysmographic waveform. Comput. Biol. Med. 2009, 39, 1145–1152. [Google Scholar] [CrossRef] [PubMed]
- McDuff, D.; Gontarek, S.; Picard, R.W. Remote detection of photoplethysmographic systolic and diastolic peaks using a digital camera. IEEE Trans. Biomed. Eng. 2014, 61, 2948–2954. [Google Scholar] [CrossRef] [PubMed]
- McCombie, D.B. Development of a Wearable Blood Pressure Monitor Using Adaptive Calibration of Peripheral Pulse Transit Time Measurements; Massachusetts Institute of Technology: Cambridge, MA, USA, 2008. [Google Scholar]
- Douniama, C.; Sauter, C.; Couronne, R. Blood pressure tracking capabilities of pulse transit times in different arterial segments: A clinical evaluation. In Proceedings of the 2009 36th Annual Computers in Cardiology Conference (CinC), Park City, UT, USA, 13–16 September 2009; pp. 201–204. [Google Scholar]
- O’brien, E.; Pickering, T.; Asmar, R.; Myers, M.; Parati, G.; Staessen, J.; Mengden, T.; Imai, Y.; Waeber, B.; Palatini, P.; et al. Working Group on Blood Pressure Monitoring of the European Society of Hypertension International Protocol for validation of blood pressure measuring devices in adults. Blood Press. Monit. 2002, 7, 3–17. [Google Scholar] [CrossRef] [PubMed]
- O’brien, E.; Petrie, J.; Little, W.; de Swiet, M.; Padfield, P.L.; Altma, D.G.; Bland, M.; Coats, A.; Atkins, N. Short report: An outline of the revised British Hypertension Society protocol for the evaluation of blood pressure measuring devices. J. Hypertens. 1993, 11, 677–679. [Google Scholar] [CrossRef] [PubMed]
- Ribezzo, S.; Spina, E.; di Bartolomeo, S.; Sanson, G. Noninvasive techniques for blood pressure measurement are not a reliable alternative to direct measurement: A randomized crossover trial in ICU. Sci. World J. 2014, 2014, 363628. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.-L.; Ding, X.-R.; Poon, C.C.Y.; Lo, B.P.L.; Zhang, H.; Zhou, X.-L.; Yang, G.-Z.; Zhao, N.; Zhang, Y.T. Unobtrusive sensing and wearable devices for health informatics. IEEE Trans. Biomed. Eng. 2014, 61, 1538–1554. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, V.; Dantu, R.; Jonnada, S.; Thiyagaraja, S.; Subbu, K.P. Cuffless differential blood pressure estimation using smart phones. IEEE Trans. Biomed. Eng. 2013, 60, 1080–1089. [Google Scholar] [CrossRef] [PubMed]
| Algorithm | Time Delay | Calibration Technique | Results | Refs | ||
|---|---|---|---|---|---|---|
| SBP | DBP | MAP | ||||
| PTTf | Subject specific | −0.22 ± 0.46 2 | - | - | [82] | |
| PATf | −0.85 ± 0.09 2 | |||||
| PTTf | 0.9 3 | |||||
| PATp | A: Dependent on Height B: Subject specific | 0.0790 ± 11.32 1 | - | - | [73] | |
| PATf | Subject specific | 0.99–0.90 2 | - | - | [65] | |
| PATp | Subject specific | −0.92 2 | −0.38 2 | - | [83] | |
| RT: −0.87 2,* | RT: −0.30 2,* | |||||
| PATm | Subject specific | 0.701 3 | 0.401 3 | - | [84] | |
| PATp | Subject specific | 0.95–0.87 3 | 0.01–0.73 3 | - | [85] | |
| PATp | Subject specific | −0.71 2 | −0.69 2 | - | [25] | |
| PATm | −0.32 2 | −0.22 2 | ||||
| PATf | −0.09 2 | −0.02 2 | ||||
| PATp | Subject specific | 0.32 2 | [28] | |||
| PATm | 0.27 2 | |||||
| PATf | 0.45 2 | |||||
| PATp | Subject specific | 0.95 3 | 0.26 3 | [69] | ||
| PATm | 0.89 3 | 0.78 3 | [86] | |||
| PATp | 0.96 3 | 0.70 3 | - | [69] | ||
| PATp | Subject specific | 0.97 ± 0.87 3 | 0.54 ± 0.05 3 | - | [85] | |
| PATf | Subject specific | 0.93 2 | - | 0.83 2 | [87] | |
| PATf | 0.94 2 | 0.86 2 | ||||
| PATm | Subject specific, Maximum Likelihood | 0.978 3 | 0.974 3 | - | [88] | |
| PATm | Subject specific, Adaptive Kalman filter | 0.976 3 | 0.989 3 | - | ||
| PATm | Subject specific | 0.85 3 | 0.74 3 | - | [84] | |
| PTTf | and are calculated for a demographically similar group. | - | −1.49 ± 6.51 1 | - | [61,63] | |
| 2.16 ± 6.23 1 | - | |||||
| PATm | Subject specific | 0.6 ± 9.81 | 0.9 ± 5.6 1 | - | [30] | |
| PATm | Universal | 0.83 2 | - | - | [89] | |
2 | PATm | Subject specific | 0.91 2 | 0.88 2 | 0.89 2 | [90] |
| Procedure | Description | Refs |
|---|---|---|
| Physical Exercise | Graded Bicycle Test, Running, Sit-ups | [87,99] |
| Posture | Sitting, standing and lying supine | [100] |
| Valsalva Maneuver | Breathing against closed nose/mouth for 30 s | [101] |
| Cold Pressure | Placement of ice wrapped in wet cloth on subject’s forehead for 2 min. Hand in 4 °C water for 1 min | [102,103] |
| Mental Arithmetic | Counting backwards from 500 in intervals of 7, Continuous addition of 3 digit numbers for 2 min | [104] |
| Relaxation | Slow breathing/Meditative music | [105,106] |
| Amyl Nitrate | Inhalation of vasodilator | [107] |
| Anesthesia | Dental anesthesia | [84,108] |
| Isometric Exercise | Raising legs/arms against pressure | [109] |
| Sustained Handgrip | Clenching one’s fist forcefully | [110,111] |
| Algorithm/Characteristic Point | PATf | PATm | PATp | |
|---|---|---|---|---|
| SBP | aln(PAT) + b | 0.1 ± 11 | 8.9 | 0.3 ± 11 |
| a/PAT2 + b | 0.1 ± 12 | 0.1 ± 12 | 0.1 ± 12 | |
| a/PAT + b | 0.1 ± 13 | 0.1 ± 13 | 0.1 ± 13 | |
| aPAT + bHR + c | 0.1 ± 14 | 0.1 ± 14 | 0.1 ± 14 | |
| MAP | aln(PAT) + b | 0.1 ± 15 | 0.1 ± 15 | 0.1 ± 15 |
| a/PAT2 + b | 0.1 ± 16 | 0.1 ± 16 | 0.1 ± 16 | |
| a/PAT + b | 0.1 ± 17 | 0.1 ± 17 | 0.1 ± 17 | |
| aPAT + bHR + c | 0.1 ± 18 | 0.1 ± 18 | 0.1 ± 18 | |
| DBP | aln(PAT) + b | 0.1 ± 19 | 0.1 ± 19 | 0.1 ± 19 |
| a/PAT2 + b | 0.1 ± 20 | 0.1 ± 20 | 0.1 ± 20 | |
| a/PAT + b | 0.1 ± 21 | 0.1 ± 21 | 0.1 ± 21 | |
| aPAT + bHR + c | 0.1 ± 22 | 0.1 ± 22 | 0.1 ± 22 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, M.; Barbosa, K.; Ho, V.; Griggs, D.; Ghirmai, T.; Krishnan, S.K.; Hsiai, T.K.; Chiao, J.-C.; Cao, H. Cuff-Less and Continuous Blood Pressure Monitoring: A Methodological Review. Technologies 2017, 5, 21. https://doi.org/10.3390/technologies5020021
Sharma M, Barbosa K, Ho V, Griggs D, Ghirmai T, Krishnan SK, Hsiai TK, Chiao J-C, Cao H. Cuff-Less and Continuous Blood Pressure Monitoring: A Methodological Review. Technologies. 2017; 5(2):21. https://doi.org/10.3390/technologies5020021
Chicago/Turabian StyleSharma, Manuja, Karinne Barbosa, Victor Ho, Devon Griggs, Tadesse Ghirmai, Sandeep K. Krishnan, Tzung K. Hsiai, Jung-Chih Chiao, and Hung Cao. 2017. "Cuff-Less and Continuous Blood Pressure Monitoring: A Methodological Review" Technologies 5, no. 2: 21. https://doi.org/10.3390/technologies5020021
APA StyleSharma, M., Barbosa, K., Ho, V., Griggs, D., Ghirmai, T., Krishnan, S. K., Hsiai, T. K., Chiao, J.-C., & Cao, H. (2017). Cuff-Less and Continuous Blood Pressure Monitoring: A Methodological Review. Technologies, 5(2), 21. https://doi.org/10.3390/technologies5020021






