Quantum Sensing of Noisy and Complex Systems under Dynamical Control
Abstract
:1. Introduction
2. Bath-Optimized Task-Oriented Control (BOTOC)
2.1. General Formulation of BOTOC
2.2. Dynamical Control of Qubit Dephasing (Decoherence)
2.3. Modulation Forms
2.4. Optimal Decoherence Control of a Qubit
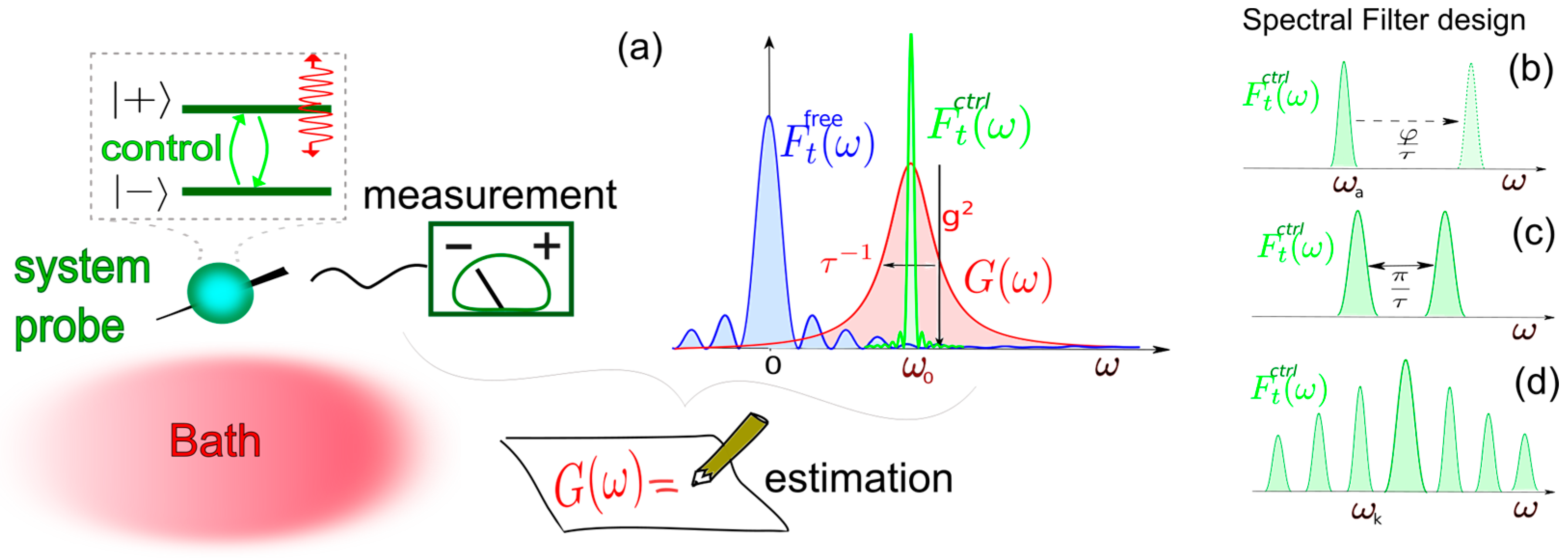
3. Control for Bath Diagnostics
4. Maximized Information on Bath’s Parameters by Dynamical Control
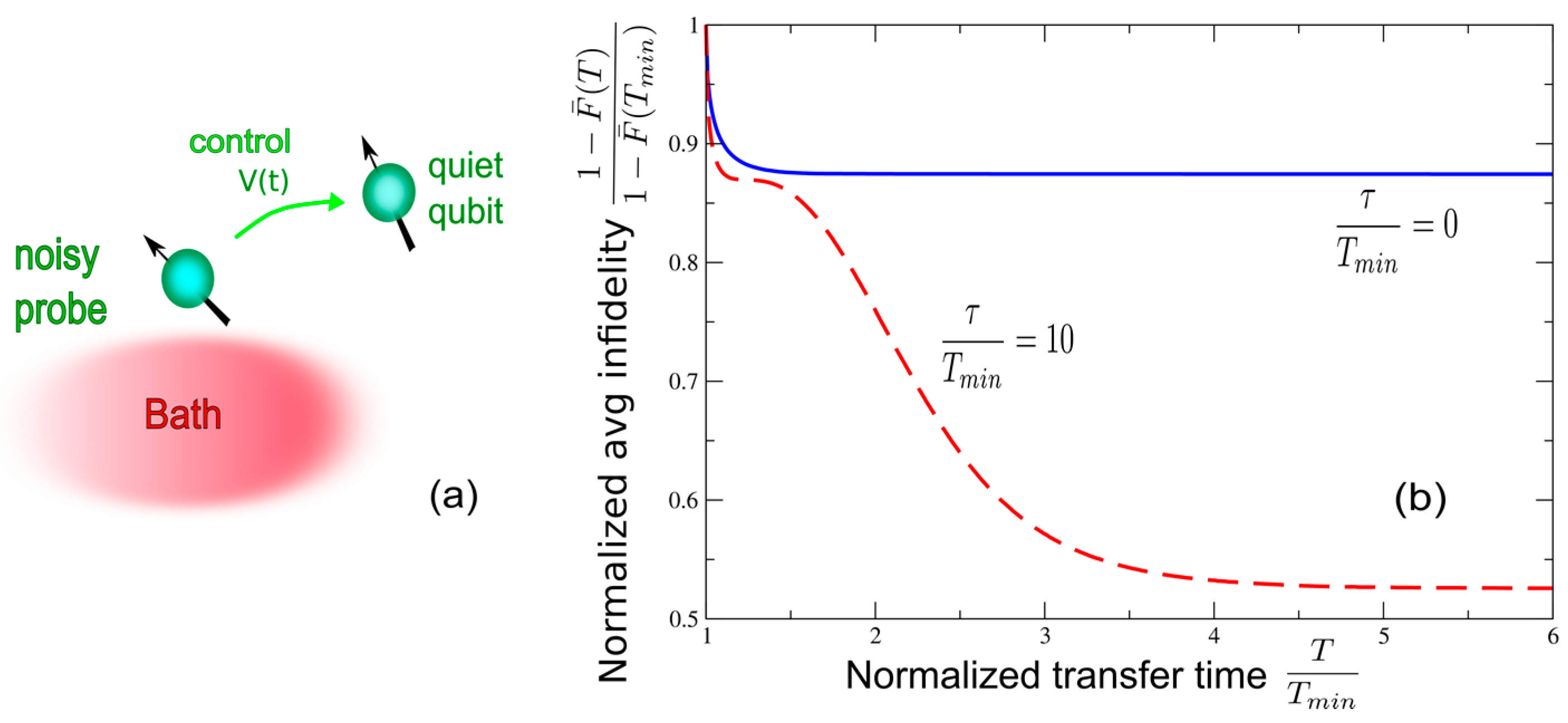
5. Dynamical Control of Quantum Transfer as Means of Diagnosing a Bath in Hybrid Systems
Optimized Transfer from Noisy to Quiet Qubits
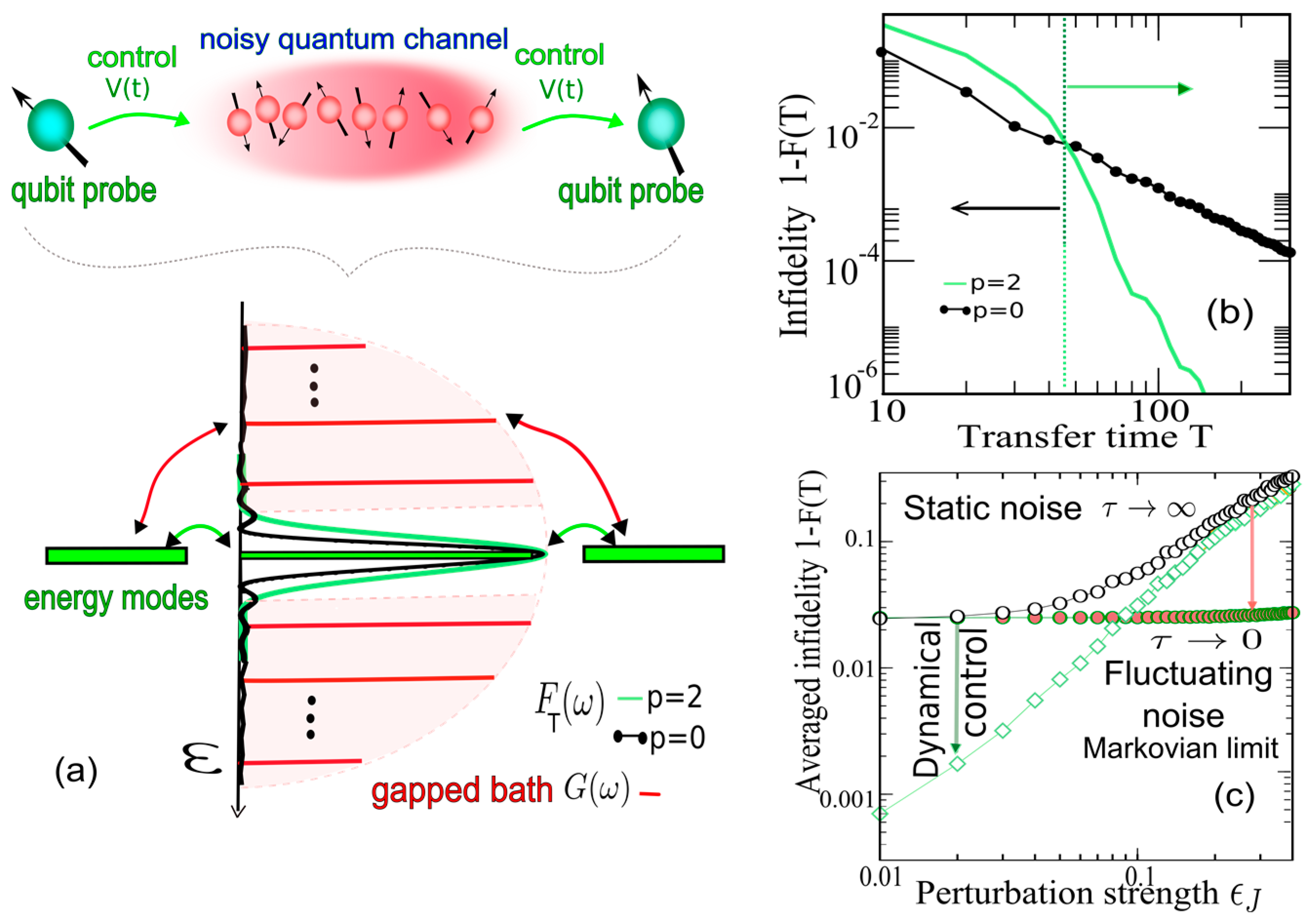
6. Dynamical Control of State Transfer via Noisy Quantum Channels and the Implications for Sensing Diagnostics
6.1. Boundary Qubit Probes and State Transfer through a Quantum Channel
6.2. Optimized Filter Design for Channel Diagnostics
6.3. Diagnosing Noise Effects in Quantum Channels
- (i)
- Dynamical boundary-control can make the channel most robust against static noise, because it filters out the bath-energies that damage the transfer. In Figure 3c control is shown to be advantageous compared with the static control case , at the expense of increasing the transfer time by only a factor of 2.
- (ii)
- Modulation is not helpful against Markovian noise. Remarkably, arbitrarily high fidelities can then be achieved by slowing down the transfer time, i.e., by decreasing , because in a Markovian bath, the fast coupling fluctuations suppress disorder-localization effects that hamper the transfer fidelity.
- (iii)
- For non-Markovian fluctuating noise that randomly varies with correlation time (Figure 3b), in contrast to Markovian noise with , optimized dynamical control can strongly reduce the infidelity that lies between the static and Markovian limits, provided the bath-spectrum is gapped.
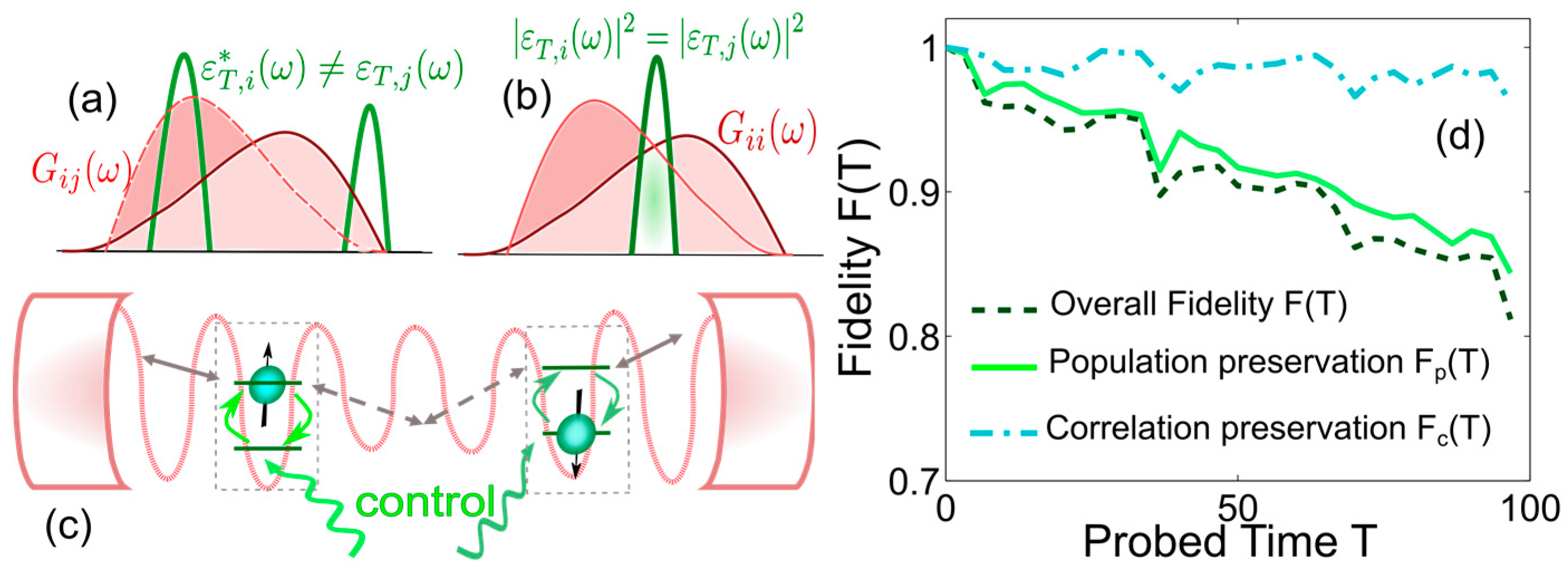
7. Dynamical Control of Multipartite Probes for Bath Diagnostics
7.1. Multipartite Decoherence Matrix
7.2. Multiqubit Probe Modulations for Reconstructing Coupling Spectra
8. Conclusions
- Local modulation can effectively decorrelate the different dephasings of the multiple qubits, i.e., eliminate their cross-decoherence, resulting in their equal dephasing rates. For two qubits, the singlet and triplet Bell-states acquire the same dynamically modified decoherence rate.
- For different couplings to a bath, one can better preserve any initial state by local modulation, which can reduce the mixing with other states, than by global modulation. Local modulation which eliminates the cross-decoherence terms, increases the fidelity more than the global modulation alternative. For two qubits, local modulation better preserves an initial Bell-state, whether a singlet or a triplet, compared to global π-phase “parity kicks.”
8.1. Comparison of Bath-Optimized Task-Oriented Control (BOTOC) to Dynamical Decoupling (DD)
- (i)
- BOTOC relaxes the DD assumption that the control fields must be either very short or very strong. In our formalism, the control fields are considered concurrently with the coupling to the bath, hence allowing a much wider variety of pulse sequences, ranging from continuous modulation all the way to DD sequences.
- (ii)
- Dynamical decoupling suggests using the same pulse sequence (be it periodic, optimized or concatenated), regardless of the shape of the bath spectrum. By contrast, BOTOC explicitly considers the bath spectrum and allows optimal tailoring of the modulation to a given bath spectrum. In many cases, the standard π-phase “bang-bang” is then found to be inadequate or non-optimal compared to dynamic control based on the optimization of the universal formula. Whereas our BOTOC approach reduces to the DD method in the particular case of proper dephasing or decay via coupling to spectrally symmetric (e.g., Lorentzian or Gaussian) noise baths with limited spectral width, phase modulation advocated for the suppression of coupling to baths with frequency cutoff or other non-monotonic spectra is, however, drastically different from the DD method which may fail for multipeak spectra.
- (iii)
- Our BOTOC universal strategy has far broader applicability than DD: It can simultaneously control, unlike DD [10,11], both decay and decoherence (proper dephasing) by either pulsed or continuous wave (CW) modulation of the system-bath coupling governed by a simple universal formula. BOTOC has been generalized by us to finite temperatures and to qubits driven by an arbitrary time-dependent field, which may cause the failure of the rotating-wave approximation [11]. It has also been extended to the analysis of multi-level systems, where quantum interference between the levels may either inhibit or accelerate the decay [19].
- (iv)
- Even if DD is adequate for independently decohering qubits, its extension to correlated multipartite systems is highly nontrivial. By contrast, BOTOC modulations with low energy decorrelate the different proper dephasings of the multiple two-level systems (TLS), resulting in equal dephasing rates for all states. For two TLS, we have shown that the singlet and triplet Bell-states acquire the same dynamically modified dephasing rate. This should be beneficial compared to standard DD based on global “bang-bang” (π-phase flips) if both the triplet and the singlet states are used (intermittently) for information transmission or storage.
8.2. Open Issues—Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Modi, K.; Cable, H.; Williamson, M.; Vedral, V. Quantum correlations in mixed-state metrology. Phys. Rev. X 2011, 1, 021022. [Google Scholar] [CrossRef]
- Kurizki, G.; Bertet, P.; Kubo, Y.; Molmer, K.; Petrosyan, D.; Rabl, P.; Schmiedmayer, J. Quantum technologies with hybrid systems. Proc. Natl. Acad. Sci. 2015, 112, 3866–3873. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, G.; Chan, I.Y.; Kolesov, R.; Al-Hmoud, M.; Tisler, J.; Shin, C.; Kim, C.; Wojcik, A.; Hemmer, P.R.; Krueger, A.; et al. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 2008, 455, 648–651. [Google Scholar] [CrossRef] [PubMed]
- Steinert, S.; Ziem, F.; Hall, L.T.; Zappe, A.; Schweikert, M.; Götz, N.; Aird, A.; Balasubramanian, G.; Hollenberg, L.; Wrachtrup, J. Magnetic spin imaging under ambient conditions with sub-cellular resolution. Nat. Commun. 2013, 4, 1607. [Google Scholar] [CrossRef] [PubMed]
- Kucsko, G.; Maurer, P.C.; Yao, N.Y.; Kubo, M.; Noh, H.J.; Lo, P.K.; Park, H.; Lukin, M.D. Nanometre-scale thermometry in a living cell. Nature 2013, 500, 54–58. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R.; Yacoby, A.; Walsworth, R.; Lukin, M.D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. [Google Scholar] [CrossRef]
- Meriles, C.A.; Jiang, L.; Goldstein, G.; Hodges, J.S.; Maze, J.; Lukin, M.D.; Cappellaro, P. Imaging mesoscopic nuclear spin noise with a diamond magnetometer. J. Chem. Phys. 2010, 133, 124105. [Google Scholar] [CrossRef] [PubMed]
- Treutlein, P.; Genes, C.; Hammerer, K.; Poggio, M.; Rabl, P. Hybrid Mechanical Systems. In Cavity Optomechanics; Aspelmeyer, M., Kippenberg, T.J., Marquardt, F., Eds.; Quantum Science and Technology; Springer Berlin Heidelberg: Berlin, Germany, 2014; pp. 327–351. [Google Scholar]
- Zwick, A.; Alvarez, G.A.; Kurizki, G. Maximizing information on the environment by dynamically controlled qubit probes. Phys. Rev. Appl. 2016, 5, 014007. [Google Scholar] [CrossRef]
- Almog, I.; Sagi, Y.; Gordon, G.; Bensky, G.; Kurizki, G.; Davidson, N. Direct measurement of the system-environment coupling as a tool for understanding decoherence and dynamical decoupling. J. Phys. B Mol. Opt. Phys. 2011, 44, 154006. [Google Scholar] [CrossRef]
- Álvarez, G.A.; Suter, D. Measuring the spectrum of colored noise by dynamical decoupling. Phys. Rev. Lett. 2011, 107, 230501. [Google Scholar] [CrossRef] [PubMed]
- Bylander, J.; Gustavsson, S.; Yan, F.; Yoshihara, F.; Harrabi, K.; Fitch, G.; Cory, D.G.; Nakamura, Y.; Tsai, J.-S.; Oliver, W.D. Noise spectroscopy through dynamical decoupling with a superconducting flux qubit. Nat. Phys. 2011, 7, 565–570. [Google Scholar] [CrossRef]
- Zwick, A.; Alvarez, G.A.; Kurizki, G. Criticality of environmental information obtainable by dynamically controlled quantum probes. Phys. Rev. A 2016, 94, 042122. [Google Scholar] [CrossRef]
- Smith, P.E.S.; Bensky, G.; Álvarez, G.A.; Kurizki, G.; Frydman, L. Shift-driven modulations of spin-echo signals. PNAS 2012, 109, 5958–5961. [Google Scholar] [CrossRef] [PubMed]
- Bretschneider, C.O.; Álvarez, G.A.; Kurizki, G.; Frydman, L. Controlling spin-spin network dynamics by repeated projective measurements. Phys. Rev. Lett. 2012, 108, 140403. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, G.A.; Shemesh, N.; Frydman, L. Coherent dynamical recoupling of diffusion-driven decoherence in magnetic resonance. Phys. Rev. Lett. 2013, 111, 080404. [Google Scholar] [CrossRef] [PubMed]
- Shemesh, N.; Álvarez, G.A.; Frydman, L. Measuring small compartment dimensions by probing diffusion dynamics via Non-uniform Oscillating-Gradient Spin-Echo (NOGSE) NMR. J. Magn. Reson. 2013, 237, 49–62. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, G.A.; Shemesh, N.; Frydman, L. Diffusion-assisted selective dynamical recoupling: A new approach to measure background gradients in magnetic resonance. J. Chem. Phys. 2014, 140, 084205. [Google Scholar] [CrossRef] [PubMed]
- Shemesh, N.; Álvarez, G.A.; Frydman, L. Size distribution imaging by Non-uniform Oscillating-Gradient Spin Echo (NOGSE) MRI. PLoS ONE 2015, 10, e0133201. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Sergienko, A.V. Quantum Communications and Cryptography; CRC Press, Inc.: Boca Raton, FL, USA, 2005. [Google Scholar]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Wolfgramm, F.; Vitelli, C.; Beduini, F.A.; Godbout, N.; Mitchell, M.W. Entanglement-enhanced probing of a delicate material system. Nat. Photonics 2013, 7, 28–32. [Google Scholar] [CrossRef]
- Schmidt, P.O.; Rosenband, T.; Langer, C.; Itano, W.M.; Bergquist, J.C.; Wineland, D.J. Spectroscopy using quantum logic. Science 2005, 309, 749–752. [Google Scholar] [CrossRef] [PubMed]
- Hempel, C.; Lanyon, B.P.; Jurcevic, P.; Gerritsma, R.; Blatt, R.; Roos, C.F. Entanglement-enhanced detection of single-photon scattering events. Nat. Photonics 2013, 7, 630–633. [Google Scholar] [CrossRef]
- Ockeloen, C.F.; Schmied, R.; Riedel, M.F.; Treutlein, P. Quantum metrology with a scanning probe atom interferometer. Phys. Rev. Lett. 2013, 111, 143001. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Minimal universal quantum heat machine. Phys. Rev. E 2013, 87, 012140. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Work and energy gain of heat-pumped quantized amplifiers. Europhys. Lett. 2013, 103, 60005. [Google Scholar] [CrossRef]
- Kolář, M.; Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Quantum Bath Refrigeration towards Absolute Zero: Challenging the Unattainability Principle. Phys. Rev. Lett. 2012, 109, 090601. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Erez, N.; Alicki, R.; Kurizki, G. Work extraction via quantum nondemolition measurements of qubits in cavities: Non-Markovian effects. Phys. Rev. A 2013, 88, 022112. [Google Scholar] [CrossRef]
- Alicki, R.; Gelbwaser-Klimovsky, D.; Kurizki, G. Periodically driven quantum open systems: Tutorial. arXiv 2012. [Google Scholar]
- Gelbwaser-Klimovsky, D.; Kurizki, G. Work extraction from heat-powered quantized optomechanical setups. Sci. Rep. 2015, 5, 7809. [Google Scholar] [CrossRef] [PubMed]
- Clausen, J.; Bensky, G.; Kurizki, G. Bath-optimized minimal-energy protection of quantum operations from decoherence. Phys. Rev. Lett. 2010, 104, 040401. [Google Scholar] [CrossRef] [PubMed]
- Clausen, J.; Bensky, G.; Kurizki, G. Task-optimized control of open quantum systems. Phys. Rev. A 2012, 85, 052105. [Google Scholar] [CrossRef]
- Viola, L.; Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 1998, 58, 2733–2744. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Scully, M.O.; Walther, H. Accelerating decay by multiple 2 pi pulses. Phys. Rev. A 2001, 63, 044101. [Google Scholar] [CrossRef]
- Agarwal, G.S. Control of decoherence and relaxation by frequency modulation of a heat bath. Phys. Rev. A 2000, 61, 013809. [Google Scholar] [CrossRef]
- Shiokawa, K.; Lidar, D.A. Dynamical decoupling using slow pulses: Efficient suppression of 1/f noise. Phys. Rev. A 2004, 69, 030302. [Google Scholar] [CrossRef]
- Vitali, D.; Tombesi, P. Heating and decoherence suppression using decoupling techniques. Phys. Rev. A 2001, 65, 012305. [Google Scholar] [CrossRef]
- Viola, L.; Knill, E. Robust dynamical decoupling of quantum systems with bounded controls. Phys. Rev. Lett. 2003, 90, 037901. [Google Scholar] [CrossRef] [PubMed]
- Khodjasteh, K.; Lidar, D.A. Fault-tolerant quantum dynamical decoupling. Phys. Rev. Lett. 2005, 95, 180501. [Google Scholar] [CrossRef] [PubMed]
- Zwick, A.; Álvarez, G.A.; Bensky, G.; Kurizki, G. Optimized dynamical control of state transfer through noisy spin chains. New J. Phys. 2014, 16, 065021. [Google Scholar] [CrossRef]
- Gordon, G.; Kurizki, G.; Kofman, A.G. Universal dynamical control of local decoherence for multipartite and multilevel systems. Opt. Comm. 2006, 264, 398. [Google Scholar] [CrossRef]
- Barone, A.; Kurizki, G.; Kofman, A.G. Dynamical control of macroscopic quantum tunneling. Phys. Rev. Lett. 2004, 92, 200403. [Google Scholar] [CrossRef] [PubMed]
- Gordon, G.; Kurizki, G.; Kofman, A.G. Universal dynamical control of decay and decoherence in multilevel systems. J. Opt. B 2005, 7, 283. [Google Scholar] [CrossRef]
- Gordon, G.; Kurizki, G. Preventing multipartite disentanglement by local modulations. Phys. Rev. Lett. 2006, 97, 110503. [Google Scholar] [CrossRef] [PubMed]
- Gordon, G.; Erez, N.; Kurizki, G. Universal dynamical decoherence control of noisy single- and multi-qubit systems. J. Phys. B Mol. Opt. Phys. 2007, 40, S75–S93. [Google Scholar] [CrossRef]
- Gordon, G.; Kurizki, G. Universal dephasing control during quantum computation. Phys. Rev. A 2007, 76, 042310. [Google Scholar] [CrossRef]
- Kofman, A.G.; Kurizki, G. Theory of dynamical control of qubit decay and decoherence. IEEE Trans. Nanotechnol. 2005, 4, 116. [Google Scholar] [CrossRef]
- Erez, N.; Gordon, G.; Nest, M.; Kurizki, G. Thermodynamic control by frequent quantum measurements. Nature 2008, 452, 724. [Google Scholar] [CrossRef] [PubMed]
- Gordon, G.; Bhaktavatsala Rao, D.D.; Kurizki, G. Equilibration by quantum observation. New J. Phys. 2010, 12, 053033. [Google Scholar] [CrossRef]
- Gordon, G.; Bensky, G.; Gelbwaser-Klimovsky, D.; Rao, D.; Erez, N.; Kurizki, G. Cooling down quantum bits on ultrashort time scales. New J. Phys. 2009, 11, 123025. [Google Scholar] [CrossRef]
- Misra, B.; Sudarshan, E.C.G. Zeno’s paradox in quantum theory. J. Math. Phys. 1977, 18, 756–763. [Google Scholar] [CrossRef]
- Kofman, A.G.; Kurizki, G. Acceleration of quantum decay processes by frequent observations. Nat. Lond. 2000, 405, 546–550. [Google Scholar]
- Kofman, A.G.; Kurizki, G. Universal dynamical control of quantum mechanical decay: Modulation of the coupling to the continuum. Phys. Rev. Lett. 2001, 87, 270405. [Google Scholar] [CrossRef] [PubMed]
- Facchi, P.; Nakazato, H.; Pascazio, S. From the quantum Zeno to the inverse quantum Zeno effect. Phys. Rev. Lett. 2001, 86, 2699. [Google Scholar] [CrossRef] [PubMed]
- Lane, A.M. Decay at early times—Larger or smaller than the Golden Rule. Phys. Lett. A 1983, 99, 359–360. [Google Scholar] [CrossRef]
- Fischer, M.C.; Gutierrez-Medina, B.; Raizen, M.G. Observation of the quantum Zeno and anti-Zeno effects in an unstable system. Phys. Rev. Lett. 2001, 87, 040402. [Google Scholar] [CrossRef] [PubMed]
- Kofman, A.G.; Kurizki, G. Unified theory of dynamically suppressed qubit decoherence in thermal baths. Phys. Rev. Lett. 2004, 93, 130406. [Google Scholar] [CrossRef] [PubMed]
- Kofman, A.G.; Kurizki, G.; Opatrný, T. Zeno and anti-Zeno effects for photon polarization dephasing. Phys. Rev. A 2001, 63, 042108. [Google Scholar] [CrossRef]
- Kofman, A.G.; Kurizki, G. Quantum Zeno effect on atomic excitation decay in resonators. Phys. Rev. A 1996, 54, R3750–R3753. [Google Scholar] [CrossRef] [PubMed]
- Facchi, P.; Pascazio, S. Quantum Zeno subspaces. Phys. Rev. Lett. 2002, 89, 080401. [Google Scholar] [CrossRef] [PubMed]
- Brion, E.; Akulin, V.M.; Comparat, D.; Dumer, I.; Harel, G.; Kèbaili, N.; Kurizki, G.; Mazets, I.; Pillet, P. Coherence protection by the quantum Zeno effect and nonholonomic control in a Rydberg rubidium isotope. Phys. Rev. A 2005, 71, 052311. [Google Scholar] [CrossRef]
- Bhaktavatsala Rao, D.D.; Kurizki, G. From Zeno to anti-Zeno regime: Decoherence-control dependence on the quantum statistics of the bath. Phys. Rev. A 2011, 83, 032105. [Google Scholar] [CrossRef]
- Petrosyan, D.; Bensky, G.; Kurizki, G.; Mazets, I.; Majer, J.; Schmiedmayer, J. Reversible state transfer between superconducting qubits and atomic ensembles. Phys. Rev. A 2009, 79, 040304. [Google Scholar] [CrossRef]
- Bensky, G.; Amsüss, R.; Majer, J.; Petrosyan, D.; Schmiedmayer, J.; Kurizki, G. Controlling quantum information processing in hybrid systems on chips. Quant. Inf. Proc. 2011, 10, 1037–1060. [Google Scholar] [CrossRef]
- Escher, B.M.; Bensky, G.; Clausen, J.; Kurizki, G. Optimized control of quantum state transfer from noisy to quiet qubits. J. Phys. B Mol. Opt. Phys. 2011, 44, 154015. [Google Scholar] [CrossRef]
- Bensky, G.; Petrosyan, D.; Majer, J.; Schmiedmayer, J.; Kurizki, G. Optimizing inhomogeneous spin ensembles for quantum memory. Phys. Rev. A 2012, 86, 012310. [Google Scholar] [CrossRef]
- Álvarez, G.A.; Rao, D.D.B.; Frydman, L.; Kurizki, G. Zeno and anti-Zeno polarization control of spin ensembles by induced dephasing. Phys. Rev. Lett. 2010, 105, 160401. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, G.A.; Bretschneider, C.O.; Fischer, R.; London, P.; Kanda, H.; Onoda, S.; Isoya, J.; Gershoni, D.; Frydman, L. Local and bulk 13C hyperpolarization in nitrogen-vacancy-centred diamonds at variable fields and orientations. Nat. Commun. 2015, 6, 8456. [Google Scholar] [CrossRef] [PubMed]
- Kurizki, G.; Kofman, A.G.; Yudson, V. Resonant photon exchange by atom pairs in high-Q cavities. Phys. Rev. A 1996, 53, R35. [Google Scholar] [CrossRef] [PubMed]
- Bhaktavatsala Rao, D.D.; Bar-Gill, N.; Kurizki, G. Generation of macroscopic superpositions of quantum states by linear coupling to a bath. Phys. Rev. Lett. 2011, 106, 010404. [Google Scholar] [CrossRef] [PubMed]
- Bar-Gill, N.; Rao, D.D.B.; Kurizki, G. Creating nonclassical states of Bose-Einstein condensates by dephasing collisions. Phys. Rev. Lett. 2011, 107, 010404. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.; Caves, C. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439–3443. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Wu, L.-A.; Kurizki, G.; Brumer, P. Master equation and control of an open quantum system with leakage. Phys. Rev. Lett. 2009, 102, 080405. [Google Scholar] [CrossRef] [PubMed]
- Laraoui, A.; Dolde, F.; Burk, C.; Reinhard, F.; Wrachtrup, J.; Meriles, C.A. High-resolution correlation spectroscopy of 13C spins near a nitrogen-vacancy centre in diamond. Nat. Commun. 2013, 4, 1651. [Google Scholar] [CrossRef] [PubMed]
- Almeida, M.P.; de Melo, F.; Hor-Meyll, M.; Salles, A.; Walborn, S.P.; Ribeiro, P.H.S.; Davidovich, L. Environment-induced sudden death of entanglement. Science 2007, 316, 579. [Google Scholar] [CrossRef] [PubMed]
- Gordon, G.; Kurizki, G. Scalability of decoherence control in entangled systems. Phys. Rev. A 2011, 83, 032321. [Google Scholar] [CrossRef]
- Gordon, G.; Kurizki, G.; Lidar, D.A. Optimal dynamical decoherence control of a qubit. Phys. Rev. Lett. 2008, 101, 010403. [Google Scholar] [CrossRef] [PubMed]
- Norris, L.M.; Paz-Silva, G.A.; Viola, L. Qubit noise spectroscopy for non-Gaussian dephasing environments. Phys. Rev. Lett. 2016, 116, 150503. [Google Scholar] [CrossRef] [PubMed]
- Paz-Silva, G.A.; Viola, L. General transfer-function approach to noise filtering in open-loop quantum control. Phys. Rev. Lett. 2014, 113, 250501. [Google Scholar] [CrossRef] [PubMed]
- Lang, J.E.; Liu, R.B.; Monteiro, T.S. Dynamical-decoupling-based quantum sensing: Floquet spectroscopy. Phys. Rev. X 2015, 5, 041016. [Google Scholar] [CrossRef]
- Zhao, N.; Wrachtrup, J.; Liu, R.-B. Dynamical decoupling design for identifying weakly coupled nuclear spins in a bath. Phys. Rev. A 2014, 90, 032319. [Google Scholar] [CrossRef]
- Ball, H.; Biercuk, M.J. Walsh-synthesized noise filters for quantum logic. EPJ Quantum Technol. 2015, 2, 11. [Google Scholar] [CrossRef]
- Yan, F.; Gustavsson, S.; Bylander, J.; Jin, X.; Yoshihara, F.; Cory, D.G.; Nakamura, Y.; Orlando, T.P.; Oliver, W.D. Rotating-frame relaxation as a noise spectrum analyser of a superconducting qubit undergoing driven evolution. Nat. Commun. 2013, 4, 2337. [Google Scholar] [CrossRef] [PubMed]
- Loretz, M.; Rosskopf, T.; Degen, C.L. Radio-frequency magnetometry using a single electron spin. Phys. Rev. Lett. 2013, 110, 017602. [Google Scholar] [CrossRef] [PubMed]
- Yoshihara, F.; Nakamura, Y.; Yan, F.; Gustavsson, S.; Bylander, J.; Oliver, W.D.; Tsai, J.-S. Flux qubit noise spectroscopy using Rabi oscillations under strong driving conditions. Phys. Rev. B 2014, 89, 020503. [Google Scholar] [CrossRef]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurizki, G.; Alvarez, G.A.; Zwick, A. Quantum Sensing of Noisy and Complex Systems under Dynamical Control. Technologies 2017, 5, 1. https://doi.org/10.3390/technologies5010001
Kurizki G, Alvarez GA, Zwick A. Quantum Sensing of Noisy and Complex Systems under Dynamical Control. Technologies. 2017; 5(1):1. https://doi.org/10.3390/technologies5010001
Chicago/Turabian StyleKurizki, Gershon, Gonzalo A. Alvarez, and Analia Zwick. 2017. "Quantum Sensing of Noisy and Complex Systems under Dynamical Control" Technologies 5, no. 1: 1. https://doi.org/10.3390/technologies5010001
APA StyleKurizki, G., Alvarez, G. A., & Zwick, A. (2017). Quantum Sensing of Noisy and Complex Systems under Dynamical Control. Technologies, 5(1), 1. https://doi.org/10.3390/technologies5010001





