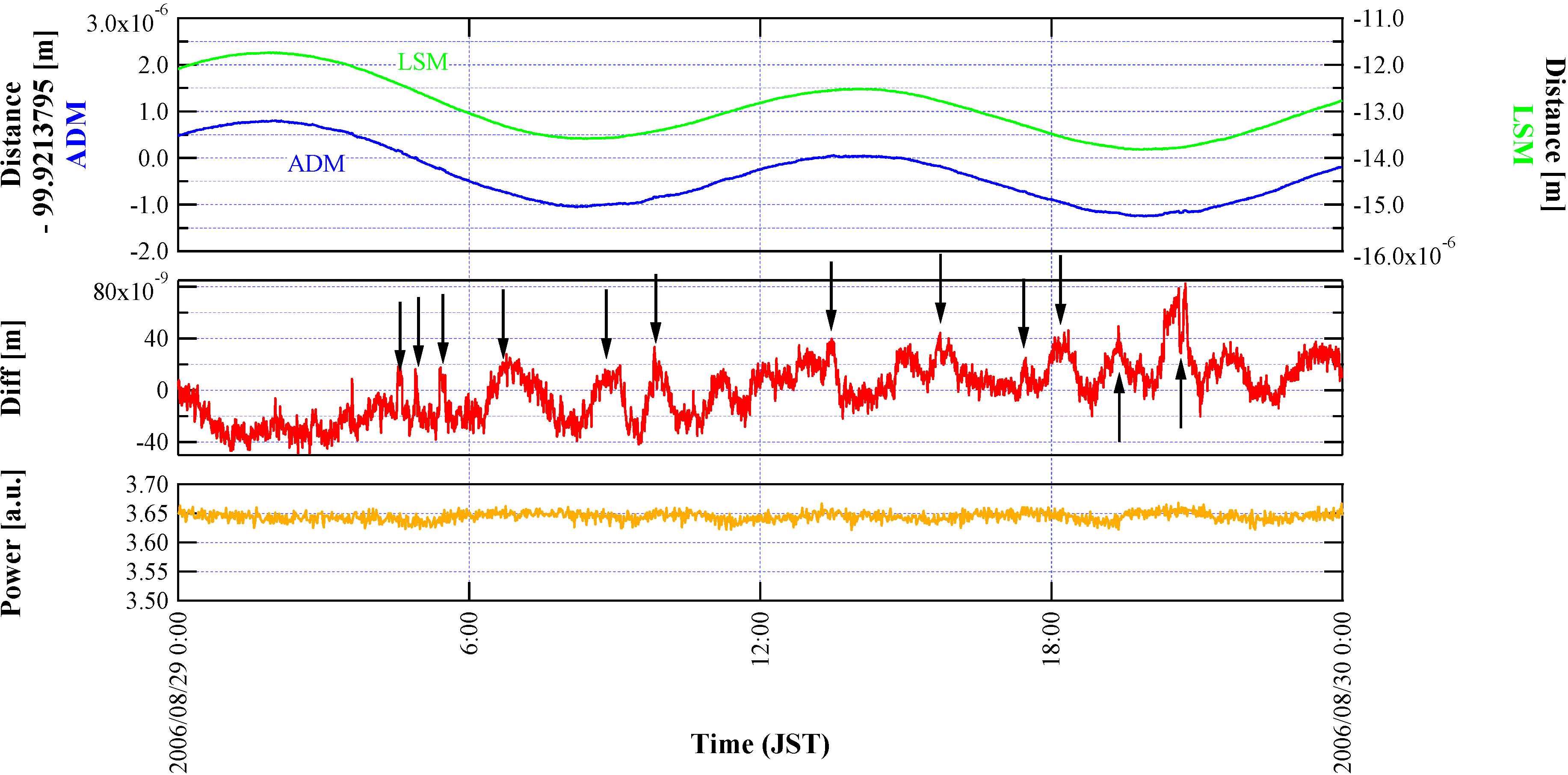
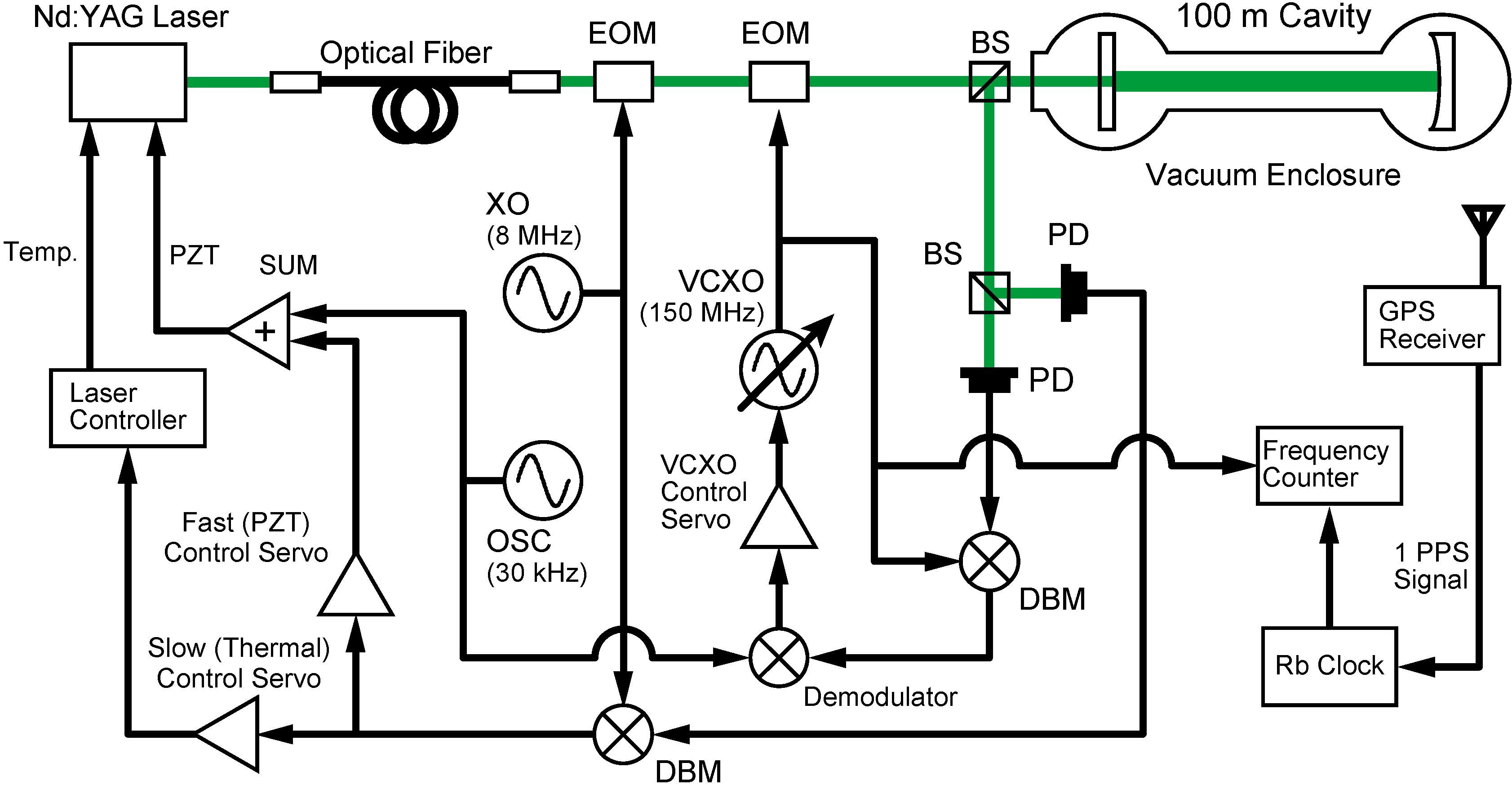
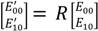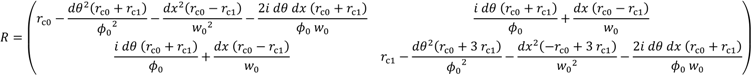2.1. ADM System Overview
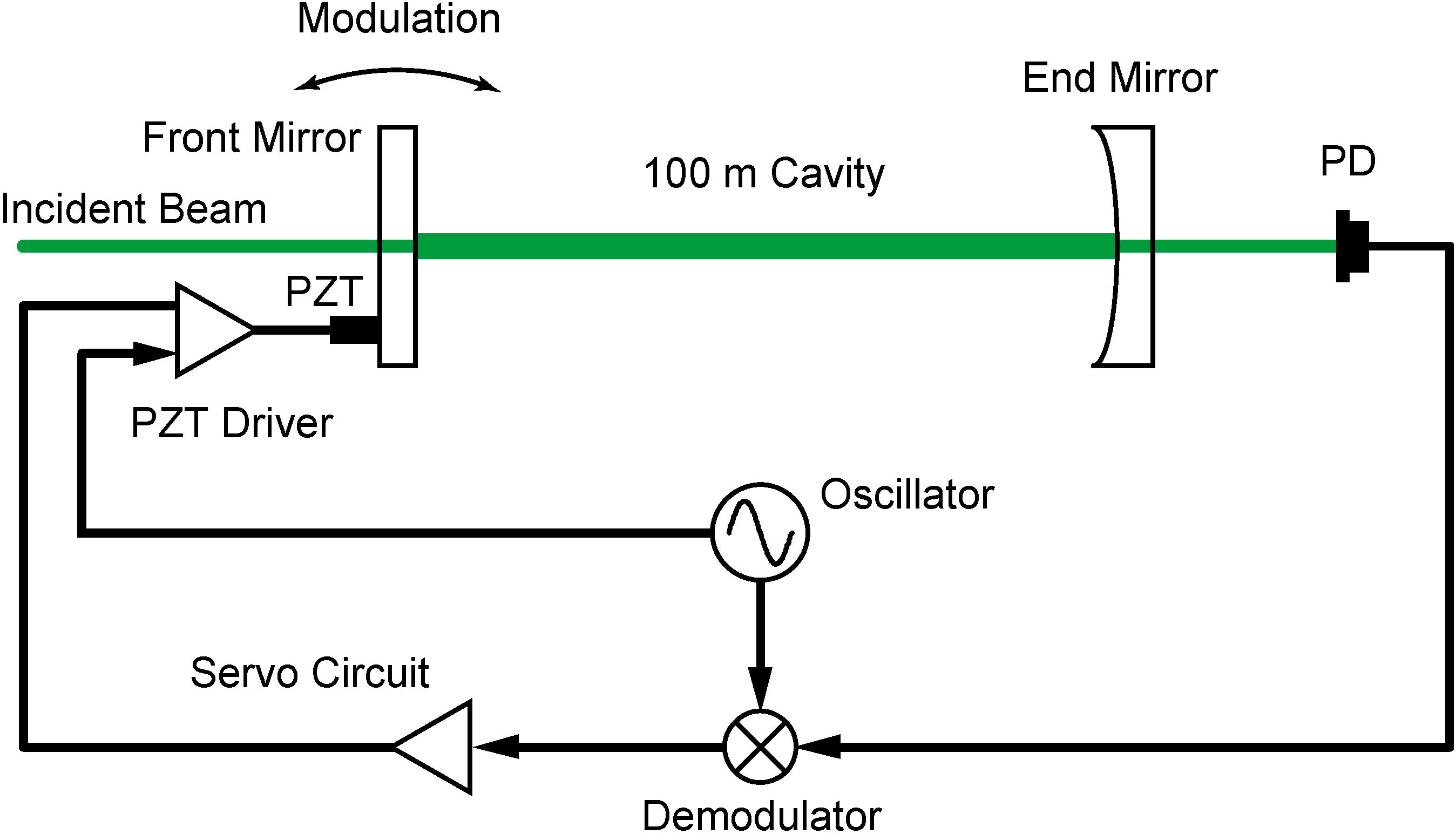
A schematic diagram of the ADM is shown in
Figure 1. A frequency-doubled Nd:YAG laser (wave length λ = 532 nm) is used as a light source, and the beam is delivered to input optics through a polarization maintaining fiber. Phase modulations at 8 MHz and ~150 MHz are applied to the laser beam via electro-optic modulators (EOMs) that are driven by a fixed frequency quartz crystal oscillator (XO) and a voltage controlled crystal oscillator (VCXO), respectively, before the light enters the 100-m optical cavity. Frequency modulation (FM) at an audio frequency (30 kHz) is applied via a piezoelectric transducer (PZT) attached to the laser crystal, as well. The cavity is oriented north–south and is formed by a flat front mirror and concave end mirror with a design radius of curvature (
Re) of 150 m. The mirrors are dielectric-multilayer coated and held by gimbals that are mounted on granite platforms firmly fixed to the bedrock. The mirror orientation is controlled by an alignment control system (described later) to maintain the optimal state. The optical cavity is under a high vacuum of the order of 10
−4 Pa to eliminate disturbances to the optical path length, because of the atmospheric refractive index. The vacuum tanks, which accommodate the cavity optics, are bolted to the granite platforms mentioned above and decoupled from the rest of the vacuum system by having flexible bellows inserted between them, as illustrated in [
10]. This assures that the cavity optics follow the Earth movement precisely. The output beam returning from the cavity is detected by two photo detectors (PDs) after being split by a beam splitter. One of the PD signals is demodulated by a double-balanced mixer (DBM) with the 8-MHz signal generated by XO to maintain the laser (carrier) frequency locked to the cavity (Pound–Drever–Hall method [
11]), while the other PD signal is demodulated by another DBM with VCXO. The DBM output signal is further demodulated at the FM frequency to obtain the error signal that is used to control the VCXO frequency to maintain the sidebands resonant in the cavity. The VCXO frequency is monitored by a frequency counter that is synchronized to a 10-MHz Rb atomic clock stabilized to the order of 10
−11 to 10
−12 using the GPS one pulse per second signal. All servo controls are implemented with analog circuits and are enabled or disabled according to the lock status of the instrument by a digital control system based on a PC for automatic operation.
The 100-m optical cavity is sealed in a vacuum enclosure to eliminate atmospheric disturbances. Double-phase modulation is applied to the incident beam. The laser beam is frequency modulated via a PZT attached to the laser crystal and using EOMs driven by the fixed frequency XO and the VCXO to generate sidebands. The error signal for the Pound–Drever–Hall method is extracted by demodulating the reflected beam signal at the XO frequency. By demodulating the PD signal at the VCXO frequency and then the FM frequency, the error signal for sideband locking is obtained.
Figure 1.
Block diagram of the absolute distance meter (ADM). EOM, electro-optic modulator; PZT, piezoelectric transducer; XO, quartz crystal oscillator; VCXO, voltage controlled crystal oscillator; PD, photo detector; DBM, double-balanced mixer.
Figure 1.
Block diagram of the absolute distance meter (ADM). EOM, electro-optic modulator; PZT, piezoelectric transducer; XO, quartz crystal oscillator; VCXO, voltage controlled crystal oscillator; PD, photo detector; DBM, double-balanced mixer.
2.2. Absolute Distance Determination
When considering only the fundamental transverse electromagnetic mode (TEM
00), the resonant frequencies (ν
n) of an optical cavity in vacuum are:
where
n,
c, and denote an integer, the speed of light and the cavity length, respectively [
12]. The geometric constant γ is defined by the radii of curvature of the mirrors (
Rf and
Re for the front and end mirrors, respectively) as:
The incident beam is doubly phase-modulated at a frequency of 8 MHz for the carrier lock and ν
m (VCXO frequency: 150 MHz) to generate sidebands. When the carrier is locked to the cavity, ν
m needs to satisfy:
to make the sidebands resonant in the cavity, as well (
m is an integer). Since
L is coarsely determined by a supplemental measurement to be 99.92 ± 0.01 m and the wave length that corresponds to ν
m is much longer than the error of
L,
m must be equal to 100 without uncertainty. Therefore, the exact distance between two mirrors can be determined by measuring the VCXO frequency accurately and substituting for
m into Equation (3):
A more detailed explanation is available in our earlier publication [
13].
2.3. Alignment Control of the Optical Cavity
As the target of the ADM covers geophysical events whose durations vary from short (sub-second) to long (years) periods of time, the optical cavity needs to be maintained highly stable. One of the expected sources of instability is the misalignment of the incident beam with respect to the main cavity caused by the ground tilts, which are mainly induced by the seasonal change of groundwater distribution and atmospheric pressure Changes of tilt angles of the cavity optics cause errors in the length determination, coupling with beam miscentering. To resolve these problems, the tilt of the cavity mirrors is monitored and controlled to maintain an optimal state. The block diagram of the alignment control system is shown in
Figure 2. A PD is located behind the end mirror to monitor the power of the beam transmitted from the cavity. The detected power reaches maximum only when the cavity mirrors are best aligned with the incident beam. Each mirror was mounted in a gimbal equipped with two PZTs to change the angle of the mirror about two axes perpendicular to the cavity axis. The rotations about the vertical and horizontal axes are defined as the yaw and pitch, respectively. The PZTs assigned to four degrees of freedom (DoF)—pitch and yaw of the front and end mirrors—were driven at different frequencies ranging from 61–109 Hz with a small amplitude for the mechanical modulation of the mirror angles. The derivatives of the output power signal were extracted by demodulating the output PD signal at these frequencies. They were used as the error signals in the control system, which sets all four demodulated signals to null, the unique condition for which the cavity is optimally aligned. The separation between modulation frequencies was carefully determined to prevent interference between each DoF. The bandwidth of the alignment control was limited from DC to several hertz to avoid interference with the modulation. The wave front sensing technique was used in our earlier experiment [
13]. That technique is suitable to resolve the misalignment of the optical system with more DoF (the cavity was a part of the TAMA300 gravitational wave detector), but it requires complicated optical design and electrics. The mechanical modulation system developed for this ADM is simpler and effective in a single cavity that is specifically designed for geophysical observations.
Figure 2.
Block diagram of automatic alignment control.
Figure 2.
Block diagram of automatic alignment control.
The angle of the cavity mirror is mechanically modulated using PZTs mounted on its gimbal holder. The photo detector located behind the end mirror monitors the intensity of the transmitted beam, and its signal is demodulated to obtain the error and is then processed by the servo circuit. The feedback signal is added to the PZT input to maintain the PD signal maximum, i.e., the best cavity alignment.
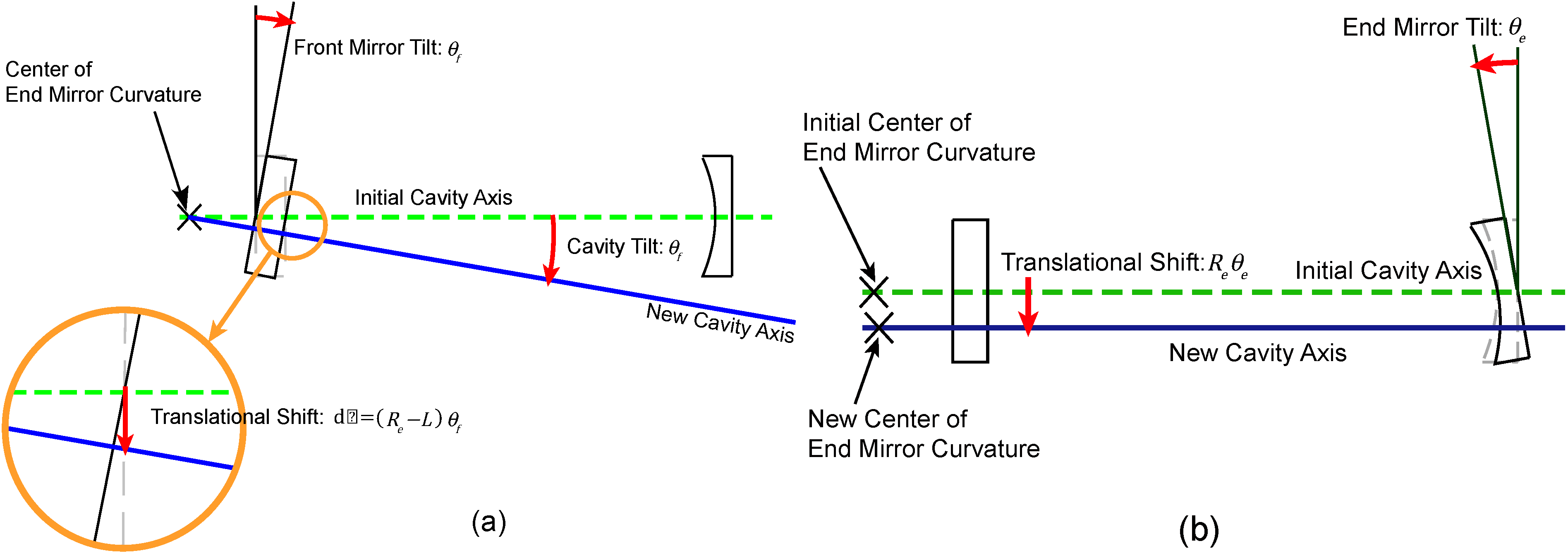
Tilts of the front and end mirrors introduce different effects on the transmitted beam power, depending on their radii of curvature. Starting with a cavity that was perfectly aligned initially, when the flat front mirror rotates by θ
f, it causes not only a tilt of the cavity axis, but also a translational shift. The cavity axis will be redefined by rotating and shifting the original axis by θ
f and d
x = (
Re −
L) θ
f, respectively, as shown in
Figure 3a. Meanwhile, the tilt of the end mirror only causes the cavity axis to shift by
Reθ
e (θ
e is the tilt angle of the end mirror), because the cavity finds a point on the end mirror surface where the beam reflects normally to the front mirror, as shown in
Figure 3b.
Figure 3.
Geometric effect caused by the cavity mirror tilt. The tilt of the flat front mirror induces the cavity axis to tilt and shift sideways simultaneously (a), while the end mirror tilt causes only a perpendicular shift, because of its concave shape (b).
Figure 3.
Geometric effect caused by the cavity mirror tilt. The tilt of the flat front mirror induces the cavity axis to tilt and shift sideways simultaneously (a), while the end mirror tilt causes only a perpendicular shift, because of its concave shape (b).
It is a good approximation that the incident beam comprises only the fundamental mode (TEM
00), and it will be converted partially to the first higher order spatial mode (TEM
10) when the beam returns from the tilted cavity. Considering only these modes, when the cavity axis rotates and shifts by
dθ and
dx with respect to the incident beam, respectively, the amplitudes of the electric fields of the reflected beam (
![Technologies 02 00129 i007]()
and
![Technologies 02 00129 i008]()
for TEM
00 and TEM
10, respectively) are calculated by using those of the input beam (
E00 and
E10 for TEM
00 and TEM
10, respectively) as:
where
rc0 and
rc1 denote the reflectivity of the cavity for the TEM
00 and TEM
10 modes, respectively [
14].
w0 and
ϕ0 are the size (radius) of the beam at its waist position and the divergence angle, respectively (designed to be located at the front mirror surface as
w0 = 3.5 mm and
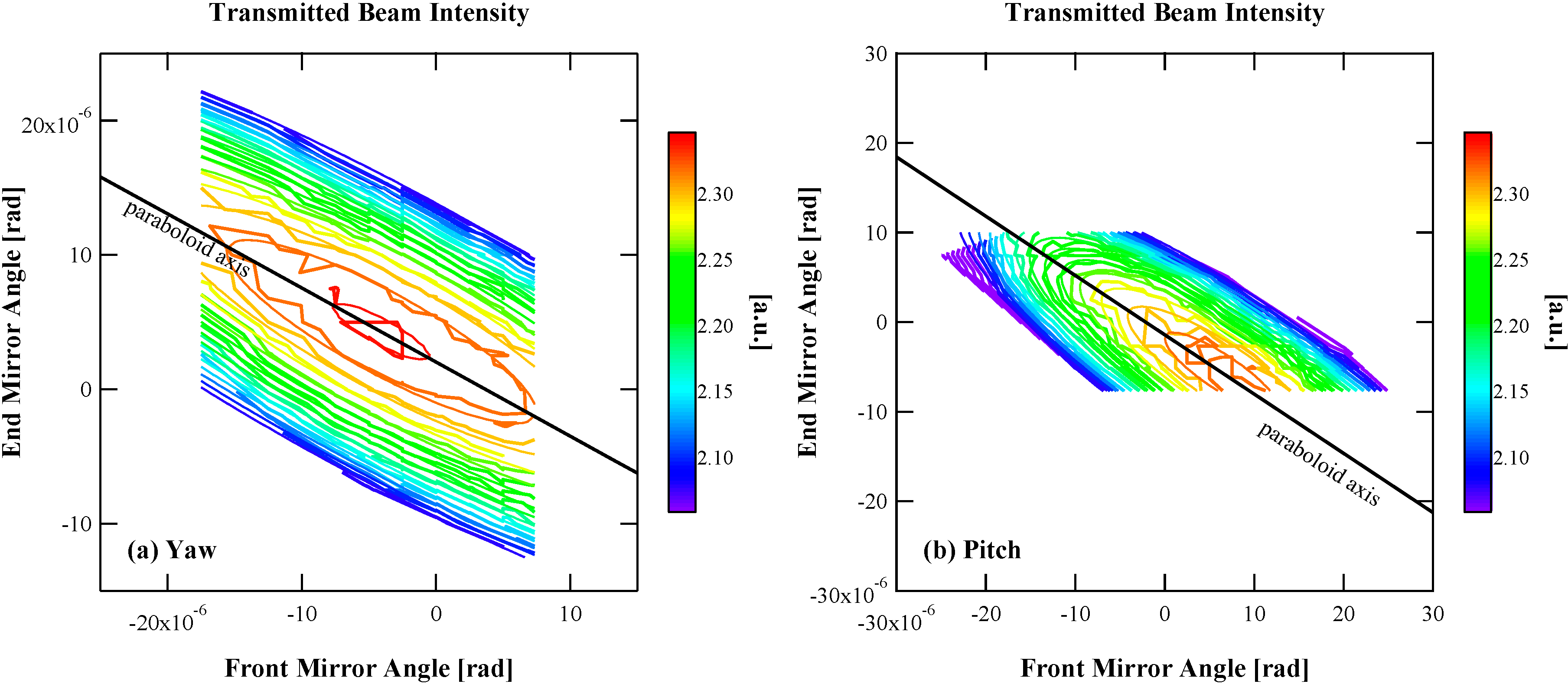
ϕ0 = 34 μrad in our configuration). By substituting the physical parameters, the equivalent rotational angle and the perpendicular shift of the cavity axis produced by the mirror tilts in Equation (6), one can compute the reflectivity of the cavity and obtain the intensity of the transmitted beam. The transmitted beam intensity as a parametric function of θ
f and θ
e is plotted in
Figure 4, normalized to unity at its maximum, and forms a skewed elliptical paraboloid. Skewing occurs because the rotation of the front mirror changes the beam spot position on the end mirror surface, and the reflected beam is no longer parallel to the incident beam. This breaks the optical resonance, except when the cavity length is equal to the radius of curvature of the end mirror (
i.e.,
L =
Re). Therefore, the end mirror needs to be rotated to correct the non-parallelism and to maintain the resonance. A coupling between mirror rotation in the orthogonal directions (yaw and pitch) is expected, because of the concave shape of the end mirror, but this higher order effect is small and is not observed. The skew angle of the elliptical axes depends on the discrepancy between
L and
Re and other parameters. For ADM specifications, the radius of curvature of the end mirror was most responsible for determining the skew angle among these parameters. The skew angles estimated by varying the radius of curvature are plotted in
Figure 5.
The pitch and yaw angles of the mirrors were independently controlled by servo controllers to reduce the error signal to zero in each DoF. Since only the unique condition (peak of the paraboloid) fulfils the optimal condition and no local minima exist, this simple strategy was successful.
Figure 4.
Transmitted beam intensity (model).
Figure 4.
Transmitted beam intensity (model).
The intensity of the beam transmitted from the optical cavity is computed by assuming that the beam waist is located at the front mirror surface and that the radius of curvature of the end mirror is 150 m. The intensity is plotted as a function of the tilt angles of the front and end mirrors and forms a skewed elliptic paraboloid with a skew angle of 28.8° in this case. This plot is scaled arbitrarily.
Figure 5.
Skew angles of the transmitted beam intensity paraboloid (model).
Figure 5.
Skew angles of the transmitted beam intensity paraboloid (model).
The skew angles of the elliptic paraboloid, which the transmitted beam intensity draws as a function of the radius of curvature of the end mirror, are estimated by using the theoretical model.
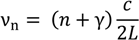
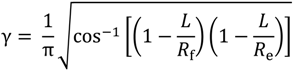
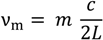
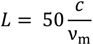
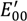 and
and 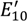 for TEM00 and TEM10, respectively) are calculated by using those of the input beam (E00 and E10 for TEM00 and TEM10, respectively) as:
for TEM00 and TEM10, respectively) are calculated by using those of the input beam (E00 and E10 for TEM00 and TEM10, respectively) as: