Influence of Performance Metrics Emphasis in Hyperparameter Tuning for Aircraft Skin Defect Detection: An Early Inspection of Weighted Average Objectives
Abstract
1. Introduction
2. Related Work
3. Objectives and Settings
3.1. Experiment Datasets
3.2. Computer Vision Model
3.3. Performance Metrics
3.4. Hyperparameter Tuning Objective
3.5. Optimization Procedure
3.6. Inspection Procedure
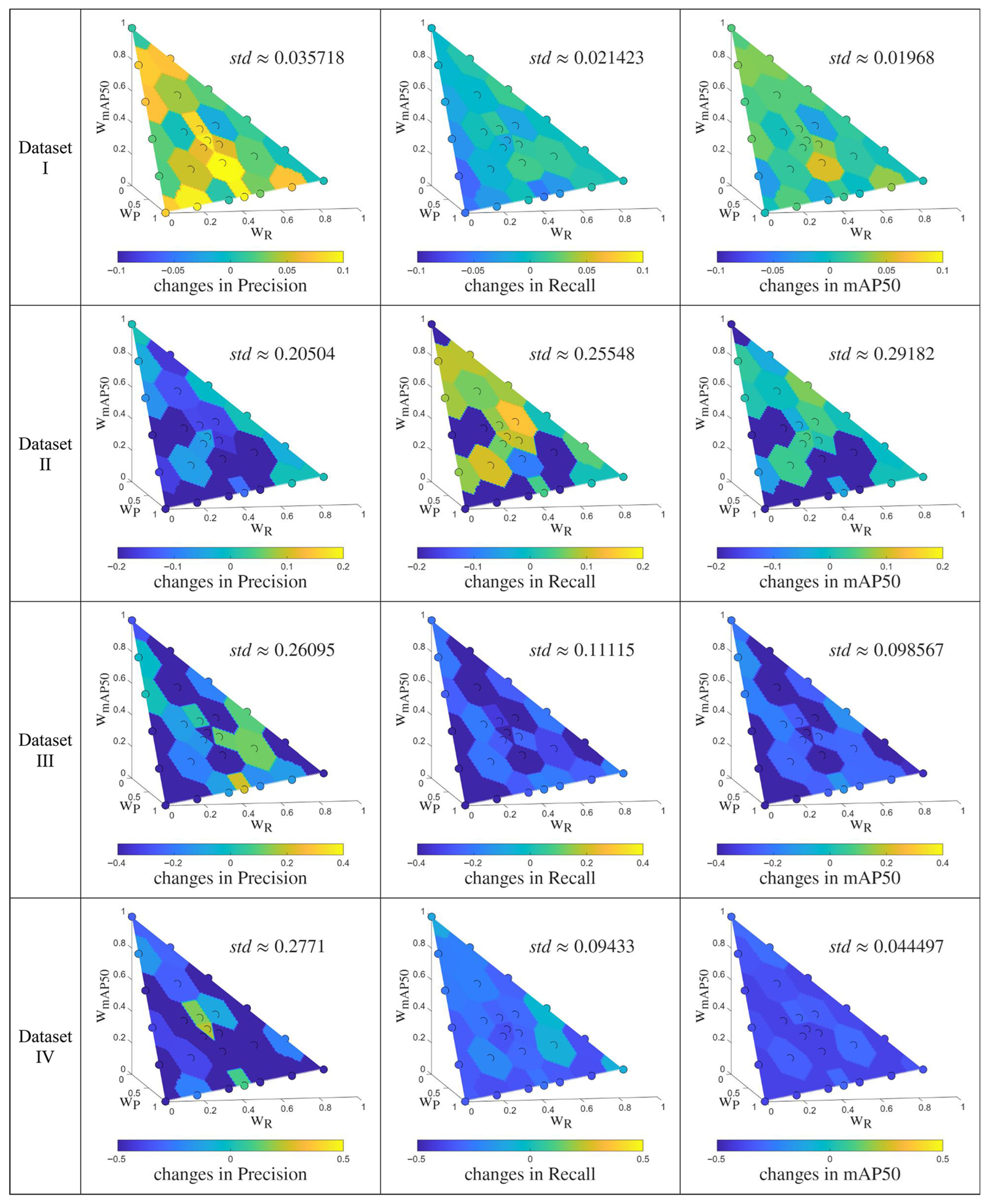
4. Results and Discussion
5. Limitations and Future Works
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cusati, V.; Corcione, S.; Memmolo, V. Impact of Structural Health Monitoring on Aircraft Operating Costs by Multidisciplinary Analysis. Sensors 2021, 21, 6938. [Google Scholar] [CrossRef] [PubMed]
- Ballarin, P.; Sala, G.; Airoldi, A. Cost-Effectiveness of Structural Health Monitoring in Aviation: A Literature Review. Sensors 2025, 25, 6146. [Google Scholar] [CrossRef]
- Gholizadeh, S. A Review of Non-Destructive Testing Methods of Composite Materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Wronkowicz-Katunin, A. A Brief Review on NDT&E Methods For Structural Aircraft Components. Fatigue Aircr. Struct. 2018, 2018, 73–81. [Google Scholar] [CrossRef]
- Rahman, M.S.U.; Hassan, O.S.; Mustapha, A.A.; Abou-Khousa, M.A.; Cantwell, W.J. Inspection of Thick Composites: A Comparative Study Between Microwaves, X-Ray Computed Tomography and Ultrasonic Testing. Nondestruct. Test. Eval. 2024, 39, 2054–2071. [Google Scholar] [CrossRef]
- Leiva, J.R.; Villemot, T.; Dangoumeau, G.; Bauda, M.A.; Larnier, S. Automatic Visual Detection and Verification of Exterior Aircraft Elements. In Proceedings of the 2017 IEEE International Workshop of Electronics, Control, Measurement, Signals and Their Application to Mechatronics (ECMSM), Donostia-San Sebastian, Spain, 24–26 May 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Yasuda, Y.D.; Cappabianco, F.A.; Martins, L.E.G.; Gripp, J.A. Aircraft visual inspection: A systematic literature review. Comput. Ind. 2022, 141, 103695. [Google Scholar] [CrossRef]
- Sprong, J.P.; Jiang, X.; Polinder, H. Deployment of Prognostics to Optimize Aircraft Maintenance—A Literature Review. J. Int. Bus. Res. Mark. 2020, 5, 26–37. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, J.; Li, Y.; Gong, X.; Wang, J. A UAV-Based Aircraft Surface Defect Inspection System via External Constraints and Deep Learning. IEEE Trans. Instrum. Meas. 2022, 71, 5019315. [Google Scholar] [CrossRef]
- Papa, U.; Ponte, S. Preliminary Design of An Unmanned Aircraft System for Aircraft General Visual Inspection. Electronics 2018, 7, 435. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E.; Gibson, S.; Cross, E.; Parente, A.; Vinuesa, R. Improving Aircraft Performance Using Machine Learning: A Review. Aerosp. Sci. Technol. 2023, 138, 108354. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of Hyperparameters of Machine Learning Algorithms. J. Mach. Learn. Res. 2019, 20, 1–32. [Google Scholar]
- Weerts, H.J.P.; Mueller, A.; Vanschoren, J. Importance of Tuning Hyperparameters of Machine Learning Algorithms. arXiv 2020, arXiv:2007.07588. [Google Scholar] [CrossRef]
- Suvittawat, N.; Kurniawan, C.; Datephanyawat, J.; Tay, J.; Liu, Z.; Soh, D.W.; Ribeiro, N.A. Advances in Aircraft Skin Defect Detection Using Computer Vision: A Survey and Comparison of YOLOv9 and RT-DETR Performance. Aerospace 2025, 12, 356. [Google Scholar] [CrossRef]
- Liu, G.; Gao, W.; Liu, W.; Xu, J.; Li, R.; Bai, W. LFM-Chirp-Square Pulse-Compression Thermography for Debonding Defects Detection in Honeycomb Sandwich Composites Based on THD-Processing Technique. Nondestruct. Test. Eval. 2024, 39, 832–845. [Google Scholar] [CrossRef]
- Vu, T.P.; Luong, V.S.; Le, M. Hidden Corrosion Detection in Aircraft Structures with A Lightweight Magnetic Convolutional Neural Network. Nondestruct. Test. Eval. 2025, 40, 1797–1819. [Google Scholar] [CrossRef]
- Scarselli, G.; Nicassio, F. Machine Learning for Structural Health Monitoring of Aerospace Structures: A Review. Sensors 2025, 25, 6136. [Google Scholar] [CrossRef]
- Zhang, S.; He, Y.; Gu, Y.; He, Y.; Wang, H.; Wang, H.; Yang, R.; Chady, T.; Zhou, B. UAV Based Defect Detection and Fault Diagnosis for Static and Rotating Wind Turbine Blade: A Review. Nondestruct. Test. Eval. 2025, 40, 1691–1729. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, O. Drone-based Automated Exterior Inspection of an Aircraft using Reinforcement Learning Technique. In Proceedings of the AIAA SCITECH 2023 Forum, Online, 23–27 January 2023; p. 0107. [Google Scholar] [CrossRef]
- Rodríguez, D.A.; Lozano Tafur, C.; Melo Daza, P.F.; Villalba Vidales, J.A.; Daza Rincón, J.C. Inspection of Aircrafts and Airports Using UAS: A Review. Results Eng. 2024, 22, 102330. [Google Scholar] [CrossRef]
- Connolly, L.; Garland, J.; O’Gorman, D.; Tobin, E.F. Deep-Learning-Based Defect Detection for Light Aircraft with Unmanned Aircraft Systems. IEEE Access 2024, 12, 83876–83886. [Google Scholar] [CrossRef]
- Zurita-Gil, M.A.; Ortiz-Torres, G.; Sorcia-Vázquez, F.D.J.; Rumbo-Morales, J.Y.; Gascon Avalos, J.J.; Reynoso-Romo, J.R.; Rosas-Caro, J.C.; Brizuela-Mendoza, J.A. Nonlinear Control Design for a PVTOL UAV Carrying a Liquid Payload with Active Sloshing Suppression. Technologies 2026, 14, 31. [Google Scholar] [CrossRef]
- Ramalingam, B.; Manuel, V.H.; Elara, M.R.; Vengadesh, A.; Lakshmanan, A.K.; Ilyas, M.; James, T.J.Y. Visual Inspection of the Aircraft Surface Using a Teleoperated Reconfigurable Climbing Robot and Enhanced Deep Learning Technique. Int. J. Aerosp. Eng. 2019, 2019, 5137139. [Google Scholar] [CrossRef]
- Chatterjee, S.; Byun, Y.C. Highly Imbalanced Fault classification of Wind Turbines using Data Resampling and Hybrid Ensemble Method Approach. Eng. Appl. Artif. Intell. 2023, 126, 107104. [Google Scholar] [CrossRef]
- Lahr, G.J.G.; Godoy, R.V.; Segreto, T.H.; Savazzi, J.O.; Ajoudani, A.; Boaventura, T.; Caurin, G.A.P. Improving Failure Prediction in Aircraft Fastener Assembly Using Synthetic Data in Imbalanced Datasets. arXiv 2025, arXiv:2505.03917. [Google Scholar] [CrossRef]
- Liu, B.; Tsoumakas, G. Dealing with Class Imbalance in Classifier Chains via Random Undersampling. Knowl.-Based Syst. 2020, 192, 105292. [Google Scholar] [CrossRef]
- Dong, Y.; Jiang, H.; Liu, Y.; Yi, Z. Global Wavelet-Integrated Residual Frequency Attention Regularized Network for Hypersonic Flight Vehicle Fault Diagnosis with Imbalanced Data. Eng. Appl. Artif. Intell. 2024, 132, 107968. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, S.; Li, Q.; Liu, Y.; Gu, X.; Liu, W. A New Bearing Fault Diagnosis Method Based on Signal-to-Image Mapping and Convolutional Neural Network. Measurement 2021, 176, 109088. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Liu, Y. Aircraft Skin Defect Detection Based on Fourier GAN Data Augmentation under Limited Samples. Measurement 2025, 245, 116657. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, H.; Zeng, T.; Dong, Y. An Adaptive Fused Domain-Cycling Variational Generative Adversarial Network for Machine Fault Diagnosis under Data Scarcity. Inf. Fusion 2026, 126, 103616. [Google Scholar] [CrossRef]
- Bouarfa, S.; Doğru, A.; Arizar, R.; Aydoğan, R.; Serafico, J. Towards Automated Aircraft Maintenance Inspection. A Use Case of Detecting Aircraft Dents using Mask R-CNN. In Proceedings of the AIAA SCITECH 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Doğru, A.; Bouarfa, S.; Arizar, R.; Aydoğan, R. Using Convolutional Neural Networks to Automate Aircraft Maintenance Visual Inspection. Aerospace 2020, 7, 171. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Liu, Y. YOLO-FDD: Efficient defect detection network of aircraft skin fastener. Signal Image Video Process. 2024, 18, 3197–3211. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, J.; Yan, Z.; Zhao, M.; Fu, X.; Zhu, H. FC-YOLO: An aircraft skin defect detection algorithm based on multi-scale collaborative feature fusion. Meas. Sci. Technol. 2024, 35, ad6bad. [Google Scholar] [CrossRef]
- Xiong, J.; Li, P.; Sun, Y.; Xiang, J.; Xia, H. An Aircraft Skin Defect Detection Method with UAV Based on GB-CPP and INN-YOLO. Drones 2025, 9, 594. [Google Scholar] [CrossRef]
- Kurkin, E.I.; Quijada Pioquinto, J.G.; Lukyanov, O.E.; Chertykovtseva, V.O.; Nikonorov, A.V. Aircraft Propeller Design Technology Based on CST Parameterization, Deep Learning Models, and Genetic Algorithm. Technologies 2025, 13, 469. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Sun, L.; Hu, B.; Zhu, L.; Zhang, J. Deep learning-based defects detection of certain aero-engine blades and vanes with DDSC-YOLOv5s. Sci. Rep. 2022, 12, 13067. [Google Scholar] [CrossRef]
- Pasupuleti, S.; K, R.; Pattisapu, V.M. Optimization of YOLOv8 for Defect Detection and Inspection in Aircraft Surface Maintenance using Enhanced Hyper Parameter Tuning. In Proceedings of the 2024 International Conference on Electrical Electronics and Computing Technologies (ICEECT), Greater Noida, India, 29–31 August 2024; Volume 1, pp. 1–6. [Google Scholar] [CrossRef]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential Model-Based Optimization for General Algorithm Configuration. In Learning and Intelligent Optimization, Proceedings of the 5th International Conference, LION 5, Rome, Italy, 17–21 January 2011; Coello, C.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: Lake Tahoe, NV, USA, 2012; Volume 25, pp. 1–9. [Google Scholar]
- Bischl, B.; Richter, J.; Bossek, J.; Horn, D.; Thomas, J.; Lang, M. mlrMBO: A Modular Framework for Model-Based Optimization of Expensive Black-Box Functions. arXiv 2018, arXiv:1703.03373. [Google Scholar]
- Azadi, S.; Okabe, Y.; Carvelli, V. Bayesian-Optimized 1D-CNN for Delamination Classification in CFRP Laminates Using Raw Ultrasonic Guided Waves. Compos. Sci. Technol. 2025, 264, 111101. [Google Scholar] [CrossRef]
- Vashishtha, G.; Chauhan, S.; Kumar, S.; Kumar, R.; Zimroz, R.; Kumar, A. Intelligent fault diagnosis of worm gearbox based on adaptive CNN using amended gorilla troop optimization with quantum gate mutation strategy. Knowl.-Based Syst. 2023, 280, 110984. [Google Scholar] [CrossRef]
- SUTD. Aircraft AI Dataset. 2024. Available online: https://universe.roboflow.com/sutd-4mhea/aircraft-ai-dataset (accessed on 22 March 2024).
- Innovation Hangar. Innovation Hangar v2 Dataset. 2023. Available online: https://universe.roboflow.com/innovation-hangar/innovation-hangar-v2/dataset/1 (accessed on 24 April 2024).
- Meng, D.; Boer, W.; Juan, X.; Kasule, A.N.; Hongfu, Z. Visual Inspection of Aircraft Skin: Automated Pixel-Level Defect Detection by Instance Segmentation. Chin. J. Aeronaut. 2022, 35, 254–264. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2015, arXiv:1506.02640. [Google Scholar]
- Ramos, L.T.; Sappa, A.D. A Decade of You Only Look Once (YOLO) for Object Detection. arXiv 2025, arXiv:2504.18586. [Google Scholar] [CrossRef]
- Tian, Y.; Ye, Q.; Doermann, D. YOLOv12: Attention-Centric Real-Time Object Detectors. arXiv 2025, arXiv:2502.12524. [Google Scholar]
- Ultralytics. Models Supported by Ultralytics. 2025. Available online: https://docs.ultralytics.com/models/ (accessed on 15 August 2025).
- Ultralytics. YOLO12: Attention-Centric Object Detection. 2025. Available online: https://docs.ultralytics.com/models/yolo12/ (accessed on 15 August 2025).
- Ultralytics. Performance Metrics Deep Dive. 2025. Available online: https://docs.ultralytics.com/guides/yolo-performance-metrics/ (accessed on 15 August 2025).
- Ultralytics. Model Training with Ultralytics YOLO. 2023. Available online: https://docs.ultralytics.com/modes/train/ (accessed on 25 April 2024).
- Head, T.; Kumar, M.; Nahrstaedt, H.; Louppe, G.; Shcherbatyi, I. Scikit-Optimize/Scikit-Optimize. 2020. Available online: https://github.com/scikit-optimize/scikit-optimize (accessed on 1 April 2024).
- MathWorks. griddata: Interpolate 2-D or 3-D Scattered Data. 2025. Available online: https://www.mathworks.com/help/matlab/ref/griddata.html#bvkwume-method (accessed on 15 November 2025).


| Defect | Dataset I (983 Images) | Dataset II (10,722 Images) | ||||
|---|---|---|---|---|---|---|
| Types | Training | Validation | Test | Training | Validation | Test |
| rust | 1430 | 425 | 183 | - | - | - |
| instances | instances | instances | ||||
| missing- | 921 | 327 | 162 | 822 | 54 | 32 |
| head | instances | instances | instances | instances | instances | instances |
| scratch | 1429 | 422 | 211 | 180 | 16 | 7 |
| instances | instances | instances | instances | instances | instances | |
| crack | - | - | - | 9606 | 607 | 386 |
| instances | instances | instances | ||||
| dent | - | - | - | 8577 | 554 | 413 |
| instances | instances | instances | ||||
| paint-off | - | - | - | 711 | 34 | 23 |
| instances | instances | instances | ||||
| number of | 688 | 197 | 98 | 9651 | 642 | 429 |
| images | images | images | images | images | images | images |
| Defect | Dataset III (200 Images) | Dataset IV (600 Images) | ||||
|---|---|---|---|---|---|---|
| Types | Training | Validation | Test | Training | Validation | Test |
| rust | 197 | 125 | 112 | - | - | - |
| instances | instances | instances | ||||
| missing- | 122 | 87 | 63 | 18 | 12 | 10 |
| head | instances | instances | instances | instances | instances | instances |
| scratch | 232 | 94 | 110 | 1 | 1 | 2 |
| instances | instances | instances | instances | instances | instances | |
| crack | - | - | - | 308 | 142 | 107 |
| instances | instances | instances | ||||
| dent | - | - | - | 314 | 139 | 85 |
| instances | instances | instances | ||||
| paint-off | - | - | - | 29 | 6 | 13 |
| instances | instances | instances | ||||
| number of | 100 | 50 | 50 | 350 | 150 | 100 |
| images | images | images | images | images | images | images |
| No. | Argument | Values | No. | Argument | Values |
|---|---|---|---|---|---|
| 1 | batch | 15 | hsv_h | ||
| 2 | lr0 | 16 | hsv_s | ||
| 3 | lrf | 17 | hsv_v | ||
| 4 | momentum | 18 | degrees | ||
| 5 | weight_decay | 19 | translate | ||
| 6 | warmup_epochs | 20 | scale | ||
| 7 | warmup_momentum | 21 | shear | ||
| 8 | warmup_bias_lr | 22 | perspective | ||
| 9 | box | 23 | flipud | ||
| 10 | cls | 24 | fliplr | ||
| 11 | dfl | 25 | bgr | ||
| 12 | pose | 26 | mosaic | ||
| 13 | kobj | 27 | mixup | ||
| 14 | nbs | 28 | copy_paste | ||
| 29 | erasing |
| Tuning States | Dataset I | Dataset III | ||||
|---|---|---|---|---|---|---|
| before tuning | ||||||
| highest after tuning | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| Tuning States | Dataset II | Dataset IV | ||||
|---|---|---|---|---|---|---|
| before tuning | ||||||
| highest after tuning | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | 0 | 0 | 0 | |||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
| tuned with | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Kurniawan, C.; Suvittawat, N.; Soh, D.W. Influence of Performance Metrics Emphasis in Hyperparameter Tuning for Aircraft Skin Defect Detection: An Early Inspection of Weighted Average Objectives. Technologies 2026, 14, 75. https://doi.org/10.3390/technologies14010075
Kurniawan C, Suvittawat N, Soh DW. Influence of Performance Metrics Emphasis in Hyperparameter Tuning for Aircraft Skin Defect Detection: An Early Inspection of Weighted Average Objectives. Technologies. 2026; 14(1):75. https://doi.org/10.3390/technologies14010075
Chicago/Turabian StyleKurniawan, Christian, Nutchanon Suvittawat, and De Wen Soh. 2026. "Influence of Performance Metrics Emphasis in Hyperparameter Tuning for Aircraft Skin Defect Detection: An Early Inspection of Weighted Average Objectives" Technologies 14, no. 1: 75. https://doi.org/10.3390/technologies14010075
APA StyleKurniawan, C., Suvittawat, N., & Soh, D. W. (2026). Influence of Performance Metrics Emphasis in Hyperparameter Tuning for Aircraft Skin Defect Detection: An Early Inspection of Weighted Average Objectives. Technologies, 14(1), 75. https://doi.org/10.3390/technologies14010075






