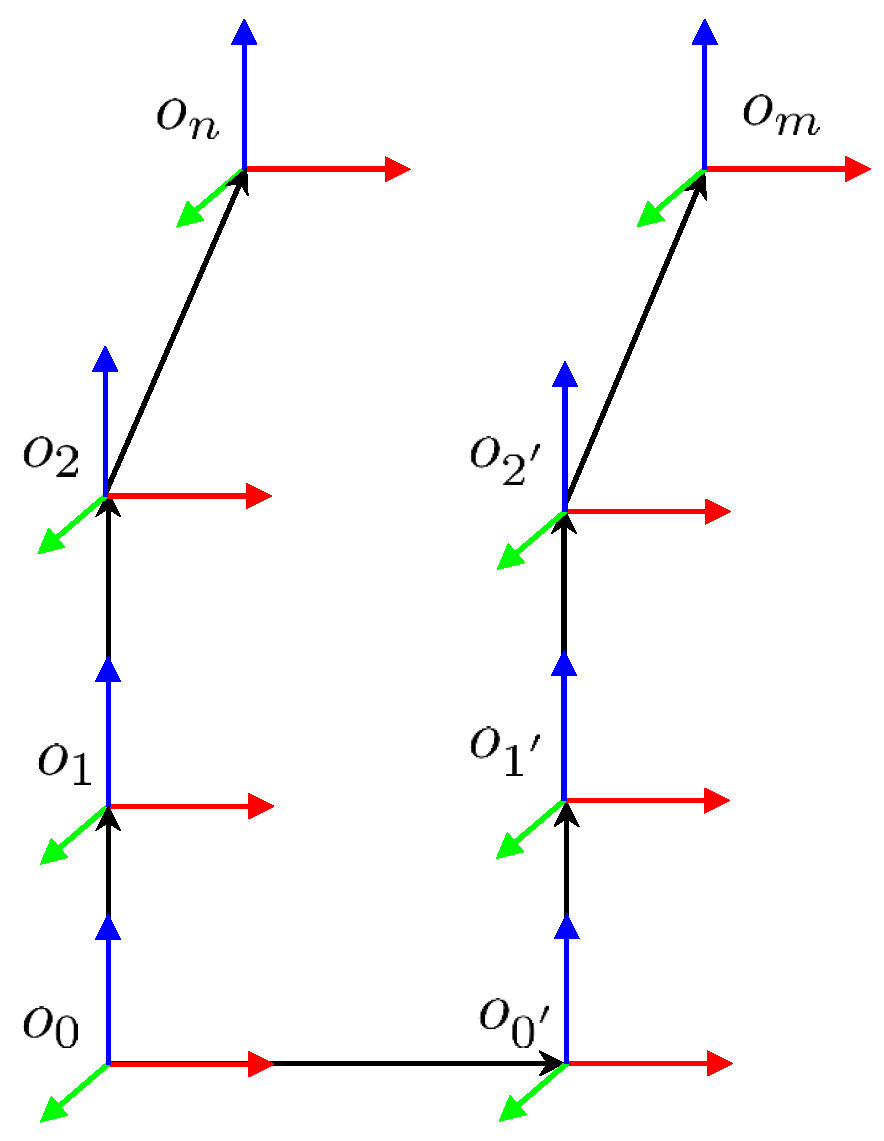
Figure 1.
General model for link boundary functions, where two arbitrary transformation paths converge at the global positions of points n and m. Their coincidence defines the collision condition.
Figure 1.
General model for link boundary functions, where two arbitrary transformation paths converge at the global positions of points n and m. Their coincidence defines the collision condition.
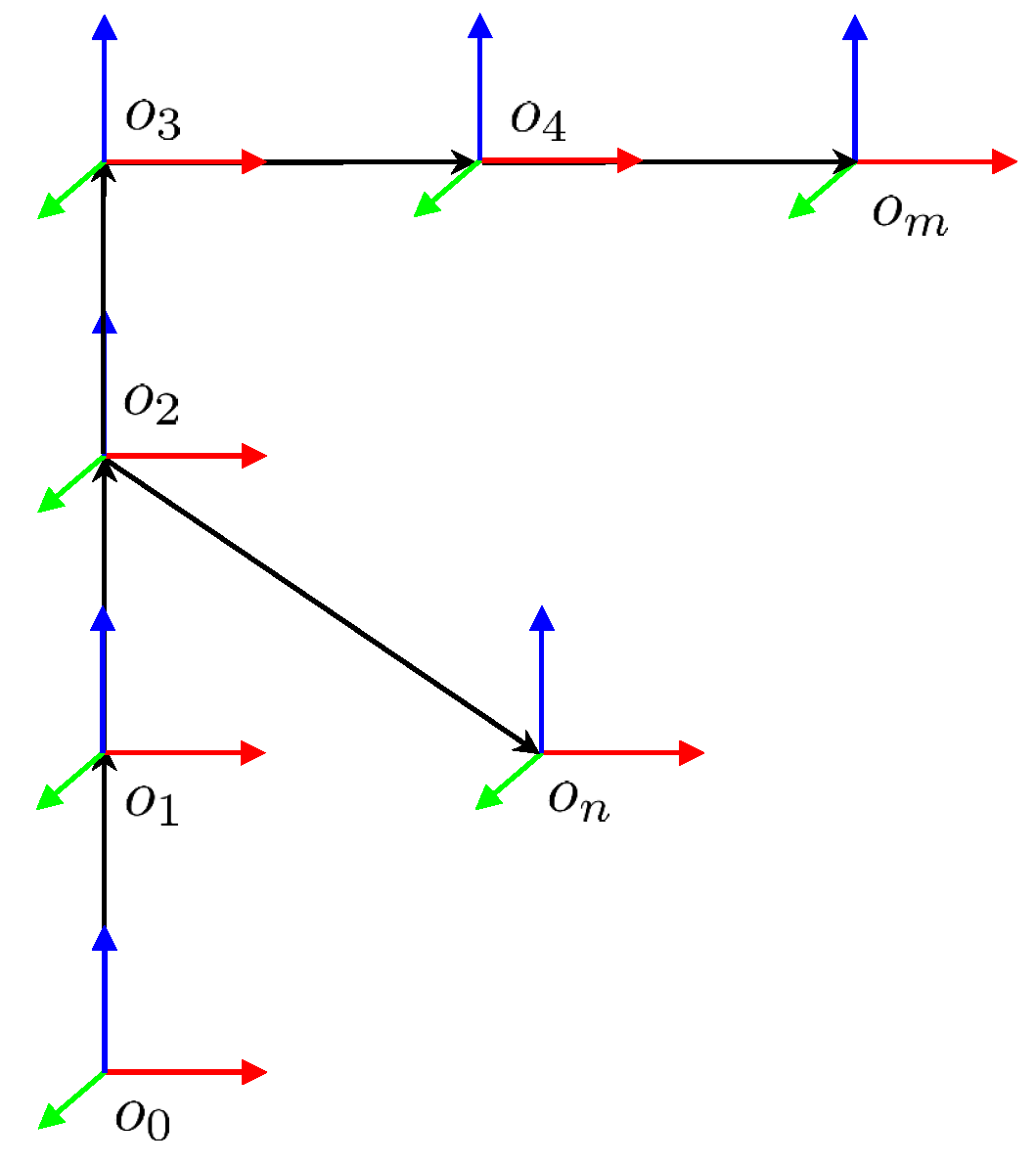
Figure 2.
Kinematic chain with non-consecutive links and local points n and m, illustrating the recursive transformation propagation that leads to the boundary function expression.
Figure 2.
Kinematic chain with non-consecutive links and local points n and m, illustrating the recursive transformation propagation that leads to the boundary function expression.
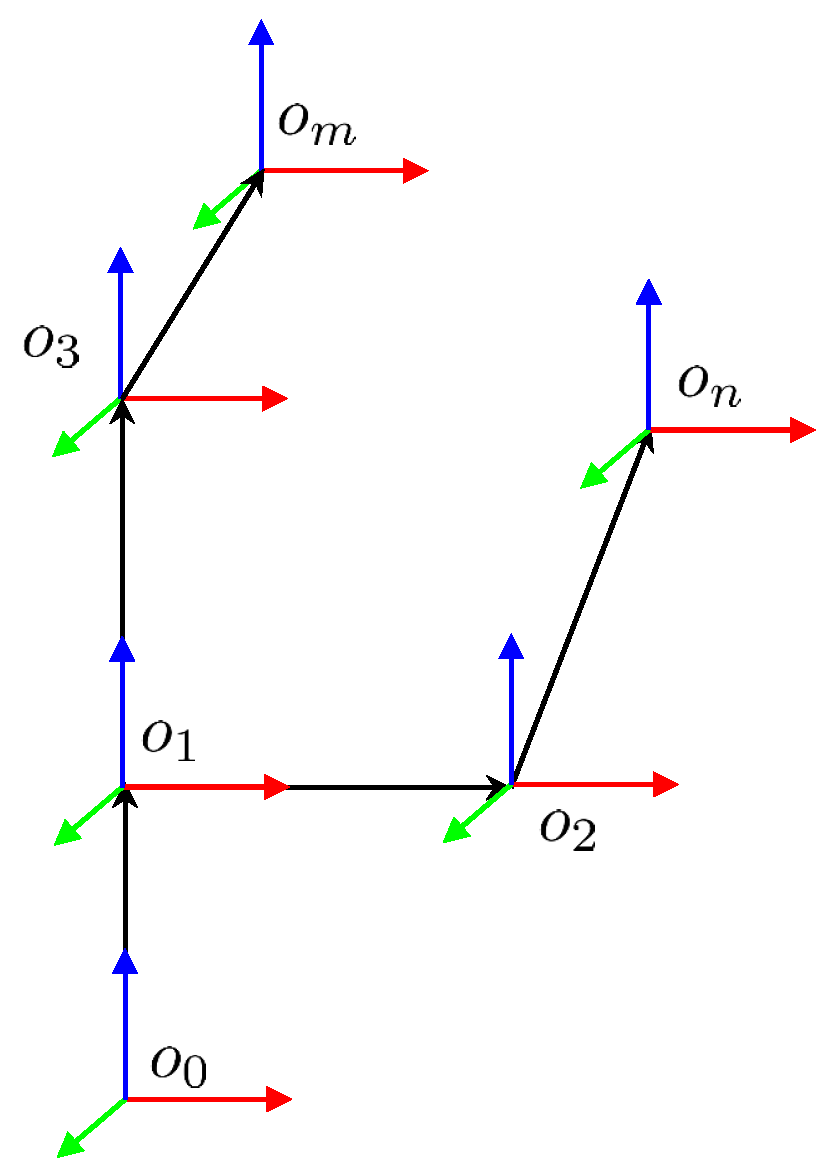
Figure 3.
Kinematic chain with consecutive links and local points n and m, showing the recursive transformation propagation and the resulting boundary function expression.
Figure 3.
Kinematic chain with consecutive links and local points n and m, showing the recursive transformation propagation and the resulting boundary function expression.
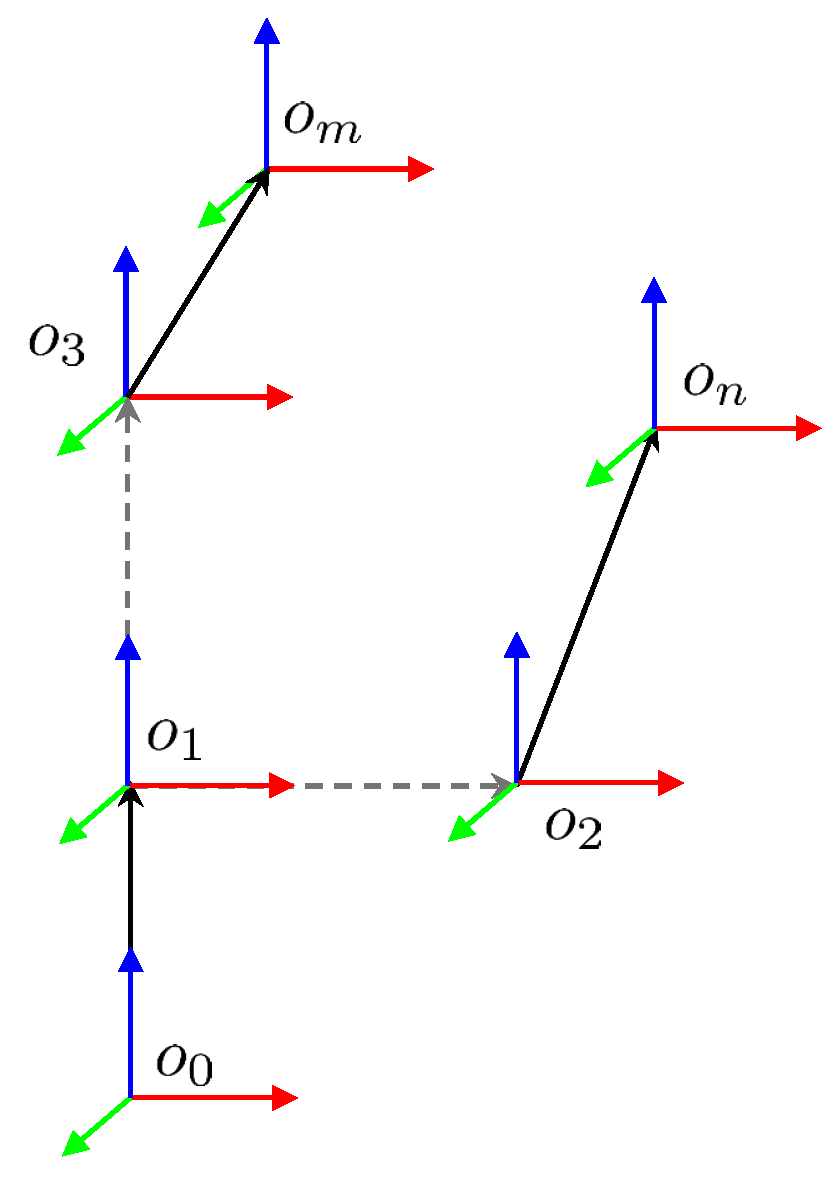
Figure 4.
Kinematic chain with a bifurcation at frame , leading to separate branches containing points n and m. The spatial relationship and resulting boundary function are illustrated.
Figure 4.
Kinematic chain with a bifurcation at frame , leading to separate branches containing points n and m. The spatial relationship and resulting boundary function are illustrated.
Figure 5.
Kinematic chain with a symmetric bifurcation where . The collision condition depends solely on the branches’ local orientations and internal geometry.
Figure 5.
Kinematic chain with a symmetric bifurcation where . The collision condition depends solely on the branches’ local orientations and internal geometry.
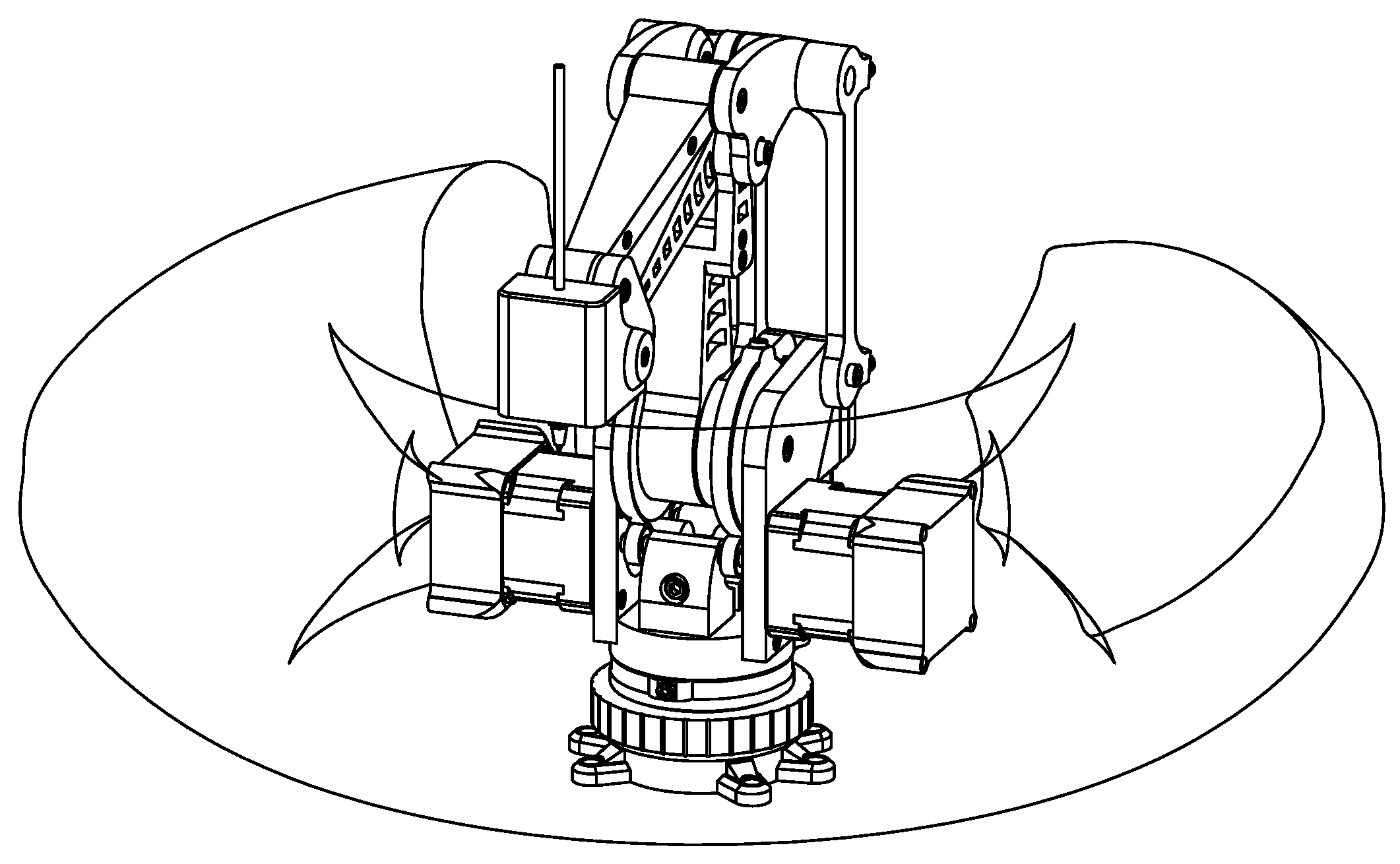
Figure 6.
MinervaBotV3 palletizing robot by Mythbots, scaled at 1:2 for educational applications.
Figure 6.
MinervaBotV3 palletizing robot by Mythbots, scaled at 1:2 for educational applications.
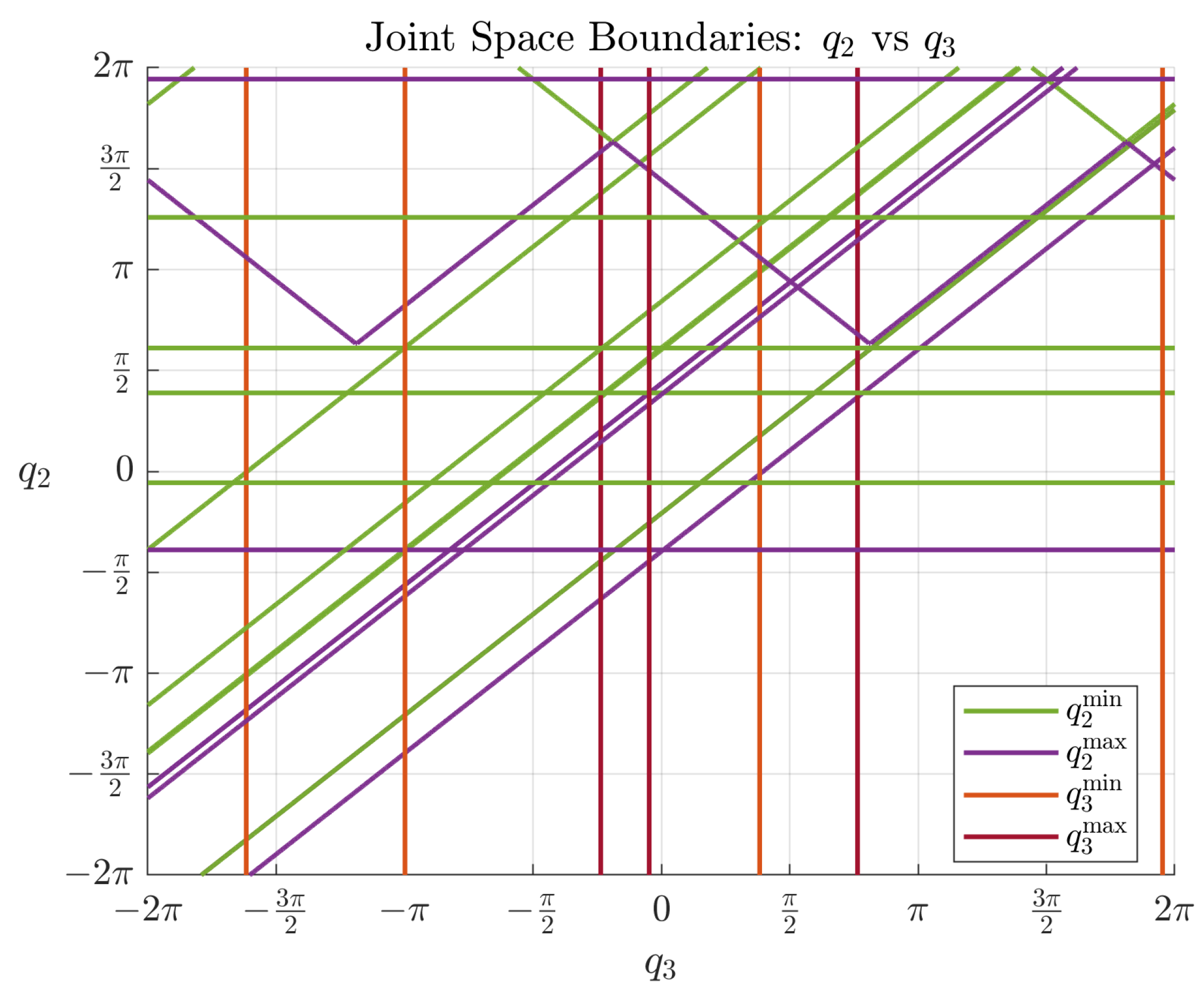
Figure 8.
Joint-space limits defined by the lower and upper boundary functions for the angular variables and . The curves , , , and were numerically evaluated over a dense grid and plotted to visualize the feasible joint region. These boundary functions were previously constructed using the symbolic formulation of collision constraints.
Figure 8.
Joint-space limits defined by the lower and upper boundary functions for the angular variables and . The curves , , , and were numerically evaluated over a dense grid and plotted to visualize the feasible joint region. These boundary functions were previously constructed using the symbolic formulation of collision constraints.
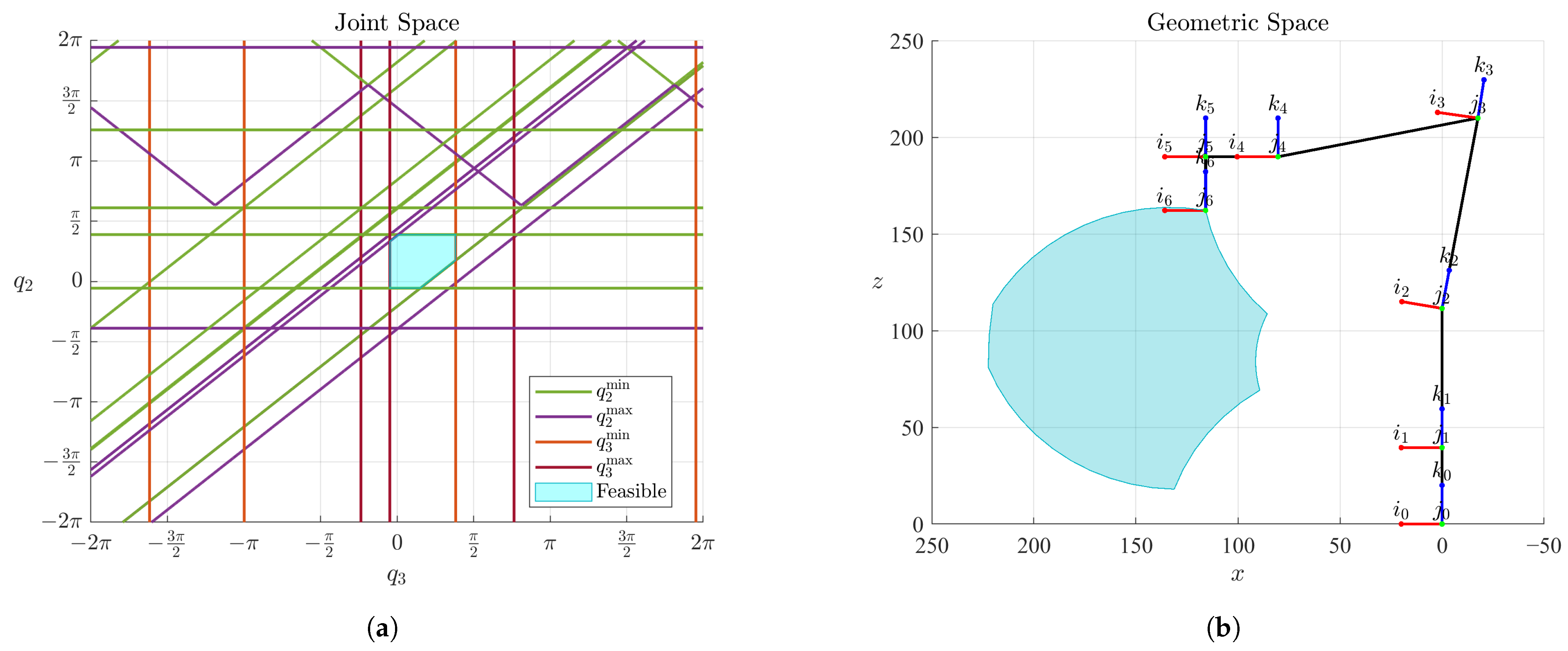
Figure 9.
Feasible workspace construction from joint-space analysis. (a) Closed contour formed by interpolating intersection points of selected boundary functions, yielding the valid configuration region in joint space. (b) Corresponding geometric workspace obtained via direct kinematic mapping of the closed trajectory, representing the principal kinematic chain.
Figure 9.
Feasible workspace construction from joint-space analysis. (a) Closed contour formed by interpolating intersection points of selected boundary functions, yielding the valid configuration region in joint space. (b) Corresponding geometric workspace obtained via direct kinematic mapping of the closed trajectory, representing the principal kinematic chain.
Figure 10.
Comparison between original and scaled trajectories. (a) Feasible joint-space regions before and after centroid-based scaling transformation. (b) Corresponding spatial trajectories, where the scaled region preserves a collision-free configuration throughout its motion.
Figure 10.
Comparison between original and scaled trajectories. (a) Feasible joint-space regions before and after centroid-based scaling transformation. (b) Corresponding spatial trajectories, where the scaled region preserves a collision-free configuration throughout its motion.
Figure 11.
Swept volume generated by rotating the scaled joint-space boundary around axis , forming a continuous and symmetric volumetric region.
Figure 11.
Swept volume generated by rotating the scaled joint-space boundary around axis , forming a continuous and symmetric volumetric region.
Figure 12.
CAD-based rendering of the MinervaBotV3 workspace, visualizing the spatial region that can be reached without self-collision.
Figure 12.
CAD-based rendering of the MinervaBotV3 workspace, visualizing the spatial region that can be reached without self-collision.
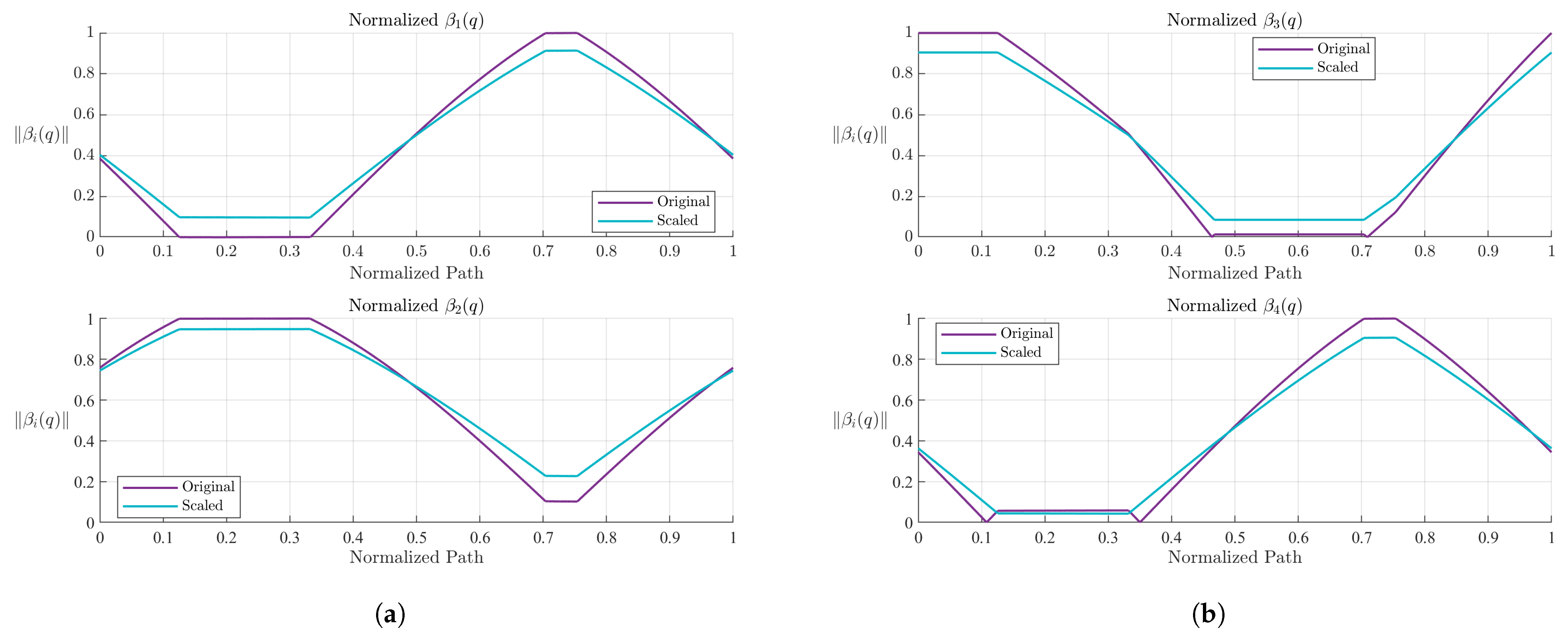
Figure 13.
Norms of the first four boundary functions along the original and scaled trajectories. The scaled path increases distance to constraint surfaces, enhancing robustness. (a) and . (b) and .
Figure 13.
Norms of the first four boundary functions along the original and scaled trajectories. The scaled path increases distance to constraint surfaces, enhancing robustness. (a) and . (b) and .
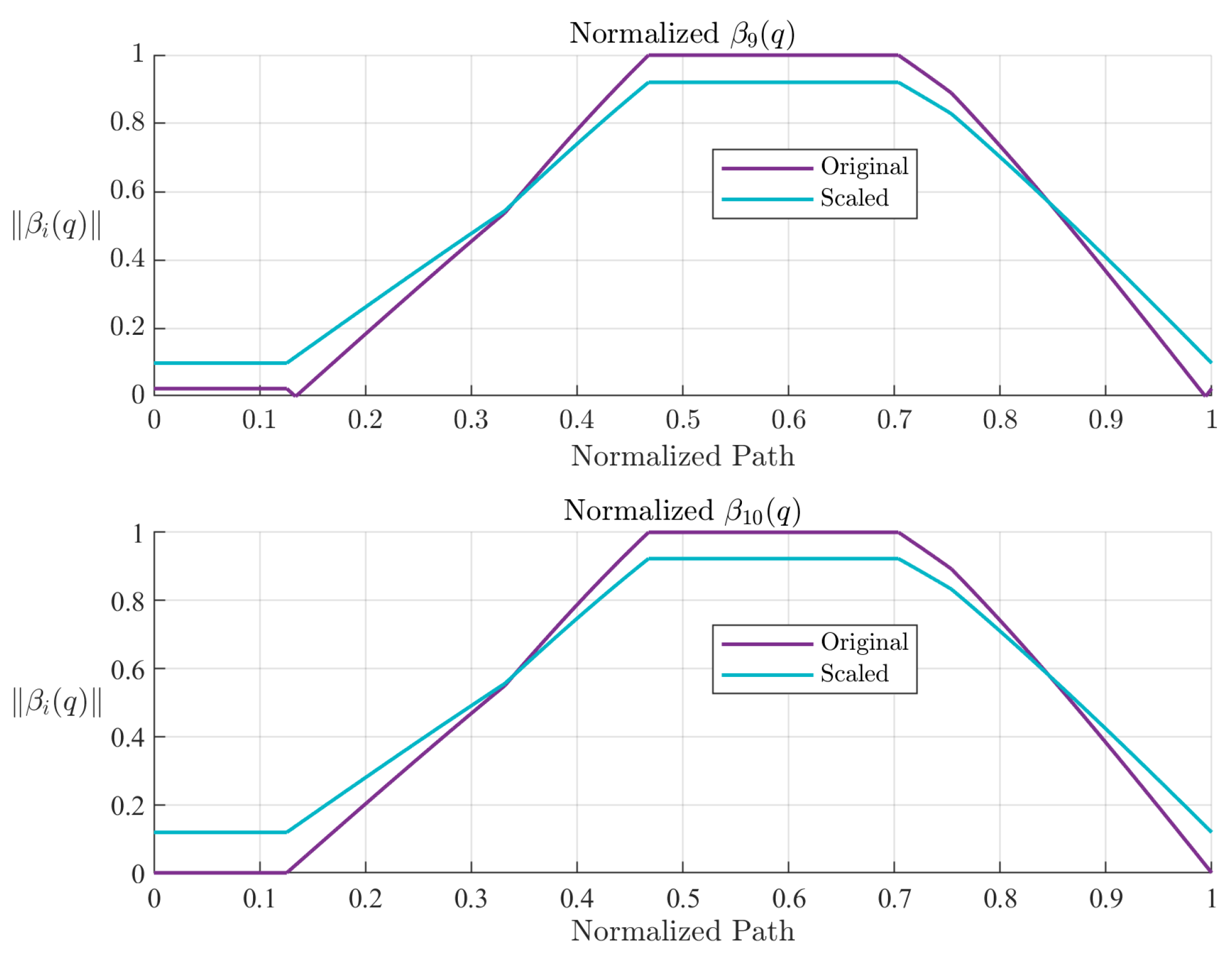
Figure 14.
Norms for through along original and scaled trajectories, showing increased clearance from constraint boundaries due to scaling. (a) and . (b) and .
Figure 14.
Norms for through along original and scaled trajectories, showing increased clearance from constraint boundaries due to scaling. (a) and . (b) and .
Figure 15.
Norms of the final pair of boundary functions. The scaled trajectory consistently maintains a safer distance from constraint surfaces.
Figure 15.
Norms of the final pair of boundary functions. The scaled trajectory consistently maintains a safer distance from constraint surfaces.
Figure 16.
Accumulated norm surface over joint space. The surface height corresponds to the sum of normalized constraint functions . Transparent coloring distinguishes the feasible region (turquoise) from its surroundings (purple).
Figure 16.
Accumulated norm surface over joint space. The surface height corresponds to the sum of normalized constraint functions . Transparent coloring distinguishes the feasible region (turquoise) from its surroundings (purple).
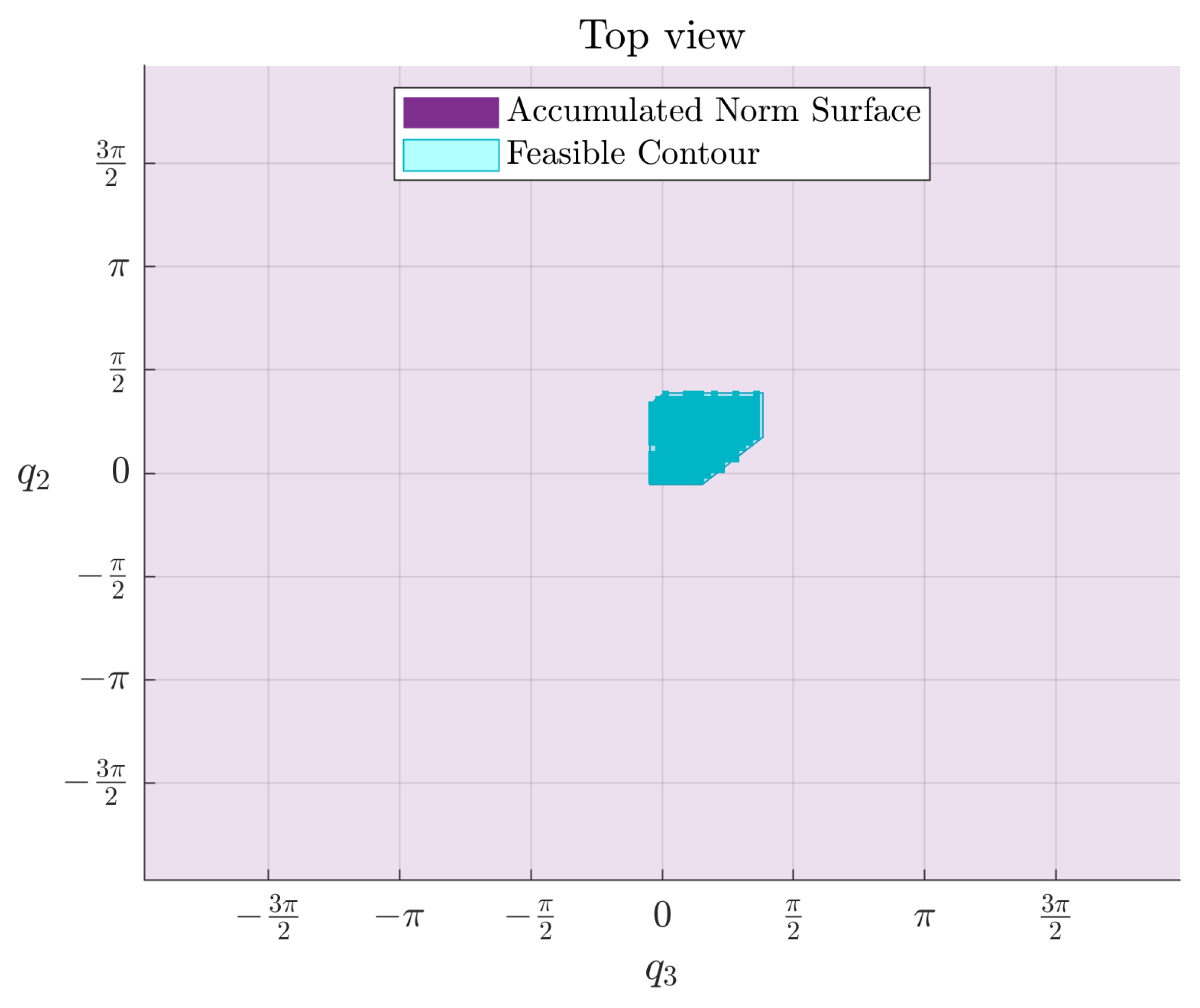
Figure 17.
Top-down view of the accumulated constraint surface. The polygonal feasible region is shown in cyan, surrounded by a gradient field representing increasing constraint activity.
Figure 17.
Top-down view of the accumulated constraint surface. The polygonal feasible region is shown in cyan, surrounded by a gradient field representing increasing constraint activity.
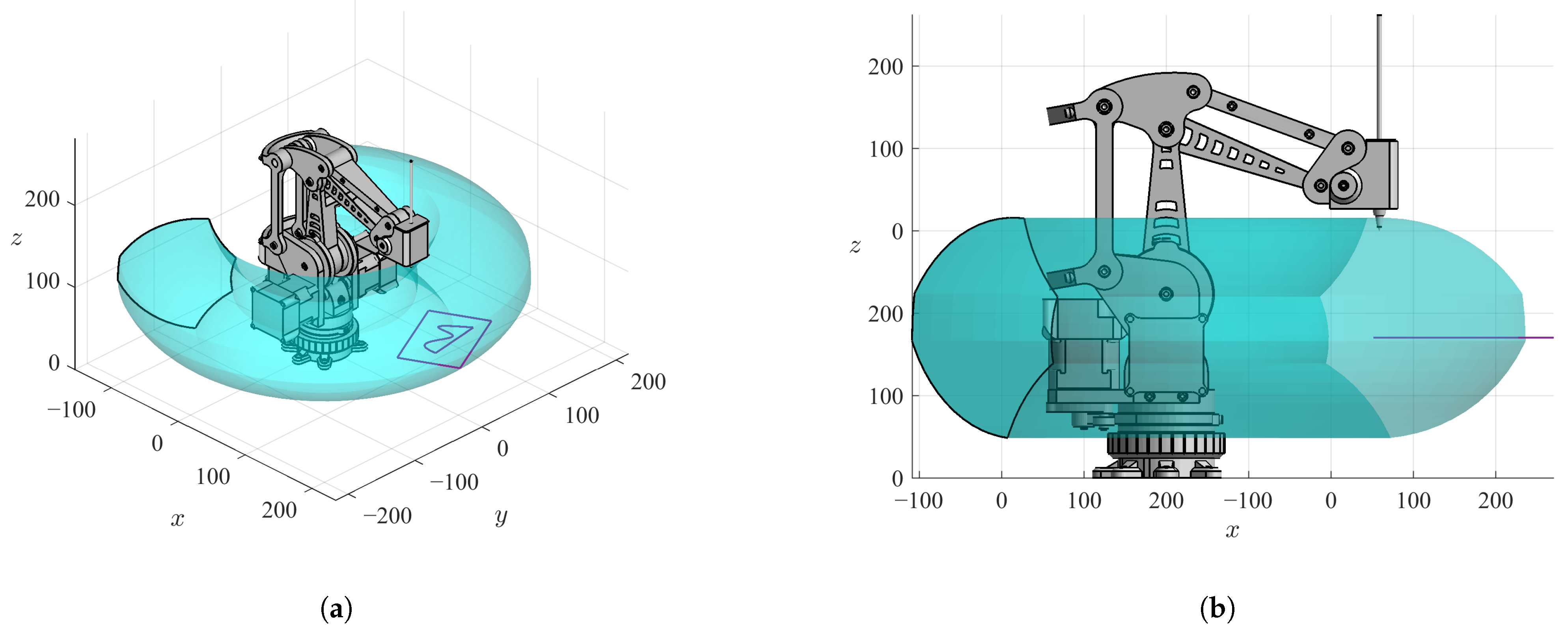
Figure 18.
Geometric evaluation of the proposed trajectory: global spatial context. (a) Isometric view of the proposed trajectory within the feasible workspace of the robot. (b) Lateral view of the robot and the geometric path used for validation.
Figure 18.
Geometric evaluation of the proposed trajectory: global spatial context. (a) Isometric view of the proposed trajectory within the feasible workspace of the robot. (b) Lateral view of the robot and the geometric path used for validation.
Figure 19.
Geometric evaluation of the proposed trajectory: local and detailed views. (a) Top-down view of the trajectory over the planar workspace of the robot. (b) Zoomed visualization of the scaled trajectory traced in the 3D workspace (bridges included).
Figure 19.
Geometric evaluation of the proposed trajectory: local and detailed views. (a) Top-down view of the trajectory over the planar workspace of the robot. (b) Zoomed visualization of the scaled trajectory traced in the 3D workspace (bridges included).
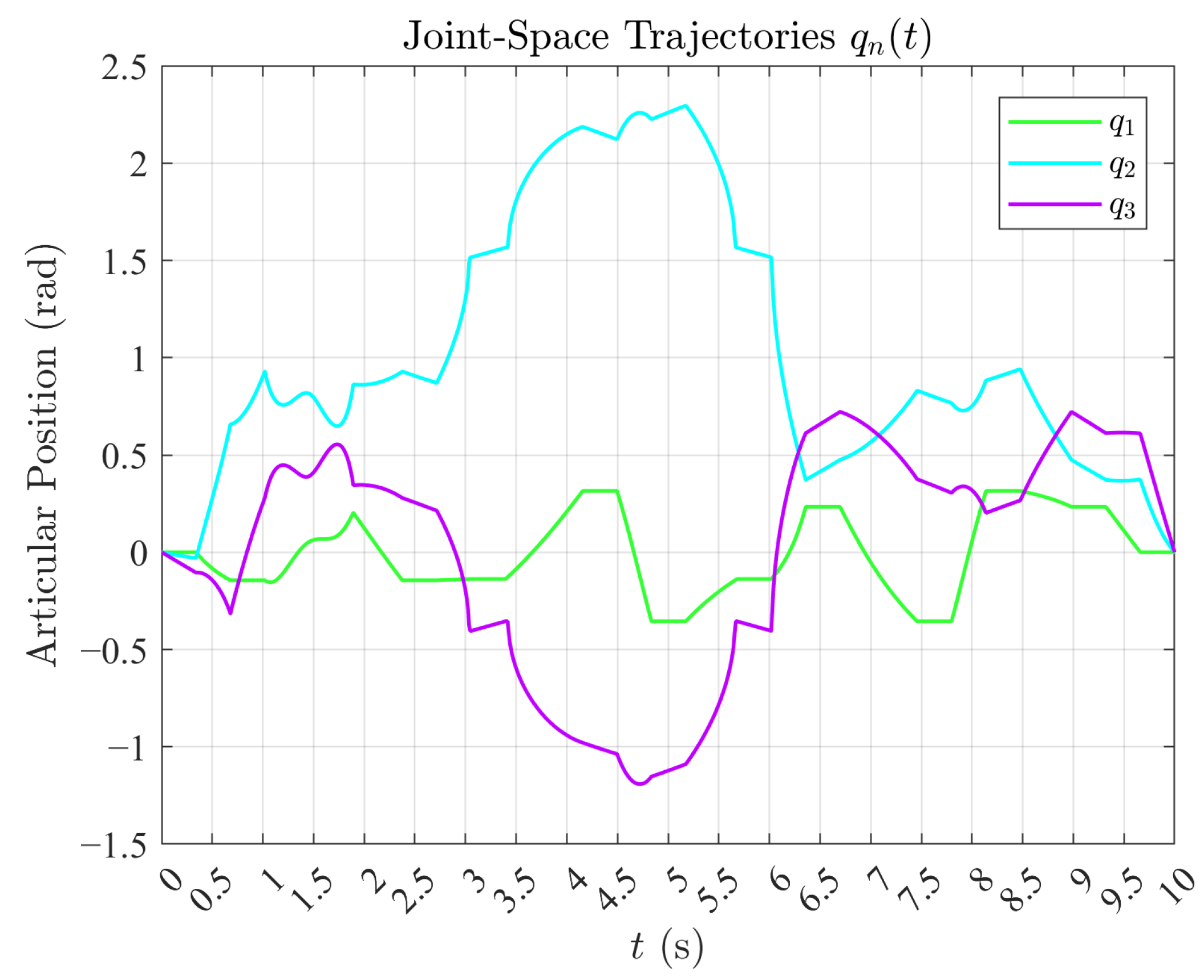
Figure 20.
Time-varying joint positions along the proposed trajectory. The curves , , and reveal the complexity and diversity of motion patterns included for symbolic evaluation (bridges included).
Figure 20.
Time-varying joint positions along the proposed trajectory. The curves , , and reveal the complexity and diversity of motion patterns included for symbolic evaluation (bridges included).
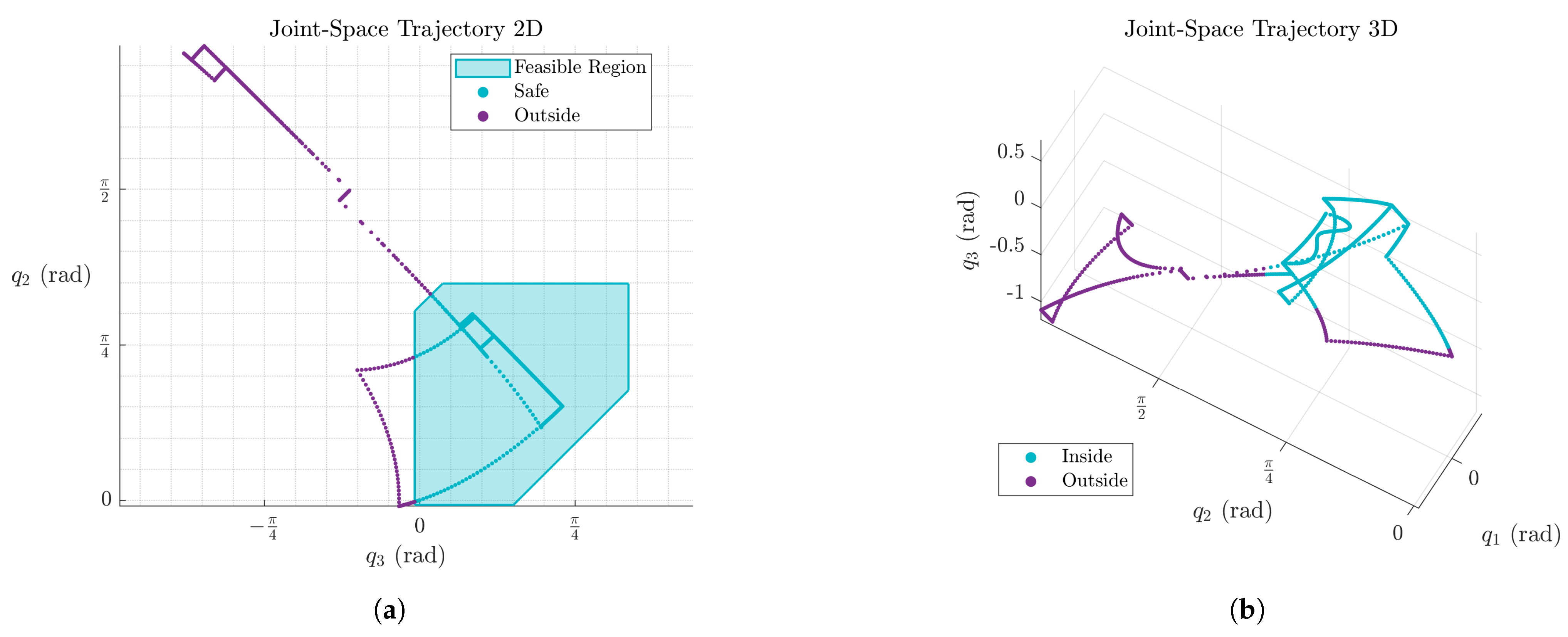
Figure 21.
Symbolic feasibility classification of the proposed trajectory. The 2D and 3D views confirm that the symbolic boundary functions successfully detect constraint violations. The joint limits for were arbitrarily set to . (a) Symbolic classification of the joint trajectory in the plane. (b) The 3D projection of the joint trajectory in space.
Figure 21.
Symbolic feasibility classification of the proposed trajectory. The 2D and 3D views confirm that the symbolic boundary functions successfully detect constraint violations. The joint limits for were arbitrarily set to . (a) Symbolic classification of the joint trajectory in the plane. (b) The 3D projection of the joint trajectory in space.
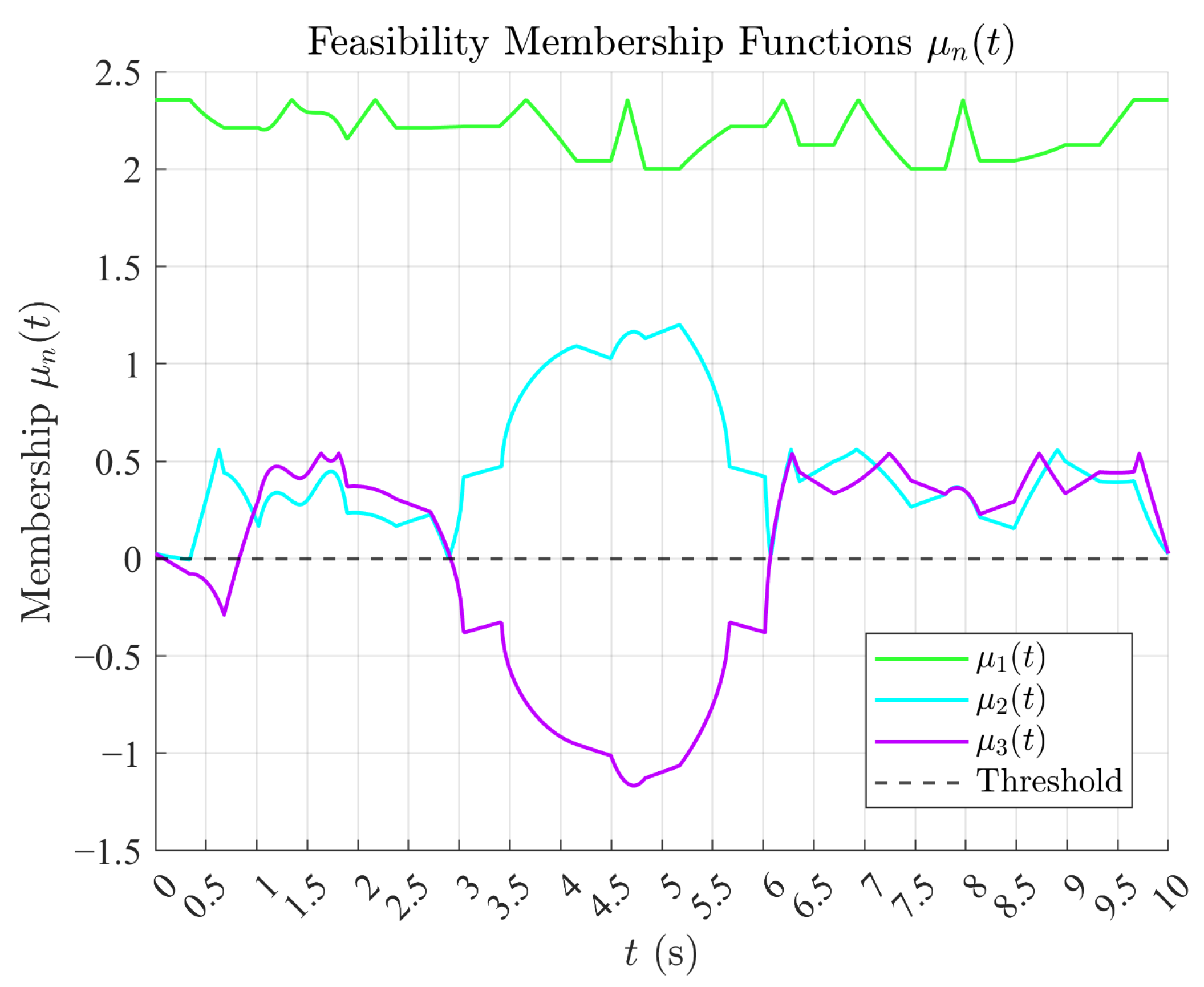
Figure 22.
Symbolic membership functions for each joint variable. Positive values indicate feasibility, zero denotes contact with the constraint, and negative values correspond to violations.
Figure 22.
Symbolic membership functions for each joint variable. Positive values indicate feasibility, zero denotes contact with the constraint, and negative values correspond to violations.
Table 1.
Robots.
| No. Serie | Manufacturer | Parallelograms | Relevant Characteristics |
|---|
| KR 700PA | KUKA | 2 | Total load: 700 kg, maximum reach: 3320 mm. |
| IRB 760 | ABB | 3 | Axes: 4, long reach, full-layer palletizer. |
| IRB 4400 | ABB | 1 | Robust construction, double bearing joints, optimized torque. |
| M-410iB/700 | FANUC | 2 | Controlled axes: 4, payload: 700 kg, reach: 3143 mm. |
| HP 160 O | HYUNDAI | 2 | Payload: 160 kg, max reach: 3128 mm, high speed. |
| PAL-260-3.1 | COMAU | 1 | Axes: 4, max wrist payload: 260 kg. |
| PAL-180-3.1 | COMAU | 1 | Axes: 4, max wrist payload: 180 kg. |
| FD-LP130 | OTC | 2 | Axes: 4, type of robot: palletizing, capacity: 130 kg or 180 kg. |
| MC1000DL | NACHI | 2 | Designed for lifting up to 1000 kg, superior strength, long reach. |
| SC700DL | NACHI | 2 | Payload: 700 kg, axes: 6, robot mass: 7000 kg. |
| MC600 | NACHI | 1 | Heavy lifting: 600 kg, work envelope: 2890 mm. |
| FD-A20 | DAIHEN | 1 | Payload: 20 kg for laser welding torch, axes: 6, high accuracy. |
| TC1010B-140 | TANG CHENG | 2 | Payload: 10 kg, axes: 4, repeat precision: ±0.08 mm. |
| M-410iC/110 | FANUC | 2 | Controlled axes: 4, payload: 110 kg, reach: 2403 mm. |
| M-410iC/185 | FANUC | 1 | Controlled axes: 4, payload: 185 kg, reach: 3143 mm. |
| PL500 | YASKAWA | 1 | Axes: 4, robot category: palletizing. |
| RMD08 | GSK | 2 | Axes: 4, max payload: 8 kg, robot mass: 180 kg. |
| RMD20 | GSK | 2 | Axes: 4, max payload: 20 kg, robot mass: 256 kg. |
| RMD120 | GSK | 2 | Axes: 4, max payload: 120 kg, robot mass: 1500 kg. |
| CP180L | KAWASAKI | 1 | Payload: 180 kg, max reach: 3255 mm, robot category: palletizing. |
| MPL160-100II | KAWASAKI | 2 | Axes: 4, payload: 100 kg, max working range: 3159 mm. |
| MPL160 II | KAWASAKI | 2 | Axes: 4, robot category: palletizing, vertical reach: 3024 mm, horizontal reach: 3159 mm. |
| ER60-2000-PL | ESTUN | 2 | Axes: 4, payload: 60 kg, reach: 2000 mm. |
| ER120-2400-PL | ESTUN | 2 | Axes: 4, payload: 120 kg, reach: 2400 mm. |
| SF15-C1538 | CHAIFU | 2 | Maximum radius: 53 mm, payload: 15 kg, repeatability: ± 0.08 mm. |
| SF8-K1400 | CHAIFU | 2 | Maximum radius: 1492 mm, payload: 8 kg, repeatability: ± 0.07 mm. |
| QJRB30-1 | QJAR | 2 | Axes: 4, payload: 30 kg, repeat positioning: ±0.05 mm. |
| QJRB800-1 | QJAR | 2 | Axes: 4, payload: 800 kg, repeat positioning: ±0.05 mm. |
| BRTIRPZ2250A | BORUTE | 2 | Axes: 4, reach: 2200 mm, payload: 50 kg, high precision. |
| BRTIRPZ3013A | BORUTE | 2 | Max load: 130 kg, reach: 3020 mm, designed for repetitive industrial tasks. |
| BRTIRPZ1508A | BORUTE | 2 | Max load: 8 kg, max reach: 1500 mm. |
| JZJ10B-140 | JZJRT | 2 | Axes: 6, weight capacity: 20 kg, position repeatability: ±0.08 mm. |
| JZJ25B-180 | JZJRT | 2 | Axes: 4, reach: 1800 mm, payload capacity: 25 kg. |
Table 2.
Symbols used in the formulation of joint and link boundary functions.
Table 2.
Symbols used in the formulation of joint and link boundary functions.
| Symbol | Description |
|---|
| Vector of joint variables |
| n-th joint variable as a function of time |
| Symbolic membership function for |
| Feasible region in joint space |
| Feasible geometric workspace in |
| Geometric position mapped from joint configuration |
| Scalar boundary function |
| i-th boundary function |
| Position vector from frame i to frame or point j |
| Relative vector between local points on links a and b |
| Euclidean norm (vector magnitude) |
| Rotation matrix from frame j to frame i |
| Recursive composition of orientation matrices |
| Local point n rigidly attached to frame a |
| Local point m rigidly attached to frame b |
| n, m | Point indices relative to their local frames |
| a, b | Frames along a kinematic chain |
| , | Common ancestor frame for branched topologies |
| 0, | Global or alternative base frames |
| Minimum allowable distance to prevent collision |
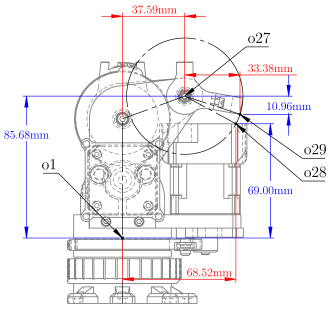
Table 3.
Geometric offsets of MinervaBotV3.
Table 3.
Geometric offsets of MinervaBotV3.
| Parameter | Symbol | Value (mm) |
|---|
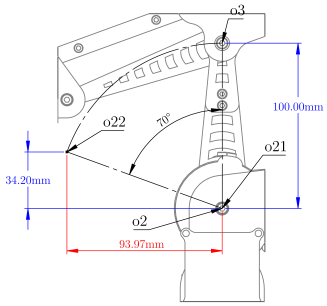
| Offset z (Base to Joint 1) | | 38.5 |
| Offset z (Joint 1 to Joint 2) | | 72 |
| Offset z (Joint 2 to Joint 3) | | 100 |
| Offset x (Joint 3 to Joint 4) | | 93.97 |
| Offset z (Joint 3 to Joint 4) | | −34.20 |
| Offset x (Joint 4 to Joint 5) | | 35.46 |
| Offset z (Joint 5 to End Effector) | | −27.71 |
Table 4.
Recursive notation of the position vectors of the MinervaBotV3.
Table 4.
Recursive notation of the position vectors of the MinervaBotV3.
| Point | Position Vector | Matrix | Orientation |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | I |
| | | |
| | | |
| | | |
| | | |
| | | |
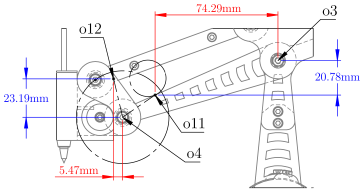
Table 5.
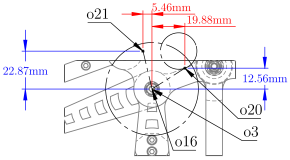
Type: Consecutive Link Boundary Function . This boundary function corresponds to a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in .
Table 5.
Type: Consecutive Link Boundary Function . This boundary function corresponds to a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i001 Technologies 13 00404 i001]() | |
Table 6.
Type: Consecutive Link Boundary Function . This boundary function corresponds to a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
Table 6.
Type: Consecutive Link Boundary Function . This boundary function corresponds to a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i002 Technologies 13 00404 i002]() | |
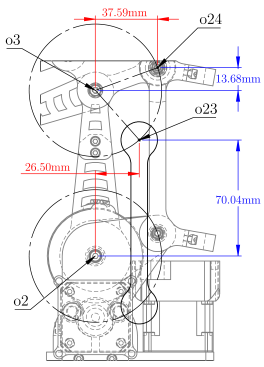
Table 7.
Type: Consecutive Link Boundary Function . This boundary function corresponds to a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
Table 7.
Type: Consecutive Link Boundary Function . This boundary function corresponds to a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i003 Technologies 13 00404 i003]() | |
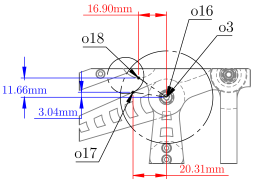
Table 8.
Type: Coincident Branched Link Boundary Function . This function models a potential collision between two components attached to separate branches. and belong to distinct kinematic chains and are both expressed with respect to the common reference system . The scalar function measures their distance in that shared frame. A collision occurs when .
Table 8.
Type: Coincident Branched Link Boundary Function . This function models a potential collision between two components attached to separate branches. and belong to distinct kinematic chains and are both expressed with respect to the common reference system . The scalar function measures their distance in that shared frame. A collision occurs when .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i004 Technologies 13 00404 i004]() | |
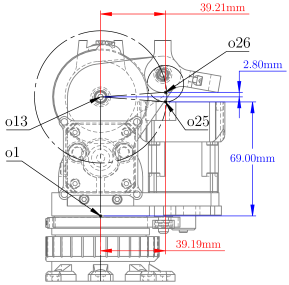
Table 9.
Type: Coincident Branched Link Boundary Function . This function models a potential collision between two components attached to separate branches originating from a common ancestor. and belong to distinct branches and are both expressed with respect to the shared reference system . The scalar function evaluates the distance between them. A collision is detected when .
Table 9.
Type: Coincident Branched Link Boundary Function . This function models a potential collision between two components attached to separate branches originating from a common ancestor. and belong to distinct branches and are both expressed with respect to the shared reference system . The scalar function evaluates the distance between them. A collision is detected when .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i005 Technologies 13 00404 i005]() | |
Table 10.
Type: Coincident Branched Link Boundary Function . This function represents a potential collision between two components belonging to distinct kinematic branches. and are defined in different branches and are transformed into the shared reference system . The scalar function evaluates the distance between them. A collision is detected when .
Table 10.
Type: Coincident Branched Link Boundary Function . This function represents a potential collision between two components belonging to distinct kinematic branches. and are defined in different branches and are transformed into the shared reference system . The scalar function evaluates the distance between them. A collision is detected when .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i006 Technologies 13 00404 i006]() | |
Table 11.
Type: Coincident Branched Link Boundary Function . This function models a potential collision between two components belonging to different branches of the kinematic structure. is defined in system , and in system . Both are transformed into the common reference frame , and the scalar function evaluates the distance between them. A collision occurs when .
Table 11.
Type: Coincident Branched Link Boundary Function . This function models a potential collision between two components belonging to different branches of the kinematic structure. is defined in system , and in system . Both are transformed into the common reference frame , and the scalar function evaluates the distance between them. A collision occurs when .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i007 Technologies 13 00404 i007]() | |
Table 12.
Type: Consecutive Link Boundary Function . This function models a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
Table 12.
Type: Consecutive Link Boundary Function . This function models a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i008 Technologies 13 00404 i008]() | |
Table 13.
Type: Consecutive Link Boundary Function . This function models a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
Table 13.
Type: Consecutive Link Boundary Function . This function models a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i009 Technologies 13 00404 i009]() | |
Table 14.
Type: Consecutive Link Boundary Function . This function models a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
Table 14.
Type: Consecutive Link Boundary Function . This function models a potential collision between two consecutive components. is defined in system , and in system . The scalar function evaluates the Euclidean distance between their transformed representations in . A collision occurs if and only if .
| Graphic | Geometric Offsets and Boundary Functions |
|---|
![Technologies 13 00404 i010 Technologies 13 00404 i010]() | |