Optimizing TSCH Scheduling for IIoT Networks Using Reinforcement Learning

Abstract

In the context of industrial applications, ensuring medium access control is a fundamental challenge. Industrial IoT devices are resource-constrained and must guarantee reliable communication while reducing energy consumption. The IEEE 802.15.4e standard proposed time-slotted channel hopping (TSCH) to meet the requirements of the industrial Internet of Things. TSCH relies on time synchronization and channel hopping to improve performance and reduce energy consumption. Despite these characteristics, configuring an efficient schedule under varying traffic conditions and interference scenarios remains a challenging problem. The exploitation of reinforcement learning (RL) techniques offers a promising approach to address this challenge. AI enables TSCH to dynamically adapt its scheduling based on real-time network conditions, making decisions that optimize key performance criteria such as energy efficiency, reliability, and latency. By learning from the environment, reinforcement learning can reconfigure schedules to mitigate interference scenarios and meet traffic demands. In this work, we compare various reinforcement learning (RL) algorithms in the context of the TSCH environment. In particular, we evaluate the deep Q-network (DQN), double deep Q-network (DDQN), and prioritized DQN (PER-DQN). We focus on the convergence speed of these algorithms and their capacity to adapt the schedule. Our results show that the PER-DQN algorithm improves the packet delivery ratio and achieves faster convergence compared to DQN and DDQN, demonstrating its effectiveness for dynamic TSCH scheduling in Industrial IoT environments. These quantifiable improvements highlight the potential of prioritized experience replay to enhance reliability and efficiency under varying network conditions.

1. Introduction

The Industrial Internet of Things (IIoT) is revolutionizing various fields by enabling automation and real-time data exchange [1]. At the core of this transformation lies wireless communication, which serves as the foundation for interactions between sensors, actuators, and control systems. These networks form the backbone of IIoT systems, enabling seamless data transmission and coordination among distributed components.

However, ensuring reliable communication within IIoT networks remains a significant challenge, especially in industrial environments prone to high levels of interference [2]. Interference in such settings can arise from numerous sources, including coexisting wireless networks [3], physical disturbances, and environmental noise. These disruptions can severely affect communication quality, resulting in increased packet loss, higher latency, and increased energy consumption [4]. Consequently, managing interference and maintaining robust communication is crucial to meeting the stringent reliability and performance demands of mission-critical industrial applications.

To address these challenges, the IEEE 802.15.4-2015 time-slotted channel hopping (TSCH) mode has been widely adopted. TSCH improves communication reliability and energy efficiency by taking advantage of two key mechanisms: time synchronization and channel hopping. These mechanisms work in tandem to reduce the impact of interference from various devices, thereby improving overall network robustness [5]. TSCH has been recognized for its capacity to support low-power, resilient, and deterministic communication, which makes it particularly suitable for industrial scenarios.

Despite these advantages, the performance of TSCH can still degrade significantly in the presence of interference, particularly in dynamic or harsh industrial environments. This limitation highlights the need for adaptive and intelligent scheduling strategies that can respond to changing network conditions in real time.

In this study, we introduce an innovative approach that leverages reinforcement learning (RL) to dynamically adapt the TSCH schedule, aiming to mitigate interference and enhance overall network performance [6]. By continuously interacting with the network environment, RL techniques learn optimal scheduling policies and adjust the TSCH schedule in real time [7].

This paper aims to enhance the scheduling performance of TSCH (time-slotted channel hopping) in industrial IoT networks by integrating reinforcement learning techniques to enable adaptive, interference-aware decision-making. The specific objectives of this study are:

• Model TSCH scheduling as a reinforcement learning (RL) problem: We formalize the TSCH scheduling process as a Markov decision process (MDP), in which the RL agent observes network states (e.g., interference levels, retransmissions, link quality) and learns optimal actions (i.e., slot and channel selection) to improve communication performance.
• Design an interference-aware reward function: We propose a novel reward function that accounts for packet delivery ratio (PDR), encouraging the agent to adopt scheduling strategies that improve reliability and minimize energy waste.
• Evaluate and compare advanced RL algorithms: We implement and evaluate three reinforcement learning algorithms—the deep Q-network (DQN), double DQN (DDQN), and prioritized experience replay DQN (PER-DQN)—to assess their effectiveness in terms of convergence speed, adaptability, and network performance.
• Demonstrate the effectiveness of RL-based TSCH scheduling under interference: Through simulation in interference-prone environments, we assess the RL-based schedulers’ ability to dynamically adapt schedules in real time and improve network metrics such as reliability.

To the best of our knowledge, this is among the first works to systematically evaluate and compare these RL algorithms for adaptive TSCH scheduling. Our study contributes a flexible and intelligent scheduling solution capable of operating in real-time, interference-heavy industrial environments.

2. Technical Background

Before presenting the proposed approach, it is important to provide the necessary technical background. This section introduces the fundamental concepts that will be used throughout the paper, namely time-slotted channel hopping (TSCH) and reinforcement learning (RL). These foundations are essential to understanding both the problem formulation and the motivation for applying RL techniques in wireless communication networks.

2.1. Overview of Time-Slotted Channel Hopping

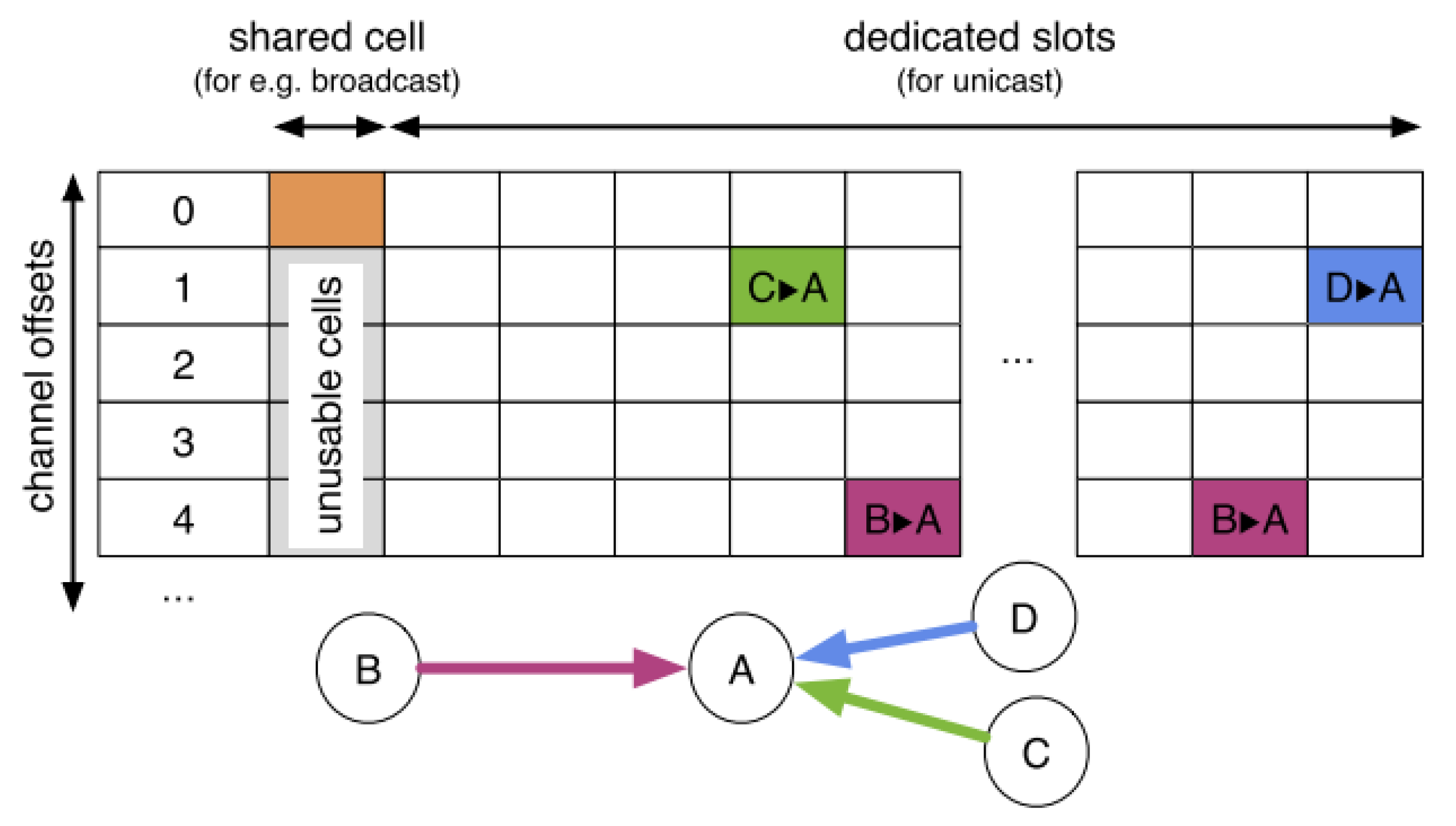
IEEE 802.15.4-e has proposed TSCH to ensure medium access control for industrial low-power wireless networks. TSCH improves reliability and reduces energy consumption by combining channel hopping and synchronization. Communications are organized as a slotframe structure. Each slotframe is a collection of cells that repeat over time. Each cell is defined by a channel offset and a timeslot as described in Figure 1.

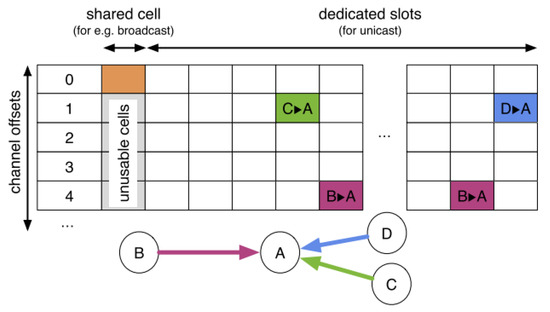
Figure 1. Schedule in an IEEE 802.15.4—TSCH network.

At the beginning of each slot, devices can decide to receive, send, or sleep, turning their radio off to save energy. Let us consider three nodes (B, C, and D) transmitting data to the border router (A) (cf. Figure 1). At the beginning of the slotframe, some shared cells (highlighted in orange) are allocated for control packets on channel offset 0. All links involving a common node (A) must be scheduled in different timeslots. In this example, two dedicated cells are assigned for the transmissions from B to A.

TSCH calculates the number of slots since network creation using the Absolute Sequence Number (ASN) parameter. ASN and channel offset are used to calculate the physical frequency, freq, used during the communication as follows:

$$\mathrm{Freq}=\mathrm{Map}\left((\mathrm{SlotNumber}+\mathrm{Offset})\%\mathrm{SeqLength}\right)$$

where

• Freq represents the physical frequencythat will be used during the exchange.
• Map[] is the mapping function that translates an integer into a physical frequency.
• SlotNumber represents the current slot number.
• Offset is the channel offset, which shifts the sequence to avoid interference.
• SeqLength is the length of the mapping sequence, determining how many possible frequencies can be chosen from the sequence.

TSCH defines dedicated and shared cells to optimize performance. Dedicated cells are used by radio links that do not interfere. In shared cells, the contention mechanism is executed to ensure retransmission in case of collision.

The efficiency of TSCH networks depends heavily on the scheduling algorithm. Scheduling must manage complex and often unpredictable network conditions, such as interference and varying traffic loads. These factors affect communication reliability and energy efficiency. Traditional scheduling methods are typically static or heuristic, limiting their adaptability to real-time changes in the network environment.

Despite its advantages, effective scheduling in TSCH remains a challenge due to the dynamic nature of industrial environments, variable traffic patterns, and interference. These challenges motivate the exploration of adaptive scheduling mechanisms, such as those based on reinforcement learning (RL), to dynamically learn and adjust schedules in real time.

2.2. Overview on Reinforcement Learning

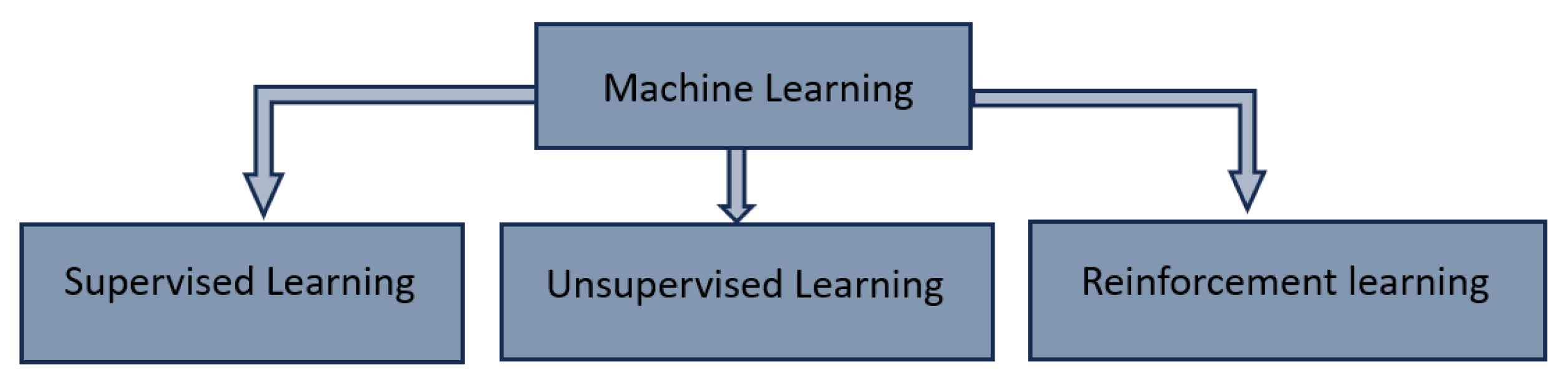
Machine learning is divided into three main classes, as described in Figure 2: supervised learning, unsupervised learning, and reinforcement learning [8].

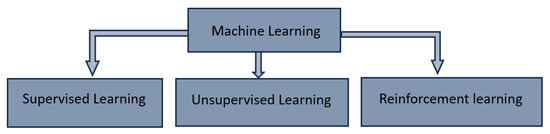
Figure 2. Categories of machine learning.

Supervised Learning relies on labeled data, where algorithms map inputs to known outputs [9]. It is used in classification and regression. Unsupervised learning is suitable for clustering and anomaly detection [10]. It relies on unlabeled datasets.

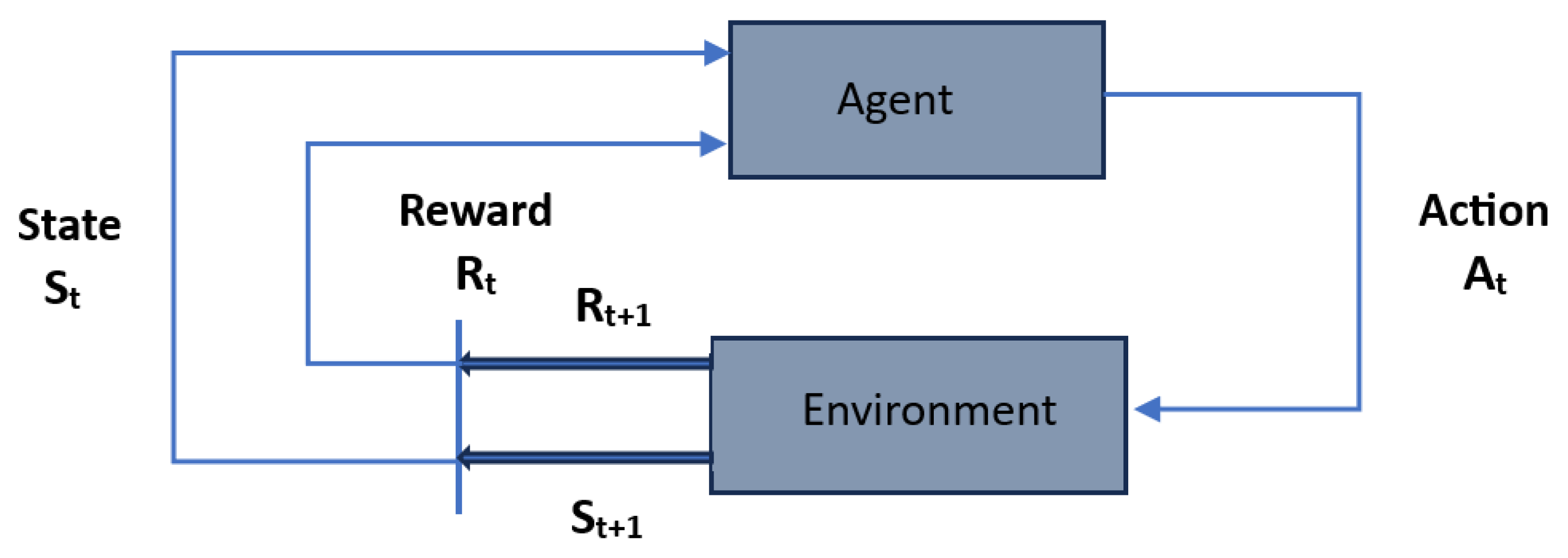
Reinforcement learning (RL) is based on an agent that interacts with an environment [11]. It learns optimal actions through rewards and penalties. The objective is to develop a strategy that maximizes cumulative rewards over time. This mechanism is used in environments where conditions change over time, requiring adaptive and intelligent decision making. RL is applied in various domains such as robotics, automated control systems, and gaming. Figure 3 illustrates the action and reward strategy of a generic RL mechanism. The agent has to explore new states and maximize its reward simultaneously. It should make the best overall decision in the future by collecting enough information from its environment.

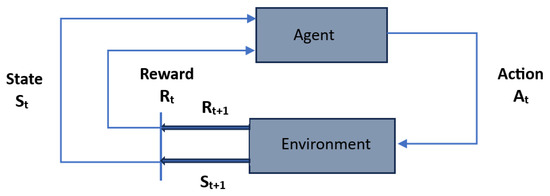
Figure 3. Reinforcement learning.

Basic elements of RL are as follows:

• Environment: Physical space in which the agent operates;
• State: The actual situation of the agent;
• Reward: The received feedback from the agent’s environment;
• Policy: The strategy used in order to map actions to the agent’s state;
• Value: Future reward that an agent would receive by taking an action in a particular state.

Reinforcement learning is a decision-making process where an agent interacts with an environment to learn optimal decisions. At each time step, the agent notices its state $S_t$ and selects an action $A_t$ based on a policy that defines its strategy for choosing actions. The environment responds by transitioning to a new state $S_{t+1}$ and providing a reward $R_t$, which serves as feedback. The agent’s goal is to maximize cumulative rewards, considering a discount factor $\gamma$. Over time, the agent enhances its policy through exploration and exploitation, progressively improving its decisions to achieve optimal performance in the considered environment.

3. Related Work

Having introduced the necessary technical background, we now turn to the existing research that applies reinforcement learning in the context of wireless and IoT networks. This review highlights how prior work has leveraged RL to address challenges such as resource allocation, access control, and scheduling, while also providing a taxonomy of the different RL methods that have been adopted.

3.1. Reinforcement Learning in Wireless Networks

Beyond classical reinforcement learning, various neural network-based decision-making approaches have been proposed to handle complex control tasks. For instance, neural network techniques have been applied to spacecraft dynamics, navigation, and control to enhance modeling accuracy and guidance robustness [12]. Similarly, generalized optimal game theory has been leveraged in virtual decision-making systems where multiple agents operate under uncertainty [13]. These game-theoretic frameworks, including those applied to CGF (computer-generated forces), use multi-granular reasoning to model layered decision-making processes in complex scenarios. Although our work does not explicitly implement game theory, its ideas support the need for flexible and context-aware control, which inspired our RL-based scheduling for TSCH.

In this context, reinforcement learning (RL) has emerged as a promising paradigm for optimizing resource allocation and enhancing efficiency in various wireless network contexts [14]. Agents are capable of autonomously learning optimal access strategies by continuously interacting with the environment and adapting to evolving network conditions [15]. For instance, Jaber et al. introduced a Q-learning-based scheduling mechanism, QL-TS-ESMACP, designed specifically for wireless sensor networks [16]. This method aims to maintain robust network connectivity while minimizing energy consumption, which is a critical requirement in environments with limited energy resources, such as IoT deployments.

In the context of vehicular ad hoc networks (VANETs), where high mobility and rapidly changing topologies pose significant challenges, RL has been employed to improve routing decisions. The work in [17] demonstrates how RL can be used to reduce end-to-end latency in such dynamic environments. Building on this, Lu et al. proposed a decentralized, multi-agent RL-based routing protocol, where each vehicle acts as an autonomous agent that learns to interact with its surrounding environment and neighboring nodes to ensure efficient communication [18].

Moreover, in the emerging 5G landscape, RL techniques are increasingly applied to optimize network performance and fulfill stringent Quality of Service (QoS) requirements. In particular, RL has been leveraged to enhance scheduling strategies by improving throughput and minimizing latency [19]. Additionally, ref. [20] explores the application of machine learning (ML) methods, including reinforcement learning (RL), for resource allocation in dynamic RAN slicing scenarios where efficient management of radio resources is essential. The survey in [21] further underscores the significance of RL in managing user mobility within ultra-dense 5G small-cell networks. It illustrates how AI techniques can contribute to the realization of key 5G service categories such as massive machine-type communications (mMTC), enhanced mobile broadband (eMBB), and ultra-reliable low-latency communications (uRLLC), all of which are essential for the scalability and reliability of IoT-based applications.

Beyond vehicular networks, similar RL-driven strategies have gained attention in Internet of Things (IoT) environments, where decentralized decision-making and adaptability are equally critical. The Internet of Things (IoT) facilitates autonomous decision-making and supports real-time communication, enabling the development of intelligent, adaptive systems. In this context, deep reinforcement learning (DRL) has emerged as a key mechanism for optimizing IoT control processes and modeling sequential decision-making tasks. Among the various machine learning (ML) paradigms, reinforcement learning (RL) has shown particular promise in empowering IoT devices to make autonomous decisions for networking operations, especially in environments constrained by limited resources [22].

In [23], the authors present an edge-based selection technique aimed at enhancing traffic delivery within distributed IoT systems. Their approach leverages DRL to enable multiple edge devices to collaboratively train a shared backhaul (BH) selection policy, thereby improving overall training efficiency and system scalability.

Building upon the integration of RL into networking, Nguyen et al. [24] propose a monitoring framework tailored for software-defined networking (SDN)-based IoT environments. Their method incorporates an intelligent agent capable of dynamically adjusting flow rule match-fields. This control process is modeled as a Markov decision process (MDP), and optimized using a double deep Q-network (DDQN) to derive an efficient match-field configuration policy.

Additionally, the work in [25] explores the use of RL to manage traffic dynamics in SDN-based networks. The proposed system is designed to autonomously identify and route critical data flows, ensuring efficient network performance under varying traffic conditions.

3.2. Taxonomy of Reinforcement Learning Methods

The advancement of IoT and IIoT has introduced multiple challenges for access control, where the primary objective is to ensure optimal resource utilization while maintaining security and data privacy. Traditional static mechanisms often fail to adapt to the dynamic and heterogeneous nature of IoT environments. In this context, reinforcement learning (RL) has been widely recognized as a promising paradigm, as it enables agents to interact with the network environment and progressively adapt their decisions. Several RL approaches have been investigated in the literature, each with distinct problem formulations, challenges, and performance trade-offs.

Q-learning is one of the most fundamental RL algorithms, where an agent learns the expected utility of actions through iterative interaction with the environment. In clustered M2M communication, Q-learning has been employed for resource allocation and access policy optimization, thereby improving throughput and reducing congestion in dynamic environments. Its main limitation is scalability, since large state-action spaces result in slow convergence [26].

To overcome these scalability issues, the deep Q-network (DQN) was introduced [27]. By combining reinforcement learning with deep neural networks, DQN approximates the Q-value function more effectively. This approach has been applied to smart grid and IIoT environments, where energy management and latency optimization are critical. By leveraging deep representations, DQN offers improved generalization in high-dimensional state spaces, though at the cost of increased computational complexity.

Alongside Q-learning and DQN, another widely studied method is SARSA (state-action-reward-state-action). Unlike Q-learning, which is off-policy, SARSA is an on-policy algorithm where updates are based on the action actually taken. In IoT applications such as smart cities, SARSA enables adaptive traffic management and dynamic security policy adjustments. However, its more conservative strategy can reduce performance in complex scenarios with large action spaces [28]. Building on DQN, the double deep Q-network (DDQN) was proposed to reduce the overestimation bias inherent in standard DQN. By decoupling action selection from value estimation, DDQN improves decision-making accuracy and stability. This makes it especially suitable for IIoT applications such as secure authentication and anomaly detection in environments with noisy or uncertain observations [29].

Beyond value-based methods, policy-gradient approaches such as proximal policy optimization (PPO) directly optimize the policy [30]. PPO has gained attention in healthcare IoT systems, where secure data transmission must be balanced with privacy and energy efficiency. Compared to earlier policy-gradient methods, PPO provides more stable updates, although it requires careful parameter tuning to perform reliably.

A hybrid family of algorithms, known as actor–critic methods (e.g., A3C, DDPG, and TD3), combines the strengths of value-based and policy-based approaches. These methods maintain separate models for policy learning (actor) and value estimation (critic). In industrial control systems, they have been applied to adapt resource allocation and enforce security policies under dynamic network conditions. Their flexibility comes at the expense of higher computational requirements [31].

In addition to single-agent approaches, multi-agent reinforcement learning extends RL to collaborative or competitive settings involving multiple agents [32]. In smart home environments, multi-agent strategies enable coordination of access control policies and device scheduling. While effective for distributed IoT systems, these methods face challenges related to convergence and coordination overhead.

Finally, hierarchical reinforcement learning (HRL) introduces a task decomposition perspective. By breaking complex decision-making tasks into smaller sub-tasks, HRL enhances interpretability and adaptability. In IIoT security, it allows critical devices to be assigned higher protection levels. However, ensuring that sub-tasks remain aligned with the overall system goal adds additional complexity [33].

This taxonomy demonstrates the diversity of RL techniques and highlights their suitability for different IoT and IIoT scenarios. Each method offers specific advantages and limitations depending on the problem complexity, scalability requirements, and computational resources available.

We present in Table 1 a summary of different RL techniques adopted in industrial settings. As explained in Table 1, each approach has multiple strengths and limitations. To meet industrial applications requirements, some of these mechanisms are not convenient. For example, due to the high tuning and computational requirements of PPO, it is not adequate for IIOT. SARSA is convenient for simple environments. However, it faces difficulties in handling many actions and states in complex environments since information is stored in large tables. HRL devides complex tasks into simpler actions. This hierarchy introduces more complexity to verify that all tasks are aligned to the main goal. Moreover, multi-agent RL has an increased overhead, which makes it unsuitable for resource-constrained environments.

Table 1. Survey of RL techniques for access control in IoT and industrial applications.

Year	Domain	RL Technique	Objective	State Representation	Action Space	Reward Function	Metrics
2020 [34]	Industrial IoT	Q-Learning	Mitigating congestion and optimizing access control in IIoT networks	Network congestion, device state	Grant/deny access	Throughput, latency	Access success rate
2023 [35]	Smart Grid	DQN	Dynamic pricing-based access control for balancing energy demand	Energy demand, user priority	Adjust pricing, limit access	Load balancing efficiency	Energy savings, user fairness
2016 [36]	Smart Cities	SARSA	Adaptive traffic management to reduce congestion and improve security	Traffic load, security risk	Traffic signal timing	Safety, congestion level	Delay reduction
2021 [37]	IIoT	DDQN	Secure device authentication and anomaly detection in industrial environments	Device authentication status	Allow/block communication	Attack detection accuracy	False-positive rate
2020 [38]	Healthcare IoT	PPO	Ensuring secure and efficient patient data transmission in IoT-based healthcare	Patient device health data	Allow/disallow data transmission	Data integrity, privacy level	Security breach rate
2023 [39]	5G-enabled IoT	A3C	Adaptive access control for network resource allocation in ultra-dense 5G IoT	Network congestion, latency	Adjust bandwidth allocation	QoS metrics	Packet loss, delay
2022 [40]	Industrial control systems	DDPG	Dynamic security policy adaptation to detect and prevent cyber-attacks	Sensor reliability, historical access patterns	Adaptive security policy	System resilience, anomaly detection	Detection accuracy
2020 [41]	Smart homes	Multi-agent RL	Managing access rights and security policies for interconnected IoT devices	User behavior, device activity logs	Grant/revoke access permissions	Privacy preservation, security level	Unauthorized access attempts
2022 [42]	Smart Factories	Hierarchical RL	Optimizing access control in multi-tier IIoT systems with varying security levels	Device hierarchy, role-based access	Assign security levels, enforce policies	Security efficiency, policy violations	Compliance rate, risk exposure
2023 [43]	Vehicular IoT	Meta-RL	Enhancing adaptive authentication and access control in V2X communication	Vehicle trust level, real-time network conditions	Authenticate, adjust security policies	Communication reliability, security robustness	False acceptance/rejection rate
2016 [44]	IWSN	TD3	Improving energy-efficient access control under network constraints	Sensor battery level, data transmission priority	Schedule data access, allocate bandwidth	Energy efficiency, real-time access	Network lifetime, response time

Given the high-dimensional state space of TSCH scheduling and the need for adaptive decision-making under interference, the deep Q-network (DQN) provides a balance between efficiency and scalability by leveraging deep learning to approximate the Q-value function. Additionally, prioritized experience replay (prioritized DQN) enhances learning by prioritizing critical transitions, allowing faster convergence and better adaptation to dynamic interference conditions. These properties make DQN and prioritized DQN ideal candidates for optimizing TSCH scheduling, ensuring improved packet delivery ratio (PDR), reduced latency, and interference-aware slot allocation in IIoT environments.

4. Problem Statement

TSCH has emerged as the de facto MAC standard for industrial IoT (IIoT) applications due to its ability to provide reliable and energy-efficient communication. By combining time-slot scheduling with frequency hopping, TSCH addresses the stringent reliability and latency requirements of industrial environments. However, its performance significantly degrades under unpredictable traffic patterns and rapidly changing network conditions. In the presence of interference, the packet delivery ratio (PDR) is reduced and latency increases, which undermines the reliability guarantees expected in mission-critical scenarios. Existing predefined scheduling mechanisms are limited by their static nature; they lack adaptability to dynamic traffic loads and fail to prevent collisions efficiently in environments with interference. This limitation creates a clear gap between TSCH’s theoretical potential and its real-world performance in harsh IIoT conditions.

To bridge this gap, adaptive and intelligent scheduling is required. Reinforcement learning (RL) provides a promising solution by enabling agents to interact with the network environment and progressively optimize scheduling decisions. In particular, deep Q-networks (DQNs) and their extensions, such as double DQNs and prioritized DQNs, offer the capacity to learn effective scheduling policies in high-dimensional state spaces. By modeling slot and channel selection as a Markov decision process (MDP), an RL agent can dynamically adapt to interference, ensuring improved network performance compared to static approaches.

The objectives of this research are as follows:

• Define TSCH scheduling as an RL problem where the agent makes decisions based on observed network states.
• Develop and compare the performance of DQN, double DQN, and prioritized DQN for adaptive scheduling.
• Evaluate the proposed solutions using key metrics such as packet delivery ratio (PDR), and reward convergence.

The expected outcome is an adaptive and interference-aware scheduling framework that enhances TSCH performance in IIoT applications. By leveraging advanced RL techniques, the solution aims to ensure robust, efficient, and resilient communication, thereby overcoming the shortcomings of predefined scheduling mechanisms and meeting the stringent requirements of industrial networks.

5. Formulation of DQN-Based TSCH Scheduling

In this part, we formulate the use of deep Q-networks (DQNs) in the context of time-slotted channel hopping (TSCH) scheduling. While designing our proposed RL scheduling mechanism, we have to consider different constraints such as energy consumption optimization, interference avoidance, and transmission reliability:

• Collision Avoidance: The objective of the proposed solution is to assign the channel that minimizes interference by avoiding channels that may lead to collisions.
• Energy Efficiency: Efficient scheduling strategies reduce energy consumption, which is a critical factor in low-power wide-area networks (LPWANs). Therefore, we have to implement an efficient communication strategy to balance network performance and power usage.
• Packet Delivery Ratio (PDR): This metric measures the reliability of transmission. Low PDR indicates that interference has occurred. An adaptive scheduling strategy may reduce packet loss and improve the PDR.

We model the TSCH network as a Markov decision process (MDP) based on the state space, action space, and reward function. The state space represents network conditions such as interference levels and link quality. The action space consists of selecting slots and channels for packet transmission. We design the reward function to avoid collisions and maximize the packet delivery ratio. The goal of our solution is to model the TSCH environment as a reinforcement learning (RL) task, where the agent (RL model) learns to optimize the scheduling process.

5.1. State Modeling

For a given hop i, we model the state $S_t$ at time t as a vector that represents key transmission characteristics across all hops within a packet. Specifically, the state is defined as:

$$S_t=\left[A_1,R_1,F_1,{\mathrm{RSSI}}_1,A_2,R_2,F_2,{\mathrm{RSSI}}_2,\dots ,A_n,R_n,F_n,{\mathrm{RSSI}}_n\right]$$

where n is the total number of hops. Each hop is represented by four parameters:

• $A_i$: Address of the hop;
• $R_i$: Number of retransmissions;
• $F_i$: Assigned transmission frequency;
• ${\mathrm{RSSI}}_i$: Received signal strength indicator, reflecting the link quality.

Results are structured in a vector that captures the link quality indicators and topology parameters. DQN uses this representation to learn optimal decisions in order to improve network performance.

5.2. Action Representation

The action state consists of the possible decisions the agent can take to maximize rewards. Actions are selected using an ϵ-greedy policy, where an agent can take the following actions:

• Exploit: Choose the action with the highest Q-value (greedy choice).
• Explore: Select a random action with probability ϵ to improve learning.

At time t, the action state represents all channel assignments that the agent can select from the current hop. We denote Nchannels the total number of channels that a node can select. In TSCH, the agent has 16 channels to select from at each step. We denote the action state as the action space:

$$A_t\in \{0,1,2,\dots ,N_{\mathrm{channels}}-1\}$$

5.3. Reward Function

To improve scheduling decisions, the RL agent has to maximize rewards over time. Positive rewards represent the effectiveness of actions.

In TSCH scheduling, the reward function $R_t$ is used to evaluate the selection of channels based on PDR values. At each step, the reward function is calculated as a function of the packet delivery ratio (PDR). We encourage the agent to adopt a strategy that improves communication reliability.

We define the reward function as:

$$R_t=\alpha ·\mathrm{PDR}$$

where

• PDR represents the ratio of successfully delivered packets.
• α is a factor that adjusts the impact of PDR on the reward function.

By relying on PDR, the reward function promotes successful transmissions. The agent adopts scheduling strategies that maximize network performance and data delivery.

5.4. State Transition Function

The state transition $S_{t+1}$ models the new state after the RL agent selects an action $A_t$. The transition depends on the current packet’s hop parameters and the selected channel selected by the agent:

$$s_{t+1}=f(S_t,A_t)$$

where f is a function that models the update of the state based on the action. The state modification reflects the following:

• The presence of successful transmission on the selected channel.
• The quality of the transmission due to interference or successful communication.

5.5. DQN Update Rule

The goal of DQN is to learn the optimal action strategy that improves the expected future rewards. The Q-value for a state-action pair $(S_t,A_t)$ depends on the Bellman equation:

$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha \left[R_t+\gamma \underset{a^{\prime }}{max}Q(S_{t+1},a^{\prime })-Q(S_t,A_t)\right]$$

where

• $\alpha$ represents the learning rate. It evaluates how much new information overrides the old.
• $\gamma$ represents the importance of future rewards.
• ${max}_{a^{\prime }}Q(s_{t+1},a^{\prime })$ is the maximum predicted Q-value for the next state $S_{t+1}$.

To determine Q-values, we use a neural network instead of a Q-table. We update the neural network in order to obtain an optimal strategy.

5.6. Proposed Algorithm

The proposed algorithm leverages deep Q-networks (DQNs) to optimize TSCH (time-slotted channel hopping) scheduling by dynamically selecting communication channels to minimize interference. The detailed steps are presented in Algorithm 1.

Algorithm 1: Summary of TSCH Scheduling Algorithm with DQN

The process begins with initializing the simulation environment and the DQN agent, which is trained through multiple episodes. In each episode, the agent verifies the network state, selects an action (a communication channel) using an $ϵ$-greedy policy, and receives a reward based on the effectiveness of the selection. The experience is stored and used to update the DQN model through replay of experiences, ensuring improved decision-making over time.

As training progresses, the exploration rate $ϵ$ is gradually reduced to favor exploitation over exploration.

The final model aims to optimize scheduling by reducing interference and thus improving network performance.

6. Double DQN for TSCH Scheduling

The double deep Q-network (double DQN) is an enhanced form of the deep Q-network (DQN). This algorithm is proposed to minimize over-estimation in Q-learning. In standard DQN, the use of the same neural network in both selecting and evaluating actions leads to Q-value overestimation.

The problem of overestimation is addressed by DDQN. It proposes to use two different networks to select the best action and estimate its value. The first network is called an online network, it selects the action with the highest Q-value. The second one is the target network. It is used to evaluate the action in order to reduce the overestimation.

Double DQN offers good performance in complex environments since it improves learning efficiency.

Double DQN (DDQN) improves DQN by using two separate neural networks to reduce the overestimation of Q-values. Given a state–action pair $(S,A)$, the Q-value update in the standard DQN is defined in the following section.

6.1. Mathematical Formulation of DDQN

Double DQN aims to learn the optimal action strategy that enhances future rewards. The Q-value for a state–action pair $(S_t,A_t)$ is updated using the Bellman equation as follows:

$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha \left[R_t+\gamma Q(S_{t+1},arg\underset{a^{\prime }}{max}Q(S_{t+1},a^{\prime };\theta ))-Q(S_t,A_t)\right]$$

where

• $\alpha$ models the learning rate used to override old information.
• $\gamma$ evaluates how much the agent cares about future rewards. If this parameter is close to zero, it means that the agent is focused on intermediate rewards. Otherwise, the agent focuses on long-term rewards.
• $arg{max}_{a^{\prime }}Q(S_{t+1},a^{\prime };\theta )$ represents the action selected by the online network for the next state $S_{t+1}$.
• $Q(S_{t+1},arg{max}_{a^{\prime }}Q(S_{t+1},a^{\prime };\theta ))$ is the Q-value of the action selected evaluated by the target network. It serves to reduce overestimation.

The target Q-value in double DQN is updated as follows:

$$y_t=R_t+\gamma Q_{{\theta }^{-}}\left(S_{t+1},arg\underset{a^{\prime }}{max}{Q}_{\theta }(S_{t+1},a^{\prime })\right)$$

where

• $R_t$ is the reward at time t.
• $\gamma$ is the discount factor.
• $Q_{{\theta }^{-}}$ is the target network, and $Q_{\theta }$ is the online network.
• $S_{t+1}$ is the state at time $t+1$.
• $arg{max}_{a^{\prime }}{Q}_{\theta }(S_{t+1},a^{\prime })$ selects the action that maximizes the Q-value in the next state $S_{t+1}$.

The objective is to maximize the cumulative discounted rewards.

$$G_t=\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k}$$

(1)

where $\gamma$ is the discount factor that determines the importance of future rewards.

6.2. Proposed DDQN Algorithm

As shown in Algorithm 2, we apply a Double DQN approach to optimize TSCH scheduling.

Algorithm 2: Double DQN for TSCH scheduling

7. Formulation of Prioritized Experience Replay Deep Q-Network (PER-DQN) for TSCH Scheduling

7.1. Mathematical Formulation

As described previously, the environment is represented by the TSCH network state $S_t$, It includes available channels, interference indicators, and slots. The action $A_t$ represents the scheduling choices made by the agent at time t.

We define the following components:

• Replay Buffer $𝒟$: This buffer is used to store experiences $(S_t,A_t,R_t,S_{t+1})$, where $S_t$ is the state, $A_t$ is the selected action, $R_t$ is the given reward, and $S_{t+1}$ is the next state after the execution of the action $A_t$.
• Action–Value Function $Q(S,S;\theta )$: A neural network parameterized by $\theta$ that estimates the expected return (reward) for taking action A in state S.
• Target network $Q(S,A;{\theta }^{-})$: Represents the action-value function network. It is updated periodically with the parameters of the main network.

For each episode, the first step consists of initializing the state and resetting the environment. Then, we select actions using the $ϵ$-greedy policy, while balancing exploration and exploitation. The selected action is executed, offering a reward and passing to the next state. The temporal difference (TD) error is calculated, followed by computing the priority for storing the experience in the buffer. Experiences are stored with prioritized sampling, and once the buffer has enough samples, a mini-batch is replayed. For each experience, importance-sampling weights and target values are calculated, followed by the computation of the loss function using the weighted mean squared error. The Q-network is updated via gradient descent, and priorities in the buffer are adjusted. Periodically, the target network is updated, and exploration gradually shifts toward exploitation. Finally, the agent’s performance is analyzed based on metrics such as reward and packet delivery ratio (PDR) for the task at hand.

7.2. Proposed Algorithm

We further enhance the DQN approach using Prioritized Experience Replay, as detailed in Algorithm 3.

Algorithm 3: Prioritized Experience Replay Deep Q-Network (PER-DQN)

The prioritized experience replay deep Q-network (PER-DQN) algorithm is an enhancement of the standard deep Q-network (DQN) that improves learning efficiency by prioritizing important transitions in the replay buffer. In this algorithm, a TSCH network’s state, including interference, slot matrix, and channels, is used to optimize scheduling and minimize interference. Initially, the algorithm sets up the replay buffer, action-value function, and a target network. During training, an $ϵ$-greedy policy is used to select actions, and transitions are stored in the buffer with a priority determined by the temporal difference (TD) error. When the buffer contains enough samples, a mini-batch is sampled based on these priorities, and a gradient descent step is performed to minimize the loss and update the priorities. The target network is periodically updated, and $ϵ$ and $\beta$ are adjusted over time. Ultimately, the algorithm optimizes the scheduling process by continuously updating its policy to minimize interference in the network.

8. Simulation Environment

The simulation environment replicates TSCH scheduling in a multi-hop industrial IoT network. Each packet is modeled with global identifiers and hop-specific data for up to six hops, including node address, retransmission count, channel frequency, and RSSI.

The action space is defined as the selection of one frequency channel from 16 available channels. At each step, the reinforcement learning agent chooses a channel, and the environment evaluates the resulting transmission outcome based on interference, retransmissions, and signal quality.

The reward function is based on the packet delivery ratio (PDR) calculated for each packet during the scheduling process. Specifically, the PDR is defined as the ratio of successful transmissions within all the hops of the current packet. A successful transmission corresponds to a hop where the RSSI is above -80 dBm and the number of retransmissions is less than or equal to two. This approach provides timely and localized feedback to the agent after each scheduling decision, enabling effective learning. The cumulative reward over an episode reflects the overall performance of the scheduling policy across multiple packets.

The training process spans 500 episodes, with parameters set as follows: learning rate = 0.001, discount factor $\gamma =0.95$, and exploration rate starting from $ϵ=1.0$ with exponential decay $ϵ\leftarrow max(ϵ\times 0.995,0.01)$.

9. Realization and Simulation Evaluation

In this section, we describe the work conducted. We implemented the deep Q-network (DQN), double DQN, and prioritized experience replay DQN (prioritized DQN) in the context of the TSCH (time-slotted channel hopping) scheduling mechanism. The objective was to enhance scheduling decisions in a dynamic and power-constrained network environment.

Thus, we propose a reinforcement learning (RL) agent that interacts with the TSCH environment. We model the action value state using deep learning techniques. We train the agent using a neural network.

For prioritized DQN, we implemented a priority-based experience replay mechanism to enhance the learning process by prioritizing important transitions. This approach aims to improve convergence speed and learning efficiency compared to the standard DQN method.

The reinforcement learning setup is based on RL, where the state space represents the hop information of each packet, including address, retransmissions, frequency, and RSSI. The action space consists of selecting one of the 16 frequency channels for scheduling. The reward function incentivizes interference-free scheduling by penalizing actions that cause frequency collisions and rewarding those that enhance successful transmissions. Training was conducted over 500 episodes with an initial exploration rate ($ϵ$) of 1.0, gradually decaying to 0.01, using a learning rate of 0.001 and a discount factor ($\gamma$) of 0.95. The simulations aimed to allow the agent to learn optimal scheduling policies, minimizing interference and maximizing packet delivery efficiency under varying network conditions.

10. Performance of DQN in TSCH

10.1. Results of DQN Performance in TSCH

The following figures depict the performance of the DQN algorithm in a time-slotted channel hopping (TSCH) environment. Each figure highlights key performance metrics over 500 training episodes. First, we evaluate the convergence of DQN and its ability to adapt the schedule and improve transmission effeciency.

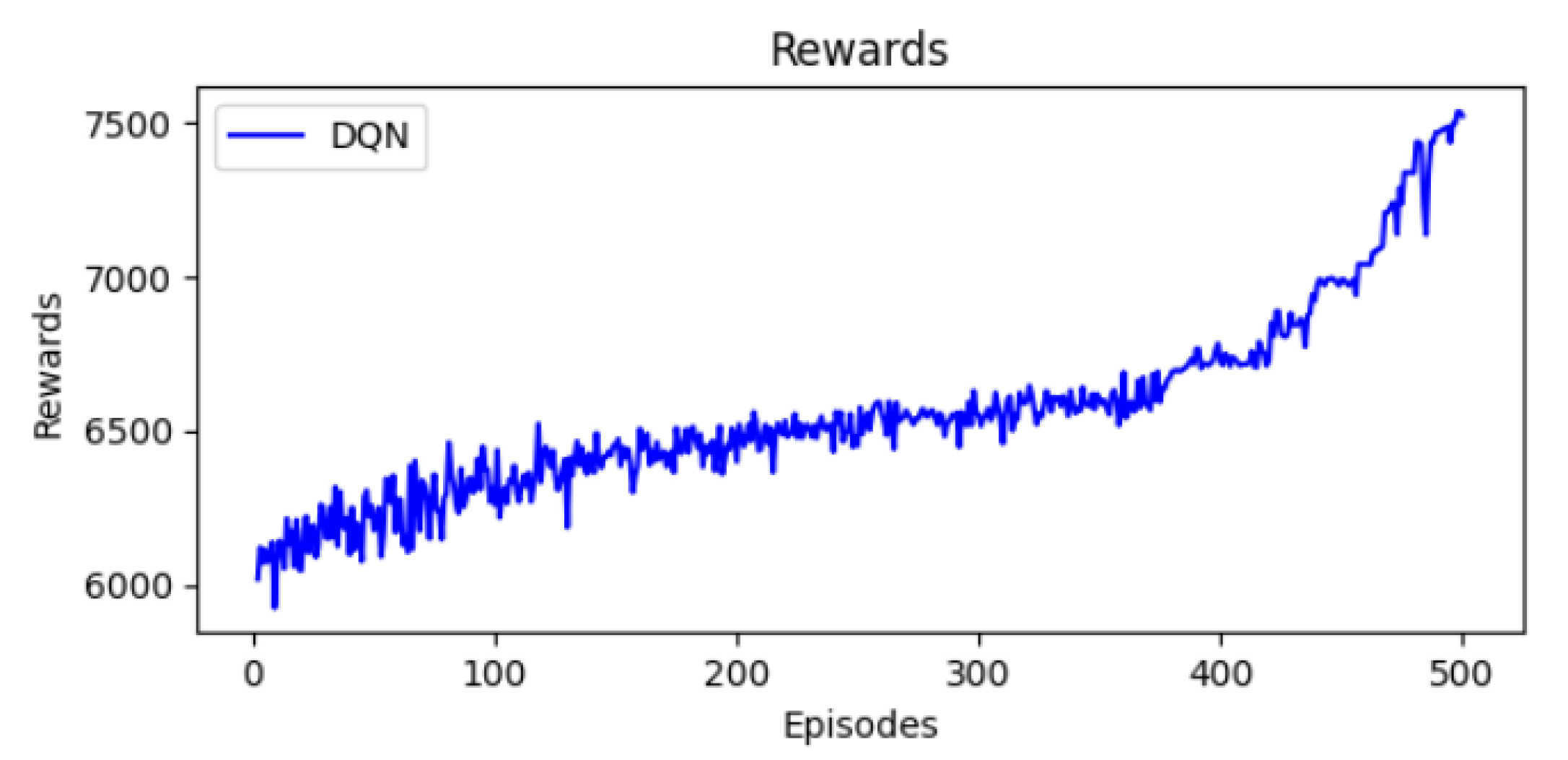
10.2. Reward Progression

Figure 4 presents the evolution of rewards over training. Reward values are fluctuating due to the dynamic interaction with the TSCH environnement. First, the rewards are equal to 6000. Then, they increase to 7500 in the last stages. This evolution means that the DQN agent can improve its decision strategy.

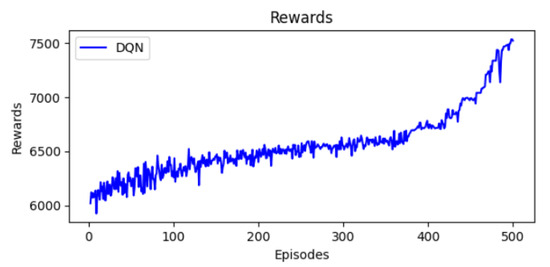
Figure 4. Evolution of rewards.

10.3. Packet Delivery Ratio Evaluation

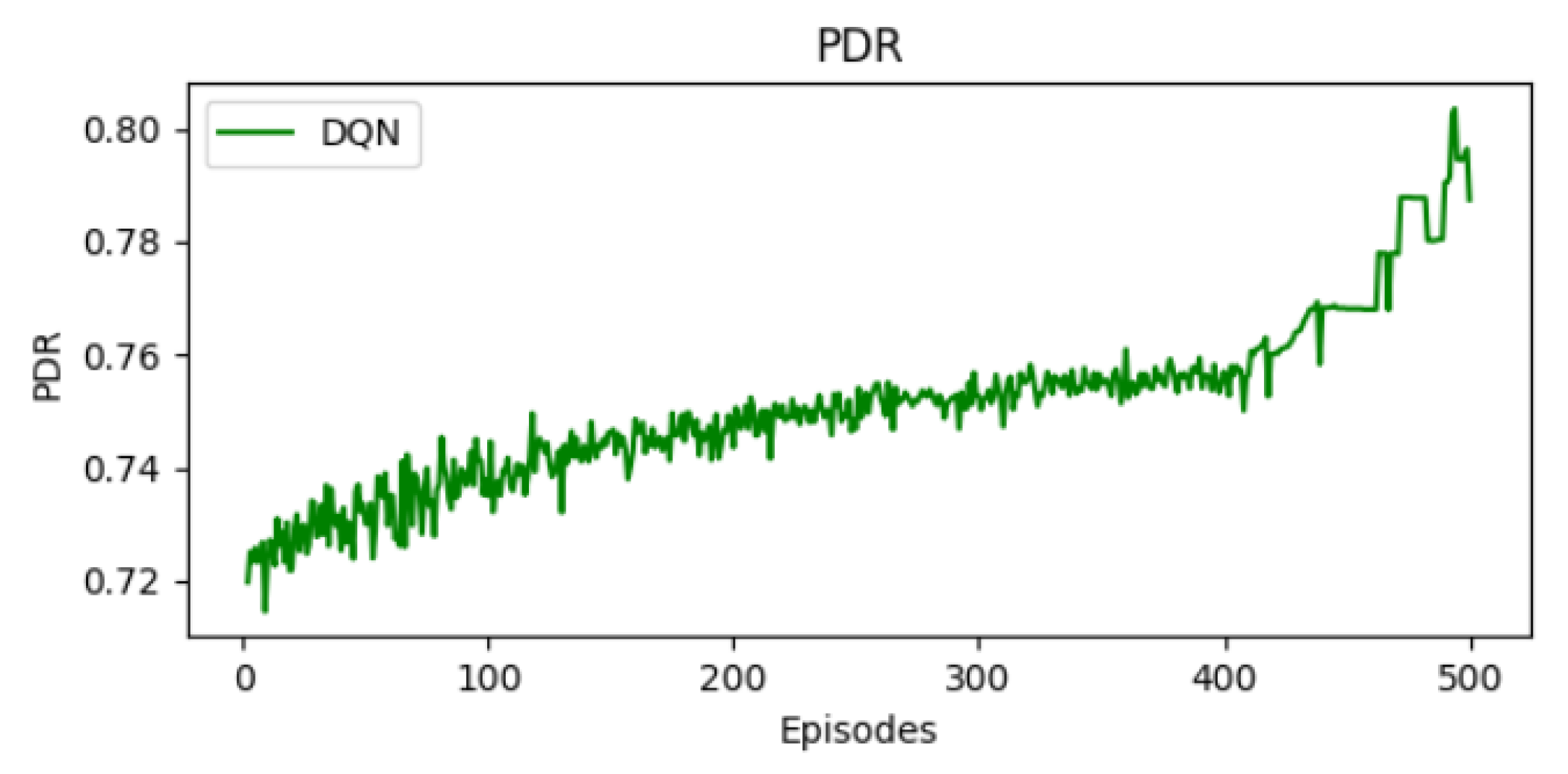
Figure 5 depicts the packet delivery ratio (PDR) over episodes. We observe a clear progression in terms of PDR. It starts around 0.72 and increases to 0.8 in the final stages. This improvement indicates that the agent is able to optimize its scheduling decisions. A large proportion of packets are successfully transmitted. The TSCH network is able to ensure data transmission with lower packet loss.

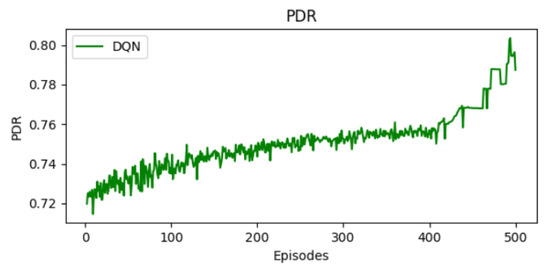
Figure 5. Evolution of PDR.

10.4. Epsilon Decay over Episodes

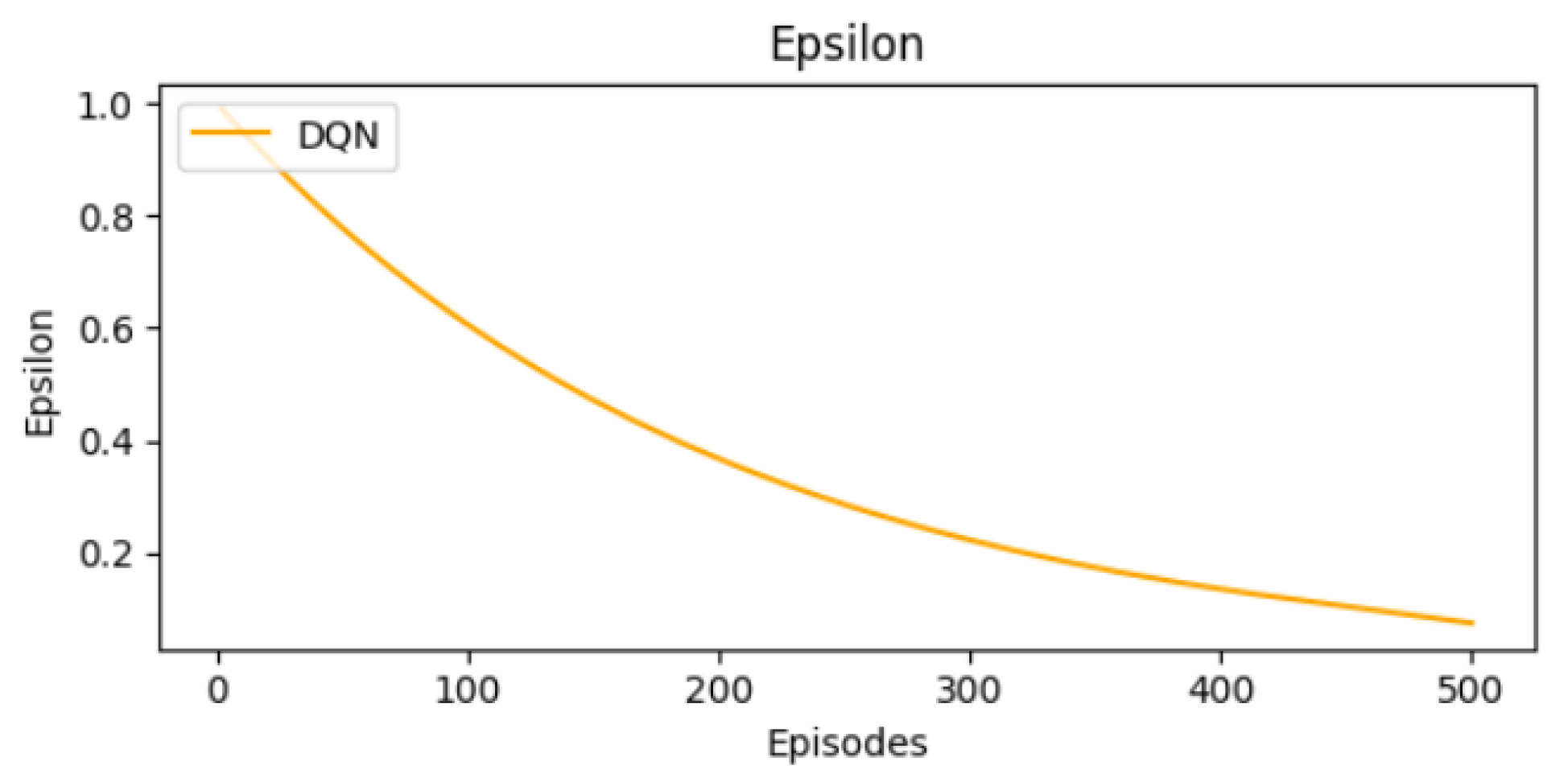
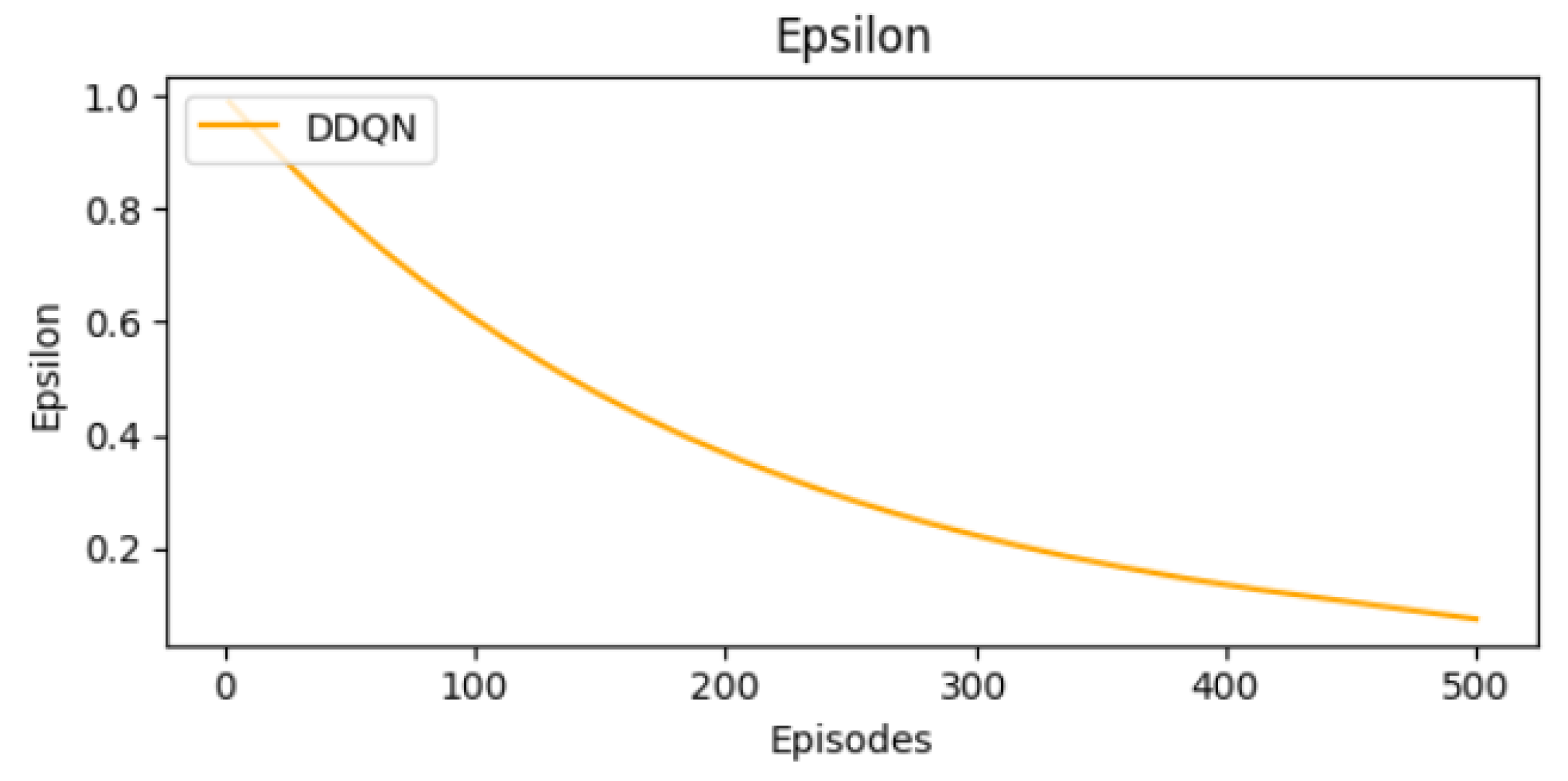
We illustrate in Figure 6 the progression of epsilon over training episodes. Epsilon implements a greedy strategy that balances exploration and exploitation. Epsilon is equal to 1 at the beginning of training. Higher values of epsilon indicate that the agent selects random actions to explore the environment. As epsilon decreases, the agent moves to an exploitative phase. It converges to an optimal strategy that prioritizes actions offering higher rewards.

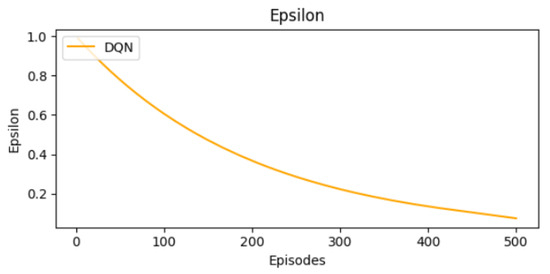
Figure 6. Epsilon decay curve.

11. Analysis of DDQN Effectiveness in TSCH

11.1. DDQN Performance Metrics

In this section, we present the results of implementing the double deep Q-network (DDQN) within the time-slotted channel hopping (TSCH) network. Our objective is to study the effectiveness of the DDQN in optimizing TSCH scheduling.

11.2. Reward Progression

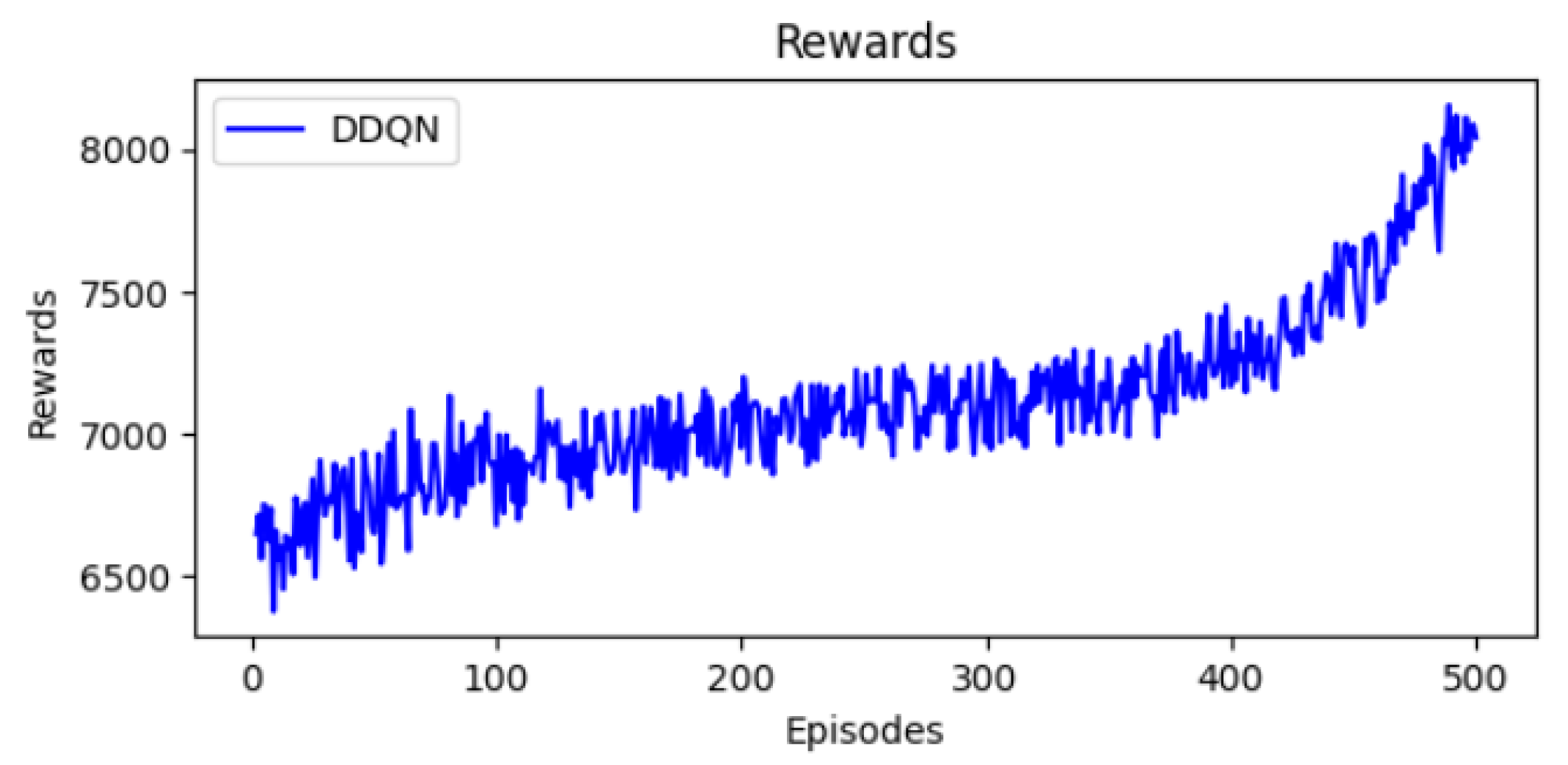
The reward values presented in Figure 7 show a clear evolution from initial to final episodes. The DDQN agent is able to maximize rewards compared to the DQN agent. While moving from exploration to exploitation, the agent is able to learn and select an optimal schedule. The ability of DDQN to achieve higher rewards improves the network performance and the efficiency of packet transmission.

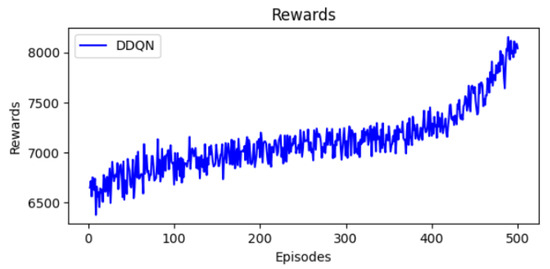
Figure 7. Evolution of rewards.

11.3. Evolution of Packet Delivery Ratio

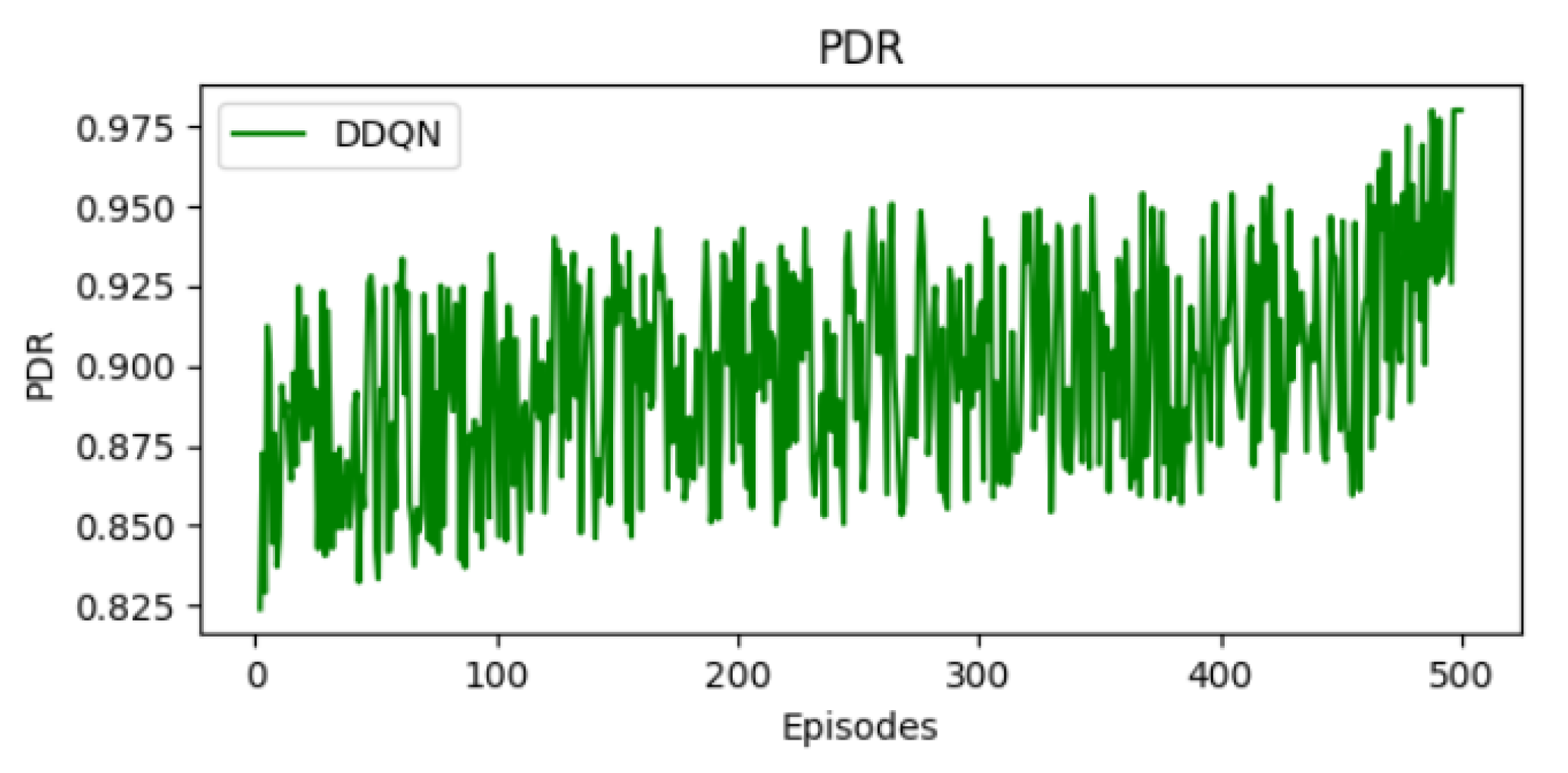
As training progresses, the PDR described in Figure 8 exhibits a gradual upward trend, reaching up to 97% in the final episodes. While the curve presents fluctuations due to the exploration process and environmental dynamics, a general improvement in PDR is observed over time. The DDQN agent learns to prioritize slots with lower interference and reduced packet loss. Despite some variance, the PDR values commonly center around 90%, reflecting the agent’s ability to converge toward an effective and robust scheduling policy that enhances network performance.

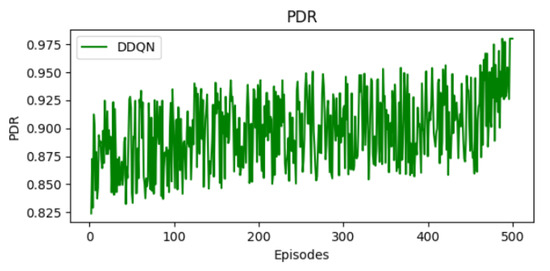
Figure 8. Evolution of PDR.

As outlined earlier, the epsilon value decreases progressively throughout the training (Figure 9). This indicates a transition from an exploration phase to an exploitation phase. After testing different actions in the first phase, the agent relies on the learned strategies and applies them to optimize performance.

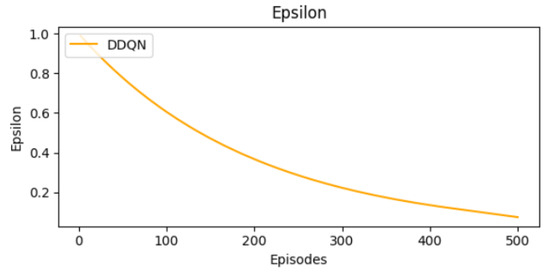
Figure 9. Epsilon decay curve.

12. Analysis of PER-DQN Effectiveness in TSCH

12.1. PER-DQN Performance Metrics

In this part, we evaluate the performance of applying the deep Q-network (DQN) enhanced with prioritized experience replay (PER) to the time-slotted channel hopping (TSCH) protocol. We focus on the same metrics: rewards, epsilon values, and packet delivery ratio (PDR).

12.2. Evolution of Rewards

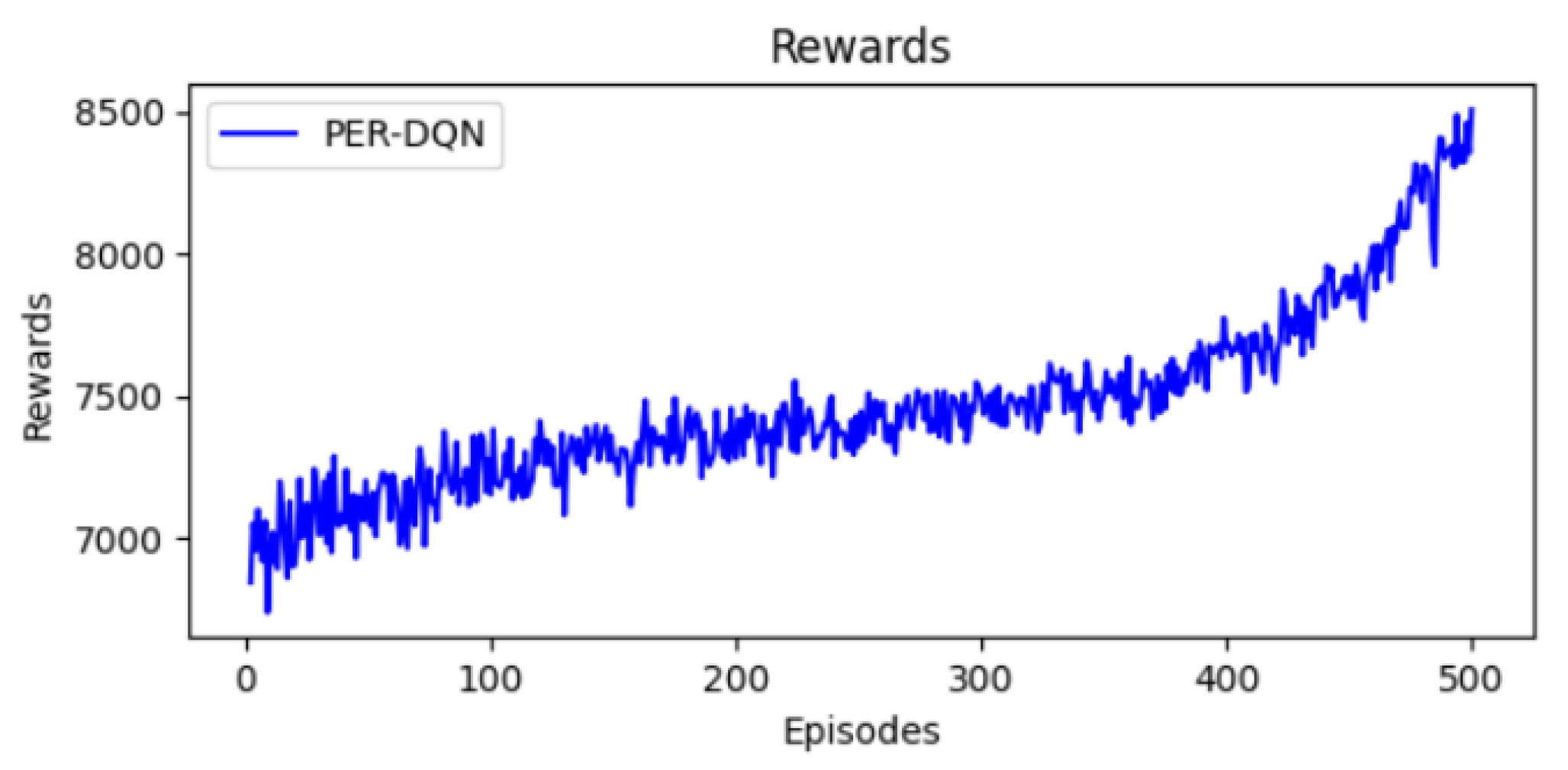
As shown in Figure 10, the reward progression in PER-DQN shows a steady improvement throughout training. Initially, rewards fluctuate around 7000, reflecting the model’s early exploration phase. As training advances, rewards increase to approximately 7500 by mid-training and eventually peak at 8500 in the final episodes. This consistent growth suggests that PER-DQN effectively optimizes scheduling decisions, leading to better network performance. Unlike traditional DQN and double DQN, the use of prioritized experience replay allows the model to focus on crucial experiences, accelerating learning and reducing suboptimal decisions.

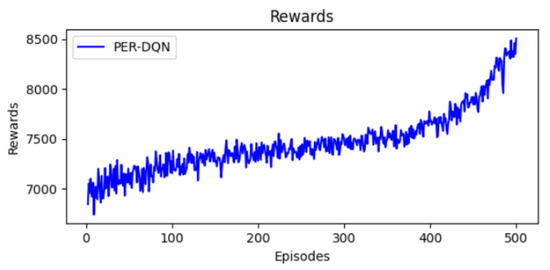
Figure 10. Evolution of rewards.

12.3. Packet Delivery Ratio (PDR) Trends

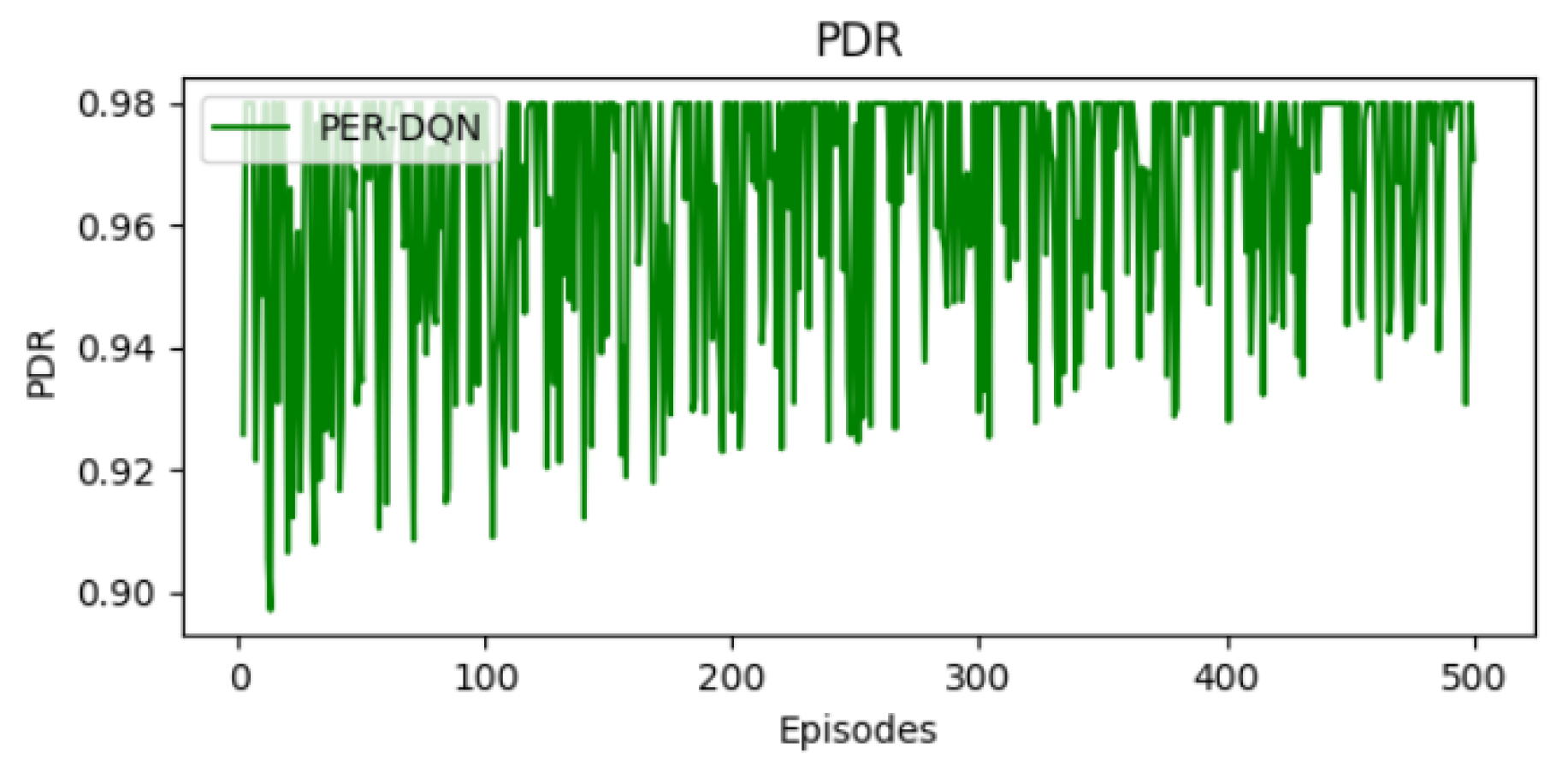
Figure 11 illustrates that the PDR begins at approximately 0.93, reflecting a relatively high initial transmission success rate. As training progresses, the PDR stabilizes with occasional variations. By the final episodes, the PDR reaches 0.98, demonstrating a significant improvement in packet transmission reliability. Although the PDR curve shows some fluctuations during training, this is expected in reinforcement learning due to the exploration mechanism and the stochastic nature of the environment. The agent continues to explore different actions to improve its performance, which can occasionally result in lower PDR values. However, the overall trend remains high—mostly above 96%, indicating that the agent has learned an effective policy. These fluctuations do not reflect instability but are a normal part of the learning process in dynamic environments. Compared to standard DQN, PER-DQN converges to a higher PDR, likely due to its ability to prioritize critical experiences and adapt more effectively to dynamic conditions.

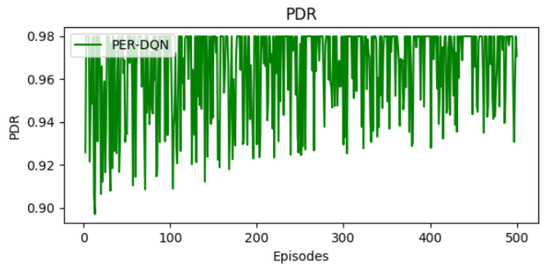
Figure 11. Evolution of PDR.

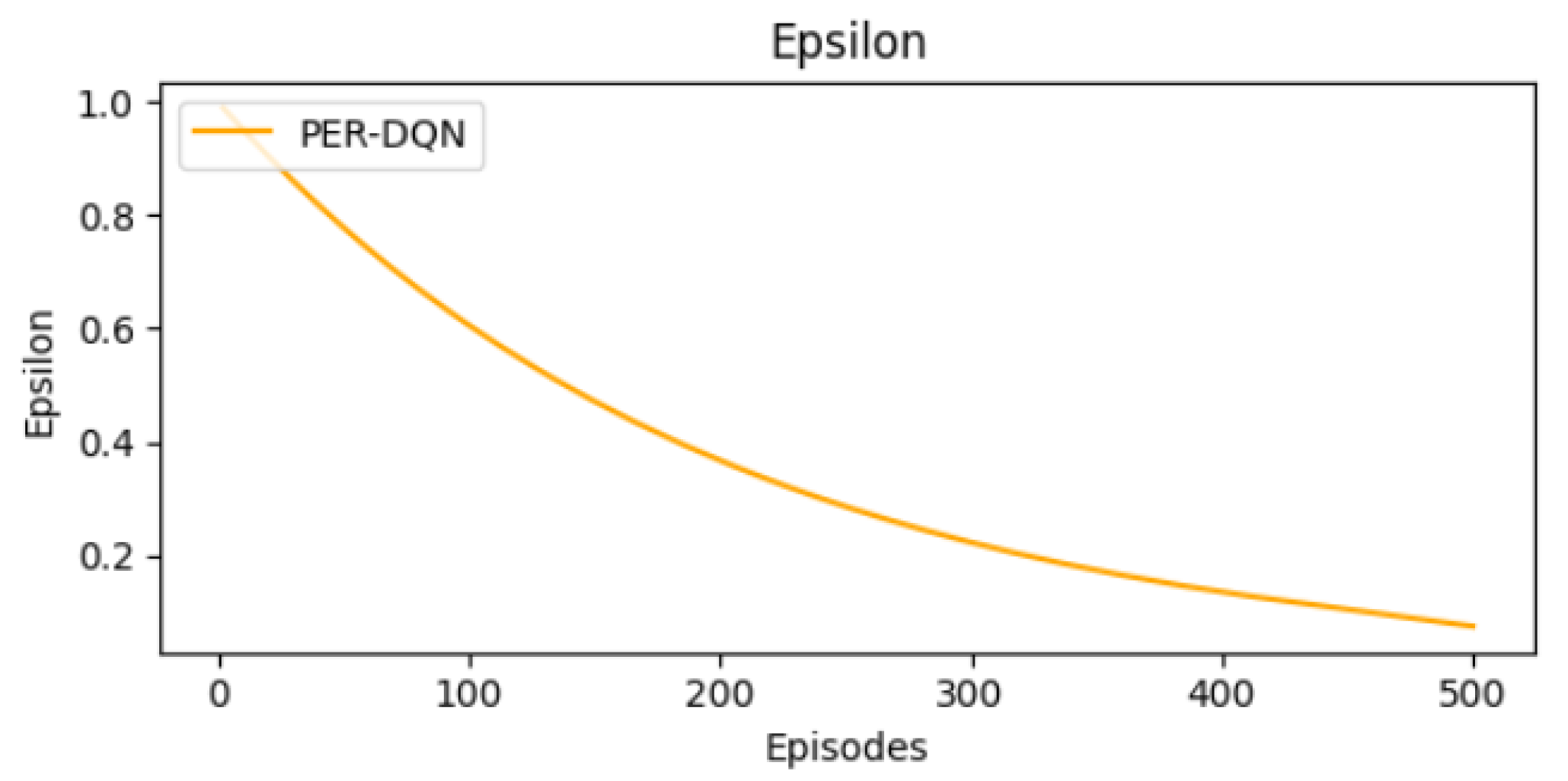
The shift from exploration to exploitation is described in Figure 12. Epsilon values follow a typical pattern. They start at 0.995 and decrease to 0 in the final episodes.

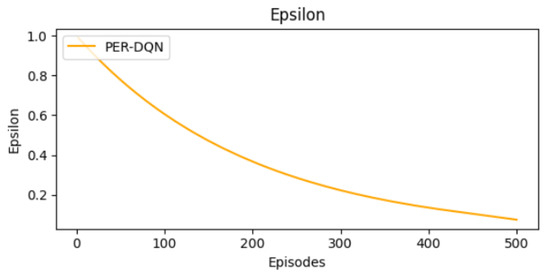
Figure 12. Epsilon decay curve.

13. Discussion and Interpretation of Results

Our simulations outline the advantages of using reinforcement learning in TSCH environments. RL is a promising technique for scheduling in industrial Internet of Things applications.

The results indicate that all RL algorithms ensure good learning efficiency and convergence. However, the prioritized DQN, compared to the DQN and the double DQN, converges faster and presents the best performance. Thus, PER-DQN is well suited for industrial applications that require rapid decision-making and scheduling to manage processes efficiently, often in real time.

14. Conclusions

In this paper, we evaluated the performance of reinforcement learning mechanisms to optimize scheduling in TSCH-based networks. We applied deep Q-learning (DQN), double DQN, and prioritized DQN (PDQN) in a TSCH environment. Through simulations, we proved that all reinforcement learning mechanisms minimize interference and improve the packet delivery ratio under varying network conditions. By leveraging DQN, double DQN, and PDQN, the RL agent learns optimal frequency channel allocation policies. Adaptative scheduling decisions help to enhance fiability and network performance.

The obtained results indicate that applying prioritized DQN guarantees faster convergence. Moreover, PER-DQN results in the best performance compared to other RL techniques due to replaying experiences with higher TD-error. Thus, the RL agent is able to optimize its scheduling decisions by prioritizing the most significant experiences.

While the proposed approaches show promising results, future contributions may extend the models to consider more complex network topologies. We also plan to investigate dynamic traffic patterns with varying packet generation rates and bursty behavior, as well as advanced interference scenarios involving cross-technology interference and multi-channel contention. In addition, we aim to adapt the current RL models by refining the state representation and reward formulation to better capture these complexities. Finally, we plan to validate the proposed methods in real environments through experimental tests on IoT platforms to assess their practical applicability.