Abstract
The exponential growth of multi-modal data in the real world poses significant challenges to efficient retrieval, and traditional single-modal methods are no longer suitable for the growth of multi-modal data. To address this issue, hashing retrieval methods play an important role in cross-modal retrieval tasks when referring to a large amount of multi-modal data. However, effectively embedding multi-modal data into a common low-dimensional Hamming space remains challenging. A critical issue is that feature redundancies in existing methods lead to suboptimal hash codes, severely degrading retrieval performance; yet, selecting optimal features remains an open problem in deep cross-modal hashing. In this paper, we propose an end-to-end approach, named Robust Supervised Deep Discrete Hashing (RSDDH), which can accomplish feature learning and hashing learning simultaneously. RSDDH has a hybrid deep architecture consisting of a convolutional neural network and a multilayer perceptron adaptively learning modality-specific representations. Moreover, it utilizes a non-redundant feature selection strategy to select optimal features for generating discriminative hash codes. Furthermore, it employs a direct discrete hashing scheme (SVDDH) to solve the binary constraint optimization problem without relaxation, fully preserving the intrinsic properties of hash codes. Additionally, RSDDH employs inter-modal and intra-modal consistency preservation strategies to reduce the gap between modalities and improve the discriminability of learned Hamming space. Extensive experiments on four benchmark datasets demonstrate that RSDDH significantly outperforms state-of-the-art cross-modal hashing methods.
1. Introduction
Single-modality tasks have already demonstrated very satisfactory results, such as Image Tagging [1], Document Summarization [2], and Keyword Tagging [3]. However, with the development of technology, real-world data is increasingly showing a trend of multi-modal development. For example, in social networks such as Flickr and Facebook, users may record events by images and associated texts. Multi-modal data have been rapidly increasing following the fast development of techniques during the past few years. Cross-modal retrieval aims to take the data of one modality as a query and retrieve relevant data of another modality, such as using an image to search relevant text documents or using text to search relevant images. In recent years, cross-modal retrieval has attracted increasing attention and has been extensively studied in many application fields. And a number of cross-modal retrieval methods have been proposed. For example, canonical correlation analysis [4] and partial least squares regression [5,6] are popular cross-modal retrieval methods.
Considering the efficiency of cross-modal retrieval, hashing has recently been paid more and more attention from the approximate nearest neighbor research community [7] due to its low storage cost and fast retrieval speed. The goal of hashing is to map the data points from original space into a Hamming space of binary hash codes, where the similarity in the original space is preserved in the Hamming space. A great number of methods based on hashing have been proposed to perform cross-modal retrieval tasks. For instance, by extending spectral hashing [8] to multi-modal data, cross-view hashing [9] and inter-media hashing [10] have been proposed to accomplish cross-modal retrieval.
Although existing hashing methods have made contributions to effectively and efficiently perform cross-modal retrieval tasks, the retrieval performance of most of them is still far from satisfactory. One reason may be that those methods usually employ traditional hand-crafted feature representations for cross-modal retrieval. For example, local binary patterns (LBPs), scale-invariant feature transform (SIFT) and histogram of oriented gradients (HOG) are usually used for depicting image features. As for text, latent Dirichlet allocation (LDA), the replicated softmax model (RSM) and bag of words (BoW) are typically used for describing text features. However, those hand-crafted features are not universal for different cross-modal retrieval tasks. As a result, the achieved cross-modal retrieval performance is usually dissatisfactory. Another reason for the dissatisfactory retrieval performance may be that most of those methods are based on shallow architectures which cannot thoroughly exploit useful information for specific cross-modal retrieval tasks.
1.1. Motivation
Recently, deep learning has proved its powerful learning capacity and has been successfully applied in different applications [11,12]. A few cross-modal retrieval methods based on deep learning have also been proposed [7,13,14,15,16,17]. Those methods have shown that deep learning-based cross-modal retrieval methods can exploit useful information more effectively than shallow architecture-based learning methods. In this paper, we mainly focus on formulating an end-to-end cross-modal hashing retrieval model with deep learning architecture, and anticipate that the learned deep learning features can be optimally compatible with specific cross-modal retrieval tasks. Simultaneously, we expect that heterogeneous correlations of multi-modal data can be effectively exploited for conducting cross-modal retrieval.
Furthermore, in each modality, the discriminant capabilities of different types of features are different, and there might be redundancies in those features. For existing cross-modal hashing retrieval methods, without employing a feature selection strategy, suboptimal binary hash codes might be generated. In particular, for existing deep cross-modal hashing retrieval methods, although the learned deep features and specific cross-modal retrieval tasks are highly compatible, more appropriate and non-redundant features also might not be selected for generating binary hash codes. It is necessary to select suitable and non-redundant features for generating optimal hash codes to effectively perform cross-modal retrieval. How to conduct feature selection in end-to-end deep cross-modal hashing retrieval is another main concern addressed in this paper.
Moreover, existing deep cross-modal hashing retrieval methods have demonstrated that they can always achieve promising cross-modal retrieval performance [7,18]. Unfortunately, since binary hash code learning is essentially a discrete learning problem, it cannot be solved easily. A number of existing hashing methods solve the discrete learning problem by conducting a relaxation for the discrete constraint and transforming the problem into a continuous learning problem [19,20]. In this way, although the discrete learning problem can be solved easily, the relaxation procedure may adversely affect the learned binary hash codes. In this paper, we also formulate the cross-modal retrieval problem as a discrete hash code learning problem. How to directly solve the discrete learning problem in our cross-modal hashing approach is also our concern in this paper.
1.2. Contribution
In this paper, we make efforts to address the issues stated above. The main contributions of our study are summarized as the following four points:
(1) To effectively and fully exploit useful information, we design an end-to-end deep cross-modal hashing model by simultaneously employing intra-modal and inter-modal consistency preservation strategies. On the one hand, the deep learning architecture of the model can make the learned features optimally compatible with specific cross-modal retrieval tasks. On the other hand, heterogeneous correlations can be effectively exploited to reduce the gap between modalities by the inter-modal consistency preservation strategy, and the intra-modal consistency preservation strategy can improve the discriminability of learned Hamming space.
(2) Aiming to select discriminative and non-redundant features in our end-to-end deep cross-modal hashing model, we design a non-redundant feature selection strategy based on spectral regression with regularization. With the feature selection strategy, robust and discriminative features with minimum redundancy can be selected for generating binary hash codes with more discriminability to effectively improve cross-modal retrieval performance. To the best of our knowledge, the non-redundant feature selection problem has not been studied in existing deep cross-modal hashing retrieval methods.
(3) To directly solve the discrete learning problem in our cross-modal hashing approach, a discrete hashing scheme called Singular Value Decomposition-based Discrete Hashing (SVDDH) is proposed to obtain better binary hash codes for enhancing the performance of cross-modal retrieval.
(4) Experimental results on three widely used datasets demonstrate that our proposed approach can achieve superior cross-modal retrieval performance to the state-of-the-art methods.
1.3. Organization
The rest of the paper is organized as follows. In Section 2, we briefly review the related work. Section 3 details our RSDDH approach. The optimization of RSDDH is given in Section 4. In Section 5, experimental results are reported. Section 6 provides a further discussion and analysis. And conclusions are drawn in Section 7.
2. Related Work
2.1. Deep Learning
During the past several years, a large number of deep learning methods have been proposed [12,21,22,23,24,25,26,27,28,29], and some of them have been successfully applied in different applications. For instance, Lecun et al. [30] proposed a convolutional neural network (CNN) structure to deal with handwritten digit recognition. AlexNet proposed in [23] achieved superior image classification performance on the ImageNet large-scale visual recognition challenge. Jia et al. [31] provided a CaffeNet implementation of deep convolutional neural networks (CNNs). For natural language processing, a number of deep learning methods were also proposed. For example, Graves et al. [11] proposed a deep learning model based on deep recurrent neural networks for speech recognition. And the multilayer perceptron (MLP) [32] is also a widely used deep learning model in natural language processing.
2.2. Shallow Cross-Modal Hashing
Hashing is a promising solution to the cross-modal retrieval problem due to its efficiency of searching in large-scale multi-modal datasets [33]. According to whether semantic labels are used or not, existing shallow cross-modal hashing methods can be categorized into unsupervised methods and supervised methods. Unsupervised methods generally utilize only the features of training data in different modalities to exploit intra-modality and inter-modality correlations for learning hash functions that project features from original modality spaces into Hamming spaces. For example, Liu et al. [34] proposed a fusion similarity hashing method, which explicitly embeds the graph-based fusion similarity across modalities into a common Hamming space. Ding et al. [35] proposed a collective matrix factorization hashing (CMFH) method, which learns unified hash codes by collective matrix factorization with a latent factor model from different modalities of one instance. Wang et al. [36] proposed a semantic-rebased cross-modal hashing method, which utilizes sparse graph structures to exploit similarity information to address the degradation problem. Wang et al. presented a robust and flexible discrete hashing method and semantic topic multi-modal hashing method in [37].
Supervised cross-modal hashing methods aim to further distill cross-modal correlation and reduce semantic gaps by exploiting available supervised information like semantic labels or semantic affinities of training data [38]. For example, based on collective matrix factorization, Tang et al. [39] proposed supervised matrix factorization hashing (SMFH) to learn unified hash codes for different modalities of an instance, which considers both the label consistency across different modalities and the local geometric consistency in each modality. Wang et al. [40] proposed a label-consistent matrix factorization hashing method which focuses on directly utilizing semantic labels to guide the hashing learning procedure. To preserve label separability, kernel discriminant analysis is used to enrich the discrimination ability of learned binary codes [41]. Shen et al. [42] proposed a method exploiting subspace relation, which exploits relation information of labels in semantic space to make similar data from different modalities closer in the low-dimensional Hamming subspace. Zhang and Li [43] proposed semantic correlation maximization (SCM) to seamlessly integrate semantic labels into a hashing learning procedure for large-scale data modeling, which utilizes all supervised information for training with linear-time complexity by avoiding explicitly computing the pairwise similarity matrix. Mandal et al. [44] proposed a generalized semantic preserving hashing method, which can work in single-label, multi-label, and both paired and unpaired scenarios while preserving the semantic similarity between data points. Meng et al. [45] proposed an asymmetric, supervised, consistent and specific hashing method, which explicitly decomposes the mapping matrices into consistent and modality-specific ones to sufficiently exploit the intrinsic correlation between different modalities. Song et al. [46] proposed Deep Self-Enhanced Hashing (DSEH), which simultaneously preserves the multi-level semantic similarity of known multi-label data while learning OOD-robust hash codes through bounded cosine quadruplet loss that explicitly constrains distances between known and pseudo-OOD samples in Hamming space.
2.3. Deep Cross-Modal Hashing
Some existing deep learning methods for multi-modal embedding [47,48] have proven that deep learning can discover useful information more effectively than shallow learning methods. Inspired by those works, a few deep cross-modal hashing methods were proposed for the cross-modal retrieval problem. For example, Ma et al. [49] proposed a multi-level correlation adversarial hashing method to integrate multi-level correlation information into hash codes. Xie et al. [50] proposed a multi-task consistency-preserving adversarial hashing method, in which a multi-task adversarial learning module is used to make modality-common representations of different modalities close to each other in feature distribution and semantic consistency. Jiang et al. [7] formulated an end-to-end deep learning framework, which preserves cross-modal similarity by minimizing a negative log likelihood. Wu et al. [51] proposed a deep generative method to learn hash functions in the absence of paired training samples through cycle consistency loss. Cao et al. [18] proposed a collective deep quantization (CDQ) approach, which attempts to introduce quantization in an end-to-end deep architecture for cross-modal retrieval. Yang et al. [52] proposed a deep cross-modal hashing method named pairwise relationship-guided deep hashing (PRDH), which integrates different types of pairwise constraints to determine the similarities of the hash codes from an intra-modal view and an inter-modal view, respectively. Liong et al. [53] proposed a cross-modal deep variational hashing (CMDVH) method to obtain unified binary hash codes for image and text modalities. Deng et al. [54] proposed a triplet-based deep hashing network that utilizes triplet labels for cross-modal retrieval.
In this paper, we propose a deep cross-modal hashing approach termed Robust Supervised Deep Discrete Hashing (RSDDH) for cross-modal retrieval. RSDDH is an end-to-end deep learning architecture seamlessly integrating deep feature learning and hash code learning. In the learning process, deep feature learning can give feedback to hash code learning and vice versa. RSDDH can adaptively learn optimal feature representations for specific tasks via the deep learning architecture. The inter-modal consistency preservation strategy used in RSDDH can capture the heterogeneous correlations across different modalities to reduce the gap between them. In RSDDH, the intra-modal consistency preservation strategy can enhance the discriminability of the learned Hamming space. Additionally, RSDDH can select robust and discriminative features with minimum redundancy to generate superior binary hash codes. Figure 1 illustrates the overall framework of our proposed approach, RSDDH.
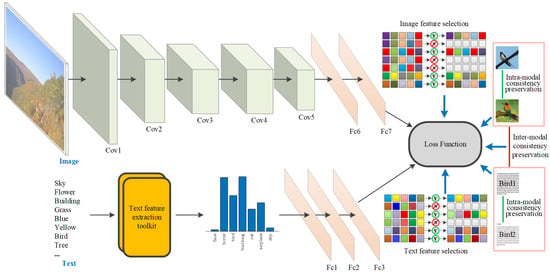
Figure 1.
Overall framework of our proposed approach, RSDDH. The deep neural networks for image and text modalities can make the learned deep features (i.e., the output of Fc3 and Fc7) be optimally compatible. By employing the formulated feature selection strategies for image and text modalities, discriminative features with minimum redundancy can be selected from the learned deep features to generate binary hash codes. The intra-modal consistency preservation strategy can improve the discriminability of learned Hamming space. The inter-modal consistency preservation strategy can reduce the gap between modalities in learned Hamming spaces of image and text modalities. The loss function of RSDDH is formulated according to the aforementioned strategies.
3. Robust Supervised Deep Discrete Hashing
3.1. Symbol Definition and Problem Formulation
Suppose that we have n training instances with image–text pairs denoted by , where denotes raw pixels of the n training instances in the image modality. Moreover, denotes features of the n training instances in the text modality, where is typically the tag information related to the image of the ith training instance. We denote the class label information corresponding to the n training instances by , where c is the class number. For the class label vector , if the ith instance belongs to the kth class, then the kth element of the vector is 1. Otherwise, the kth element of the vector is 0.
The goal of our RSDDH approach is to learn binary hash codes and for training instances in the image modality and text modality, respectively. For out-of-sample instances, RSDDH learns hash functions and for the image modality and text modality, respectively. In this paper, we utilize commonly used linear hash functions. Then, the hash functions in image and text modalities are respectively defined as and , where is an element-wise sign function, and denotes the transpose of a matrix. and are the deep learning features of one training instance in image and text modalities. and are the network parameters of the deep neural networks for the image modality and text modality, respectively. and are linear projection matrices that map the deep learning features and to latent spaces. Table 1 tabulates important symbols of the paper and their definition.

Table 1.
List of important symbols.
3.2. Feature Learning
3.2.1. Image Feature Learning
The deep neural network (DNN) for the image modality is a CNN adapted from AlexNet [23] with seven layers. For the CNN model, we make the first six layers the same as those in the AlexNet model. And we employ a fully connected layer as the last layer with the output of this layer being the learned image features. The details of each layer are tabulated in Table 2.

Table 2.
Configurationof the CNN for image modality.
In the CNN for the image modality, seven layers are divided into five convolutional layers and two fully connected layers, which are denoted as “Conv1-Conv5” and “Fc6-Fc7”, respectively. The images are fed into the CNN as input. ReLU (Rectified Linear Unit) is utilized as the nonlinear activation function for the first six layers. For the layer Fc6, dropout is applied with a rate of 0.5 to prevent overfitting. The output features of Fc6 are fed to the fully connected layer Fc7, which has neurons. And hyperbolic tangent (TanH) is employed as the activation function of the last layer Fc7. Finally, the features of size corresponding to the input images are obtained. Using RELU as the activation function does not require exponential operations, which accelerates the convergence of training and avoids the vanishing gradient problem. It is the best choice to balance our retrieval performance and efficiency.
3.2.2. Text Feature Learning
Since text features are usually more discriminative than image features, the relationship between text features and their semantics can be more easily built. We adopt the multilayer perceptron (MLP) [32] comprising three fully connected layers to construct an MLP DNN to map text features from original feature space into semantic space. And the three fully connected layers are denoted as Fc1, Fc2 and Fc3, respectively. Similar to the fully connected layers of the text modality in [7], ReLU is utilized as the nonlinear activation function for the first two fully connected layers. And hyperbolic tangent (TanH) is employed as the activation function of the last layer Fc3. The dimension of the text DNN is ; in other words, there are neurons in the last layer of the text DNN. The detailed configuration of the MLP DNN for the text modality is shown in Table 3.

Table 3.
Configurationof the DNN for text modality.
It is worth mentioning that other DNNs might also be employed to conduct feature learning for deep cross-modal retrieval in this paper, which will be left for future study.
3.3. Hash Code Learning
For the ith instance , let denote the learned image feature which corresponds to the output of the DNN for the image modality. denotes the deep learning feature matrix of the training instances in the image modality with the ith column vector being . Furthermore, let denote the learned text features which correspond to the output of the MLP DNN for the text modality. represents the deep learning feature matrix of the n training instances in the text modality with the ith column vector being .
3.3.1. Deep Hash Code Learning with Non-Redundant Feature Selection Strategy
Assume that the projected deep learning features and of the ith training instance in image and text modalities can produce binary hash codes and in Hamming spaces, respectively. In general, image and text modalities contain redundant features. It is beneficial to minimize the redundancy among the features in the image modality and text modality. Inspired by the theory of spectral feature selection [55], we formulate a non-redundant feature selection strategy based on spectral regression with -norm regularization for conducting feature selection in both the image modality and text modality. Then, we formulate the following optimization problem to obtain binary hash codes for the instances in image and text modalities:
where , and are non-negative trade-off parameters, 1 represents a vector with all elements being 1, and respectively denote the Frobenius norm and -norm of a matrix [56]. Following the reference [55], and are obtained based on two similarity matrices and singular value decomposition, where and .
The first and third terms of in Equation (1) are the quantization errors in the image modality and text modality, respectively. The terms and in Equation (1) are employed to make each bit of binary hash code balanced on all the training instances. More specifically, the numbers of +1 and −1for each bit on all the training instances should be almost the same. This constraint can be used to maximize the information provided by each bit.
The terms and in Equation (1) are respectively formulated to select discriminative and non-redundant features from the image modality and text modality to generate binary hash codes with more discriminability. For the -norm based regularization terms and in the above-stated two terms, when they are applied together with regression, they can select features across all data points with joint sparsity, i.e., each feature either has small scores for all data points or large scores over all data points [57]. We call the above-stated feature selection strategy as the non-redundant feature selection strategy in our RSDDH approach.
3.3.2. Intra-Modal Consistency Preservation
Intra-modal similarity can reflect the neighborhood relationships among feature vectors in each modality. The intra-modal similarity of two feature vectors and in the image modality can be defined as follows:
where denotes the set of -nearest neighbors of the feature data point . Similarly, the intra-modal similarity of two feature vectors and in the text modality can be defined as follows:
where denotes the set of -nearest neighbors of the feature data point .
To preserve the intra-modal consistency of each modality between original feature space and Hamming space, we formulate the minimization problem as follows:
Overall, by conducting intra-modal consistency preservation, i.e., by ensuring that the neighborhood structure of each data point in original space can be well preserved in Hamming space, we can improve the discriminability of learned Hamming space.
3.3.3. Inter-Modal Consistency Preservation
By using label information, we can define the semantic affinity matrix of feature vectors from the image modality and from the text modality as follows:
To clarify, we consider and to have the same semantics if shares at least one label with , i.e., is satisfied. To preserve inter-modal consistency between the image modality and text modality in Hamming spaces, we formulate the minimization problem as follows:
In short, performing inter-modal consistency preservation can effectively exploit the heterogeneous correlations across the image modality and text modality and reduce the gap between the two modalities in Hamming spaces.
3.4. Overall Objective Function
According to the above analysis, the overall objective function of our RSDDH approach can be formulated as follows:
Existing works demonstrate that if data described in different modal spaces have the same semantics, they are expected to have the same common latent space [9,58]. In this paper, we assume that the instances in image and text modalities with the same semantics are eventually represented by the same binary hash codes in a low-dimensional common Hamming space. Then, we set . Further, the problem in Equation (7) can be transformed to the following problem:
where
Through a simple derivation, can be rewritten as follows:
where . can be reformulated as
where is Laplacian matrix, D is diagonal matrix with the ith diagonal element being , W is a matrix with the element of the ith row and jth column being , and is the matrix trace operator. Combining Equations (12) and (13), Equation (8) can be rewritten as follows:
4. Optimization
To the best of our knowledge, the objective function in Equation (14) is not jointly convex over all variables B, , , and . We adopt an alternating optimization strategy to solve the unknown variables [7,37,40,52,59]. In other words, we update one variable with the other variables fixed each time.
4.1. Update of Image Modality with B, , and Fixed
When B, , and are fixed, we learn the DNN parameter of the image modality by using a back-propagation (BP) algorithm. As most existing deep learning methods [23], we utilize stochastic gradient descent (SGD) with the BP algorithm to learn . More specifically, in each iteration, we sample a mini-batch of instances from the training instance set, and then carry out our learning algorithm based on the sampled instances.
Concretely, for each image feature data point of the sampled instances, we first compute the following gradient:
Then we can compute with by using the chain rule, based on which BP can be used to update the parameter . Algorithm 1 displays the algorithm for obtaining the DNN parameter .
| Algorithm 1 Algorithm for obtaining DNN parameter . |
Input: image feature matrix v, projection matrix , binary hash code matrix B, mini-batch size , and iteration number . Output: DNN parameter . 1: Initialize DNN parameter; 2: for do; 3: Randomly sample feature vectors from v to construct a mini-batch; 4: For each sampled point in the mini-batch, calculate by forward propagation; 5: Calculate the derivative according to Equation (15); 6: Update the DNN parameter by using back propagation; 7: end for |
4.2. Update of Text Modality with B, , and Fixed
When B, , and are fixed, we also learn the DNN parameter of the text modality by using SGD with a BP algorithm. More specifically, for each text feature data point of the sampled instances, we first compute the following gradient:
Then we can compute with by using the chain rule, based on which BP can be used to update the parameter . We employ an algorithm similar to Algorithm 1 to obtain DNN parameter .
4.3. Update with B, , and Fixed
When B, , and are fixed, the problem in Equation (14) is reformulated as follows:
We propose an iterative algorithm based on the half-quadratic minimization [56,60,61] to solve the objective function in Equation (17).
The minimization problem in Equation (17) can be reformulated as follows:
In Equation (18), is a diagonal matrix with the ith diagonal element being
where is a smoothing term, which is usually set to a small constant value [62].
By differentiating the objective function in Equation (18) with respect to and setting the derivative of to zero, we obtain
Through a simple derivation, we have
where denotes the inverse of a matrix.
Since the problem in Equation (18) is a convex problem, is a global optimum solution to the problem if and only if Equation (21) is satisfied. Note that is dependent on and is also an unknown variable. In this paper, we employ an iterative algorithm to obtain the solution such that Equation (21) is satisfied. It can be proved that the iterative algorithm will converge to the global optimum [57]. Algorithm 2 briefly illustrates the iterative algorithm for solving projection matrix .
| Algorithm 2 The iterative algorithm for solving projection matrix . |
Input: features F, binary hash code matrix B, maximum iteration number , threshold . Output: projection matrix . 1: Initialize ; 2: for do; 3: Compute according to Equation (19) and construct diagonal matrix ; 4: Compute ; 5: if then 6: break 7: end if 8: end for |
4.4. Update with B, , and Fixed
When B, , and are fixed, the problem in Equation (14) is reformulated as follows:
Similar to the optimization for solving
, we can achieve
where is a diagonal matrix with the ith diagonal element being . Then, we solve by using an algorithm similar to Algorithm 2.
4.5. Update B with , , and Fixed
4.5.1. Objective Function Reformulation
When , , and are fixed, the problem in Equation (14) is reformulated as follows:
By conducting a simple derivation for Equation (24), we have
Since , , and are fixed, and are constant terms. They can be ignored as they do not affect the optimization of B. Due to , it can be known that . Then, the term can also be omitted. By dropping the constant terms, Equation (25) can be reformulated as follows:
where . It can be seen that the Q incorporates the feature information from both image and text modalities.
4.5.2. Singular Value Decomposition-Based Discrete Hashing
Due to the discrete constraint, it is hard to directly solve the objective function in Equation (26) to obtain the solution of the unknown binary hash code matrix B. Inspired by the discrete cyclic coordinate descent method [63], we propose a Singular Value Decomposition-based Discrete Hashing (SVDDH) scheme to solve the unknown discrete variable B.
We can obtain by conducting singular value decomposition [64] for matrix L. Then, Equation (26) can be rewritten as follows:
Through a simple derivation, we have
where , and respectively denote the ith row of B, and ; , and represent all other rows in B, and excluding , and respectively; denotes the ith column of Q; represents all other columns in Q excluding .
According to Equations (28) and (29), the solution of the unknown variable B in Equation (27) can be obtained by solving the problem with respect to as follows:
Through a simple derivation, the problem in Equation (30) can be transformed to the optimization problem as follows:
The problem in Equation (31) has a closed-form solution as follows:
Algorithm 3 briefly summarizes the procedures of SVDDH.
| Algorithm 3 SVDDH scheme. |
Input: deep learning feature matrices F and G, projection matrices and , Laplacian matrix L. Output: binary hash code matrix B=. 1: Compute ; 2: Obtain , and ∑ by conducting SVD for matrix L; 3: for do 4: Obtain , and from , and Q, respectively; 5: Obtain , and from B, and , respectively; 6: Compute according to Equation (32); 7: end for |
4.6. Complexity Analysis
In this subsection, we detail the time complexity of our RSDDH approach. The objective function of RSDDH is optimized by iteratively updating five different variables. In the training phase, the time complexity of each iteration is + , where N denotes the number of trainable neural network parameters in image and text modalities [65], and are the iteration numbers of the iteration procedures for solving and , respectively.
5. Experiments
5.1. Datasets
We conduct experiments on three widely used multi-modal datasets, i.e.,Wiki [66], MIRFlickr [67], NUS-WIDE [68] and MSCOCO [69] datasets, to evaluate the performance of our RSDDH approach.
The Wikidataset [66] contains 2866 pairs of images and documents from 10 categories. The dataset was randomly split into a training set of 2173 image–document pairs and a query set of the remaining 693 image–document pairs. Each document associated with the corresponding image consists of several paragraphs, resulting in at least 70 words. For each image, a 128-dimensional SIFT bag-of-visual words (BoVW) vector is used to feed the hand-crafted feature-based methods. For texts, following the practices in [13] and [70], each instance in the text modality is represented by a 3000-dimensional bag of words (BoW) vector.
The MIRFlickr dataset [67] is a real-word dataset originally containing 25,000 instances collected from the Flickr website, each being an image with its associated textual tags. For each instance, i.e., each image–tag pair, it is annotated with at least 1 of 24 provided semantic categories. Following the pretreatment in [7], we select those instances which have at least 20 textual tags for our experiment. We randomly select 10,000 instances to construct a training set, and 1000 instances to construct a query set. The text of each instance in the text modality is represented as a 1386-dimensional BoW vector. For the hand-crafted feature-based methods, each image is represented by a 512-dimensional GIST feature vector.
The NUS-WIDE dataset [68] is a web image dataset downloaded from Flickr. The dataset contains images with annotated tags from 81 semantic concepts. Each image with its tag annotations can be taken as an image–text pair. Since some concepts contain scarce image–text pairs, following state-of-the-art work [7], we choose those image–text pairs that belong to the 21 largest concept categories as the experimental data. The selected 21 categories include animal, buildings, clouds, grass, lakes, etc. In the chosen experimental data, we randomly select 100 image–text pairs per category as the query set, and 500 image–text pairs per category as the training set. The text of each instance in the text modality is represented as a 1000-dimensional BoW vector. The hand-crafted feature for each image is a 500-dimensional BoVW vector which is only used for hand-crafted feature methods.
The MSCOCO dataset [69] serves as a broadly adopted benchmark that spans object recognition, multimedia retrieval and semantic segmentation. It aggregates 123,287 real-world images whose objects have been meticulously segmented from complex daily scenes. For our experiments, we retained 87,081 images annotated with 91 concept classes; associated captions were encoded as 2000-dimensional bag of words vectors. From these, 5000 image–caption pairs were randomly designated as queries, and the remainder formed the retrieval pool. A further random subset of 10,000 image–phrase pairs from this pool was chosen for training.
5.2. Evaluation Metrics
We perform two kinds of cross-modal retrieval tasks. One is Img-to-Txt, i.e., using images as a query to retrieve relevant texts. The other is Txt-to-Img, i.e., using texts as queries to retrieve relevant images. We employ two popular metrics, i.e., mean average precision (MAP) and precision–recall, to evaluate the performance of cross-modal retrieval. The larger value of MAP demonstrates the better cross-modal retrieval performance. The precision–recall metric shows the precision at different recall levels, which can be obtained by varying the Hamming radius of the retrieved instances in a certain range and calculating the precision and recall accordingly.
To obtain the MAP, average precision (AP) needs to be computed first. Given a query with a group of retrieved instances, the value of its AP is defined as follows:
where N is the number of relevant instances in the retrieved set, denotes the precision of the top r retrieved instances, of the rth retrieved instance is a truly relevant instance of the query instance, and otherwise . In this paper, for a query, its truly relevant instances are defined as those sharing at least one label with it. Finally, the MAP can be obtained by averaging the APs of all queries in the query set.
5.3. Baseline Methods and Experimental Settings
Baseline Methods. We compare our RSDDH approach with several recently published state-of-the-art cross-modal hashing methods, including three shallow cross-modal hashing methods, i.e.,CMFH [35], SCM [43] and SMFH [39], and four deep cross-modal hashing methods, i.e., CDQ [18], PRDH [52], DCMH [7] and DNPH [71]. For CMFH, SCM, SMFH, CDQ, DCMH and DNPH methods, we use the codes kindly provided by the authors. We carefully implement the PRDH method as its code is not publicly available.
Parameter Settings. For our deep cross-modal hashing approach RSDDH, we use mini-batch SGD with momentum being 0.9 and weight decay being 0.0001. And the mini-batch size is fixed as 128. We employ the AlexNet pre-trained on the ImageNet dataset to initialize the first five layers of the DNN for the image modality. A similar initialization strategy has also been adopted by other deep cross-modal hashing methods [7]. All the other parameters of the DNNs in our RSDDH approach are randomly initialized. For image DNN, we set the learning rate of the last fully connected layer to 0.01. We reduce the learning rate of the remaining layers to 0.0001 to avoid overfitting and destroying the representative abstract features already learned during pre-training. For text DNN, the learning rate of all fully connected layers is set to 0.01. Similar to [53,72], the output dimensions of the image and text DNNs are both set as 2048. The optimal values of three hyper-parameters , and are set by employing cross-validation. We tune the parameters of the other compared methods as suggested in the corresponding studies, and then report the optimal results of them. It is important to point out that all the reported results are averaged over 10 independent trials.
Feature Representation. For the image modality, the raw image pixels are used as the input of those deep cross-modal hashing methods, and the hand-crafted features mentioned in the dataset description are utilized as the input of those shallow cross-modal hashing methods. For the text modality, all the compared methods use BoW vectors of texts as the input.
Software and Hardware Settings.We implemented our RSDDH approach using Python 3.8 and utilized TensorFlow version 1.15.0 for the computations. All the experiments are conducted on a computer which has an Intel(R) Core(TM) i7-7700K 4.20 GHz CPU, NVIDIA TITAN Xp GPU, 128 GB DDR4 RAM and Ubuntu 16.04 64bit operating system. And we use OpenCV 3.2, CUDA 8.0, and cuDNN v5.1 in TensorFlow. For the deep cross-modal hashing methods, we train deep networks on a single NVIDIA TITAN Xp GPU.
5.4. Overall Comparison with Baseline Methods
In this subsection, we compare the cross-modal retrieval performance of our RSDDH approach with that of the other compared methods. We first evaluate the cross-modal retrieval performance of all compared methods by employing MAP. Subsequently, the precision–recall metric is used to further investigate the cross-modal retrieval performance of all compared methods.
Table 4 reports the experimental results with respect to MAP of all compared methods on Wiki, MIRFlickr, NUS-WIDE and MSCOCO datasets at different code lengths. It can be seen from Table 4 that the MAPs of deep cross-modal hashing methods outperform those of shallow cross-modal hashing methods on Wiki and MSCOCO datasets at the four different lengths of binary hash codes. But in some cases, our deep hashing method is at a slight disadvantage to the latest deep hashing methods. The experimental phenomenon illustrates that the deep architecture-based learning model can learn preferable features for generating binary hash codes in cross-modal hashing retrieval. Additionally, the experimental results in Table 4 show that our RSDDH approach outperforms the other deep cross-modal hashing methods in both two cross-modal retrieval tasks on Wiki, MIRFlickr, NUS-WIDE and MSCOCO datasets at all four different code lengths. It indicates that our RSDDH approach can exploit more discriminative features for improving cross-modal retrieval performance.

Table 4.
The MAPs of all compared methods on Wiki, MIRFlickr, NUS-WIDE and MSCOCO datasets.
Figure 2 shows the precision–recall curves of all compared methods on Wiki, MIRFlickr and NUS-WIDE datasets at the code length of 32 bits. We find that our RSDDH approach outperforms the other compared methods in two retrieval tasks on all three datasets. This observation is consistent with the evaluation with regard to MAP for all the compared methods in Table 4. It again demonstrates that our RSDDH approach can exploit more discriminative features for improving cross-modal retrieval performance. Additionally, we find that our RSDDH approach can also achieve the best retrieval performance on other cases with different values of code length such as 16, 64 and 128 bits. For brevity, we omit those experimental results.
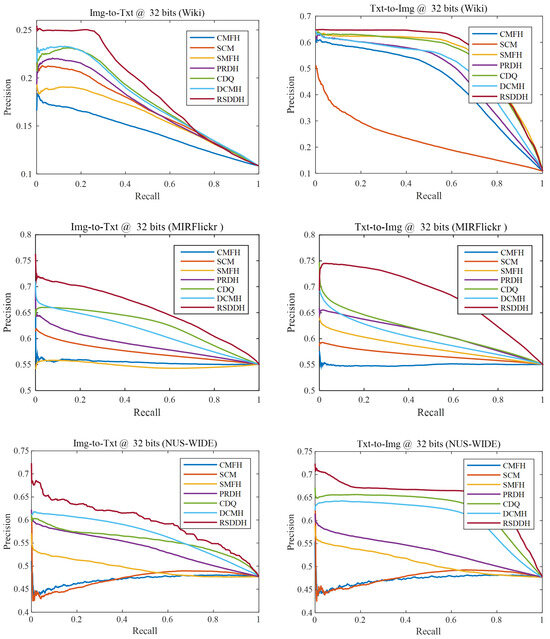
Figure 2.
The precision–recall curves of RSDDH and the other compared methods on Wiki, MIRFlickr and NUS-WIDE datasets.
5.5. Further Comparison with Shallow Learning-Based Baseline Methods
To further verify the effectiveness of our proposed approach RSDDH, we feed deep feature representations into shallow cross-modal hashing retrieval methods, i.e., CMFH, SCM and SMFH methods, to perform cross-modal retrieval. Concretely, for the image modality, we employ the AlexNet pre-trained on the ImageNet dataset, which is the same as the initial DNN of the image modality in our RSDDH approach, to conduct fine-tuning on Wiki, MIRFlickr, NUS-WIDE datasets and MSCOCO datasets, respectively. And then we extract the deep features of each image from the Fc7 layer to feed shallow cross-modal hashing retrieval methods. For the text modality, we utilize ReLU as the nonlinear activation function for the first two fully connected layers, and employ TanH as the activation function of the last layer. Then the output of the last fully connected layer is fed into a softmax, which generates predictive scores (i.e., semantic features) over c classes. And the learning rate for each fully connected layer is set to 0.01 at the beginning and dynamically changed according to the squared loss. The output of the last fully connected layer Fc3 is used as deep feature representations of text. Table 5 summarizes the MAPs of RSDDH, CMFH, SCM and SMFH methods on Wiki, MIRFlickr and NUS-WIDE datasets at different code lengths. It is noticeable that our RSDDH approach outperforms the other methods in two cross-modal retrieval tasks on all three datasets at all four different lengths of hash codes. The experimental phenomenon demonstrates that our end-to-end deep cross-modal hashing approach RSDDH can learn more discriminative features than the other methods even though they are fed with deep feature representations for training cross-modal hashing models.

Table 5.
The MAPs of our RSDDH approach and three shallow hashing methods fed with deep learning features.
6. Discussion
6.1. Effect of Non-Redundant Feature Selection Strategy
In this subsection, we investigate the effectiveness of a non-redundant feature selection strategy in our approach RSDDH. Concretely, we reformulate the objective function by discarding the two feature selection terms of the objective function of RSDDH, obtaining a variant of RSDDH. For convenience, we denote the variant by supervised deep discrete hashing (SDDH). The two feature selection terms are used to select optimal features with minimum redundancy to generate hash codes with more discriminability. Then we evaluate the retrieval performance of SDDH and RSDDH. The performance drop in SDDH (Figure 3) and RDDH (Figure 4) quantitatively reflects the necessity of feature selection and consistency preservation. Figure 3 shows the MAPs of RSDDH and SDDH methods on the MIRFlickr dataset at 16, 32, 64 and 128 bits. We can see that the MAPs of the RSDDH method for Img-to-Txt and Txt-to-Img tasks are both superior to those of the SDDH method for the same tasks, which demonstrates that RSDDH can learn hash codes with higher discriminability than the SDDH method. And it also illustrates that our non-redundant feature selection strategy is beneficial for generating hash codes with more discriminability to effectively accomplish cross-modal retrieval. Similar phenomena also exist in the other two datasets.
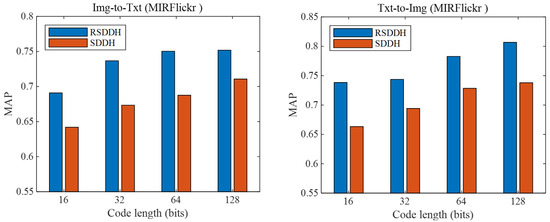
Figure 3.
The MAPs of RSDDH and SDDH methods on the MIRFlickr dataset at different code lengths.
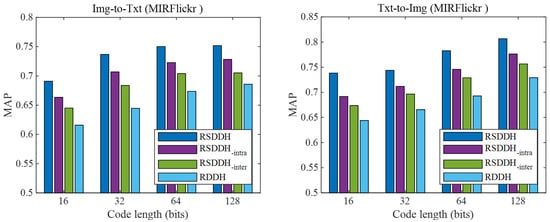
Figure 4.
The MAPs of RSDDH and its three variants on the MIRFlickr dataset at different code lengths.
6.2. Effect of Inter-Modal and Intra-Modal Consistency Preservation Strategies
In this subsection, we investigate the effectiveness of inter-modal and intra-modal consistency preservation strategies in our approach RSDDH. Specifically, we make three variants of RSDDH by abnegating one of the strategies and both of the strategies. The inter-modal consistency preservation strategy is utilized to reduce the gap between modalities. And the intra-modal consistency preservation strategy can enhance the discriminability of learned Hamming space. For convenience, we denote the variant of RSDDH without the inter-modal consistency preservation strategy by RSDDH-Inter. And RSDDH-Intra represents the variant of RSDDH without the intra-modal consistency preservation strategy. The variant of RSDDH without both inter-modal and intra-modal consistency preservation strategies is denoted as RDDH. We evaluate the effectiveness of the consistency preservation strategies according to the MAPs of RSDDH and its three variants. Figure 4 shows the MAPs of RSDDH and its variants on the MIRFlickr dataset. From Figure 4, we can find that our RSDDH approach outperforms RSDDH-Inter, RSDDH-Intra and RDDH methods, which illustrates that inter-modal and intra-modal consistency preservation strategies are crucial and beneficial. And the effectiveness of the two consistency preservation strategies is also confirmed by the experimental results. On Wiki and NUS-WIDE datasets, analogous phenomena can also be found.
6.3. Effect of Discrete Hashing Scheme
In this subsection, we evaluate the effectiveness of our discrete hashing scheme in our approach RSDDH. For the overall objective function in our RSDDH, the unknown discrete variable B can also be solved by relaxing it as a continuous variable. Here, we denote the method that solves the discrete variable B in a continuous manner by robust supervised deep hashing (RSDH). We evaluate the effectiveness of our discrete hashing scheme by investigating the MAPs of RSDDH and RSDH methods. Note that RSDH shares identical consistency preservation mechanisms and feature selection with RSDDH, differing only in the optimization of binary codes. Figure 5 shows the MAPs of RSDDH and RSDH methods on the MIRFlickr dataset at 16, 32, 64 and 128 bits, respectively. From Figure 5, we can see that the MAPs of the RSDDH method are superior to those of the RSDH method, which demonstrates that directly solving the discrete variable B can preserve the binary property and avoid the adverse effects caused by relaxation. As a result, binary hash codes with more discriminability can be learned to effectively accomplish cross-modal retrieval. We find similar phenomena on Wiki and NUS-WIDE datasets as well.
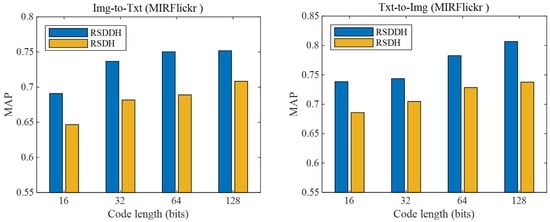
Figure 5.
The MAPs of RSDDH and RSDH methods on the MIRFlickr dataset at different code lengths.
6.4. Training Time Comparison
Table 6 shows the training time of different methods on Wiki, MIRFlickr and NUS-WIDE datasets. The code length is set to 32 bits in this experiment. As shown in Table 6, deep cross-modal hashing methods are slower than shallow cross-modal hashing methods. That is because those deep methods employ more complex architecture to learn hash codes compared with shallow methods. According to Table 6, it is obvious that the training times of the four deep cross-modal hashing methods are similar. However, our RSDDH approach achieves superior cross-modal retrieval performance to shallow methods. Therefore, RSDDH possesses a competitive computational speed as well as superior performance compared with existing state-of-the-art deep cross-modal hashing methods.

Table 6.
Training time (in seconds) of all compared methods on the Wiki, MIRFlickr and NUS-WIDE datasets.
6.5. Effect of the Size of Training Set
For all the experiments in this paper except that in this subsection, the training sets on MIRFlickr and NUS-WIDE datasets are formulated following the practice in [7]. To investigate the effect of the size of the training set on the cross-modal retrieval performance of our RSDDH approach, we conduct experiments on the training sets with different sizes of sets. Table 7 and Table 8 tabulate the MAPs and training time of our RSDDH approach on MIRFlickr and NUS-WIDE datasets. The code length is set to 32 bits in the experiments. From Table 7 and Table 8, it is obvious that when the size of training sets on MIRFlickr and NUS-WIDE increases, MAPs improve slowly while training time increases quickly. The phenomenon shows that compromise is needed between MAP and training time for the cross-modal retrieval in large-scale dataset scenarios. For the other comparison methods, similar phenomena can also be observed.

Table 7.
MAPs of RSDDH at different sizes of training set.

Table 8.
Training time of RSDDH at different sizes of training set.
6.6. Parameter Sensitivity Analysis
In this subsection, we conduct experiments to analyze the effects of different hyper-parameter settings on the cross-modal retrieval performance. Concretely, we analyze the effects based on investigating the performance variation of Img-to-Txt and Txt-to-Img tasks on the MIRFlickr dataset. The MAPs are used to demonstrate the cross-modal retrieval performance variation with respect to different hyper-parameter values. And we fix the length of hash codes to 32 bits. There are three hyper-parameters in our RSDDH approach, including , and in the objective function. Hyper-parameters and are the parameters of two feature selection terms, which are used to control the importance of feature selection. Hyper-parameter is used to control the significance of hash code balance terms. When we investigate the effect of one hyper-parameter, we perform experiments by varying the value of the hyper-parameter and fixing the other two hyper-parameters. We change the values of hyper-parameters , and in the set of . Figure 6 illustrates the MAPs of our RSDDH approach versus different values of , and on the MIRFlickr dataset. It can be seen from Figure 6 that RSDDH can achieve stable and satisfactory performance under a wide range of hyper-parameter values. It verifies that RSDDH is robust to hyper-parameters. Similar phenomena can be observed on the Wiki and NUS-WIDE datasets as well.
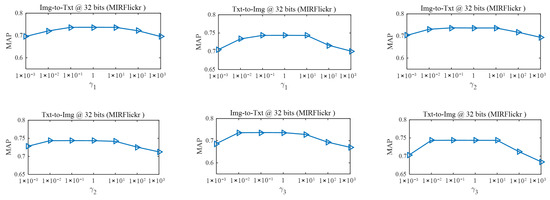
Figure 6.
MAPsof RSDDH with different values of the hyper-parameters , and on the MIRFlickr dataset at 32 bits.
7. Conclusions
In this paper, we propose a novel cross-modal hashing approach termed RSDDH. It can learn more appropriate feature representations for specific cross-modal retrieval tasks by employing an end-to-end hybrid deep learning architecture. The non-redundant feature selection strategy in RSDDH can select optimal and non-redundant features in each modality to generate hash codes which contain more discriminability. With the inter-modal consistency preservation strategy, RSDDH can effectively bridge heterogeneous modalities and reduce the semantic gap between different modalities in Hamming spaces. With the intra-modal consistency preservation strategy, the learned Hamming space can possess more discriminability. And the two binary hash code balance terms in RSDDH can maximize the information provided by each bit. Additionally, the SVDDH scheme designed for our RSDDH approach can enable the generated hash codes to possess beneficial characteristics.
Experimental results on three standard cross-modal retrieval datasets demonstrate that our approach RSDDH is superior to state-of-the-art cross-modal hashing methods. And the results also illustrate that our RSDDH approach can outperform several state-of-the-art shallow cross-modal hashing methods which are fed with deep learning features. According to the experimental results, the effectiveness of the non-redundant feature selection strategy, discrete hashing scheme, and inter-modal and intra-modal consistency preservation strategies are all confirmed. Additionally, experimental results also demonstrate the robustness of our RSDDH to hyper-parameters. In the future, we will extend our work to the weakly supervised case even with unpaired cross-modal data. In addition, we will further investigate the effectiveness on multi-modal data with audio or video.
Author Contributions
Conceptualization, X.D. (Xiwei Dong) and F.W.; methodology, X.D. (Xiwei Dong) and X.-Y.J.; software, J.Z.; validation, F.M., G.W. and T.L.; formal analysis, J.Z.; investigation, X.D. (Xiwei Dong); resources, F.W.; data curation, J.Z. and X.D. (Xiaogang Dong); writing—original draft preparation, X.D. (Xiwei Dong); writing—review and editing, F.W.; visualization, J.Z.; supervision, X.D. (Xiwei Dong); project administration, X.D. (Xiwei Dong); funding acquisition, X.D. (Xiwei Dong) and F.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jiangxi Province (grant numbers 20232BAB202053, 20232BAB202054), National Natural Science Foundation of China (grant number 62367004), Natural Science Foundation of Shandong Province (grant number ZR2020MF105), and Science and Technology Project of Education Department of Jiangxi Province (grant number GJJ2201915).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
We are deeply grateful to the researchers who shared their data and the students, teachers, and staff who helped us process data, as well as the social network users and the school for their support in our research work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yasuda, K.; Aritsugi, M.; Takeuchi, Y.; Shibayama, A. Disaster image tagging using generative AI for digital archives. In Proceedings of the 24th ACM Joint Conference on Digital Libraries, Hong Kong, China, 16–20 December 2025; p. 11. [Google Scholar]
- Mai Chau, P.P.; Bakkali, S.; Doucet, A. DocSum: Domain-adaptive pre-training for document abstractive summarization. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision Workshops, Tucson, AZ, USA, 28 February–4 March 2025; pp. 1213–1222. [Google Scholar]
- Liu, Y.; Wu, J.; Xin, G. Multi-keywords carrier-free text steganography based on part of speech tagging. In Proceedings of the International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery, Guilin, China, 29–31 July 2017; pp. 2102–2107. [Google Scholar]
- Hardoon, D.R.; Szedmak, S.; Shawe-Taylor, J. Canonical correlation analysis: An overview with application to learning methods. Neural Comput. 2004, 16, 2639–2664. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta. 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, L.; Wang, W.; Zhang, Z. Continuum regression for cross-modal multimedia retrieval. In Proceedings of the IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 1949–1952. [Google Scholar]
- Jiang, Q.Y.; Li, W.J. Deep cross-modal hashing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3232–3240. [Google Scholar]
- Weiss, Y.; Torralba, A.; Fergus, R. Spectral hashing. In Proceedings of the Annual Conference on Neural Information Processing Systems, Vancouver, BC, USA, 8–10 December 2008; pp. 1753–1760. [Google Scholar]
- Kumar, S.; Udupa, R. Learning hash functions for cross-view similarity search. In Proceedings of the International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 1360–1365. [Google Scholar]
- Song, J.; Yang, Y.; Yang, Y.; Huang, Z.; Shen, H.T. Inter-media hashing for large-scale retrieval from heterogeneous data sources. In Proceedings of the ACM International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 785–796. [Google Scholar]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, USA, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Jiao, Z.; Gao, X.; Wang, Y.; Li, J.; Xu, H. Deep convolutional neural networks for mental load classification based on EEG data. Pattern Recognit. 2018, 76, 582–595. [Google Scholar] [CrossRef]
- Feng, F.; Wang, X.; Li, R. Cross-modal retrieval with correspondence autoencoder. In Proceedings of the ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 7–16. [Google Scholar]
- Qian, X.; Xue, W.; Zhang, Q.; Tao, R.; Li, H. Deep cross-modal retrieval between spatial image and acoustic speech. IEEE Trans. Multimed. 2024, 26, 4480–4489. [Google Scholar] [CrossRef]
- Chen, C.; Wang, D. CausMatch: Causal matching learning with counterfactual preference framework for cross-modal retrieval. IEEE Access 2025, 13, 12734–12745. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Liu, L.; Liu, D.; Lu, X.; Meng, H. Primary code guided targeted attack against cross-modal hashing retrieval. IEEE Trans. Multimed. 2025, 27, 312. [Google Scholar] [CrossRef]
- Qi, X.; Zeng, X.; Tang, H. Cross-Modal hashing retrieval based on density clustering. IEEE Access 2025, 13, 44577–44589. [Google Scholar] [CrossRef]
- Cao, Y.; Long, M.; Wang, J.; Liu, S. Collective deep quantization for efficient cross-modal retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 3974–3980. [Google Scholar]
- Zhu, X.; Huang, Z.; Shen, H.T.; Zhao, X. Linear cross-modal hashing for efficient multimedia search. In Proceedings of the ACM International Conference on Multimedia, Barcelona, Spain, 21 October 2013; pp. 143–152. [Google Scholar]
- Liu, W.; Mu, C.; Kumar, S.; Chang, S.F. Discrete graph hashing. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3419–3427. [Google Scholar]
- Cun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Fei, L.; He, Z.; Wong, W.K.; Zhu, Q.; Zhao, S.; Wen, J. Semantic decomposition and enhancement hashing for deep cross-modal retrieval. Pattern Recognit. 2025, 160, 111225. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; p. 25. [Google Scholar]
- Hu, W.; Fan, Y.; Xing, J.; Sun, L.; Cai, Z.; Maybank, S. Deep constrained siamese hash coding network and load-balanced locality-sensitive hashing for near duplicate image detection. IEEE Trans. Image Process. 2018, 27, 4452–4464. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Sun, Z.; He, R.; Tan, T. A general framework for deep supervised discrete hashing. Int. J. Comput. Vision. 2020, 128, 2204–2222. [Google Scholar] [CrossRef]
- Yang, H.F.; Lin, K.; Chen, C.S. Supervised learning of semantics-preserving hash via deep convolutional neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 437–451. [Google Scholar] [CrossRef]
- Oh, Y.; Park, S.; Ye, J.C. Deep learning COVID-19 features on CXR using limited training data sets. IEEE Trans. Med. Imaging 2020, 39, 2688–2700. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Weng, Z.; Li, R.; Zhuang, H.; Lin, Z. Online weighted hashing for cross-modal retrieval. Pattern Recognit. 2025, 161, 111232. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Y.; Li, J.; Chen, J.; Akutsu, T.; Cheung, Y.M.; Cai, H. Unsupervised dual deep hashing with semantic-index and content-code for cross-modal retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 387–399. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the ACM International Conference on Multimedia, Mountain View, CA, USA, 3–7 November 2014; pp. 675–678. [Google Scholar]
- Raji, C.G.; Chandra, S.V. Long-term forecasting the survival in liver transplantation using multilayer perceptron networks. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2318–2329. [Google Scholar] [CrossRef]
- Ding, G.; Guo, Y.; Zhou, J.; Gao, Y. Large-scale cross-modality search via collective matrix factorization hashing. IEEE Trans. Image Process. 2016, 25, 5427–5440. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Ji, R.; Wu, Y.; Huang, F.; Zhang, B. Cross-modality binary code learning via fusion similarity hashing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7380–7388. [Google Scholar]
- Ding, G.; Guo, Y.; Zhou, J. Collective matrix factorization hashing for multimodal data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2083–2090. [Google Scholar]
- Wang, W.; Shen, Y.; Zhang, H.; Yao, Y.; Liu, L. Set and rebase: Determining the semantic graph connectivity for unsupervised cross modal hashing. In Proceedings of the International Joint Conference on Artificial Intelligence, Yokohama, Japan, 7–15 January 2020; pp. 853–859. [Google Scholar]
- Wang, D.; Wang, Q.; Gao, X. Robust and hashing for cross-modal similarity search. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2703–2715. [Google Scholar] [CrossRef]
- Smeulders, A.W.M.; Worring, M.; Santini, S.; Gupta, A.; Jain, R. Content-based image retrieval at the end of the early years. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1349–1380. [Google Scholar] [CrossRef]
- Tang, J.; Wang, K.; Shao, L. Supervised matrix factorization hashing for cross-modal retrieval. IEEE Trans. Image Process. 2016, 25, 3157–3166. [Google Scholar] [CrossRef]
- Wang, D.; Gao, X.; Wang, X.; He, L. Label consistent matrix factorization hashing for large-scale cross-modal similarity search. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2466–2479. [Google Scholar] [CrossRef]
- Fang, Y.; Ren, Y. Supervised discrete cross-modal hashing based on kernel discriminant analysis. Pattern Recognit. 2020, 98, 107062. [Google Scholar] [CrossRef]
- Shen, H.T.; Liu, L.; Yang, Y.; Xu, X.; Huang, Z.; Shen, F.; Hong, R. Exploiting subspace relation in semantic labels for cross-modal hashing. IEEE Trans. Knowl. Data Eng. 2020, 33, 3351–3365. [Google Scholar] [CrossRef]
- Zhang, D.; Li, W.J. Large-scale supervised multimodal hashing with semantic correlation maximization. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014; pp. 1–7. [Google Scholar]
- Mandal, D.; Chaudhury, K.N.; Biswas, S. Generalized semantic preserving hashing for cross-modal retrieval. IEEE Trans. Image Process. 2019, 28, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Meng, M.; Wang, H.; Yu, J.; Chen, H.; Wu, J. Asymmetric supervised consistent and specific hashing for cross-modal retrieval. IEEE Trans. Image Process. 2021, 30, 986–1000. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Su, H.; Huang, K. Deep Self-enhancement hashing for robust multi-label cross-modal retrieval. Pattern Recognit. 2024, 147, 110079. [Google Scholar] [CrossRef]
- Karpathy, A.; Li, F.F. Deep visual-semantic alignments for generating image descriptions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3128–3137. [Google Scholar]
- Long, M.; Cao, Y.; Wang, J.; Jordan, M. Learning transferable features with deep adaptation networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 97–105. [Google Scholar]
- Ma, X.; Zhang, T.; Xu, C. Multi-level correlation adversarial hashing for cross-modal retrieval. IEEE Trans. Multimed. 2020, 22, 3101–3114. [Google Scholar] [CrossRef]
- Xie, D.; Deng, C.; Li, C.; Liu, X.; Tao, D. Multi-task consistency-preserving adversarial hashing for cross-modal retrieval. IEEE Trans. Image Process. 2020, 29, 3626–3637. [Google Scholar] [CrossRef]
- Wu, L.; Wang, Y.; Shao, L. Cycle-consistent deep generative hashing for cross-modal retrieval. IEEE Trans. Image Process. 2019, 28, 1602–1612. [Google Scholar] [CrossRef]
- Yang, E.; Deng, C.; Liu, W.; Liu, X.; Tao, D.; Gao, X. Pairwise relationship guided deep hashing for cross-modal retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1618–1625. [Google Scholar]
- Liong, V.E.; Lu, J.; Tan, Y.P.; Zhou, J. Cross-modal deep variational hashing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4077–4085. [Google Scholar]
- Deng, C.; Chen, Z.; Liu, X.; Gao, X.; Tao, D. Triplet-based deep hashing network for cross-modal retrieval. IEEE Trans. Image Process. 2018, 27, 3893–3903. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Wang, L.; Liu, H. Efficient spectral feature selection with minimum redundancy. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 673–678. [Google Scholar]
- He, R.; Tan, T.N.; Wang, L.; Zheng, W. l2,1 regularized correntropy for robust feature selection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2504–2511. [Google Scholar]
- Nie, F.; Huang, H.; Cai, X.; Ding, C.H. Efficient and robust feature selection via joint l2,1-norms minimization. In Proceedings of the Annual Conference on Neural Information Processing Systems, Vancouver, BC, USA, 6–9 December 2010; pp. 1813–1821. [Google Scholar]
- Zhen, Y.; Yeung, D.Y. A probabilistic model for multimodal hash function learning. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 940–948. [Google Scholar]
- Tseng, P. Convergence of a block coordinate descent method for nondifferentiable minimization. J. Optim. Theory Appl. 2001, 109, 475–494. [Google Scholar] [CrossRef]
- He, R.; Zheng, W.; Hu, B. Maximum correntropy criterion for robust face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1561–1576. [Google Scholar]
- Nikolova, M.; Ng, M.K. Analysis of half-quadratic minimization methods for signal and image recovery. SIAM J. Sci. Comput. 2005, 27, 937–966. [Google Scholar] [CrossRef]
- Wang, K.; He, R.; Wang, L.; Wang, W.; Tan, T. Joint feature selection and subspace learning for cross-modal retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2010–2023. [Google Scholar] [CrossRef]
- Shen, F.; Shen, C.; Liu, W.; Shen, H.T. Supervised discrete hashing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 37–45. [Google Scholar]
- Sun, R.; Sun, H.; Yao, T. A SVD-and quantization based semi-fragile watermarking technique for image authentication. In Proceedings of the International Conference on Signal Processing, Beijing, China, 26–30 August 2002; pp. 1592–1595. [Google Scholar]
- He, K.; Sun, J. Convolutional neural networks at constrained time cost. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5353–5360. [Google Scholar]
- Rasiwasia, N.; Pereira, J.C.; Coviello, E.; Doyle, G.; Lanckriet, G.R.G.; Levy, R.; Vasconcelos, N. A new approach to cross-modal multimedia retrieval. In Proceedings of the ACM International Conference on Multimedia, Firenze Italy, 25–29 October 2010; pp. 251–260. [Google Scholar]
- Huiskes, M.J.; Lew, M.S. The MIR Flickr retrieval evaluation. In Proceedings of the 1st ACM International Conference on Multimedia Information Retrieval, Vancouver, BC, USA, 30–31 October 2008; pp. 39–43. [Google Scholar]
- Chua, T.S.; Tang, J.; Hong, R.; Li, H.; Luo, Z.; Zheng, Y. NUS-WIDE: A real-world web image database from National University of Singapore. In Proceedings of the ACM International Conference on Multimedia, Beijing, China, 19–24 October 2009; pp. 1–9. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Peng, Y.; Huang, X.; Qi, J. Cross-media shared representation by hierarchical learning with multiple deep networks. In Proceedings of the International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 3846–3853. [Google Scholar]
- Qin, Q.; Huo, Y.; Huang, L. Deep neighborhood-preserving hashing with quadratic spherical mutual information for cross-modal retrieval. IEEE Trans. Multimed. 2024, 26, 6361–6374. [Google Scholar] [CrossRef]
- Kang, C.; Liao, S.; Li, Z.; Cao, Z.; Xiong, G. Learning deep semantic embeddings for cross-modal retrieval. In Proceedings of the Asian Conference on Machine Learning, Seoul, Republic of Korea, 15–17 November 2017; pp. 471–486. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).