Structural Design of a Multi-Stage Variable Stiffness Manipulator Based on Low-Melting-Point Alloys
Abstract
1. Introduction
2. Materials and Methods
2.1. Selection of LMPAs
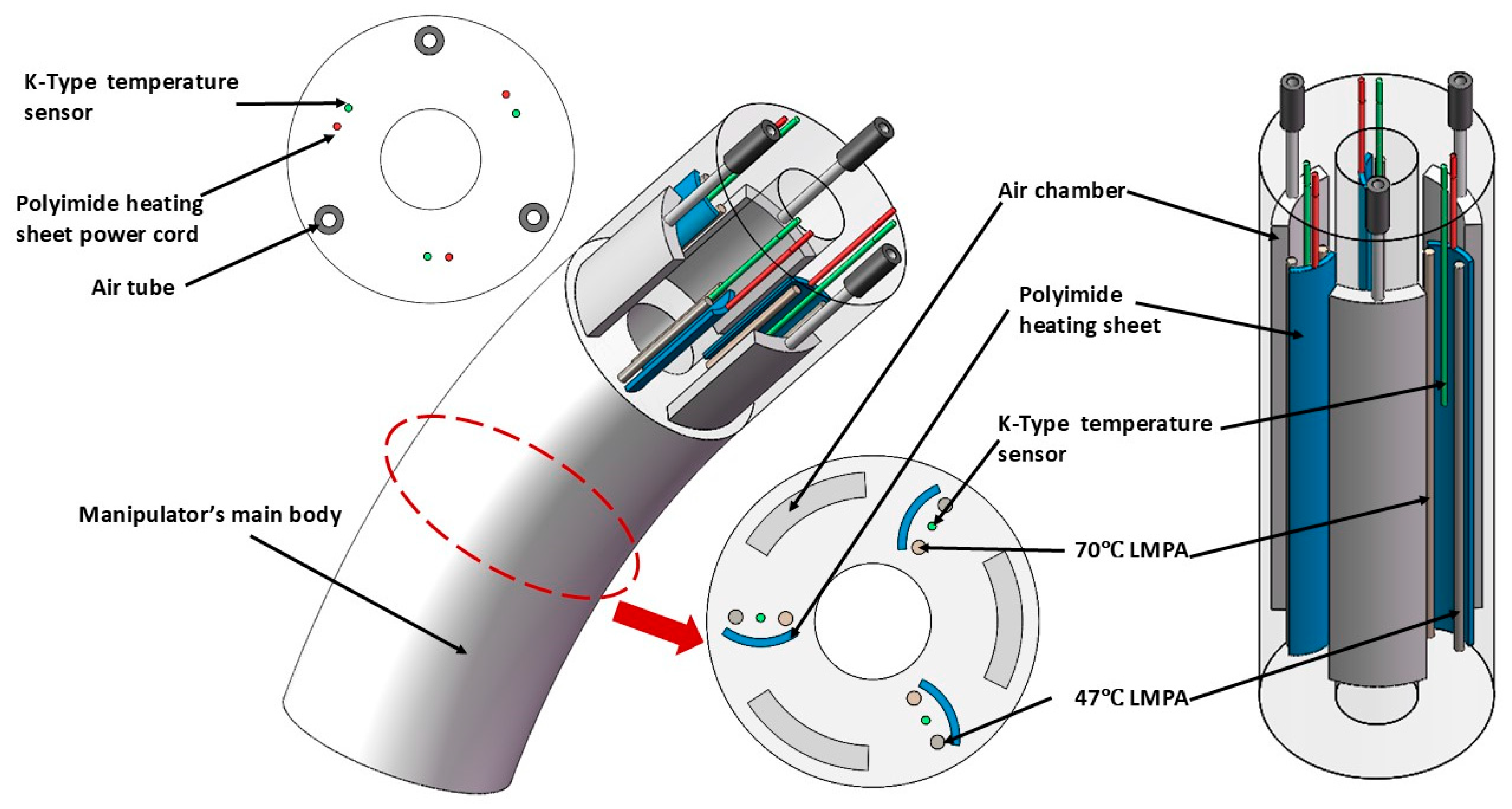
2.2. Design Concept and Structure of the Manipulator
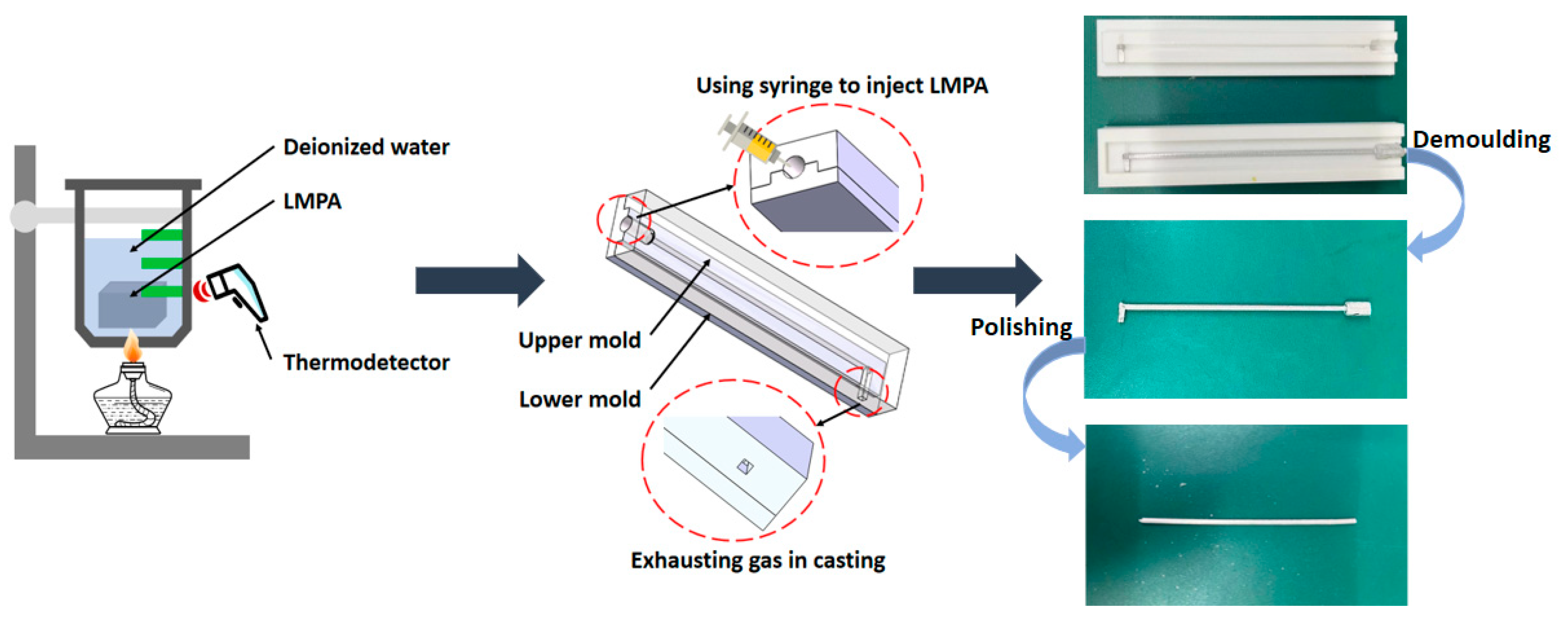
2.3. Fabrication Method of LMPA
- 1.
- First, the LMPAs are immersed in a beaker containing deionized water and heated to achieve a molten state. In the molten state, the LMPAs exhibit a higher density and are immiscible with deionized water, resulting in stratification and settling at the bottom.
- 2.
- Molds fabricated via 3D printing are used for casting the LMPAs. To accommodate the self-healing properties of the LMPAs during operation, the diameter of the mold cavity is designed to be slightly larger than the target dimensions of the final LMPA components. The molten LMPA is extracted using a syringe and promptly injected into the mold, allowing it to solidify at room temperature for 2–4 h.
- 3.
- After the curing step is completed, demolding is performed to obtain the preliminary LMPA. At this stage, the LMPA does not yet meet the application requirements. The LMPA is subjected to a polishing process to achieve the desired dimensions, resulting in a final diameter of 1.8 mm.
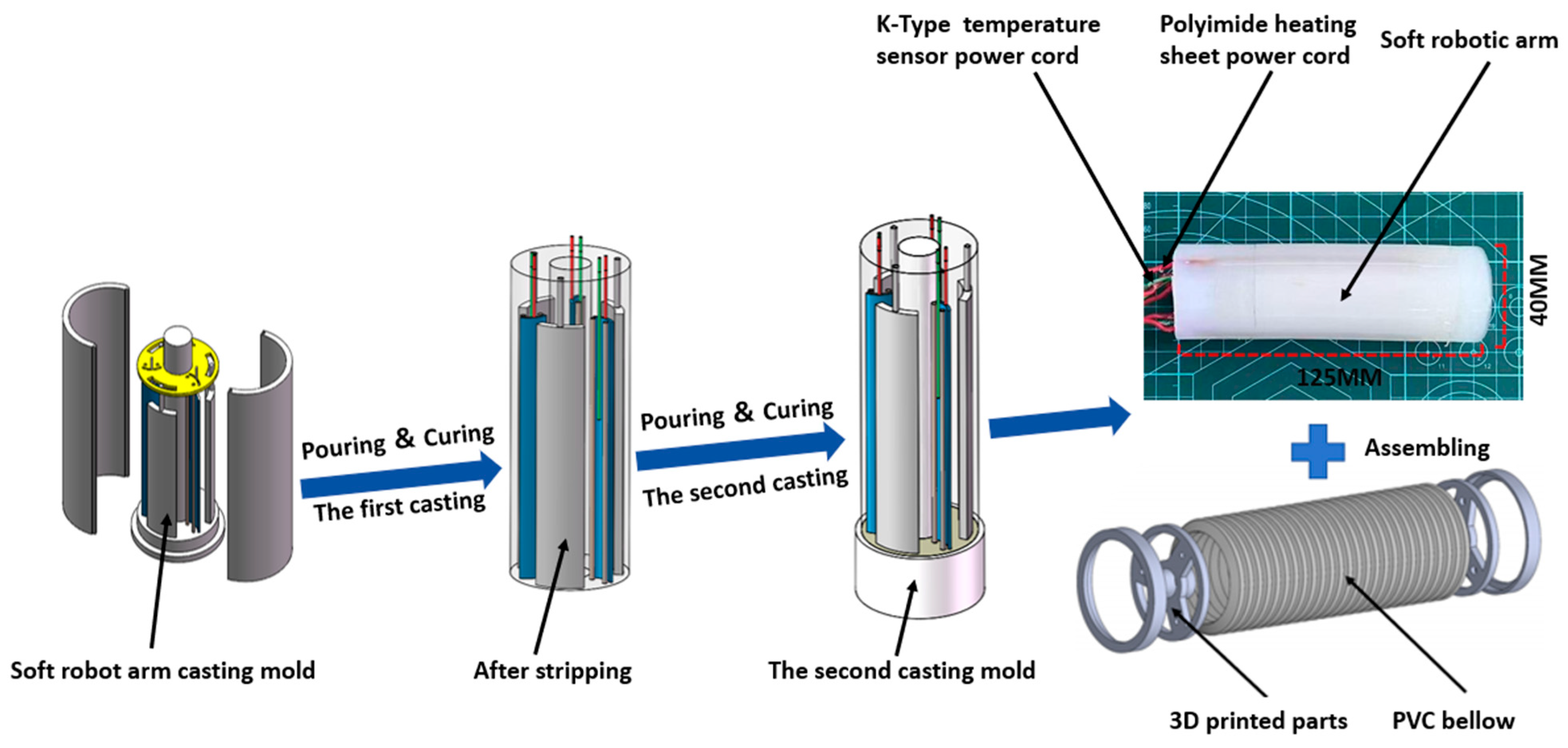
2.4. Fabrication Process of the Manipulator
- 1.
- Nylon material, which has higher material strength, is selected as the 3D printing material for mold fabrication, followed by mold assembly. Due to the dimensional constraints of the manipulator, molds printed with PLA suffer from low precision, whereas nylon effectively overcomes this limitation.
- 2.
- The main body of the manipulator is fabricated from silicone rubber (SJ3211, Shore hardness 15A). The silicone rubber is prepared by mixing components A and B in a 1:1 weight ratio. The mixture is stirred manually for 2–3 min and then placed in a vacuum chamber for 2 min to remove air bubbles. The degassed silicone rubber is then poured into the mold to complete the first casting step.
- 3.
- The first casting is cured at room temperature for 6 h before being demolded. The first casting forms the manipulator’s main body, as well as the reserved chambers for built-in components and air channels. The LMPAs, K-type temperature sensors, and polyimide heating sheets are assembled into the reserved chambers. The assembled manipulator is then inverted into the mold, and the second casting step is performed by repeating the previous procedure.
- 4.
- The second casting cures at room temperature for 6 h before being demolded. This step seals the manipulator, resulting in the formation of a fully assembled structure.
- 5.
- Final assembly of the manipulator is performed. To limit the ballooning effect during bending, 3D-printed components are used to integrate a matching PVC bellow with the manipulator, forming the final soft robotic structure.
3. Theory and Simulation
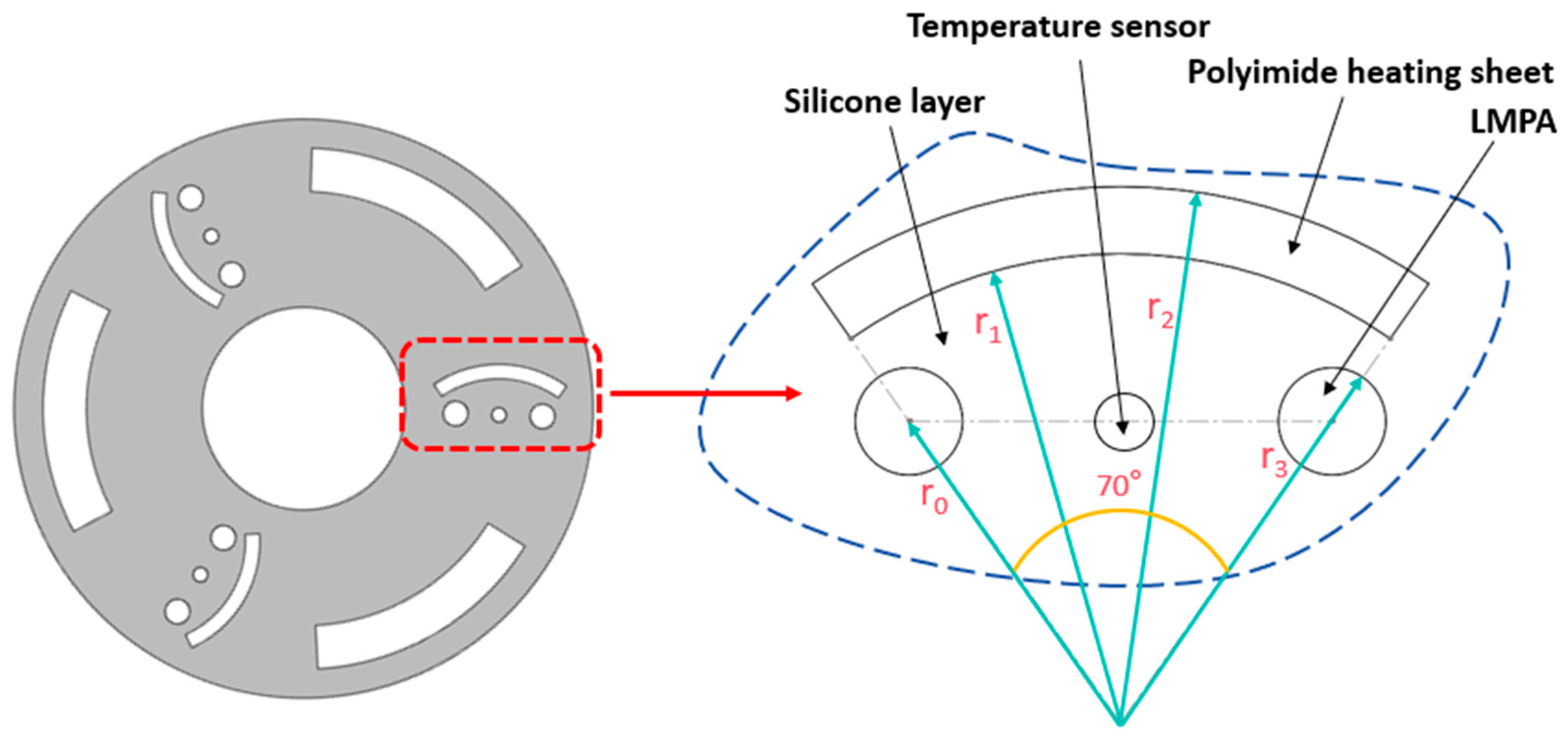
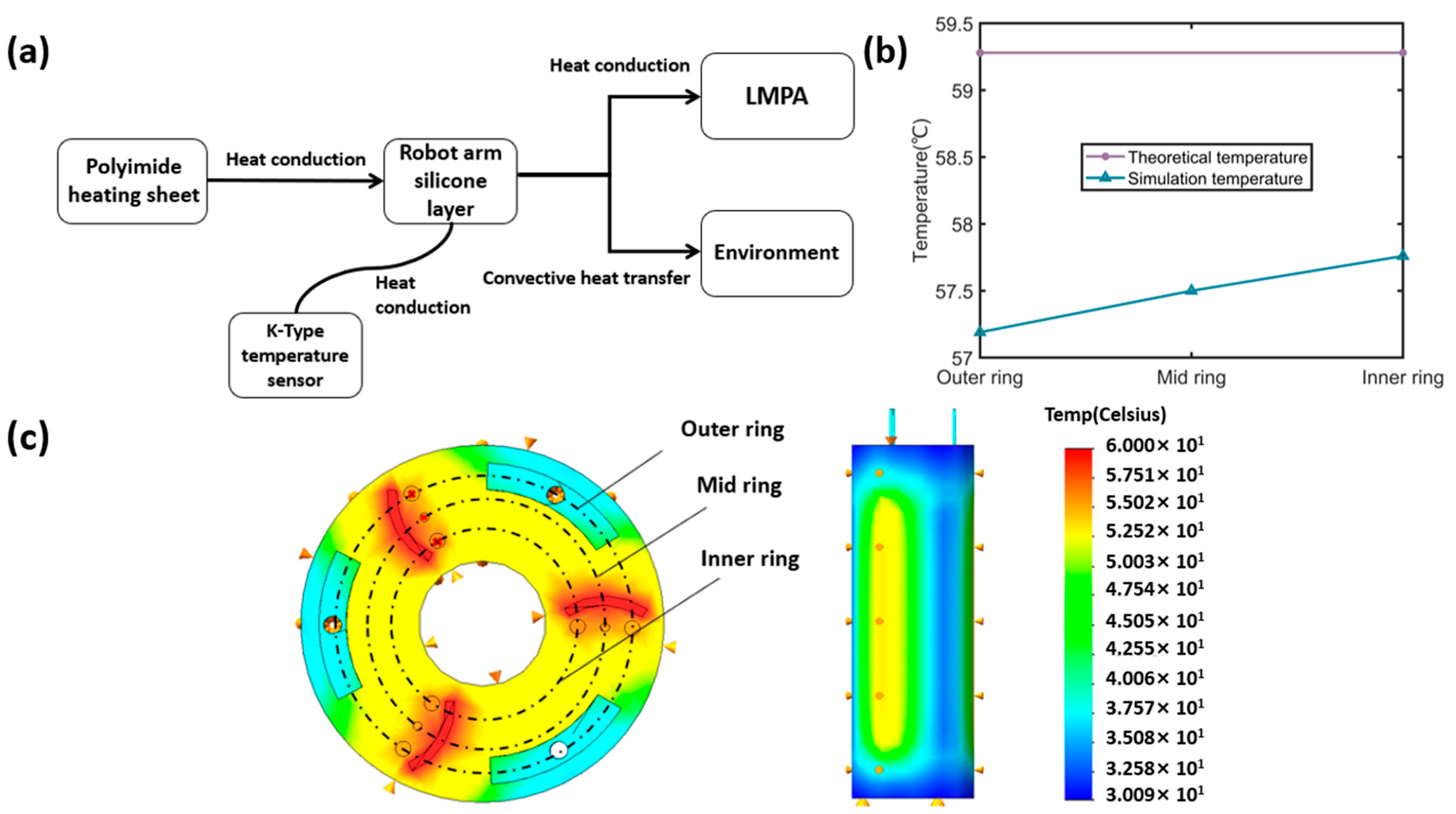
3.1. Temperature Field Model of Manipulator
3.2. Steady-State Thermodynamic Simulation of the Model
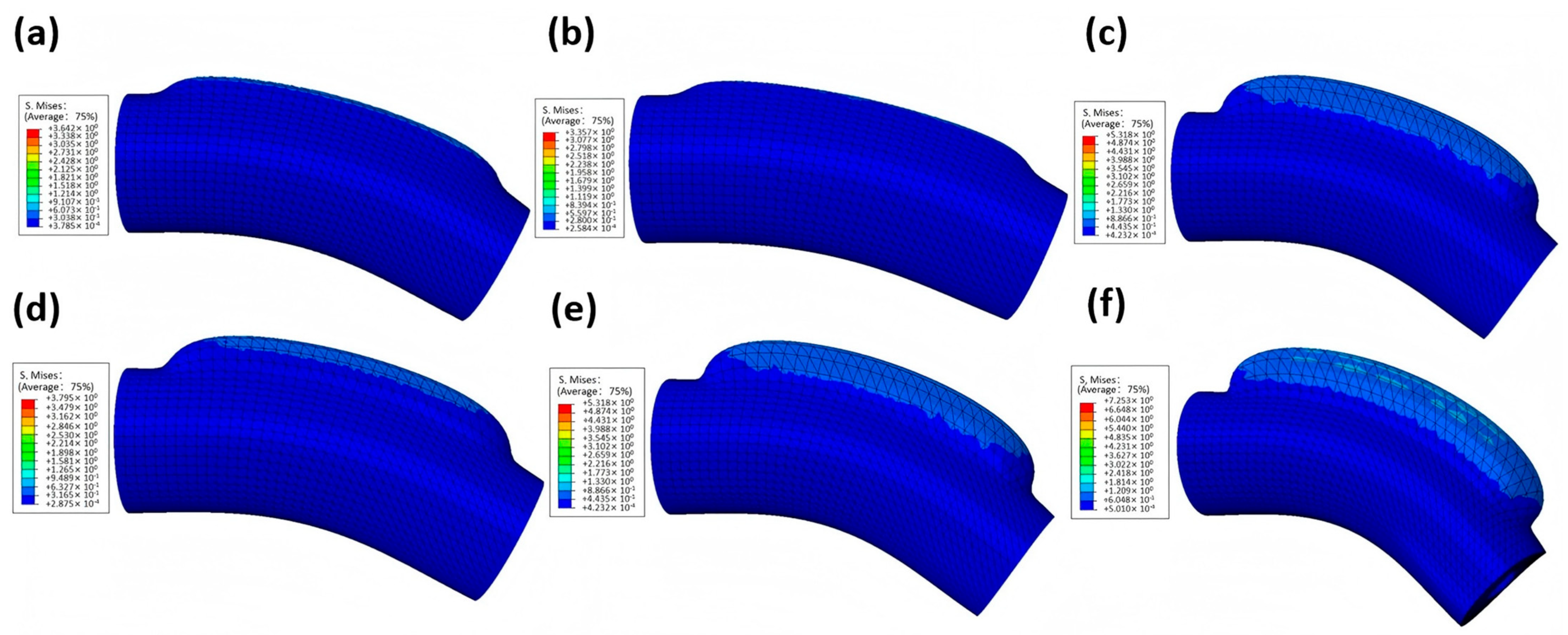
3.3. Air-Driven Simulation of the Manipulator
4. Experiment Validation and Assessment
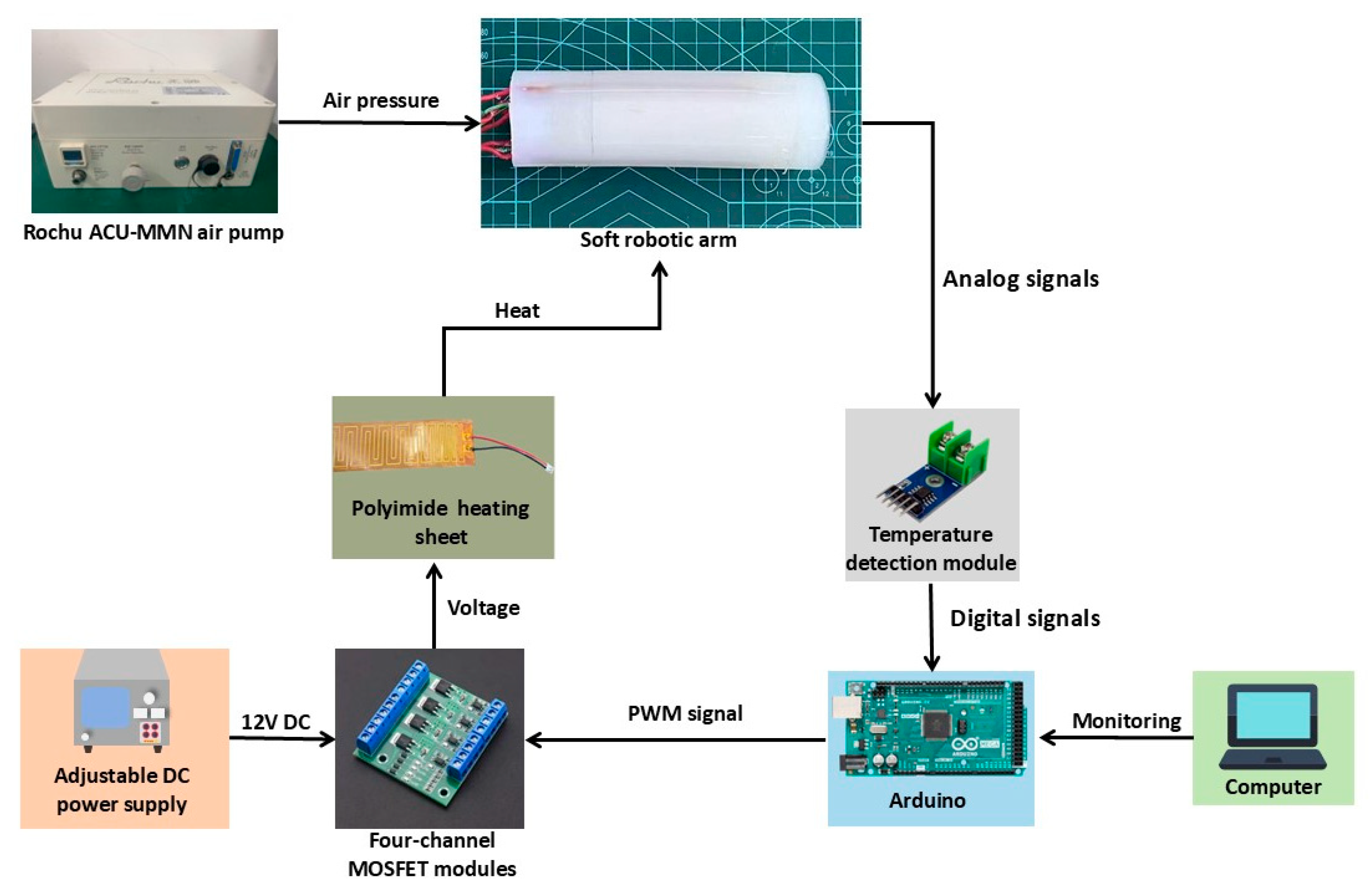
4.1. Soft Manipulator Control System
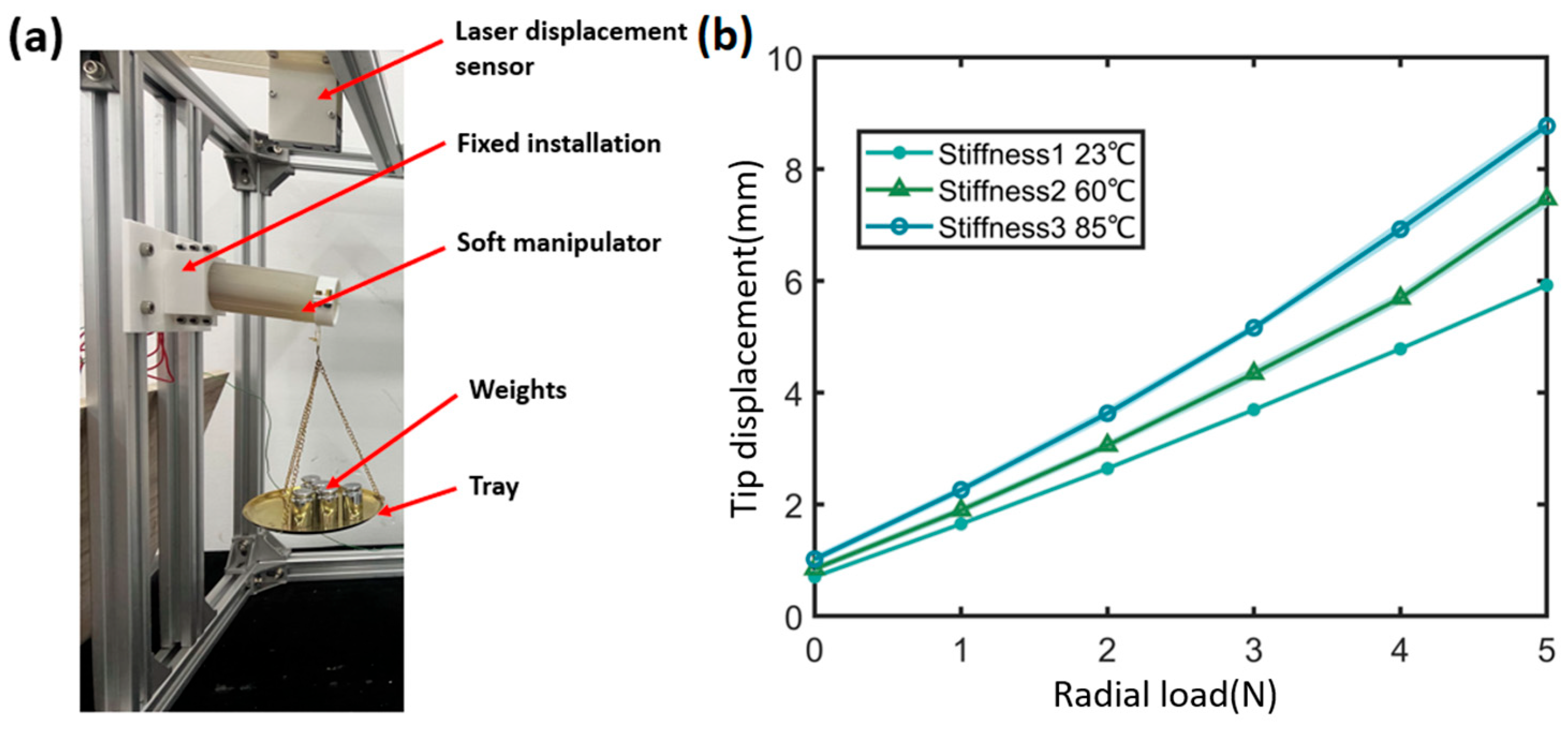
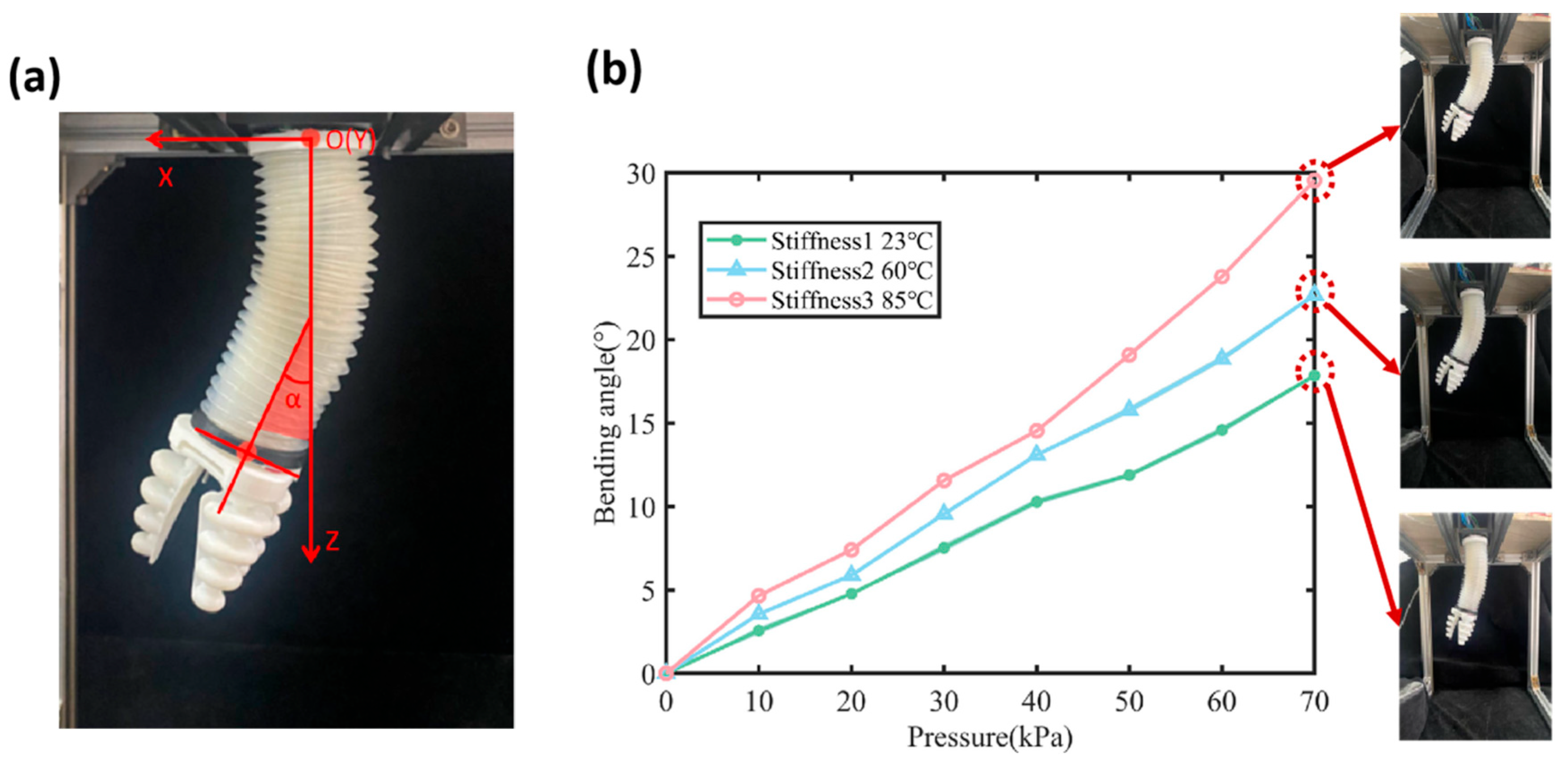
4.2. Stiffness Characterization Under Static Loading
4.3. Characterization of Pneumatic Actuation Under Variable Stiffness
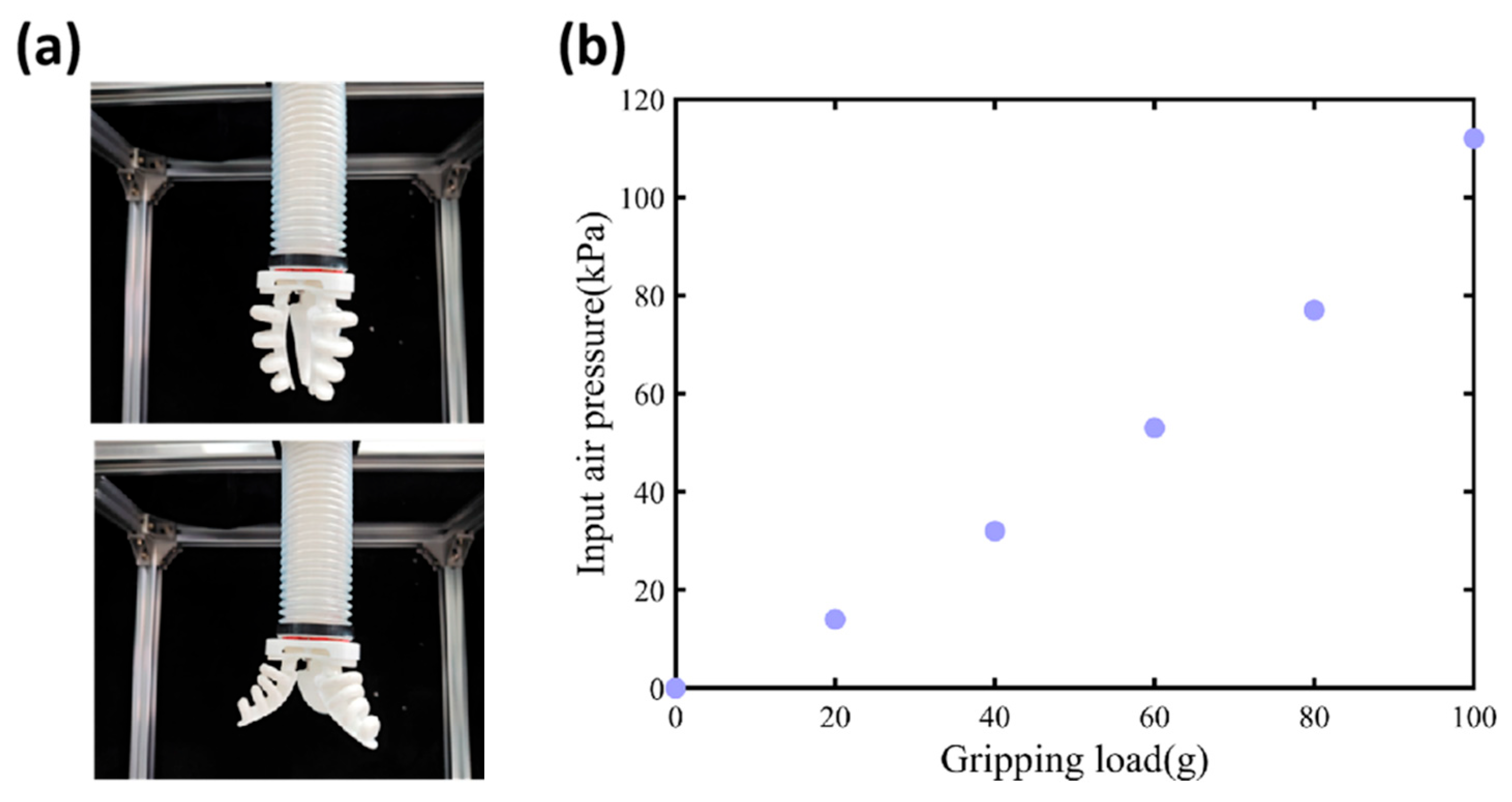
4.4. Object Grasping Experiments for Functional Verification
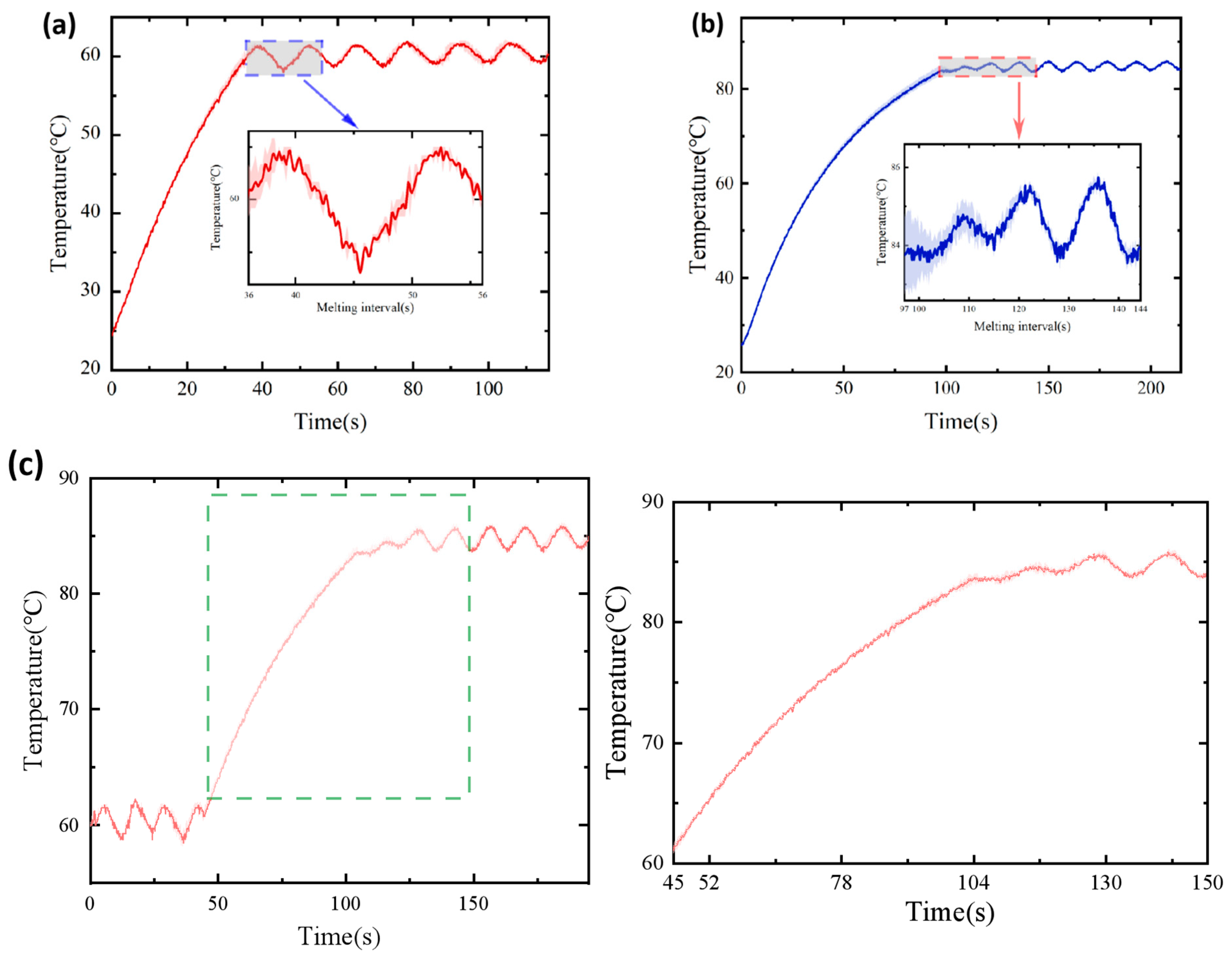
4.5. Response Time Assessment of LMPA Activation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| LMPAs | Low-melting-point alloys |
References
- Yoshida, S.; Morimoto, Y.; Zheng, L.; Onoe, H.; Takeuchi, S. Multipoint Bending and Shape Retention of a Pneumatic Bending Actuator by a Variable Stiffness Endoskeleton. Soft Robot. 2018, 5, 718–725. [Google Scholar] [CrossRef] [PubMed]
- Dou, W.; Zhong, G.; Cao, J.; Shi, Z.; Peng, B.; Jiang, L.-z. Soft Robotic Manipulators: Designs, Actuation, Stiffness Tuning, and Sensing. Adv. Mater. Technol. 2021, 6, 2100018. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Zuo, S. Flexible manipulator with low-melting-point alloy actuation and variable stiffness. Soft Robot. 2022, 9, 577–590. [Google Scholar] [CrossRef] [PubMed]
- Das, R.; Babu, S.P.M.; Visentin, F.; Palagi, S.; Mazzolai, B. An earthworm-like modular soft robot for locomotion in multi-terrain environments. Sci. Rep. 2023, 13, 1571. [Google Scholar] [CrossRef]
- Rozen-Levy, S.; Messner, W.; Trimmer, B.A. The design and development of branch bot: A branch-crawling, caterpillar-inspired, soft robot. Int. J. Robot. Res. 2021, 40, 24–36. [Google Scholar] [CrossRef]
- Piskarev, Y.; Shintake, J.; Chautems, C.; Lussi, J.; Boehler, Q.; Nelson, B.J.; Floreano, D. A variable stiffness magnetic catheter made of a conductive phase-change polymer for minimally invasive surgery. Adv. Funct. Mater. 2022, 32, 2107662. [Google Scholar] [CrossRef]
- Sut, D.J.; Sethuramalingam, P. Soft manipulator for soft robotic applications: A review. J. Intell. Robot. Syst. 2023, 108, 10. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, P.; Lin, Y.; Jiao, Z.; Zou, J. Modular soft robotics: Modular units, connection mechanisms, and applications. Adv. Intell. Syst. 2020, 2, 1900166. [Google Scholar] [CrossRef]
- Mohammadi, A.; Hajizadeh, E.; Tan, Y.; Choong, P.; Oetomo, D. A bioinspired 3D-printable flexure joint with cellular mechanical metamaterial architecture for soft robotic hands. Int. J. Bioprinting 2023, 9, 696. [Google Scholar] [CrossRef]
- Pagliarani, N.; Arleo, L.; Albini, S.; Cianchetti, M. Variable Stiffness Technologies for Soft Robotics: A Comparative Approach for the STIFF-FLOP Manipulator. Actuators 2023, 12, 96. [Google Scholar] [CrossRef]
- Manti, M.; Cacucciolo, V.; Cianchetti, M. Stiffening in soft robotics: A review of the state of the art. IEEE Robot. Autom. Mag. 2016, 23, 93–106. [Google Scholar] [CrossRef]
- Blanc, L.; Delchambre, A.; Lambert, P. Flexible medical devices: Review of controllable stiffness solutions. Actuators 2017, 6, 23. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Chen, Y.; Majidi, C.; Iida, F.; Askounis, E.; Pei, Q. Controllable and reversible tuning of material rigidity for robot applications. Mater. Today 2018, 21, 563–576. [Google Scholar] [CrossRef]
- De Falco, I.; Cianchetti, M.; Menciassi, A. A soft multi-module manipulator with variable stiffness for minimally invasive surgery. Bioinspiration Biomim. 2017, 12, 056008. [Google Scholar] [CrossRef] [PubMed]
- Ranzani, T.; Cianchetti, M.; Gerboni, G.; De Falco, I.; Menciassi, A. A soft modular manipulator for minimally invasive surgery: Design and characterization of a single module. IEEE Trans. Robot. 2016, 32, 187–200. [Google Scholar] [CrossRef]
- Ranzani, T.; Gerboni, G.; Cianchetti, M.; Menciassi, A. A bioinspired soft manipulator for minimally invasive surgery. Bioinspiration Biomim. 2015, 10, 035008. [Google Scholar] [CrossRef] [PubMed]
- Arezzo, A.; Mintz, Y.; Allaix, M.E.; Arolfo, S.; Bonino, M.; Gerboni, G.; Brancadoro, M.; Cianchetti, M.; Menciassi, A.; Wurdemann, H. Total mesorectal excision using a soft and flexible robotic arm: A feasibility study in cadaver models. Surg. Endosc. 2017, 31, 264–273. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Cheng, S.; Kim, S.; Iagnemma, K. A novel layer jamming mechanism with tunable stiffness capability for minimally invasive surgery. IEEE Trans. Robot. 2013, 29, 1031–1042. [Google Scholar] [CrossRef]
- Shah, D.S.; Yang, E.J.; Yuen, M.C.; Huang, E.C.; Kramer-Bottiglio, R. Jamming skins that control system rigidity from the surface. Adv. Funct. Mater. 2021, 31, 2006915. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, J.; Li, Y.; Hong, J.; Wang, M.Y. Electrostatic layer jamming variable stiffness for soft robotics. IEEE/ASME Trans. Mechatron. 2019, 24, 424–433. [Google Scholar] [CrossRef]
- Shiva, A.; Stilli, A.; Noh, Y.; Faragasso, A.; De Falco, I.; Gerboni, G.; Cianchetti, M.; Menciassi, A.; Althoefer, K.; Wurdemann, H.A. Tendon-based stiffening for a pneumatically actuated soft manipulator. IEEE Robot. Autom. Lett. 2016, 1, 632–637. [Google Scholar] [CrossRef]
- Althoefer, K. Antagonistic actuation and stiffness control in soft inflatable robots. Nat. Rev. Mater. 2018, 3, 76–77. [Google Scholar] [CrossRef]
- Stilli, A.; Wurdemann, H.A.; Althoefer, K. A novel concept for safe, stiffness-controllable robot links. Soft Robot. 2017, 4, 16–22. [Google Scholar] [CrossRef]
- Alambeigi, F.; Seifabadi, R.; Armand, M. A continuum manipulator with phase changing alloy. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 758–764. [Google Scholar]
- Hao, Y.; Wang, T.; Xie, Z.; Sun, W.; Liu, Z.; Fang, X.; Yang, M.; Wen, L. A eutectic-alloy-infused soft actuator with sensing, tunable degrees of freedom, and stiffness properties. J. Micromechanics Microengineering 2018, 28, 024004. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, Z.; Liu, J.; Fang, X.; Fang, B.; Nie, S.; Guan, Y.; Sun, F.; Wang, T.; Wen, L. A soft gripper with programmable effective length, tactile and curvature sensory feedback. Smart Mater. Struct. 2020, 29, 035006. [Google Scholar] [CrossRef]
- Yuen, M.C.; Bilodeau, R.A.; Kramer, R.K. Active variable stiffness fibers for multifunctional robotic fabrics. IEEE Robot. Autom. Lett. 2016, 1, 708–715. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, N.; Hingorani, H.; Ding, N.; Wang, D.; Yuan, C.; Zhang, B.; Gu, G.; Ge, Q. Fast-response, stiffness-tunable soft actuator by hybrid multimaterial 3D printing. Adv. Funct. Mater. 2019, 29, 1806698. [Google Scholar] [CrossRef]
- Schubert, B.E.; Floreano, D. Variable stiffness material based on rigid low-melting-point-alloy microstructures embedded in soft poly (dimethylsiloxane)(PDMS). Rsc Adv. 2013, 3, 24671–24679. [Google Scholar] [CrossRef]
- Dong, H.; Hu, B.; Zhang, W.; Xie, W.; Mo, J.; Sun, H.; Shang, J. Robotic-assisted automated in situ bioprinting. Int. J. Bioprinting 2022, 9, 629. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Weng, T.; Zheng, K.; Sun, H.; Chen, B. Application of 3D Printing Technology in Soft Robots. 3D Print. Addit. Manuf. 2024, 11, 954–976. [Google Scholar] [CrossRef]
- Keong, B.A.W.; Hua, R.Y.C. A novel fold-based design approach toward printable soft robotics using flexible 3D printing materials. Adv. Mater. Technol. 2018, 3, 1700172. [Google Scholar] [CrossRef]
- Tawk, C.; Spinks, G.M.; in het Panhuis, M.; Alici, G. 3D printable linear soft vacuum actuators: Their modeling, performance quantification and application in soft robotic systems. IEEE/ASME Trans. Mechatron. 2019, 24, 2118–2129. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, Y.; Peng, Y.; Yuan, F.; Zhang, X.; Wang, J. Medical Image Segmentation: A Comprehensive Review of Deep Learning-Based Methods. Tomography 2025, 11, 52. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Yang, X.; Li, D.; Ma, Z.; Liu, Z.; Bai, X.; Mao, Z. Predicting flow status of a flexible rectifier using cognitive computing. Expert Syst. Appl. 2025, 264, 125878. [Google Scholar] [CrossRef]
- Zhou, K.; Tang, Z.; Lu, Y.; Wang, T.; Wang, H.; Li, T. Composition, Microstructure, Phase Constitution and Fundamental Physicochemical Properties of Low-Melting-Point Multi-Component Eutectic Alloys. J. Mater. Sci. Technol. 2017, 33, 131–154. [Google Scholar] [CrossRef]
- Wang, F.; Xing, Z.; Yang, P.; Lin, J.; Zhao, J. Study on Steady-state Heat Transfer of Soft Manipulators with Variable Stiffness Based on Low-melting-point Alloy Phase Transition. China Mech. Eng. 2021, 32, 793. [Google Scholar]


| Solubility Range (°C) | Element (%) | Autoflow Point | Note | |||||
|---|---|---|---|---|---|---|---|---|
| Start Melting Point | End Melting Point | In | Bi | Sn | Cd | Pb | ||
| 46.70 | 46.70 | 19.10 | 44.70 | 8.30 | 5.30 | 22.60 | 46.70 | eutectic |
| 47.00 | 48.00 | 15.00 | 42.34 | 11.00 | 8.46 | 22.86 | 47.00 | |
| 58.00 | 58.00 | 21.00 | 49.40 | 11.60 | - | 18.00 | 58.00 | eutectic |
| 70.00 | - | 50.00 | 13.30 | 10.00 | 26.70 | 70.00 | eutectic | |
| 78.80 | 78.80 | 25.20 | 57.05 | 17.30 | - | - | 78.80 | eutectic |
| 91.50 | 91.00 | - | 51.65 | - | 8.15 | 40.20 | 91.50 | eutectic |
| 95.00 | 95.00 | - | 52.50 | 15.50 | - | 32.00 | 95.00 | eutectic |
| Parameter | Value |
|---|---|
| Diameter of the manipulator (mm) | 40 |
| Diameter of the central channel (mm) | 14 |
| Length of the manipulator (mm) | 125 |
| Diameter of the variable stiffness column (mm) | 1.6 |
| Length of the variable stiffness column (mm) | 90 |
| Length of polyimide heating sheet (mm) | 98 |
| No. | Object | Weight (g) | Size (mm) (L × W × H or D × H) |
|---|---|---|---|
| 1 | Egg | 56 | D: 44 × H: 56 |
| 2 | Toothpaste tube | 55 | 133 × 34 × 22 |
| 3 | Tissue | 15 | 74 × 53 × 25 |
| 4 | Cereal sachet | 34 | 150 × 52 × 18 |
| 5 | Liquid glue bottle | 62 | D: 30 × H: 125 |
| 6 | Bread slice | 50 | 145 × 110 × 23 |
| 7 | Biscuit box | 48 | 122 × 64 × 35 |
| 8 | Stapler | 26 | 57 × 32 × 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Guo, L.; Wang, A.; Dong, W.; Gao, Y.; Dong, H. Structural Design of a Multi-Stage Variable Stiffness Manipulator Based on Low-Melting-Point Alloys. Technologies 2025, 13, 338. https://doi.org/10.3390/technologies13080338
Ye M, Guo L, Wang A, Dong W, Gao Y, Dong H. Structural Design of a Multi-Stage Variable Stiffness Manipulator Based on Low-Melting-Point Alloys. Technologies. 2025; 13(8):338. https://doi.org/10.3390/technologies13080338
Chicago/Turabian StyleYe, Moufa, Lin Guo, An Wang, Wei Dong, Yongzhuo Gao, and Hui Dong. 2025. "Structural Design of a Multi-Stage Variable Stiffness Manipulator Based on Low-Melting-Point Alloys" Technologies 13, no. 8: 338. https://doi.org/10.3390/technologies13080338
APA StyleYe, M., Guo, L., Wang, A., Dong, W., Gao, Y., & Dong, H. (2025). Structural Design of a Multi-Stage Variable Stiffness Manipulator Based on Low-Melting-Point Alloys. Technologies, 13(8), 338. https://doi.org/10.3390/technologies13080338






