Abstract
It is demonstrated that neuromorphic materials designed for computational tasks can be effectively implemented by drawing an analogy with trigger-based systems built upon classical binary elements. Among the most promising approaches in this context are systems that perform computations based on the Residue Number System (RNS). A specific implementation of a trigger-based adder employing the proposed methodology is presented and tested through simulation modeling. This adder utilizes the representation of natural numbers as elements of a subtraction ring modulo P, where P is the product of Mersenne prime numbers. This configuration enables component-wise, independent execution of arithmetic operations. It is further shown that analogous trigger-based systems can be realized using recurrent neural network analogs, particularly those implemented with neuromorphic materials. The study emphasizes that it is possible to construct a neural network, especially one based on neuromorphic substrates, that can perform logical operations equivalent to those executed by conventional binary circuitry. A key challenge in the proposed approach lies in implementing an operation analogous to the carry mechanism employed in classical binary adders. An algorithm addressing this issue is proposed, based on the transition from computations modulo P to computations modulo 2P.
1. Introduction
At present, increasing attention is being paid to the development of computing systems based on fundamentally new physico-chemical principles. In particular, the literature reflects numerous attempts to design computing devices using biological polymers, including DNA-based architectures [1,2,3]. These efforts are closely aligned with extensive research in the domain of organic electronics [4,5,6], including organic transistors [7,8,9], organic optoelectronic components [10,11,12], and related technologies.
The demand for computing platforms built on unconventional physico-chemical foundations is well justified. As emphasized in [13,14,15], the potential for further advancement of traditional semiconductor technology—especially that based on the von Neumann architecture—has been largely exhausted. A similar perspective is adopted in [16,17], where it is noted that the von Neumann model leads to significant energy inefficiencies due to the continuous data transfer between processing units and memory elements.
Of particular interest in this context are neuromorphic materials, which aim to physically implement neural networks [18,19,20]. Various classes of such materials, many of them derived from organic electronics, are currently under active development [21,22,23]. One of their distinguishing features is the inherent capacity for parallel computation, enabling substantial improvements in both performance and energy efficiency.
Neuromorphic materials have already shown promising practical results. For instance, ref. [24] demonstrated that they can effectively address sensory multitask learning, facilitating the creation of systems analogous to the human retina for pattern recognition tasks. Moreover, studies such as [25,26] have shown that organic transistors can serve as the foundational elements of neural networks (or their analogs), supporting on-substrate, decentralized learning directly on the carrier medium (e.g., crystal).
It is also worth noting the growing body of research focused on the integration of artificial intelligence (AI) with neuromorphic substrates [27,28,29].
Nevertheless, an important contradiction (previously highlighted in [15]) remains unresolved. On the one hand, neuromorphic materials are predominantly designed to support learning procedures typical of classical neural networks [24,25,26]. On the other hand, their application in computational hardware inherently demands transparent and interpretable logic operations. In this regard, it is important to recognize that most existing types of neural networks are often logically opaque: while their training algorithms are well established, the resulting behavior of such networks is frequently difficult not only to predict but also to interpret. As a result, these limitations have prompted the emergence of research focused on explainable neural networks [30,31,32] and, more broadly, explainable AI [33,34,35].
As previously noted in [15], resolving the aforementioned contradiction remains an urgent research priority. In particular, studies such as [24,25,26] have shown that the operational logic of neuromorphic materials effectively represents a hybrid model, combining elements of neural network algorithms with those traditionally used in classical logic circuitry. Building upon these observations, ref. [15] proposed that it is both necessary and promising to develop specialized algorithms specifically tailored to support the operation of neuromorphic materials as the physico-chemical foundation for future computing systems.
Moreover, there is growing evidence to suggest that different classes of neuromorphic materials will ultimately be associated with distinct algorithmic frameworks, including those based on multi-valued logic. This perspective aligns well with the views expressed in [36], where the authors advocate for the formation of a new paradigm for biological artificial intelligence.
The problem of improving the operational algorithms of information processing systems based on neuromorphic materials is closely related to the methods that enable the construction of equivalent electronic circuits for such systems. At the very least, this approach ensures the transparency of the obtained results, as evidenced by the widespread use of equivalent electronic circuits in describing systems of various natures. For instance, the chips used in practice essentially represent multilayer structures comprising alternating p-type and n-type conductivity regions. Nevertheless, the operational characteristics of such structures can be analyzed through equivalent circuits assembled from transistors and other classical electronic components [37,38].
The method of constructing equivalent circuits is also extensively employed in electrochemistry (e.g., impedance modeling of elements [39,40]), biophysics (e.g., modeling the properties of cell membranes, where RC circuits are specifically used to describe ion channels [41,42]), and geophysical surveys involving electrical prospecting (e.g., modeling the properties of soil media [43,44]).
This method is likewise widely applied in studies of neuromorphic materials. For example, the behavior of memristive materials (including those based on titanium and hafnium oxides) can be modeled using equivalent circuits comprising variable resistors and nonlinear RC networks [45,46,47]. The behavior of materials undergoing phase transitions (such as those based on Ge2Sb2Te5 (GST) or VO2) can be modeled with equivalent circuits incorporating state switches, thermally sensitive resistors, and RC circuits capable of retaining thermal history, among other components [48,49,50]. Equivalent circuits for materials with ionic conductivity often employ RC networks with voltage-controlled nonlinear elements [51,52,53]. To further advance this approach, it appears advisable to adopt a combined methodology. In addition to developing equivalent circuits for existing neuromorphic materials, it is reasonable to pursue the design of equivalent circuits for promising neuromorphic systems—taking into account their fundamental characteristics, of course. This approach is justified, among other reasons, by the fact that the use of a nontrivial physico-chemical basis for computing technologies also necessitates a substantial modernization of their algorithmic foundation. The development and testing of such algorithms should reasonably be carried out using equivalent electronic circuits. As demonstrated for the first time in the present study, the specific characteristics of many neuromorphic materials capable of forming local memory cells [54,55] call for close attention to circuit architectures that serve as analogs of trigger elements.
In this study, we demonstrate that there exists an algorithm, structurally based on neural networks, capable of implementing an equivalent of a binary adder. Current trends in computing system design suggest that such functionality is sufficient to emulate the core logic of conventional processors.
The core of the proposed algorithm lies in the use of the Residue Number System (RNS)—a computational model that has recently seen increasing adoption in various fields [56,57,58]. Residue number systems can be interpreted in terms of a specific class of finite algebraic rings, namely rings of residue classes of integers under a given modulus.
It should also be noted that electronic adders and multipliers operating modulo an integer [59,60], which have been developed for a wide range of practical applications [61,62] and are compatible with RNS-based computing, have received significant attention in both academic and industrial research. In fact, ongoing developments in the domain of modular arithmetic circuits are also well documented in the patent literature [63,64,65,66]. The key feature of the algorithm proposed in this study lies in its orientation toward the use of a hybrid number system. For its sequential implementation, we introduce (also for the first time) an analog of the carry operation traditionally employed in binary adders.
A major advantage of the proposed algorithm, particularly in the context of neuromorphic material implementation, lies in its inherent support for parallel computation. This property enables the algorithm to natively exploit one of the fundamental strengths of physically realized neural networks—high-performance, energy-efficient parallel processing.
2. Methods
This study relies on several properties of algebraic rings, specifically those defined as rings of residue classes modulo an integer . Such rings can be decomposed into a direct sum of algebraic ideals, each of which can be associated with a corresponding Galois field [67]. In particular, when the modulus P is expressed as the product of prime numbers, this decomposition becomes especially structured and computationally tractable.
and the next formula is valid:
where is an arbitrary element of the ring of subtraction classes of the ring of integers modulo , are idempotent elements, and the values can be put in correspondence to the elements of the Galois field .
Idempotent elements have the property:
Formula (2) corresponds to the classical framework of modular arithmetic, which, as noted above, is finding an increasing number of practical applications. To illustrate the underlying idea more clearly, one may refer to an operation frequently encountered in practice—for instance, the addition of two decimal numbers by hand-written calculation. Each such number has a least significant digit, and the rules of addition de facto involve two operations applied to this digit. One of them is precisely modular addition modulo 10. For example, when adding 7 and 4, the least significant digit of the result is 1, which corresponds to the sum modulo 10 (i.e., the remainder after dividing the total by 10).
The second operation is the carry-over. Similarly, in multiplication, if the least significant digits of two numbers are 4 and 7, the least significant digit of the product is 8, again corresponding to the remainder modulo 10. Notably, in such operations, the result may be zero even when the multiplied numbers are nonzero modulo 10. In algebra, such numbers are referred to as “zero divisors.” For instance, the least significant digit of the product is zero when the numbers 2 and 5 are multiplied. Likewise, it is zero when summing numbers ending in 4 and 6.
The existence of zero divisors, in turn, leads to the emergence of multiple analogs of the multiplicative identity in the algebraic structure under consideration. Specifically, these are elements whose squares equal themselves, commonly referred to as idempotent elements.
They are formed according to the rule
where is an integer. These numbers are chosen on the basis of condition (4).
Idempotent elements cancel each other:
This follows, in particular, from the fact that the product includes all the somnomials of the number .
The possibility of using the representation (2) for parallel-sequential computations follows from the fact that there is
Comparison (7) is valid by virtue of the fact that the ring under consideration possesses a unit which is represented in the form of
From Formula (8), in particular, it follows that the computation of the sums is actually performed in the sense of an addition operation in the Galois field , since the addition is performed modulo since , which follows from (5).
Consequently,
where denotes the -th component of the number n in the sense of the decomposition (2).
This formula demonstrates that when the value is incremented by one, each component is also increased by one, but such addition is performed modulo . Formula (7), as well as its analog for the multiplication operation, can be the basis for the implementation of parallel (more precisely, parallel-sequential computations), which has been repeatedly reflected in the current literature, including the brief review presented above.
Thus, the question about the realization of a convenient and effective way of parallel-sequential calculations is reduced to finding a convenient and effective way of realizing the addition operation in Galois fields , where are prime numbers into which the number is decomposed, which can be interpreted as the maximum for this particular computing device.
The algorithm proposed in this study is based on the use of Mersenne prime numbers, defined as
This algorithm is analogous to the one previously developed using quasi-Mersenne numbers, as discussed in our earlier work [68]. The primary advantage of employing Mersenne primes lie in the possibility of implementing computations using highly simplified analogs of neural networks, including those compatible with polymer-based architectures. Such simplifications are especially relevant for the physical realization of neuromorphic systems, where minimalistic and energy-efficient structures are preferred.
3. Results
3.1. Utilization of Trigger-Based Systems for Computation Modulo Mersenne Numbers
As demonstrated in [69], a neural network composed of binary elements with threshold activation functions can be represented by components that perform binary logic operations. This correspondence can be formally proven through the representation of the threshold function via the Zhegalkin polynomial, which is widely used in information theory [70,71]. Moreover, this representation can be generalized to multivalued logic systems as well [72].
The reverse is also true: a neural network can be constructed—or trained—based on an analogy with a specific logical circuit composed of standard logical gates that perform a predefined set of operations. However, an important nuance must be considered. As shown in [15,73], neural network analogs based on elements with threshold (or near-threshold) characteristics and equipped with branched feedback loops are, in general, analogous to triggers.
The simplest form of such a system was examined in [73], and its schematic is presented in Figure 1. This configuration is simultaneously an analog of the classical RS flip-flop and a minimal feedback neural network, consisting of only two interconnected threshold elements. This circuit can be viewed as the simplest (more precisely, a degenerate) variant of a Hopfield neural processor [74], with the key distinction that feedback is present not only between elements but also from each element’s output to its own input (as highlighted in the caption to Figure 1). The purpose of this schematic is to clearly illustrate that the boundary between trigger-based systems and neural networks with feedback is not rigid. More specifically, it may already be inferred from this model that there exist neural networks in which local elements function as memory cells.
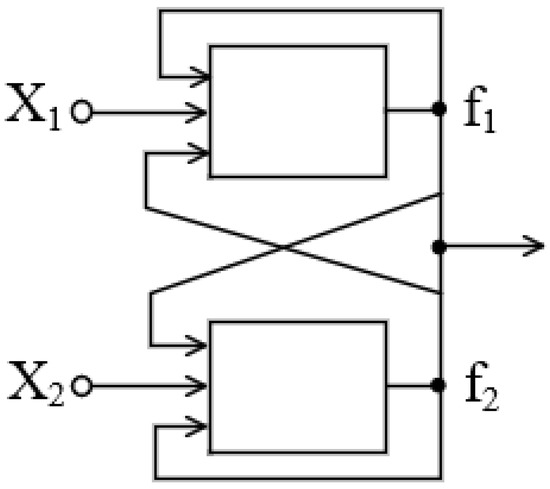
Figure 1.
Schematic representation of an RS-trigger analog with additional feedback loops [15]; are logical variables representing the input state, while denote the output state.
Consequently, in the context of training neural networks for computational purposes, it is advisable to initially focus on adder structures that serve as analogs of trigger systems. The rationale for employing such systems to train neural networks implemented with neuromorphic materials lies in the fact that a broad class of polymer-based systems inherently exhibit behavior analogous to flip-flops.
In particular, as demonstrated in [75], hysteresis phenomena can occur during phase transitions in systems based on hydrophilic polymers. This implies the existence of a range of external conditions under which the system can reside in two distinct stable states, thus functioning as a physical analog of a trigger.
A specific implementation of a trigger-based adder capable of performing modular addition using a Mersenne number as the modulus, and suitable for constructing neural network analogs of the aforementioned type, was proposed in [76]. The schematic of this adder is shown in Figure 2. (Notably, this design has been granted a patent in Kazakhstan [77].)
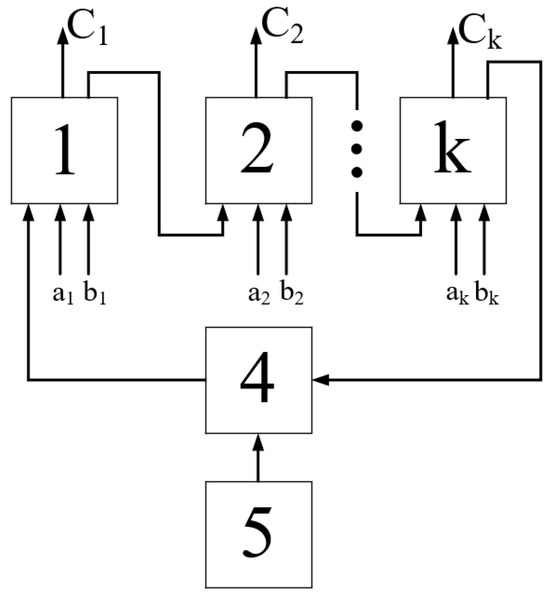
Figure 2.
Diagram of a modulo adder using feedback [57].
This circuit can also be regarded as a special case of the general trigger-based adder architecture introduced in [68], which supports addition modulo an arbitrary integer. The adder is based on the following property of Mersenne prime numbers represented in binary form:
Indeed, the number is obtained from the number by subtracting the number .
A detailed description of the operation of this circuit—consistent with the findings presented in [68,76]—is provided in the Supporting Information. This description also includes the results of simulation-based testing, conducted using the Proteus 8.17 software environment.
Let us now examine how this circuit can be applied to support series-parallel computations, leveraging its structural features for efficient neuromorphic implementation.
Formula (7) shows that at summation modulo , where are prime numbers, the components of summands are summarized independently, and for each of the components, summation is performed modulo , which corresponds to the operation of addition in the Galois field .
Consequently, when the summands are represented in the form corresponding to Formula (2), a set of independent adders, each of which can be assembled according to the scheme of Figure 2, can be used to provide summation.
Such an approach, obviously, really meets the realization of parallel-sequential computations, since adders corresponding to different Galois fields operate independently of each other. This property is of critical importance for the use of neuromorphic materials in computational architectures, as it enables a reduction in bit width for each independent adder unit, thereby contributing to overall system efficiency.
Moreover, a circuit similar to the adder shown in Figure 2 can also be employed to reduce an arbitrary binary number to its residue modulo a Mersenne number. This operation is essential for transforming a number from its original binary representation into separate “components”, as defined by Equation (7). Such decomposition forms the foundation for implementing parallel residue-based arithmetic, which is particularly well suited for neuromorphic computing environments.
Let us consider the reduction of some number written in binary form to one of the Mersenne prime numbers, , whose binary representation contains k binary digits. If this binary number contains exactly k binary digits, it is enough to feed it to the input of the adder of the type discussed above, i.e., by default, assume that the second summand is equal to 0. The trigger circuit will lead it to a number modulo . If the number of digits satisfies the inequality
then we can also use the proposed adder circuit. Indeed, consider the notation
In order to take the number (13) modulo , we must subtract the next number from it
and add the number .
Both of these operations are reduced to the number , corresponding to digits of the number modulo by adding the number . The special case where all binary symbols are 1 is eliminated by the proposed trigger circuit.
The block diagram implementing the above procedure for the case of and is presented in Figure 3, while the results of its testing, obtained via simulation modeling in the Proteus software, are shown in Figure 4. This diagram illustrates a converter that transforms a 5-bit binary number into its equivalent modulo 7 representation, with the output directly displayed on a seven-segment indicator. The circuits shown in Figure 3 and Figure 4 are directly based on Formula (14). Specifically, from the perspective of electronic circuit implementation, the removal of the higher-order digits that form the number expressed by Formula (14) implies that these digits are ignored—that is, the components corresponding to these digits are not included in the circuit design. Consequently, the operational principle of the circuit reduces to the addition of the binary number , which represents the lower-order digits, with the number , which corresponds to the number defined by Formula (14) divided by .
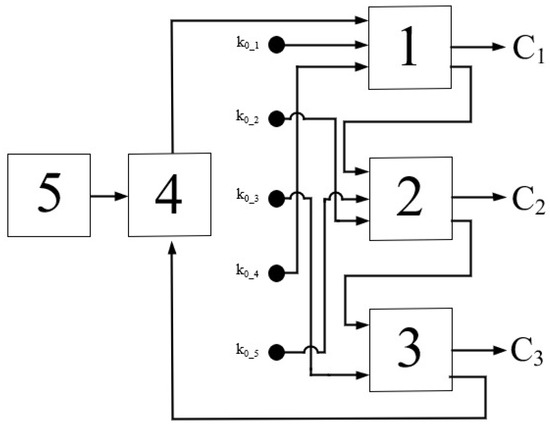
Figure 3.
Block diagram for converting a number containing 5 binary digits to modulo 7.
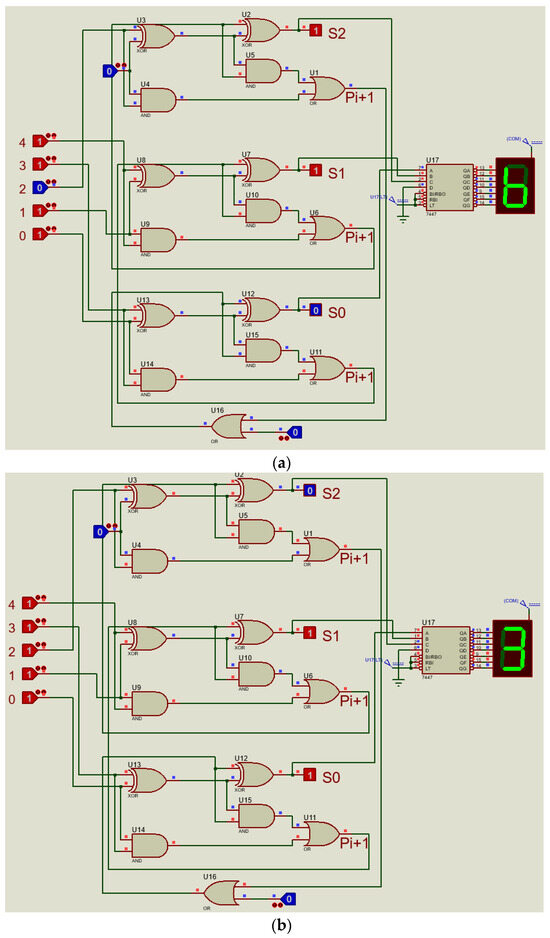
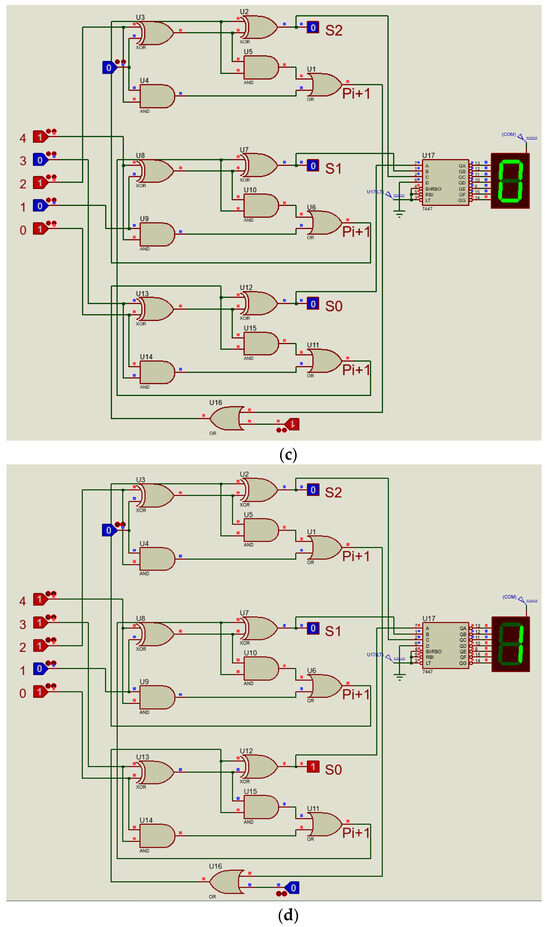
Figure 4.
Scheme for converting a number containing 5 binary digits to a number modulo 7: (a) input value: 27, output: 6; (b) input value: 31, output: 3; (c) input value: 21, output: 0; (d) input value: 29, output: 1.
Figure 4 presents specific results of circuit testing conducted in the Proteus software. The illustrated figures reflect the outcomes of testing under various cases, thereby confirming the validity of the adopted methodology. The simulation circuit used for testing was constructed as follows.
The circuit employs three cascaded single-bit full adders, each implemented using two XOR gates, two AND gates, and one OR gate. The inputs to the first adder correspond to signals at inputs 0 and 3 in the circuit shown in Figure 4. The carry-in input, i.e., the input of the XOR gate (U12), receives the carry-out signal from the higher-order adder via the OR gate (U16). The sum and carry-out values are computed by the gates U13 and U12 (XOR), U14 and U15 (AND), and U11 (OR), with the carry-out connected to the carry-in of the subsequent adder.
The second adder receives input signals from inputs 1 and 4 of the circuit, as well as the carry-out from the lower-order adder. This adder is constructed using XOR gates U8 and U7 for the sum, AND gates U9 and U10 for partial carry generation, and OR gate U6. The highest-order (third) adder accepts the signal from input 2, while its second input is tied to a constant logical zero. XOR gates U3 and U2, AND gates U4 and U5, and OR gate U1 generate the higher-order sum bit S2 and the final carry, which is not utilized in this circuit.
The three resulting bits S2, S1, and S0 are fed into inputs A, B, and C of the 74LS47 decoder (U17), which converts the binary signal combination into a decimal digit. This provides a clear correspondence between the test results of the circuit and the expected output. The decoder input D is hardwired to ground (“0”), ensuring the correct display of digits ranging from 0 to 7.
A similar approach can be used when inequality (12) is not satisfied. In this case, the above procedure should be repeated as many times as the number of digits exceeds .
The reverse procedure, i.e., the transition to the binary representation in the usual form, can be realized directly on the basis of Formula (2), for which ordinary processors operating in standard binary logic can be used.
It should be noted that the trigger-based system variant considered here, which is natural for performing computational operations, is by no means unique. As demonstrated in [15], the circuit depicted in Figure 1 exhibits multidimensional hysteresis behavior (see Figure 5 and Figure 6).
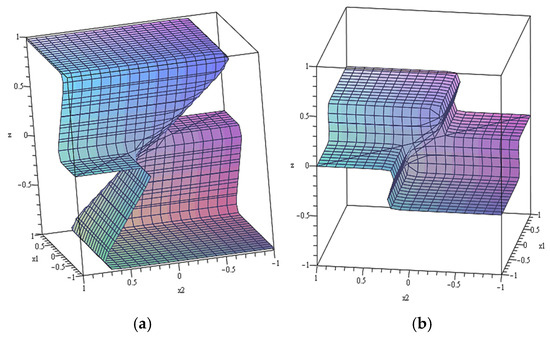
Figure 5.
Three-dimensional graph of the dependence of the solution of the system of Equation (15) on different values of variables , ; , (a); , (b) [15].
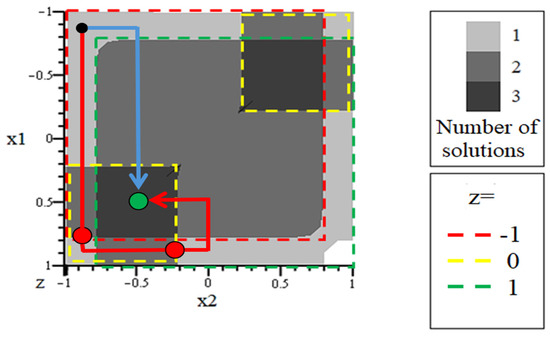
Figure 6.
Decision map for the considered analog of a trigger based on two neurons [15]; parameters: a = 10, k = 0.5; the darkest color shows the areas that correspond to three possible solutions of the system of Equation (15); the lightest color shows the areas that correspond to only one possible solution; the intermediate color corresponds to two solutions; the dashed lines also show the areas that correspond to the three possible solutions of the system of Equation (15). , , .
Figure 5 presents a three-dimensional graph corresponding to the following system of equations that describe the trigger analog shown in Figure 1.
where are variables describing the states of the inputs (assumed to vary within the range from −1 to +1), and the activation function is defined as follows:
As noted in [15], Figure 5 demonstrates that for identical values of the control parameters , the system under consideration can be in several different states. Moreover, the realization of a particular state of the system depends not only on the current values of but also on the trajectory of the representing point on the map, schematically represented in Figure 6. This map represents a projection of the figure shown in Figure 5a onto the coordinate plane corresponding to the control parameters. The folded nature of this figure results in regions on the map that correspond to different numbers of solutions of the considered system of equations. The temporal variation of the control parameters corresponds to the movement of the representative point across the map. The current values of the control parameters determine the specific position of the representative point.
Figure 6 shows two possible trajectories of the imaging point. It can be seen that at the same initial and final values of a pair of control parameters, the point can move along different paths. The trajectory shown in red corresponds to two jump transitions shown by the bold red dots. One of these transitions is from a state to a state , and the other is from a state to a state , which corresponds to the endpoint of the trajectory. When moving along the trajectory shown in blue, there are no transitions, i.e., when reaching the endpoint of the trajectory, the system remains in state .
The fact that the representative point may follow different trajectories depending on the nature of external influences (interpreted as an applied coded sequence) can be understood as follows. Specifically, it can be asserted that the final state of the system under consideration depends not only on the current parameters but also on its “prehistory,” that is, on the character of the stimuli previously applied to the system. Consequently, there is a potential to employ systems exhibiting multidimensional hysteresis for the implementation of computational architectures of the following type. One set of control parameters (corresponding, for example, to the first term when the system is used as an adder) is utilized for its “programming,” thereby defining the “prehistory.” A second set of control parameters, applied to the system at subsequent moments in time, ensures the desired summation result.
Thus, there exists a fundamental possibility for the modernization of computational systems, where the classical concept of an “input,” as traditionally understood in modern electronics, is also transformed. This approach is justified by the ongoing miniaturization of computational elements. In such a scenario, the formation of communication channels between system elements inevitably becomes a challenging task (especially for neuromorphic materials) since the volume allocated for information transmission channels may become significant as miniaturization progresses. The use of programmable structures promises to reduce this number in the future.
The sequential realization of this approach is, of course, a matter for the future; however, the considerations presented here provide additional justification for the development of equivalent circuits for neuromorphic materials based on trigger analogs.
Other possibilities also exist for the implementation of systems under consideration. Essentially, any system capable of residing in multiple stable states under identical values of thermodynamic variables is suitable for this purpose.
Let us now proceed to compare the computational capabilities of circuits based on trigger analogs with those of classical binary processors.
3.2. Comparison of the Effective Digit Capacity of an Adder Based on Mersenne Numbers with the Capacity of Existing Adders
Let us start from the obvious fact that any physically realizable adders actually perform summation modulo operation. Thus, a 16-bit adder, widely used in practice [78], actually performs summation modulo 216, because the bit with number 17 will be discarded after summation (even if it acquires a non-zero value). The corresponding element is not in the circuit. Special measures must be taken to ensure that this highest bit is taken into account when using 16-bit adders. Many processors use the carry bit as a flag register that includes carry, zero, overflow, and sign flags.
The summation result will correspond to the summation result in the sense of ordinary arithmetic if it does not exceed the maximum allowable number defined by the adder design. Consequently, it is permissible to proceed from summation modulo 216 to summation modulo any other number. Ultimately, this is no more than a matter of agreement and convenience. In particular, it is convenient to use numbers P, which are the product of Mersenne prime numbers for parallel-sequential calculations.
The first prime numbers of this type are 3, 7, 31, 127, and 8191. To compare the adder built on independent blocks corresponding to Mersenne numbers with existing types of adders, it is convenient to use Table 1. The first columns of this table contain Mersenne numbers, which are multipliers of the number P; the penultimate column contains the logarithm of the product on base 2; and the last column contains numbers rounded down to an integer value. This allows us to compare an adder built on Mersenne prime numbers with traditional binary ones.

Table 1.
Toward a comparison of the effective binary digit capacity of the adder on Mersenne prime numbers with binary adders.
It can be seen that the same range that corresponds to the 16-bit adder overlaps the adder realized on the basis of the product of the first four Mersenne numbers. The use of the product of the first five numbers allows us to come quite close to the 32-bit adder.
Thus, we can conclude that the development of a scheme of computations modulo Mersenne prime numbers (or, equivalently, computations in their corresponding Galois fields) really provides the transition to parallel-sequential computations, and the effective binary digit capacity in this case correlates with the computational elements actually used in practice (16-summarizer, 32-adder).
This type of adder is of independent interest, similar to that of 16- and 32-summarizers, on the basis of which arithmetic-logic units (ALUs) as well as processors are designed.
There is, however, a nuance. Namely, such a scheme performs only calculations modulo P. Consequently, we should also consider the case when the sum of two numbers is equal to or greater than P, i.e., we are actually talking about the analog of the operation of bit transfer.
The significance of this issue stems from the following considerations. Depending on the specific implementation of the neural network analog performing binary addition functions, it may be convenient to operate with different moduli P. In particular, it is quite feasible to utilize separate adders corresponding to Mersenne numbers not exceeding 31. Such a scenario is especially likely during the initial stages of developing processor analogs based on novel physico-chemical hardware platforms.
Consequently, the relevant problem becomes the implementation of adders—operating according to Equation (7)—that handle only a single group of digits. Specifically, if polymer materials are used, which facilitate the realization of separate adders for Mersenne numbers up to 31, it is reasonable to employ at least two groups of adders, each containing adders corresponding to the moduli 3, 7, and 31.
As follows from Table 1, these two groups combined provide computational power that slightly exceeds that of a typical 16-bit binary adder (approximately 18 bits).
Therefore, implementing an analog of a 16-bit or 32-bit processor in this context necessitates the development of an algorithm that serves as an equivalent to the carry operation used in classical binary adders. The specificity of this task lies in the fact that this operation must be performed not on a single digit but rather on an entire group of digits.
3.3. Algorithm for the Carry Operation Across Groups of Digits
From our perspective, the operation considered in this section is crucial for the functioning of computational devices built upon nontrivial physico-chemical foundations and employing separate adders. This conclusion is illustrated by Figure 7, which emphasizes that the use of a numeral system based on a finite algebraic ring corresponding to an arbitrary modulus P generally implies a partitioning of a number into specific digit groups.
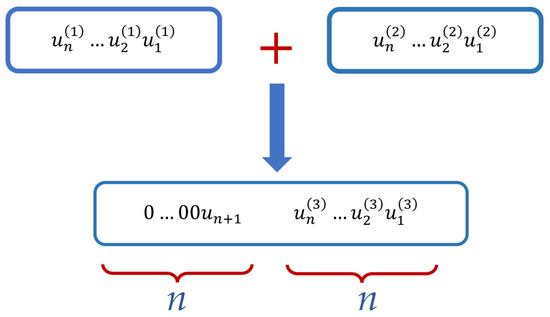
Figure 7.
Illustration of the carry operation in a hybrid numeral system.
Indeed, a generalization of representing a number in binary or decimal numeral systems can be expressed by the following formula:
Indeed, by analogy with the decimal or binary representation of a number, instead of Formula (17), we can write down
However, if a numeral system with a base of the form (1) is used—which technically corresponds to employing separate adders—then each symbol in Equation (18) effectively represents the use of a group of digits (or, more precisely, their analogs).
Therefore, instead of the symbols corresponding to the base P, we can denote the corresponding groups of digits associated with addition modulo a prime number.
This notation can also be interpreted as a representation of an integer in a number system with a hybrid base [79]. In this context, the number P is interpreted as the base of a hybrid numeral system.
Let us consider the simplest case illustrated in Figure 7. The result U of the addition of two numbers not exceeding P can also be represented in the form (17), and in the most general case,
The value is exactly the remainder of the division of by P, i.e., the number U taken modulo P. The value of can take a value of either 1 or 0, which corresponds to the operation of transfer of a digit, which is highlighted by Figure 7. The figure emphasizes that, whereas the terms can be represented as a single group , the summation corresponds to a representation through two such groups, with only one component, , in the higher-order group being nonzero; its value is either zero or one.
Let us consider the algorithm that allows performing this operation when using trigger adders.
Due to the fact that two summands, each of which does not exceed P, are summed, this sum can be represented through the elements of a finite algebraic ring corresponding to the classes of deductions modulo . The number 2 is also prime, so the next formula is valid:
in which the number of digits and, correspondingly, the number of idempotent elements is increased by one.
The idempotent element corresponds to the multiplier 2, respectively, it is easy to show that
Let us refer to Formula (9). In particular, it shows that if we consider the elements of the ring corresponding to the natural numbers , then the value of the digits will remain unchanged by the addition of one more idempotent element.
Formula (9) also shows that the elements of the considered algebraic ring, which correspond to the natural numbers satisfying the inequality
will correspond to the same set of values .
As one would expect from Formula (9), these values change periodically with period P. However, the number P is odd. Hence, if we consider a number n satisfying the inequality
then the parity of the component will coincide with the parity of the value .
On the contrary, if the number n satisfies the inequality (23), then the values and will have different parity.
For the sake of clarity, let us consider a concrete example of using the additional digit in the case when the circuit contains two independent adders corresponding to the fields and . According to Formula (2), the use of two such adders covers the range of integers up to and including 20. With respect to the operations of addition and multiplication, any number less than 21 is representable as a sum modulo 21.
where take the following values:
In operations modulo 21, the elements of the ring of subtraction classes appearing in (25) act as idempotent elements, i.e., there is
The elements cancel each other because they contain the multiplier 21, and their sum modulo 6 is equal to one.
Let us extend the representation (25) to the case when the computation is modulo 21 · 2 = 42, which corresponds to the discharge transfer procedure discussed above. Then, any number smaller than 42 is representable in the form
where
In accordance with the above, the comparison of Formulas (24) and (29) leads to the following result, which is illustrated in Table 2.

Table 2.
Values used in the implementation of the carry operation algorithm for the particular case of a hybrid number system with bases 3 and 7.
The first column of this table shows the natural number n; the next three columns show the quantities , representing the number n taken modulo 3, 7, and 2, respectively. The fifth column shows the quantity , which represents the number n taken modulo 21 (or, equivalently, the result of applying Formula (25) to the quantities and ). The sixth column represents the quantity taken modulo 2, i.e., the result of determining its parity . In the last column is the product of . Table 2 emphasizes that for the first 21 numbers, the parity of and coincide.
It can be seen that the values and , regardless of the appearance of an additional digit, provide summation modulo 21. This corresponds to the calculation of the lowest digit in the number system (16).
Determination of the parity of this value will allow us to form the operation of carrying the digit. Indeed, if the parity of coincides with the parity of , there is no discharge transfer. The discharge transfer is performed in the opposite case.
In fact, this operation is a direct analog of the bit carry operation used in binary logic-based systems. The corresponding block diagram can also be constructed based on the exclusive OR operation (Figure 8). Blocks “3” and “7” perform addition of the original numbers modulo 3 and 7, respectively. Block “2” carries out addition modulo 2, effectively determining the parity of the summation result. The “Q” block determines the parity of the summation result based on the outputs of blocks “3” and “7.” The Exclusive Or block compares the parities. If the parities differ, a logical one is generated at its output, corresponding to the carry operation; otherwise, the output is logical zero. Nevertheless, we emphasize once again that even without using this operation the analog of a 16-bit adder can be realized, and by the number of logic elements involved, it does not differ significantly from the analog built entirely on binary logic.
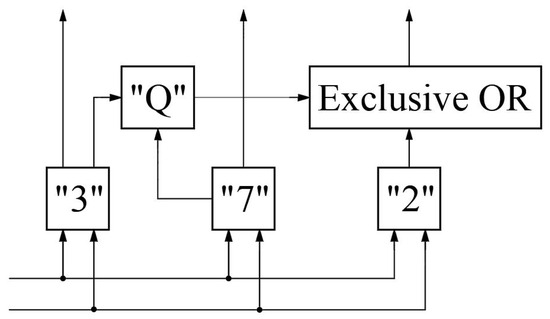
Figure 8.
Block diagram illustrating the carry operation for the hybrid number system with bases 3 and 7.
4. Discussion
Any neural network constructed from elements possessing threshold characteristics (or characteristics close to threshold) can be reduced to a circuit built from classical binary elements. Moreover, if the number of elements in the neural network is relatively small, this reduction can be performed analytically, for example, using methods from projective geometry [80]. Therefore, it is possible to first develop a promising computational circuit based on classical binary components and subsequently implement a neural network—potentially using neuromorphic materials—that performs the same operations. In this process, it is, of course, advisable to fully leverage the specific physico-chemical properties of the systems underlying the neuromorphic materials.
It is well known that many polymer-based systems, including hydrophilic polymers, undergo phase transitions [81]. As noted above, such transitions are often accompanied by hysteresis phenomena [75], meaning that under certain conditions, the system can exist in two distinct stable states for the same values of controlling thermodynamic parameters. This fact renders such systems analogous to flip-flops (triggers), as a defining characteristic of a trigger (including the classical RS flip-flop) is its ability to reside in two distinct stable states.
Consequently, as fundamental electronic circuits intended for subsequent implementation as neural networks, it is reasonable to use trigger-based adders. Such adders performing modular arithmetic with respect to an integer modulus were first proposed in [76]. Their distinctive feature is the use of a minimal number of logic elements compared to designs described in the literature [62,63,64,65,66]. This efficiency is achieved because the operation of reducing an integer modulo is realized through feedback loops, which make the circuit an analog of a trigger.
In this work, it is shown that the simplest trigger-based adder corresponds to the case where the modulus is the product of numbers expressible in the form .
The use of modular arithmetic with respect to an integer composed of prime factors is of particular interest for implementing computing systems based on neuromorphic materials. Specifically, as follows from Equation (7), the addition and multiplication operations for each “component” of the integer are performed independently. Consequently, a modular adder with modulus decomposes into a collection of independent adders, each executing addition modulo —an individual prime factor in the factorization of . This implies that relatively simple neural networks can be used to implement each individual computational unit, which facilitates their physical realization in the form of neuromorphic materials.
In particular, adders corresponding to numbers 3, 7, and 31 correspond to neural networks constructed from two, three, and five fundamental elements, respectively. The implementation of such neural networks is a feasible task at the current level of research in this field. Furthermore, as follows from Table 1, the aggregate of these simplest adders corresponds to a 9-bit adder. However, adders corresponding to larger Mersenne primes require neural networks with substantially more basic elements. Therefore, scenarios exist in which it is reasonable to employ two groups of adders, each corresponding to the primes 3, 7, and 31. Two such groups provide the implementation of an 18-bit adder, which exceeds the bit width of the 16-bit adders frequently used in contemporary practice.
The use of more than one group of adders of the type described above effectively corresponds to computations within a hybrid numeral system (the term is understood in accordance with the arguments presented in [79]). The employment of such a numeral system, in turn, necessitates the development of an algorithm that implements an operation analogous to the carry operation fundamental to classical binary adders.
As follows from the materials presented above, this algorithm can also be constructed based on the residue number system (RNS) by transitioning from computations modulo a prime number P to computations modulo 2P. The advantage of this algorithm lies in the fact that operations within the main digit group remain unchanged, corresponding to computations modulo P. The carry operation analog thereby reduces to determining the parity of the resulting quantities, which directly follows from Table 2.
The most significant conclusion that can be drawn from the presented materials is as follows. Analogies between electronic circuits realized with classical binary logic elements and neural networks implemented on neuromorphic materials provide an additional foundation for creating programmable molecular- and supramolecular-level structures. It goes without saying that such tasks have long been and remain fundamental within nanotechnology as a whole. In particular, the aforementioned programmable structures offer additional opportunities for the creation of drug delivery systems, and corresponding trends are already emerging in practice [82,83,84,85,86]. The proposed approach potentially enables the use of equivalent electronic circuits for such systems and, accordingly, paves the way for the development of algorithmic languages for molecular programming.
While solving such challenges is clearly a matter for the future, a number of practical applications exist where computational systems based on hydrophilic polymers are of particular interest. Specifically, this relates to self-tuning systems requiring controlled modulation of hydrogel states. The examples of such systems are described in [87,88], which is of interest regarding the practical implementation of the smart house concept, currently developing across various domains [89,90,91].
The core idea underpinning [87] is based on the readily demonstrable fact that only a small fraction of the energy consumed by any household necessarily relates to electricity (computers, smartphones, etc.). The operation of heating, air conditioning, refrigeration, and similar systems does not inherently require the conversion of energy, such as that derived from wind turbines, into electricity. For example, a wind-driven heating system for residential spaces may be constructed around the circulation of saline solution within a circuit that includes a heat-generating element based on a polyelectrolyte hydrogel. The operation of such an element may be controlled conventionally (via a computer interface), or it may be realized through self-regulation.
This challenge is prospectively addressed by employing simple programs embedded within the heat-generating element, where the hydrogel itself serves as the program carrier. Crucially, in solving such problems, there are no significant spatial limitations on the size of individual logic elements (or neuron analogs) enabling system programming. This, in particular, means that existing developments [92,93,94] in creating analogs of traditional electronic components (transistors, diodes, etc.) based on alternative physico-chemical foundations can be utilized.
For clarity, Table 3 presents a comparison of prospective computational systems based on neuromorphic materials utilizing trigger circuits with other approaches.

Table 3.
Comparison of different types of adders.
5. Conclusions
Thus, it is possible to establish a correspondence between operations performed by neural networks, assuming their elements have threshold-like characteristics, and electronic circuits constructed from binary logic elements.
This enables the design of neural networks intended for computation, based on analogs assembled from binary logic elements. In this regard, trigger-based adders are optimal for the modeling of neuromorphic materials, as they are analogs of bistable systems realized using polymer-based materials. There is a direct analogy between neural networks constructed from threshold elements with feedback loops and trigger-like systems. This analogy, among other things, facilitates the transition to equivalent electronic circuits based on polymer materials, which are capable of existing in multiple stable states under identical thermodynamic parameters. This prospectively enables the realization of equivalent electronic circuits for neuromorphic materials and the development of devices based on such materials, relying on these types of circuits refined through well-established simulation tools.
A significant step in this direction is associated with the possibility of proposing a scheme of an adder that performs parallel-sequential calculations by utilizing the residue number system (RNS).
In the considered case, a natural number n, not exceeding the maximum number representable by logical variables corresponding to the adder output states, is uniquely mapped to an element of the ring of classes modulo an integer P, which is the product of Mersenne prime numbers. Since P is a product of Mersenne primes, computation modulo P reduces to independent computations modulo each of its prime factors. This allows the use of independent adders performing addition modulo the respective Mersenne number.
A distinctive feature of the considered adder is that for certain summands, the circuit transforms into an analog of an RS flip-flop; i.e., in this case, the circuit becomes bistable.
For the implementation of this approach, an analog of the carry operation is critically important. In the case of employing the residue number system, this analog exhibits significant peculiarities. The corresponding algorithm can be constructed by transitioning from computations modulo P to computations modulo 2P.
Overall, the method of equivalent electronic circuits represents a promising tool for the advancement of computational systems based on neuromorphic materials. In particular, it is conceivable to consider, in the future, the development of software that facilitates the design of neuromorphic materials through the use of equivalent electronic circuits of individual “blocks.”
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/technologies13080326/s1, Figure S1. Illustration of the appearance of two different stable states in the circuit of Figure 2 in the case when the sum of binary numbers is 7; (a)—there are ones at the outputs of all three adders, (b)—there are zeros at the output of all three adders; The circuit was compiled in the Proteus 8 program.
Author Contributions
Conceptualization, I.S.; Formal analysis, D.S. and K.K.; Funding acquisition, D.S., K.K. and I.S.; Investigation, K.K., J.C. and Y.V.; Methodology, D.S., J.C. and I.S.; Project administration, Y.V.; Resources, K.K. and J.C.; Software, K.K.; Supervision, Y.V.; Validation, K.K.; Visualization, Y.V.; Writing—original draft, I.S.; Writing—review and editing, D.S., J.C. and Y.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP23490107).
Institutional Review Board Statement
Ethical review and approval were waived for this study because it did not involve human participants or animal subjects.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Yelizaveta Vitulyova was employed by the “Institute of Digital Engineering and Technology” JSC. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Demir, B.; Akin Gultakti, C.; Koker, Z.; Anantram, M.P.; Oren, E.E. Electronic Properties of DNA Origami Nanostructures Revealed by In Silico Calculations. J. Phys. Chem. B 2024, 128, 4646–4654. [Google Scholar] [CrossRef]
- Katz, E. DNA- and RNA-Based Computing Systems, 1st ed.; Wiley-VCH: Weinheim, Germany, 2021. [Google Scholar]
- Fan, D.; Wang, J.; Wang, E.; Dong, S. Propelling DNA Computing with Materials’ Power: Recent Advancements in Innovative DNA Logic Computing Systems and Smart Bio-Applications. Adv. Sci. 2020, 7, 2001766. [Google Scholar] [CrossRef] [PubMed]
- Krauhausen, I.; Coen, C.; Spolaor, S.; Gkoupidenis, P.; Van De Burgt, Y. Brain-Inspired Organic Electronics: Merging Neuromorphic Computing and Bioelectronics Using Conductive Polymers. Adv. Funct. Mater. 2024, 34, 2307729. [Google Scholar] [CrossRef]
- Friederich, P.; Fediai, A.; Kaiser, S.; Konrad, M.; Jung, N.; Wenzel, W. Toward Design of Novel Materials for Organic Electronics. Adv. Mater. 2019, 31, 1808256. [Google Scholar] [CrossRef] [PubMed]
- Casalini, S.; Bortolotti, C.A.; Leonardi, F.; Biscarini, F. Self-Assembled Monolayers in Organic Electronics. Chem. Soc. Rev. 2017, 46, 40–71. [Google Scholar] [CrossRef]
- Kukhta, N.A.; Marks, A.; Luscombe, C.K. Molecular Design Strategies Toward Improvement of Charge Injection and Ionic Conduction in Organic Mixed Ionic–Electronic Conductors for Organic Electrochemical Transistors. Chem. Rev. 2021, 122, 4325–4355. [Google Scholar] [CrossRef]
- Rivnay, J.; Inal, S.; Salleo, A.; Owens, R.M.; Berggren, M.; Malliaras, G.G. Organic Electrochemical Transistors. Nat. Rev. Mater. 2018, 3, 17086. [Google Scholar] [CrossRef]
- Huang, W.; Chen, J.; Yao, Y.; Zheng, D.; Ji, X.; Feng, L.W.; Facchetti, A. Vertical Organic Electrochemical Transistors for Complementary Circuits. Nature 2023, 613, 496–502. [Google Scholar] [CrossRef]
- Bryce, M.R. A Review of Functional Linear Carbon Chains and Their Applications as Molecular Wires in Electronics and Optoelectronics. J. Mater. Chem. C 2021, 9, 10524–10546. [Google Scholar] [CrossRef]
- Yu, P.; Zhen, Y.; Dong, H.; Hu, W. Crystal Engineering of Organic Optoelectronic Materials. Chem 2019, 5, 2814–2853. [Google Scholar] [CrossRef]
- Ullbrich, S.; Benduhn, J.; Jia, X.; Nikolis, V.C.; Tvingstedt, K.; Piersimoni, F.; Vandewal, K. Emissive and Charge-Generating Interfaces for Optoelectronics. Nat. Mater. 2019, 18, 459–464. [Google Scholar] [CrossRef]
- Shalf, J. The Future of Computing Beyond Moore’s Law. Philos. Trans. R. Soc. A 2020, 378, 2166. [Google Scholar] [CrossRef]
- Leiserson, C.E.; Thompson, N.C.; Emer, J.S.; Kuszmaul, B.C.; Lampson, B.W.; Sanchez, D.; Schardl, T.B. There’s Plenty of Room at the Top: What Will Drive Computer Performance After Moore’s Law? Science 2020, 368, eaam9744. [Google Scholar] [CrossRef] [PubMed]
- Suleimenov, I.; Gabrielyan, O.; Kopishev, E.; Kadyrzhan, A.; Bakirov, A.; Vitulyova, Y. Advanced Applications of Polymer Hydrogels in Electronics and Signal Processing. Gels 2024, 10, 715. [Google Scholar] [CrossRef] [PubMed]
- Niu, X.; Tian, B.; Zhu, Q.; Dkhil, B.; Duan, C. Ferroelectric Polymers for Neuromorphic Computing. Appl. Phys. Rev. 2022, 9, 021309. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, W.; Zeng, J.; Fan, F.; Gu, J.; Chen, X.; Yan, L.; Xie, G.; Liu, S.; Yan, Q.; et al. 90% Yield Production of Polymer Nano-Memristor for In-Memory Computing. Nat. Commun. 2021, 12, 1984. [Google Scholar] [CrossRef]
- Gumyusenge, A.; Melianas, A.; Keene, S.T.; Salleo, A. Materials Strategies for Organic Neuromorphic Devices. Annu. Rev. Mater. Res. 2021, 51, 47–71. [Google Scholar] [CrossRef]
- Melianas, A.; Quill, T.J.; LeCroy, G.; Tuchman, Y.; Loo, H.V.; Keene, S.T.; Giovannitti, A.; Lee, H.R.; Maria, I.P.; McCulloch, I.; et al. Temperature-Resilient Solid-State Organic Artificial Synapses for Neuromorphic Computing. Sci. Adv. 2020, 6, eabb2958. [Google Scholar] [CrossRef]
- Park, M.H.; Kim, Y.; Choi, M.J.; Kim, Y.B.; Yun, J.M.; Jeong, J.H.; Kang, S.J. Enhanced In-Sensor Computing with Spike Number-Dependent Plasticity in an InGaSnO Neuromorphic Device. ACS Nano 2025, 19, 13107–13117. [Google Scholar] [CrossRef]
- Hoch, F.L.; Wang, Q.; Lim, K.G.; Loke, D.K. Multifunctional Organic Materials, Devices, and Mechanisms for Neuroscience, Neuromorphic Computing, and Bioelectronics. Nano-Micro Lett. 2025, 17, 251. [Google Scholar] [CrossRef]
- Kim, K.N.; Sung, M.J.; Park, H.L.; Lee, T.W. Organic Synaptic Transistors for Bio-Hybrid Neuromorphic Electronics. Adv. Electron. Mater. 2022, 8, 2100935. [Google Scholar] [CrossRef]
- Tuchman, Y.; Mangoma, T.N.; Gkoupidenis, P.; Van De Burgt, Y.; John, R.A.; Mathews, N.; Salleo, A. Organic Neuromorphic Devices: Past, Present, and Future Challenges. MRS Bull. 2020, 45, 619–630. [Google Scholar] [CrossRef]
- Wu, X.; Wang, S.; Huang, W.; Dong, Y.; Wang, Z.; Huang, W. Wearable In-Sensor Reservoir Computing Using Optoelectronic Polymers with Through-Space Charge-Transport Characteristics for Multi-Task Learning. Nat. Commun. 2023, 14, 468. [Google Scholar] [CrossRef] [PubMed]
- Krauhausen, I.; Koutsouras, D.A.; Melianas, A.; Keene, S.T.; Lieberth, K.; Ledanseur, H.; Sheelamanthula, R.; Giovannitti, A.; Torricelli, F.; Mcculloch, I.; et al. Organic Neuromorphic Electronics for Sensorimotor Integration and Learning in Robotics. Sci. Adv. 2021, 7, eabl5068. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Jiang, Y.; Zhong, D.; Zhang, Z.; Choudhury, S.; Lai, J.-C.; Gong, H.; Niu, S.; Yan, X.; Zheng, Y.; et al. Neuromorphic Sensorimotor Loop Embodied by Monolithically Integrated, Low-Voltage, Soft e-Skin. Science 2023, 380, 735–742. [Google Scholar] [CrossRef]
- Choi, Y.; Jeong, S.; Jeong, H.; Han, S.; Ko, J.; Yu, S.E.; Bae, S.H. Advanced AI Computing Enabled by 2D Material-Based Neuromorphic Devices. npj Unconv. Comput. 2025, 2, 8. [Google Scholar] [CrossRef]
- Gandolfi, D.; Mapelli, J.; Puglisi, F.M. Brain-Inspired Computing: From Neuroscience to Neuromorphic Electronics for New Forms of Artificial Intelligence. Front. Neurosci. 2025, 19, 1565811. [Google Scholar] [CrossRef]
- Li, Y.; Ding, G.; Zhai, Y.; Lv, Z.; Yan, Y.; Xue, S.; Han, S.T. MXene-Based Flexible Memory and Neuromorphic Devices. Small 2025, 2410914. [Google Scholar] [CrossRef]
- Ibrahim, R.; Shafiq, M.O. Explainable Convolutional Neural Networks: A Taxonomy, Review, and Future Directions. ACM Comput. Surv. 2023, 55, 1–37. [Google Scholar] [CrossRef]
- Damilola, S. A Review of Unsupervised Artificial Neural Networks with Applications. Int. J. Comput. Appl. 2019, 181, 22–26. [Google Scholar] [CrossRef]
- Dike, H.U.; Zhou, Y.; Deveerasetty, K.K.; Wu, Q. Unsupervised Learning Based on Artificial Neural Network: A Review. In Proceedings of the 2018 IEEE International Conference on Cyborg and Bionic Systems (CBS), Shenzhen, China, 25–27 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 322–327. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Carloni, G.; Berti, A.; Colantonio, S. The Role of Causality in Explainable Artificial Intelligence. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2025, 15, e70015. [Google Scholar] [CrossRef]
- Mersha, M.; Lam, K.; Wood, J.; AlShami, A.K.; Kalita, J. Explainable Artificial Intelligence: A Survey of Needs, Techniques, Applications, and Future Direction. Neurocomputing 2024, 599, 128111. [Google Scholar] [CrossRef]
- Perera, J.; Balasubramaniam, S.; Somathilaka, S.; Wen, Q.; Li, X.; Kasthurirathna, D.; Nelson, T. Wet-Neuromorphic Computing: A New Paradigm for Biological Artificial Intelligence. IEEE Intell. Syst. 2025, 40, 39–48. [Google Scholar] [CrossRef]
- Shi, X.; Ma, J.-G.; Yeo, K.S.; Do, M.A.; Li, E. Equivalent Circuit Model of On-Wafer CMOS Interconnects for RFICs. IEEE Trans. VLSI Syst. 2005, 13, 1060–1071. [Google Scholar] [CrossRef]
- Gielen, G.; Dehaene, W. Analog and Digital Circuit Design in 65 nm CMOS: End of the Road? In Proceedings of the Design, Automation and Test in Europe, Munich, Germany, 7–11 March 2005; Volume 1, pp. 37–42. [Google Scholar] [CrossRef]
- Zhang, L.; Dai, Y.; Li, C.; Dang, Y.; Zheng, R.; Wang, Z.; Wang, Y.; Cui, Y.; Arandiyan, H.; Shao, Z.; et al. Recent Advances in Electrochemical Impedance Spectroscopy for Solid-State Batteries. Energy Storage Mater. 2024, 69, 103378. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of Electrochemical Impedance Spectroscopy to Commercial Li-Ion Cells: A Review. J. Power Sources 2020, 480, 227742. [Google Scholar] [CrossRef]
- Hille, B. Ion Channels of Excitable Membranes, 3rd ed.; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Koch, C. Biophysics of Computation: Information Processing in Single Neurons; Oxford Academic: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Binley, A.; Kemna, A. DC Resistivity and Induced Polarization Methods. In Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 129–156. [Google Scholar] [CrossRef]
- Revil, A.; Florsch, N. Determination of Permeability from Spectral Induced Polarization in Granular Media. Geophys. J. Int. 2010, 181, 1480–1498. [Google Scholar] [CrossRef]
- Li, Y.; Su, K.; Chen, H.; Zou, X.; Wang, C.; Man, H.; Liu, K.; Xi, X.; Li, T. Research Progress of Neural Synapses Based on Memristors. Electronics 2023, 12, 3298. [Google Scholar] [CrossRef]
- Ali, M.; Lee, D.; Ahmad, I.; Kim, H.-D. Recent Progress in Memristor-Based Gas Sensors: Device Modeling, Mechanisms, Performance, and Prospects. Sens. Actuators Rep. 2025, 9, 100269. [Google Scholar] [CrossRef]
- Zeumault, A.; Alam, S.; Wood, Z.; Weiss, R.J.; Aziz, A.; Rose, G.S. TCAD Modeling of Resistive-Switching of HfO2 Memristors: Efficient Device-Circuit Co-Design for Neuromorphic Systems. Front. Nanotechnol. 2021, 3, 734121. [Google Scholar] [CrossRef]
- Zhang, W.; Mazzarello, R.; Wuttig, M.; Ma, E. Designing Crystallization in Phase-Change Materials for Universal Memory and Neuro-Inspired Computing. Nat. Rev. Mater. 2019, 4, 150–168. [Google Scholar] [CrossRef]
- AlZaabi, M.; Halawani, Y.; Mohammad, B. In-Memory Computing Using Phase Change Memory. In In-Memory Computing Hardware Accelerators for Data-Intensive Applications; Mohammad, B., Halawani, Y., Eds.; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Driscoll, T.; Kim, H.-T.; Chae, B.-G.; Di Ventra, M.; Basov, D.N. Phase-Transition Driven Memristive System. Appl. Phys. Lett. 2009, 95, 043503. [Google Scholar] [CrossRef]
- Berdan, R.; Vasilaki, E.; Khiat, A.; Indiveri, G.; Serb, A.; Prodromakis, T. Emulating Short-Term Synaptic Dynamics with Memristive Devices. Sci. Rep. 2016, 6, 18639. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, H.; Burr, G.W.; Hwang, C.S.; Wang, K.L.; Xia, Q.; Yang, J.J. Resistive Switching Materials for Information Processing. Nat. Rev. Mater. 2020, 5, 173–195. [Google Scholar] [CrossRef]
- Yarragolla, S.; Hemke, T.; Jalled, F.; Gergs, T.; Trieschmann, J.; Arul, T.; Mussenbrock, T. Identifying and Understanding the Nonlinear Behavior of Memristive Devices. Sci. Rep. 2024, 14, 31633. [Google Scholar] [CrossRef]
- Zhou, Y.; Ramanathan, S. Mott Memory and Neuromorphic Devices. Proc. IEEE 2015, 103, 1289–1310. [Google Scholar] [CrossRef]
- Ryndin, E.; Andreeva, N.; Luchinin, V. Compact Model for Bipolar and Multilevel Resistive Switching in Metal-Oxide Memristors. Micromachines 2022, 13, 98. [Google Scholar] [CrossRef]
- Oke, A.A.; Nathaniel, B.A.; Bukola, B.F.; Ayopo, O.A. Residue Number System Based Applications: A Literature Review. Ann. Comput. Sci. Ser. 2021, 19, 1. [Google Scholar]
- Chang, C.H.; Molahosseini, A.S.; Zarandi, A.A.E.; Tay, T.F. Residue Number Systems: A New Paradigm to Datapath Optimization for Low-Power and High-Performance Digital Signal Processing Applications. IEEE Circuits Syst. Mag. 2015, 15, 26–44. [Google Scholar] [CrossRef]
- Younes, D.; Steffan, P. Efficient Image Processing Application Using Residue Number System. In Proceedings of the 20th International Conference Mixed Design of Integrated Circuits and Systems-MIXDES 2013, Gdynia, Poland, 20–22 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 468–472. [Google Scholar]
- Beuchat, J.-L. Some Modular Adders and Multipliers for Field Programmable Gate Arrays. In Proceedings of the International Parallel and Distributed Processing Symposium, Nice, France, 22–26 April 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 1–8. [Google Scholar] [CrossRef]
- Kuo, C.-T.; Wu, Y.-C. FPGA Implementation of a Novel Multifunction Modulo (2n ± 1) Multiplier Using Radix-4 Booth Encoding Scheme. Appl. Sci. 2023, 13, 10407. [Google Scholar] [CrossRef]
- Abd-Elkader, A.A.H.; Rashdan, M.; Hasaneen, E.A.M.; Hamed, H.F.A. Efficient Implementation of Montgomery Modular Multiplier on FPGA. Comput. Electr. Eng. 2022, 97, 107585. [Google Scholar] [CrossRef]
- Patel, B.K.; Kanungo, J. Efficient Tree Multiplier Design by Using Modulo 2n + 1 Adder. In Proceedings of the 2021 Emerging Trends in Industry 4.0 (ETI 4.0), Raigarh, India, 19–21 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Irkhin, V.P.; Obukhov, A.N.; Gul’bin, S.S. Device for Modulo Addition and Subtraction of Numbers. RU Patent 2 145 112 C1, 27 January 2000. [Google Scholar]
- Ebihara, H.; Kiyoto. Circuit for Modulo Multiplication and Exponentiation Arithmetic. EP Patent EP0801345B1, 10 October 2002. [Google Scholar]
- Suprun, V.P. Modulo Four Adder. EA Patent EA030205B1, 31 July 2018. [Google Scholar]
- Petrenko, V.I.; Stepanian, N.E.; Nelidin, I.R. Multi-Digit Parallel Adder Modulo with Serial Transfer. RU Patent RU2724597C1, 25 June 2020. [Google Scholar]
- Suleimenov, I.; Kadyrzhan, A.; Matrassulova, D.; Vitulyova, Y. Peculiarities of Applying Partial Convolutions to the Computation of Reduced Numerical Convolutions. Appl. Sci. 2024, 14, 6388. [Google Scholar] [CrossRef]
- Kadyrzhan, A.; Kadyrzhan, K.; Bakirov, A.; Suleimenov, I. Prospects for the Use of Quasi-Mersen Numbers in the Design of Parallel-Serial Processors. Appl. Sci. 2025, 15, 741. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Bakirov, A.S.; Matrassulova, D.K. A Technique for Analyzing Neural Networks in Terms of Ternary Logic. J. Theor. Appl. Inf. Technol. 2021, 99, 2537–2553. [Google Scholar]
- Barotov, D.N.; Barotov, R.N. Polylinear Transformation Method for Solving Systems of Logical Equations. Mathematics 2022, 10, 918. [Google Scholar] [CrossRef]
- Barotov, D.N.; Barotov, R.N.; Soloviev, V.; Feklin, V.; Muzafarov, D.; Ergashboev, T.; Egamov, K. Development of Suitable Inequalities and Their Application to Systems of Logical Equations. Mathematics 2022, 10, 1851. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Vitulyova, Y.S.; Kabdushev, S.B.; Bakirov, A.S. Improving the Efficiency of Using Multivalued Logic Tools. Sci. Rep. 2023, 13, 1108. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Gabrielyan, O.A.; Bakirov, A.S. Initial Study of General Theory of Complex Systems: Physical Basis and Philosophical Understanding. Bull. Electr. Eng. Inform. 2025, 14, 774–789. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neurons with Graded Response Have Collective Computational Properties Like Those of Two-State Neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Guven, O.; Mun, G.A.; Uzun, C.; Gabrielyan, O.A.; Kabdushev, S.B.; Agibaeva, L.; Nurtazin, A. Hysteresis Effects During the Phase Transition in Solutions of Temperature Sensitive Polymers. Eurasian Chem. Tech. J. 2017, 19, 41. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Vitulyova, Y.S.; Shaltykova, D.B.; Matrassulova, D.K.; Bakirov, A.S. Pattern Recognition Methods as a Base of Development of New Instruments for Investigations in Physical Chemistry. In Proceedings of the 2022 European Symposium on Software Engineering, Rome, Italy, 27–29 October 2022; pp. 127–132. [Google Scholar]
- Mun, G.A.; Baipakbaeva, S.T.; Kadyrzhan, K.N.; Kabdushev, S.B.; Vitulyova, E.S.; Konshin, S.V.; Suleimenov, I.E. Adder by Module 22 − 1. U.S. Patent 36236, 26 May 2023. [Google Scholar]
- Kornstein, H. 8086—Its Development and Capability. Microprocessors 1978, 2, 166–169. [Google Scholar] [CrossRef]
- Suleimenov, I.; Vitulyova, Y.; Bakirov, A. Hybrid Number Systems: Application for Calculations in Galois Fields. In Proceedings of the 2022 3rd Asia Conference on Computers and Communications (ACCC), Shanghai, China, 16–18 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 126–130. [Google Scholar]
- Vitulyova, Y.S.; Bakirov, A.S.; Shaltykova, D.B.; Suleimenov, I.E. Prerequisites for the Analysis of the Neural Networks Functioning in Terms of Projective Geometry. In Proceedings of the 2020 4th International Conference on Information Processing and Control Engineering University of California, Berkeley, CA, USA, 27–29 June 2020; Volume 946, p. 012001. [Google Scholar]
- Radecki, M.; Spěváček, J.; Zhigunov, A.; Sedláková, Z.; Hanyková, L. Temperature-Induced Phase Transition in Hydrogels of Interpenetrating Networks of Poly(N-isopropylacrylamide) and Polyacrylamide. Eur. Polym. J. 2015, 68, 68–79. [Google Scholar] [CrossRef]
- Yang, X.; Ahmad, K.; Yang, T.; Fan, Y.; Zhao, F.; Jiang, S.; Hou, H. Collagen-Based Hydrogel Sol-Gel Phase Transition Mechanism and Their Applications. Adv. Colloid Interface Sci. 2025, 340, 103456. [Google Scholar] [CrossRef]
- Liu, X.; Li, B.; Wang, W.; Zhang, Y.; Li, H.; Li, Z. Multistimuli-Responsive Hydrogels with Both Anisotropic Mechanical Performance and Anisotropic Luminescent Behavior. Chem. Eng. J. 2022, 449, 137718. [Google Scholar] [CrossRef]
- Ruiz, A.L.; Ramirez, A.; McEnnis, K. Single and Multiple Stimuli-Responsive Polymer Particles for Controlled Drug Delivery. Pharmaceutics 2022, 14, 421. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, Q.; Yu, S.; Akhavan, B. Poly (Ethylene Glycol)-Based Hydrogels for Drug Delivery in Cancer Therapy: A Comprehensive Review. Adv. Healthc. Mater. 2023, 12, 2300105. [Google Scholar] [CrossRef]
- Rust, T.; Jung, D.; Langer, K.; Kuckling, D. Stimuli-Accelerated Polymeric Drug Delivery Systems. Polym. Int. 2023, 72, 5–19. [Google Scholar] [CrossRef]
- Suleimenov, I.; Egemberdieva, Z.; Bakirov, A.; Baipakbayeva, S.; Kopishev, E.; Mun, G. Efficiency Problem of Renewable Energetics Systems in the Context of “Smart House” Concept. E3S Web Conf. 2020, 164, 13002. [Google Scholar] [CrossRef]
- Suleimenov, I.; Kadyrzhan, K.; Kabdushev, S.; Bakirov, A.; Kopishev, E. New Equipment for Aromatherapy and Related Mobile App: A Tool to Support Small Peasant Farms in Kazakhstan in Crisis. In Robotics, Machinery and Engineering Technology for Precision Agriculture; Springer: Singapore, 2021; pp. 347–355. [Google Scholar]
- Yar, H.; Imran, A.S.; Khan, Z.A.; Sajjad, M.; Kastrati, Z. Towards Smart Home Automation Using IoT-Enabled Edge-Computing Paradigm. Sensors 2021, 21, 4932. [Google Scholar] [CrossRef]
- Agee, P.; Gao, X.; Paige, F.; McCoy, A.; Kleiner, B. A Human-Centred Approach to Smart Housing. Build. Res. Inf. 2021, 49, 84–99. [Google Scholar] [CrossRef]
- Taiwo, O.; Ezugwu, A.E.; Oyelade, O.N.; Almutairi, M.S. Enhanced Intelligent Smart Home Control and Security System Based on Deep Learning Model. Wirel. Commun. Mob. Comput. 2022, 2022, 9307961. [Google Scholar] [CrossRef]
- Ho, J.C.; Lin, Y.C.; Chen, C.K.; Hsu, L.C.; Chen, W.C. Hydrogel-Based Sustainable and Stretchable Field-Effect Transistors. Org. Electron. 2022, 100, 106358. [Google Scholar] [CrossRef]
- Beck, A.; Obst, F.; Gruner, D.; Voigt, A.; Mehner, P.J.; Gruenzner, S.; Richter, A. Fundamentals of Hydrogel-Based Valves and Chemofluidic Transistors for Lab-on-a-Chip Technology: A Tutorial Review. Adv. Mater. Technol. 2023, 8, 2200417. [Google Scholar] [CrossRef]
- Zhang, Y.; Jeong, C.K.; Wang, J.; Chen, X.; Choi, K.H.; Chen, L.Q.; Wang, Q. Hydrogel Ionic Diodes Toward Harvesting Ultralow-Frequency Mechanical Energy. Adv. Mater. 2021, 33, 2103056. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).