Long Short-Term Memory Mixture Density Network for Remaining Useful Life Prediction of IGBTs
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
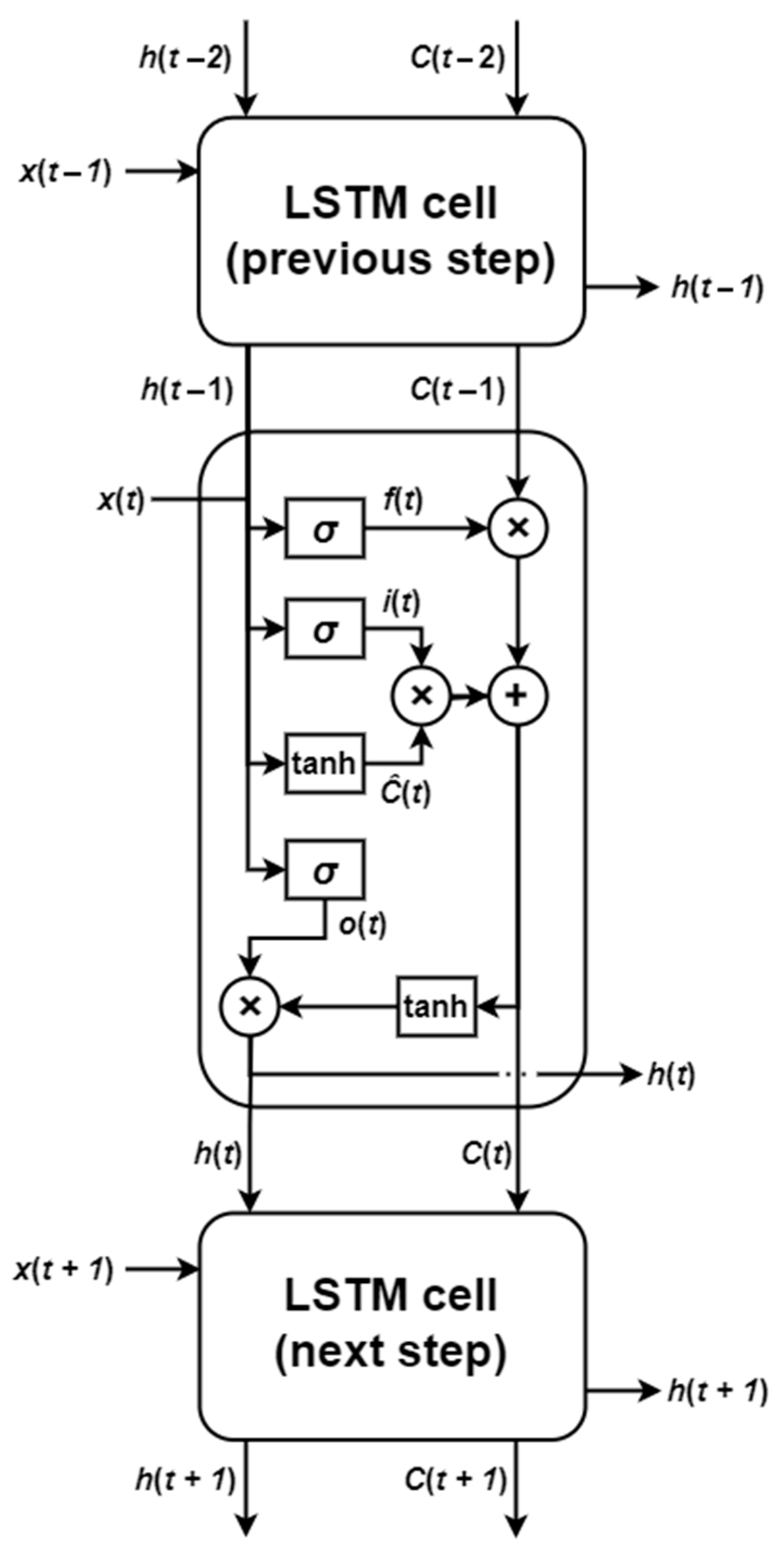
3.1. Network Architecture
3.2. Experimental Setup
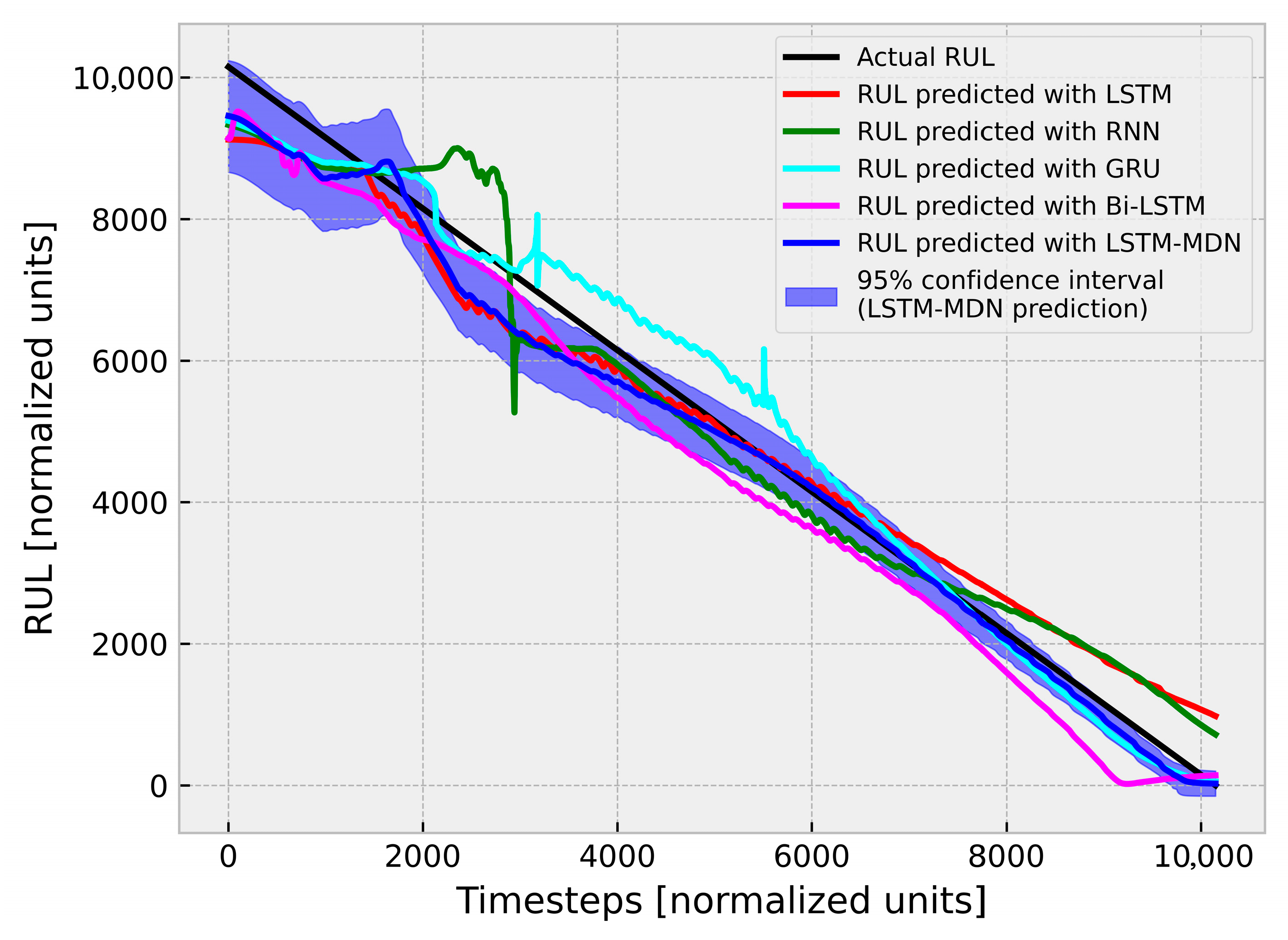
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IGBT | Insulated Gate Bipolar Transistor |
| RUL | Remaining Useful Life |
| LSTM | Long Short-Term Memory |
| MDN | Mixture Density Network |
| CNN | Convolutional Neural Network |
| SVR | Support Vector Regression |
| GPR | Gaussian Process Regression |
| NASA | National Aeronautics and Space Administration |
| Bi-LSTM | Bi-directional LSTM |
| RNN | Recurrent Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| RMSE | Root Mean Squared Error |
| R2 | Coefficient of Determination |
| GRU | Gated Recurrent Unit |
References
- Dai, J.; Kim, C.; Mukundhan, P. Applications of Picosecond Laser Acoustics to Power Semiconductor Device: IGBT and MOSFET. In Proceedings of the 2023 China Semiconductor Technology International Conference (CSTIC), Shanghai, China, 17–26 June 2023; pp. 1–3. [Google Scholar]
- Zhuang, L.; Xu, A.; Wang, X.-L. A Prognostic Driven Predictive Maintenance Framework Based on Bayesian Deep Learning. Reliab. Eng. Syst. Saf. 2023, 234, 109181. [Google Scholar] [CrossRef]
- Wang, K.; Sun, P.; Zhu, B.; Luo, Q.; Du, X. Monitoring Chip Branch Failure in Multichip IGBT Modules Based on Gate Charge. IEEE Trans. Ind. Electron. 2023, 70, 5214–5223. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, F.; Zhao, T.; Li, Z.; Li, M.; Liu, D. IGBT Status Prediction Based on PSO-RF with Time-Frequency Domain Features. In Proceedings of the 2022 IEEE 11th Data Driven Control and Learning Systems Conference (DDCLS), Chengdu, China, 3–5 August 2022; pp. 337–341. [Google Scholar]
- Cruz, Y.J.; Rivas, M.; Quiza, R.; Beruvides, G.; Haber, R.E. Computer Vision System for Welding Inspection of Liquefied Petroleum Gas Pressure Vessels Based on Combined Digital Image Processing and Deep Learning Techniques. Sensors 2020, 20, 4505. [Google Scholar] [CrossRef] [PubMed]
- Cruz, Y.J.; Rivas, M.; Quiza, R.; Villalonga, A.; Haber, R.E.; Beruvides, G. Ensemble of Convolutional Neural Networks Based on an Evolutionary Algorithm Applied to an Industrial Welding Process. Comput. Ind. 2021, 133, 103530. [Google Scholar] [CrossRef]
- Sommeregger, L.; Pilz, J. Regularizing Lifetime Drift Prediction in Semiconductor Electrical Parameters with Quantile Random Forest Regression. Technologies 2024, 12, 165. [Google Scholar] [CrossRef]
- Perçuku, A.; Minkovska, D.; Hinov, N. Enhancing Electricity Load Forecasting with Machine Learning and Deep Learning. Technologies 2025, 13, 59. [Google Scholar] [CrossRef]
- Ali, A.R.; Kamal, H. Time-to-Fault Prediction Framework for Automated Manufacturing in Humanoid Robotics Using Deep Learning. Technologies 2025, 13, 42. [Google Scholar] [CrossRef]
- El Bazi, N.; Guennouni, N.; Mekhfioui, M.; Goudzi, A.; Chebak, A.; Mabrouki, M. Predicting the Temperature of a Permanent Magnet Synchronous Motor: A Comparative Study of Artificial Neural Network Algorithms. Technologies 2025, 13, 120. [Google Scholar] [CrossRef]
- Alomari, Y.; Andó, M.; Baptista, M.L. Advancing Aircraft Engine RUL Predictions: An Interpretable Integrated Approach of Feature Engineering and Aggregated Feature Importance. Sci. Rep. 2023, 13, 13466. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, S.; Qiu, L.; Zhang, Y.; Wang, Y.; Wang, Z.; Yang, G. A Remaining Useful Life Prediction Method Based on PSR-Former. Sci. Rep. 2022, 12, 17887. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W.D. A Data-Driven Approach With Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2021, 68, 3170–3180. [Google Scholar] [CrossRef]
- Chechkin, A.; Pleshakova, E.; Gataullin, S. A Hybrid KAN-BiLSTM Transformer with Multi-Domain Dynamic Attention Model for Cybersecurity. Technologies 2025, 13, 223. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, J.; Wong, D.; Sun, C.; Yan, R. Probabilistic Remaining Useful Life Prediction Based on Deep Convolutional Neural Network. In Proceedings of the 9th International Conference on Through-life Engineering Services (TESConf 2020), Cranfield, UK, 3-4 November 2020. [Google Scholar]
- Zhao, D.; Liu, F. Cross-Condition and Cross-Platform Remaining Useful Life Estimation via Adversarial-Based Domain Adaptation. Sci. Rep. 2022, 12, 878. [Google Scholar] [CrossRef] [PubMed]
- Kerin, M.; Hartono, N.; Pham, D.T. Optimising Remanufacturing Decision-Making Using the Bees Algorithm in Product Digital Twins. Sci. Rep. 2023, 13, 701. [Google Scholar] [CrossRef]
- Unni, R.; Yao, K.; Zheng, Y. Deep Convolutional Mixture Density Network for Inverse Design of Layered Photonic Structures. ACS Photonics 2020, 7, 2703–2712. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, B.; Liu, J.; Zhang, G.; Wang, J. IGBT Aging Monitoring and Remaining Lifetime Prediction Based on Long Short-Term Memory (LSTM) Networks. Microelectron. Reliab. 2020, 114, 113902. [Google Scholar] [CrossRef]
- Ma, L.; Huang, J.; Chai, X.; He, S. Life Prediction for IGBT Based on Improved Long Short-Term Memory Network. In Proceedings of the 2023 IEEE 18th Conference on Industrial Electronics and Applications (ICIEA), Ningbo, China, 18–22 August 2023; pp. 868–873. [Google Scholar]
- Wang, X.; Zhou, Z.; He, S.; Liu, J.; Cui, W. Performance Degradation Modeling and Its Prediction Algorithm of an IGBT Gate Oxide Layer Based on a CNN-LSTM Network. Micromachines 2023, 14, 959. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Li, Y. Remaining Useful Life Prediction for IGBT Based on SO-Bi- ALSTM. In Proceedings of the 2023 IEEE 9th International Conference on Cloud Computing and Intelligent Systems (CCIS), Dali, China, 12–13 August 2023; pp. 193–198. [Google Scholar]
- Lu, Z.; Guo, C.; Liu, M.; Shi, R. Remaining Useful Lifetime Estimation for Discrete Power Electronic Devices Using Physics-Informed Neural Network. Sci. Rep. 2023, 13, 10167. [Google Scholar] [CrossRef] [PubMed]
- Yousuf, S.; Khan, S.A.; Khursheed, S. Remaining Useful Life (RUL) Regression Using Long–Short Term Memory (LSTM) Networks. Microelectron. Reliab. 2022, 139, 114772. [Google Scholar] [CrossRef]
- Castano, F.; Cruz, Y.J.; Villalonga, A.; Haber, R.E. Data-Driven Insights on Time-to-Failure of Electromechanical Manufacturing Devices: A Procedure and Case Study. IEEE Trans. Industr. Inform. 2023, 19, 7190–7200. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.; Li, X. Machine Remaining Useful Life Prediction via an Attention-Based Deep Learning Approach. IEEE Trans. Ind. Electron. 2021, 68, 2521–2531. [Google Scholar] [CrossRef]
- Fei, Z.; Huang, Z.; Zhang, X. Voltage and Temperature Information Ensembled Probabilistic Battery Health Evaluation via Deep Gaussian Mixture Density Network. J. Energy Storage 2023, 73, 108587. [Google Scholar] [CrossRef]
- Kim, G.; Yang, S.M.; Kim, S.; Kim, D.Y.; Choi, J.G.; Park, H.W.; Lim, S. A Multi-Domain Mixture Density Network for Tool Wear Prediction under Multiple Machining Conditions. Int. J. Prod. Res. 2023, 1–20, 2289076. [Google Scholar] [CrossRef]
- Bazzani, L.; Larochelle, H.; Torresani, L. Recurrent Mixture Density Network for Spatiotemporal Visual Attention. arXiv 2017, arXiv:1603.08199. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, R.; Chevalier, G.; Shah, R.C.; Romijnders, R. Applying Deep Bidirectional LSTM and Mixture Density Network for Basketball Trajectory Prediction. Optik 2018, 158, 266–272. [Google Scholar] [CrossRef]
- Felder, M.; Kaifel, A.; Graves, A. Wind Power Prediction Using Mixture Density Recurrent Neural Networks. In Proceedings of the European Wind Energy Conference & Exhibition 2010 (EWEC 2010), Warsaw, Poland, 20-23 April 2010; pp. 3417–3424. [Google Scholar]
- Mukherjee, S.; Shankar, D.; Ghosh, A.; Tathawadekar, N.; Kompalli, P.; Sarawagi, S.; Chaudhury, K. ARMDN: Associative and Recurrent Mixture Density Networks for ERetail Demand Forecasting. arXiv 2018, arXiv:1803.03800. [Google Scholar] [CrossRef]
- Schwab, D.; O’Rourke, S.M.; Minnehan, B.L. Combining LSTM and MDN Networks for Traffic Forecasting Using the Argoverse Dataset. In Proceedings of the 2021 IEEE 24th International Conference on Information Fusion (FUSION), Sun City, South Africa, 1–4 November 2021; pp. 1–6. [Google Scholar]
- Chen, M.; Chen, R.; Cai, F.; Li, W.; Guo, N.; Li, G. Short-Term Traffic Flow Prediction with Recurrent Mixture Density Network. Math. Probl. Eng. 2021, 2021, 6393951. [Google Scholar] [CrossRef]
- Gugulothu, N.; Subramanian, E.; Bhat, S.P. Sparse Recurrent Mixture Density Networks for Forecasting High Variability Time Series with Confidence Estimates. In Artificial Neural Networks and Machine Learning—ICANN 2019: Deep Learning: 28th International Conference on Artificial Neural Networks, Munich, Germany, September 17–19, 2019, Proceedings, Part II; Springer: Berlin/Heidelberg, Germany, 2019; pp. 422–433. ISBN 978-3-030-30483-6. [Google Scholar]
- Lei, Y.; Karimi, H.R.; Chen, X. A Novel Self-Supervised Deep LSTM Network for Industrial Temperature Prediction in Aluminum Processes Application. Neurocomputing 2022, 502, 177–185. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, Y.; Yan, J.; Han, S.; Li, L.; Long, Q. Improved Deep Mixture Density Network for Regional Wind Power Probabilistic Forecasting. IEEE Trans. Power Syst. 2020, 35, 2549–2560. [Google Scholar] [CrossRef]
- Bishop, C.M. Mixture Density Networks; Aston University: Birmingham, UK, 1994. [Google Scholar]
- Celaya, J.; Wysocki, P.; Goebel, K. IGBT Accelerated Aging Data Set; NASA Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2009. [Google Scholar]
- Xiao, D.; Qin, C.; Ge, J.; Xia, P.; Huang, Y.; Liu, C. Self-Attention-Based Adaptive Remaining Useful Life Prediction for IGBT with Monte Carlo Dropout. Knowl. Based Syst. 2022, 239, 107902. [Google Scholar] [CrossRef]
- Boutrous, K.; Bessa, I.; Puig, V.; Nejjari, F.; Palhares, R.M. Data-Driven Prognostics Based on Evolving Fuzzy Degradation Models for Power Semiconductor Devices. PHM Soc. Eur. Conf. 2022, 7, 68–77. [Google Scholar] [CrossRef]
- Ismail, A.; Saidi, L.; Sayadi, M.; Benbouzid, M. A New Data-Driven Approach for Power IGBT Remaining Useful Life Estimation Based On Feature Reduction Technique and Neural Network. Electronics 2020, 9, 1571. [Google Scholar] [CrossRef]
- Ge, J.; Huang, Y.; Tao, Z.; Li, B.; Xiao, D.; Li, Y.; Liu, C. RUL Predict of IGBT Based on DeepAR Using Transient Switch Features. PHM Soc. Eur. Conf. 2020, 5, 11. [Google Scholar] [CrossRef]
- Cruz, Y.J.; Castaño, F.; Haber, R.E.; Villalonga, A.; Ejsmont, K.; Gladysz, B.; Flores, Á.; Alemany, P. Self-Reconfiguration for Smart Manufacturing Based on Artificial Intelligence: A Review and Case Study BT—Artificial Intelligence in Manufacturing: Enabling Intelligent, Flexible and Cost-Effective Production Through AI; Soldatos, J., Ed.; Springer Nature: Cham, Switzerland, 2024; pp. 121–144. ISBN 978-3-031-46452-2. [Google Scholar]
- Cruz, Y.J.; Villalonga, A.; Castaño, F.; Rivas, M.; Haber, R.E. Automated Machine Learning Methodology for Optimizing Production Processes in Small and Medium-Sized Enterprises. Oper. Res. Perspect. 2024, 12, 100308. [Google Scholar] [CrossRef]






| Model | RNN | GRU | LSTM | Bi-LSTM | LSTM-MDN (Our Approach) | ||
|---|---|---|---|---|---|---|---|
| Validation device | 2 | (cycles) | 543.72 | 453.83 | 514.53 | 561.26 | 384.33 |
| 0.96 | 0.98 | 0.96 | 0.96 | 0.98 | |||
| 3 | (cycles) | 558.99 | 447.81 | 520.16 | 593.89 | 352.27 | |
| 0.96 | 0.98 | 0.97 | 0.95 | 0.98 | |||
| 4 | (cycles) | 534.18 | 416.52 | 544.11 | 460.60 | 381.50 | |
| 0.96 | 0.98 | 0.96 | 0.97 | 0.98 | |||
| 5 | (cycles) | 542.85 | 534.68 | 522.75 | 450.06 | 396.89 | |
| 0.96 | 0.96 | 0.96 | 0.97 | 0.98 | |||
| Average | (cycles) | 544.94 | 463.21 | 525.39 | 516.45 | 378.75 | |
| 0.96 | 0.98 | 0.96 | 0.96 | 0.98 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz, Y.J.; Castaño, F.; Haber, R.E. Long Short-Term Memory Mixture Density Network for Remaining Useful Life Prediction of IGBTs. Technologies 2025, 13, 321. https://doi.org/10.3390/technologies13080321
Cruz YJ, Castaño F, Haber RE. Long Short-Term Memory Mixture Density Network for Remaining Useful Life Prediction of IGBTs. Technologies. 2025; 13(8):321. https://doi.org/10.3390/technologies13080321
Chicago/Turabian StyleCruz, Yarens J., Fernando Castaño, and Rodolfo E. Haber. 2025. "Long Short-Term Memory Mixture Density Network for Remaining Useful Life Prediction of IGBTs" Technologies 13, no. 8: 321. https://doi.org/10.3390/technologies13080321
APA StyleCruz, Y. J., Castaño, F., & Haber, R. E. (2025). Long Short-Term Memory Mixture Density Network for Remaining Useful Life Prediction of IGBTs. Technologies, 13(8), 321. https://doi.org/10.3390/technologies13080321








