Abstract
Monitoring Peripheral Oxygen Saturation (SpO2) is an important vital sign both in Intensive Care Units (ICUs), during surgery and convalescence, and as part of remote medical consultations after of the COVID-19 pandemic. This has made the development of new SpO2-measurement tools an area of active research and opportunity. In this paper, we present a new Deep Learning (DL) combined strategy to estimate SpO2 without contact, using pre-magnified facial videos to reveal subtle color changes related to blood flow and with no calibration per subject required. We applied the Eulerian Video Magnification technique using the Hermite Transform (EVM-HT) as a feature detector to feed a Three-Dimensional Convolutional Neural Network (3D-CNN). Additionally, parameters and hyperparameter Bayesian optimization and an ensemble technique over the dataset magnified were applied. We tested the method on 18 healthy subjects, where facial videos of the subjects, including the automatic detection of the reference from a contact pulse oximeter device, were acquired. As performance metrics for the SpO2-estimation proposal, we calculated the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and other parameters from the Bland–Altman (BA) analysis with respect to the reference. Therefore, a significant improvement was observed by adding the ensemble technique with respect to the only optimization, obtaining 14.32% in RMSE (reduction from 0.6204 to 0.5315) and 13.23% in MAE (reduction from 0.4323 to 0.3751). On the other hand, regarding Bland–Altman analysis, the upper and lower limits of agreement for the Mean of Differences (MOD) between the estimation and the ground truth were 1.04 and −1.05, with an MOD (bias) of −0.00175; therefore, MOD = −0.00175 ± 1.04. Thus, by leveraging Bayesian optimization for hyperparameter tuning and integrating a Bagging Ensemble, we achieved a significant reduction in the training error (bias), achieving a better generalization over the test set, and reducing the variance in comparison with the baseline model for SpO2 estimation.
1. Introduction
Peripheral Oxygen Saturation (SpO2) is and important vital sign for monitoring in Intensive Care Units (ICUs) during surgery and convalescence [1]. It has become an important component of remote medical monitoring and the diagnosis of respiratory conditions related to COVID-19, caused by SARS-CoV-2 [2]. For example, specific symptoms such as fatigue, fever, and respiratory distress are associated with SARS-CoV-2, where the patient frequently experiences shortness of breath, leading to a reduction in blood oxygen saturation levels [3,4]. During the COVID-19 pandemic, SpO2 monitoring was included in the protocol for tracking and diagnosing this disease. Hence, the development of tools to measure SpO2 became incontrovertible. In general, non-contact monitoring of vital signs has been the subject of much work in the recent decades [5], and Deep Learning (DL) has been used particularly in the monitoring of heart rate [6,7,8,9,10,11] and respiratory rate [12,13,14,15]. Studies focused on non-contact monitoring of SpO2 have increased considerably in the recent years [16,17,18,19,20,21,22,23,24,25] but there are fewer approaches based on DL compared to the other vital signs [26,27,28,29,30,31,32].
The two major families of methods to estimate SpO2 can be classified according to the subject-based calibration stage. In the first group, a calibration step is necessary for each subject or for specific conditions of acquisition. Historically, the first works belong to this group. In this group, in [16], a method was introduced that acquires three monochromatic photoplethysmography (PPG) signals in the near-infrared spectrum. In this proposal, it was observed that the signals showed a high correlation with near-infrared wavelengths, opening a new avenue for estimating SpO2 through images. In [22], the authors proposed an estimation method based on an analysis of color variations and intensity changes in an extracted face ROI correlated with the pulsatile blood flow and oxygen saturation levels. The signals are extracted from the RGB channels of the image and are characterized by Independent Component Analysis (ICA). In [24], Lan et al. proposed a method based on the principle of Dynamic Spectrum (DS). The authors used a multi-spectral camera with 24 wavelengths to capture video on cheek regions of the subjects. Then, the PPG signal was extracted from the two-dimensional images, followed by the extraction of the DS values for the 24 wavelengths, and the optimal wavelength combination was obtained by wavelength screening using the one-by-one elimination method. Finally, a Partial Least Squares (PLS) model was established using the SpO2 reference values. In several works, the estimation is based on the Rate of Ratios (RoR) principle defined as the ration of the AC component normalized by the DC component of the two pulsatile components related to the red and blue channels on the image [18,19,23,25]. Nagakawa et al. [23] reported an SpO2 measurement based on the RoR using a near-infrared camera. The acquisition conditions are controlled by asking the subjects to hold their breath during the beginning of the acquisition. Takahashi et al. [25] proposed a method to select the optimal combination of bands from multi-band video images using a Monte Carlo Simulation (MS) of light scattering on the skin to obtain a regression model to correlate the measurement based on the RoR to perform the estimation of the SpO2. Al-Naji et al. [18] proposed a signal-decomposition technique of the PPG signals based on a complete Ensemble Empirical Mode Decomposition (EEMD) technique and ICA technique to obtain the optical properties of two channels of the RGB image. In [19], De Fatima Galvao et al. proposed to magnify the red and blue components of the image frame and then compute the RoR to estimate the SpO2). Other works proposed a global calibration model based on statistics from individual calibration regression for given conditions of acquisition [20,33,34,35,36]. Shao et al. [33] proposed a normalization method of the RoR by aligning individual calibrations of the data with a general calibration model for SpO2 estimation for all subjects. Hence, this general model mitigates the cross-user variation, the different camera configurations, and the lighting changes. In [20,34], the authors proposed an empirical model for all the subjects for thew same conditions of acquisition during the experiment. In [35], the empirical model calibration was carried out with hypoxia and normal subjects. In [36], the model used the YCbCr color space instead the RGB model to compute the RoR.
The second group, which does not require calibration per subject, includes recent works based on machine learning approaches. Among these works are those that directly use the raw spatio-temporal data of the video for the estimation [26,27,28,29,30,31]. Cheng et al. [26] proposed a deep learning model to estimate SpO2 from facial videos using a spatial–temporal representation to encode the information acquired by conventional RGB cameras and then directly pass it to a Convolutional Neural Networks (CNN) to estimate SpO2. Wang et al. [27] proposed a method using Three-Dimensional Convolutional Neural Networks (3D-CNN) and 3D multi-modal Visible Near-Infrared (VIS-NIR). In [28], Stogiannopoulos et al. explore SpO2 estimation under not-optimal lightning conditions. They use the Eulerian Video Magnification (EVM) technique as input to two different approaches: Generalized Additive Model (GAM) and a 3D-CNN architecture. In [30], Stogiannopoulos et al. compared it to a proposal using Video Vision Transformer (ViT) with the previous methods presented in [28]. In [31], the authors proposed a end-to-end DL strategy using a Residual and Coordinate Attention (RCA) network and a Color Channel Model (CCM) for the SpO2 estimation. In [29], the authors presented a non-contact strategy using a Eulerian Video Magnification technique based on Hermite Transform (EVM-HT) and a 3D-CNN from a Region of Interest (ROI) detected automatically using transfer learning over YOLOv5.
Finally, other approaches extract features from the rPPG signals before the machine learning estimation step [17,32,37,38]. Akamatsu et al. [32] proposed an end-to-end approach extracting the DC and AC components from PPG signals via convolutional layers and then from the spatio-temporal map to train the CNN models to estimate the SpO2. It captures a reflected signal from the tissue, originating from the wavelength source, which is correlated with blood SpO2 levels. In [37], Arefin et al. reported a DL facial-recognition and signal-processing techniques to extract the remote photoplethysmography (rPPG) signal and then estimate the SpO2) using a support vector regression machine learning model. For signal noise and motion artifact reduction, the proposal uses relevant characteristics from the rPPG signal such as peak heights, time intervals between peaks, and systolic and diastolic slops. In [17], Tommoy et al. extract relevant features including peak characteristics and AC and DC components as input to a logistic regression model for the estimation. Lee et al. [38] proposed a method for estimating diffused spectral absorbance of ROIs by means of the shading bias representing the discrepancy between the measured and actual diffused absorbances estimated by the Monte Carlo Modeling (MCML) of light transport in multilayered tissues. Furthermore, the resulting Rate of Ratios (RoR) of the AC and DC components computed by the shading bias are spatio-temporally regressed by a Long Short-Term Memory (LSTM) network to improve the accuracy and robustness of the SpO2 prediction.
For the non-contact strategies, the initial proposals used infrared spectrum cameras [23,24,27,28,30]; however, Guazzi et al. [39] demonstrated that the SpO2 changes could be tracked through the red and blue channels by utilizing wide-spectrum light during the acquisition. Finally, other works have used RGB cameras and ambient light to estimate SpO2 with good results [18,19,20,21,22,25,26,29,31,32].
On the other hand, to extract the SpO2 signal, an ROI is generally defined in those areas with a very high vascularity, for example, the face and forehead [18,19,21,29,31,32]. However, other authors have defined an area near the iris tissue to estimate SpO2 [40].
In Table 1, we summarize the most representative non-contact SpO2 estimations works. In the first column, the work reference is displayed; the second column shows the methods used; the third column presents the evaluation metrics: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Bland–Altman (BA) analysis, and the Coefficient of Determination (R2); the fourth column indicates the number of subjects or the dataset used; the fifth column presents the acquisition camera modality; and the sixth column indicates whether a calibration step is required.

Table 1.
Principal SpO2 non-contact estimation works.
In this paper, we present a novel blended strategy to estimate SpO2 by means of a 3D-CNN architecture that does not require any supplementary stage for the reduction of motion and noise artifacts. As reported in [41], deep learning strategies are a new approach for noise reduction. A parameter and hyperparameter Bayesian optimization and an ensemble technique over a magnified dataset are also used for the estimation. First, we applied Eulerian Video Magnification based on Hermite Transform (EVM-HT) [29] over an ROI located on the forehead of each subject of the dataset. Then, the proposal starts from an 3D-CNN architecture and iterates in order to decrease bias through optimization and variance using an ensemble. The contributions of this work are summarized as follows:
- EVM-HT approach:
- -
- We used the EVM-HT method as a feature detector, which is used as input by the 3D-CNN to estimate the SpO2.
- -
- This makes it easier for the 3D-CNN to focus on those regions where there are chrominance changes.
- New DL combined strategy to estimate SpO2:
- -
- We applied a Bayesian optimization approach to reduce the training error or bias compared to our previous baseline CNN model [29].
- -
- We used the Bagging technique to achieve a better generalization over the test set with respect to the optimized model, which reduces the variance.
- No calibration required per subject:
- -
- In the proposed DL SpO2-estimation approach, a calibration process per subject is not necessary, allowing its implementation in real conditions.
To the best of our knowledge, the specific application of the combined techniques of Bayesian optimization and Bagging in DL on rPPG SpO2 estimation has not been already explored in the state-of-the-art methods.
The paper is organized as follows: the methodology of the proposed strategy, computational resources, dataset, model architecture, optimization, and ensemble approach are described in Section 2. Section 3 presents the experimental results, and in Section 4 the discussion. Finally, conclusions are given in Section 5.
2. Materials and Methods
This proposal focuses on improving the strategy for estimating SpO2 without contact using face videos. The strategy relies on the principle that SpO2 can be estimated using high-vascularity-zone RGB images (using the red and blue channels) for tracking the intensity changes during a time window. The proposed SpO2-estimation method uses a preprocessed video dataset with the Eulerian Video Magnification technique using Hermite Transform. The EVM-HT method acts as a feature detector by amplifying the chrominance changes, related to blood perfusion, which are used by the 3D-CNN to estimate the SpO2.
To estimate SpO2, different techniques were applied to decrease the SpO2-estimation error using a DL approach (see Figure 1). First, a 3D-CNN is used to estimate the SpO2 (Section 2.5). Next, a Bayesian optimization of parameters is applied to reduce bias (Section 2.6). Finally, the optimal architecture is identified as the unit model within the meta-technique of Bootstrap Aggregating (Bagging) described in Section 2.7, which was used to reduce the variance of the proposal. Both the Bayesian optimization and Bagging are implemented using a validation dataset with early stopping. The final Bagging Ensemble is retrained on the joint train–val data and evaluated with a separate test set.
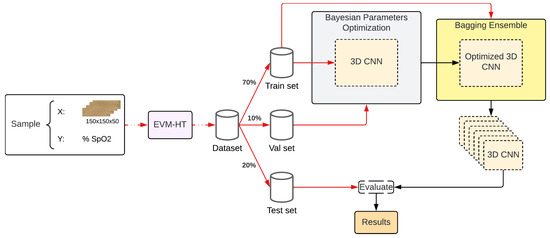
Figure 1.
General workflow followed in order to improve the performance of a base CNN.
The main purpose of this methodology is to take the human intervention out of the loop, improving the results observed in SpO2 estimation, bias, and variance using DL techniques. The focus in this paper is shifted to the use of classic meta-techniques in Machine Learning (ML), such as optimization and Bagging, on the specific field of PPG, not in the model architecture as in recent works.
2.1. Experimental Setup
All the computations were performed on a 12-core (AMD Ryzen 5900X) PC running Ubuntu 20.04 LTS with 64 GB memory and an NVIDIA RTX 3090 GPU. The following relevant software modules were installed: CUDA 11.8, Hyperopt 0.2.7, NumPy 1.26.2, Python 3.9.16, PyTorch 2.0.0, and Scikit-learn 1.3.0.
2.2. Dataset
In this work, we use the dataset presented by Escobedo-Gordillo et al. [29]. This dataset consists of videos of 18 healthy subjects (13 male and 5 female). Prior to the study, all subjects voluntarily completed an agreement with the principal investigator and the School of Engineering, and signed informed consent forms in accordance with applicable regulations and data policies.
The dataset was acquired using a smartphone camera mounted on a tripod positioned approximately 40 cm horizontally from the subject. Videos at resolution and 30 fps were recorded under everyday conditions, including various locations and lighting environments. Additionally, the subjects simultaneously used a commercial oximeter visible in the video to extract reference values, which were automatically labeled for every second of the recording using a YOLOv5s detection model. Next, the videos were magnified using a coefficient applied only to the red and blue channels. Finally, an ROI crop/selection was performed in order to obtain the subject’s forehead in each frame through another YOLOv5s model.
2.3. Eulerian Video Magnification Technique Using Hermite Transform
The Eulerian magnification method works like a magnifying lens for visual motion, enhancing subtle movements in a video sequence to make normally imperceptible visible motions and to uncover hidden details. In the classical Eulerian magnification approach, a spatial frequency decomposition of the image sequence is performed using a Laplacian pyramid. Then, temporal filtering is applied to the video sequence decomposition to hold the relevant motion information. Next, a factor is used to amplify the spatial frequency bands. Then, inverse decomposition is performed to reconstruct the magnified video, which is finally added to the original video [42].
In [42], Eulerian Video Magnification with Hermite Transform was introduced as an alternative to the traditional Laplacian pyramid decomposition used in the Eulerian magnification method. Hermite Transform is a mathematical model that decomposes images into relevant visual patterns by emulating certain retinal ganglion cell responses found in the early stages of the human visual system [42]. Figure 2 shows the stages of the EVM-HT process.
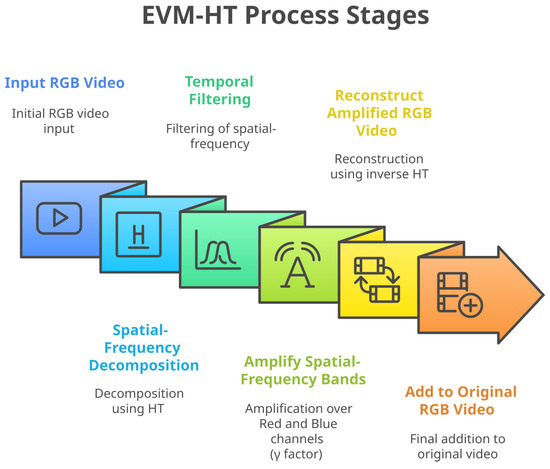
Figure 2.
EVM-HT stages.
In [42], it was shown that Hermite Transform decomposition improved the image-reconstruction step in motion magnification, allowing one to amplify subtle motions and preserving image quality. Thus, in [43], the EVM-HT was also used to estimate the breathing rate in natural videos, outperforming the classical Laplacian approach. Additionally, other works estimating the breathing rate from natural videos using the EVM-HT approach have shown high agreement with the reference. For example, ref. [12] used a CNN framework, while ref. [44] employed an artificial organic network.
In addition, a modified version of the EVM-HT using a low-spatial-frequency decomposition of the Hermite Transform and a typical CNN was presented in [45]. This decomposition allows the amplification of chrominance changes, instead of motion changes, related to blood perfusion, enabling estimation of the heart rate at the subjects’ wrists, and obtaining an RMS value of 2.7815 bpm. Additionally, in [7], a Fourier analysis of the chrominance changes using the EVM-HT method and a trained neuronal network were used to estimate the heart rate with an RMS value of 1.86 bpm. This chrominance magnification approach and signal-processing techniques were used in [21] to estimate the SpO2 and obtain a hight agreement with respect to the reference in a dataset composed of five subjects. Finally, [29] reported an SpO2-estimation system using the low-spatial-frequency EVM-HT and a transfer learning approach, obtaining a strong agreement with respect to the reference using a larger set of videos
In this work, we fixed the parameter values used for both heart rate and SpO2 estimation using the EVM-HT method: a factor of 50 and a range of 0.833–1.583 Hz (50–95 bpm) for the cut-off frequencies in the temporal filtering, the latter corresponding to the typical heart rate range in rest. These parameter values were defined and tested in [7,21,29,45], as they provided the best heart rate and SpO2-estimation results.
2.4. Data Processing
The dataset for the prediction model consisted of 827 volumes of 150 frames, equivalent to 5 s with a reference. The dataset was created based on the following criteria:
- 150 ROI batches were generated by stacking ROIs from the dataset. The target for each batch was derived from the oximeter value in the final frame.
- A 125-ROI sliding window technique was used as a data-augmentation strategy.
- To ensure a consistent input size, each ROI was resized to .
- A split ratio of 70-10-20 was applied to divide the dataset into training, validation, and testing sets.
- The target was normalized with mean and standard deviation.
Figure 3 illustrates the distribution of the ground truth SpO2 values for the samples generated after the stated data processing.
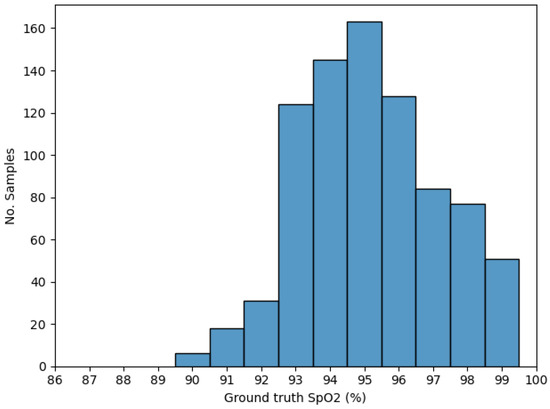
Figure 3.
Ground truth SpO2 (%) distribution generated after data processing.
The training and validation datasets were used during parameter optimization (Section 2.6) and Bootstrap aggregation (Section 2.7), while the test set is only used as a final assessment.
2.5. Model Architecture
The 3D-CNN architecture (Figure 4) is based on the one presented by Escobedo-Gordillo et al. [29], which takes as input 150 frames of an ROI in a video, each with a size of 150 × 50 pixels.
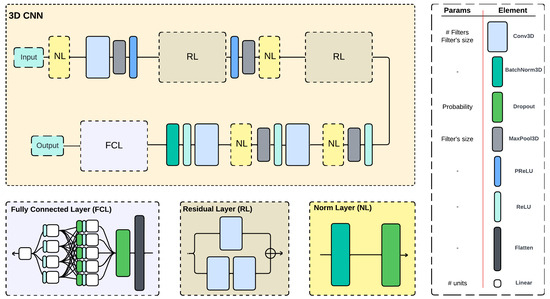
Figure 4.
Architecture of the 3D-CNN used, with some components grouped and displayed below; legend and modifiable parameters are to the left.
The network was implemented using PyTorch and is composed of convolution (Conv3D), batch normalization (BatchNorm3D), dropout, max pooling (MaxPool3D), PReLU, ReLU, flatten, and linear layers; in addition, there are three grouped components, The Fully Connected Layer (FCL), the Residual Layer (RL), and the Norm Layer (NL). The corresponding parameters of each, such as number and size of filters in Conv3D, were not defined in advance and set as variables to optimize.
The RL component receives its input and splits it; the first branch uses two cascade Conv3D, while the other uses a Conv3D with a cubic filter of size 1 whose only purpose is to reshape the input of the component to the output of the other branch, therefore allowing the summation and the residual behavior.
To normalize and prevent overfit, the NL block was used, which is composed of a BatchNorm3D and a dropout layer. The dropout rate was set as a variable to optimize.
The output of the convolution layers passes through the FCL, which contains firstly a flatten and a dropout and then two hidden layers, both with ReLU’s and the first also with a dropout. The output is a single linear unit.
2.6. Parameter Optimization
Hyperopt [46] (https://hyperopt.github.io/hyperopt/, accessed on 13 February 2025) is an open-source Python library for Bayesian optimization that implements Sequential Model Based Optimization (SBMO) using the Tree-structured Parzen Estimator (TPE) for the surrogate function. In ML, it is applied to parameters and hyperparameters of a given model to reduce the bias over a training dataset. The optimization process is composed of four parts: the objective function, the domain space (prior), the optimization algorithm, and the results.
This work used Hyperopt in a parameter- and hyperparameter-optimization cycle (Figure 5) that started with prior knowledge of the domain space based on experimentation performed in previous works [29] and is represented with either a uniform distribution for continuous values or a set for ordinal values, as can be seen in Table 2. The different parameters to optimize are the learning rate (LR), the cubic filter size of a convolution layer (f# from 1 to 3), the dropout rate before convolutions (d1) and linear layers (d2), the number of convolution filters (n# from 1 to 7), and the number of units at the linear layers (n# from 8 to 9).
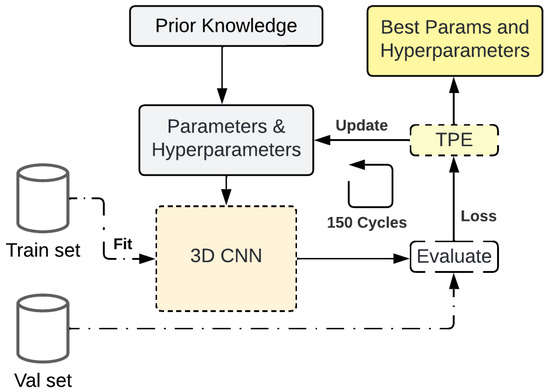
Figure 5.
Workflow for the parameter and hyperparameter optimization followed for the 3D-CNN.

Table 2.
Hyperopt Bayesian prior.
3D-CNN was trained in each step of the cycle with the parameters and hyperparameters selected by the Bayesian algorithm with a train set and evaluated with a validation set on the objective function selected (L1 loss) that goes into the TPE to update the prior parameters and repeat the cycle 150 times. At the end, the best loss is achieved and its corresponding parameters and hyperparameters are returned.
For each training iteration, the model ran for 150 epochs using Stochastic Gradient Descent (SGD) as the weight optimizer and it tracked the L1 loss and the MSE loss in the validation set; in addition, the L1 loss was used as a metric for early stop with a patience level of 35 epochs.
2.7. Bagging Ensemble
The basic idea of ensemble methods is to learn several models and combine them instead of learning only one. As averaging reduces variance, averaging models reduce the variance present in those models. Bagging consists of the generation of many Bootstrap sample sets of the training data (random sampling with replacement) and the training of a model with each of those sets.
The methodology followed in order to apply Bagging to our 3D-CNN (Figure 6) consists of the use of the training set to generate 20 different Bootstrap sets. Hence, they were used to train one CNN with each one, where the individual model parameters and hyperparameters were optimized in Section 2.6. With this model, we analyzed the performance achieve by stacking from 2 models up to the 20 models on the validation set. The results would determine if, for a given number of models, the performance stagnates and if the computation would be wasted to keep increasing this number. This is an important fact as the models are DL models and not weak learners.
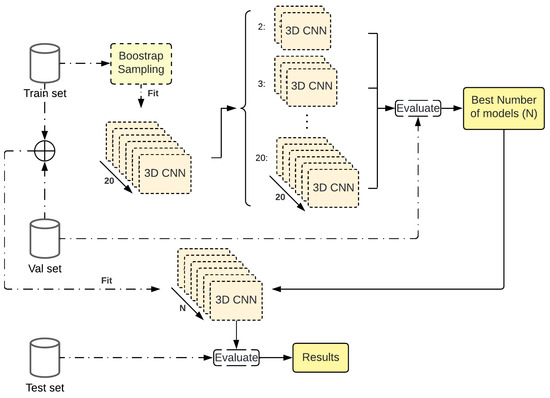
Figure 6.
Workflow for the Bagging technique applied over the best parameters found.
With a defined number of learners, the models will be retrained taking the training and the validation set. Finally, the resulting ensemble is evaluated on the test set to compute the final performance.
3. Results
3.1. Parameter Optimization
The optimization process time was 240:39:54 h and the L1 loss across iterations can be seen in Figure 7. It can be noted that from early on (Iteration 26), a good approximation was found, which was not surpassed until Iteration 140.
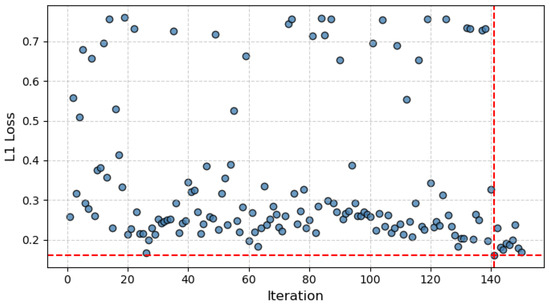
Figure 7.
L1 loss (blue dots) measured on the validation set across all iterations of the parameter-optimization cycle, where the intersection of the red dashed lines represents the minimum loss achieved.
The hyperparameters and parameters selected are display in Table 3, Table 4 and Table 5; split by the hyperparameters, the convolution filter’s cubic size, and the number of filters (convolutions) and units (fully connected).

Table 3.
Hyperparameters obtained for the best model found.

Table 4.
Convolution filter’s cubic size obtained for the best model found.

Table 5.
Number of filters and units obtained for the best model found.
The distributions of the parameter selection across iterations can be split into continuous and discrete and are summarized in Figure A1, Figure A2, Figure A3 and Figure A4 (Appendix A).
3.2. Bagging Ensemble
The ensemble iterations were carried out based on the newly trained 20 Bootstrapped models. In order to match the results obtained to real world cases, the predictions were de-normalized with the original mean and standard deviation and used to calculate three metrics: MAE directly quantifies the difference between predicted and target values; RMSE gives greater weight to larger errors, being sensitive to outliers and larger deviations; and R2 score measures the variance in the target that the model can explain.
MAE, RMSE, and R2 metrics were tracked for each ensemble of size N (ranging from 1 to 20 Bootstrap trained models). The results (Figure 8) showed an increase in the performance as N grows until the 13th model, where it reaches a plateau.
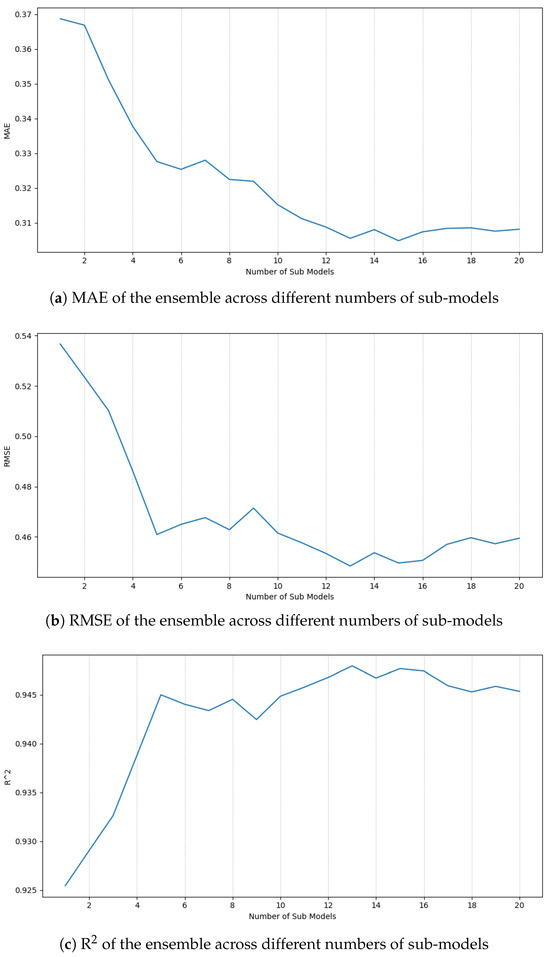
Figure 8.
Ensemble performance across different numbers of sub-models.
With this results, 13 models were trained on the combined dataset (train + validation) and evaluated on the test set (Table 6). We obtained an MAE of 0.3751, an RMSE of 0.5315 and an R2 that displays a great fit of 0.9249. In addition, results for the optimized only model are displayed for comparison purposes.

Table 6.
Results obtained by the optimized model and ensemble on the validation and test set.
Finally, we performed a Bland–Altman analysis to assess the level of agreement between the results of the proposed system and the reference. In total, of the limits of agreements were defined as Mean of Differences (MOD) (bias = MOD ), with representing the standard deviation of the MOD between the reference and the true value. Additionally, the Pearson’s Correlation Coefficient (PCC), the Spearman Correlation Coefficient (SCC), and the RMSE were used to evaluate the relationship between the estimated values and the true values.
Figure 9 shows the Bland–Altman plots, and the corresponding statistics, for SpO2 estimations using only the optimization and using both the optimization and the Bagging Ensemble. An MOD of was obtained with Limits of Agreement (LoA) of and . Then, the bias = MOD . The statistics are and , corresponding to a strong correlation for only the optimization model. On the other hand, an MOD of was obtained with Limits of Agreement (LoA) of and . Then, the bias = MOD . The statistics are and , corresponding to a strong correlation for the optimization and Bagging model.
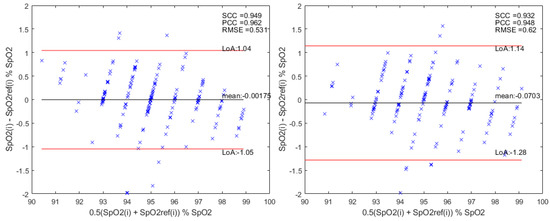
Figure 9.
Bland-Altman analysis for the Bagging Ensemble method on the left and optimization without Bagging Ensemble on the right. is the estimation value and the reference value of SpO2.
4. Discussion
In this work, we use TPE for parameter and hyperparameter optimization of a 3D-CNN as a basis of a Bagging Ensemble in order to decrease both the bias and variance present in the model by taking the human out of the loop. The results showed how the optimization alone presents good results (RMSE = 0.6204, MAE = 0.4323), but the addition of the Ensemble technique successfully achieves better results, mainly minimizing the larger deviations (RMSE = 0.5315, MAE = 0.3751); there is also a difference of almost 3 percentage points in the R2 between both approaches with the Ensemble being the best.
In general, the comparison of our proposal with previous works can be seen in Table 7. For the MAE, we obtain a value of 0.375, a result comparable with Wang et al. [27] (MAE = 2.31), Cheng et al. [26] (MAE = 1.274), Arefin et al. [37] (MAE = 0.9), Lee et al. [38], Brieva et al. [21] (MAE = 0.45), and our previous work [29] (MAE = 0.363). For the RMSE, our result of 0.532 is the best among the presented papers, Brieva et al. [21] (RMSE = 0.802), Hu et al. [31] (RMSE = 0.8), Escobedo et al. [29] (RMSE = 0.926), Cheng et al. [26] (RMSE = 1.71), Arefin et al. [37] (RMSE = 1.4), Lee et al. [38] (RMSE = 0.71); for R2, the result is an improvement with respect to our previous work [29] of almost 1.5 percentage points. Regarding the Bland–Altman analysis, in [19], De Fatima et al. obtained an agreement with a bias of and Brieva et al. [21] an agreement with a bias of . These two works are consistent with the results obtained in our previous work [29], with an agreement with bias = . Therefore, the current proposal slightly outperforms the three existing works, showing a stronger agreement regarding a bias of .

Table 7.
Results Comparison of results between the proposal and other works.
Overall, this shows the importance of an optimized training process, where the addition of Ensemble techniques, even in deep learning, can bring some important benefits such as the reduction in the variance in the model.
It is important to note that the dataset used is relatively small regarding a DL project, and 18 healthy subjects are by no means representative of individuals with different skin conditions due to race, gender, or age, and in real-world scenarios where SpO2 ranges are wider. This is thought of as a proof of concept of the benefits in performance of this strategy regarding SpO2 estimation; further evaluation on a bigger dataset needs to be carried out to fully validate the approach.
This proposal is an end-to end approach that does not require any supplementary stage for the reduction of motion and noise artifacts. It is not a necessary supplementary stages for filtering the rPPG signals as in [18,19,23,25], or extracting specific features of the rPPG signals as input to the deep learning architecture as in [17,32,37,38]. In addition, the model is general enough to not require per subject calibration.
Limitations of the current work include the relatively small, demographically limited dataset and controlled lighting conditions.
5. Conclusions
In this study, we present a novel combined strategy to estimate SpO2 using a deep learning 3D Convolutional Neural Network, parameters and hyperparameter Bayesian optimization, and an ensemble technique over a dataset magnified by the Eulerian Video Magnification technique using Hermite Transform. To the best of our knowledge, this is the first time an end-to-end pipeline such as this has been applied to rPPG SpO2 estimation.
By applying Bayesian optimization to our baseline CNN [29], we reduced training bias—raising validation R2 from 0.787 to 0.890—and, by Bagging the optimized model, we improved generalization—boosting test R2 from 0.898 to 0.925. Together, these techniques yield a robust ensemble for SpO2 estimation. Furthermore, the current proposal eliminates the need for subject-specific calibration, which enhances its applicability in real-world conditions.
These results confirm that we have met our research objectives and demonstrate clear academic and practical value. The novelty lies in integrating advanced video magnification, deep Bayesian tuning, and ensemble learning within a single framework for rPPG SpO2.
As future work, a larger database should be used, with variations in lighting and different skin types of the subjects, health status, gender, and age to study the robustness of this proposal.
Author Contributions
Conceptualization, A.E.-G., J.B. and E.M.-A.; methodology, A.E.-G., J.B. and E.M.-A.; software, A.E.-G. and J.B.; validation, J.B. and E.M.-A.; formal analysis A.E.-G., J.B. and E.M.-A.; investigation, J.B. and E.M.-A.; resources, A.E.-G., J.B. and E.M.-A.; data curation, A.E.-G.; writing—original draft preparation, A.E.-G., J.B. and E.M.-A.; writing—review and editing, J.B. and E.M.-A.; visualization, A.E.-G. and J.B.; supervision, J.B.; project administration, J.B.; funding acquisition, J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universidad Panamericana through the grant Fomento a la Investigación 2023 under project code UP-CI-2023-MX-14-ING.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of the Engineering School of Universidad Panamericana (protocol code: CI-2023-MX-14-ING and date of approval: 27 July 2023).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Andrés Escobedo-Gordillo, Jorge Brieva and Eresto Moya-Albor would like to thank the Facultad de Ingeniería of Universidad Panamericana for all support in this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BA | Bland–Altman |
| bmp | beats per minute |
| CNN | Convolutional Neural Networks |
| 3D-CNN | Three-Dimensional Convolutional Neural Network |
| CCM | Color Channel Model |
| COVID-19 | Coronavirus Disease 2019 |
| DL | Deep Learning |
| DS | Dynamic Spectrum |
| EEMD | Ensemble Empirical Mode Decomposition |
| EVM | Eulerian Video Magnification |
| EVM-HT | Eulerian Video Magnification - Hermite Transform |
| FCL | Fully Connected Layer |
| ICA | Independent Component Analysis |
| ICU | Intensive Care Unit |
| LoA | Limits of Agreement |
| LSTM | Long Short- Term Memory |
| ML | Machine Learning |
| MCML | Monte Carlo Modeling |
| MAE | Mean Absolute Error |
| MOD | Mean of Differences |
| MS | Monte Carlo Simulation |
| NL | Normalization Layer |
| PCC | Pearson’s Correlation Coefficient |
| PLS | Partial Least Squares |
| PPG | Photoplethysmography |
| RCA | Residual and Coordinate Attention |
| RMSE | Root Mean Square Error |
| rPPG | remote Photoplethysmography |
| R2 | Coefficient of Determination |
| RL | Residual Layer |
| ROI | Region Of Interest |
| SARS-CoV-2 | Severe Acute Respiratory Syndrome Coronavirus 2 |
| SBMO | Sequential Model-Based Optimization |
| SCC | Spearman Correlation Coefficient |
| SGD | Stochastic gradient descent |
| SpO2 | Peripheral Oxygen Saturation |
| SVR | Support Vector Regression |
| TPE | Tree-structured Parzen Estimator |
| ViT | Video Vision Transformer |
| VIS-NIR | Visible–near infrared |
Appendix A
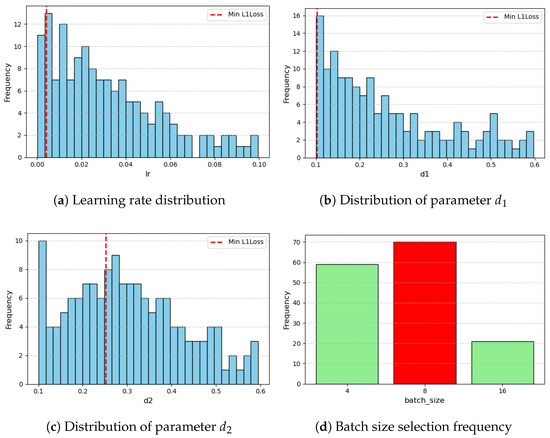
Figure A1.
Parameter and hyperparameter distributions from optimization. Red line indicates the value associated with minimum L1 loss (1/4).
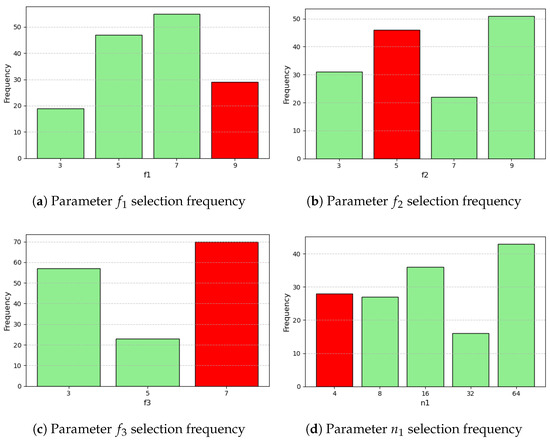
Figure A2.
Parameter and hyperparameter distributions from optimization. Red indicates the value associated with minimum L1 loss (2/4).
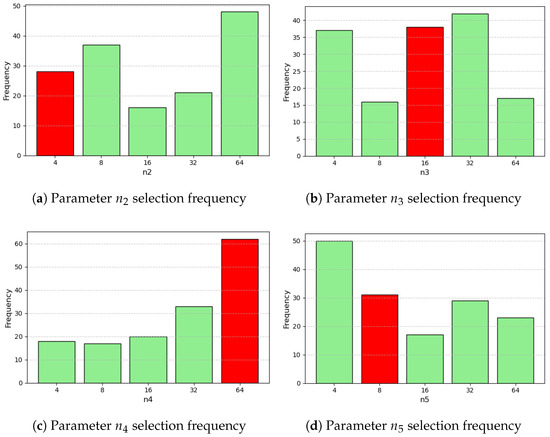
Figure A3.
Parameter and hyperparameter distributions from optimization. Red indicates the value associated with minimum L1 loss (3/4).
Figure A4.
Parameter and hyperparameter distributions from optimization. Red indicates the value associated with minimum L1 loss (4/4).
References
- Hackett, K. Guidance on oxygen use in adults. Emerg. Nurse J. RCN Accid. Emerg. Nurs. Assoc. 2017, 25, 11. [Google Scholar] [CrossRef] [PubMed]
- Paules, C.I.; Marston, H.D.; Fauci, A.S. Coronavirus Infections—More Than Just the Common Cold. JAMA 2020, 323, 707–708. [Google Scholar] [CrossRef] [PubMed]
- Struyf, T.; Deeks, J.J.; Dinnes, J.; Takwoingi, Y.; Davenport, C.; Leeflang, M.M.; Spijker, R.; Hooft, L.; Emperador, D.; Dittrich, S.; et al. Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19 disease. Cochrane Database Syst. Rev. 2020, 7, CD013665. [Google Scholar] [CrossRef] [PubMed]
- Moro, E.; Priori, A.; Beghi, E.; Helbok, R.; Campiglio, L.; Bassetti, C.L.; Bianchi, E.; Maia, L.F.; Ozturk, S.; Cavallieri, F.; et al. The international European Academy of Neurology survey on neurological symptoms in patients with COVID-19 infection. Eur. J. Neurol. 2020, 27, 1727–1737. [Google Scholar] [CrossRef] [PubMed]
- Hajr, A.; Tarvirdizadeh, B.; Alipour, K.; Ghamari, M. Contactless Health Monitoring: An Overview of Video-Based Techniques Utilising Machine/Deep Learning. IET Wirel. Sens. Syst. 2025, 15, e70009. [Google Scholar] [CrossRef]
- Poh, M.Z.; McDuff, D.; Picard, R. Non-contact, automated cardiac pulse measurements using video imaging and blind source separation. Opt. Express 2010, 18, 10762–10774. [Google Scholar] [CrossRef] [PubMed]
- Moya-Albor, E.; Brieva, J.; Ponce, H.; Martínez-Villaseñor, L. A non-contact heart rate estimation method using video magnification and neural networks. IEEE Instrum. Meas. Mag. 2020, 23, 56–62. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Yu, Z.; Lu, H.; Yue, H.; Yang, J. rppg-mae: Self-supervised pretraining with masked autoencoders for remote physiological measurements. IEEE Trans. Multimed. 2024, 26, 7278–7293. [Google Scholar] [CrossRef]
- Othman, W.; Kashevnik, A.; Ali, A.; Shilov, N.; Ryumin, D. Remote heart rate estimation based on transformer with multi-skip connection decoder: Method and evaluation in the wild. Sensors 2024, 24, 775. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.X.; Sun, H.M.; Hao, R.R.; Pan, A.; Jia, R.S. TransPhys: Transformer-based unsupervised contrastive learning for remote heart rate measurement. Biomed. Signal Process. Control 2023, 86, 105058. [Google Scholar] [CrossRef]
- Cheng, C.H.; Wong, K.L.; Chin, J.W.; Chan, T.T.; So, R.H. Deep learning methods for remote heart rate measurement: A review and future research agenda. Sensors 2021, 21, 6296. [Google Scholar] [CrossRef] [PubMed]
- Brieva, J.; Ponce, H.; Moya-Albor, E. A contactless respiratory rate estimation method using a hermite magnification technique and convolutional neural networks. Appl. Sci. 2020, 10, 607. [Google Scholar] [CrossRef]
- Bian, D.; Mehta, P.; Selvaraj, N. Respiratory rate estimation using PPG: A deep learning approach. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5948–5952. [Google Scholar]
- Hashim, H.A. Non-Contact Automatic Respiratory Rate Monitoring for Newborns Using Digital Camera Technology and Deep Learning. J. Biomed. Photonics Eng. 2024, 10, 040317-1–040317-12. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.; Kwon, Y.; Kwon, J.; Park, S.; Sohn, R.; Park, C. Multitask siamese network for remote photoplethysmography and respiration estimation. Sensors 2022, 22, 5101. [Google Scholar] [CrossRef] [PubMed]
- Wieringa, F.P.; Mastik, F.; van der Steen, A.F.W. Contactless multiple wavelength photoplethysmographic imaging: A first step toward “SpO2 camera” technology. Ann. Biomed. Eng. 2005, 33, 1034–1041. [Google Scholar] [CrossRef] [PubMed]
- Tonmoy, A.S.; Ahmed, M.S.; Chowdhury, A.; Chowdhury, M.H. Estimation of Oxygen Saturation from PPG Signal using Smartphone Recording. In Proceedings of the 2024 International Conference on Advances in Computing, Communication, Electrical, and Smart Systems: Innovation for Sustainability, iCACCESS 2024, Dhaka, Bangladesh, 8–9 March 2024. [Google Scholar] [CrossRef]
- Al-Naji, A.; Khalid, G.; Mahdi, J.; Chahl, J. Non-Contact SpO2 Prediction System Based on a Digital Camera. Appl. Sci. 2021, 11, 4255. [Google Scholar] [CrossRef]
- De Fatima Galvao Rosa, A.; Betini, R. Noncontact SpO2 Measurement Using Eulerian Video Magnification. IEEE Trans. Instrum. Meas. 2020, 69, 2120–2130. [Google Scholar] [CrossRef]
- Wu, B.J.; Wu, B.F.; Dong, Y.C.; Lin, H.C.; Li, P.H. Peripheral Oxygen Saturation Measurement Using an RGB Camera. IEEE Sensors J. 2023, 23, 26551–26563. [Google Scholar] [CrossRef]
- Brieva, J.; Moya-Albor, E.; Ponce, H. A non-contact SpO2 estimation using a video magnification technique. In Proceedings of the 17th International Symposium on Medical Information Processing and Analysis, Campinas, Brazil, 17–19 November 2021; Rittner, L., Romero Castro, E., Lepore, N., Brieva, J., Linguraru, M.G., Eds.; International Society for Optics and Photonics. SPIE: Bellingham, WA, USA, 2021; Volume 12088, pp. 10–18. [Google Scholar] [CrossRef]
- Yaythish Kannaa, G.; Bhattacharya, S.; Aishwarya, N. Remote Photoplethysmography (rPPG) for Contactless Blood Oxygen Saturation Monitoring. In Proceedings of the 2024 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 12–14 July 2024. [Google Scholar] [CrossRef]
- Nakagawa, K.; Kawamoto, H.; Sankai, Y. Noncontact Measurement of Oxygen Saturation with Dual Near Infrared Imaging for Daily Health Monitoring. In Proceedings of the 2022 IEEE/SICE International Symposium on System Integration (SII), Narvik, Norway, 9–12 January 2022; pp. 736–741. [Google Scholar] [CrossRef]
- Lan, T.; Li, G.; Lin, L. A non-contact oxygen saturation detection method based on dynamic spectrum. Infrared Phys. Technol. 2022, 127, 104421. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, R.; Ashida, K.; Kobayashi, Y.; Tokunaga, R.; Kodama, S.; Tsumura, N. Oxygen saturation estimation based on optimal band selection from multi-band video. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 19–25 June 2021; pp. 3845–3851. [Google Scholar] [CrossRef]
- Cheng, C.H.; Yuen, Z.; Chen, S.; Wong, K.L.; Chin, J.W.; Chan, T.T.; So, R.H.Y. Contactless Blood Oxygen Saturation Estimation from Facial Videos Using Deep Learning. Bioengineering 2024, 11, 251. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, Z.; Alić, B.; Wildenauer, A.; Dietz-Terjung, S.; Sucre, J.G.O.; Sutharsan, S.; Schöbel, C.; Seidl, K.; Notni, G. Leveraging 3D Convolutional Neural Network and 3D visible-near-infrared multimodal imaging for enhanced contactless oximetry. J. Biomed. Opt. 2024, 29, S33309. [Google Scholar] [CrossRef]
- Stogiannopoulos, T.; Cheimariotis, G.A.; Mitianoudis, N. A non-contact SpO2 estimation using video magnification and infrared data. In Proceedings of the ICASSP 2023–2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023. [Google Scholar] [CrossRef]
- Escobedo-Gordillo, A.; Brieva, J.; Moya-Albor, E.; Ponce, H. A non-contact oxygen saturation estimation using Video Magnification and a Deep Learning method. In Proceedings of the 2023 19th International Symposium on Medical Information Processing and Analysis (SIPAIM), Mexico City, Mexico, 15–17 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Stogiannopoulos, T.; Cheimariotis, G.A.; Mitianoudis, N. A Study of Machine Learning Regression Techniques for Non-Contact SpO2 Estimation from Infrared Motion-Magnified Facial Video. Information 2023, 14, 301. [Google Scholar] [CrossRef]
- Hu, M.; Wu, X.; Wang, X.; Xing, Y.; An, N.; Shi, P. Contactless blood oxygen estimation from face videos: A multi-model fusion method based on deep learning. Biomed. Signal Process. Control 2023, 81, 104487. [Google Scholar] [CrossRef] [PubMed]
- Akamatsu, Y.; Onishi, Y.; Imaoka, H. Blood oxygen saturation estimation from facial video via dc and ac components of spatio-temporal map. In Proceedings of the ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Shao, Q.; Zhu, L.; Ahmed, M.; Vatanparvar, K.; Gwak, M.; Rashid, N.; Bae, J.; Kuang, J.; Gao, A. Normalization is All You Need: Robust Full-Range Contactless SpO2 Estimation Across Users. In Proceedings of the ICASSP 2024–2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 1646–1650. [Google Scholar] [CrossRef]
- Cheng, J.C.; Pan, T.S.; Hsiao, W.C.; Lin, W.H.; Liu, Y.L.; Su, T.J.; Wang, S.M. Using Contactless Facial Image Recognition Technology to Detect Blood Oxygen Saturation. Bioengineering 2023, 10, 524. [Google Scholar] [CrossRef] [PubMed]
- van Gastel, M.; Verkruysse, W. Contactless SpO2 with an RGB camera: Experimental proof of calibrated SpO2. Biomed. Opt. Express 2022, 13, 6791–6802. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.H.; Yu, S.G.; Kim, S.E.; Lee, E.C. Non-contact oxygen saturation measurement using ycgcr color space with an rgb camera. Sensors 2021, 21, 6120. [Google Scholar] [CrossRef] [PubMed]
- Arefin, K.Z.; Alam, K.S.; Mamun, S.M.; Sabith, N.U.S.; Rabbani, M.; Sridevi, P.; Ahamed, S.I. PulseSight: A novel method for contactless oxygen saturation (SpO2) monitoring using smartphone cameras, remote photoplethysmography and machine learning. Smart Health 2025, 36, 100542. [Google Scholar] [CrossRef]
- Lee, S.; Park, H. Noncontact Multispectral SpO2 Prediction Based on Deep Ratio-of-Ratio Refinement with Optimal Band Selection and Shading Bias Removal. IEEE Access 2025, 13, 109513–109527. [Google Scholar] [CrossRef]
- Guazzi, A.R.; Villarroel, M.; Jorge, J.; Daly, J.; Frise, M.C.; Robbins, P.A.; Tarassenko, L. Non-contact measurement of oxygen saturation with an RGB camera. Biomed. Opt. Express 2015, 6, 3320–3338. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Hung, C.J.; Shen, C.H.; Chen, S.J. A new oxygen saturation images of iris tissue. In Proceedings of the SENSORS, 2010 IEEE, Waikoloa, HI, USA, 1–4 November 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1386–1389. [Google Scholar] [CrossRef]
- Naqvi, R.A.; Haider, A.; Kim, H.S.; Jeong, D.; Lee, S.W. Transformative Noise Reduction: Leveraging a Transformer-Based Deep Network for Medical Image Denoising. Mathematics 2024, 12, 2313. [Google Scholar] [CrossRef]
- Brieva, J.; Moya-Albor, E.; Gomez-Coronel, S.L.; Escalante-Ramírez, B.; Ponce, H.; Mora Esquivel, J.I. Motion magnification using the Hermite Transform. In Proceedings of the 11th International Symposium on Medical Information Processing and Analysis (SIPAIM 2015), Cuenca, Ecuador, 17–19 November 2015; Volume 9681. [Google Scholar] [CrossRef]
- Brieva, J.; Moya-Albor, E.; Rivas-Scott, O.; Ponce, H. Non-contact breathing rate monitoring system based on a Hermite video magnification technique. In Proceedings of the 14th International Symposium on Medical Information Processing and Analysis, Mazatlán, Mexico, 24–26 October 2018; Volume 10975. [Google Scholar] [CrossRef]
- Brieva, J.; Ponce, H.; Moya-Albor, E. Non-Contact Breathing Rate Estimation Using Machine Learning with an Optimized Architecture. Mathematics 2023, 11, 645. [Google Scholar] [CrossRef]
- Moya-Albor, E.; Brieva, J.; Ponce, H.; Rivas-Scott, O.; Gomez-Pena, C. Heart Rate Estimation using Hermite Transform Video Magnification and Deep Learning. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 2595–2598. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; number PART 1. pp. 115–123. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
