Agent-Based Modeling of Epidemics: Approaches, Applications, and Future Directions

Abstract

The spread of infectious diseases is inherently linked to human social behavior, characterized by complexity, diversity, and openness. Intelligent agents in computer science provide a powerful framework for capturing such dynamics, enabling complex epidemic patterns to emerge from simple local rules. These agents exhibit self-organization, adaptability, and self-optimization, making them well suited for individual-level modeling. Agent-based models (ABMs) have shown promising results in epidemic simulation and policy evaluation. However, current implementations often suffer from simplistic behavioral assumptions and rigid interaction mechanisms, limiting their realism and flexibility. This paper first reviews the current landscape of epidemic modeling approaches. It then analyzes the underlying mechanisms of advanced intelligent agents, highlighting their modeling capabilities. The study focuses on four key advantages of intelligent agent-based modeling and elaborates on three critical roles these agents play in evaluating and optimizing intervention strategies.

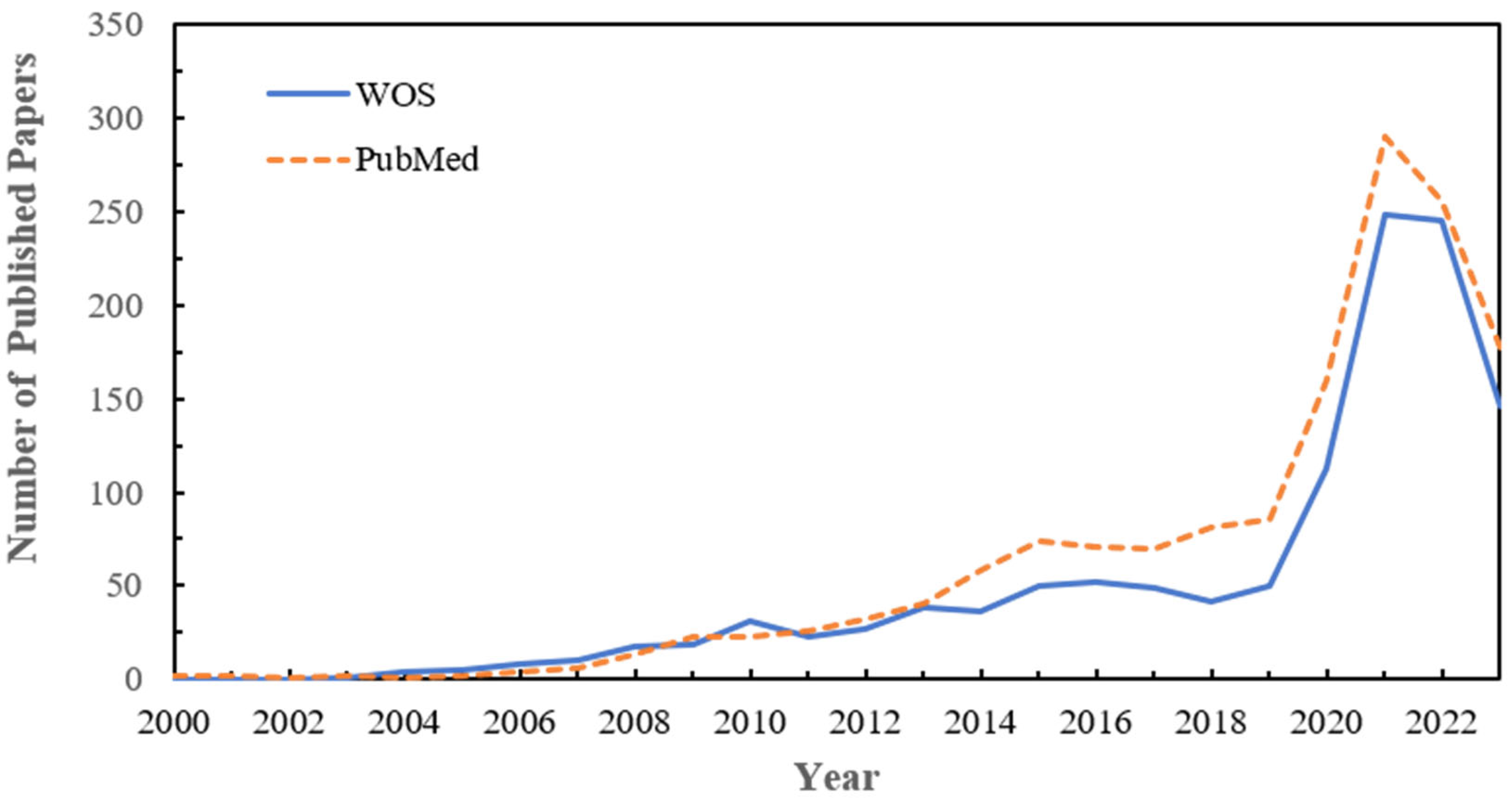
1. Introduction

From ancient times to the present, humanity has been plagued and tormented by diseases, especially by large-scale infectious diseases that have erupted repeatedly throughout history, posing serious threats to life and health, impacting economic development, and exacerbating social unrest. Faced with global outbreaks of pandemics such as COVID-19, various sectors of society urgently need accurate and real-time predictions of disease spread to formulate rational prevention and control strategies. In the prevention and control of infectious diseases, while accelerating vaccine development and optimizing the allocation of medical resources, numerous scholars tirelessly strive to reveal the patterns of disease transmission by collecting the geographic distribution and movement trajectories of infection cases and develop effective isolation measures and containment measures to slow down the spread of the epidemic.

Traditional prediction methods, such as models based on epidemiological principles and statistical methods, have played a crucial role in past epidemics. However, as diseases evolve and the complexity of social interactions increases, their limitations become increasingly apparent. Traditional methods often overlook the complex dynamic relationships between individuals, the interactions between different groups, and the comprehensive effects of multiple factors, lacking in-depth analysis of transmission mechanisms. Particularly when facing rapidly spreading, highly variable pathogens, the accuracy of predictions may be limited. Therefore, predicting infectious diseases requires a more intelligent prediction model that comprehensively considers multiple factors to better cope with the challenges of unknown epidemics.

In this context, ABMs have emerged and attracted great interest from the academic community and the field of epidemic prevention. The application of ABMs in the field of infectious diseases has been steadily increasing since the beginning of this century. With the global spread of COVID-19 and its significant impact on people’s lives, work, and daily activities, research in the direction of intelligent agents has begun to show explosive growth, as shown in Figure 1. Agent-based models, based on the behavior and interactions of individual agents, can more accurately simulate the dynamic changes in individuals and populations in the real world. Highly flexible agents not only can consider people’s social activities but also adapt flexibly to different scenarios, thereby improving the accuracy and applicability of predictions. The incorporation of real-time interactive simulation features enhances their capacity to accurately depict alterations within social networks, thereby advancing the comprehension of epidemic transmission dynamics. This approach offers a more efficacious strategy for managing complexity and enhancing the reliability of predictions.

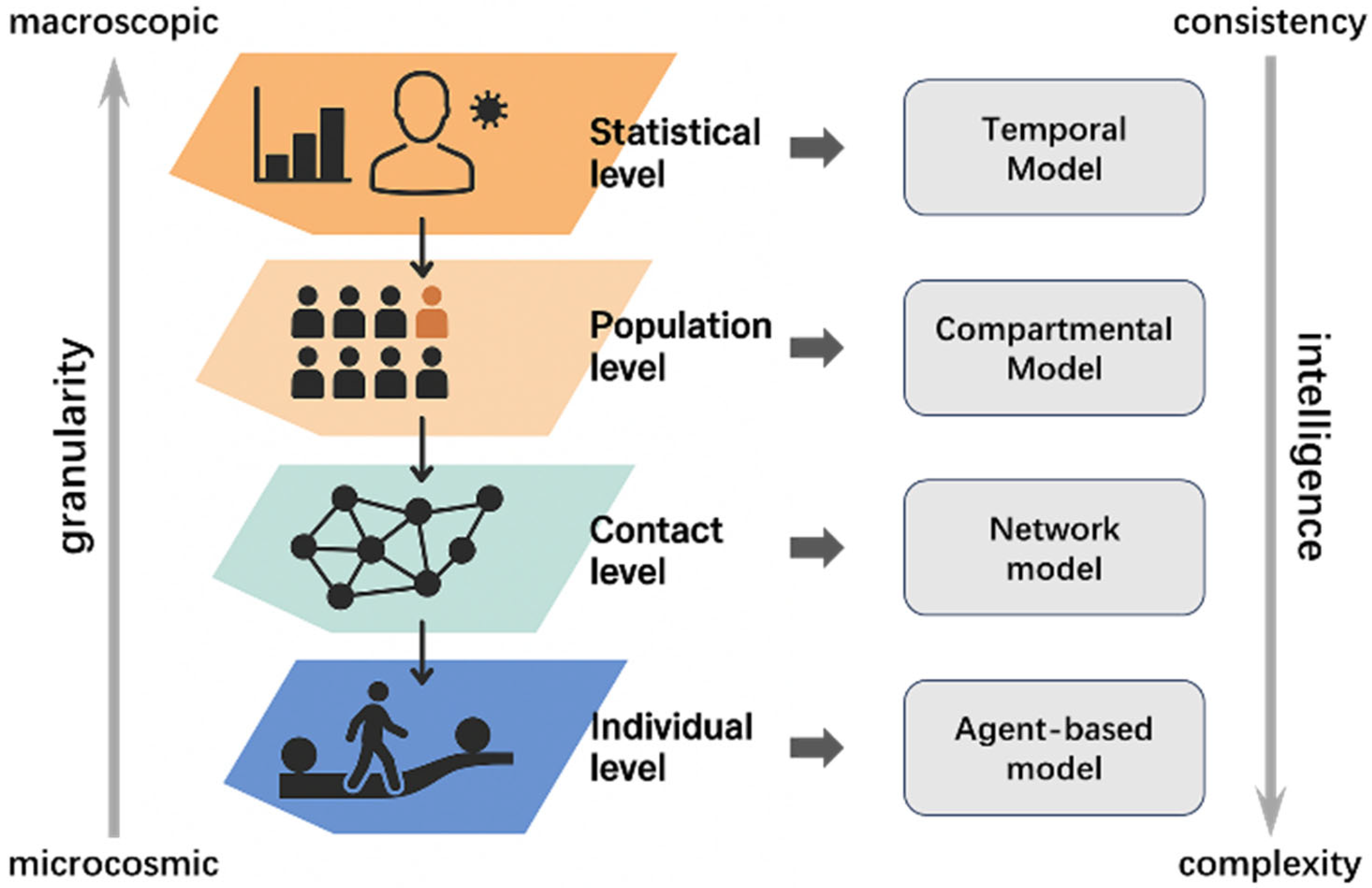
2. Related Works on Infectious Disease Modeling

Against the backdrop of continuously evolving global infectious diseases, researchers are actively exploring various advanced methods with unprecedented urgency to enhance the accuracy and practicality of infectious disease models. With the development of modern transportation networks, people’s mobility has become more convenient and fast, and the cross-border flow of populations has greatly increased, making it much more challenging to establish accurate infectious disease models. In this challenging context, the introduction of emerging technologies, including machine learning, big data analysis, and artificial intelligence, has become a key breakthrough point in addressing these challenges. Currently, mainstream infectious disease prediction methods include compartmental models, network models, time series models, and agent-based models [1]. These models reflect different levels of granularity—from macroscopic statistical abstractions to fine-grained individual-level simulations—as illustrated in Figure 2. At each level, “intelligence” manifests differently: temporal and compartmental models often embed intelligence in parameter estimation and dynamic fitting; network models capture structural complexity and heterogeneity; and agent-based models allow for adaptive, goal-driven behavior at the individual scale. In the following section, we briefly review the first three model types, focusing on their assumptions, strengths, and limitations in epidemic prediction.

2.1. Compartmental Model

Compartmental models, also known as dynamic models, are a classic epidemiological method for predicting infectious diseases. They involve analyzing epidemiological data to establish mathematical models, which include parameters such as the number of cases, infection rates, recovery rates, and possible mortality rates. These models describe the interactions between susceptible individuals, infected individuals, and recovered individuals. They rely on actual data and use mathematical equations and statistical methods to transform epidemiological data into computable models. Typical model methods include the SI model (Susceptible–Infectious), SIR model (Susceptible–Infectious–Recovered) and SEIR model (Susceptible–Exposed–Infectious–Recovered). For common infectious diseases with well-understood transmission mechanisms and relatively stable pathogen characteristics, these models perform well in predicting disease spread.

Dynamic modeling of infectious disease emerged as early as the 18th century, with Daniel Bernoulli’s seminal SI model (1766) for smallpox, in which he used demographic data to estimate the impact of inoculation on life expectancy, laying the groundwork for modern compartmental approaches [2]. Later, Sir Ronald Ross’s dynamic malaria model earned him the 1927 Nobel Prize and further established the framework of using differential equations to simulate disease spread. Since then, compartmental models, particularly SIR and SEIR variants, have become essential tools in epidemiology.

During the COVID-19 pandemic, researchers rapidly deployed these models alongside enhanced data and AI techniques: Alberto adopted a generalized SEIR to analyze global SARS-CoV-2 trends [3], Zhong Nanshan’s team integrated mobility data with AI-augmented SEIR simulations to forecast epidemic peaks [4], and institutions like China CDC applied meta-population SEIR frameworks to assess travel restrictions [5]. Additionally, extensions such as deep learning-enhanced SEIRD models, network-augmented SEIR frameworks, and multifractal-adjusted SIR models have provided nuanced insights into COVID-19 dynamics [6,7,8,9,10]. Collectively, these efforts illustrate the continual evolution of dynamic compartmental modeling from Bernoulli’s SI age-structured analysis to AI-informed, network-sensitive epidemic simulations.

The compartmental model, as one of the most commonly used infectious disease research models, also has its drawbacks. Firstly, it typically relies on previous knowledge of the transmission patterns of known pathogens, which can lead to inaccurate predictions for emerging pathogens due to a lack of sufficient experience. Additionally, compartmental models often simplify complex diseases that consider social networks and individual behaviors. For instance, they may overlook factors such as people’s mobility patterns, social contact frequencies, and behavioral changes that influence disease spread. Therefore, while compartmental models can provide useful insights in certain cases, researchers should exercise caution when applying these models and integrate other methods to gain a more comprehensive understanding and prediction of disease.

2.2. Network Model

The network model captures the spread of infectious diseases by simulating interpersonal interactions through graph structures, where individuals are represented as nodes and their social ties as edges. By incorporating parameters such as transmission rate, recovery rate, and diverse network topologies, the model enables dynamic simulations of disease propagation. Unlike purely dynamics-based approaches, network models emphasize the heterogeneity of real-world social connections—considering both the intensity and scale of contacts—and can integrate complex structures such as community clusters and hierarchical layers. This allows for a more granular understanding of transmission pathways, enhancing both the realism and predictive precision of epidemic modeling.

Network-based epidemic models have evolved to capture the heterogeneity and dynamics of human interactions. Eden introduced an agent-based network evolution model tailored for low-prevalence diseases like HIV, combining adaptive network generation with individual-level simulation to improve inference in sparse-contact settings [11]. Steijvers used data from the SaNAE cohort, distinguished the roles of strong and weak social ties in respiratory infection prevention, suggesting structural differences in behavioral influence and information diffusion [12].

The integration of mobility networks into early outbreak modeling has also yielded key insights. Read utilized airline travel data to estimate SARS-CoV-2’s basic reproduction number and case trajectories [13] while correlating inter-city traffic volume in the Republic of Korea with COVID-19 case rates, indicating rapid spread via urban mobility [14]. Lau further revealed that international air traffic patterns significantly influenced cross-border transmission dynamics [15].

Complementary approaches enhanced inference and strategy design. Li applied a network-based meta-population model with Bayesian inference to estimate hidden transmission parameters [16]. Cui demonstrated that targeted testing of close contacts in a network setting can effectively suppress outbreaks [17]. Kiskowski and Chowell emphasized the role of individual behavior and stochastic contact patterns in epidemic control [18]. In recent years, multilayer and multi-strain network models have been widely employed to capture the complexity arising from pathogen evolution and heterogeneous contact structures [19,20].

However, network models have a strong dependency on network structure. Their applicability may be limited in cases where detailed social network information is lacking or where structural dynamics change rapidly. Pinter used network simulations to model interpersonal contacts within a community. By individualizing the transmission process for each contact, the phenomenon of generating different results in various simulation runs was observed [21]. In practical applications, network models may contain intertwined coupling structures, making them difficult to interpret and adjust. Therefore, it is necessary to comprehensively consider issues such as model flexibility and interpretability.

2.3. Temporal Models

Temporal models leverage historical and current data for predicting future trends. This field integrates advanced mathematical, statistical, and machine learning techniques to analyze data, identifying and inferring underlying patterns. There are three primary approaches: statistical models, machine learning models, and deep learning models.

In the face of large-scale data, emerging information technologies such as machine learning and deep learning exhibit not only enhanced processing power, but also advanced capabilities for data analysis and pattern recognition. Prediction models based on deep learning (such as RNN) are more flexible, capable of handling nonlinear relationships, implementing automatic feature learning, and avoiding the need for differencing or other preprocessing of data, thus exhibiting significant advantages in modeling and analyzing complex raw data. In practical applications, it is essential to fully understand the characteristics of the data and select appropriate models based on actual needs and available resources.

Recent studies have explored diverse hybrid architectures to enhance forecasting accuracy. For instance, Sujath proposed a Multilayer Perceptron (MLP) and Vector Autoregression (VAR)-based method to predict COVID-19 spread in India, showing that MLP outperforms conventional methods such as Linear Regression [22]. Pinter proposed a hybrid machine learning approach combining the Adaptive Neuro-Fuzzy Inference System (ANFIS) with the Multilayer Perceptron–Imperialist Competitive Algorithm (MLP-ICA) to predict daily COVID-19 infection rates and mortality in Hungary [23]. Zivkovic further developed an enhanced hybrid framework incorporating ANFIS and a Beetle Antennae Search metaheuristic for COVID-19 case forecasting [24]. Beyond individual models, Lalmuanawma reviewed the rapid deployment of artificial intelligence in pandemic response, highlighting its effectiveness in improving diagnosis, prediction, contact tracing, and vaccine development [25].

Temporal models supported by big data have played a crucial role in large-scale epidemic outbreaks. However, the accuracy of temporal models heavily relies on the quality and quantity of input data. Selecting an appropriate temporal model for specific data can be challenging, as different models may be suitable for different types of data and problems. Additionally, some intervention measures may result in delayed effects, and temporal models need to accurately capture these delayed effects to effectively guide epidemic control measures in real-world scenarios.

3. Agent-Based Model and Characteristic Analysis

Agent-based models (ABMs), also referred to as individual-based models, represent a class of microsimulation techniques that model systems from the bottom up by simulating the behavior and interactions of autonomous individuals (“agents”). Unlike traditional compartmental models that assume a homogeneous mixing of populations, ABMs emphasize individual-level heterogeneity, localized interaction, and adaptive behavior, making them particularly suited for simulating the complex dynamics of infectious disease transmission in realistic social systems.

3.1. Current Status and Evolution

Recent work has demonstrated the widespread application and expansion of ABMs in pandemic modeling. For instance, Sun reviewed over 200 COVID-19 modeling studies from February 2020 to May 2022 and found that ABMs were the most frequently employed method, surpassing system dynamics, discrete event simulations, and hybrid models [26]. Lukens introduced an individual infection model that links infectivity and symptoms to viral load, host age, and pathogen phenotype, improving biological realism [27]. De-Leon developed a Dynamic Monte Carlo Agent Model (MAM) based on statistical physics principles, demonstrating superior predictive performance over traditional SIR models using epidemic data from Israel [28].

The growing reliance on ABMs also stems from the increasing availability of modeling platforms that support complex, scalable simulations. Abar provided a comprehensive comparison of 85 ABM platforms, offering design guidelines for researchers and system engineers [29]. Several modeling engines have since been developed to simulate a wide range of infectious disease dynamics: Waleed introduced a multi-disease engine supporting SIR/SIS/SI models [30], while Lee built the Regional Healthcare Ecosystem Analyzer (RHEA) to examine infection pathways within healthcare networks [31]. Notably, OpenABM, developed by Oxford researchers, supports age-stratified and country-specific simulations of SARS-CoV-2, enabling the assessment of interventions such as contact tracing and vaccination strategies [32]. Similarly, Kerr developed Covasim, an open-source ABM platform tailored for COVID-19 analysis, which incorporates demographic, contact network, and behavioral data to simulate complex events such as intra-household transmission, school-based clustering, and super-spreader dynamics [33].

While simple models remain valuable for rapid assessment during early outbreak stages, the scale and complexity of pandemics like COVID-19 have driven the demand for granular, data-rich, and behavior-aware models. The widespread availability of high-resolution population data and increased computational capacity has further accelerated the adoption of ABMs [34], shifting research focus toward more sophisticated aspects such as individual heterogeneity modeling, spatial population structuring, dynamic contact networks, and high-risk scenario identification.

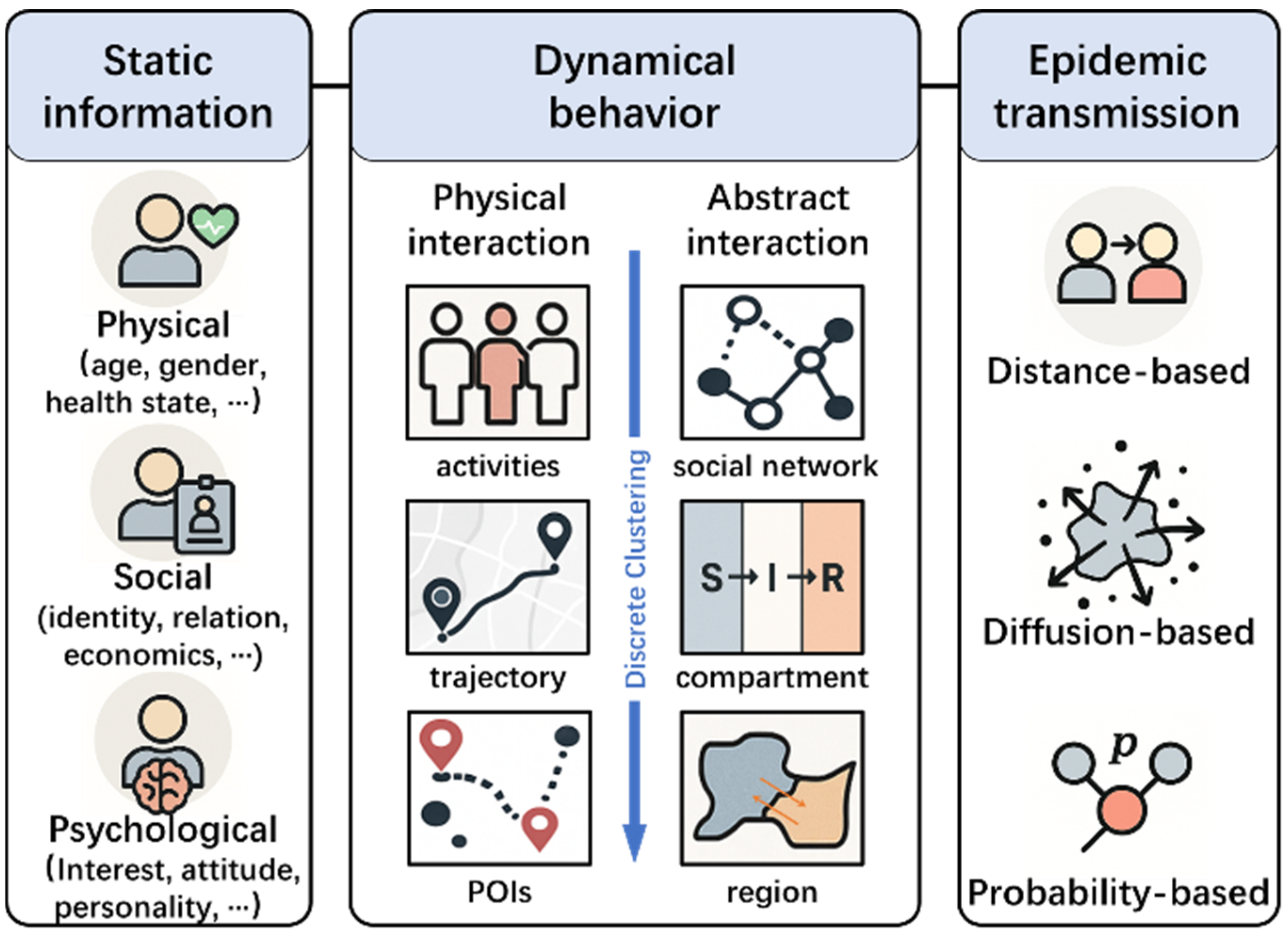
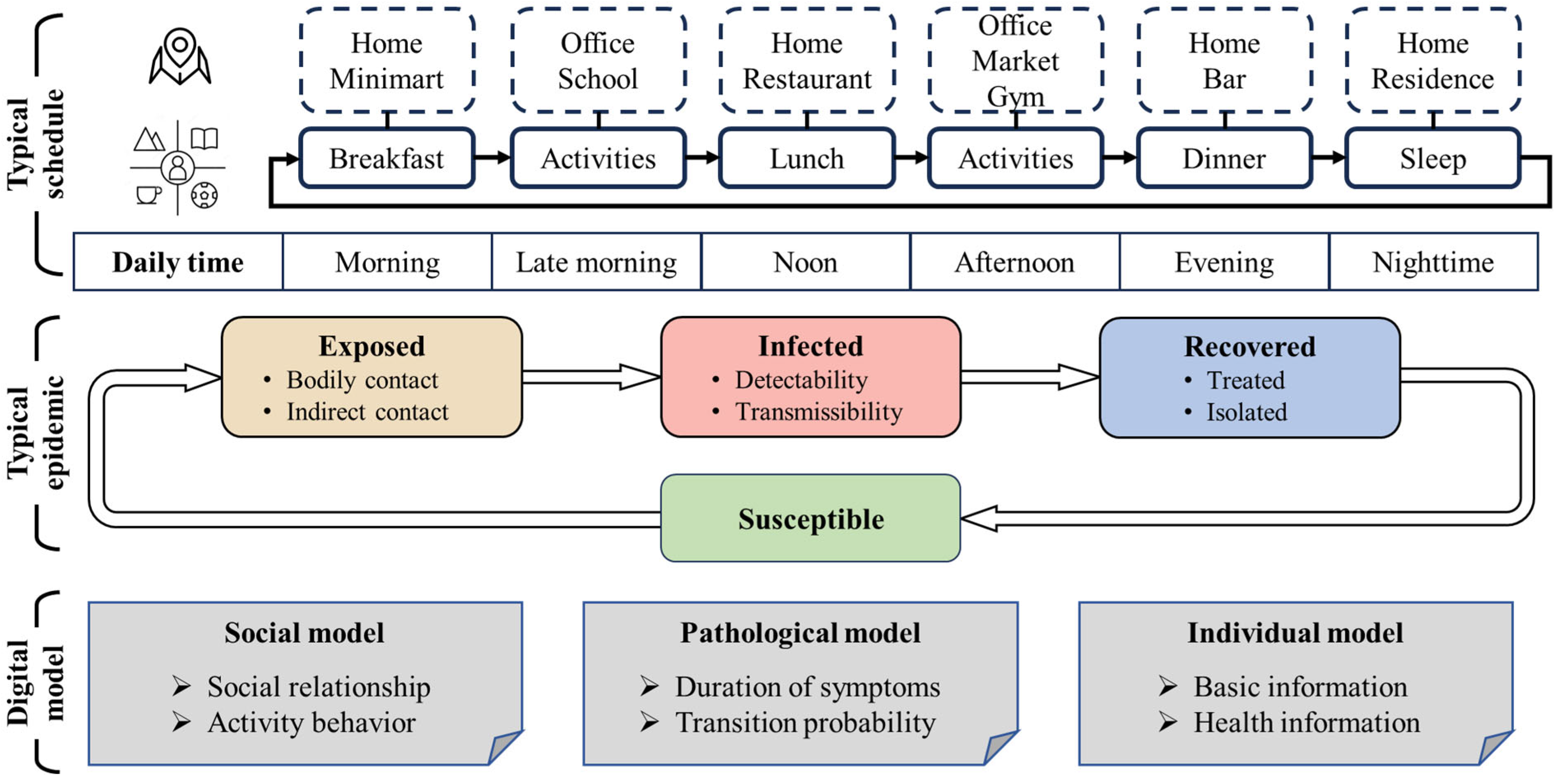
3.2. Agent Modeling Framework and Characteristics

At their core, ABMs characterize each agent as an independent decision-making entity endowed with specific attributes (e.g., age, health status, cognition) and behavioral rules, enabling high-resolution modeling of inter-individual differences and responses. These agents interact within dynamic environments, adjusting their behavior in response to external stimuli, perceived risk, or peer influence. To summarize the specific features of existing intelligent agents in infectious disease modeling, Figure 3 illustrates a multi-faceted agent-based modeling framework that captures the static heterogeneity, dynamic behavioral evolution, and context-specific transmission mechanisms crucial for epidemic simulation. The framework is divided into three hierarchical modules—Static Information, Dynamical Behavior, and Epidemic Transmission—each representing a critical layer in capturing the complexity of infectious disease spread and control.

The Static Information module encodes agents with essential attributes, including physiological conditions, demographic characteristics, cognitive awareness, and spatial location. These elements define the foundational heterogeneity across the population. For instance, physiological and immunological diversity has been emphasized through the explicit modeling of individual antibody levels and waning immunity [35]. Age-based infection pathways and symptom expression have been captured through calibrated agent-based simulations [36]. Xu constructed statistically accurate synthetic populations using census and land-use data, enabling realistic social structures at the household level [37]. Spatially embedded agents further reflect population distribution patterns, urban density, and neighborhood composition [38,39,40,41,42,43]. Cognitive features such as risk awareness and trust, which significantly influence health-related decision making, have also been embedded during initialization [44,45,46]. By integrating such multifactorial information, this module allows ABMs to differentiate infection risks at the individual level and serves as a basis for constructing fine-grained policy simulations.

Building upon this, the Dynamical Behavior module models how agents evolve over time through mobility, interaction, and behavior adaptation. This layer captures both routine spatial behaviors and responses to perceived epidemic risk. Multiple studies simulate realistic human mobility and activity patterns using GPS trajectories, transportation networks, and behavioral schedules [42,47,48,49]. Social and emotional feedback loops play a central role in shaping individual decisions—such as vaccine acceptance or avoidance of crowded locations—which are often influenced by fear, institutional trust, or misinformation [44,46,50,51,52,53]. These behaviors are modeled through frameworks like fuzzy cognitive maps, machine-learning-augmented protection motivation models, and dynamic awareness distribution functions. Moreover, collective behavior changes under social pressure or external information exposure have been examined to assess large-scale behavioral tipping points and their epidemic consequences [50,54,55]. This behavioral modeling capacity is critical to capturing the nonlinear feedback loops inherent in real-world outbreaks.

The Epidemic Transmission module connects agent behavior with transmission dynamics through spatiotemporally resolved contact networks and disease propagation rules. It incorporates multiple transmission pathways, such as direct contact, aerosol, and fomite-based spread, especially in enclosed environments like airports and shopping centers [48,56].

At the micro-scale, distance-based transmission models quantify infection risk between individuals i and j as an exponentially decaying function of physical distance:

$$P_{ij}(t)=\beta ·\exp \left(-{\displaystyle \frac{d_{ij}^2}{2{\sigma }^2}}\right),$$

(1)

where β represents the peak transmission probability and σ characterizes the spatial decay rate. Such formulations are particularly effective in modeling indoor environments where proximity plays a dominant role.

To account for stochastic individual-level interactions, ABMs often adopt probabilistic models of infection transitions. For a susceptible individual j in contact with a set of infectious agents ${\mathcal{I}}_j(t)$, the infection probability is given by

$$P(\mathrm{Susceptible} \to \mathrm{Infected})=1-{\displaystyle \prod _{k\in {\mathcal{I}}_j(t)}\left(1-{\lambda }_k\right)},$$

(2)

where λ_k denotes the transmission probability per contact with infectious individual k. This can be extended to multi-pathway formulations, combining transmission via direct contact, aerosol, and fomites.

At the mesoscopic scale, compartmental dynamics (e.g., SIR) are embedded in agent decision processes to simulate the evolution of the disease within the population,

$$\begin{array}{l}{\displaystyle \frac{dS}{dt}}=-\beta ·{\displaystyle \frac{I}{N}}·S,\\ {\displaystyle \frac{dI}{dt}}=\beta ·{\displaystyle \frac{I}{N}}·S-\gamma I,\\ {\displaystyle \frac{dR}{dt}}=\gamma I,\end{array}$$

(3)

where the classic S-I-R transitions are realized at the agent level through rule-based updates. Each agent a_i updates its epidemiological state through a rule-based function that reflects both individual behavior and networked exposures:

$$s_i(t+1)=\mathcal{T}\left(s_i(t),\left\{s_j(t)\mid j\in {\mathcal{N}}_i\right\},\theta \right),$$

(4)

Numerous scenario-specific simulations have been conducted to assess epidemic progression and control efficacy in diverse contexts. These include high-risk institutional environments (schools [57,58,59,60], hospitals [61,62,63,64], refugee camps [65,66], construction sites [67,68]), household and community transmission [49,69,70,71], and public infrastructure (e.g., malls [72], airports [56]). Studies have used such settings to evaluate the impact of intervention strategies such as social distancing, vaccination, hybrid teaching, and contact tracing [59,69,72,73,74,75]. Advanced ABMs integrate Monte Carlo simulations and real-time data to model uncertainties, stress-test interventions, and generate robust decision-making insights [67,76,77].

By organizing prior research within this structured framework, Figure 3 demonstrates how static heterogeneity, dynamic behavior, and context-specific transmission mechanisms are jointly modeled to simulate the full lifecycle of an epidemic. This three-part modularity allows agent-based models to remain adaptable across scales and domains while ensuring fidelity to real-world complexities. It also provides a systematic reference for aligning model inputs, behavioral rules, and transmission pathways with targeted research objectives and policy needs.

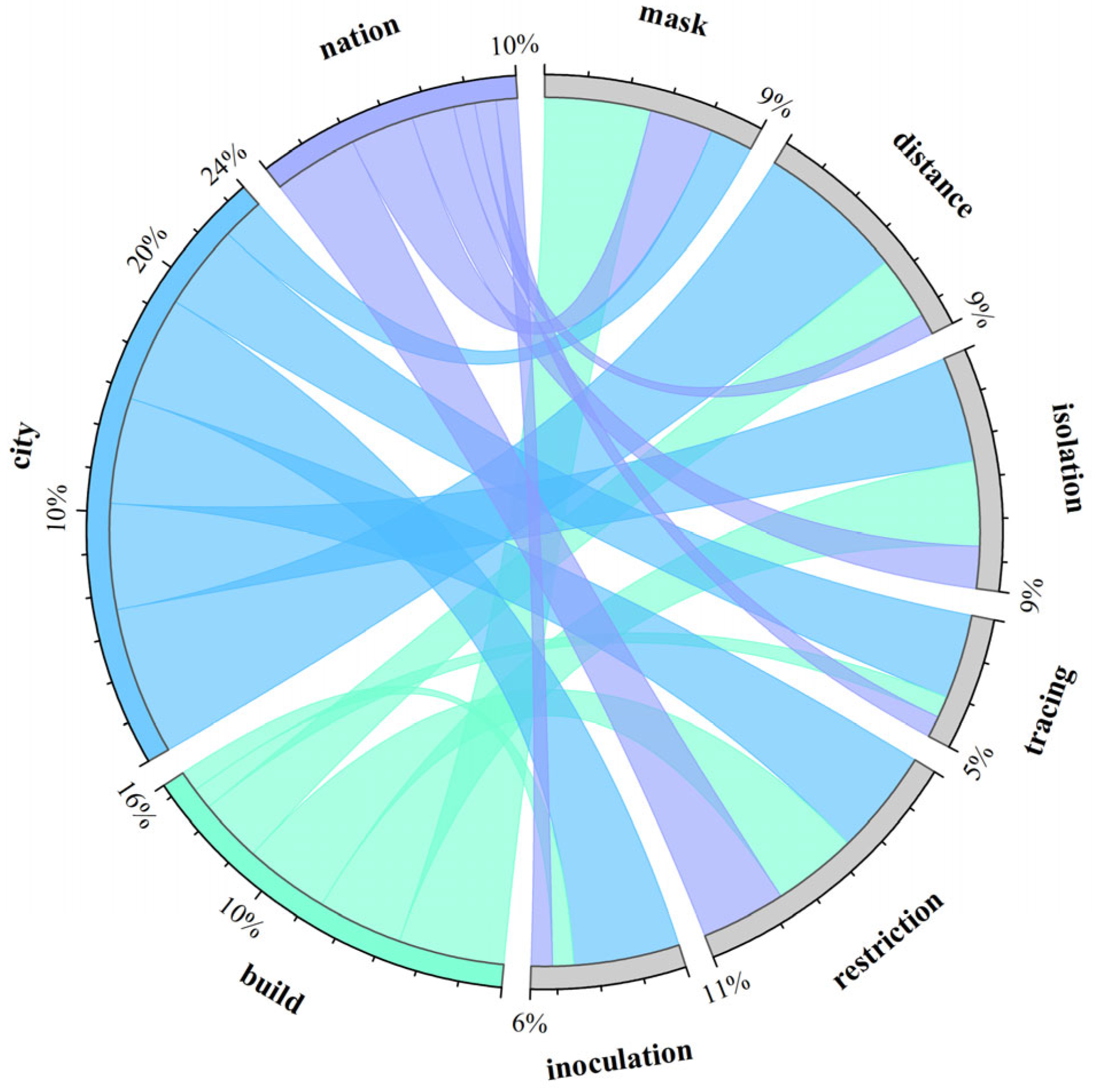
4. Intervention Measures Evaluation Based on ABM

This section focuses on the application of intelligent agent models in assessing intervention strategies for infectious diseases. While intelligent agent models have the capability to predict the number and trend of infections, their functionality extends far beyond this. Through the interaction between individuals and intervention strategies, intelligent agent models can manifest more complex and profound impacts, thereby providing a powerful tool for the comprehensive evaluation of the effectiveness of various intervention measures.

4.1. Revealing Transmission Chains and Sites of Disease Outbreak

ABMs excel in identifying early transmission chains and outbreak sites, especially when epidemiological data are limited. Unlike compartmental models that rely on population-level assumptions, ABMs simulate individual behaviors over social and mobility networks to infer potential transmission pathways, offering critical support in the early phase of epidemics [78,79,80].

As epidemics evolve with variant emergence, reinfection, and shifting interventions, accurate modeling becomes increasingly data-demanding. ABMs, by simulating individual-level interactions and scenarios, infer latent transmission routes without requiring extensive real-time data, supporting timely decision making [81,82].

Recent studies validate ABMs’ capacity in reconstructing outbreak dynamics. Syga combined Bayesian inference with ABM to estimate key transmission parameters during Germany’s first COVID-19 wave [83]. Cliff used nearly 20 million simulated agents to model influenza spread in Australia [84]. Ajelli showed that tracing 5–10 contacts per Ebola case was crucial during elimination [85]. López [86] found that digital contact tracing with 30% adoption could suppress COVID-19 at R0 = 1.7 [86]. Shamil demonstrated city-level containment with 75% smartphone tracking [87].

Large-scale geospatial ABMs have revealed how mobility and contact patterns shape outbreak risk. Aleta integrated mobility and census data to model COVID-19 in Boston, showing that targeted isolation and testing could substitute for broad lockdowns [88]. Kustudic highlighted how urban connectivity affects spatial predictability [89]. Studies on smallpox [90] and lab-released influenza [91] further confirmed ABMs’ ability to assess containment feasibility under high-risk scenarios.

At the micro-scale, ABMs have uncovered transmission contexts in diverse environments. Cooley estimated subways could account for 4% of flu transmission in New York City [92]. Rajabi [93] and Tabasi [94] used GIS-integrated ABMs to identify environmental drivers of leishmaniasis spread, including desert zones and seasonal patterns.

In summary, ABMs provide a flexible, data-efficient approach to reveal transmission chains and outbreak hotspots. Their capacity to simulate individual behaviors, mobility, and contacts underpins early detection and targeted intervention, especially when empirical data remain scarce.

4.2. Prospective Assessment of Vaccine Efficacy

Vaccination remains a cornerstone of infectious disease control by offering both direct protection to individuals and indirect community-wide immunity. Agent-based models (ABMs) offer distinctive advantages in prospectively evaluating vaccine efficacy, particularly during the early stages of an outbreak when uncertainty is high. Through fine-grained simulation of individual behavior, ABMs can assess the effects of various vaccination strategies—including target population selection, rollout timing, prioritization policies, and distribution logistics—on transmission dynamics and outbreak mitigation. These models provide actionable insights for public health authorities seeking to optimize immunization programs.

Unlike traditional compartmental models, which often assume homogenous vaccine implementation across space and time, ABMs account for behavioral heterogeneity, operational constraints, and dynamic feedback between vaccination coverage and disease spread. Addressing this gap, Tao proposed an SIRV model to identify optimal vaccine diffusion rates under resource limitations, suggesting that moderate distribution speeds may achieve localized herd immunity while minimizing outbreak size [95]. Similarly, Lee demonstrated that influenza vaccination remains impactful even during epidemic decline, with effectiveness shaped by compliance, timing, and priority settings [96,97]. Zachreson highlighted that targeted vaccination of high-risk groups, as implemented in Australia, can reduce lockdown intensity and early epidemic growth by 43% and 52%, respectively [98]. Faucher further emphasized the superiority of reactive vaccination strategies in schools and workplaces during large-scale outbreaks [99]. Liu explored how vaccination coverage and immune clustering interact with contact tracing to affect measles outbreak probability and scale across households, schools, and workplaces [100].

Several studies focus on age-based prioritization. Laskowski evaluated cross-protective antibody levels and recommended child-targeted vaccination to reduce epidemic burden on children [101]. In regional simulations, Cattaneo used Covasim to model the Lombardy region and found that prioritizing elderly and high-risk individuals greatly reduced infection and mortality [102]. Moghadas, using U.S. demographics and COVID-19 severity data, demonstrated that prioritizing healthcare workers and vulnerable populations while excluding children under 18 significantly reduced incidence, hospitalizations, and deaths [103].

While vaccine efficacy against infection may be limited in some scenarios, these studies collectively affirm that strategic vaccination, when informed by agent-based simulations, can effectively suppress epidemic spread. Importantly, continued adherence to non-pharmaceutical interventions remains essential to maximize overall control.

4.3. Assessment of Nucleic Acid Testing and Mixed Intervention Measures

ABMs offer powerful tools for assessing epidemic detection and control strategies, particularly through their ability to simulate heterogeneous behaviors, spatial interactions, and policy impacts across varying populations and contexts. By modeling interventions across regions, time frames, and social settings, ABMs provide critical insights for evaluating the effectiveness of testing protocols, vaccination efforts, behavioral restrictions, and compound strategies.

In the realm of testing strategies, ABMs have been widely applied to simulate the impact of rapid diagnostic interventions. Abeysuriya evaluated a “test-to-stay” strategy using daily rapid antigen tests (RATs) for school-based close contacts, balancing outbreak control with in-person learning [104]. Vilches incorporated Ontario census data and waning immunity into an ABM to design cost-effective workplace testing plans [105]. Asgary assessed school-based testing under varying classroom structures, revealing that frequent, rapid testing combined with at-home isolation could effectively mitigate school outbreaks [106]. In Canadian long-term care facilities (LTCFs), Vilches showed that weekly staff testing reduced resident infections by over 25% compared with baseline symptom screening [107]. Huang found antigen-based testing, particularly in combination strategies, outperformed PCR testing in reducing healthcare burden [108].

Addressing the challenge of asymptomatic transmission, Sah reviewed 350+ studies and estimated over 1/3 of COVID-19 cases are asymptomatic, especially among children [109]. This silent spread highlights the importance of population-wide behavioral interventions [110]. In modeling non-pharmaceutical interventions, ABMs further reveal the conditions under which behavior-based strategies can effectively reduce transmission. Li showed that widespread surgical mask use and adherence to distancing protocols could contain SARS-CoV-2 spread without lockdowns [111]. Bagger proposed a personalized return-to-work strategy and found restricting population mixing more impactful than limiting absolute numbers [112]. Hoertel simulated post-lockdown resurgence and demonstrated that continued masking, distancing, and protection of vulnerable groups substantially reduce mortality and ICU burden [113]. Mao found that extending weekends could significantly curb influenza transmission in urban regions [114]. Finally, Peak compared isolation and symptom-monitoring strategies for seven diseases and concluded that intervention effectiveness is tightly coupled with disease natural history, transmissibility, and health system capacity [115].

In summary, ABMs’ ability to simulate nuanced social dynamics, intervention timing, and heterogeneous adherence makes them indispensable for scenario-based epidemic response planning.

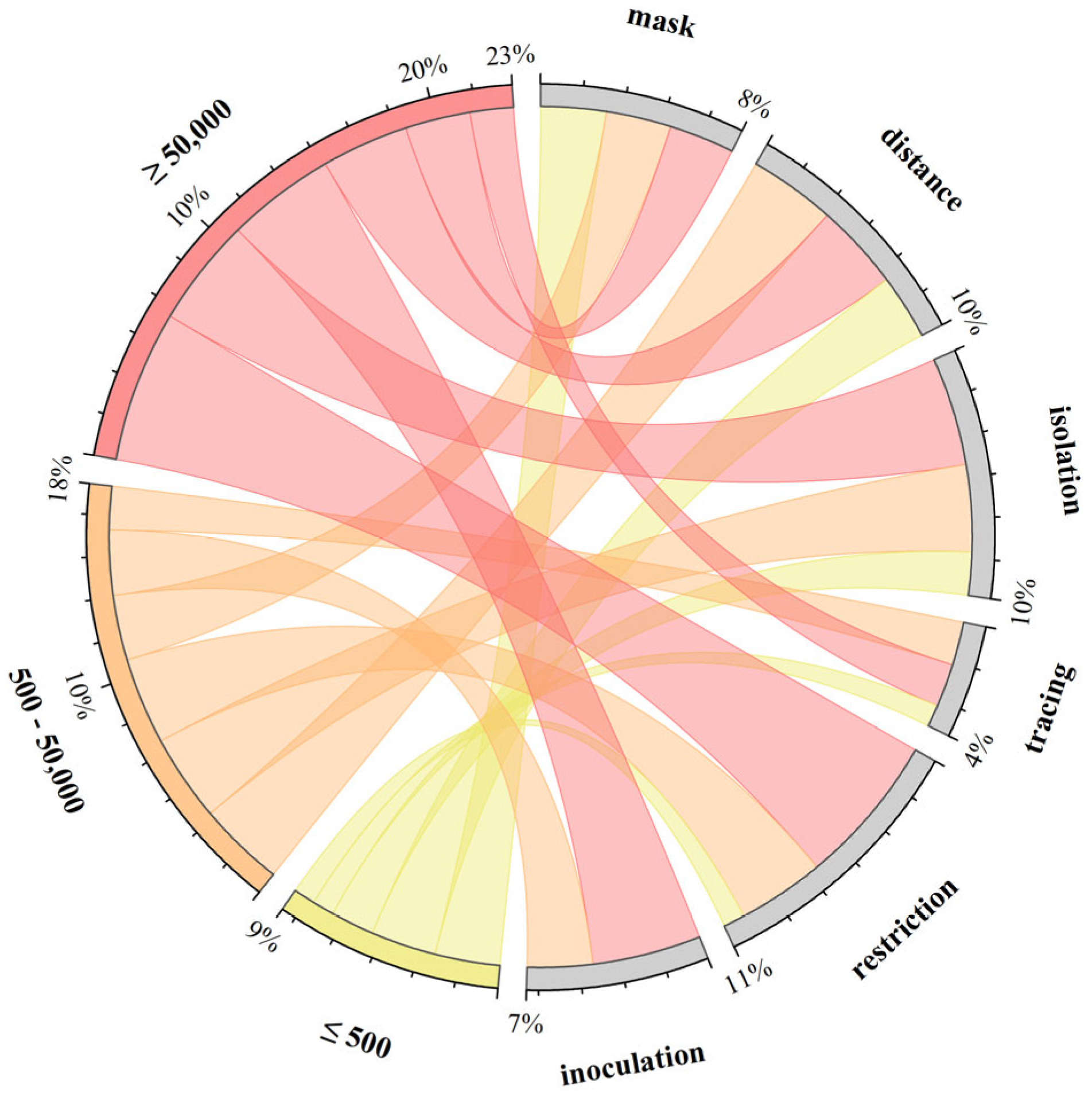
4.4. Cluster and Visual Analysis of Intervention Strategies

Incorporating contextual background information and data from specific scenarios facilitates the intelligent agent in providing meaningful assessments of various intervention measures across multiple scope levels. This approach furnishes scientific grounds and decision support across different scales, including individual, familial, communal, urban, and even national or global tiers.

At the national and global levels, ABMs simulate cross-regional transmission and policy responses. Silva clustered U.S. states to assess H7N9 outbreak burdens [116], while Mehra modeled inter-city consensus-based control through travel-mediated disease spread [117]. Novakovic [118] and Zhang [119] quantified the impact of non-pharmaceutical interventions (NPIs) like masking and lockdowns in national populations, revealing the importance of timely and targeted measures.

At the urban level, ABMs capture complex mobility and interaction networks. Borkowski used a discrete-space pedestrian model in a city of 650,000 agents to simulate outbreak dynamics [120]. Gomez modeled one million virtual agents in Bogotá under different distancing policies [121]. Zhou integrated testing and treatment resource allocation in a multi-city framework [122]. Other studies focused on city-specific epidemic dynamics and responses: CystiAgent validated in Peru [123], simulations of Nunavut [124], and regional comparisons in Wisconsin and New York City [125].

At the community and household levels, ABMs simulate dense, high-contact environments where household clustering significantly affects disease spread. Scott emphasized scenario-driven modeling in Victoria’s COVID-19 response [126], while Laskowski showed the role of age structure and immunity in Indigenous communities [127]. Tiwari used cellular automata to explore distancing and movement restrictions [128]. Longini evaluated antivirals, isolation, and vaccination in Southeast Asia [129], and Scott demonstrated that reopening high-contact venues (e.g., bars, transport) drives resurgence more than structured, small-scale gatherings [130].

School environments require special attention due to their enclosed spaces and repetitive interactions. Lyu [131] and Benneyan [132] analyzed transmission drivers like density and operational flexibility. Tatapudi simulated the effects of campus reopening in U.S. cities [133]. Duan used parallel simulations to test intervention strategies for H1N1 outbreaks [134]. Potter concluded that prolonged school closures, guided by local incidence thresholds, are key to epidemic mitigation [135].

To better clarify the relationship between intelligent agent modeling features and intervention strategies, we present a synthesis of the key literature discussed in Section 2 and Section 3, as shown in

Table 1. Key modeling features statistics in agent-based modeling research.

Duration of Simulation			Agent Number			Territorial Scope
Hour	Year	Month(s)	<500	500~50,000	>50,000	Building(s)	City	Nation
[48,63]	[36,70,103,110,118]	[5,16,18,44,49,57,59,60,67,68,72,74,76,86,88,97,98,99,100,101,105,106,111,115,119,124,125,130,131,135,136,137,138,139]	[48,49,63,67,68,72,91,106]	[18,44,57,59,60,70,74,101,103,105,110,111,115,124,128,130,131]	[16,36,76,86,88,97,98,99,100,118,119,125,135,136,137,138,139]	[18,48,49,59,60,63,67,68,70,72,101,105,106,128,131]	[36,74,86,88,91,97,99,100,124,125,130,135,136,138,139]	[5,16,76,86,98,111,118,119,137]
Intervention Measures						Result
Mask	Social Distance	Isolation	Contact Tracing	Travel Restriction	Inoculation	Infection	Death	Risk
[59,60,67,68,74,106,111,118,119,139]	[57,68,72,74,88,91,111,125,128,130,136,139]	[44,76,86,88,91,105,106,115,128,131,136,139]	[70,86,91,130,139]	[5,49,59,60,76,110,118,119,130,131,135,136,138,139]	[36,57,59,60,68,72,76,97,98,99,100,101,103,124]	[5,16,18,44,49,57,59,60,67,68,70,74,76,86,88,97,99,103,105,106,110,111,115,119,124,125,130,131,135,136,139]	[67,103]	[5,36,48,63,72,91,98,100,101,137,138]

. Our literature selection focused on peer-reviewed articles published between 2000 and 2024, using search terms such as “agent-based model,” “epidemic simulation,” “intervention strategy,” and “infectious disease control.” We consulted major academic databases, including Web of Science, Scopus, PubMed, and Google Scholar. Studies were selected based on their relevance, methodological innovation, and representativeness across different modeling frameworks and application scenarios. This table provides a structured overview to support the mapping between agent modeling features and intervention contexts. When summarizing, we adhered to the following rules:

• Modeling of infectious diseases transmitted through modes such as animals, water sources, or transmission via injection, sexual activity, etc., was not included temporarily, with the focus primarily on diseases spread through respiratory and physical contact.
• Modeling of transmission in specific environments (e.g., prisons, refugee camps, hospitals) with unique characteristics was not included for comparison due to the special considerations necessitated by these environments.
• The term “build(s)” denotes small social units formed by a group of people within a specific geographical area, such as a floor, a building, or adjacent buildings within a region.
• The term “risk” refers to parameters not directly mentioned in the corresponding paper that denote specific infection quantities or approximate meanings, such as infection risk or probability of illness.

Further, we provide a visual analysis based on proportional chord diagrams for well-structured agent models identified in the literature, as shown in Figure 4. It should be noted that the interventions listed in this article are primarily based on those commonly observed in clusters, making it challenging to encompass all measures. Here are some other measures not included and specific reasons for their omission:

• Although nucleic acid testing is considered a significant measure, it was not explicitly listed here as it does not fall under direct intervention measures.
• Measures such as ventilation, disinfection, and improving sanitation, while present in a small number of studies, were not directly quantified in the corresponding literature.
• For the purpose of clustering and summarization, measures related to movement restrictions mentioned in the article, such as sheltering in place, staggered travel, population grouping management, etc., are collectively referred to as travel restriction measures.

As shown in Figure 4, it is evident that the majority of research efforts in modeling intelligent agents for epidemic spread are primarily focused on simulating medium- to large-scale populations within urban and sub-urban contexts. This aligns with the propensity of intelligent agents to excel in meso-level simulations. Simultaneously, the duration of infection–recovery cycles in infectious diseases, typically lasting 1 to 2 weeks, and the characteristic of staggered population infection, correspond to the prolonged durations of intelligent agent simulations, often spanning several months. Regarding intervention measures, it is notable that various interventions have been digitally implemented within intelligent agent systems. In contrast to conventional control measures, emerging technologies such as contact tracing, supported by intelligent agent modeling, have also been employed. This facilitates more precise differential prevention and control efforts, thereby minimizing the spatial and severity impacts of epidemics on society to the greatest extent possible.

To further analyze the relationship between agent-specific features and intervention measures, we have constructed a corresponding relational diagram, as shown in Figure 5 and Figure 6. Given that simulation durations are primarily set as per experimental requirements rather than inherent features of agent modeling, we refrain from delving deeper into this aspect in our discussion.

In Figure 5, it becomes evident that across various scales of agent modeling, research tends to gravitate toward modeling and studying moderate to large-scale populations. Foundational preventive measures (e.g., mask wearing, social distancing, isolation) are reflected across different scales of agent models. However, more targeted intervention strategies (e.g., contact tracing, travel restrictions, vaccination strategies) are better suited for agent models dealing with larger population bases. In terms of territorial scope, additional findings have been obtained, as shown in Figure 6. There is a greater emphasis on modeling and inference at the community and city levels in research. Within urban control measures, there is a heightened focus on population control, with relatively less research dedicated to individual mask-wearing behavior. Conversely, community-level controls emphasize comprehensive measures at the individual level, such as mask wearing, isolation, and travel management.

5. Challenges and Prospects

Although intelligent agents still face numerous challenges and difficulties in infectious disease modeling, we are optimistic about their prospects in the field, owing to continuous technological advancements, particularly in artificial intelligence and machine learning as well as enhanced interdisciplinary collaboration. As we further research and innovate, intelligent agent models are expected to provide deeper insights and better equip us to understand and address the challenges posed by infectious diseases. This section briefly analyzes the primary challenges encountered by intelligent agent technology and proposes strategies for addressing these issues, aiming to foster interdisciplinary applications of intelligent agent technology and bring about new breakthroughs and opportunities in infectious disease research and control efforts.

5.1. The Current Challenges

As illustrated in Figure 7, agent-based epidemic models typically integrate three sub-models—individual, social, and pathological—to simulate state transitions across daily schedules and SEIR dynamics. Each agent carries personal health and demographic attributes (individual model), engages in time-structured social interactions (social model), and transitions between epidemiological states based on disease-specific parameters (pathological model). However, this fine-grained representation results in substantial computational and modeling challenges.

Firstly, the computational complexity of modeling large populations with heterogeneous schedules and contact networks is immense. Simulating city- or nation-level epidemics requires handling millions of agents and high-frequency behavioral updates [140]. To address this, methods such as meta-modeling [141], hybrid asynchronous execution [142], data locality optimization [143], and parallel acceleration via GPUs or high-performance computing [144,145,146] have been adopted. More recently, equation-learning frameworks reduce the reliance on full simulations by approximating dynamic outputs with fewer runs [147].

Second, parameter calibration remains difficult due to the expanded configuration space across individual, social, and pathological layers. As shown in Figure 7, the typical epidemic model segment depicts a standard SEIR-like state transition framework in which agents move through four disease-related states: Susceptible, Exposed, Infected, and Recovered. Adaptive surrogate-based optimizers like DYCORS-XGBoost and MSRS-SVM have achieved high accuracy in fitting epidemic curves [148], while mathematical [139] and spatial–statistical approaches [149] assist in refining transmission parameters and identifying risk factors. Sensitivity analysis models such as CystiAgent further support uncertainty reduction in localized epidemic contexts [150].

Most critically, current models often suffer from behavioral rigidity. As shown in Figure 7, agents typically follow predefined, fine-grained daily schedules, such as sequential transitions between home, work, restaurants, and recreational spaces, combined with deterministic state transitions in the epidemic process. While this structure enables detailed modeling of activity patterns and contact events, it also reflects a critical limitation: the absence of cognitive adaptation. Lacking perception, reasoning, and learning capabilities, these agents cannot respond to unexpected events such as novel policy changes, misinformation, or dynamic risk environments. This limits the model’s capacity to capture real-world behavioral heterogeneity and responsiveness in crisis situations.

In sum, while the modular integration of individual, social, and pathological layers enhances realism, addressing the computational, parametric, and cognitive challenges remains essential for the future advancement of intelligent epidemic modeling.

5.2. Fusion Innovation in Interdisciplinary Studies

Integrating intelligent agent models with disciplines beyond epidemiology opens broad avenues for innovation and application. Fields such as journalism, GIS, genomics, and economics benefit from agent-based modeling through enhanced behavioral realism, network-driven inference, and policy scenario evaluation.

Siettos highlighted the potential of large-scale agent models incorporating data from molecular biology, sociology, and demography and proposed network–theoretic frameworks to link epidemiology with social dynamics [151]. Du explored the interplay between social media and human behavior, demonstrating how platforms can both improve public risk awareness and exacerbate outbreaks through misinformation [152]. In genomics, Rockett integrated SARS-CoV-2 sequencing data with agent models to trace unidentified transmission chains and clarify epidemiological links [137]. From an economic perspective, Kerr modeled alternative COVID-19 control strategies (e.g., test–trace–isolate), revealing their ability to mitigate social and economic disruptions [136]. Zhu proposed an ACP-based agent modeling framework to evaluate the economic cost of interventions via carbon emissions, offering insights into balancing public health and development [138]. Further, Shoukat assessed the cost-effectiveness of Zika vaccination strategies across 18 countries, concluding that targeting reproductive-age women was highly efficient under specific incidence thresholds and cost conditions [153]. Together, these studies demonstrate the adaptability of intelligent agent models in supporting decision making across complex, multidisciplinary contexts.

6. Conclusions

The present study synthesizes the current research status of epidemic modeling techniques with a particular emphasis on the application of agent-based modeling in infectious disease research. Agent-based models, as an innovative modeling approach, possess unique characteristics enabling more accurate simulations of complex population behaviors and disease transmission dynamics. We intricately analyze four key features of agent-based models, including individual heterogeneity, population distribution characteristics, awareness of safety and behaviors, and the versatility of multiscale scenarios. These features endow a more realistic social context in infectious disease research and provide effective means for a deeper exploration of epidemic transmission mechanisms.

Furthermore, we delve into the proprietary functionalities of agent-based control strategy development, encompassing risk exploration and prediction, vaccine efficacy assessment, and nucleic acid testing alongside various strategy evaluations. Finally, we employ proportional chord diagrams to analyze the relationship between agent characteristics modeling and intervention measures and outcomes, aiding epidemiologists in better planning and designing agent-based models tailored to different scenario requirements.

In summary, this paper consolidates the application cases of agent-based modeling in infectious disease research, offering a systematic overview of novel technological research in the field of epidemiology at the current stage. Simultaneously, by deepening the understanding of infectious disease transmission mechanisms, it provides theoretical support and practical guidance for guiding epidemic prevention and control efforts, holding significant theoretical and practical implications.