Abstract
Cross-laminated timber (CLT) is a high-performance engineered timber that is very widely adopted. In several conditions, such as strength improvement at vulnerable connection points, local stress concentrations, existing structure retrofitting, and others, it is desirable to enhance the mechanical performance of CLT by applying additional reinforcement systems. This paper reports on an experimental campaign aimed at assessing the mechanical behavior of CLT panels reinforced with steel-reinforced polymers (SRPs). Twenty Sardinian Maritime Pine CLT panels, including unreinforced, SRP single- and double-layer reinforced panels, have been subjected to bending tests to determine the bending strength, stiffness, failure mechanism and enhancement of the reinforced panels compared to the unreinforced ones. In addition, an analytical model has been proposed to understand the mechanical behavior of SRP-reinforced CLT panels. The results show that SRP reinforcement significantly increases the strength and stiffness and influences the failure mechanism of CLT panels. The strength improvement induced by the reinforcement, however, is not proportional to its amount, since the increase due to the SRP double layer is only slightly higher than that due to the SRP single layer. The stiffness enhancement is less relevant, as expected. Attention has been paid to the possible shear failures of reinforced panels.
1. Introduction
Cross-laminated timber (CLT) is a high-performance structural material that belongs to the family of engineered timber. It is made up of solid timber boards placed side by side, arranged in crossed layers, stacked typically in odd numbers and glued together under pressure, or sometimes screwed, to form a single planar element with load-bearing capacity in all directions that can be loaded both in-plane and out-of-plane.
In addition to the intrinsic sustainability, with wood being a natural material, CLT structural systems offer high load-bearing capacity against vertical and horizontal actions such as wind and earthquake, which is also thanks to the high strength-to-weight ratio, the in-plane stiffness and the ability of the connections to confer ductility to the entire system. Moreover, relevant fire resistance and excellent thermal and acoustic performance are guaranteed. This construction system also promotes the use of prefabrication, which helps contain the construction site and logistics costs. CLT, being an industrial construction product, must satisfy specific quality and performance requirements; therefore, the boards that it is composed of are strength-graded according to established European standards [1,2,3,4]. By virtue of its characteristics, CLT represents the most innovative and cutting-edge timber construction technology and is very widely adopted.
In several conditions, it is advantageous to enhance the mechanical performance of CLT panels by applying additional reinforcement systems. This is particularly useful for addressing issues like large spans (without increasing thickness and weight), local stress concentrations due to openings in floors and walls (e.g., for staircases, windows, etc.) and other geometric irregularities, employment of medium–low-quality wood, strength improvement at vulnerable connection points, specific exceptional events (e.g., blows and fire), existing structure retrofitting, design errors, accidental load variations in existing structures, decreases in load-bearing sections due to degradation, and crack occurrence due to differentiated shrinkage. In addition, other goals can be addressed, like reducing the forest resource consumption and meeting the increasing demand for high-quality timber.
Although the literature on reinforced CLT is rather recent and therefore not yet very extensive, current findings indicate that strengthening of CLT panels can be achieved through the application of various types of reinforcement methods. Türer et al. [5] tested CLT formwork beams, damaged up to 85% of the ultimate capacity, retrofitted with carbon-fiber-reinforced polymer (CFRP) strips and CFRP fan-type anchors. The ultimate load-carrying capacity was almost completely restored. Song et al. [6] investigated the bending performance of three-ply CLT panels reinforced with CFRP bars and plates. The modulus of elasticity (MOE) and modulus of rupture (MOR) increased by 9% and 8%, respectively, in the case of the CFRP rod reinforcements, and by 27% for the MOE and 48% for the MOR in the case of the CFRP plate reinforcements. In addition, the ultimate bending moment was 14% higher than that of five-ply CLT panels (175 mm thick), calculated by the limit state design method. The authors ascribed the less effective performance of the CFRP rod reinforcement to the increase in the panel’s cross-section caused by the bars. Qingfang Lv et al. [7] tested bamboo CLT panels strengthened with CFRP grids under a four-point monotonic loading configuration. The application of CFRP grids via pressing them into the bamboo layer significantly increased the ultimate load; conversely, CFRP grids bonded at the interfaces of adjacent layers negatively affected the load-carrying capacity. Lopez-Molina and Doudak [8] simulated blast loading on CLT elements retrofitted with steel straps and glass-fiber-reinforced polymers (GFRPs). Steel straps increased the post-peak resistance and ductility, while GFRP enhanced the overall behavior of the slabs. Song et al. [9] compared the strength performance of the edge connections between CLT panels to that of connections reinforced with GFRP. GFRP increased the yield strength by 7% and the stiffness by 92%. Valdes et al. [10] carried out bending tests on three-layer and five-layer maritime pine CLT panels reinforced with a single or double strip of flax fibers. For the three-layer panels, a significant increment in the load-carrying capacity and stiffness has been achieved, whilst for five-layer panels, the effectiveness of the reinforcement was negligible. Rostampour Haftkhani and Shakiba [11] studied the bending behavior of three-layer screwed CLT reinforced with two types of reinforcements: aluminum sheets and glass fiber reinforcement polymer (GFRP) wraps. The MOR and MOE of the CLT reinforced with aluminum sheets were higher than those reinforced with GFRP wraps. Bhat [12] tested different binding/wrapping techniques for enhancing the axial strength of CLT columns. Cold-formed steel (CFS) sheets and double cross-helix wrapping of fiber-reinforced polymer (FRP) improved the strength by about 32% and 50%, respectively. Sharari et al. [13] investigated the effect of CLT strengthening with GFRP on the lateral resistance of single shear lap joints, which increased up to 53%. Rostampour Haftkhani et al. [14] investigated the lateral resistance of double shear lap joints in CLT panels reinforced by GFRP with 0-90-0 arrangements in two strength directions. The lateral resistance of the reinforced panels increased by about 26.5% and the value in the major strength direction was 4.2% greater than that in the minor strength direction. Rostampour-Haftkhani et al. [15] compared the embedment strength of lag screws in densified three-ply CLT under both longitudinal and transverse loading conditions with that of CLT reinforced with GFRP. Densification and reinforcement determined higher embedment strength than that of the control specimens. Hao Li et al. [16] analyzed the out-of-plane bending behavior of three-layer CLT specimens strengthened with carbon or basalt FRP (CFRP, BFRP) bonded to the bottom of the element. One tested configuration combined CFRP in the intrados with an inner layer of BFRP. The reinforcements enhanced the bending strength by up to 23.8% and the global bending stiffness with infinite shear stiffness by up to 18.4%. Arabi and Rostampour-Haftkhani [17] investigated the effects of GFRP on the withdrawal capacity of wood, lag screws, and steel nails in CLT. The withdrawal resistance of the nails, wood screws, and lag screws increased by 280.4%, 29.2%, and 83.3%, respectively, when increasing the number of GFRP layers in the CLT. Swinea et al. [18] tested CLT panels manufactured with various reinforcement materials (solid steel plates, perforated metal plates, FRP), placed between wood laminations, against various ballistic threats. The reinforced CLT specimens exhibited greater ballistic resistance than standard CLT. Baek et al. [19] evaluated the bending performance of CLT reinforced with glass fiber cloth (GFC) or a CFRP sheet applied at different locations: at the outermost tensile side, between the outermost tensile layer and the minor strength direction layer, and between all the layers. CFRP suppressed the tensile failure and improved the bending performance by introducing rolling shear failure. GFC improved the bending performance but suffered delamination.
As can be seen from the existing literature, the most studied reinforcement systems are the so-called FRPs (fiber-reinforced polymers), which are materials usually made up of two phases, one of which is the reinforcement, in a discontinuous form (typically bars, nets, sheets, etc.), characterized by high mechanical performance, and the other is the matrix, a continuous and mechanically weaker element. Therefore, FRP represents a family of composite systems made up of a polymer matrix that a fiber reinforcement, with high mechanical properties, is embedded in. The fibers give strength and stiffness to the composite, while the matrix binds, protects and stabilizes the fibers and determines the collaboration and the transfer of loads from the substrate. The main qualities of FRP systems are high strength and stiffness, lightness, speed of application, versatility, immunity to corrosion, and partial reversibility of the intervention. The FRP family includes SRP (steel-reinforced polymers), systems for structural reinforcement that employ steel fibers instead of the more common carbon, glass, basalt, or poliparafenilenbenzobisoxazolo (PBO) fibers. SRP systems are based on fabrics made of unidirectional high-strength twisted steel wires of a small diameter held together by a thin fiberglass mesh or other material that facilitates installation, which can be impregnated and glued on site with either epoxy or polyester resin [20,21,22,23,24]. The twisting of the wires allows some mechanical interlocking between the cords and the matrix and may also induce overall ductile behavior upon stretching. The cords are also coated with either brass or zinc, making the material potentially free of any corrosion and suitable for different kinds of environmental exposure. Relevant advantages of SRP over other FRPs are the higher steel wire MOE than carbon or glass fibers, larger displacement capacity, relatively ductile behavior, higher energy dissipation at failure and better cost efficiency [20,21,25]. SRPs have been widely used for about two decades in the strengthening of reinforced concrete structures [26,27,28,29,30,31,32,33,34,35,36,37,38,39] and masonry buildings [40,41,42,43,44,45,46,47,48], where steel-reinforced grout (SRG) is frequently preferred [49,50,51,52,53,54,55] due to its better compatibility with the substrate. The application of SRPs in the strengthening of timber structures is still quite limited [56,57,58,59], and to the best of the authors’ knowledge, there are no documented uses of SRP for CLT strengthening. In this regard, the characteristics of SRP, especially the ductility, high strength, and lower energy cost compared to carbon- or glass-based FRP [60], highlight the need for various alternative strengthening solutions beyond traditional FRPs and inspire researchers to explore the potential of SRP in CLT structure strengthening. Indeed, the reinforcement of CLT with SRP can be beneficial in various structural and functional situations, including (i) improvement of the in-plane and out-of-plane bending and shear strength of slabs, beams and shear walls, useful in cases of elements subjected to high loads; (ii) crack control, useful for elements exposed to load cycles or thermo-hygrometric variations; (iii) non-invasive reinforcement of existing buildings, in cases of renovations or seismic retrofitting of structures; (iv) increased robustness in extreme events, due to the enhanced toughness and energy absorption capacity provided by SRP; (v) optimization of the structural design, for example in architectural projects with large spans or complex geometries, thanks to the possibility of reducing structural sections while maintaining required performance; and (vi) optimization of structural details such as openings, reducing the risk of stress concentrations and improving the structural integration.
Although the use of SRP in timber structure reinforcement is not yet widespread, in general, with respect to more established reinforcing systems such as CFRP (carbon-fiber-reinforced polymers), SRPs are expected to offer greater plastic deformation capacity before failure due to the presence of steel, which makes the structure more resistant to dynamic and seismic loads. Moreover, since SRPs retain a certain load-bearing capacity even after cracking due to the ductility of steel, they are expected to enhance the structural safety and offer better performance in shear reinforcement thanks to their greater plasticity and mechanical adhesion.
This paper aims to contribute to evaluating the effects and the effectiveness of SRP in terms of the structural performance of CLT elements subjected to bending. An experimental program has been run by carrying out bending tests on CLT panels unreinforced and reinforced with one or two SRP layers to determine the bending strength, stiffness, failure mechanism and enhancement of reinforced panels compared to the unreinforced ones. In addition, an analytical capacity model has been developed to evaluate the CLT performance increase due to the presence of SRP reinforcement, aiming to shed more light on the mechanical behavior of the composite panel and implement an effective tool for the design of CLT reinforcement systems.
2. Experimental Tests
The objective of the experimentation was to assess the mechanical behavior of CLT panels reinforced with SRP by means of bending tests aimed at the evaluation of relevant structural parameters, such as the failure loads, collapse mechanisms and global stiffness, and to evaluate the possible increase in the strength and stiffness of the fiber-reinforced panels compared to unreinforced panels.
2.1. Materials
The tests were carried out on 20 3-layer Sardinian Maritime Pine CLT panels (Figure 1), with the dimensions shown in Table 1. Three of them were not reinforced (U), the other 17 were reinforced with a single (R) or double (RR) reinforcement layer. Type RR* refers to a single layer of double-weight reinforcement. One panel (P14) was discarded due to a malfunction in the acquisition system.

Figure 1.
Three-layer 60 mm thick CLT panels made of Sardinian Maritime Pine.

Table 1.
Labeling and geometry of the specimens.
The employed reinforcement was the GeoSteel® G600 (Figure 2a) SRP system supplied by Kerakoll (Sassuolo, Italy), consisting of a unidirectional extra-high-strength galvanized steel fiber sheet, made of steel micro-cords, arranged in a fiberglass micromesh and embedded in a two-component epoxy thixotropic gel, the GeoLite® Gel (Figure 2b). In the case of the reinforcement labeled RR*, double-weight sheet GeoSteel® G1200 has been used. The technical characteristics of the reinforcing system are shown in Table 2, as supplied by the producer.

Figure 2.
(a) GeoSteel® steel fiber reinforcement fabric. (b) Two-component GeoLite® Gel matrix.

Table 2.
Mechanical properties of the SRP.
The steel-fiber-reinforced composite was applied after smoothing the surface of the panel to obtain a homogeneous substrate and clean off grease traces or glue residues, with the proper roughness, to allow effective bonding of the matrix. The effective application of the reinforcement to the panels respected the following steps: (i) cutting of the steel fiber fabric into properly sized portions (Figure 3a); (ii) preparing the GeoLite® Gel epoxy matrix by mixing the two components in the ratio of 3:1 using a drill stirrer until a soft paste of uniform light-gray color is obtained (Figure 3b); and (iii) applying the GeoSteel® SRP system.

Figure 3.
(a) Cutting of the GeoSteel® fiber reinforcement fabric. (b) Preparation of the GeoLite® Gel matrix.
The matrix was applied to the panel by creating a first layer 1 ÷ 2 mm thick with a flat spreader and a paint roller, ensuring that enough material was employed; then, the steel fabric was accurately incorporated, taking care to level any micro-irregularity and applying enough pressure to ensure the correct impregnation and elimination of any air bubbles, working in a direction parallel to the fibers and from the center of the section toward the edge; and finally, a second layer of matrix was applied until the steel sheet was completely covered (Figure 4). Working fresh-on-fresh, these operations were repeated in cases where a double-layer reinforcement was required.

Figure 4.
Application of the steel fiber reinforcement to the panel.
2.2. Bending Test
Bending tests were carried out on (see Table 1):
- 3 unreinforced panels (U), sized 1200 × 240 × 60 mm (L × W × h);
- 8 panels reinforced with a single SRP layer (R), sized 1200 × 240 × 60 mm;
- 3 panels reinforced with a double SRP layer (RR), sized 1200 × 240 × 60 mm;
- 2 panels reinforced with a double SRP layer (RR), sized 1500 × 240 × 60 mm;
- 4 panels reinforced with a double-weight SRP single layer (RR*), sized 1500 × 240 × 60 mm.
The tests were carried out according to [61,62], which prescribe four-point bending tests, where the span length is 18 ÷ 20 h [61] (h is the panel height) or 24 ÷ 30 h [62] and two symmetric loading points are located at the span center with a distance 6 h from each other. The set-up is depicted in Figure 5 and shown in Figure 6. The load was applied at a constant rate of 0.18 mm/s using a load actuator with a maximum capacity of 200 kN and an accuracy of 0.1% of the maximum applied load. The displacements were measured at the mid-span and at the center of the tension edge using a linear displacement transducer (LDT) with a nominal range of 50 mm, linearity and hysteresis of 0.10%, and a standard output of 2 mV/V. All the tests were conducted under controlled laboratory conditions of (18 ± 2) °C and (65 ± 2)% relative humidity. The moisture content of the panels remained constant during the testing and was approximately 12%.
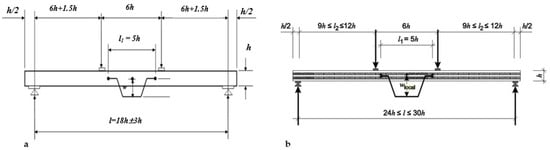
Figure 5.
Layout of the bending tests according to [61] (a) and [62] (b).

Figure 6.
Arrangement of the bending test in the laboratory.
To trace the load–displacement curve, a testing machine equipped with a load cell and a displacement transducer was used; moreover, an LVDT transducer was positioned at the centerline of the specimen to measure the CLT vertical displacements and calculate the global stiffness. Once the estimated maximum load was nearly reached, the LVDT transducer was removed and the load further increased until failure.
The data collected during each test comprised:
- Fu = failure load (N);
- wmax = maximum vertical displacement (mm) corresponding to the peak load;
- (F-w) = dataset of forces (F) and vertical displacements (w) recorded via the force and displacement transducers for tracking the load–displacement curves.
The maximum moment Mu at the mid-span and the maximum shear force Vu at the supports were calculated as follows:
where a is the distance between the loading point and the nearest support.
The bending strength fm (MPa) of the panels was calculated as:
where:
- h = total height of the specimen;
- Jeff = effective moment of inertia of the CLT panel.
Instead of the moment of inertia (bh3/12) of the solid timber section, the effective moment of inertia Jeff was assumed [63,64], considering the composite configuration of the CLT panels. In fact, in CLT technology, timber layers are stacked crosswise so that the layers’ grain orientation is alternatively aligned (0°-oriented layers) or orthogonal (90°-oriented layers) with the specimen’s longitudinal direction, where the bending forces act. 0°-oriented layers exploit the best timber properties, such as the longitudinal MOE E0, and are at least placed at the outer locations of the section. Conversely, the 90°-oriented layers are characterized by minimal strength and stiffness contribution in the specimen’s longitudinal direction due to timber intrinsic anisotropy. For example, the orthogonal MOE E90 is on average assumed to be 30 times smaller than E0 [63,65], which causes the transversal layers to barely contribute to the stiffness and stress distribution under the hypothesis of planar section in bending, as in the case of the intermediate layer in a 3-layer CLT element. The effective moment of inertia (Equation (4)), which neglects the contribution of the 90°-oriented layers to the stress distribution, was thus evaluated, as depicted in Figure 7 for the cases of the 5- and 3-layer CLT cross-sections.
where:

Figure 7.
Strain and stress distribution in the 5- or 3-layer CLT section under bending.
- Ji = moment of inertia of the generic 0°-oriented layer i;
- Ai = cross-sectional area of the generic 0°-oriented layer i;
- zi = the distance between the centroid of the generic 0°-oriented layer i and the CLT section centroid.
Equation (3) yields a good approximation derived from the current stress distribution only in the case of an unreinforced CLT cross-section; when a reinforcement is applied to the section, the stress distribution changes, as will be discussed further on. However, if applied to SRP-reinforced specimens, Equation (3) yields a “conventional” enhanced strength that is, in the authors’ opinion, suitable for comparing the panel performances in various configurations and takes on significance as a design reference.
In the light of this, the authors evaluated the specimens’ stiffness straight from the experimental response, as it provides a straightforward way to assess the enhancement provided by the reinforcement and make a comparison among different configurations. In accordance with the evaluation of the global MOE proposed in [61], the sectional global stiffness (EJ)exp was experimentally estimated by applying Equation (5), based on a linear regression of the experimental load–displacement curve in the range [0.1Fu; 0.4Fu]:
where:
- (F2 − F1) = load increment (N) on the regression line with a correlation coefficient of 0.99 or better;
- (w2 − w1) = vertical displacement increment (mm) corresponding to (F2 − F1);
- l = span of the specimen between the supports;
- b = width of the specimen;
- G0 = timber shear modulus in the direction parallel to the grain (N/mm2).
The shear modulus G0 has been assumed to be 500 MPa (~E0/16) according to [65], being the mean MOE of the employed Sardinian Maritime Pine E0 ~8000 MPa [66].
In addition, the rolling shear (RS) failure has been constantly monitored. The RS refers to a shear component acting on the 90–90° plane orthogonal to the grain direction of each layer. This type of failure, usually ignored when dealing with structural solid timber and barely monitored in glue-laminated timber, deserves great attention in CLT elements under bending due to the involvement of the intermediate 90°-oriented layers [63,64]. These internal layers, exposed to significant shear stresses, are highly susceptible to failure because of the small RS resistance (fv,RS) of timber in the 90–90° plane with respect to the grain direction, which is directly involved; failure occurs suddenly, and no residual strength is possible since the intermediate layers can no longer grant the transmission between the tension and compression 0°-oriented layers. Moreover, the RS modulus largely affects the deformation of panels in out-of-plane bending. The maximum shear stresses in the cross-sections have been evaluated according to Jourawsky’s theory by means of Equation (6) [63].
where Q and J are, respectively, the static moment and the moment of inertia of the cross-section with respect to the elastic neutral axis, calculated neglecting the contribution of the 90°-oriented layers based on the hypothesis that E90 = E0/30 [63,64,65] but accounting for the reinforcement when present, so that an estimation of the actual shear stresses is accomplished. As stated, the RS strength is generally very low compared to the longitudinal shear strength. EN 16351 [62] suggests considering the characteristic RS strength equal to 1.10 MPa independently of the timber strength class. Therefore, this issue is critical in CLT capable of driving the panel design, especially when the flexural strength is high or enhanced by means of reinforcement, as in this case.
3. Results
3.1. Unreinforced Panels (U)
The results of the bending tests carried out on the unreinforced panels according to [61] are summarized in Table 3, while Figure 8 and Figure 9 illustrate the experimental load–displacement curves and some examples of the failure mechanisms, respectively.

Table 3.
Experimental results of the unreinforced CLT panels.
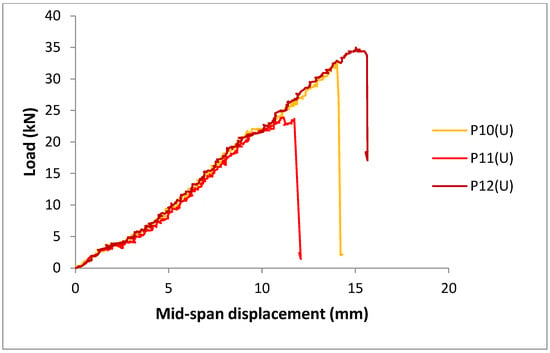
Figure 8.
Load–displacement curves for the unreinforced CLT panels.

Figure 9.
Typical failure mechanisms of the unreinforced panels.
Table 3, as well as the subsequent Table 4 and Table 5, reports the following data: the specimen’s label, span in bending l, failure load Fu, maximum shear force at failure Vu, maximum bending moment at failure Mu, bending strength fu, shear stress at failure τmax, maximum mid-span deflection wmax, bending stiffness (EJ)exp, and failure mode type.

Table 4.
Experimental results and elaboration for the single-layer reinforced CLT panels.

Table 5.
Experimental results and elaboration for the double-layer and double-weight reinforced CLT panels.
The outcomes of the bending tests clearly show that the unreinforced panels exhibit a substantially linear elastic behavior with brittle failure due to the excessive tensile stress in approximately the central uniform bending area of the specimen and cracks starting from the bottom layer at the panel intrados.
3.2. Single-Layer Reinforced Panels (R)
The results of the bending test carried out according to [61] on the panels reinforced with one SRP layer are summarized in Table 4, while Figure 10 and Figure 11 illustrate the experimental load–displacement curves and some examples of the failure mechanisms, respectively.
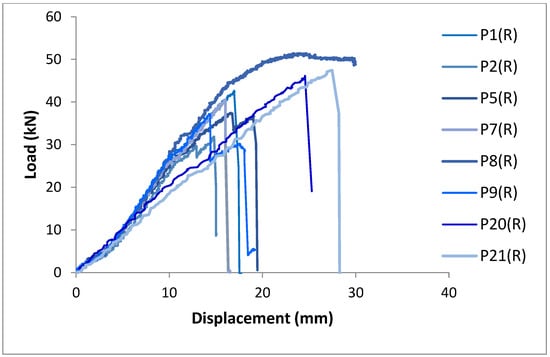
Figure 10.
Load–displacement curves for the single-layer reinforced CLT panels.

Figure 11.
Specimen P8’s bending failure mechanism.
The results of this experimental dataset highlight that the overall behavior of the panels is essentially linear elastic, with few exceptions, and exhibits brittle failure due to bending. One exception is represented by the P8 specimen, which shows a ductile flexural collapse mode (Figure 10 and Figure 11), different from all the other panels. The behavior of panels P2, P5 and P9 clearly shows a force drop in the load–displacement curve as if, after the critical load was reached for the first time, a secondary capacity mode took over until the final rupture. This behavior can be associated with the presence of the SRP reinforcement, which, after the first crack in tension in the outer CLT layer, has been capable of bridging the cracks and promoting the transfer of the load to the upper compressed layer, until collapse. Although not evident from the load–displacement curve, a different collapse mode has emerged in specimen P7 due to the RS (Figure 12).

Figure 12.
Rolling shear failure mode of specimen P7.
3.3. Double-Reinforced Panels (RR and RR*)
A group of three CLT panels 1200 mm long were reinforced with a double-layer SRP reinforcement (RR) and tested according to [61]. To prevent RS collapse due to the expected increase in the flexural strength, a further group of six panels with a longer length, equal to 1500 mm, were also prepared to force bending failures. Of this group, two panels (P13, P15) were reinforced with the same SRP reinforcement (RR), while four panels (P16, P17, P18, P19) were reinforced with one layer of a double-weight steel mesh GeoSteel® G1200 (RR*), assumed to provide the same enhancement as two layers of GeoSteel® G600, at least in terms of the strength. These six panels were tested according to [62], maintaining the distance between the loading points equal to 6 h and growing the ratio span-to height (l/h) suitable to minimize shear collapses.
The results of the bending tests on the double-reinforced RR and RR* panels are shown in Table 5, while Figure 13 and Figure 14 illustrate the load–displacement curves. Figure 15, Figure 16, Figure 17 and Figure 18 illustrate the failure mechanisms.
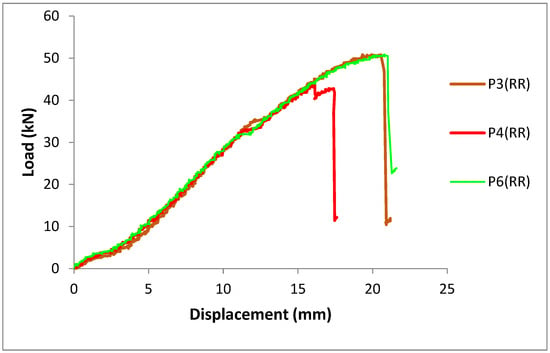
Figure 13.
Load–displacement curves for double-layer reinforced panels of 1200 mm length.
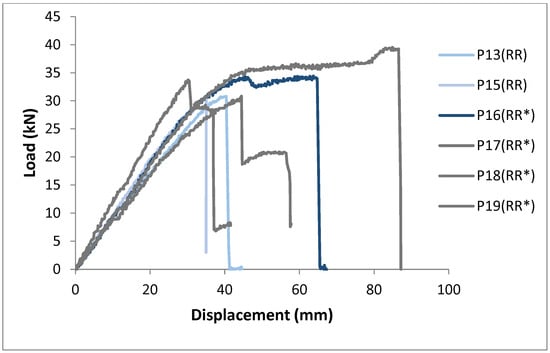
Figure 14.
Load–displacement curves for the double-layer reinforced panels of 1500 mm length.

Figure 15.
Failure mechanism in double-reinforced 1200 mm long panels. Rolling shear in the P4 panel (a). Bending in the P6 panel (b).

Figure 16.
Rolling shear failure mechanism in the double-layer reinforced 1200 mm long panels: P3 (a) and P4 (b).

Figure 17.
Bending failure mechanisms in the double-layer reinforced 1500 mm long panels.

Figure 18.
Rolling shear failure mechanism in the double-layer reinforced panel P19.
As expected, the double-layer reinforced panels 1200 mm long (span l = 1080 mm) collapse due to RS failure in two out of three cases. Despite the load–displacement curves in Figure 13 not highlighting the phenomenon, as the P3 and P6 curves are quite similar, with failure achieved almost simultaneously, the mechanism of rupture differs significantly, as shown in Figure 15 and Figure 16, where the ruptures of panels P3 (a) and P4 (b) are pointed out. Conversely, most of the double-reinforced panels 1500 mm long (span l = 1380 mm) show bending failures triggered by the maximum tensile stresses at the intrados (Figure 17). Panel P19 is an exception, showing RS failure (Figure 18). Looking at the load–displacement curves of these panels (Figure 14), it is evident that P13, P15 and P18 collapse under modest load values, around 30 kN. Notably, P19 shows higher stiffness than the others, which may have induced a different failure mechanism. In contrast, P16 and P17 exhibit both higher deflections (more than 60 mm) and significant strength at failure. Their performance is characterized by unexpected elastoplastic behavior, then collapse occurs suddenly, leading to the complete splitting of the section (Figure 17), as if they accumulated high elastic energy instantaneously released at failure, along with unstable fracture propagation.
4. Discussion
The effectiveness of the reinforcement is doubtless when comparing the outcomes of the bending tests of the unreinforced and the SRP-reinforced panels. Table 6 summarizes the results (average moment at failure Mu, average “conventional” bending strength fm and average bending stiffness (EJ)exp) along with their percentage variation with respect to the unreinforced panels. In addition, the table reports the results of the Student’s t-test carried out to assess the statistical significance of the variations in the strength and stiffness shown by the reinforced panels compared to the unreinforced ones. The results of this analysis indicate that the group means are statistically different at a significance level of p ≤ 0.05, except for the RR (1380) panel group, which includes only two specimens.

Table 6.
Summary of the average experimental results.
It is noteworthy that the application of SRP reinforcement to the 1200 mm long panels (span equal to 1080 mm) increases both the “conventional” bending strength fm and the bending stiffness (EJ)exp. The strength increases by 37.0% in the case of an SRP single-layer and up to 58.8% for double-layer reinforcement, while the stiffness increases by 12.2% in the case of SRP single-layer reinforcement and up to 27.3% for double-layer reinforcement. This enhancement shows how the SRP effectively increases the mechanical characteristics of the panels, significantly in terms of the strength, less so in terms of the stiffness. However, this effectiveness is not better in the case of double-layer reinforcement, since it produces a further increase in strength and stiffness of 15.89% and 13.40%, respectively, compared to single-layer reinforcement, highlighting that the mechanical properties’ improvement is not proportional to the employed amount of reinforcement. This finding makes the use of two or more SRP layers questionable, at least for three-layer Sardinian Maritime Pine CLT panels and for its potential role in activating RS failure modes.
In the single-layer applications, only one out of eight cases ends up with an RS failure, which can be regarded as an anomaly due to material variability. Conversely, in the case of the double-reinforced panels of 1200 mm length, RS failures occur in two out of three cases, showing that the amount of reinforcement possibly modified the hierarchy of the bending/RS shear capacity. Hence, in the following tests, we have moved to more slender panels of length 1500 to prevent shear collapses. Indeed, in the case of double-layer reinforcement applied to the 1500 mm long panels (span equal to 1380 mm), the RS criticalities have been bypassed, with only one exception in six panels, since the shear stresses have been widely lowered, as shown in Table 5. Nevertheless, the improvement in strength and stiffness compared to the 1200 mm long panels reinforced with a double layer is negligible for both the RR and RR* reinforcement types, even in the presence of the prevailing bending collapse modes. While the cases of the two panels P13 and P15 represent a small anomaly, the remaining four panels with RR* reinforcement confirm the substantial equivalence in terms of the strength and stiffness enhancement of the double layer of GeoSteel® G600 (RR) and the single layer of double-weight GeoSteel® G1200 (RR*). Remarkedly, in this last case, some evidence of ductility is registered in the panels’ behavior, as shown in Figure 14.
Finally, RS failure has been confirmed as a key issue in CLT design, especially in the examined case, where the bending strength is enhanced by means of reinforcements, which are meant only for panels’ flexural behavior. During design, careful checking is needed of structural elements’ slenderness and further provisions may be necessary to enhance the RS strength as well. Regarding the resulting shear strength, the unreinforced panels exhibit bending failure and evolve mean shear stress of about 1.50 MPa, meaning that the shear strength of Sardinian Maritime Pine CLT panels is higher, as experimentally investigated in other studies [66,67], than the conventional value of 1.10 MPa proposed in [62]. In fact, the reinforced panels exhibit shear stresses up to and greater than 2 MPa, which reasonably represent an indication of the RS strength of the employed Maritime Pine. It is important to underline that no debonding issues arose during the tests until failure, neither at the specimens’ edge nor at intermediate locations.
5. Analytical Model
An analytical capacity model based on the Italian Standard Guidelines [68], which currently do not explicitly consider the case of CLT, and on a previous contribution of the authors [67], is proposed to evaluate the SRP reinforcement effect and contribution to CLT panels’ bending strength.
5.1. Timber Constitutive Behavior
Composite beam-like behavior is addressed based on common assumptions in bending:
- Planar section under loading.
- Full composite behavior.
Consequently, a linear distribution of normal strains is involved. Simple transformations based on the elastic moduli of the materials permit the evaluation of the effective properties of the composite section of the timber and reinforcement in the elastic field, provided that no debonding occurs between the two materials so that assumption 2 is fulfilled. The experiments confirm that debonding of the reinforcement is not likely to happen. As already stated, the contribution of the central 90°-oriented layer can be neglected with good approximation in the overall behavior, since it is barely involved in the stress distribution due to the ratio E90/E0 [63,64,65]. This holds in the proposed model when investigating both the linear elastic behavior and the ultimate capacity.
In small defect-free specimens, failure occurs abruptly in tension with no plasticity due to the fibrous anatomy of timber; therefore, linear elastic behavior is commonly assumed until failure. In full-scale specimens instead, the presence of anatomic defects, like knots or local grain deviation, cannot be avoided and significantly affects the strength of the structural elements, which has an impact on the assignment of the strength class [2,3,4]. When bending is concerned, defects located in the tensile zone of the cross-section still predominantly affect the specimens’ failure, although to a different extent depending on their distance from the neutral axis, i.e., they have a full effect when located at the tensile edge, a minor effect when near the neutral axis, and almost no effect if in the compression zone. This is among the reasons for the tensile strength along grain direction (ft,0) and the bending strength (fm) being distinct and almost independent in the strength classes profiles. According to [65], when grading tests are carried out on softwood specimens in tension (T-Classes), a set of empirical correlations is available to determine the elastic and strength properties starting from the experimental tensile strength ft,0; a different set of empirical correlations is employed when grading tests are performed in bending (C-Classes) and the bending strength fm is experimentally evaluated. It is worth noting that these sets of correlations refer to the characteristic values of the parameters; in the following, they have been employed, under a certain approximation, with average strength values.
In this model, the tensile strength ft,0 has been involved instead of the bending strength fm according to [67,68]. Thus, the T-Classes set of correlations has been adopted to determine other relevant parameters, such as the compressive strength fc,0. In the literature, this assumption could lead to some controversy, and in [68], no justification other than conservativeness is provided for it. The authors’ choice is clarified by comparing the effect of the presence of defects in solid or glue-laminated timber and CLT exposed to tensile and bending stress. As already stated, solid and glue-laminated timber specimens exposed to bending tests statistically offer higher average strength than specimens exposed to traction, with higher scattering of the results. Conversely, in solid timber specimens in tension, the presence of the defect drastically reduces the tensile strength regardless of its position within the section. In the case of bending tests on three-layer CLT, since the lamella at the extrados is in compression and the central layer is barely effective, the main contribution to the bending strength is made by the lamella placed at the intrados, exposed to excentric traction, where the defects cause the failure to occur because the tensile strength ft,0 has been reached. Since in the following calculations the tensile strength is retrieved directly from experimentation, this controversial issue is partially overcome and affects only the choice between the T-Class and C-Class correlation formulas.
On the other hand, the compressive failure of timber implies the collapse of the lignin matrix, in both the 0° and 90° directions, and the instability of the cellulose fibers in the 0° direction [64]. Therefore, compressive failures show up differently to tensile ruptures, exhibiting plasticity and significant ultimate strains. Several types of constitutive laws have been proposed for uniaxial compressive behavior [69,70], all of them with the linear elastic part having the same elastic modulus as in tension, followed by the plastic field. The numerical model here proposed adopts a simplified elastic–perfectly plastic constitutive law, maintaining the same elastic modulus in tension and compression, and a compressive strength fc,0 derived from [65] for the T-classes grading. Lower performance is shown for compression in the 90° direction, which is of minor concern in this investigation, apart from the contact areas at the supports and loading points.
5.2. SRP Reinforcement Behavior
The properties of the SRP reinforcement considered in the analytical model are the same as provided by the manufacturer and reported in Table 3. The constitutive behavior follows a typical linear elastic law with perfectly plastic behavior at yield stress until maximum deformation is reached. Since steel’s ultimate properties are hardly exploited in this application, as failure occurs in timber way before the reinforcement steel yields, no major concern has been devoted to these properties.
5.3. Capacity Model
According to the Italian Standard Guidelines [68], two main failure modes can affect solid and glue-laminated timber sections under pure bending, with or without reinforcements, both of them involving tensile failure; that is to say, the strains in the tension side reach the ultimate value:
- tensile failure without plasticity in the compression edge: εt = εtu and εc ≤ εcy
- tensile failure with plasticity in the compression edge: εt = εtu and εcy ≤ εc ≤ εcu
where εt and εc are, respectively, the maximum tensile and compressive strain at the section edges; εtu is the ultimate strain at tensile failure, evaluated as the ratio between the average tensile strength ft,0 and the MOE E0 according to a brittle failure model; εcy is the strain at which plasticity starts in compressed timber, evaluated as the ratio between the average 0° compressive strength fc,0 and the MOE E0; and εcu is the ultimate compressive strain, assumed conventionally to be 1.00% according to [68]. The average tensile strength ft,0 has been retrieved directly from the bending tests performed on the non-reinforced panels U. The average MOE E0 has been experimentally determined in [66] on timber boards used to manufacture CLT panels.
More ultimate states could be invoked, but they are outside the scope of the present case. The two ultimate states depend on the neutral axis position at failure, schematically depicted in Figure 19.
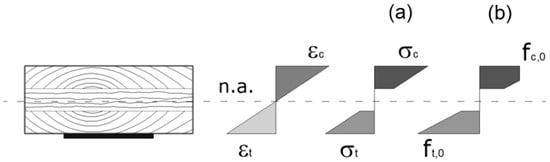
Figure 19.
Stress–strain behavior in bending for the CLT-reinforced cross-section.
In (a), a linear elastic stress distribution at tensile failure is shown, where the contribution of the 90°-oriented layer is neglected. The position of the neutral axis is determined by simple geometric considerations since it corresponds to the barycentric axis of the effective section. In (b), the compressed upper layer exhibits strain values beyond the elastic limit εcy, and the plasticity is evaluated according to the assumed constitutive model. In this case, the neutral axis position is estimated by an iterative procedure that checks for the horizontal equilibrium of the tensile and compressive stress resultants, including the reinforcement contribution. Again, considering the contribution of the stresses acting on the central 90°-oriented layer is irrelevant in this procedure. Finally, rotational equilibrium is used to assess the ultimate bending moment.
The proposed capacity model is susceptible to be adapted automatically to different types of timber and several reinforcement systems by simply employing the appropriate values of the material properties stated in Table 7 and Table 8, in accordance with the orientations of [68]. The model has already been used for a five-layer CLT configuration and a different type of reinforcement (natural fiber FRP) in [67]. Since the contribution of each layer is evaluated separately then summed, the case of hybrid CLT can be easily treated. Different types of SRPs are thus automatically treated, as well as the majority of FRPs, provided they behave consistently to the products used by [68].

Table 7.
Mechanical properties of the timber.

Table 8.
Mechanical properties of the SRP reinforcement.
5.4. Comparison to Experimental Results
As already stated, to compare the experimental results and validate the capacity model, the following constitutive parameters need to be evaluated: ft,0, εtu, fc,0, εcy, εcu, and E0, whose meanings have been previously established. These parameters can be retrieved according to [66] on the basis of the experimental evaluation of the timber strength and MOE. The average MOE E0 has been experimentally determined in [66] on boards used to manufacture the tested CLT panels. Furthermore, the RS strength fv,90 of Sardinian Maritime Pine has been experimentally investigated in [66,67], pointing out that it is significantly higher than the conventional values adopted for softwood [62].
Table 7 and Table 8 restate the data used in the analytical model for the timber and SRP system, respectively. In Table 8, the equivalent thickness tf of a single layer of GeoSteel® G600 reinforcement is reported as well, as derived from the producer’s technical sheets. In the case of GeoSteel® G1200, the thickness is exactly doubled.
Table 9 provides the results gained by applying the analytical capacity model to the tested CLT panels.

Table 9.
Summary of the analytical results and comparison to the experimental results.
The outcomes in Table 9 are expressed in terms of the ultimate bending moment Mu, with the subscript “exp” and “mod” referring to the experimental and model, respectively, the neutral axis position x with reference to the compressed edge, the timber compressive and tensile maximum strain εc and εt, and the percentage error of the analytical prediction toward the experimental one. Note that the experimental average results presented in Table 9 disregard, for the sake of consistency, the cases of RS failures, and aggregate the outcomes of the RR and RR* 1500 mm long reinforced panels. The results concern the hypothesis of tensile maximum strain εtu occurrence, i.e., the tensile strength achieved at the intrados of the panels, in both the unreinforced and reinforced panels. The model yields a small amount of plasticity, i.e., εc > εcy, at the upper compressed edge even when there is no reinforcement. This unexpected occurrence derives from the formulas provided by [65], which yield, for a high tensile strength as in the case, compressive strength lower than the tensile one, as expected for defect-free timber. When reinforcement is considered, the plasticity at the compression edge increases as the neutral axis moves downward. The accuracy of the model is satisfactory, especially if the scattering of the experimental results is considered. If the results concerning the 1500 long panels with reinforcement types of RR and RR* are considered, the error in the model prediction with the doubled reinforcement falls under 15%.
When analyzing the resulting ultimate bending moment prediction, it turns out that the classical approach proposed in [68] to evaluate the effect of composite flexural reinforcements on timber members underestimates the actual CLT panels’ capacity. In general, the planar section assumption, though shared with the majority of bending capacity models in the literature (see e.g., [63]), in the presence of high shear deformation can lead to an overestimation of the bending stresses. Nevertheless, the predictions are conservative also in the case of the examined four-point bending tests with negligible shear deformations in the central part of the specimens where the bending failures occurred. This outcome, together with the experimental evidence of the absence of debonding between the reinforcement and the panel until failure, highlights the presence of a “bridging effect” of the SRP reinforcement and corroborate the authors’ opinion [67], as also tracked in other literature references [56,70,71], on the capability of the reinforcement system not only to collaborate with its own tensile strength but also to mitigate and redistribute the stress concentrations arising in correspondence with the timber defects in the tension layers, like knots, responsible for crack onset and propagation. In other words, reinforcements are likely to provide apparent extra tensile strength to the CLT tension layer. Nevertheless, it should be emphasized that the experimental tests have not clearly detected the occurrence of plasticity in the compressed fibers, even though panels P8, P16 and P18 have shown distinctive ductile behavior. More studies are needed to gain a deeper understanding of this phenomenon; for instance, by employing advanced analytical models for the bending behavior of laminated materials, meshless numerical techniques that can also be applied to engineered wood, and layer-wise approaches that could be adapted to multilayer CLT models [72].
Remarkably, the analytical model confirms the issue already pointed out by the experimental tests, i.e., doubling the reinforcement amount yields a negligible capacity gain.
6. Conclusions
This paper presents the results of an experimental program aimed at evaluating the effect of a commercial SRP reinforcement system on three-layer Sardinian Maritime Pine CLT panels.
Bending tests have been carried out on 20 panels divided into five groups:
- Three unreinforced panels (U), sized 1200 × 240 × 60 mm (L × W × h).
- Eight panels reinforced with single SRP layer (R), sized 1200 × 240 × 60 mm.
- Three panels reinforced with double SRP layer (RR), sized 1200 × 240 × 60 mm.
- Two panels reinforced with double SRP layer (RR), sized 1500 × 240 × 60 mm.
- Four panels reinforced with double-weight SRP single layer (RR*), sized 1500 × 240 × 60 mm.
The results can be summarized as follows:
- Compared to unreinforced panels, the SRP single-layer reinforced panels show an increase in bending strength and bending stiffness on average equal to 37.0% and 12.2%, respectively, while the double-layer reinforced panels show an increase in bending strength and bending stiffness on average equal to 58.8% and 27.3%, respectively.
- The increase in bending strength due to the reinforcement favors the increase in shear stresses and the possible occurrence of failure due to rolling shear. This is particularly evident in the case of double-layer reinforcement.
- Since the strength improvement induced by the reinforcement is not proportional to its amount, and the increase in the amount of reinforcement increases the possibility of shear failures, the convenience of double-layer reinforcement must be carefully evaluated in the design phase, as the rolling shear failures can set the limit of the possible panel strengthening.
- The strength and stiffness enhancement provided by the double-layer and double-weight reinforcements confirms the substantial equivalence, except in terms of the ductility, of the two reinforcement systems.
In addition to the experimental tests, an analytical capacity model, based on an authors’ adaptation to the case of CLT of the Italian Standard Guidelines relating to the reinforcement of structural timber, has been developed to evaluate the SRP reinforcement effect and contribution to CLT panels’ bending strength. The results show that the approach proposed in the current standard, when applied to reinforced CLT, underestimates the actual CLT panels’ capacity, providing a conservative prediction affected by an acceptable error of about 15%.
The set of experimental and analytical results supports the hypothesis that SRP reinforcement has the capacity to mitigate and redistribute the stress concentrations arising in correspondence with timber defects, like knots, in the tension layers, responsible for crack onset and propagation, being likely to provide an apparently enhanced tensile strength to CLT panels.
More studies are needed to develop greater insight into this phenomena and to extend it to further CLT layouts, and improvements are advisable to the proposed analytical model to tackle more precisely the undoubtable improvement provided by the SRP reinforcement in CLT panels. Moreover, to assess the validity of the proposed model across a broader range of cases, future research will address more complex configurations and more demanding structural conditions.
Author Contributions
Conceptualization, G.C., D.M. and M.V.; methodology, G.C., D.M. and M.V.; validation, G.C., D.M. and M.V.; formal analysis, G.C., D.M. and M.V.; investigation, G.C., D.M. and M.V.; resources, G.C.; data curation, G.C., D.M. and M.V.; writing—original draft preparation, G.C., D.M. and M.V.; writing—review and editing, G.C., D.M. and M.V.; visualization, G.C., D.M. and M.V.; project administration, G.C.; funding acquisition, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research and the APC were funded by DICAAR—University of Cagliari, Research Project ISEC (Ingegneria Strutturale ed Economia Circolare), grant number 63830-RICDIP_2025_CONCU.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- EN 338:2016; Structural Timber—Strength Classes. European Committee for Standardization: Brussels, Belgium, 2016.
- EN 14081-1:2016+A1:2019; Timber Structures—Strength Graded Structural Timber with Rectangular Cross Section—Part 1: General Requirements. European Committee for Standardization: Brussels, Belgium, 2019.
- EN 14081-2:2018+A1:2022; Timber Structures—Strength Graded Structural Timber with Rectangular Cross Section—Part 2: Machine Grading; Additional Requirements for Type Testing. European Committee for Standardization: Brussels, Belgium, 2022.
- EN 14081-3:2022; Timber Structures—Strength Graded Structural Timber with Rectangular Cross Section—Part 3: Machine Grading; Additional Requirements for Factory Production Control. European Committee for Standardization: Brussels, Belgium, 2022.
- Türer, A.; Dönmez, Ü.; Çevik, A.; Anıl, Ö. Behavior of CLT Formwork Beams Retrofitting with CFRP Strip under Static Loading. In Proceedings of the 2nd International Symposium on Innovative Approaches in Scientific Studies (ISAS2018-Winter), Samsun, Turkey, 30 November–2 December 2018; SETSCI Conference Proceedings. Volume 3, pp. 277–281. [Google Scholar]
- Song, Y.-J.; Lee, I.-H.; Song, D.-B.; Hong, S.-I. Evaluation of Delamination and Bending Performance of Composite CLT Reinforced with CFRP. Wood Fiber Sci. 2019, 51, 354–363. [Google Scholar] [CrossRef]
- Lv, Q.; Wang, W.; Liu, Y. Flexural Performance of Cross-Laminated Bamboo (CLB) Slabs and CFRP Grid Composite CLB Slabs. Hindawi Adv. Civ. Eng. 2019, 2019, 6980782. [Google Scholar] [CrossRef]
- Lopez-Molina, A.; Doudak, G. Retrofit techniques for Cross-Laminated Timber (CLT) elements subjected to blast loads. Eng. Struct. 2019, 197, 109450. [Google Scholar] [CrossRef]
- Song, Y.-J.; Lee, I.-H.; Hong, S.-I. An Evaluation of Strength Performance of the Edge Connections between Cross-laminated Timber Panels Reinforced with Glass Fiber-reinforced Plastic. BioResources 2019, 14, 7719–7733. [Google Scholar] [CrossRef]
- Valdes, M.; Giaccu, G.F.; Meloni, D.; Concu, G. Reinforcement of maritime pine cross-laminated timber panels by means of natural flax fibers. Constr. Build. Mater. 2020, 233, 117741. [Google Scholar] [CrossRef]
- Haftkhani, A.R.; Shakiba, S. Reinforcement of flexural performance of screwed cross laminated timber (CLT) panels constructed of poplar by aluminum sheet and glass fiber reinforced polymer wrap. For. Wood Prod. 2020, 73, 317–331. [Google Scholar] [CrossRef]
- Bhat, J.A. Improved Strength and Stiffness Characteristics of Cross-laminated Poplar Timber Columns. Int. J. Eng. Trans. A Basics 2021, 34, 803–810. [Google Scholar] [CrossRef]
- Sharari, M.; Haftkhani, A.R.; Ahmadi, M.; Moezipour, B.; Hajializadeh, F. Strengthening of the cross-laminated timber using glass fiber-reinforced polymer on the lateral performance of the single shear lap joints. Iran. J. Wood Pap. Ind. 2022, 13, 1–14. [Google Scholar]
- Rostampour Haftkhani, A.; Rashidi, M.; Abdoli, F.; Gerami, M. The Effect of GFRP Wrapping on Lateral Performance of Double Shear Lap Joints in Cross-Laminated Timber as a Part of Timber Bridges. Buildings 2022, 12, 1678. [Google Scholar] [CrossRef]
- Rostampour-Haftkhani, A.; Abdoli, F.; Arabi, M.; Nasir, V.; Rashidi, M. Effect of Wood Densification and GFRP Reinforcement on the Embedment Strength of Poplar CLT. Appl. Sci. 2023, 13, 12249. [Google Scholar] [CrossRef]
- Li, H.; Wang, L.; Wei, Y.; Semple, K.E.; Dai, C. Out-of-plane bending behavior of cross-laminated timber members enhanced with fiber-reinforced polymers. J. Build. Eng. 2023, 66, 105862. [Google Scholar] [CrossRef]
- Arabi, M.; Rostampour Haftkhani, A. Improved withdrawal capacity of nail and screw in cross-laminated timber (CLT) made of poplar (Populus alba) using glass fiber-reinforced polymer (GFRP). J. For. Wood Prod. 2023, 76, 23–32. [Google Scholar]
- Swinea, J.; Sanborn, K.; Weaver, M.; Lo Ricco, M.; Adam Senalik, C.; Stewart, L.K. Enhanced cross laminated timber (ECLT) for ballistic resistant design. Int. J. Impact Eng. 2024, 189, 104931. [Google Scholar] [CrossRef]
- Baek, S.; Song, Y.; Hong, S. Bending performance of domestic larch cross-laminated timber reinforced with fiber-reinforced polymer. Wood Mater. Sci. Eng. 2025, 20, 686–696. [Google Scholar] [CrossRef]
- Casadei, P.; Nanni, A.; Alkhrdaji, T. Steel-Reinforced Polymer: An Innovative and Promising Material for Strengthening the Infrastructures. Concr. Eng. Int. 2005, 9, 54–56. [Google Scholar]
- De Santis, S.; de Felice, G.; Napoli, A.; Realfonzo, R. Strengthening of structures with Steel Reinforced Polymers: A state-of-the-art review. Compos. Part B Eng. 2016, 104, 87–110. [Google Scholar] [CrossRef]
- Napoli, A.; de Felice, G.; De Santis, S.; Realfonzo, R. Bond behaviour of Steel Reinforced Polymer strengthening systems. Compos. Struct. 2016, 152, 499–515. [Google Scholar] [CrossRef]
- Krzywoń, R. Steel-Reinforced Polymers and Steel-Reinforced Composite Mortars for Structural Applications—An Overview. J. Compos. Sci. 2020, 4, 142. [Google Scholar] [CrossRef]
- Krzywoń, R. Assessment of Existing Bond Models for Externally Bonded SRP Composites. Appl. Sci. 2020, 10, 8593. [Google Scholar] [CrossRef]
- Ascione, F.; Lamberti, M.; Napoli, A.; Razaqpur, A.G.; Realfonzo, R. Modeling SRP-concrete interfacial bond behavior and strength. Eng. Struct. 2019, 187, 220–230. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Hao, H.; Su, Y. Experimental and numerical study on steel wire mesh reinforced concrete slab under contact explosion. Mater. Des. 2017, 116, 77–91. [Google Scholar] [CrossRef]
- Napoli, A.; Realfonzo, R. Compressive behavior of concrete confined by SRP wraps. Constr. Build. Mater. 2016, 127, 993–1008. [Google Scholar] [CrossRef]
- Ascione, F.; Lamberti, M.; Napoli, A.; Razaqpur, G.; Realfonzo, R. An experimental investigation on the bond behavior of steel reinforced polymers on concrete substrate. Compos. Struct. 2017, 181, 58–72. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Nawaz, W.; Abdalla, J.A. Flexural behavior of reinforced concrete beams externally strengthened with Hardwire Steel-Fiber sheets. Constr. Build. Mater. 2018, 172, 562–573. [Google Scholar] [CrossRef]
- Ascione, F.; Napoli, A.; Realfonzo, R. Experimental and analytical investigation on the bond of SRP systems to concrete. Compos. Struct. 2020, 242, 112090. [Google Scholar] [CrossRef]
- Al Nuaimi, N.; Sohail, M.G.; Hawileh, R.A.; Abdalla, J.A.; Douier, K. Durability of reinforced concrete beams strengthened by galvanized steel mesh-epoxy systems under harsh environmental conditions. Compos. Struct. 2020, 249, 112547. [Google Scholar] [CrossRef]
- Bonati, A.; Franco, A.; Occhiuzzi, A. Long-Term Behaviour of Steel Reinforced Polymer (SRP) Systems Bonded to Concrete Substrates. In Proceedings of the Italian Concrete Conference 2020/21; di Prisco, M., Menegotto, M., Eds.; ICC 2021, Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2024; Volume 351. [Google Scholar] [CrossRef]
- Al-Khafaji, A.F.; Myers, J.J.; Wang, W. Bond assessment of two types of SRP strengthening systems subjected to severe conditions. Constr. Build. Mater. 2021, 273, 121968. [Google Scholar] [CrossRef]
- Baietti, G.; Kahangi Shahreza, S.; Santandrea, M.; Carloni, C. Concrete columns confined with SRP: Effect of the size, cross-sectional shape and amount of confinement. Constr. Build. Mater. 2021, 275, 121618. [Google Scholar] [CrossRef]
- Sohail, M.G.; Al Nuaimi, N.; Hawileh, R.A.; Abdalla, J.A.; Douier, K. Durability of plain concrete prism strengthened with galvanized steel mesh and CFRP laminates under harsh environmental conditions. Constr. Build. Mater. 2021, 286, 122904. [Google Scholar] [CrossRef]
- Bencardino, F.; Nisticò, M. A Theoretical Model for Debonding Prediction in the RC Beams Externally Strengthened with Steel Strip and Inorganic Matrix. Materials 2021, 14, 4961. [Google Scholar] [CrossRef]
- Sneed, L.H.; Verre, S.; Ombres, L.; Carloni, C. Flexural behavior RC beams strengthened and repaired with SRP composite. Eng. Struct. 2022, 258, 114084. [Google Scholar] [CrossRef]
- Kekez, S.; Krzywon, R. Prediction of Bonding Strength of Externally Bonded SRP Composites Using Artificial Neural Networks. Materials 2022, 15, 1314. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; McBurney, K.L.; Sneed, L.H. A spike-shaped anchorage for steel reinforced polymer (SRP)-strengthened concrete structures. Constr. Build. Mater. 2023, 389, 131710. [Google Scholar] [CrossRef]
- Parsekian, G.A.; El-Hacha, R.; Shrive, N.G. Strengthening and Retrofitting Unreinforced Masonry Walls with Various FRP Systems. In Proceedings of the Asia-Pacific Conference on FRP in Structures (APFIS 2007), Hong Kong, China, 12–14 December 2007; pp. 263–270. [Google Scholar]
- Capozucca, R. Experimental FRP/SRP–historic masonry delamination. Compos. Struct. 2010, 92, 891–903. [Google Scholar] [CrossRef]
- Grande, E.; Imbimbo, M.; Sacco, E. Bond Behavior of Historical Clay Bricks Strengthened with Steel Reinforced Polymers (SRP). Materials 2011, 4, 585–600. [Google Scholar] [CrossRef]
- Valluzzi, M.R.; Oliveira, D.V.; Caratelli, A.; Castori, G.; Corradi, M.; De Felice, G.; Garbin, E.; Garcia, D.; Garmendia, L.; Grande, E.; et al. Round Robin Test for composite-to-brick shear bond characterization. Mater. Struct. 2012, 45, 1761–1791. [Google Scholar] [CrossRef]
- Girardello, P.; Pappas, A.; da Porto, F.; Valluzzi, M.R. Experimental testing and numerical modelling of masonry vaults. In Proceedings of the International Conference on Rehabilitation and Restoration of Structures, Chennai, India, 13–16 February 2013. [Google Scholar]
- Valluzzi, M.R.; da Porto, F.; Garbin, E.; Panizza, M. Out-of-plane behaviour of infill masonry panels strengthened with composite materials. Mater. Struct. 2014, 47, 2131–2145. [Google Scholar] [CrossRef]
- Garmendia, L.; Larrinaga, P.; San-Mateos, R.; San-José, J.T. Strengthening masonry vaults with organic and inorganic composites: An experimental approach. Mater. Des. 2015, 85, 102–114. [Google Scholar] [CrossRef]
- De Felice, G.; Aiello, M.A.; Bellini, A.; Ceroni, F.; De Santis, S.; Garbin, E.; Leone, M.; Lignola, G.P.; Malena, M.; Mazzotti, C.; et al. Experimental characterization of composite-to-brick masonry shear bond. Mater. Struct. 2016, 49, 2581–2596. [Google Scholar] [CrossRef]
- Gentilini, C.; Yuan, Y.; Carloni, C.; Franzoni, E. Adhesion between SRP and masonry: Laboratory simulations of the field moisture and salt conditions. Constr. Build. Mater. 2020, 264, 120697. [Google Scholar] [CrossRef]
- Garcia-Ramonda, L.; Pelà, L.; Roca, P.; Camata, G. Experimental cyclic behaviour of shear masonry walls reinforced with single and double layered Steel Reinforced Grout. Constr. Build. Mater. 2022, 320, 126053. [Google Scholar] [CrossRef]
- Ombres, L.; Guglielmi, M.; Verre, S. Structural Performances of Clay Brick Masonry Columns Partially Confined with FRCM/SRG Composites. Key Eng. Mater. 2022, 916, 297–304. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Bond Behavior Investigation Between Steel Reinforced Grout Composites and Masonry Substrate. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 3519–3535. [Google Scholar] [CrossRef]
- Garcia-Ramonda, L.; Pelà, L.; Roca, P.; Camata, G. Experimental and numerical insights on the in-plane behaviour of unreinforced and TRM/SRG retrofitted brick masonry walls by diagonal compression and shear-compression testing. Constr. Build. Mater. 2023, 402, 132997. [Google Scholar] [CrossRef]
- Al-Jaberi, Z.; Myers, J.J. Prediction of compressive strength and evaluation of different theoretical standards and proposed models of brick columns confined with FRP, FRCM, or SRG system. Case Stud. Constr. Mater. 2023, 18, e01875. [Google Scholar] [CrossRef]
- Pingaro, N.; Milani, G. Simple non-linear numerical modelling of masonry arches reinforced with SRG using elasto-fragile and elasto-ductile truss finite elements. Eng. Struct. 2023, 293, 116637. [Google Scholar] [CrossRef]
- Canestri, M.; Ferretti, F.; Mazzotti, C. Confinement of masonry columns through SRG: Experimental results and analytical prediction. Procedia Struct. Integr. 2023, 44, 2198–2205. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M. Strengthening of timber beams with high strength steel cords. Compos. Part B Eng. 2011, 42, 1480–1491. [Google Scholar] [CrossRef]
- Corradi, M.; Maheri, A.; Osofero, A.I. Design of reinforced and unreinforced timber beams subject to uncertainties. In Proceedings of the Twelfth International Conference on Computational Structures Technology, Naples, Italy, 2–5 September 2014; Topping, B.H.V., Iványi, P., Eds.; Civil Comp Press: Stirlingshire, UK, 2014; p. 134. [Google Scholar] [CrossRef]
- Uzel, M.; Togay, A.; Anil, Ö.; Söğütlü, C. Experimental investigation of flexural behavior of glulam beams reinforced with different bonding surface materials. Constr. Build. Mater. 2018, 158, 149–163. [Google Scholar] [CrossRef]
- Ulasan, H.; Bajraktari, A.; Döngel, N.; Imirzi, H.Ö.; Sögütlü, C. Modulus of Elasticity and Flexural Behavior of Glulam Beams Reinforced with Steel Mesh in Different Mesh Openings. Materials 2023, 16, 4307. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R.; Gutowski, T.G. Life cycle energy analysis of fiber-reinforced composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1257–1265. [Google Scholar] [CrossRef]
- EN 408:2010+A1:2012; Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. European Committee for Standardization: Brussels, Belgium, 2012.
- EN 16351:2021; Timber Structures—Cross Laminated Timber—Requirements. European Committee for Standardization: Brussels, Belgium, 2021.
- Canadian CLT Handbook, 2019 ed; FPInnovations: Point-Claire, QC, Canada, 2019; Volume I, Special Publication SP-532E; ISBN 978-0-86488-590-6.
- Blass, H.J.; Fellmoser, P. Design of solid wood panels with cross layers. In Proceedings of the 8th World Conference on Timber Engineering 2004, Lahti, Finland, 14–17 June 2004. [Google Scholar]
- EN 384:2022; Structural Timber—Structural Timber—Determination of Characteristic Values of Mechanical Properties and Density. European Committee for Standardization: Brussels, Belgium, 2022.
- Riu, R. Caratterizzazione di Pannelli XLam in Pino Marittimo Sardo. Ph.D. Thesis, University of Cagliari, Cagliari, Italy, 2016. (In Italian). [Google Scholar]
- Concu, G.; Giaccu, G.F.; Meloni, D.; Valdes, M.; Riu, R. Advances in reinforcing of cross laminated timber panels. In Proceedings of the WCTE 2021, World Conference on Timber Engineering, Santiago, Chile, 9–12 August 2021. [Google Scholar]
- CNR-DT 201-2005; Preliminary Studies Addressed to Drawing Up Guidelines for Static Consolidation Interventions on Timber Structures by Means of Fiber-Reinforced Composites. National Research Council: Rome, Italy, 2005.
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Borri, A.; Corradi, M.; Grazini, A. A method for flexural reinforcement of old wood beams with CFRP materials. Compos. Part B 2005, 36, 143–153. [Google Scholar] [CrossRef]
- Fiorelli, J.; Alves Dias, A. Analysis of the strength and stiffness of timber beams reinforced with carbon fiber and glass fiber. Mater. Res. 2003, 6, 193–202. [Google Scholar] [CrossRef]
- Xia, Q.; Xiang, P.; Jiang, L.; Yan, J.; Peng, L. Bending and free vibration and analysis of laminated plates on Winkler foundations based on meshless layerwise theory. Mech. Adv. Mater. Struct. 2021, 29, 6168–6187. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).