Impact of Log-Normal Particle Size Distribution in Holby–Morgan Degradation Model on Aging of Pt/C Catalyst in PEMFC
Abstract
1. Introduction
2. Model
3. Materials
4. Methods
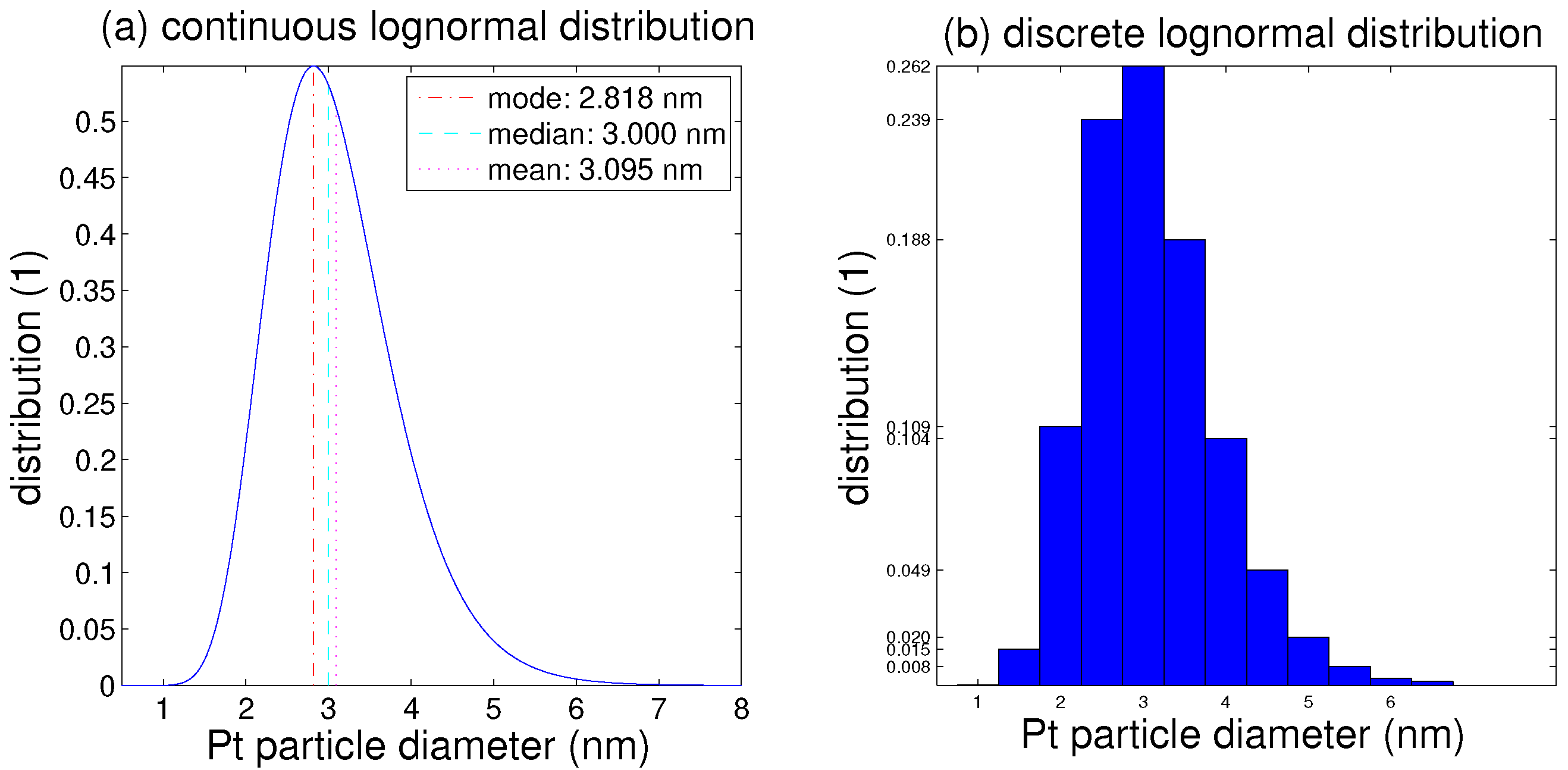
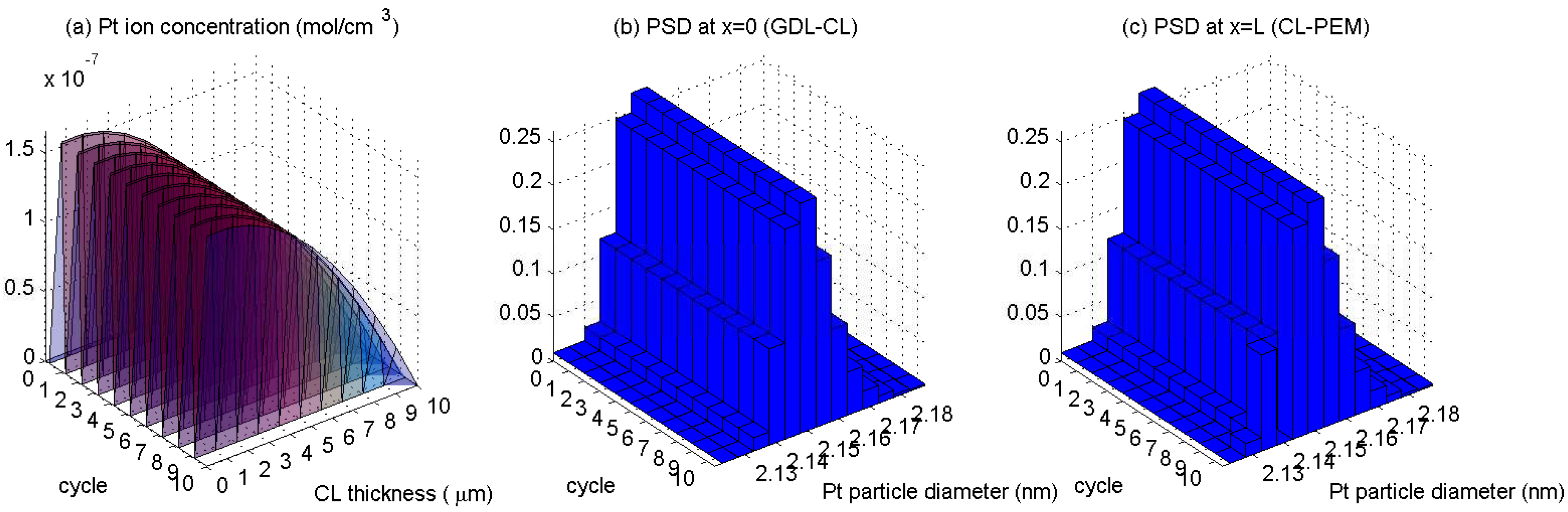
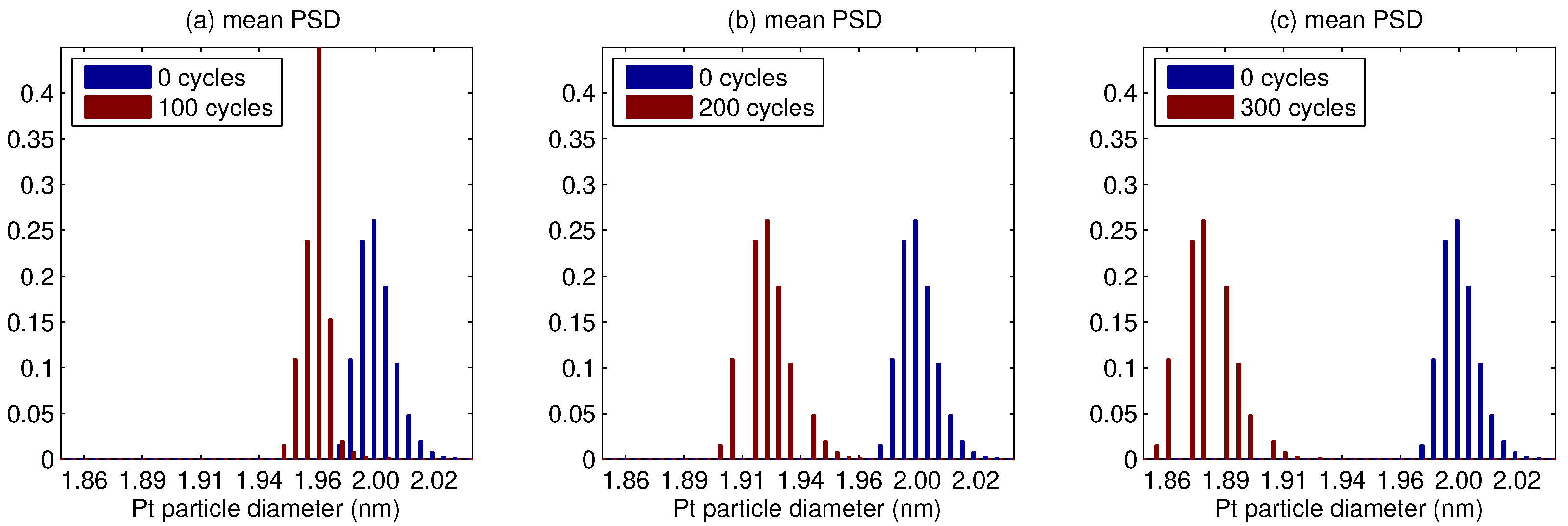
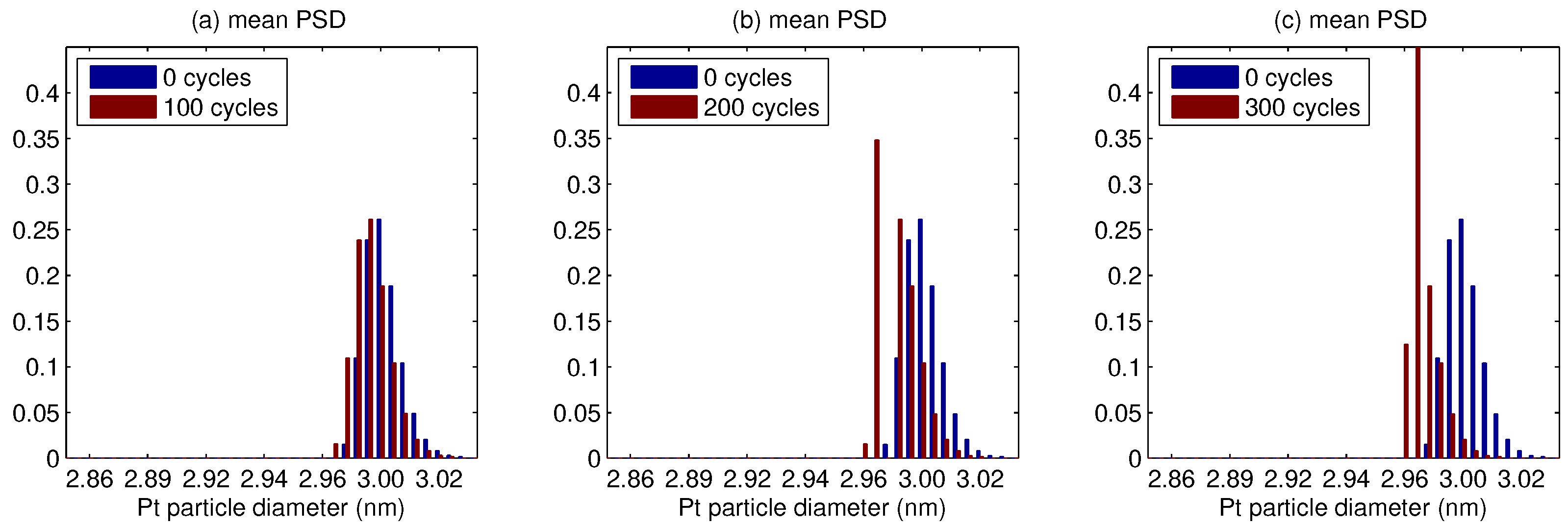
5. Results
6. Discussion
7. Conclusions
- Without diffusion, platinum nanoparticles decrease for small sizes, and increase when the particles are larger than 5 nm in diameter.
- The Pt ion diffusion is nonuniform, it is less into the membrane, and becomes larger when interface with the gas diffusion layer is approaching.
- In overall, Pt particle sizes reduce under the accelerated stress test which results in the loss of both the electrochemical active area and relative mass: smaller diameter, larger loss.
- The probability distribution of sizes is determined by the median and standard deviation, and it can be approximated within groups of finite breadth.
- The platinum particle size distribution (PSD) broadens for a median smaller than 5 nm, and shrinks for a larger median.
- PSD tails towards large particles, and the probability for each of their own size group can decrease as well as increase.
- In whole PSD changes towards a smaller size, the change is faster for a small median, and conversely slower for a large median.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ball, M.; Basile, A.; Veziroǧlu, T. Compendium of Hydrogen Energy: Hydrogen Use, Safety and the Hydrogen Economy; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Barbir, F.; Basile, A.; Veziroǧlu, T. Compendium of Hydrogen Energy: Hydrogen Energy Conversion; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Basile, A.; Gupta, R.; Veziroǧlu, T. Compendium of Hydrogen Energy: Hydrogen Storage, Distribution and Infrastructure; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Subramani, V.; Basile, A.; Veziroǧlu, T. Compendium of Hydrogen Energy: Hydrogen Production and Purification; Woodhead Publishing: Sawston, UK, 2015. [Google Scholar]
- Eikerling, M.; Kulikovsky, A. Polymer Electrolyte Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Kulikovsky, A. Analytical Modeling of Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Hacker, V.; Mitsushima, S. Fuel Cells and Hydrogen; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Foniok, K.; Drozdova, L.; Prokop, L.; Krupa, F.; Kedron, P.; Blazek, V. Mechanisms and modelling of effects on the degradation processes of a proton exchange membrane (PEM) fuel cell: A comprehensive review. Energies 2025, 18, 2117. [Google Scholar] [CrossRef]
- Zhu, Y.; Qu, Z.; Zhang, G.; Yu, B. A one-dimensional model for Pt degradation and precipitation in proton exchange membrane fuel cell considering Pt nucleation, particle size growth, and band formation. Electrochim. Acta 2024, 475, 143590. [Google Scholar] [CrossRef]
- Jahnke, T.; Futter, G.; Baricci, A.; Rabissi, C.; Casalegno, A. Physical modeling of catalyst degradation in low temperature fuel cells: Platinum oxidation, dissolution, particle growth and platinum band formation. J. Electrochem. Soc. 2020, 167, 013523. [Google Scholar] [CrossRef]
- Ding, Y.; Fang, Z.; Yuan, Y.; Tian, M.; Yu, J.; Li, L. Particle size distribution degradation model for PEM fuel cell Pt/C catalyst based on population balance equation. Chem. Eng. Sci. 2024, 300, 120590. [Google Scholar] [CrossRef]
- Li, Y.; Moriyama, K.; Gu, W.; Arisetty, S.; Wang, C. A one-dimensional Pt degradation model for polymer electrolyte fuel cells. J. Electrochem. Soc. 2015, 162, F834–F842. [Google Scholar] [CrossRef]
- Colombo, E.; Casalegno, A.; Guetaz, L.; Bariccil, A. Revealing the critical role of low voltage excursions in enhancing PEM fuel cell catalyst degradation by automotive hydrogen/air potential cycling experiments. Int. J. Hydrogen Energy 2024, 65, 292–307. [Google Scholar] [CrossRef]
- Shojayian, M.; Kjeang, E. Simulation of cathode catalyst durability under fuel cell vehicle operation—Effects of stack size and temperature. J. Power Sources 2024, 591, 233820. [Google Scholar] [CrossRef]
- Choi, J.; Kim, E.; Cha, Y.; Ghasemi, M.; Ju, H. Probing the influence of nonuniform Pt particle size distribution using a full three-dimensional, multiscale, multiphase polymer electrolyte membrane fuel cell model. Electrochim. Acta 2022, 405, 139811. [Google Scholar] [CrossRef]
- Kobayashi, A.; Fujii, T.; Harada, C.; Yasumoto, E.; Takeda, K.; Kakinuma, K.; Uchida, M. Effect of Pt and ionomer distribution on polymer electrolyte fuel cell performance and durability. ACS Appl. Energy Mater. 2021, 4, 2307–2317. [Google Scholar] [CrossRef]
- Wang, D.; Min, H.; Sun, W.; Zeng, B.; Wu, H. Durability study of frequent dry–wet cycle on proton exchange membrane fuel cell. Energies 2023, 16, 4284. [Google Scholar] [CrossRef]
- Tarasova, N.A.; Hanif, M.B.; Janjua, N.K.; Anwar, S.; Motola, M.; Medvedev, D.A. Fluorine-insertion in solid oxide materials for improving their ionic transport and stability. A brief review. Int. J. Hydrogen Energy 2024, 50 Pt C, 104–123. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, F.; Lin, C.; Zhu, F.; Shen, S.; Wei, G.; Zhang, J. Design of gradient cathode catalyst layer (CCL) structure for mitigating Pt degradation in proton exchange membrane fuel cells (PEMFCs) using mathematical method. J. Power Sources 2020, 451, 227729. [Google Scholar] [CrossRef]
- Kravos, A.; Ritzberger, D.; Tavčar, G.; Hametner, C.; Jakubek, S.; Katrašnik, T. Thermodynamically consistent reduced dimensionality electrochemical model for proton exchange membrane fuel cell performance modelling and control. J. Power Sources 2020, 454, 227930. [Google Scholar] [CrossRef]
- Bartlechner, J.; Vrlić, M.; Hametner, C.; Jakubek, S. State-of-Health observer for PEM fuel cells—A novel approach for real-time online analysis. Int. J. Hydrogen Energy 2024, 95, 1112–1125. [Google Scholar] [CrossRef]
- Franco, A.A.; Schott, P.; Jallut, C.; Maschke, B. A dynamic mechanistic model of an electrochemical interface. J. Electrochem. Soc. 2006, 153, A1053–A1061. [Google Scholar] [CrossRef]
- Fuhrmann, J.; Guhlke, C.; Linke, A.; Merdon, C.; Müller, R. Models and numerical methods for electrolyte flows. In Topics in Applied Analysis and Optimisation; Hintermüller, M., Rodrigues, J.F., Eds.; Springer: Cham, Switzerland, 2019; Chapter 8; pp. 183–209. [Google Scholar] [CrossRef]
- Efendiev, M. Attractors for Degenerate Parabolic Type Equations. In Mathematical Surveys and Monographs; AMS: Providence, RI, USA, 2013; Volume 192. [Google Scholar] [CrossRef]
- Fellner, K.; Kovtunenko, V.A. A singularly perturbed nonlinear Poisson–Boltzmann equation: Uniform and super-asymptotic expansions. Math. Meth. Appl. Sci. 2015, 38, 3575–3586. [Google Scholar] [CrossRef]
- González-Granada, J.; Kovtunenko, V. Entropy method for generalized Poisson–Nernst–Planck equations. Anal. Math. Phys. 2018, 8, 603–619. [Google Scholar] [CrossRef]
- Kovtunenko, V.; Zubkova, A. Mathematical modeling of a discontinuous solution of the generalized Poisson–Nernst–Planck problem in a two-phase medium. Kinet. Relat. Mod. 2018, 11, 119–135. [Google Scholar] [CrossRef]
- Alekseev, G.; Spivak, Y. Stability estimates of optimal solutions for the steady magnetohydrodynamics-Boussinesq equations. Mathematics 2024, 12, 1912. [Google Scholar] [CrossRef]
- Hintermüller, M.; Kovtunenko, V.A.; Kunisch, K. A Papkovich–Neuber-based numerical approach to cracks with contact in 3D. IMA J. Appl. Math. 2009, 74, 325–343. [Google Scholar] [CrossRef]
- Itou, H.; Kovtunenko, V.; Rajagopal, K. The Boussinesq flat-punch indentation problem within the context of linearized viscoelasticity. Int. J. Eng. Sci. 2020, 151, 103272. [Google Scholar] [CrossRef]
- Khludnev, A.; Kovtunenko, V. Analysis of Cracks in Solids. In Advances in Fracture Mechanics; WIT-Press: Southampton, MA, USA, 2000; Volume 6. [Google Scholar]
- Du, S.; Guan, S.; Mehrazi, S.; Zhou, F.; Pan, M.; Zhang, R.; Chuang, P.Y.A.; Sui, P.C. Effect of dispersion method and catalyst on the crack morphology and performance of catalyst layer of PEMFC. J. Electrochem. Soc. 2021, 168, 114506. [Google Scholar] [CrossRef]
- Chan, H.S.; Bläubaum, L.; Vijayshankar, D.; Röder, F.; Nowak, C.; Weber, A.; Kwade, A.; Krewer, U. Revealing the impact of particle size distribution on ageing of Lithium-Ion batteries with frequency response analysis. Batter. Supercaps 2023, 6, e202300203. [Google Scholar] [CrossRef]
- Kovtunenko, V.; Karpenko-Jereb, L. Study of voltage cycling conditions on Pt oxidation and dissolution in polymer electrolyte fuel cells. J. Power Sources 2021, 493, 229693. [Google Scholar] [CrossRef]
- Pivac, I.; Barbir, F. Impact of shutdown procedures on recovery phenomena of proton exchange membrane fuel cells. Fuel Cells 2020, 160, 185–195. [Google Scholar] [CrossRef]
- Kovtunenko, V.; Karpenko-Jereb, L. Lifetime of catalyst under voltage cycling in polymer electrolyte fuel cell due to platinum oxidation and dissolution. Technologies 2021, 9, 80. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Kovtunenko, V. Modeling of the impact of cycling operating conditions on durability of polymer electrolyte fuel cells and its sensitivity analysis. Int. J. Hydrogen Energy 2023, 48, 15646–15656. [Google Scholar] [CrossRef]
- Kovtunenko, V. Variance-based sensitivity analysis of fitting parameters to impact on cycling durability of polymer electrolyte fuel cells. Technologies 2022, 9, 111. [Google Scholar] [CrossRef]
- Kovtunenko, V. The Holby–Morgan model of platinum catalyst degradation in PEM fuel cells: Range of feasible parameters achieved using voltage cycling. Technologies 2023, 11, 184. [Google Scholar] [CrossRef]
- Kovtunenko, V. Feasible domain of cycling operating conditions and model parameters for Holby–Morgan model of platinum catalyst degradation in PEMFC. Int. J. Hydrogen Energy 2024, 51C, 1518–1526. [Google Scholar] [CrossRef]
- Koltsova, E.; Vasilenko, V.; Zhensa, A.; Bogdanovskaya, V.; Radina, M. Mechanism of degradation of polymer fuel cell cathode catalyst: Research and modeling. Theor. Found. Chem. Eng. 2024, 58, 1945–1956. [Google Scholar] [CrossRef]
- Kovtunenko, V. Particle size distribution in Holby–Morgan degradation model of platinum on carbon catalyst in fuel cell: Normal distribution. Technologies 2024, 12, 202. [Google Scholar] [CrossRef]
- Holby, E.; Morgan, D. Application of Pt nanoparticle dissolution and oxidation modeling to understanding degradation in PEM fuel cells. J. Electrochem. Soc. 2012, 159, B578–B591. [Google Scholar] [CrossRef]
- Touil, W.; Li, Z.; Outbib, R.; Hissel, D.; Jemei, S. A system-level modeling framework for predicting Pt catalyst degradation in proton exchange membrane fuel cells. J. Power Sources 2025, 625, 235628. [Google Scholar] [CrossRef]
- Darling, R.; Meyers, J. Kinetic model of platinum dissolution in PEMFCs. J. Electrochem. Soc. 2003, 150, A1523–A1527. [Google Scholar] [CrossRef]
- Holby, E.; Sheng, W.; Shao-Horn, Y.; Morgan, D. Pt nanoparticle stability in PEM fuel cells: Influence of particle size distribution and crossover hydrogen. Energy Environ. Sci. 2009, 2, 865–871. [Google Scholar] [CrossRef]
- Taylor, S.; Fabbri, E.; Levecque, P.; Schmidt, T.J.; Conrad, O. The effect of platinum loading and surface morphology on oxygen reduction activity. Electrocatalysis 2016, 7, 287–296. [Google Scholar] [CrossRef]
- Lönn, B.; Strandberg, L.; Roth, V.; Luneau, M.; Wickman, B. Fuel cell catalyst layers with platinum nanoparticles synthesized by sputtering onto liquid substrates. ACS Omega 2024, 9, 43725–43733. [Google Scholar] [CrossRef]
- Adibi, P.T.Z.; Zhdanov, V.P.; Langhammer, C.; Grönbeck, H. Transient bimodal particle size distributions during Pt sintering on alumina and silica. J. Phys. Chem. C 2014, 119, 989–996. [Google Scholar] [CrossRef]
- Bi, W.; Fuller, T.F. Modeling of PEM fuel cell Pt/C catalyst degradation. J. Power Sources 2008, 178, 188–196. [Google Scholar] [CrossRef]
- Schröder, J.; Pittkowski, R.K.; Du, J.; Kirkensgaard, J.J.K.; Arenz, M. Investigating the particle growth in bimodal Pt/C catalysts by in-situ small-angle x-ray scattering: Challenges in the evaluation of stress test protocol-dependent degradation mechanisms. J. Electrochem. Soc. 2022, 169, 104504. [Google Scholar] [CrossRef]
- Gilbert, J.A.; Kariuki, N.N.; Wang, X.; Kropf, A.J.; Yu, K.; Groom, D.J.; Ferreira, P.J.; Morgan, D.; Myers, D.J. Pt catalyst degradation in aqueous and fuel cell environments studied via in-operando anomalous small-angle x-ray scattering. Electrochim. Acta 2015, 173, 223–234. [Google Scholar] [CrossRef]
- Sandbeck, D.; Secher, N.; Speck, F.; Sørensen, J.; Chorkendorff, J.; Cherevko, S. Particle size effect on platinum dissolution: Considerations for accelerated stability testing of fuel cell catalysts. ACS Catal. 2020, 10, 6281–6290. [Google Scholar] [CrossRef]
- Ostwald, W. Lehrbruck der Allgemeinen Chemie; W. Engelmann: Leipzig, Germany, 1896; Volume 2. [Google Scholar]
- Ascarelli, P.; Contini, V.; Giorgi, R. Formation process of nanocrystalline materials from x-ray diffraction profile analysis: Application to platinum catalysts. J. Appl. Phys. 2002, 91, 4556–4561. [Google Scholar] [CrossRef]
- Granqvist, C.G.; Buhrman, R.A. Size distributions for supported metal catalysts: Coalescence growth versus Ostwald ripening. J. Catal. 1976, 42, 477–479. [Google Scholar] [CrossRef]
- Kregar, A.; Katrašnik, T. Theoretical analysis of particle size re-distribution due to Ostwald ripening in the fuel cell catalyst layer. Open Phys. 2019, 17, 779–789. [Google Scholar] [CrossRef]
- Kregar, A.; Kravos, A.; Katrašnik, T. Methodology for evaluation of contributions of Ostwald ripening and particle agglomeration to growth of catalyst particles in PEM fuel cells. Fuel Cells 2020, 20, 487–498. [Google Scholar] [CrossRef]
- Baroody, H.A.; Stolar, D.B.; Eikerling, M.H. Modelling-based data treatment and analytics of catalyst degradation in polymer electrolyte fuel cells. Electrochim. Acta 2018, 283, 1006–1016. [Google Scholar] [CrossRef]
- Nores-Pondal, F.; Vilella, I.; Troiani, H.; Granada, M.; de Miguel, S.; Scelza, O.; Corti, H. Catalytic activity vs. size correlation in platinum catalysts of PEM fuel cells prepared on carbon black by different methods. Int. J. Hydrogen Energy 2009, 34, 8193–8203. [Google Scholar] [CrossRef]
- Gummalla, M.; Ball, S.C.; Condit, D.A.; Rasouli, S.; Yu, K.; Ferreira, P.J.; Myers, D.J.; Yang, Z. Effect of particle size and operating conditions on Pt3Co PEMFC cathode catalyst durability. Catalysts 2015, 5, 926–948. [Google Scholar] [CrossRef]
- Yu, K.; Groom, D.J.; Wang, X.; Yang, Z.; Gummalla, M.; Ball, S.C.; Myers, D.J.; Ferreira, P.J. Degradation mechanisms of platinum nanoparticle catalysts in proton exchange membrane fuel cells: The role of particle size. Chem. Mater. 2014, 26, 5540–5548. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Zhong, H.; Lu, Q.; Wang, Y.; Su, D. Effect of particle size on the activity and durability of the Pt/C electrocatalyst for proton exchange membrane fuel cells. Appl. Catal. B Environ. 2012, 111–112, 264–270. [Google Scholar] [CrossRef]
- Yu, H.; Zachman, M.J.; Reeves, K.S.; Park, J.H.; Kariuki, N.N.; Hu, L.; Mukundan, R.; Neyerlin, K.C.; Myers, D.J.; Cullen, D.A. Tracking nanoparticle degradation across fuel cell electrodes by automated analytical electron microscopy. ACS Nano 2022, 16, 12083–12094. [Google Scholar] [CrossRef]
- Zhan, F.; Hu, K.S.; Mai, J.H.; Zhang, L.S.; Zhang, Z.G.; He, H.; Liu, X.H. Recent progress of Pt-based oxygen reduction reaction catalysts for proton exchange membrane fuel cells. Rare Met. 2024, 43, 2444–2468. [Google Scholar] [CrossRef]


| Symbol | Value | Units | Description |
|---|---|---|---|
| Hz | dissolution attempt frequency | ||
| Hz | backward dissolution rate factor | ||
| 0.5 | Butler transfer coefficient for Pt dissolution | ||
| n | 2 | electrons transferred during Pt dissolution | |
| 1.118 | V | Pt dissolution bulk equilibrium voltage | |
| 9.09 | cm3/mol | molar volume of Pt | |
| J/cm2 | Pt [1 1 1] surface tension | ||
| 1 | mol/cm3 | reference Pt ion concentration | |
| J/mol | partial molar Pt dissolution activation enthalpy | ||
| cm2/s | diffusion coefficient of Pt ion in the membrane | ||
| Hz | forward Pt oxide formation rate constant | ||
| Hz | backward Pt oxide formation rate constant | ||
| mol/cm2 | Pt surface site density | ||
| 0.5 | Butler transfer coefficient for PtO formation | ||
| 2 | electrons transferred during Pt oxide formation | ||
| 0.8 | V | Pt oxide formation bulk equilibrium voltage | |
| J/mol | Pt oxide dependent kinetic barrier constant | ||
| J/mol | Pt oxide-oxide interaction energy | ||
| J/mol | partial molar oxide formation activation enthalpy |
| Group | Particle Size | Range | Probability |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovtunenko, V.A. Impact of Log-Normal Particle Size Distribution in Holby–Morgan Degradation Model on Aging of Pt/C Catalyst in PEMFC. Technologies 2025, 13, 262. https://doi.org/10.3390/technologies13070262
Kovtunenko VA. Impact of Log-Normal Particle Size Distribution in Holby–Morgan Degradation Model on Aging of Pt/C Catalyst in PEMFC. Technologies. 2025; 13(7):262. https://doi.org/10.3390/technologies13070262
Chicago/Turabian StyleKovtunenko, Victor A. 2025. "Impact of Log-Normal Particle Size Distribution in Holby–Morgan Degradation Model on Aging of Pt/C Catalyst in PEMFC" Technologies 13, no. 7: 262. https://doi.org/10.3390/technologies13070262
APA StyleKovtunenko, V. A. (2025). Impact of Log-Normal Particle Size Distribution in Holby–Morgan Degradation Model on Aging of Pt/C Catalyst in PEMFC. Technologies, 13(7), 262. https://doi.org/10.3390/technologies13070262






