Linear Average Yield Criterion and Its Application in Failure Pressure Evaluation of Defect-Free Pipelines
Abstract
1. Introduction
2. Yield Criterion and Evaluation Model
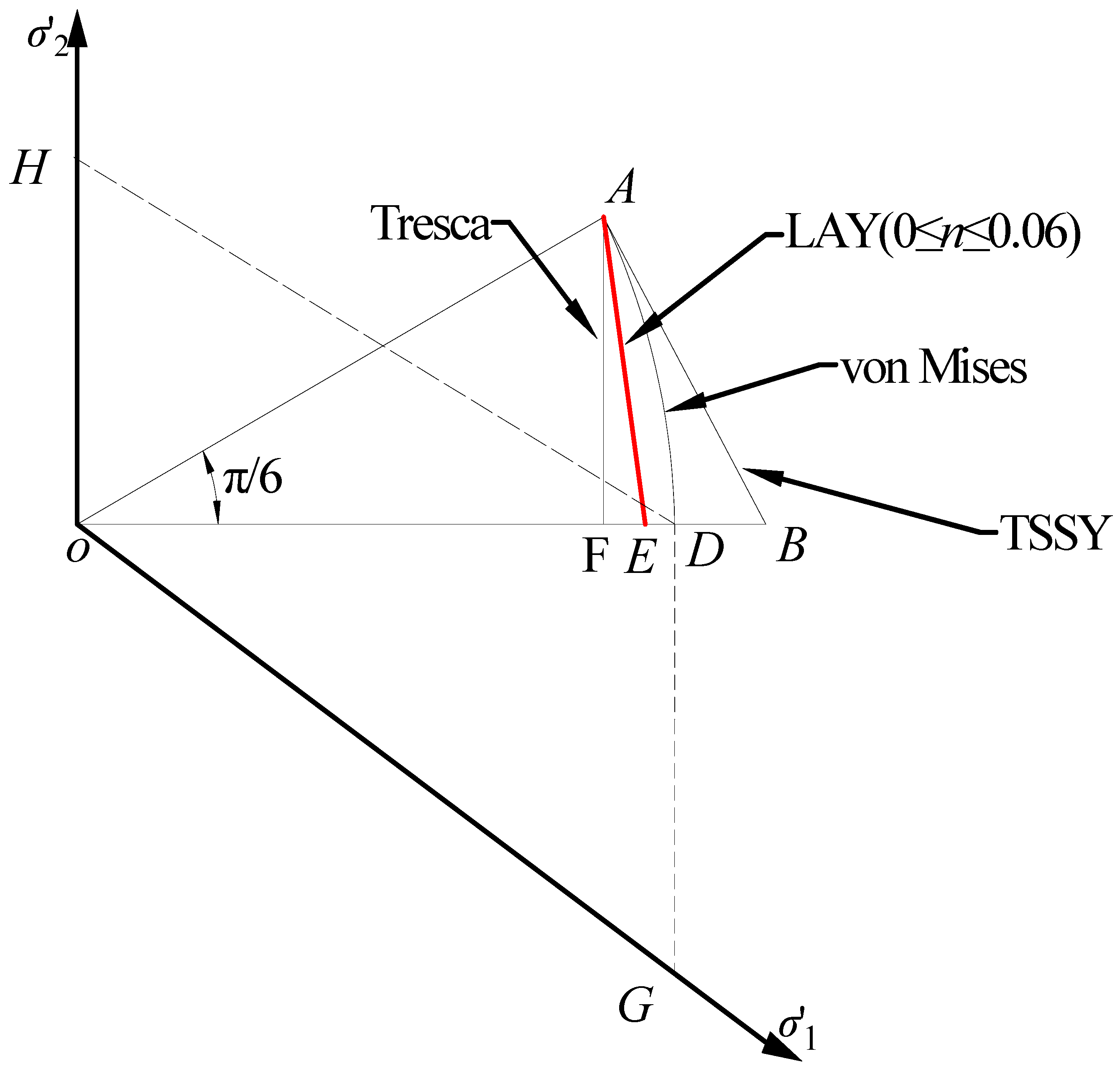
3. Applicability of Different Yield Criteria
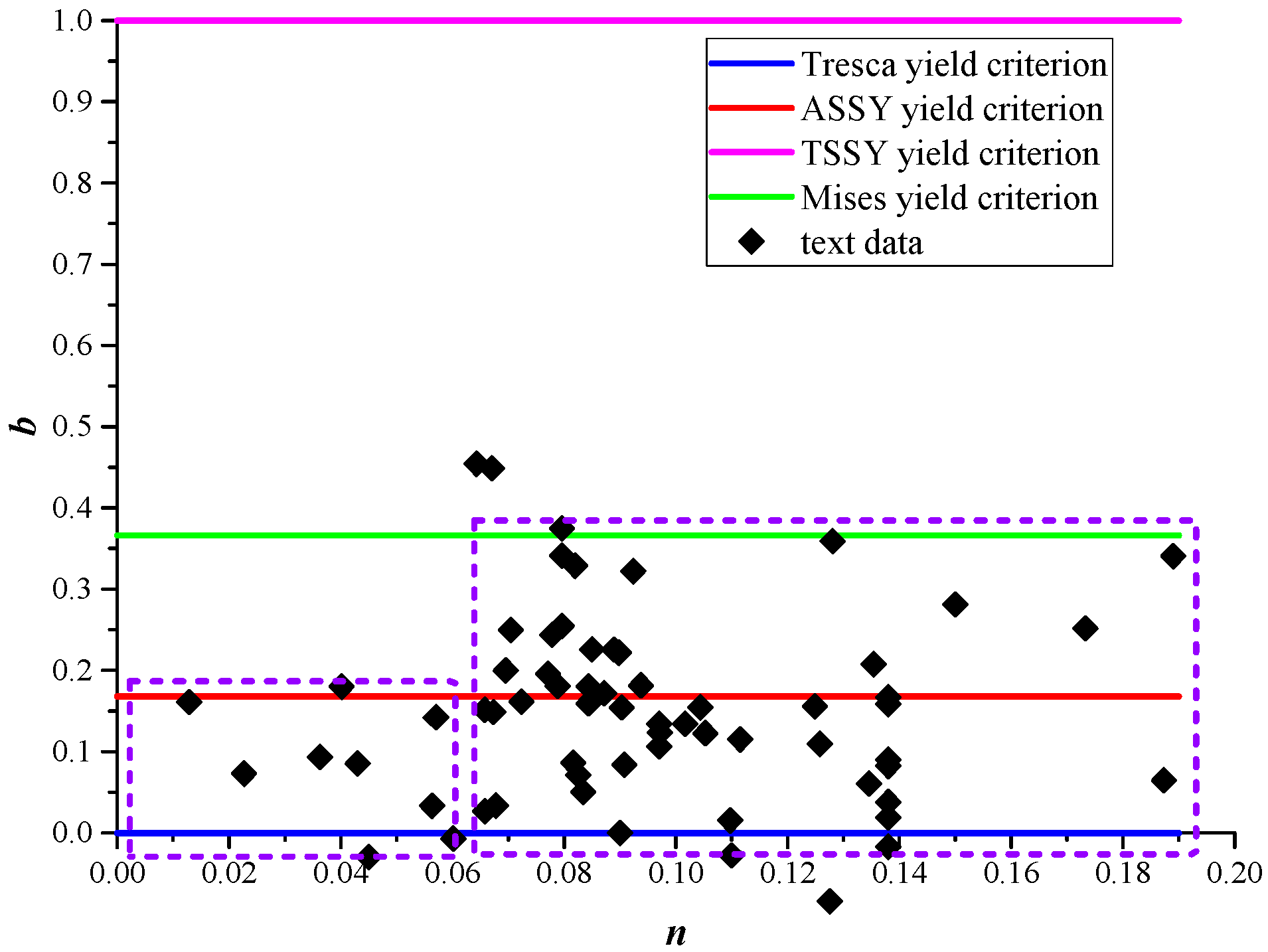
4. Development of a Novel Yield Criterion
4.1. Linear Average Yield Criterion
4.2. Yield Trajectory
4.3. Derivation of Plastic Work Rate
5. Analysis of Failure Pressure Error for the LAY Criterion
5.1. Failure Pressure Evaluation Method Based on LAY Criterion
5.2. Error Analysis of Failure Pressure Assessment
5.3. Conservativeness Analysis of Yield Criteria Under Safety Factors
5.4. Example of Predesign Assessments for Burst Pressure
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, B.; Shuai, J. Influence of Plastic Deformation Capacity On Failure Behavior of Pipelines. J. Fail. Anal. Prev. 2018, 18, 508–518. [Google Scholar] [CrossRef]
- Tresca, H. Memoir On the Flow of Solid Bodies Under Strong Pressure; Comptesrendus de l’Académie des Sciences: Paris, France, 1864; Volume 59, pp. 754–758. [Google Scholar]
- Mises, R.V. Mechanik Der Festen Körper Im Plastisch-Deformablen Zustand. Nachrichten Von Der Ges. Der Wiss. Zu Gött. Math.-Phys. Kl. 1913, 4, 582–592. [Google Scholar]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: New York, NY, USA, 1950. [Google Scholar]
- Yu, M. Twin Shear Stress Yield Criterion. Int J. Mech. Sci. 1983, 25, 71–74. [Google Scholar] [CrossRef]
- Yu, M. Advances in Strength Theories for Materials Under Complex Stress State in the 20Th Century. Appl. Mech. Rev. 2002, 55, 169–218. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, X.; Wang, G. Yield Criterion Based on the Mean Function of Tresca and Twin Shear Stress Yield Functions. J. Northeast. Univ. (Nat. Sci.) 2002, 23, 979–982. [Google Scholar]
- Zhu, X.; Leis, B.N. Average Shear Stress Yield Criterion and its Application to Plastic Collapse Analysis of Pipelines. Int. J. Pres. Ves. Pip. 2006, 83, 663–671. [Google Scholar] [CrossRef]
- Xing-yu, P.; Peng, Z.; Ying, W. Study on the Residual Strength Reliability of Corroded Oil Pipeline Based on Double Shear Yield Condition. China Saf. Sci. J. Nal. 2008, 18, 149–152. [Google Scholar]
- Zhu, X.; Leis, B.N. Evaluation of Burst Pressure Prediction Models for Line Pipes. Int. J. Pres. Ves. Pip. 2012, 89, 85–97. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Q.; Zhou, W. Implementation of the Tresca Yield Criterion in Finite Element Analysis of Burst Capacity of Pipelines. Int. J. Pres. Ves. Pip. 2019, 172, 180–187. [Google Scholar] [CrossRef]
- Chmelko, V.; Berta, I. Analytical Solution of the Pipe Burst Pressure Using Bilinear Stress-Strain Model and Influence of Corrosion Defects On It. Procedia Struct. Integr. 2019, 18, 600–607. [Google Scholar] [CrossRef]
- Chen, Z.; Chu, W.; Wang, H.; Li, Y.; Wang, W.; Meng, W.; Li, Y. Structural Integrity Assessment of Hydrogen-Mixed Natural Gas Pipelines Based On a New Multi-Parameter Failure Criterion. Ocean. Eng. 2022, 247, 110731. [Google Scholar] [CrossRef]
- Tang, Z.J.; Zhang, S.H.; Li, Y.; Li, Y.X. A Mathematical Extrapolation-Based Yield Criterion and its Application in Modeling of Burst Pressure of Defect-Free Straight Pipes. Ocean. Eng. 2022, 263, 112408. [Google Scholar] [CrossRef]
- Zhang, S.H.; Liu, J.R. A Generalized Weighted Yield Criterion: Theoretical Derivation and its Application in the Plastic Failure Analysis of Pipeline with Corroded Defects. Int. J. Pres. Ves. Pip. 2022, 200, 104832. [Google Scholar] [CrossRef]
- Sun, M.; Chen, Y.; Zhao, H.; Li, X. Analysis of the Impact Factor of Burst Capacity Models for Defect-Free Pipelines. Int. J. Pres. Ves. Pip. 2022, 200, 104805. [Google Scholar] [CrossRef]
- Zhu, X.; Wiersma, B.; Johnson, W.R.; Sindelar, R.L. Burst Pressure Solutions of Thin and Thick-Walled Cylindrical Vessels. J. Press. Vessel. Technol. 2023, 145, 041303. [Google Scholar] [CrossRef]
- Jin, C.; Wang, L.; Zhang, Y. Strength Differential Effect and Influence of Strength Criterion On Burst Pressure of Thin-Walled Pipelines. Appl. Math. Mech. 2012, 33, 1361–1370. [Google Scholar] [CrossRef]
- Sun, M.; Li, X.; Liu, J. Determination of Folias Factor for Failure Pressure of Corroded Pipeline. J. Press. Vess-T. Asme. 2020, 142, 31802. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y. Plastic Collapse Analysis of Thin-Walled Pipes Based On Unified Yield Criterion. Int. J. Mech. Sci. 2011, 53, 348–354. [Google Scholar] [CrossRef]
- Mok, D.; Pick, R.J.; Glover, A.G.; Hoff, R. Bursting of Line Pipe with Long External Corrosion. Int. J. Pres. Ves. Pip. 1991, 46, 195–216. [Google Scholar] [CrossRef]
- Liessem, A.; Graef, M.K.; Knauf, G.; Marewski, U. Influence of Thermal Treatment on Mechanical Properties of UOE Linepipe. In Proceedings of the 4th International Conference of Pipeline Technology, Ostend, Belgium, 9–13 May 2004; pp. 1263–1281. [Google Scholar]
- Hillenbrand, H.; Liessem, A.; Knauf, G.; Niederhoff, K.; Bauer, J. Development of Large-Diameter Pipe in Grade X100. In Proceedings of the 3rd International Pipeline Technology Conference, Brugge, Belgium, 21–24 May 2000; pp. 469–482. [Google Scholar]
- Okaguchi, S.P.; Makino, H.L.; Hamada, M.; Yamamoto, A.; Ikeda, T.; Takeuchi, I.; Fairchild, D.P.; Macia, M.L.; Papka, S.D.; Stevens, J.H. Development and Mechanical Properties of X120 Linepipe. In Proceedings of the The Thirteenth International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003; pp. 3–336. [Google Scholar]
- Papka, S.D.; Stevens, J.H.; Macia, M.L.; Fairchild, D.P.; Petersen, C.W. Full-Size Testing and Analysis of X120 Linepipe. In Proceedings of the the 13th International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003; pp. 50–59. [Google Scholar]
- Paslay, P.R.; Cernocky, E.P.; Wink, R. Burst Pressure Prediction of Thin-Walled, Ductile Tubulars Subjected to Axial Load. In Proceedings of the SPE Applied Technology Workshop on Risk Based Design of Well Casing and Tubing, Woodlands, TX, USA, 7–8 May 1998; p. 48327. [Google Scholar]
- Benjamin, A.C.; Freire, J.L.F.; Vieira, R.D.; Diniz, J.L.; de Andrade, E.Q. Burst Tests On Pipeline Containing Interacting Corrosion Defects. In Proceedings of the ASME 2005 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 12–17 June 2005; pp. 403–417. [Google Scholar]
- Cronin, D.S.; Pick, R.J. Experimental Database for Corroded Pipe: Evaluation of RSTRENG and B31G. In Proceedings of the 3rd International Pipeline Conference, Calgary, AL, Canada, 1–5 October 2000; pp. 757–767. [Google Scholar]
- Royer, C.P.; Rolfe, S.T. Effect of Strain-Hardening Exponent and Strain Concentrations on the Bursting Behavior of Pressure Vessels. J. Eng. Mater-T. Asme. 1974, 96, 292–298. [Google Scholar] [CrossRef]
- Gaessier, H.; Vogt, G.H. Influence of Yield to Tensile Ratio On the Safety of Pipelines. In Proceedings of the 7th Biennial Joint Technical Meeting on Line Pipe Research, Calgary, AL, Canada, 4 April 1989; pp. 165–172. [Google Scholar]
- Maxey, W.A. Y/T Significance in Line Pipe. In Proceedings of the 7th Symposium on Line Pipe Research, Houston, TX, USA, 14–16 October; 1986; pp. 1–18. [Google Scholar]
- Amano, K.; Matsuoka, M.; Ishihara, T.; Tanaka, K.; Inoue, T.; Kawaguchi, Y.; Tsukamoto, M. Significance of Yield Ratio Limitation to Plastic Deformation of Pipeline in High Pressure Proof Test. In Proceedings of the 7th Symposium on Line Pipe Research, Houston, TX, USA, 14–16 October 1986; pp. 1–21. [Google Scholar]
- Chouchaoui, B. Evaluating the Remaining Strength of Corroded Pipelines; University of Waterloo: Waterloo, ON, Canada, 1995. [Google Scholar]
- Stewart, G.; Klever, F.J.; Ritchie, D. An Analytical Model to Predict the Burst Capacity of Pipelines. In Proceedings of the 13th International Offshore Mechanics and Arctic Engineering Conference, Houston, TX, USA, February 27–March 3 1994; pp. 177–188. [Google Scholar]
- Law, M.; Bowie, G. Prediction of Failure Strain and Burst Pressure in High Yield-To-Tensile Strength Ratio Pipeline. Int J. Pres. Ves. Pip. 2007, 84, 487–492. [Google Scholar] [CrossRef]
- Law, M.; Bowie, G.; Fletcher, L. Burst Pressure and Failure Strain in Pipeline, Part 2: Comparisons of Burst-Pressure and Failure-Strain Formulas. J. Pipeline Integr. 2004, 3, 102–106. [Google Scholar]
- Law, M.; Bowie, G.; Fletcher, L.; Piper, L. Burst Pressure and Failure Strain in Linepipe: Part 1:Comparison of Ring-Expansion and Tensile Testing in Gas Linepipe. J. Pipeline Integr. 2004, 3, 95–101. [Google Scholar]
- Zhu, X.; Leis, B.N. Strength Criteria and Analytic Predictions of Failure Pressure in Line Pipes. Int. J. Offshore Polar. 2004, 14, 125–131. [Google Scholar]
- Zhu, X.; Leis, B.N. Influence of Yield-To-Tensile Strength Ratio On Failure Assessment of Corroded Pipelines. J. Press. Vess-T. Asme. 2005, 127, 436–442. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, X.; Liu, X.; Wang, G. A Dodecagon Linear Yield Criterion with Optimal Approximation to Mises Criterion. In Proceedings of the 2nd International Conference on New Development in Rock Mechanics & Rock Engineering, Shenyang, China, 10 October 2002; pp. 554–558. [Google Scholar]
- Belrhiti, Y.; Hamelin, C.; Lamagnere, P.; Knowles, D.; Mostafavi, M. A Comprehensive Comparison of Creep-Fatigue Life Assessment through Leading Industrial Codes. Int. J. Pres. Ves. Pip. 2025, 216, 105497. [Google Scholar] [CrossRef]

| Yield Criterion | Tresca | LAY (0 ≤ n ≤ 0.06) | LAY (n > 0.06) | ASSY | von Mises | TSSY |
|---|---|---|---|---|---|---|
| k | 2.000 | 1.928 | 1.866 | 1.856 | 1.732 | 1.500 |
| Computation model | ||||||
| Yield Criterion (Design Code) | Tresca (ASME B31.8) | ASSY | von Mises (RCC-MRx, R5) | LAY |
|---|---|---|---|---|
| maximum | 16.54% | 14.43% | 23.74% | 13.78% |
| minimum | 0.01% | 0.04% | 0.24% | 0.01% |
| average | 6.99% | 4.03% | 9.39% | 3.75% |
| standard deviation | 0.04 | 0.03 | 0.05 | 0.03 |
| Method | LAY | ASSY | ||
|---|---|---|---|---|
| attribute interval | 0 ≤ n ≤ 0.06 | 0.06 < n | 0 ≤ n ≤ 0.06 | 0.06 < n |
| maximum | 5.59% | 13.78% | 9.83% | 14.43% |
| minimum | 0.24% | 0.01% | 0.27% | 0.04% |
| average | 2.68% | 3.93% | 4.20% | 4.01% |
| Safety Factor SF | Yield Criterion (Design Code) | Tresca (ASME B31.8) | ASSY | von Mises (RCC-MRx, R5 [41]) | LAY |
|---|---|---|---|---|---|
| 1.1 | average | 91.09% | 99.29% | 84.82% | 92.03% |
| minimum | 81.69% | 88.42% | 75.87% | 82.13% | |
| maximum | 103.44% | 112.49% | 95.65% | 104.03% | |
| 1.15 | average | 87.13% | 94.97% | 81.14% | 88.03% |
| minimum | 78.14% | 84.58% | 72.57% | 78.56% | |
| maximum | 98.94% | 107.60% | 91.49% | 99.51% | |
| 1.2 | average | 83.50% | 91.01% | 77.76% | 84.36% |
| minimum | 74.89% | 81.05% | 69.55% | 75.29% | |
| maximum | 94.82% | 103.12% | 87.68% | 95.36% |
| Criterion | Predicted Burst Pressure (MPa) | Design Burst Pressure (MPa) |
|---|---|---|
| Tresca | 14.44 | 13.13 |
| von Mises | 18.91 | 17.19 |
| ASSY | 15.67 | 14.24 |
| LAY | 15.59 | 14.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, J.-H.; Sun, M.-M.; Zhang, J. Linear Average Yield Criterion and Its Application in Failure Pressure Evaluation of Defect-Free Pipelines. Technologies 2025, 13, 252. https://doi.org/10.3390/technologies13060252
Ji J-H, Sun M-M, Zhang J. Linear Average Yield Criterion and Its Application in Failure Pressure Evaluation of Defect-Free Pipelines. Technologies. 2025; 13(6):252. https://doi.org/10.3390/technologies13060252
Chicago/Turabian StyleJi, Jian-Hong, Ming-Ming Sun, and Jie Zhang. 2025. "Linear Average Yield Criterion and Its Application in Failure Pressure Evaluation of Defect-Free Pipelines" Technologies 13, no. 6: 252. https://doi.org/10.3390/technologies13060252
APA StyleJi, J.-H., Sun, M.-M., & Zhang, J. (2025). Linear Average Yield Criterion and Its Application in Failure Pressure Evaluation of Defect-Free Pipelines. Technologies, 13(6), 252. https://doi.org/10.3390/technologies13060252





