Center of Mass Auto-Location in Space †
Abstract
1. Introduction
- Problem Statement: Generally, inertia moments are estimated on the ground, while some recent attempts have been made to estimate them on an orbit. The estimation of inertia products is relatively rare, despite the ability to parameterize the location of the mass center using the parallel axis theorem. This study elaborates a novel process for determining the time-varying location of the mass center on orbit by using the parallel axis theorem to parameterize the problem and then estimating the time-varying inertia properties leads to the auto-location of the spacecraft’s center of mass.
- Research objectives: (1) Using only attitude empirical angle knowledge, find mass imbalanced inertia components and (2) convert mass imbalance to center of gravity coordinates, and then calculate that location.
- Key contributions: Seminal proposal of a novel mass center auto-location method is introduced, realizing improvements over the comparative state-of-the-art benchmark. Rapid convergence is validated in spaceflight experiments.
1.1. Review of the Literature
1.2. State-of-the-Art Benchmarks
- Mass center coordinate estimation based on an overall brightness average determined from a three-dimensional vision system [26].
- Reference [27] presents an exact analytic method for calculating the volume, mass, center of gravity, and inertia properties of wing segments and rotors of constant density, emphasizing analysis requiring the analytical solution of several volume integrals (necessarily a quite lengthy process). The goal of this present study is akin to this state-of-the-art benchmark, while avoiding such complications.
- Reference [28] combines multiple accelerometers and gyroscopes into an inertial measurement unit mounted on the pitch and yaw axes, where the roll axis houses the gyroscope used to determine the spin axis.
1.3. Novelties Presented
- This present manuscript presents results validating the declared state-of-the-art benchmark with tests on orbit using experimental satellites depicted in Figure 1.
- A seminal method is proposed and tested, and results are presented relative to the comparative benchmark.
- An additional novelty stems from the seminal introduction of a two-norm optimal projection learning method.
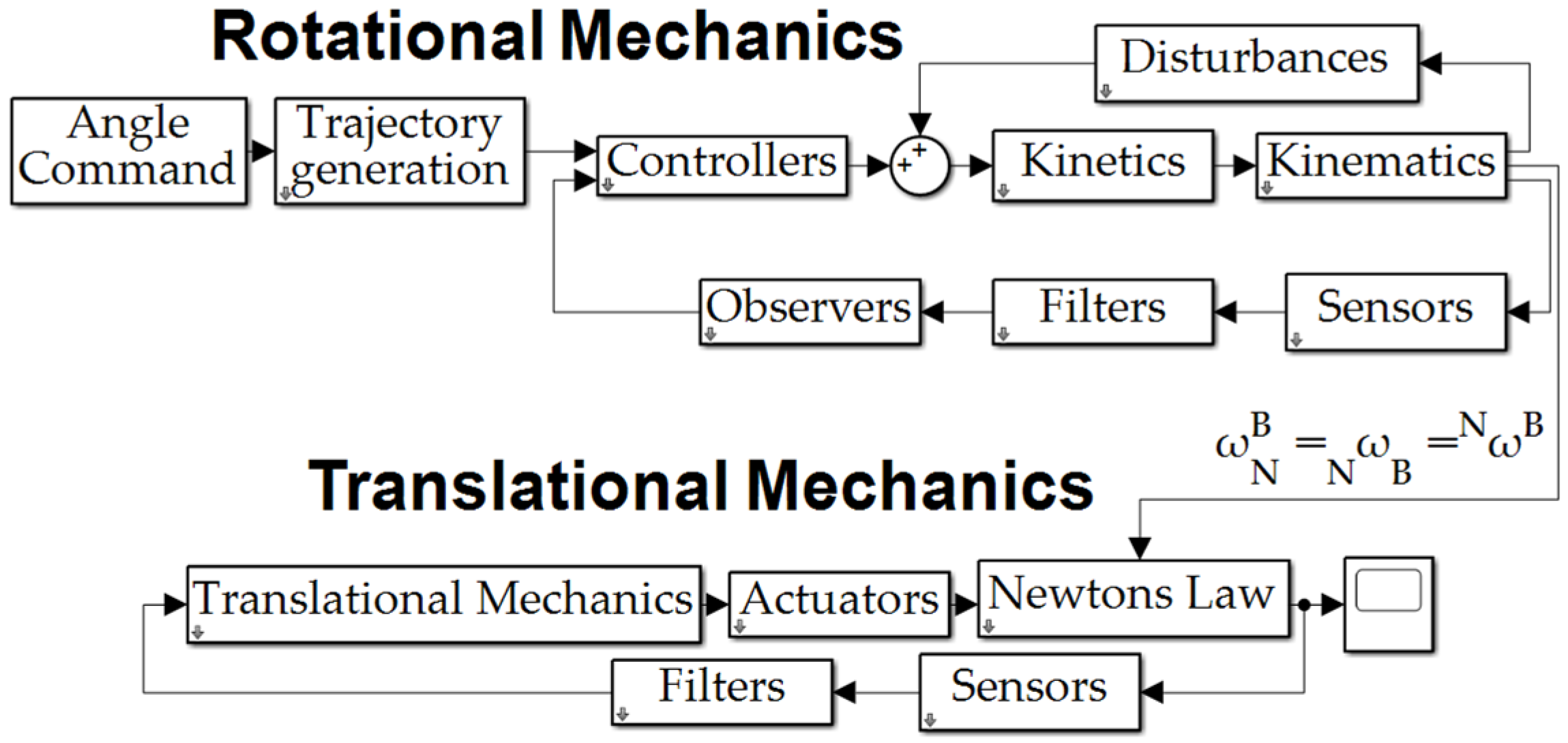
2. Materials and Methods
2.1. Inertia Matrix
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Centroidal angular momentum | Dummy variables | ||
| Radius vector to differential mass, | Radius vector to point | ||
| Differential mass, | Differential mass | ||
| Angular velocity vector | Velocity vector of differential mass, |
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Angular velocity [radians/second] | Moments of inertia | ||
| Unit vectors | Products of inertia | ||
| Positional coordinates | Moment of inertia matrix |
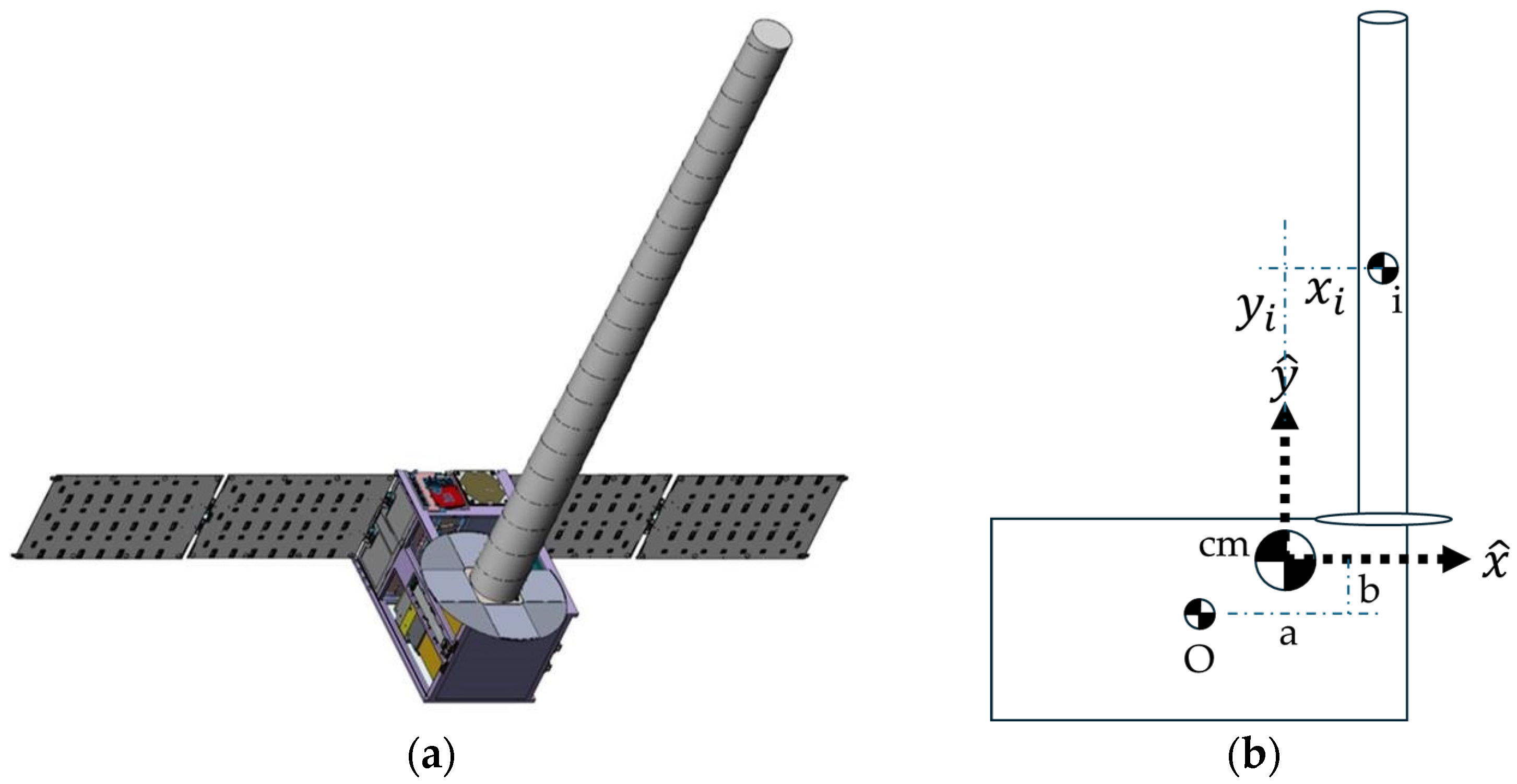
2.2. Center of Mass Location Estimation
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Inertia moment about a fixed axis along | Robot arm base parallel axis | ||
| Inertia moment about mass center | Body center parallel axis | ||
| Total system mass | Radius from parallel axis (not mass center) | ||
| Distance from O to the mass center | Radius vector to the mass center | ||
| Distance to axis | Differential mass element | ||
| Fixed axis along axis | () | Center of mass coordinates | |
| coordinate of | coordinate of |
2.3. Inertia Matrix Component Estimation
2.3.1. Classical Approach
2.3.2. Comparative Benchmark Approach (Nonlinear Adaptive Estimation)
2.3.3. Proposed Approach (Two-Norm Optimal Projection Learning)
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Desire angular velocity about | Desire angular acceleration about | ||
| Desire angular velocity about | Desire angular acceleration about | ||
| Desire angular velocity about | Desire angular acceleration about | ||
| Regression matrix of sensor data | Regression matrix of desired states | ||
| Unknown predicted variables | Estimated variables | ||
| Total control torque signal | Feedforward control signal | ||
| Estimated moment of inertia about | Estimated inertia product | ||
| Estimated moment of inertia about | Estimated inertia product | ||
| Estimated moment of inertia about | Estimated inertia product |
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Desired angular state vector | Angular state vector | ||
| Desired angular velocity vector | Angular velocity vector | ||
| Desired angular acceleration vector | Angular acceleration vector | ||
| Feedback control | Integral gain | ||
| Proportional gain | Derivative gain |
2.4. Implementation Procedure
3. Results
3.1. Key Results from Modeling and Simulation
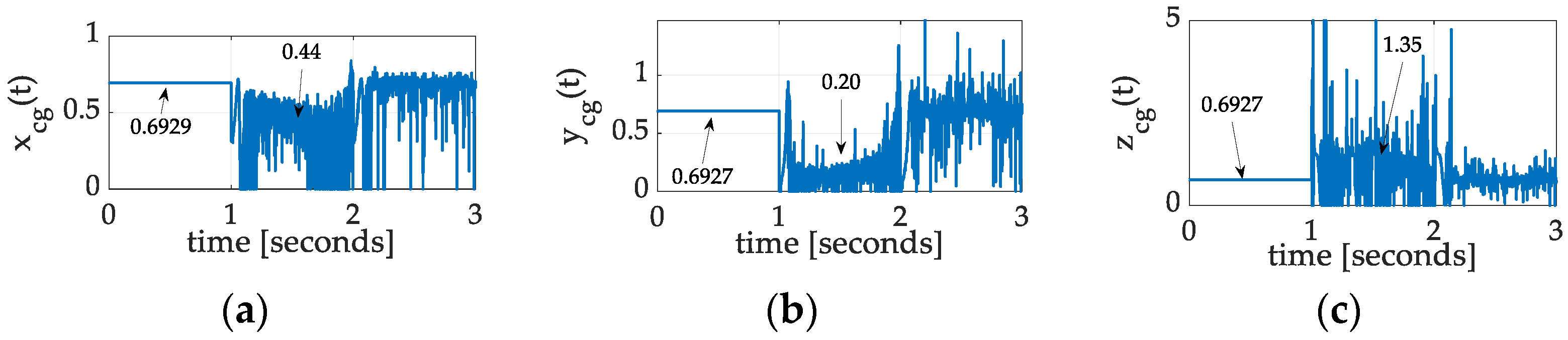
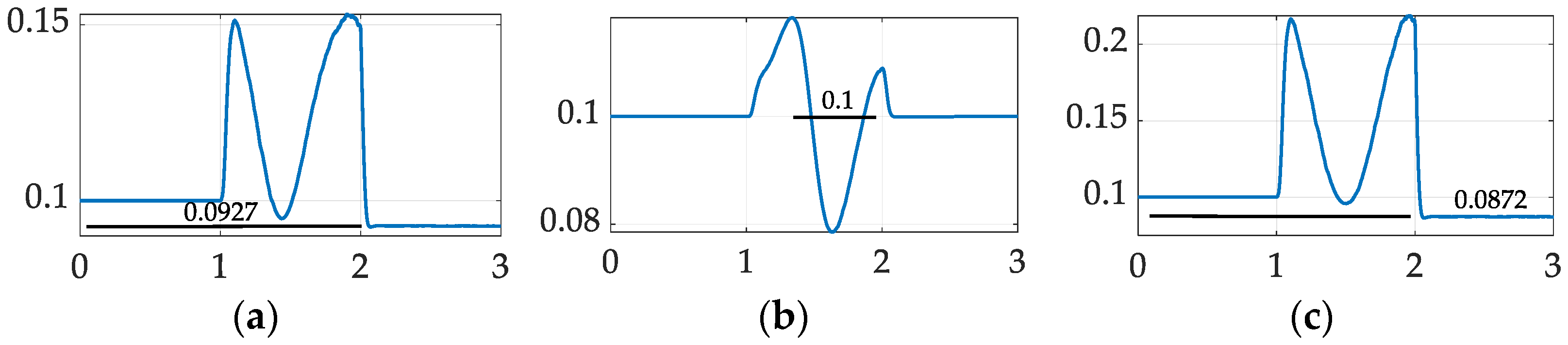
3.1.1. Center of Gravity Auto-Location by Nonlinear Adaption
3.1.2. Center of Gravity Auto-Location by Nonlinear Projection-Based Regression Learning
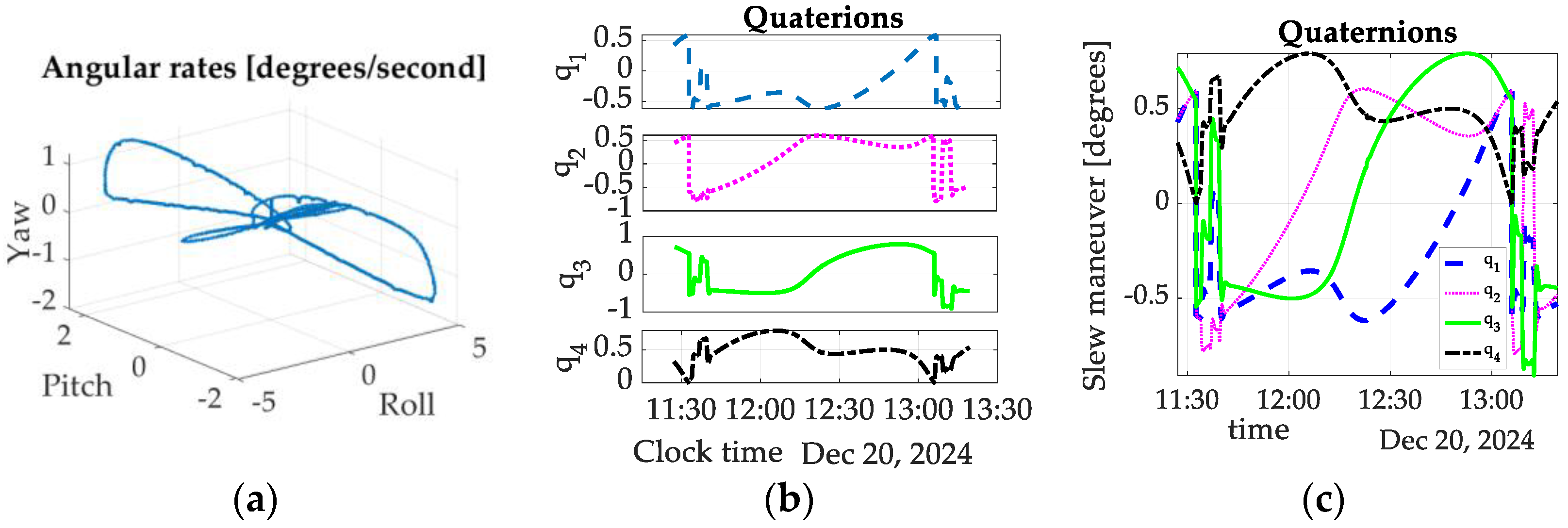
3.2. Key Results from Spaceflight Experiments Flown on 20 December 2024
3.3. Inertia Auto-Identification
3.4. Center of Mass Location Auto-Location
4. Discussion
Future Research Directions
- Enhance Luenberger observer tuning for improved accuracy.
- Rationale: Figure 13 reveals poor state estimation errors that nonetheless led to precise estimation of inertia components and mass center location. Very recent attempts to repeat these experiments produced similar results, but subsequent experiments on a different spacecraft (seeking generalizability) did not produce good inertia estimation or mass center location estimation. Since all other aspects of the proposed method are analytic, the remaining potential cause of the loss of estimation performance is the relatively poor state estimation.
- Purpose served: continue to seek generalizable application to any spacecraft.
- Expected outcomes: improved inertia estimation should lead to robust gravity center estimation.
- Empirical validation of these initial results.
- Rationale: experimental validation of analytic and simulation results necessitate repeatability and generalizability.
- Purpose served: expand the applicability of the proposed methods.
- Expected outcomes: increased inertia estimation accuracy should improve the inputs to (12), directly leading to robust mass center location estimation.
- Grapple with objects of unknown mass.
- Rationale: space robotic grappling requires rapid inertia identification and mass center location to update guidance and control systems.
- Purpose served: improves stability and accuracy.
- Expected outcomes: substantially improves robustness and accuracy.
- Recover from collision damage with significant mass losses and/or gains.
- Rationale: spacecraft that have experienced such collisions need autonomous methods to rapidly update system models to recommence operations.
- Purpose served: autonomously recovers from substantial damage.
- Expected outcomes: Equation (20) retains utility for control with updated mass center and inertia components.
- Application of these methods to flexible spacecraft.
- Rationale: flexible spacecraft modeling can be more realistic and typically follows rigid body treatments to ascertain whether the higher order modeling is necessary.
- Purpose served: potentially increases modeling accuracy.
- Expected outcomes: potential increase in grappling ability.
- Sensitivity analysis how angular velocity cross terms affect the conditioning of the regression matrix.
- Rationale: to justify using the higher order model, including the transport theorem cross products, rather than the ubiquitous so-called double integrator model.
- Purpose served: potentially ability to use simplified models without increasing model accuracy.
- Expected outcomes: potential decrease in computational burden.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


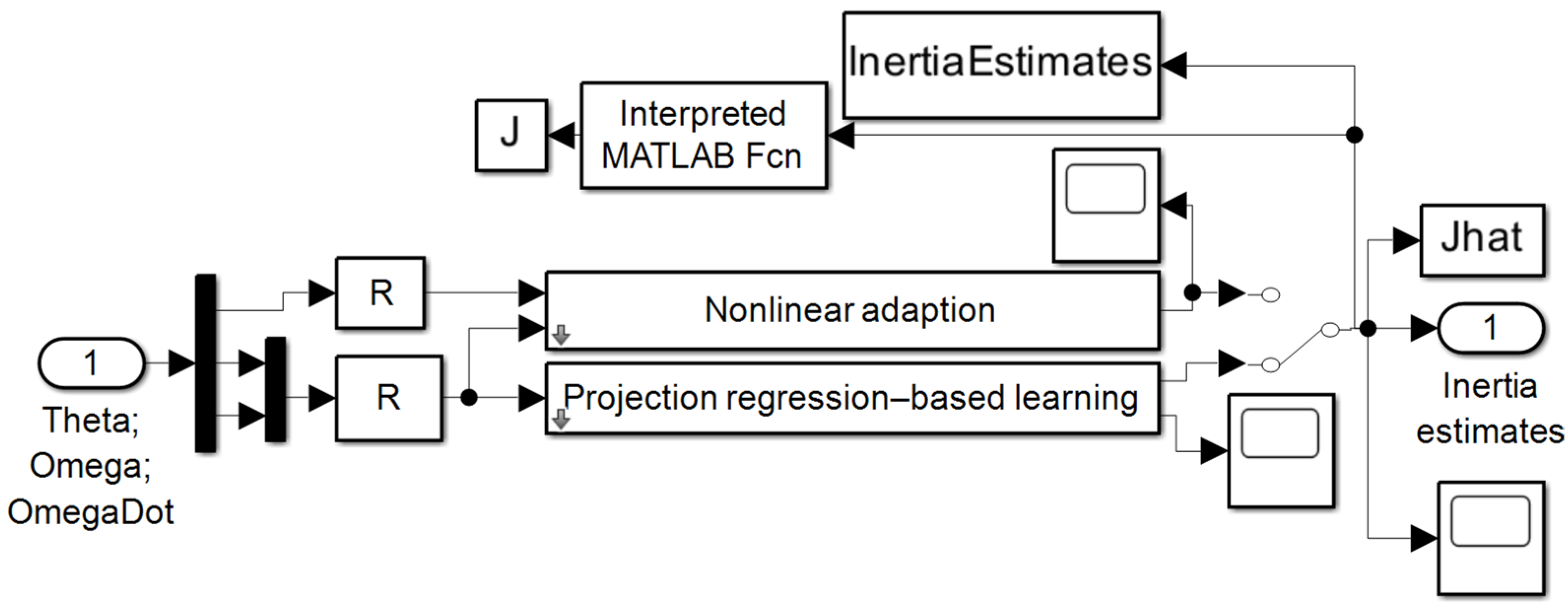
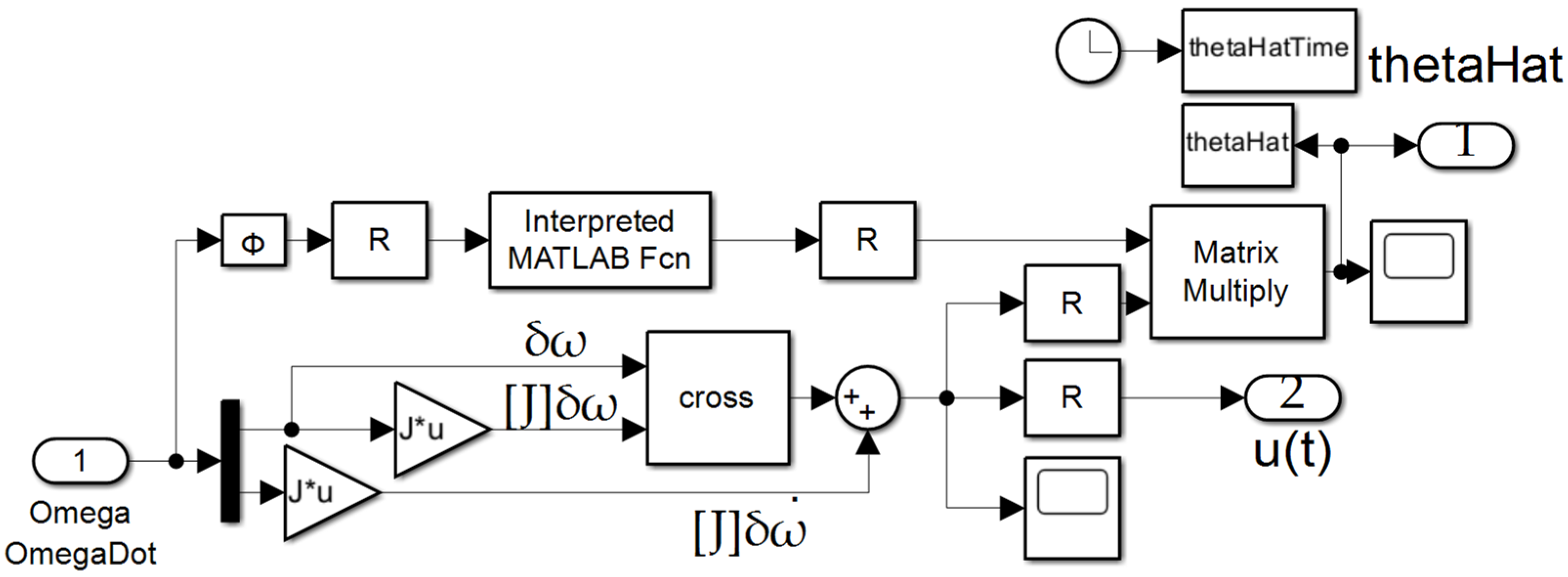
Appendix A.1. Simulink Start Function Callbacks
- clear all; close all; clc;
- Data = readtable(‘Quaternions’); %%% Open angular rate table and separate data into new chacter vectors %%%
- Torques = readtable(‘CommandedWheelTorque’);
- mass = 1; %SV mass in kg
- stoptime = max(size(Data));
- timestep = 1%1/stoptime;
- Time = Data(:,1); time = table2array(Time); [Hour,Minute,Second] = hms(time); [Year,Month,Day] = ymd(time);
- q1 = Data(:,2); q1 = table2array(q1);
- q2 = Data(:,3); q2 = table2array(q2);
- q3 = Data(:,4); q3 = table2array(q3);
- q4 = Data(:,5); q4 = table2array(q4);
- Quaternion = [q1 q2 q3 q4]; dcm = quat2dcm(Quaternion); eulerAngles = quat2eul(Quaternion,’ZYX’);
- roll = eulerAngles(:,1); pitch = eulerAngles(:,2); yaw = eulerAngles(:,3);
- torque1 = Torques(:,2); torque1 = table2array(torque1);
- torque2 = Torques(:,3); torque2 = table2array(torque2);
- torque3 = Torques(:,4); torque3 = table2array(torque3);
- tau1 = regexp(torque1,’\d+(\.)?(\d+)?’,’match’); out = strjoin([tau1{:}],’’);
- tau2 = regexp(torque2,’\d+(\.)?(\d+)?’,’match’); out = strjoin([tau2{:}],’’);
- tau3 = regexp(torque3,’\d+(\.)?(\d+)?’,’match’); out = strjoin([tau3{:}],’’);
- lambda = 10; Eta = 1;
- J = 0.1.*ones(3);
- Ko = [0.01; 0.1; 0.001];
- Ko = [0.01; 0.1; 0.001];
- Kpo = Ko(1); Kdo = Ko(2); Kio = Ko(3);
- %figure(1);
- %subplot(3,1,1); plot(time,torque1,’--‘,’linewidth’,3); grid; %axis([0 5863 -0.75 0.75]);
- % set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24,’xtick’,[]); set(text,’Color’,’k’);
- % ylabel(‘\tau_x’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- % title(‘Quaterions’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- % subplot(3,1,2); plot(time,torque1,’m:‘,’linewidth’,3); grid; %axis([0 5863 -1 0.75]);
- % set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24,’xtick’,[]); set(text,’Color’,’k’);
- % ylabel(‘\tau_y’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- % subplot(3,1,3); plot(time,torque1,’g’,’linewidth’,3); grid; %axis([0 5863 -1 1]);
- % set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24,’xtick’,[]); set(text,’Color’,’k’);
- % ylabel(‘\tau_z’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- % xlabel(‘Clock time’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- figure(2);
- subplot(4,1,1); plot(time,q1,’--‘,’linewidth’,3); grid; %axis([0 5863 -0.75 0.75]);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24,’xtick’,[]); set(text,’Color’,’k’);
- ylabel(‘q_1’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- title(‘Quaterions’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- subplot(4,1,2); plot(time,q2,’m:‘,’linewidth’,3); grid; %axis([0 5863 -1 0.75]);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24,’xtick’,[]); set(text,’Color’,’k’);
- ylabel(‘q_2’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- subplot(4,1,3); plot(time,q3,’g’,’linewidth’,3); grid; %axis([0 5863 -1 1]);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24,’xtick’,[]); set(text,’Color’,’k’);
- ylabel(‘q_3’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- subplot(4,1,4); plot(time,q4,’k-.’,’linewidth’,3); grid; %axis([0 5863 0 0.7]);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- ylabel(‘q_4’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- xlabel(‘Clock time’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- figure(3);
- plot(time,q1,’--b’,’LineWidth’,4); axis tight; hold on;
- plot(time,q2,’m:‘,’LineWidth’,2); axis tight;
- plot(time,q3,’g’,’LineWidth’,3); axis tight;
- plot(time,q4,’k-.’,’LineWidth’,3); axis tight;
- xlabel(‘time’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘Slew maneuver [degrees]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- title(‘Quaternions’,’FontName’,’Palatino Linotype’,’FontSize’,24)
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- legend(‘q_1’,’q_2’,’q_3’,’q_4’, ‘location’,’ North’)
- hold off; grid;
- figure(4);
- plot3(roll, pitch, yaw,’linewidth’,3); grid;
- xlabel(‘Roll’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘Pitch’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- zlabel(‘Yaw’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- title(‘Euler Angles [degrees]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- figure(5);
- plot(time,eulerAngles(:,1),’--b’,’LineWidth’,4); axis tight; hold on;
- plot(time,eulerAngles(:,2),’r’,’LineWidth’,2); axis tight;
- plot(time,eulerAngles(:,3),’:k’,’LineWidth’,3); axis tight;
- xlabel(‘time’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘Slew maneuver [degrees]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- title(‘Slew Maneuver’,’FontName’,’Palatino Linotype’,’FontSize’,24)
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- legend(‘Roll [degrees]’,’Pitch [degrees]’,’Yaw [degrees]’,’location’,’ North’)
- hold off; grid;
- figure(6);
- subplot(3,1,1); plot(time,eulerAngles(:,1),’--b’,’LineWidth’,4); axis tight;
- title(‘Slew Maneuver’,’FontName’,’Palatino Linotype’,’FontSize’,24)
- legend(‘Roll’,’location’,’SouthWest’); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- subplot(3,1,2); plot(time,eulerAngles(:,2),’r’,’LineWidth’,2); axis tight;
- ylabel(‘Angle [degrees]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- legend(‘Pitch’,’location’,’SouthWest’); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- subplot(3,1,3); plot(time,eulerAngles(:,3),’:k’,’LineWidth’,3); axis tight;
- legend(‘Yaw’,’location’,’SouthWest’); grid;
- xlabel(‘time’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
Appendix A.2. Simulink Stop Function Callbacks
- InertiaEstimates = squeeze(InertiaEstimates); InertiaEstimates = InertiaEstimates’;
- Jhat = squeeze(Jhat); Jhat = Jhat’;
- StateEstimates = squeeze(StateEstimates); StateEstimates = StateEstimates’;
- Luen_2 = squeeze(Luen_2); Luen_2 = Luen_2’;
- figure(7);
- thetaHat = squeeze(thetaHat);thetaHat = thetaHat’;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- subplot(2,3,1); plot(tout./15,thetaHat(:,1)); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘J_x_x’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 0 0.152]);
- subplot(2,3,2); plot(tout./15,thetaHat(:,2)); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘J_x_y’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 0 0.152]);
- subplot(2,3,3); plot(tout./15,thetaHat(:,3)); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘J_x_z’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 0 0.152]);
- subplot(2,3,4); plot(tout./15,thetaHat(:,4)); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘J_y_y’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 0 0.152]);
- subplot(2,3,5); plot(tout./15,thetaHat(:,5)); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘J_y_z’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 0 0.152]);
- subplot(2,3,6); plot(tout./15,thetaHat(:,6)); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘J_z_z’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 0 0.152]);
- figure(8);
- plot(tout./15,cg(:,1),’--b’,’LineWidth’,4); axis tight; hold on;
- plot(tout./15,cg(:,2),’r’,’LineWidth’,2); axis tight;
- plot(tout./15,cg(:,3),’:k’,’LineWidth’,3); axis tight;
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- ylabel(‘Coordinates [m]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 0 0.355]);
- title(‘Center of mass location’,’FontName’,’Palatino Linotype’,’FontSize’,24)
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- legend(‘x [m]’,’y [m]’,’z [m]’,’location’,’SouthWest’)
- hold off; grid;
- figure(9);
- title(‘Center of mass location’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- subplot(3,1,1); plot(tout./15,cg(:,1),’--b’,’LineWidth’,4); axis tight; hold on;
- title(‘CG location’,’FontName’,’Palatino Linotype’,’FontSize’,24)
- ylabel(‘x_c_g(t) [m]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- legend(‘x [m]’,’location’,’SouthWest’); grid;
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- %axis([44.45 49.2 0 0.4]);
- subplot(3,1,2); plot(tout./15,cg(:,2),’r’,’LineWidth’,4); axis tight;
- ylabel(‘y_c_g(t) [m]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- legend(‘y [m]’,’location’,’SouthWest’); grid;
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- %axis([44.45 49.2 0 0.4]);
- subplot(3,1,3); plot(tout./15,cg(:,3),’:k’,’LineWidth’,4); axis tight;
- legend(‘z [m]’,’location’,’SouthWest’); grid;
- ylabel(‘z_c_g(t) [m]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- %axis([44.45 49.2 0 0.4]);
- hold off;
- figure(10);
- subplot(3,1,1); plot(tout./15,LuenbergerError(:,1),’--b’,’LineWidth’,4); axis tight; hold on;
- ylabel(‘Roll [degrees]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- legend(‘x [m]’,’location’,’SouthWest’); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- title(‘Luenberger Estimator Errors’,’FontName’,’Palatino Linotype’,’FontSize’,24)
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 -4 4]);
- subplot(3,1,2); plot(tout./15,LuenbergerError(:,2),’r’,’LineWidth’,2); axis tight;
- ylabel(‘Pitch [degrees]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- legend(‘y [m]’,’location’,’SouthWest’); grid;
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 -4 4]);
- subplot(3,1,3); plot(tout./15,LuenbergerError(:,3),’:k’,’LineWidth’,3); axis tight;
- ylabel(‘Roll [degrees]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- legend(‘z [m]’,’location’,’SouthWest’); grid;
- xlabel(‘time’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- set(gca,’FontName’,’Palatino Linotype’,’FontSize’,24); set(text,’Color’,’k’);
- xlabel(‘time [seconds]’,’FontName’,’Palatino Linotype’,’FontSize’,24);
- %axis([44.45 49.2 -4 4]);
- hold off;
Appendix B
| Variable/Acronym | Definition |
|---|---|
| Centroidal angular momentum | |
| Radius vector to differential mass, | |
| Differential mass, | |
| Angular velocity vector | |
| Angular velocity [radians/second] | |
| Unit vectors | |
| Positional coordinates | |
| Inertia moment about a fixed axis along | |
| Inertia moment about the mass center | |
| Total system mass | |
| Distance from O to the mass center | |
| Distance to axis | |
| Fixed axis along axis | |
| Dummy variables | |
| Radius vector to point | |
| Differential mass | |
| Velocity vector of differential mass, | |
| Moments of inertia | |
| Products of inertia | |
| [] | Moment of inertia matrix |
| Robot arm base parallel axis | |
| Body center parallel axis | |
| Radius from parallel axis (not mass center) | |
| Radius vector to the mass center | |
| Differential mass element | |
| ( | Center of mass coordinates |
| coordinate of | |
| coordinate of | |
| Desired angular state vector | |
| Desired angular velocity vector | |
| Desired angular acceleration vector | |
| Feedback control | |
| Proportional gain | |
| Angular state vector | |
| Angular velocity vector | |
| Angular acceleration vector | |
| Integral gain | |
| Derivative gain |
References
- SDA Gets OK to Begin Limited Testing of Data Satellites Link 16 Nodes. Available online: https://www.sda.mil/sda-gets-ok-to-begin-limited-testing-of-data-satellites-link-16-nodes/ (accessed on 16 December 2024).
- Department of Defense Photographs and Imagery, Unless Otherwise Noted, Are in the Public Domain. Use of Department of Defense Imagery. Available online: https://www.defense.gov/Contact/Help-Center/Article/Article/2762906/use-of-department-of-defense-imagery/ (accessed on 16 December 2024).
- Nanosats Database: XVI Satellite. Available online: https://www.nanosats.eu/sat/xvi (accessed on 16 December 2024).
- Available online: https://www.usna.edu/Users/aero/kang/Research.php#panel3RSatPRoboticArmSatellitePrototype (accessed on 4 February 2025).
- Wei, X.; Huang, L.; Shen, T.; Cai, Z. Calibration of the in-orbit center-of-mass of TaiJi-1. arXiv 2024, arXiv:2307.01724v2. [Google Scholar] [CrossRef]
- Otsubo, T.; Appleby, G. System-dependent center-of-mass correction for spherical geodetic satellites. J. Geophys. Res. 2003, 108, 2201. [Google Scholar] [CrossRef]
- Rodríguez, J.; Appleby, G.; Otsubo, T. Upgraded modelling for the determination of centre of mass corrections of geodetic SLR satellites: Impact on key parameters of the terrestrial reference frame. J. Geod. 2019, 93, 2553–2568. [Google Scholar] [CrossRef]
- Rodríguez, J. Centre of Mass Corrections Updates for Geodetic Spherical Satellites: Changes in the Latest Releases in Preparation for the Computation of ITRF2020 Products; Technical Report IT-CDT 2022-11; Yebes Observatory: Yebes, Spain, 22 November 2022. [Google Scholar]
- Geosat: U.S. Navy GEOdetic SATellite. Available online: https://science.nasa.gov/mission/geosat/ (accessed on 16 December 2024).
- NASA Images and Media Usage Guidelines. Available online: https://www.nasa.gov/nasa-brand-center/images-and-media/ (accessed on 16 December 2024).
- Neubert, R. The Retro-Reflector for the CHAMP Satellite: Final Design and Realization. In Proceedings of the 11th International Laser Ranging Workshop, Deggendorf, Germany, 21–25 September 1988. [Google Scholar]
- International Laser Ranging Service: Etalon-1 and -2: Array Offset Information. Available online: https://ilrs.gsfc.nasa.gov/missions/satellite_missions/current_missions/eta1_com.html (accessed on 16 December 2024).
- International Laser Ranging Service: Galileo: Array Offset Information. Available online: https://ilrs.gsfc.nasa.gov/missions/satellite_missions/current_missions/ga01_com.html (accessed on 16 December 2024).
- Lemoine, F.; Rowlands, D.; Lillibridge, J.; Smith, W.; Zelensky, N.; Beckley, B.; Chinn, D.; Scharroo, R. Evaluation of the GEOSAT and GEOSAT Follow-On Precise Orbit Ephemeris. In Proceedings of the 2007 Ocean Surface Topography Science Team Meeting, Hobart, Australia, 12–15 March 2007; Available online: https://www.aviso.altimetry.fr/fileadmin/documents/OSTST/2007/lemoine_gfo_pod.pdf (accessed on 16 December 2024).
- Hernández-Arias, H.; Prado-Molina, J. On-Orbit Center Of Mass Relocation System For a 3U Cubesat. Int. J. Sci. Technol. Res. 2018, 7, 44–51. [Google Scholar]
- Alharam, A.; Albalooshi, A.; Sleptchenko, A. Linear cubesat center of gravity optimization. In Proceedings of the AerospaceEurop Confrence 2021, Warsaw, Poland, 23–26 November 2021. [Google Scholar]
- Al-Rawashdeh, Y.M.; Elshafei, M.; Al-Malki, M.F. In-Flight Estimation of Center of Gravity Position Using All-Accelerometers. Sensors 2014, 14, 17567–17585. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Xiao, W. Uncertainty Analysis of Aircraft Center of Gravity Deviation and Passenger Seat Allocation Optimization. Mathematics 2024, 12, 1591. [Google Scholar] [CrossRef]
- Wu, F.; Sun, C.; Li, H.; Zheng, S. Real-Time Center of Gravity Estimation for Intelligent Connected Vehicle Based on HEKF-EKF. Electronics 2023, 12, 386. [Google Scholar] [CrossRef]
- Park, G.; Choi, S.B. An Integrated Observer for Real-Time Estimation of Vehicle Center of Gravity Height. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5660–5671. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J. Real-Time Estimation of Center of Gravity Position for Lightweight Vehicles Using Combined AKF–EKF Method. IEEE Trans. Veh. Technol. 2014, 63, 4221–4231. [Google Scholar] [CrossRef]
- Lin, C.; Gong, X.; Xiong, R.; Cheng, X. A novel H∞ and EKF joint estimation method for determining the center of gravity position of electric vehicles. Appl. Energy 2017, 194, 609–616. [Google Scholar] [CrossRef]
- Fu, Z.; Hu, Q.; Li, B. Adaptive online estimation of centre of gravity height for commercial vehicles. Int. J. Heavy Veh. Syst. 2021, 28, 206–225. [Google Scholar] [CrossRef]
- Han, X.; Li, Z.; Li, H.; Huang, L.; Pang, Y. Variable mass control and parameter identification of spacecraft orbit refueling process. Math. Prob. Eng. 2022, 17, 9660218. [Google Scholar] [CrossRef]
- Gaine Technology. Probabilistic and Deterministic Results in AI Systems. 31 July 2023. Available online: https://www.gaine.com/blog/probabilistic-and-deterministic-results-in-ai-systems (accessed on 11 March 2024).
- Holubek, R.; Vagaš, M. Center of Gravity Coordinates Estimation Based on an Overall Brightness Average Determined from the 3D Vision System. Appl. Sci. 2022, 12, 286. [Google Scholar] [CrossRef]
- Moulton, B.C.; Hunsaker, D.F. Analytic Solutions for Volume, Mass, Center of Gravity, and Inertia of Wing Segments and Rotors of Constant Density. Aerospace 2024, 11, 492. [Google Scholar] [CrossRef]
- Liu, F.; Su, Z.; Zhao, H.; Li, Q.; Li, C. Attitude Measurement for High-Spinning Projectile with a Hollow MEMS IMU Consisting of Multiple Accelerometers and Gyros. Sensors 2019, 19, 1799. [Google Scholar] [CrossRef] [PubMed]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Spacecraft fine tracking pointing using adaptive control. In Proceedings of the 58th International Astronautical Congress, Hyderabad, India, 24–28 September 2007. [Google Scholar]
- Sands, T. Autonomous Real–Time Mass Center Location and Inertia Identification for Grappling Space Robotics. Technologies 2025, 13, 148. [Google Scholar] [CrossRef]
- Adams, G. Arizona State University Physics Department Proof of the Parallel Axis Theorem. Available online: https://www.public.asu.edu/~gbadams/sum00/parallelaxisT.pdf (accessed on 16 December 2024).
- SatCatalog. Available online: https://www.satcatalog.com/component/rwp050/ (accessed on 16 December 2024).
- Foust, J. SpaceX Launches Eighth Dedicated Smallsat Rideshare Mission. Available online: https://spacenews.com/spacex-launches-eighth-dedicated-smallsat-rideshare-mission/ (accessed on 11 March 2025).
- Alessia Nocerino, A.; Opromolla, R.; Fasano, G.; Grassi, M.; Balaguer, P.; John, S.; Cho, H.; Bevilacqua, R. Experimental validation of inertia parameters and attitude estimation of uncooperative space targets using solid state LIDAR. Acta Astronaut. 2023, 210, 428–436. [Google Scholar] [CrossRef]
- Gupta, D.; Kumar, A.; Giri, V. Effect of adaptation gain and reference model in MIT and Lyapunov rule–based model reference adaptive control for first- and second-order systems. Trans. Inst. Meas. Control 2024, 46, 1635–1654. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McLeland, L.; Erickson, B.; Ruchlin, B.; Daman, E.; Mejia, J.; Ho, B.; Lewis, J.; Mann, B.; Paw, C.; Ross, J.; et al. Center of Mass Auto-Location in Space. Technologies 2025, 13, 246. https://doi.org/10.3390/technologies13060246
McLeland L, Erickson B, Ruchlin B, Daman E, Mejia J, Ho B, Lewis J, Mann B, Paw C, Ross J, et al. Center of Mass Auto-Location in Space. Technologies. 2025; 13(6):246. https://doi.org/10.3390/technologies13060246
Chicago/Turabian StyleMcLeland, Lucas, Brian Erickson, Brendan Ruchlin, Eryn Daman, James Mejia, Benjamin Ho, Joshua Lewis, Bryan Mann, Connor Paw, James Ross, and et al. 2025. "Center of Mass Auto-Location in Space" Technologies 13, no. 6: 246. https://doi.org/10.3390/technologies13060246
APA StyleMcLeland, L., Erickson, B., Ruchlin, B., Daman, E., Mejia, J., Ho, B., Lewis, J., Mann, B., Paw, C., Ross, J., Reis, C., Walter, S., Coward, S., Post, T., Freeborn, A., & Sands, T. (2025). Center of Mass Auto-Location in Space. Technologies, 13(6), 246. https://doi.org/10.3390/technologies13060246







