A Novel Framework for Co-Expansion Planning of Transmission Lines and Energy Storage Devices Considering Unit Commitment
Abstract
1. Introduction
Literature Review
2. Contributions
- Formulate a stochastic optimization model for the co-expansion planning of transmission lines and energy storage devices.
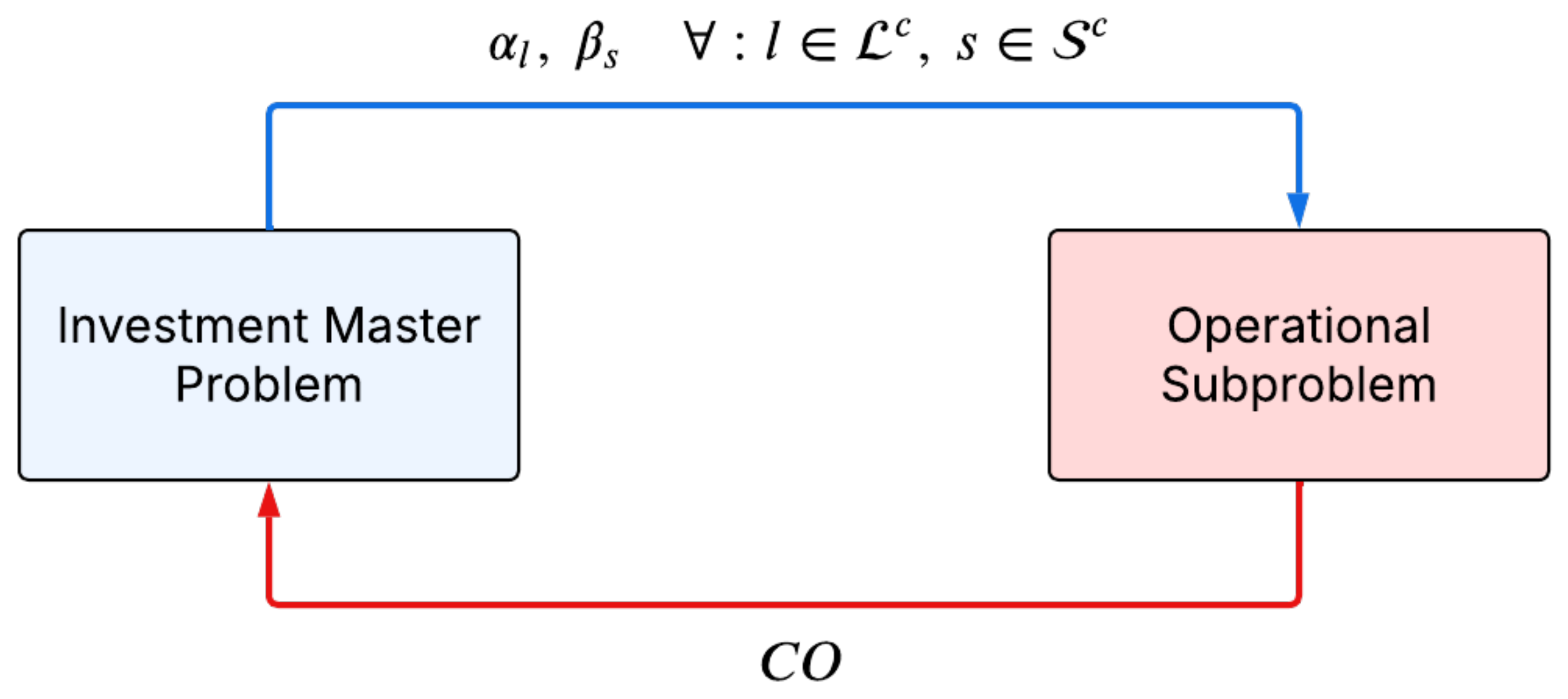
- Propose a solution strategy to address the problem, which involves decomposing the problem into a master problem and a subproblem.
3. Problem Formulation
3.1. Objective Function
3.2. Constraints
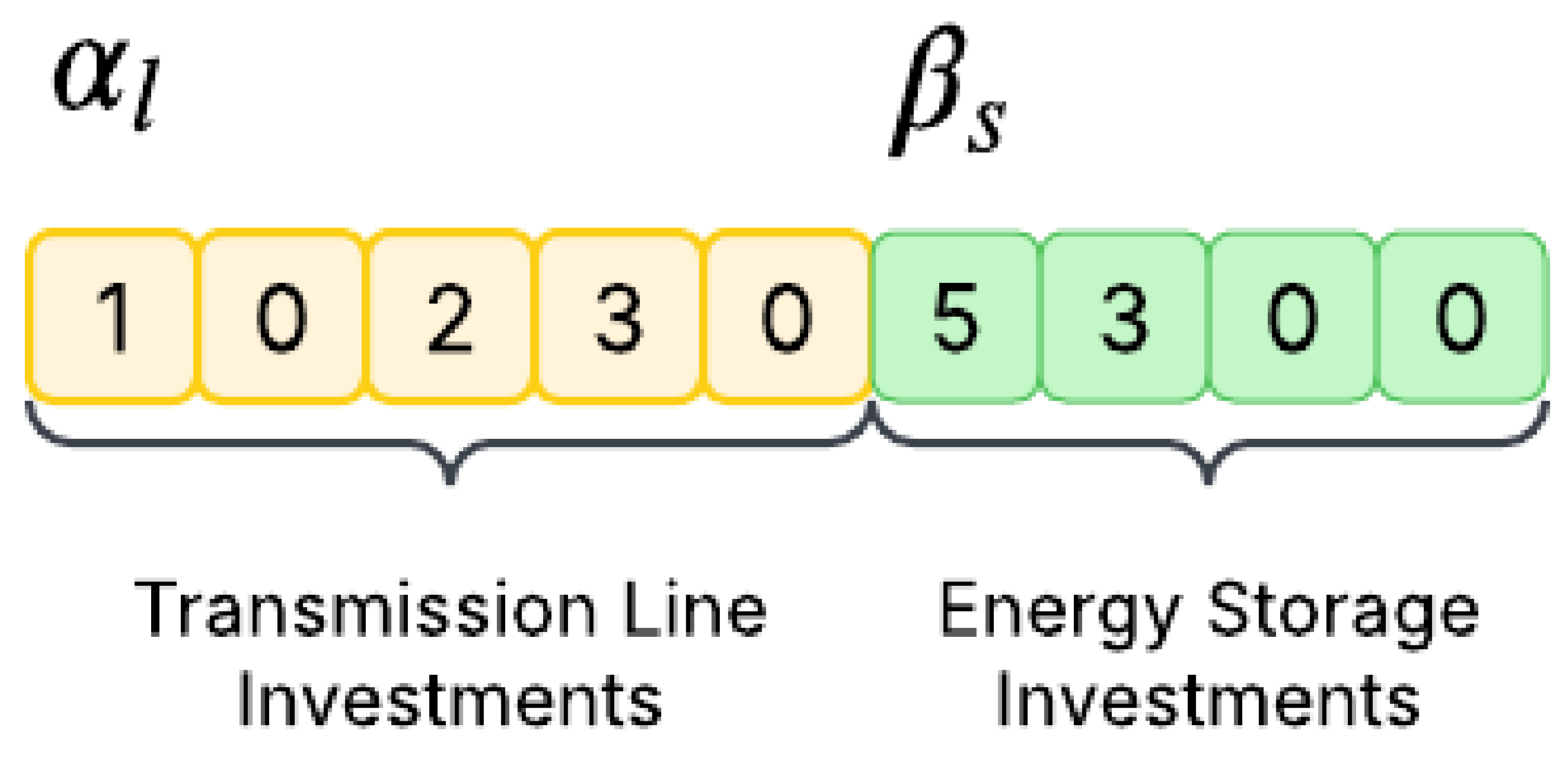
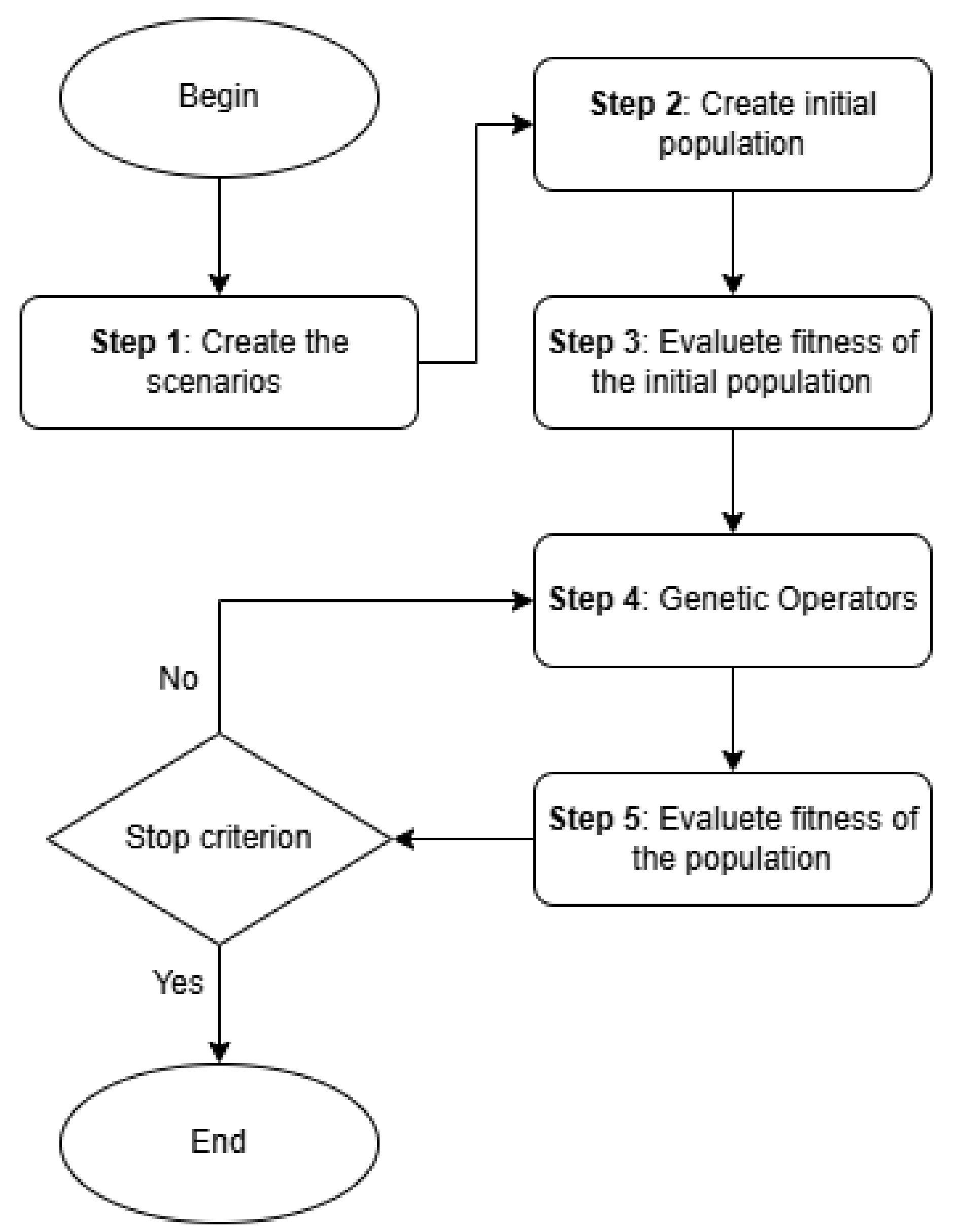
4. Solution Strategy
4.1. Investment Master Problem
4.2. Operational Subproblem
5. Simulations
- Case A: Investments in transmission line.
- Case B: Investments in transmission line and energy storage device.
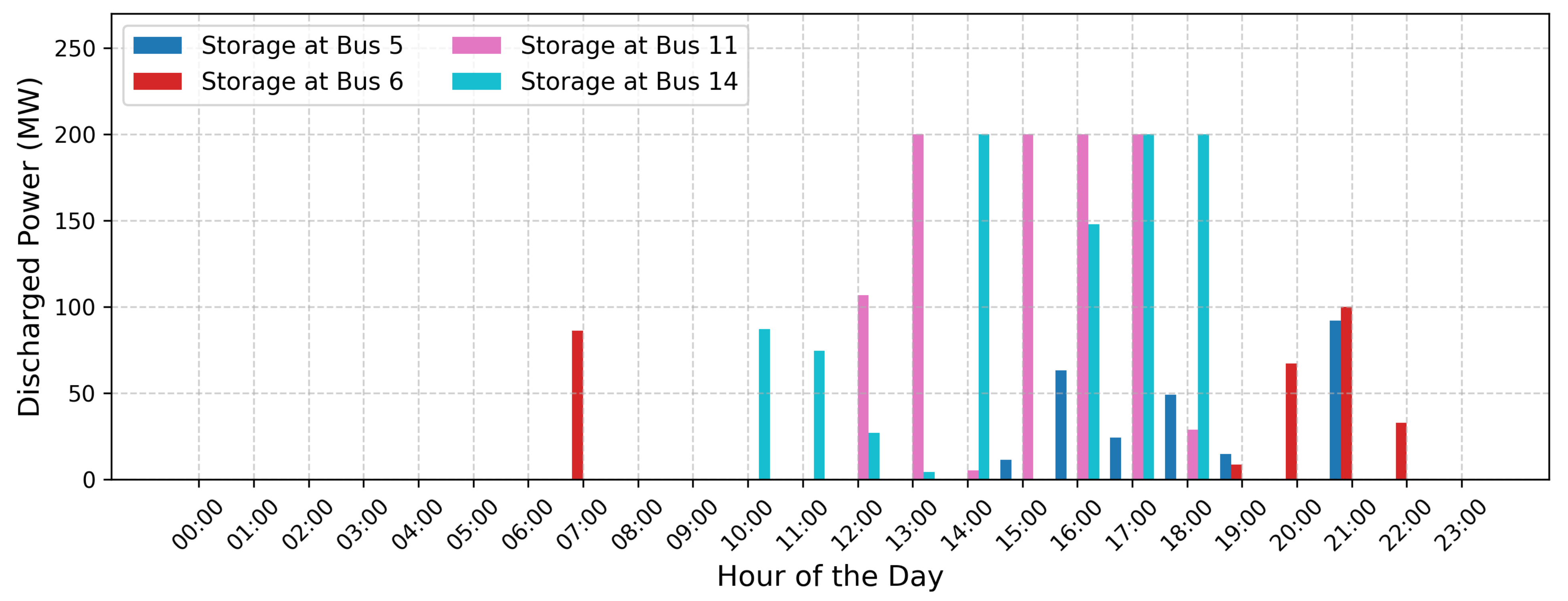
Results
6. Conclusions
Future Work
- Integration of hydroelectric power plants, introducing long-term storage capabilities and seasonal planning aspects;
- Expansion of the formulation to include AC power flow constraints, improving the electrical accuracy of the model;
- Application of the methodology to larger test systems, allowing for evaluation of scalability and computational performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| g | Index of generating units |
| h | Index of time periods |
| Index of scenarios or phases | |
| Indexes of buses | |
| l | Index of transmission lines |
| s | Index of storage units |
| w | Index of wind units |
| Set of generating units | |
| Set of time periods | |
| Set of scenarios or phases | |
| Set of buses | |
| Set of existing transmission lines | |
| Set of candidate transmission lines | |
| Set of storage units | |
| Set of existing storage units | |
| Set of candidate storage units | |
| Set of wind units | |
| Minimum power output of thermal unit g | |
| Maximum power output of thermal unit g | |
| Ramp-up limit of thermal unit g | |
| Ramp-down limit of thermal unit g | |
| Startup ramp limit of thermal unit g | |
| Shutdown ramp limit of thermal unit g | |
| Minimum up-time of thermal unit g | |
| Minimum down-time of thermal unit g | |
| Number of initial periods thermal unit g must be online | |
| Number of initial periods thermal unit g must be offline | |
| T | Total number of time periods |
| Load demand at bus i in period h and scenario | |
| Maximum power flow limit of transmission line l | |
| Reactance of transmission line l | |
| Maximum bus angle limit | |
| Minimum state of charge (SOC) of storage unit s | |
| Maximum state of charge (SOC) of storage unit s | |
| Minimum discharge power of storage unit s | |
| Maximum discharge power of storage unit s | |
| Minimum charge power of storage unit s | |
| Maximum charge power of storage unit s | |
| Discharge efficiency of storage unit s | |
| Charge efficiency of storage unit s | |
| Available wind power of wind unit w in period h and scenario | |
| Investment cost of transmission line l | |
| Energy component of the investment cost for storage unit s | |
| Power component of the investment cost for storage unit s | |
| r | Discount rate |
| Lifetime of transmission line l | |
| Lifetime of storage unit s | |
| Fixed cost of operating thermal unit g (USD) | |
| Variable cost of operating thermal unit g (USD/MW) | |
| Operational cost of storage units (USD/MW) | |
| Curtailment cost of wind generation (USD/MWh) | |
| Weight of scenario | |
| Binary variable indicating if thermal unit g is online (1) or offline (0) in period h and scenario | |
| Power output of thermal unit g in period h and scenario | |
| Maximum available power output of thermal unit g in period h and scenario | |
| Power flow in transmission line l in period h and scenario | |
| Voltage angle at bus i in period h and scenario | |
| State of charge (SOC) of storage unit s in period h and scenario | |
| Discharge power of storage unit s in period h and scenario | |
| Charge power of storage unit s in period h and scenario | |
| Curtailed wind power of wind unit w in period h and scenario | |
| Binary variable indicating if candidate transmission line l is built | |
| Binary variable indicating if candidate storage unit s is built | |
| TNEP | Transmission Network Expansion Planning |
| ESS | Energy Storage System |
| CETES | Co-expansion planning of transmission lines and energy storage devices |
| UC | Unit Commitment |
| GESS | Generic Energy Storage System |
| BESS | Battery Energy Storage System |
| CAES | Compressed Air Energy Storage |
| PHES | Pumped Hydro Energy Storage |
| MILP | Mixed-Integer Linear Programming |
| CCG | Column-and-Constraint Generation |
| GA | Genetic Algorithm |
References
- Hu, Z.; Zhang, F.; Li, B. Transmission expansion planning considering the deployment of energy storage systems. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Zhang, F.; Hu, Z.; Song, Y. Mixed-integer linear model for transmission expansion planning with line losses and energy storage systems. IET Gener. Transm. Distrib. 2013, 7, 919–928. [Google Scholar] [CrossRef]
- Hedayati, M.; Zhang, J.; Hedman, K.W. Joint transmission expansion planning and energy storage placement in smart grid towards efficient integration of renewable energy. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar]
- MacRae, C.; Ernst, A.; Ozlen, M. A Benders decomposition approach to transmission expansion planning considering energy storage. Energy 2016, 112, 795–803. [Google Scholar] [CrossRef]
- Qiu, T.; Xu, B.; Wang, Y.; Dvorkin, Y.; Kirschen, D.S. Stochastic multistage coplanning of transmission expansion and energy storage. IEEE Trans. Power Syst. 2016, 32, 643–651. [Google Scholar] [CrossRef]
- Falugi, P.; Konstantelos, I.; Strbac, G. Planning with multiple transmission and storage investment options under uncertainty: A nested decomposition approach. IEEE Trans. Power Syst. 2017, 33, 3559–3572. [Google Scholar] [CrossRef]
- Aguado, J.; de La Torre, S.; Triviño, A. Battery energy storage systems in transmission network expansion planning. Electr. Power Syst. Res. 2017, 145, 63–72. [Google Scholar] [CrossRef]
- Dvorkin, Y.; Fernández-Blanco, R.; Wang, Y.; Xu, B.; Kirschen, D.S.; Pandžić, H.; Watson, J.P.; Silva-Monroy, C.A. Co-planning of investments in transmission and merchant energy storage. IEEE Trans. Power Syst. 2017, 33, 245–256. [Google Scholar] [CrossRef]
- Zhang, X.; Conejo, A.J. Coordinated investment in transmission and storage systems representing long-and short-term uncertainty. IEEE Trans. Power Syst. 2018, 33, 7143–7151. [Google Scholar] [CrossRef]
- Nikoobakht, A.; Aghaei, J. Integrated transmission and storage systems investment planning hosting wind power generation: Continuous-time hybrid stochastic/robust optimisation. IET Gener. Transm. Distrib. 2019, 13, 4870–4879. [Google Scholar] [CrossRef]
- Wang, S.; Geng, G.; Jiang, Q. Robust co-planning of energy storage and transmission line with mixed integer recourse. IEEE Trans. Power Syst. 2019, 34, 4728–4738. [Google Scholar] [CrossRef]
- Gan, W.; Ai, X.; Fang, J.; Yan, M.; Yao, W.; Zuo, W.; Wen, J. Security constrained co-planning of transmission expansion and energy storage. Appl. Energy 2019, 239, 383–394. [Google Scholar] [CrossRef]
- Luburić, Z.; Pandžić, H.; Carrión, M. Transmission expansion planning model considering battery energy storage, TCSC and lines using AC OPF. IEEE Access 2020, 8, 203429–203439. [Google Scholar] [CrossRef]
- Mazaheri, H.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Farzin, H.; Wang, F.; Dehghanian, P. An online method for MILP co-planning model of large-scale transmission expansion planning and energy storage systems considering N-1 criterion. IET Gener. Transm. Distrib. 2021, 15, 664–677. [Google Scholar] [CrossRef]
- de Oliveira, E.J.; de Paula, A.N.; de Oliveira, L.W.; Honório, L.d.M. Block-Based Multicut Benders Decomposition Algorithm for Transmission and Energy Storage Co-Planning. Int. Trans. Electr. Energy Syst. 2022, 2022. [Google Scholar] [CrossRef]
- Carrión, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Dillon, T.S.; Edwin, K.W.; Kochs, H.D.; Taud, R. Integer programming approach to the problem of optimal unit commitment with probabilistic reserve determination. IEEE Trans. Power Appar. Syst. 1978, PAS-97, 2154–2166. [Google Scholar] [CrossRef]
- Arroyo, J.M.; Conejo, A.J. Optimal response of a thermal unit to an electricity spot market. IEEE Trans. Power Syst. 2000, 15, 1098–1104. [Google Scholar] [CrossRef]
- Morales-España, G.; Latorre, J.M.; Ramos, A. Tight and compact MILP formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2013, 28, 4897–4908. [Google Scholar] [CrossRef]
- Subcommittee, P.M. IEEE reliability test system. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 2047–2054. [Google Scholar] [CrossRef]
- Ordoudis, C.; Pinson, P.; Morales, J.M.; Zugno, M. An Updated Version of the IEEE RTS 24-Bus System for Electricity Market and Power System Operation Studies; Technical University of Denmark: Kongens Lyngby, Denmark, 2016; Volume 13. [Google Scholar]
- de Paula, A.N.; de Oliveira, E.J.; de Oliveira, L.W.; Honório, L.M. Robust static transmission expansion planning considering contingency and wind power generation. J. Control Autom. Electr. Syst. 2020, 31, 461–470. [Google Scholar] [CrossRef]
- Fernández-Blanco, R.; Dvorkin, Y.; Xu, B.; Wang, Y.; Kirschen, D.S. Optimal energy storage siting and sizing: A WECC case study. IEEE Trans. Sustain. Energy 2016, 8, 733–743. [Google Scholar] [CrossRef]
- Merrick, J.H. On representation of temporal variability in electricity capacity planning models. Energy Econ. 2016, 59, 261–274. [Google Scholar] [CrossRef]
- Nepomuce, L.; de Oliveira, E.; de Oliveira, L.; de Paula, A. Data for paper: A Novel Framework for Co-Expansion Planning of Transmission Lines and Energy Storage Devices Considering Unit Commitment. 2025. Available online: https://drive.google.com/drive/folders/1jJZeTsX8kTKbMI_zjHbBncBdxizD9wer?usp=drive_link (accessed on 21 May 2025).
| Reference | Uncertainties | Planning Horizon | UC | Network Representation | Storage Investment | Technology | Sistema | Model |
|---|---|---|---|---|---|---|---|---|
| [1] | No | S | No | Lossless DC | B | GESS | Garver 6-bus IEEE 24-bus Brazil 46-bus | MILP Solver |
| [2] | No | S | No | DC | B | GESS | Garver 6-bus IEEE 24-bus | MILP Solver |
| [3] | No | D | No | Lossless DC | B | BESS | Roy Billinton 6-bus IEEE 24-bus | MILP Solver |
| [4] | No | S | No | Lossless DC | C | GESS | Garver 6-bus IEEE 24-bus Brazil 46-bus | Benders Decomposition |
| [5] | Yes | D | Yes | Lossless DC | C | BESS | IEEE 24-bus IEEE 118-bus | MILP Solver |
| [6] | No | D | No | Lossless DC | B | BESS CAES PHES | IEEE 118-bus | Nested Benders Decomposition |
| [7] | Yes | S | No | DC | B | BESS | Garver 6-bus IEEE 24-bus | MILP Solver |
| [8] | Yes | S | No | Lossless DC | C | BESS | WECC system 240-bus | CCG |
| [9] | Yes | S | No | Lossless DC | B | GESS | IEEE 24-bus | Benders Decomposition |
| [10] | Yes | S | No | Lossless DC | B | GESS | IEEE 24-bus | Benders Decomposition |
| [10] | Yes | S | No | Lossless DC | B | GESS | IEEE 24-bus | Benders Decomposition |
| [11] | Yes | S | No | Lossless DC | C | BESS | Garver 6-bus Chinese 196-bus | CCG |
| [12] | Yes | D | No | Lossless DC | B | BESS PHES | Garver 6-bus Gansu-53 bus | Benders Decomposition |
| [13] | No | S | No | AC | C | BESS | IEEE 24-bus | Benders Decomposition |
| [14] | No | S | No | Lossless DC | B | CAES | Garver 6-bus IEEE 24-bus | MILP Solver |
| [15] | Yes | S | No | Lossless DC | B | BESS | Garver 6-bus IEEE 24-bus IEEE 118-bus | Benders Decomposition |
| This Work | Yes | S | Yes | Lossless DC | B | GESS | IEEE 24-bus | Decomposition GA MILP Solver |
| Unit | Bus | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 152.00 | 30.40 | 120.00 | 120.00 | 8 | 4 | 76.00 | 1 | 22 | 0 | 0.01 | 13.32 | 108.00 | 1430.40 | 715.20 | 152.00 | 152.00 |
| 2 | 2 | 152.00 | 30.40 | 120.00 | 120.00 | 8 | 4 | 76.00 | 1 | 22 | 0 | 0.07 | 13.32 | 108.00 | 1430.40 | 715.20 | 152.00 | 152.00 |
| 3 | 7 | 350.00 | 75.00 | 350.00 | 350.00 | 8 | 8 | 0.00 | 0 | 0 | 2 | 0.00 | 20.70 | 118.00 | 1725.00 | 862.50 | 300.00 | 300.00 |
| 4 | 13 | 591.00 | 206.85 | 240.00 | 240.00 | 12 | 10 | 0.00 | 0 | 0 | 1 | 0.01 | 20.93 | 94.00 | 3056.70 | 1528.35 | 591.00 | 591.00 |
| 5 | 15 | 60.00 | 12.00 | 60.00 | 60.00 | 4 | 2 | 0.00 | 0 | 0 | 1 | 0.03 | 26.11 | 84.00 | 437.00 | 218.50 | 60.00 | 60.00 |
| 6 | 15 | 155.00 | 54.25 | 155.00 | 155.00 | 8 | 8 | 0.00 | 0 | 0 | 2 | 0.01 | 10.52 | 118.00 | 312.00 | 156.00 | 89.20 | 89.20 |
| 7 | 16 | 155.00 | 54.25 | 155.00 | 155.00 | 8 | 8 | 124.00 | 1 | 10 | 0 | 0.01 | 10.52 | 118.00 | 312.00 | 156.00 | 89.20 | 89.20 |
| 8 | 18 | 400.00 | 100.00 | 280.00 | 280.00 | 1 | 1 | 240.00 | 1 | 50 | 0 | 0.03 | 6.02 | 177.00 | 0.00 | 0.00 | 240.00 | 240.00 |
| 9 | 21 | 400.00 | 100.00 | 280.00 | 280.00 | 1 | 1 | 240.00 | 1 | 16 | 0 | 0.03 | 5.47 | 177.00 | 0.00 | 0.00 | 240.00 | 240.00 |
| 10 | 22 | 300.00 | 300.00 | 300.00 | 300.00 | 1 | 1 | 240.00 | 1 | 24 | 0 | 0.01 | 2.00 | 177.00 | 0.00 | 0.00 | 300.00 | 300.00 |
| 11 | 23 | 310.00 | 108.50 | 180.00 | 180.00 | 8 | 8 | 248.00 | 1 | 10 | 0 | 0.01 | 10.52 | 118.00 | 624.00 | 312.00 | 178.50 | 178.50 |
| 12 | 23 | 350.00 | 140.00 | 240.00 | 240.00 | 8 | 8 | 280.00 | 1 | 50 | 0 | 0.01 | 10.89 | 118.00 | 2298.00 | 1149.00 | 210.00 | 210.0 |
| Parameters | Value |
|---|---|
| Number of chromosomes | 20 |
| Maximum number of iterations | 50 |
| Crossover rate | 0.7 |
| Mutation rate | 0.3 |
| Number of tournament participants | 4 |
| Size of the elite set | 2 |
| Case | Total Investment Cost in Lines (USD/M) | Total Investment Cost in Storage (USD/M) | Annual Operational Cost (USD/M) | Transmission Expansion | Storage Expansion |
|---|---|---|---|---|---|
| A | 1494.0 | - | 42,702.86 | 1–5 (2), 2–6, 3–9, 4–9, 6–10, 7–8, 9–11 (2), 9–12, 11–14 (2), 12–13 (2), 12–23, 14–16, 15–16, 16–17, 17–22 (2), 18–21, 20–23, 1–8 (2), 6–7 (3), 14–23 | – |
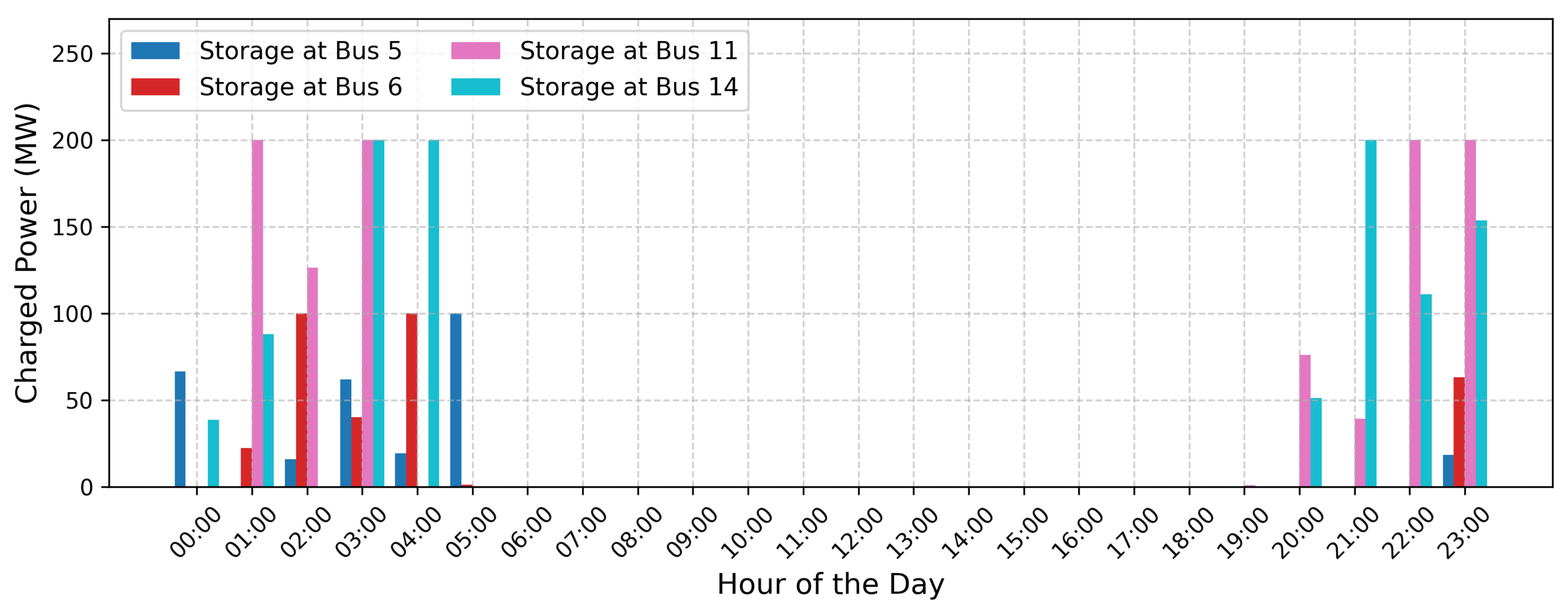
| B | 1193.00 | 81.60 | 31,520.56 | 1–5 (2), 2–6, 3–9, 3–24, 4–9, 5–10, 6–10, 7–8 (2), 8–9, 9–11, 10–11, 11–14, 12–23, 14–16, 15–21, 15–24, 16–17, 17–18, 17–22, 20–23, 1–8 (2), 13–14, 14–23 (2) | 5 (1), 6 (1), 11 (2), 14 (2) |
| Case | Stochastic Thermal Generation (MWh) | Stochastic Energy Charged (MWh) | Stochastic Energy Discharged (MWh) | Stochastic Wind Curtailment (MWh) |
|---|---|---|---|---|
| A | 43,171.06 | - | - | 391.72 |
| B | 43,083.81 | 2800.79 | 2527.72 | 31.40 |
| Hour | Power Generation of Units (MW) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 197.67 | 30.40 | 0 | 0 | 0 | 0 | 54.25 | 0 | 101.25 | 600.00 | 108.50 | 140.00 |
| 2 | 133.19 | 30.40 | 0 | 0 | 0 | 0 | 54.25 | 0 | 102.57 | 600.00 | 0 | 140.00 |
| 3 | 90.44 | 30.40 | 0 | 0 | 0 | 0 | 100.40 | 0 | 0 | 600.00 | 0 | 140.00 |
| 4 | 74.42 | 30.40 | 0 | 0 | 0 | 0 | 94.68 | 0 | 0 | 600.00 | 0 | 140.00 |
| 5 | 77.64 | 30.40 | 0 | 0 | 0 | 0 | 54.25 | 0 | 100.00 | 572.26 | 0 | 140.00 |
| 6 | 112.00 | 30.40 | 0 | 0 | 0 | 0 | 54.25 | 172.21 | 0 | 600.00 | 0 | 140.00 |
| 7 | 290.92 | 59.88 | 0 | 0 | 0 | 0 | 54.25 | 479.54 | 0 | 600.00 | 0 | 169.49 |
| 8 | 304.00 | 216.76 | 0 | 0 | 0 | 0 | 54.25 | 548.09 | 0 | 600.00 | 0 | 363.13 |
| 9 | 304.00 | 278.27 | 75.00 | 0 | 0 | 0 | 54.25 | 593.20 | 0 | 600.00 | 0 | 543.89 |
| 10 | 304.00 | 286.44 | 125.64 | 0 | 0 | 0 | 58.51 | 635.42 | 0 | 600.00 | 0 | 629.94 |
| 11 | 304.00 | 291.65 | 183.89 | 0 | 0 | 0 | 83.65 | 666.23 | 0 | 600.00 | 0 | 656.30 |
| 12 | 304.00 | 293.57 | 205.36 | 0 | 0 | 0 | 92.39 | 686.24 | 0 | 600.00 | 0 | 680.72 |
| 13 | 304.00 | 297.49 | 249.21 | 0 | 0 | 0 | 112.70 | 698.56 | 0 | 600.00 | 0 | 691.21 |
| 14 | 304.00 | 301.18 | 290.40 | 0 | 0 | 0 | 132.23 | 706.28 | 0 | 600.00 | 0 | 693.36 |
| 15 | 304.00 | 300.87 | 286.99 | 0 | 0 | 0 | 130.90 | 701.81 | 0 | 600.00 | 0 | 687.63 |
| 16 | 304.00 | 303.12 | 312.10 | 0 | 0 | 0 | 143.34 | 700.74 | 0 | 600.00 | 0 | 684.49 |
| 17 | 304.00 | 265.65 | 499.92 | 0 | 0 | 0 | 201.23 | 710.52 | 0 | 600.00 | 0 | 682.46 |
| 18 | 304.00 | 248.98 | 544.69 | 0 | 0 | 0 | 211.25 | 700.82 | 0 | 600.00 | 0 | 666.64 |
| 19 | 304.00 | 250.80 | 539.80 | 0 | 0 | 0 | 214.74 | 647.02 | 0 | 600.00 | 0 | 595.51 |
| 20 | 304.00 | 304.00 | 354.63 | 0 | 0 | 0 | 173.22 | 572.58 | 0 | 600.00 | 0 | 510.10 |
| 21 | 304.00 | 296.48 | 236.69 | 0 | 0 | 0 | 89.20 | 492.86 | 0 | 600.00 | 0 | 435.96 |
| 22 | 304.00 | 222.33 | 75.00 | 0 | 0 | 0 | 0 | 416.73 | 0 | 600.00 | 0 | 371.06 |
| 23 | 253.74 | 40.32 | 75.00 | 0 | 0 | 0 | 0 | 300.58 | 0 | 600.00 | 0 | 140.00 |
| 24 | 109.81 | 0 | 75.00 | 0 | 0 | 0 | 0 | 125.79 | 0 | 600.00 | 0 | 0 |
| Hour | Power Generation of Units (MW) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 30.40 | 30.40 | 0 | 0 | 0 | 0 | 54.25 | 0 | 373.36 | 600.00 | 108.50 | 140.00 |
| 2 | 30.40 | 30.40 | 0 | 0 | 0 | 0 | 0 | 0 | 601.29 | 600.00 | 108.50 | 0 |
| 3 | 30.40 | 30.40 | 0 | 0 | 0 | 0 | 0 | 0 | 434.06 | 600.00 | 108.50 | 0 |
| 4 | 73.42 | 30.40 | 0 | 0 | 0 | 0 | 0 | 0 | 628.96 | 600.00 | 108.50 | 0 |
| 5 | 30.40 | 30.40 | 0 | 0 | 0 | 0 | 0 | 0 | 524.33 | 600.00 | 108.50 | 0 |
| 6 | 30.40 | 30.40 | 0 | 0 | 0 | 0 | 0 | 0 | 440.52 | 600.00 | 108.50 | 0 |
| 7 | 59.07 | 30.40 | 0 | 0 | 0 | 0 | 0 | 0 | 722.64 | 600.00 | 241.96 | 0 |
| 8 | 81.49 | 30.40 | 0 | 0 | 0 | 0 | 0 | 100.00 | 788.85 | 600.00 | 399.29 | 0 |
| 9 | 302.11 | 71.97 | 0 | 0 | 0 | 0 | 0 | 150.39 | 800.00 | 600.00 | 524.16 | 0 |
| 10 | 304.00 | 129.37 | 0 | 0 | 0 | 0 | 0 | 186.60 | 800.00 | 600.00 | 619.98 | 0 |
| 11 | 230.15 | 232.75 | 0 | 0 | 0 | 0 | 0 | 215.68 | 800.00 | 600.00 | 620.00 | 0 |
| 12 | 282.37 | 258.96 | 0 | 0 | 0 | 0 | 0 | 226.42 | 800.00 | 600.00 | 620.00 | 0 |
| 13 | 304.00 | 268.98 | 0 | 0 | 0 | 0 | 0 | 226.47 | 800.00 | 600.00 | 620.00 | 0 |
| 14 | 304.00 | 268.30 | 0 | 0 | 0 | 0 | 0 | 230.92 | 800.00 | 600.00 | 620.00 | 0 |
| 15 | 304.00 | 269.52 | 0 | 0 | 0 | 0 | 0 | 213.57 | 800.00 | 600.00 | 620.00 | 0 |
| 16 | 304.00 | 271.93 | 0 | 0 | 0 | 0 | 0 | 240.66 | 800.00 | 600.00 | 620.00 | 0 |
| 17 | 304.00 | 287.82 | 0 | 0 | 0 | 0 | 0 | 241.26 | 800.00 | 600.00 | 620.00 | 0 |
| 18 | 304.00 | 276.08 | 0 | 0 | 0 | 0 | 0 | 252.16 | 800.00 | 600.00 | 620.00 | 0 |
| 19 | 304.00 | 285.72 | 0 | 0 | 0 | 0 | 0 | 264.52 | 800.00 | 600.00 | 620.00 | 0 |
| 20 | 304.00 | 273.30 | 0 | 0 | 0 | 0 | 0 | 198.99 | 800.00 | 600.00 | 620.00 | 0 |
| 21 | 304.00 | 152.00 | 0 | 0 | 0 | 0 | 0 | 132.26 | 800.00 | 600.00 | 526.89 | 0 |
| 22 | 147.71 | 0 | 0 | 0 | 0 | 0 | 0 | 100.00 | 800.00 | 558.74 | 429.90 | 0 |
| 23 | 171.29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 747.20 | 591.09 | 178.50 | 0 |
| 24 | 139.23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 608.18 | 597.87 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Oliveira, E.J.; Nepomuceno, L.S.; de Oliveira, L.W.; de Paula, A.N. A Novel Framework for Co-Expansion Planning of Transmission Lines and Energy Storage Devices Considering Unit Commitment. Technologies 2025, 13, 241. https://doi.org/10.3390/technologies13060241
de Oliveira EJ, Nepomuceno LS, de Oliveira LW, de Paula AN. A Novel Framework for Co-Expansion Planning of Transmission Lines and Energy Storage Devices Considering Unit Commitment. Technologies. 2025; 13(6):241. https://doi.org/10.3390/technologies13060241
Chicago/Turabian Stylede Oliveira, Edimar José, Lucas Santiago Nepomuceno, Leonardo Willer de Oliveira, and Arthur Neves de Paula. 2025. "A Novel Framework for Co-Expansion Planning of Transmission Lines and Energy Storage Devices Considering Unit Commitment" Technologies 13, no. 6: 241. https://doi.org/10.3390/technologies13060241
APA Stylede Oliveira, E. J., Nepomuceno, L. S., de Oliveira, L. W., & de Paula, A. N. (2025). A Novel Framework for Co-Expansion Planning of Transmission Lines and Energy Storage Devices Considering Unit Commitment. Technologies, 13(6), 241. https://doi.org/10.3390/technologies13060241







