Comparing Strategies for Optimal Pumps as Turbines Selection in Pressurised Irrigation Networks Using Particle Swarm Optimisation: Application in Canal del Zújar Irrigation District, Spain

Abstract

The modernisation of irrigation networks has enhanced water use efficiency but increased energy demand and costs in agriculture. Energy recovery (ER) is possible by utilising excess pressure to generate electricity with pumps as turbines (PATs), offering a cost-effective alternative to traditional turbines. This study assesses the use of PATs in pressurised irrigation networks for recovering wasted hydraulic energy, employing the particle swarm optimisation (PSO) algorithm for PAT sizing based on two single-objective functions. The analysis focuses on minimising the payback period (MPP) and maximising energy recovery (MER) at specific excess pressure points (EPPs). A comparative analysis of values for each EPP and objective function is conducted independently in Sector II of the Canal del Zújar Irrigation District (CZID) in Extremadura, Spain. A sensitivity analysis on energy prices and installation costs is also performed to assess socioeconomic trends and volatility, examining their effects on both objective functions. The optimisation process predicts an annual ER for an average irrigation season using 2015 data ranging from 9554.86 kWh to 43,992.15 kWh per PATs from the MER function, and payback periods (PPs) from 12.92 years to 3.01 years for the MPP function. The sensitivity analysis replicated the optimisation for the years 2022 and 2023, showing potential annual ER of up to 54,963.21 kWh and PPs ranging from 0.88 to 5.96 years for the year 2022.

1. Introduction

Water distribution systems for irrigation have undergone significant modernisation in recent years to improve the efficiency of water use [1]. These technological advances have inevitably been accompanied by an increase in the energy requirements of the agricultural sector and a consequent increase in energy costs.

Many pressurised water distribution systems have high potential for energy recovery (ER), as part of their excess of pressure energy is dissipated by regulation valves installed in the network. However, this excess of energy could be used through a reversal process to generate electricity [2]. This ER can be achieved by implementing pumps working in reverse at excess pressure points (EPPs), such as pumps as turbines (PATs), which offer a cost-effective alternative, particularly in micro-scale applications, where their cost per kW is more competitive than that of conventional turbines [3,4,5,6]. Furthermore, Ref. [7] identified the environmental and economic benefits of a system incorporating hydropower (PAT) under different energy demand scenarios in the agricultural sector, demonstrating a significant reduction in greenhouse gas emissions and fossil fuel dependency.

However, the choice of these turbines is still an obstacle to the widespread dissemination and implementation of PAT technology [8]. This is mainly due to the lack of information on the performance and operation of PATs. The fact that the characteristic curves for reverse operation of commercial pumps are usually not available, together with the limited detailed flow and pressure records of existing irrigation networks, makes it difficult to carry out an accurate analysis and implementation of these systems.

The feasibility of these systems is largely dependent on a detailed understanding of their operation, as well as on the existing conditions at the hydraulic network, as it is known that the efficiency of PATs varies significantly with flow and head fluctuations. This research line is not new and there have been significant advances in recent years, such as the experimental characterisation of PATs as energy recovery devices for the water distribution network in the laboratory [9]; the creation of predictive models that estimate the performance of centrifugal pumps used as turbines through a one-dimensional numerical code [10]; performance prediction models using the rotor–volute coincidence principle [11]; or using artificial neural networks [12]; a methodology for predicting the performance of PATs operating at off-design conditions has been evaluated experimentally and numerically [13]; a model for extrapolating the curves of turbine-like pumps from their best efficiency point (BEP) has also been developed [14]; the curves of centrifugal pumps operating as turbines at different specific speeds have been studied experimentally [15]; and a methodology to extend the solution space beyond the traditional affinity curves of commercially available PATs has been studied [16].

Another issue is the optimal location of PATs within the water network. Ref. [17] developed a methodology that considers theoretical PAT curves, focusing on maximising ER in irrigation networks. Other studies have also focused on the optimal selection of PATs to maximise ER [18,19]. Meanwhile, Ref. [20] formulated a model for PAT selection primarily aimed at minimising payback periods (PPs), considering costs associated with electromechanical components, required civil works for installation and operation, and other related expenses. Ref. [21] addressed the global optimisation of PAT location by determining a fixed number of PATs using a deterministic approach. However, several key research gaps remain unaddressed: (i) Insufficient focus has been given to the determination of the optimal strategy for the selection of PATs using particle swarm optimisation (PSO), despite its proven effectiveness in other engineering domains; (ii) Multiple objective functions, particularly the trade-off between maximising energy recovery (MER) and minimising the payback period (MPP), have not been independently analysed. These criteria are often treated jointly or simplistically; (iii) The interplay between ER and PPs under dynamic economic conditions has yet to be thoroughly explored; and (iv) Limited consideration has been given to how site-specific factors, such as irrigation management practices and the investment capacity of farmers, affect the feasibility and prioritisation of PAT implementation. Furthermore, few studies have proposed flexible and context-aware optimisation frameworks that simultaneously account for technical, economic, and operational constraints, which restricts the practical applicability of current models in real-world agricultural systems.

To address these limitations, this work has developed a PAT selection model based on the PSO algorithm, applied to nine EPPs pre-selected in a real pressurised irrigation network by [22]. The main contributions include: (i) A novel PSO framework for PAT selection tailored to real hydraulic and economic conditions in irrigation systems; (ii) Separate analysis of two independent objective functions: MPP and MER; (iii) Integration of economic viability, including energy prices and installation costs, to reflect real market dynamics; (iv) Sensitivity analysis to evaluate the impact of fluctuating external factors on the feasibility of PAT implementations; and (v) Application to a real irrigation district using flow rates data, enhancing the model’s practical relevance and transferability. It offers a practical tool for engineers, irrigation managers, and policymakers seeking to implement cost-effective and sustainable ER strategies in rural pressurised water distribution systems, with the aim of reducing energy dependence and enhancing the economic viability of irrigation infrastructure. However, the methodology is currently limited to micro-scale installations, and its application depends on the availability of EPPs in pressurised water networks.

The PSO algorithm was applied using actual flow rates data from the 2015 irrigation season. This model was applied to irrigation sector II of the Canal del Zújar Irrigation District (CZID) and a comparison of the results obtained by applying each of the objective functions was made. The determination of the optimal PAT in both objective functions is significantly impacted by energy price volatility. Consequently, a sensitivity analysis was conducted to examine fluctuations in energy prices and alterations in raw material costs. The PSO algorithm was re-applied for both objective functions using updated costs from 2022 and 2023 across the nine EPPs. This analysis facilitates the identification of trends and potential developments, as variations in total costs can influence the decision-making process and the efficacy of the selection criteria. The results were analysed, and the feasibility of implementing these systems was evaluated for each objective function under different economic scenarios.

2. Materials and Methods

2.1. Study Area

The data necessary for the development of this study were obtained from the Canal del Zújar Irrigation District (CZID), located in Extremadura (Spain). The irrigated area extends along the left bank of the Zújar River to its mouth in the Guadiana River, covering an area of 20,870 ha. The area is divided into 10 pressurised irrigation sectors, Figure 1.

The data used in this work correspond to Sector II, which irrigates 2691 ha, 90% of which is devoted to grow tomatoes, maize, and rice. The network corresponding to this sector is made up of pipes with diameters between 80 and 1000 mm, which supply water to 196 hydrants located at heights varying between 250 and 285 masl. The network has been designed to supply 1.2 L/s/ha on demand (water available 24 h per day), assuming 100% simultaneity (all hydrants simultaneously opened) and a minimum pressure service at hydrant level of 35 m. Annual rainfall, evapotranspiration and average temperature in 2024 were 322 mm, 1249 mm and 17 °C, respectively. This irrigation sector has a remote telemetry system since the 2015 irrigation season that records hourly water demand through flow meters installed on 196 hydrants [23]. This system provides flow information that is rarely available at this level of spatial and temporal resolution in irrigation districts.

2.2. Identification of EPPs Pre-Selected in CZID

Using data of real water consumption in Sector II, it is possible to determine the hourly flow rate through each pipe in the network and the hourly volume pumped throughout the district, enabling the possibility to hydraulically assess the behaviour of the network and analyse the excess pressure available through an EPANET hydraulic model of the network [22]. This irrigation sector has already been the subject of previous studies, such as the research developed by Crespo Chacón et al. [22], who validated a methodology for determining flow rates in irrigation networks on demand using real flow data records.

From these flows and the EPANET hydraulic model, nine EPPs of the network were identified (yellow dots is Figure 2), for which the ER potential was evaluated using PATs [20]. To identify the EPPs, the most unfavourable scenario was considered, namely 100% simultaneity. The EPPs were defined based on two criteria: Minimising the existing excess pressure in the irrigation network to match its service pressure and reducing the pressure in as many hydrants with excess pressure as possible. These flow data and the nine EPPs identified in this preliminary study were used in this research. The location of the EPPs is directly related to the topography of the terrain, the characteristics of the network, the flow rates fluctuations, and the operating conditions imposed by the irrigation district. It is assumed that all hydrants are open and that flow rates follow consistent patterns throughout the years, except during drought periods. In the case of pressurised irrigation networks in flat terrain, it is necessary to analyse the existing overpressures and apply the proposed methodology to assess the feasibility of implementing such systems.

2.3. Problem Approach

The objective of this methodology is to determine the optimal PAT size, according to two different optimisation criteria: maximising energy recovery (MER) and minimising payback period (MPP), for specific EPPs within a pressurised irrigation network. In an optimisation process, the objective functions define the goal by mathematically specifying the variables and criteria to be maximised or minimised, such as the MER and MPP. To achieve this, the algorithm adjusts the input variables to find the optimum value, while ensuring compliance with the constraints imposed by the decision variables.

2.3.1. Function Objective 1: Maximise Energy Recovery (MER)

This function aims to identify the PAT that ensures the highest energy production during an irrigation season for each EPP studied, resulting in the highest possible ER and, consequently, the greatest economic savings. The MER objective function, used to determine the annual energy recovery (${ER}_i$), is defined in Equation (1). It is assumed that the energy generated or recovered is destined for self-consumption, rather than the sale of energy to the grid, considering that in many cases the installation does not have grid connection points nearby [20].

$${MAXIMISE}_{{ER}_i}=\Sigma P_i·t$$

(1)

where $P_i$ is the power produced during each operational period of the turbine, and ($t$) represents the annual time scale. Since $P_i$ depends on both the flow rate ($Q_i$) and the available head ($H_i$), it is necessary to establish a methodological framework to accurately estimate these parameters.

2.3.2. Function Objective 2: Minimise Payback Period (MPP)

The optimisation of the MPP objective function, defined in Equation (2), is designed to identify the PAT that results in the shortest payback period at each analysed EPP. The simple payback period is an economic index that shows how long it takes to recover an investment, calculated as the ratio of the total installation costs ($C_{PP2}$) to the economic savings (${ES}_i$), as defined in Equation (2).

$${MINIMISE}_{PP}={\displaystyle \frac{C_{PP2}}{{ES}_i}}$$

(2)

Economic savings (${ES}_i$) are calculated as the product of the energy recovery and the value of the tariff considered ($T_i$), according to Equation (3).

$${ES}_i=\Sigma P_i·t·T_i$$

(3)

To determine the total installation costs ($C_{PP2}$) for each proposed PAT, as set out in Equation (4), consider the cost of the civil works ($C_{CW}$) necessary for correct operation and the cost of the electromechanical components (turbine + generator) ($C_{\mathrm{P}\mathrm{A}\mathrm{T}}$), as in Equation (5). The costs of PATs are determined using the equation proposed by Novara and McNabola [6] for a pump with two magnetic pole pairs which depends directly on $Q_{\mathrm{B}\mathrm{E}\mathrm{P}}$ and $H_{\mathrm{B}\mathrm{E}\mathrm{P}}$, which is referenced in other articles, including those by [17,20].

$$C_{PP2}=C_{PAT}+C_{CW}$$

(4)

$$C_{PAT}=\mathrm{12,864.77}·Q_{BEP}·\sqrt{H_{BEP}}+949.43$$

(5)

To estimates the civil works costs, the methodology proposed by Crespo Chacón [20] is followed. It is based on the estimated cost of the construction stages of the standard installation of PATs in irrigation networks, as opposed to estimates of the costs of the civil works based on the installed power or a percentage of the total installation cost. The chosen criterion is considered to be more accurate, given that the works required vary little from one case to another, beyond the specific circumstances of each site. The stages considered in cost estimation are excavation, construction of the bypass, construction of the reinforced concrete base, installation of the shelter, and backfilling with excavated land.

2.4. Methodology for Flow Estimation and PAT Operating Rules in Irrigation Networks

To effectively implement the objective functions, it is crucial to determine the flow rates ($Q_i$) circulating through each EPP and their corresponding occurrence times. Therefore, the algorithmic optimisation process will be applied independently to each of EPP using the methodology proposed by [22] to obtain the flow rates and the time of occurrence for each of them.

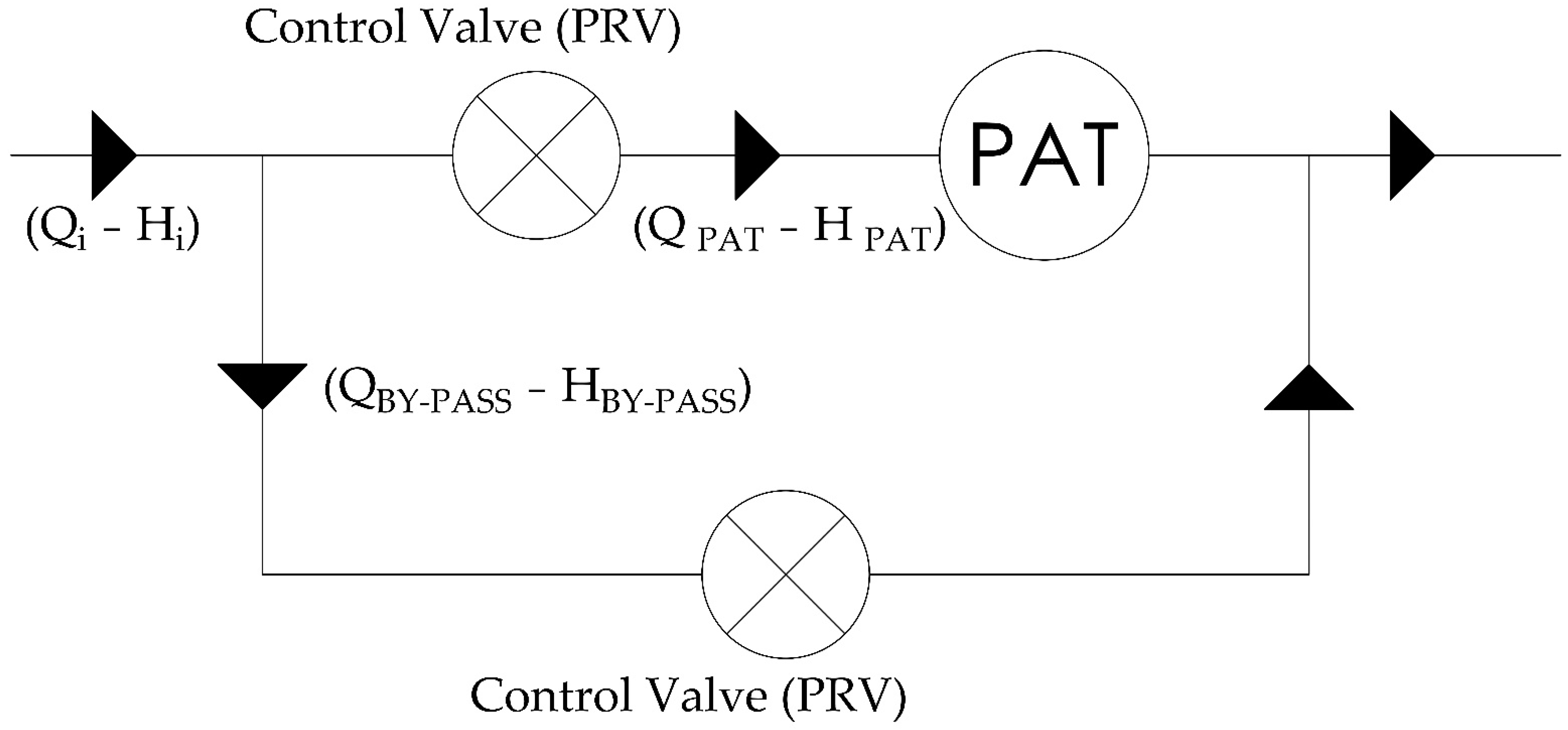
To guarantee the required operating conditions downstream flow demand of an EPP while optimising ER, the method employed by Lydon et al. [9,24] was adopted. A bypass configuration was proposed for the installation of a PAT, shown in Figure 3, comprising two control valves (pressure reducing valve (PRV), flow control valve (FCV), or similar), one in series with the PAT and one in parallel, to ensure that the desired downstream demands are fulfilled with the required conditions in terms of pressure and flow.

The methodology for the estimation of the flow within the turbine simulates the interaction between the Q–H system and PAT curves, as seen in Figure 4. The two operating rules fixed were as follows: (I) the flow demanded downstream of the EPP ($Q_i$) would fully circulate through the turbine if its value is lower than or equal to the maximum flow to be turbined ($Q_{MAX}$) (this value was calculated obtaining the intersection between both, PAT and system Q–H curves), Equation (6); (II) if $Q_i$ is greater than the maximum fixed for each scenario ($Q_{MAX}$), this flow would be diverted to the bypass ($Q_{BY-PASS}$). To obtain the amount of $Q_{BY-PASS}$, the interaction between both system and PAT curves is required again, as seen in Equation (7). The operating rules are as follows:

$$Operating rule I:if Q_i\le Q_{MAX}\left\{\left.\begin{array}{c}{Q}_{PAT}=Q_i\\ Q_{BY-PASS}=0\end{array}\right\}\right.$$

(6)

$$Operating rule II:if Q_i>Q_{MAX}\left\{\left.\begin{array}{c}{Q}_{PAT}=Q_{,PAT}\\ Q_{BY-PASS}=Q_i-Q_{PAT}\end{array}\right\}\right.$$

(7)

These operating rules ensure that the PAT functions within its optimal hydraulic conditions while guaranteeing the required irrigation flow downstream.

2.5. Optimisation Process

From the preselected PATs, the optimal PAT for each EPP is determined using the PSO algorithm applied to two single-objective functions. The input data used include the system curves, the $Q_i$ values obtained from the data recorded for each EPP, shown in Figure 4, and the average annual final energy price including taxes and non-discriminatory terms ($T_i$).

The algorithm simulates the hydraulic behaviour of the system under varying operating conditions by applying $Q_i$ and the estimation of the $H_i$ for each possible flow rate $Q_i.$ To estimate $H_i$ and Q–H characteristic curves, the approach proposed by Barbarelli [25] is used, shown in Equation (8). This model, developed as an alternative to the approach by Derakshan and Nourbakhsh [15], is based on experimental data from 12 tested PAT and provides a direct estimation of the $H_i$ for each $Q_i$, enabling the generation of Q–H characteristic curves each candidate PAT configuration.

$${\displaystyle \frac{H_i}{H_{BEP}}}=0.922{\left({\displaystyle \frac{Q_i}{Q_{BEP}}}\right)}^2-0.406\left({\displaystyle \frac{Q_i}{Q_{BEP}}}\right)+0.48$$

(8)

Each ($Q_i$ − $H_i$) pairs has an associated relative efficiency (${\eta }_i$) that determines how effectively the PAT converts hydraulic energy into mechanical energy. Novara and McNabola [14] proposed a model, through the extrapolation of 116 measured PAT characteristic curves, to estimate the relative PAT efficiency (${\eta }_i$) as a function of flow rate, shown in Equation (9).

$${\eta }_i=0.5197{\left({\displaystyle \frac{Q_i}{Q_{BEP}}}\right)}^3-2.3328·{\left({\displaystyle \frac{Q_i}{Q_{BEP}}}\right)}^2+3.0931·\left({\displaystyle \frac{Q_i}{Q_{BEP}}}\right)-0.2757$$

(9)

where ($Q_i$) is the relative flow and ($Q_{BEP}$) is the flow at the BEP.

The $P_i$ for each pair of ($Q_i$ − $H_i$) was obtained using Equation (10), assuming that the PAT operates at its BEP, where ($Q_{BEP}$, $H_{BEP}$) represent the optimal flow and head conditions. Following [8,20], we assumed that $H_{PAT}=H_{BEP}$ and ηi = efficiency at BEP, for which the maximum overall efficiency has been taken as 0.55, considering 65% for the PATs + generator efficiency and 85% to account for hydraulic regulation losses.

$$P_i=0.55·Q_{PAT}·H_{PAT}·\gamma ·{\eta }_i$$

(10)

where $\gamma$ is the specific weight of water and ${\eta }_i$ is the relative efficiency.

For very low rates, this relative efficiency has negative values, for which the device should be off, and no flow would be turbined.

Depending on the selected objective function, the algorithm either evaluates total annual energy production or the economic feasibility of the PAT installation. For the MER, the algorithm returns the total annual energy generated by the system, as seen in Equation (1), maximising turbine output based on hydraulic conditions and system performance. For the MPP, the objective function calculates the total investment cost, as seen in Equation (4), (including turbine, generator, and civil works), and annual revenue based on electricity tariffs, as seen in Equation (3). The ratio of cost to income is minimised to determine the configuration with the shortest payback period, as seen in Equation (2). Figure 5 presents a flowchart summarising the steps of this methodology.

2.6. Particle Swarm Single-Objective Optimisation

The PSO algorithm is a heuristic optimisation technique first created by Kennedy and Eberhart in 1995 [26]. This approach is commonly employed in scientific and engineering disciplines to identify the minimum or maximum of a problem. It operates based on the collective behaviour of animal groups, such as schools of fish, flocks of birds, and swarms of bees. The movement of each individual results from a combination of individual decisions and group behaviour. A collection of particles moving through the parameter space that describes their direction, velocity, and acceleration can be characterised as the possible solutions to the optimisation problem [27]. Within the swarm, each particle signifies an individual entity and possesses a position solution vector, while the best solution to the problem is defined as the most optimal position discovered by the swarm, which is accomplished by each particle. To identify the most effective local solution, the swarm particles are divided into subsets called neighbourhoods. Each particle in a neighbourhood possesses knowledge of the optimal position within its own subset. Interactions between particles are governed by the neighbourhood, therefore influencing information flow throughout the swarm and impacting the algorithm’s convergence [28]. Therefore, it should be noted that heuristic algorithms, including PSO, may become trapped into a local minimum or maximum, depending on the configuration and complexity of the problem.

The first step in the process involves creating an initial swarm of $h$ random particles. At each iteration $k$, each $P_l$consists of four components: one is the position $X_l\left(k\right)=\{x_{l1},\dots ,x_{ln}\}$, which represents a specific combination of variable values; the value of the objective function at the position where the particle is located; a velocity $V_l\left(k\right)=\{v_{l1},\dots ,v_{ln}\}$, indicating how and where the particle is moving; and a record of the best global position the particle has reached so far $G_l\left(t\right)=\{g_{l1},\dots ,g_{ln}\}$. Each particle is evaluated using the objective function, and its position and velocity are updated, providing the algorithm with optimisation capabilities. If a stopping criterion is not met, the procedure is repeated, starting from the evaluation of the particles.

To update both the position and velocity of each particle in the swarm at each iteration $k$, the following equations are used:

$$v_l\left(k+1\right)=w{v}_l\left(k\right)+c_1{r}_1\left[{\widehat{x}}_l\left(k\right)-x_l\left(k\right)\right]+c_2{r}_2\left[g\left(k\right)-x_l\left(k\right)\right]$$

(11)

$$x_l\left(k+1\right)=x_l\left(k\right)+v_l\left(k+1\right)$$

(12)

where $v_l(k+1)$ is the velocity of particle $l$ at time $k+1$, i.e., the new velocity; $v_l\left(k\right)$ is the velocity of particle $l$ at time $k$, i.e., the current velocity; $w$ is the inertia coefficient, which adjusts the particle velocity by either reducing or increasing it; $c_1$ is the cognitive coefficient; $r_1$ is a random vector with values between 0 and 1, with a length equal to that of the velocity vector; ${\widehat{x}}_l\left(k\right)$ is the best position the particle $l$ has reached up to that point; $x_l\left(k\right)$ is the position of particle$l$ at time $k$; $c_2$ is the social coefficient; $r_2$ is a random vector with values between 0 and 1, with a length equal to that of the velocity vector; and $g\left(k\right)$ is the position of the entire swarm at time $k$, representing the best global value.

2.7. Sensitivity Analysis

The determination of the optimal PAT in both objective functions is significantly impacted by energy price volatility. Consequently, a sensitivity analysis was conducted. The objective of this sensitivity analysis is to evaluate the impact of two key sources of variability on the total costs: electricity tariff fluctuations and changes in construction and PAT costs in Spain.

In the case of Spain, electricity pricing is subject to market-driven variations, influenced by the wholesale market (OMIE) regulatory adjustments, and taxation policies. Simultaneously, construction and PAT costs are affected by material price inflation, labour costs, and market conditions, which can alter investment requirements. Given the potential impact of these fluctuations on decision-making processes, this sensitivity analysis aims to assess their influence on total costs, identify trends, and evaluate the robustness of the selection criteria under different scenarios.

The price of electricity in Spain has been market-driven since July 2009, except for small consumers [29]. This market liberalisation, coupled with rising energy costs, led to significant increases in energy bills for farms and irrigation communities by 2010, with a 50% rise in contracted power costs and a 200% increase in consumption costs [30]. Corominas [29] highlights the rapid annual growth in energy costs for irrigation, which can be restrictive amid sudden energy price hikes. Since 2020, due to post-pandemic recovery and geopolitical conflicts such as the Russia–Ukraine war, energy price surges have led to increase variable term costs in contracts negotiated by Irrigation Districts, with a trend of continued rises in future contracts. According to OMIE [31], the Spanish electricity market regulator, the average energy price in 2022 reached 167.52 euros/MWh, 2.8 times higher than the 18-year average, with a peak of 700 euros/MWh.

The Spanish average annual final energy price, including taxes and non-discriminatory energy terms ($T_i$), was calculated according to Equation (13), where $i$represents the year analysed, comprises a fixed term for power (${PP}_{i,fixed}$), and a variable term for energy consumption (${PE}_{i,variable}$), with prices fluctuating overtime. Taxes applied at the national level and those specific to the agricultural sector have been considered, including all components that contribute to the final energy price.

$$T_i={PP}_{i,fixed}+{PE}_{i,variable}$$

(13)

The variable electricity price $\left({PE}_{i,variable}\right)$consists of energy production costs ($C_{production}$), access tariff costs ($C_{access tariff}$), and additional expenses like the marketer’s profit margin, equipment rental, or taxes, as seen in Equation (14).

$${PE}_{i,variable}=C_{production}+C_{access tariff}$$

(14)

The proposed scenarios are heavily influenced by price fluctuations in a volatile energy market, needing a sensitivity study on energy prices and raw material cost variations to analyse trends and inform decision-making and selection criteria effectiveness.

The following considerations will be taken for the calculation of the energy price: The average final energy prices without taxes (${FE}_i$) of the wholesale market (OMIE) [31] will be taken as a reference for the calculation assuming a uniform distribution in consumption, independent of the tariff periods $\left({TP}_n\right)$; the standard Special Electricity Tax ($IEE$) and its reductions in agriculture; value-added tax (VAT); energy term ($E_{term})$ depend on usage and periods. The weighted average value on a time and ${TP}_n$, where $n$represents the type of periods applied, is calculated for an assumed constant use, which will be added to the average final energy price.

$$T_i=\left(\left({FE}_i+E_{term}\left(P_n\right)\right)·IEE\right)·VAT$$

(15)

In order to determine the added toll (${pf}_j$) per energy term ($E_{term}$) based on the ${TP}_n$applied, where $j$ represents the number of added tolls, the average cost of each ${TP}_n$was determined ($\overline{C_{i, pf}}$). We have taken the weighted average, as in Equation (16), between the annual hours of each${pf}_j$($H_{annual}$) and the ${pf}_j$ for each ${TP}_n$for an assumed constant usage resulting in an average price of $E_{term}$ non-discriminated. The $E_{term}$is obtained with an annual time scale by dividing the average by the total hours of the year, as in Equation (17).

$$\overline{C_{i,pf}}={\displaystyle \frac{\sum _{i=1}^n(H_{annual}·{pf}_j)}{\sum _{i=1}^n{pf}_j}}$$

(16)

$$E_{term}={\displaystyle \frac{\overline{C_{i,pf}}}{8760 \left(h\right)}}·1000$$

(17)

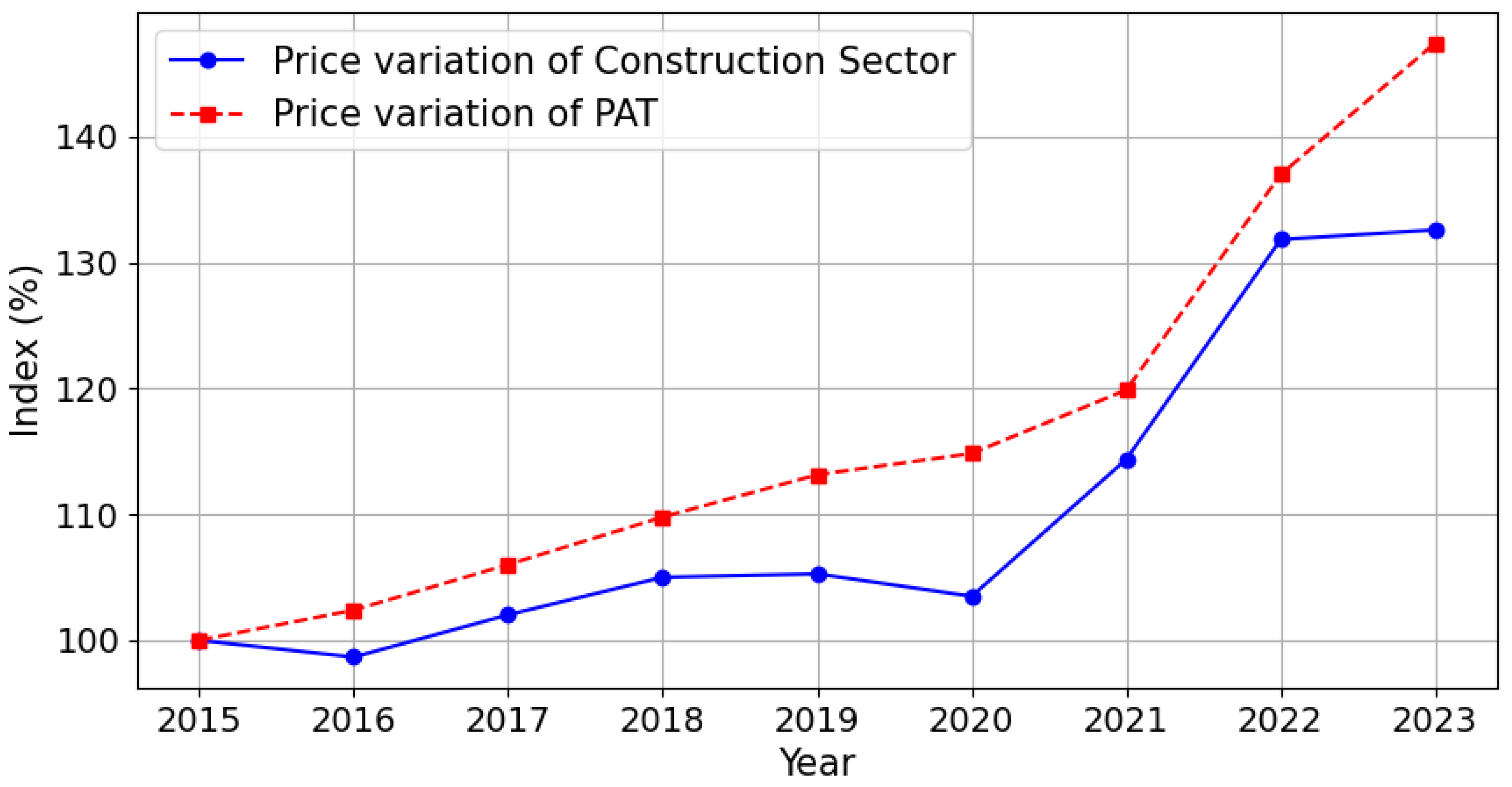
The variation in $C_{CW}$ has been determined through the cost index of the construction sector of the Spanish Ministry of Transport, Mobility and Urban Agenda, which shows the percentage variation of civil works costs taking 2015 as the relative base year, and the costs were extrapolated considering these percentages and the cost of civil works in 2015 proposed by [20]. For the variation in $C_{PAT},$ a market price evolution study was carried out by analysing the sales prices of more than 15 pumps, from three different commercial companies and with different power ratings and characteristics.

3. Results

The optimisation process was carried out independently for each of the nine EPPs using actual flow fluctuations corresponding to the year 2015. For each EPP, the irrigation flow rates ($Q_i$) were obtained from records collected from the 2015 telemetry system. Additionally, system curve coefficients for each EPP were obtained from the hydraulic model, shown in

Table 1. Input variables of the PSO algorithm.

EPP	System Curve Coefficients	Particle Swarm
	(Quadratic Equation: c + bx + ax2)	Lower Limits	Upper Limits
1	[60.616; −0.015; −0.0002]	[10.0; 10.0]	[172; 16.94]
2	[71.639; 0.0113; −0.0003]	[10.0; 10.0]	[240.31; 21]
3	[74.053; 0.0097; −0.0003]	[10.0; 10.0]	[320.01; 14.1]
4	[76.655; −0.0541; 0.00002]	[10.0; 10.0]	[228.06; 31.08]
5	[57.332; −0.023; −0.0002]	[10.0; 10.0]	[115.27; 16.89]
6	[48.045; −0.0078; −0.00006]	[10.0; 10.0]	[270.36; 7.06]
7	[68.237; 0.0194; −0.0002]	[10.0; 10.0]	[240.61; 23.2]
8	[69.654; 0.0177; −0.0002]	[10.0; 10.0]	[326.47; 17.026]
9	[64.782; −0.0069; −0.00003]	[10.0; 10.0]	[365.29; 23.96]

Source: own research.

. The lower limits were set at 10 m for the head and 10 l/s for the flow rate, while the upper limits, which are defined for each EPP, were set according to the real maximum values recorded by CZID in 2015, as shown in Table 1. The lower limits were chosen to prevent the effective operating range of each PAT, based on heuristic considerations.

During the process, the energy price ($T_i$) of 88.26 EUR/MWh (2015) was used for the income calculations. The optimisation was repeated for each of the EPPs based on the tariffs for 2022 and 2023, with the goal of minimising the PP and maximising the annual ER. The PSO algorithm was performed using $h=50$ particles ($P_l)$ and 100 iterations $k$. Adaptive inertia weights ($w)$ of 0.8, cognitive coefficients ($c_1$) of 1, and social coefficients ($c_2$) of 2 were employed, along with an early stopping criterion based on a convergence tolerance of ${10}^{-3}$ over five consecutive rounds and performance stagnation.

3.1. Particle Swarm Single-Objective Optimisation Results

Once all the data have been entered, the computation and optimisation process are carried out independently by means of a particle swarm algorithm for each EPP studied, returning the optimum position and value data for each objective function, as shown in

Table 2. Results of the algorithm for the objective functions in the year 2015.

Objective Functions
EPP	MER			MPP
	Best Position		Best Value	Best Position		Best Value
	Flow Rate (L/s)	Head (m)	ER (kWh)	Flow Rate (L/s)	Head (m)	PP (Years)
1	76.41	16.94	19,357.85	56.95	13.76	6.98
2	86.76	21.00	42,988.30	66.65	18.36	3.42
3	112.21	14.10	49,828.68	87.22	14.10	3.01
4	84.04	31.08	33,116.07	55.77	20.90	4.45
5	54.17	16.89	9554.86	40.95	14.17	12.92
6	87.07	7.06	10,421.65	72.06	6.78	12.14
7	82.01	23.20	34,225.61	60.60	18.62	4.26
8	107.37	17.03	45,442.89	81.24	15.83	3.37
9	144.42	23.96	43,992.15	89.38	14.06	3.82

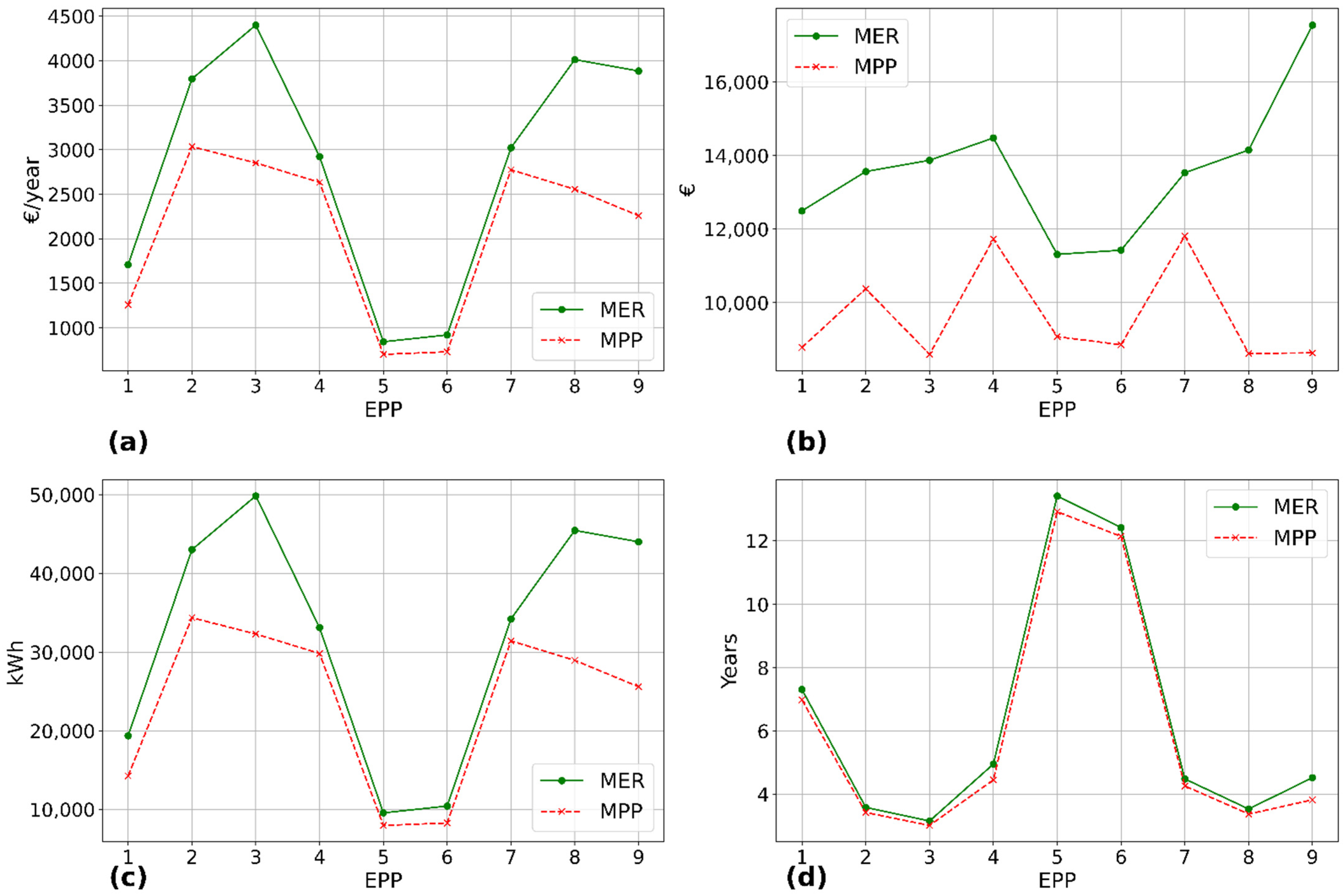
Source: own research.

. The results obtained correspond to the year 2015 and predict energy savings in the range from 9554.86 kWh (EPP5) to 49,828.68 kWh (EPP3) for the MER function, and payback periods ranging from 12.92 years for EPP5 to 3.01 years for EPP3 for the MPP function.

To compare the results of the two objective functions, the ER and PP values associated with the two operating points of each EPP listed in Table 2 are shown in Figure 6: the values of the annual savings in euros, Figure 6a; the investment required to carry out the designed installation, Figure 6b; the energy recovered for each objective function, Figure 6c; and the payback period was calculated for this function to compare it with the results of both objective functions, Figure 6d. The variation in energy recovered between the objective function MER and MPP ranges from 1597.57 kWh to 18,394.05 kWh per year. The variation in PPs between both functions ranges from 0.14 to 0.7 years.

3.2. Sensitivity Analysis Results

The methodology described in Section 2.7 was followed to estimate the annual evolution of electricity tariffs, as seen in

Table 3. Average annual final price of energy including taxes and non-discriminatory energy terms ($T_i$).

Year	$\mathit{F}\mathit{E}$ (EUR/MWh)	${\mathit{E}}_{\mathit{t}\mathit{e}\mathit{r}\mathit{m}}$ (EUR/MWh)	$\mathit{I}\mathit{E}\mathit{E}$ (%)	VAT (%)	${\mathit{T}}_{\mathit{i}}$ (EUR/MWh)
2015	62.85	6.55	5.11 (−85% BI)	21	88.26
2016	48.43	6.55	5.11 (−85% BI)	21	69.92
2017	60.54	6.55	5.11 (−85% BI)	21	85.32
2018	64.35	6.55	5.11 (−85% BI)	21	90.17
2019	53.41	6.55	5.11 (−85% BI)	21	76.25
2020	40.39	6.55	5.11 (−85% BI)	21	59.69
2021	118.65	9.00	0.5 (−85% BI)	21	155.24
2022	221.87	9.00	0.5 (−85% BI)	21	259.45
2023	100.02	9.00	0.5 (−85% BI)	21	132.59

Source: own research.

, and the costs of civil works and electromechanical components PATs, as seen in Figure 7. As can be seen in Table 3, the energy price is relatively constant in the years 2015 to 2019. In 2020, the energy price is slightly lower, possibly due to the recovery of COVID-19, and from 2021 the price shoots up to double the final price, and in 2022 it almost triples, returning to near post-pandemic levels in 2023.

The study of the cost of the variable term of the average energy price was extended to a period between January 2009 and December 2023 in Spain. Reference is made to the average final prices of energy contracted by marketers on the free market (OMIE) [31]. The energy term tariff tolls (${pf}_j$) contracted by CZID were divided into six tolls, $j=6$ (P1, P2, P3, P4, P5, and P6). There were two tariff periods $\left(T{P}_n\right)$ contracted by CZID ($n=2$): tariff 6.0A (applied until 2020 in irrigation) and 6.1TD (applied from 2021).

The VAT rate of 21% in force in Spain was considered. An 85% reduction of the taxable base (BI), which corresponds to the amount on which taxes are calculated in Spain, is applied to agricultural irrigation [32]. The standard Special Electricity Tax ($IEE$) in Spain is 5.113%. However, due to government measures implemented to mitigate high electricity prices, its value was reduced to 0.5% between 2021 and 2023 [33].

The particle swarm optimisation algorithm was also applied to each EPP considering updated costs for 2022 and 2023, and the results are shown in

Table 4. Results of the algorithm for the objective functions in the year 2022 and 2023.

Objective Functions	MER		MPP
EPP	Best Value 2022	Best Value 2023	Best Value 2022	Best Value 2023
	ER (kWh)	ER (kWh)	PP (Years)	PP (Years)
1	19,357.85	19,357.85	3.21	6.39
2	54,963.21	42,988.3	0.88	3.15
3	49,828.68	49,828.68	1.38	2.78
4	33,116.06	33,116.07	2.05	4.09
5	9554.86	9554.85	5.96	11.76
6	41,603.89	41,603.89	5.59	11.08
7	34,225.61	34,225.61	1.96	3.91
8	45,442.89	45,442.89	1.55	3.11
9	43,992.15	43,992.15	1.75	3.53

Source: own research.

.

4. Discussion

The results obtained validate the effectiveness of the algorithm as an optimisation method, yielding logical and convincing results for each EPP studied. The algorithm demonstrated rapid convergence (approximately 1 s per EPP and objective function) with a limited number of iterations (100 iterations per objective function), confirming its suitability for the selection of PAT configurations under single-objective optimisation criteria.

When comparing the values obtained in this study to those from other optimisation methods, such as genetic algorithms or linear programming approaches used in similar PAT installations, the ER values obtained here are generally within or above average. For instance, while typical PAT installations in irrigation systems recover between 10,000 and 30,000 kWh/year [34,35,36], this study reports several cases (e.g., EPP2, EPP3, EPP8, EPP9) with ER values exceeding 40,000 kWh/year, indicating strong optimisation performance. Only EPP5 and EPP6 display lower ER values (~10,000 kWh/year), as seen in Figure 6c, which are at the lower end of the expected range, primarily due to unfavourable hydraulic conditions and flow characteristics. In the case of EPP6, it is in a flat area with a high flow rate, as it is near the network’s inflow point, but with low available pressure. At EPP5, the flow diverted to the branch that supplies downstream demand is small, even though the available pressure is similar to that at other points such as EPP1, EPP3, and EPP8, which negatively affect ER.

In terms of economic viability, the PP values obtained through the MPP objective function are relatively short in most cases, ranging from 3 to 5 years, particularly in EPP2, EPP3, and EPP8. These values are considered highly competitive when compared with other small hydropower projects [36,37], which often present PP values between 5 and 10 years. The exception is EPP5 and EPP6, where PP exceeds 10 years under 2015 conditions, reflecting suboptimal investment opportunities unless energy prices increase, or installation costs are reduced.

However, when updated energy prices for 2022 and 2023 are incorporated into the model (Table 4), the scenario changes considerably. Higher electricity prices lead to a significant reduction in PP across all EPPs, most notably in 2022, where PPs are shortened to less than 6 years even in previously unviable cases like EPP5 and EPP6. This shift highlights the importance of including a temporal economic analysis in PAT project assessments, as external market conditions can drastically affect project viability. 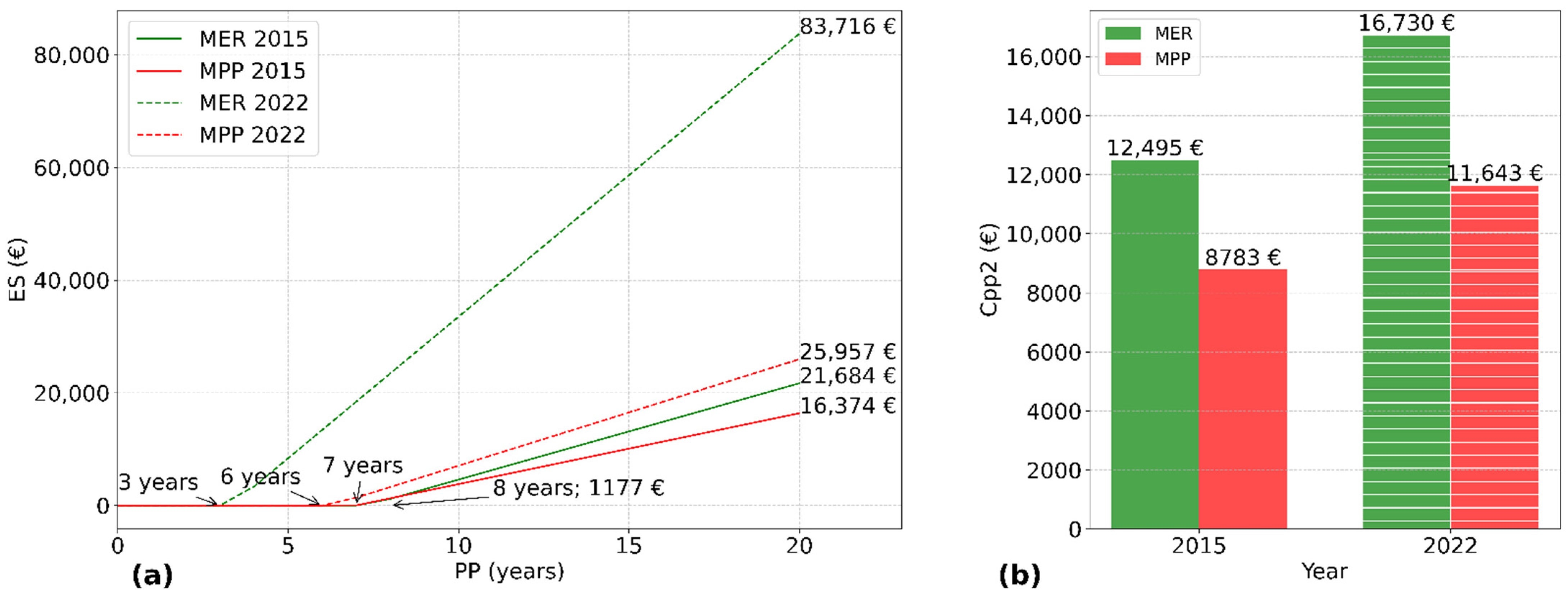To illustrate this, EPP1 was selected due to the marked differences observed between the MER and MPP objective functions under varying economic scenarios, as shown in Figure 8, using energy price and cost data from both 2015 and 2022. A 20-year average operational lifespan was considered for this type of installation in the analysis.

As shown in Figure 8a, in 2022, both objective functions yield similar PP values (approximately 6 years and 7 years) relative to the installation’s lifespan. However, there is a substantial difference in ES, amounting to nearly EUR 58,000 (EUR 83,716 vs. EUR 25,957) after 20 years of investment. This highlights the superiority of MER in terms of long-term profitability, provided the investor can afford higher initial investment. Indeed, Figure 8b shows that the investment cost difference in 2022 ($C_{PP2}$) is EUR 5087.00 in favour of MPP.

Conversely, a reverse trend in energy prices, returning them to values similar to those of 2015, combined with a decrease in installation costs, would make the MPP criterion more favourable. In this scenario, the difference in PP, shown in Figure 8a, narrows to similar values between 7 and 8 years, while the difference in ES to just over EUR 5000 (EUR 21,684 vs. EUR 16,374) between functions after 20 years. The difference in $C_{PP2}$ between both functions in 2015 is EUR 3712.00 (see Figure 8b). Taking costs into account, the final benefit would be around EUR 1598.00. This further reduces the relative advantage of MER, particularly when accounting for inflation and equipment depreciation. Under these conditions, the break-even point between the two options is reached in year 8, with net savings of only EUR 1177. This makes it difficult to justify the higher investment required for MER.

Given the sensitivity to energy and civil works costs, a multi-objective function could provide a single balanced result, while single-objective functions allow for the analysis of different outcomes that can be adapted to the context or convenience of various options (market trends, the economic capacity of the investor, sensitivity to carbon footprint, etc.), enabling the most suitable decision for each situation and expanding the range of possible solutions.

The developed model serves as a practical decision-making tool for identifying the optimal PAT configuration at hydrants with excess pressure in pressurised irrigation networks. By integrating hydraulic and economic criteria through single-objective functions, it enables the evaluation of profitability, investment effort, and ER. This allows stakeholders to tailor decisions to specific contexts—whether prioritising short PPs, maximising long-term ER, or adapting to market trends and investment capacities.

5. Conclusions

This research presents a single-objective optimisation framework using a PSO algorithm for the optimal selection and sizing of PAT-based ER systems at EPPs in pressurised irrigation networks. Two single-objective functions were analysed: maximising energy recovery (MER) and minimising payback period (MPP). The methodology proved effective, delivering logical and robust results, and enabling a comparative evaluation of technical and economic criteria under real operating conditions.

The results obtained for the reference year 2015 demonstrated substantial ER potential, with several EPPs achieving values above 40,000 kWh/year and competitive PPs below 5 years in most cases. However, specific cases such as EPP5 and EPP6 showed limited ER and extended PPs exceeding 10 years, and are not considered economically viable, highlighting the need for individualised assessments. The trade-off analysis between MER and MPP revealed that prioritising MER often incurs higher initial costs but results in only marginal increases in PPs (e.g., EPP3 and EPP8), making this strategy preferable when long-term energy yield is a priority and financing is accessible. Conversely, in unfavourable hydraulic scenarios, the MPP criterion becomes more suitable.

To address the economic uncertainty of recent years, a sensitivity analysis was conducted by incorporating updated energy tariffs and cost indices for civil and electromechanical works from 2022 and 2023. The results reveal a dramatic improvement in project viability due to rising energy prices, with PPs falling below 6 years across all EPPs in 2022, even for previously unfeasible cases like EPP5 and EPP6. These findings emphasise the necessity of including time-dependent economic variables in feasibility studies, particularly in volatile energy markets.

The advancements proposed in this research include the use of a flexible optimisation framework capable of independently evaluating multiple objective criteria; a comparative strategy for selecting PAT installations based on technical–economic trade-offs; and an extended temporal sensitivity analysis that highlights how evolving market conditions can radically alter investment decisions. These contributions support a more adaptive, cost-effective, and context-aware deployment of PATs in water–energy nexus projects.