A New Method for Camera Auto White Balance for Portrait

Abstract

Accurate skin color reproduction under varying CCT remains a critical challenge in the graphic arts, impacting applications such as face recognition, portrait photography, and human–computer interaction. Traditional AWB methods like gray-world or max-RGB often rely on statistical assumptions, which limit their accuracy under complex or extreme lighting. We propose SCR-AWB, a novel algorithm that leverages real skin reflectance data to estimate the scene illuminant’s SPD and CCT, enabling accurate skin tone reproduction. The method integrates prior knowledge of human skin reflectance, basis vectors, and camera sensitivity to perform pixel-wise spectral estimation. Experimental results on difficult skin color reproduction task demonstrate that SCR-AWB significantly outperforms traditional AWB algorithms. It achieves lower reproduction angle errors and more accurate CCT predictions, with deviations below 300 K in most cases. These findings validate SCR-AWB as an effective and computationally efficient solution for robust skin color correction.

1. Introduction

Skin color reproduction under different correlated color temperature (CCT) conditions has long been a critical topic in color science. Accurate and reliable skin color reproduction techniques have significant applications in portrait recognition [1], aesthetic photography [2], and human-computer interaction [3]. One of the key factors influencing skin color reproduction in digital photography is the accurate correction of white balance (WB), especially when converting images from RAW formats to standard output formats such as .JPG form. Under varying CCT conditions, changes in light sources can cause skin tones to appear distorted and unnatural. WB adjusts the color temperature in an image to eliminate color casts under different lighting conditions, making the image look more like the original scene [4]. However, the AWB algorithm faces many challenges when used on mobile devices, for example, smartphones, such as optical sensor performance limitations, algorithm complexity brought by mixed light source scenes, and limited chip computing resources [5]. Consequently, achieving precise white balance correction to ensure accurate skin color reproduction in complex lighting environments, while also maintaining algorithm simplicity and speed for seamless implementation on mobile devices, has become a significant technical challenge for many smartphone manufacturers today.

Traditional AWB algorithms rely on statistical assumptions about the image’s light source. One common assumption is that the average color of the image should be neutral gray, as defined by the GreyWorld algorithm [6], Perfect Reflector algorithm [7], Shades of Gray algorithm [8], and Grey-Edge algorithm [9]. Another assumption is that certain objects in the scene reflect the maximum amount of light, reaching saturation in at least one color channel, as in the Max-RGB algorithm [10] and Retinex algorithm [11]. These methods estimate AWB gain across the entire image using techniques like average grayscale or white point estimation.

However, traditional algorithms relying on global image statistics often assume uniform lighting environments, where the light source can be predicted through calculated gains. These assumptions frequently break down in complex scenarios, such as scenes with large uniform color areas (e.g., grass or sky) or extreme CCT. In such cases, relying on global color averages or edge-based information fails to achieve accurate white balance [12,13]. Similarly, brightness-focused methods or those using maximum value information perform well in brightly lit scenes but struggle in low light, monochromatic areas, or when no clear white reference points are available. Therefore, it is a good idea to consider the face as a color reference in the scene for AWB.

Previous studies [14,15,16] have also considered using skin color clustering as a clue for illuminant prediction. Traditional methods also face significant challenges in reproducing accurate skin tones under these conditions, primarily due to their inability to account for the complexity of real-world SPD. Moreover, the use of reflectance data and RGB data as fundamental concepts has been widely adopted in various color science applications, such as spectral image reconstruction [17,18]. Most of them have predominantly focused on light or East Asian skin tones. In contrast, reproducing dark skin tones poses a greater challenge due to their lower reflectivity and more complex spectral characteristics, especially under extreme CCT conditions or mixed illumination.

To address this challenge and better evaluate the robustness of the proposed algorithm, we specifically chose individuals with dark skin tones as the primary subjects in our experiments. Darker skin reflects less light in the shorter wavelengths due to higher melanin content, making it a stringent test case for white balance algorithms. Moreover, our empirical observation indicates that dark skin tends to exhibit greater inter-individual spectral variation than lighter skin tones, which further stresses the generalization capacity of the model.

Although this study focuses on dark skin individuals for the aforementioned reasons, our research team has already collected a comprehensive skin reflectance dataset across a diverse population, including Caucasian, East Asian, South Asian, and Middle Eastern groups [19]. Figure 1 demonstrates the spectral reflectance profiles of multiple ethnicities, indicating substantial variation across the spectrum. While these profiles were not the main focus of the experimental evaluation in this work, they were used during model development and motivation.

For colorists and camera manufacturers, achieving accurate skin tone reproduction requires overcoming the spectral differences among racial groups. However, conventional color correction techniques often struggle to maintain consistent skin tone appearance under varying lighting conditions, necessitating advanced computational models to enhance color fidelity. Moreover, AWB algorithms must be optimized to adaptively adjust for skin reflectance variations, ensuring color accuracy across diverse illumination environments. To address this, we propose incorporating actual skin reflectance data into the SPD computation, integrating skin color characteristics into the fundamental formula. This approach enhances the adaptability of traditional algorithms, enabling more precise skin tone reproduction in complex lighting scenarios while improving visual consistency and color fidelity.

In recent years, deep learning-based AWB algorithms have gained attention for their ability to handle complex lighting scenarios. For example, Bianco et al. [20] proposed a CNN-based model for both single and multiple illuminant estimation using raw image patches, achieving state-of-the-art accuracy. More recently, Choi [21] introduced DRANet, a deep residual architecture designed to enhance illumination estimation while maintaining a compact model size and strong generalization across varying lighting conditions and devices. By leveraging neural networks, these methods model intricate interactions within a scene to predict AWB gains [20,22,23,24]. However, most AI-based AWB models focus on spatial characteristics [6] rather than directly analyzing the spectral properties of light sources. Accurate skin tone reproduction, however, critically depends on interpreting the spectral distribution of light—an aspect often overlooked by existing AI-AWB approaches. Our work bridges this gap by emphasizing the spectral reflectance of skin tones, aiming to improve both traditional and AI-based AWB methods.

Purpose: To address these issues, this paper presents an SPD prediction AWB algorithm based on skin reflectance (SCR-AWB) that predicts the SPD using skin color information and real skin reflectance data. By directly tackling the challenges of spectral and color restoration in lighting environments with different CCT, particularly in scenarios involving dark skin color reproduction, SCR-AWB offers significant advancements over existing AWB technologies. The proposed algorithm has several key advantages:

Unlike traditional white balance algorithms, which rely on assumptions such as average grayscale or the brightest color channel in the image, SCR-AWB eliminates these dependencies. It can be applied to a variety of scenes where skin color information exists and establishes a connection with the skin color information in the image through the real skin reflectance information, thereby providing more accurate color reproduction results. In addition, more accurate SPD and CCT predictions can also be used in other key steps of the image processing pipeline. Compared to AI-AWB models, this method imposes fewer constraints on computational resources and model size, leading to improved computational efficiency. This makes it particularly well-suited for deployment in mobile devices and low-power environments, offering a practical solution with enhanced performance.

2. Materials and Methods

We propose a novel spectral prediction-based AWB algorithm, SCR-AWB, which leverages known skin reflectance and sensor sensitivity to estimate the scene’s SPD as Figure 2 shows. The pipeline includes raw image preprocessing (black level compensation and early demosaicing), followed by illuminant estimation based on segmented skin regions. The predicted SPD is used to compute the CCT and derive RGB gain values for global white balance correction.

The most important thing in the core of the algorithm is the prediction of the light source spectrum, which requires some known information: 1. Nonlinear RGB values representing skin color, obtained by segmenting and selecting skin color areas. 2. Skin reflectance information that can represent the race. 3. Basis vector values that match the light source type, including daylight and artificial light sources. 4. Sensor sensitivity function. The light source spectrum SPD predicted by the core of the algorithm is used to estimate CCT and calculate AWB gain and apply to the entire image for accurate white balance correction.

Unlike gray-world-based methods that rely on RGB-level statistical assumptions (e.g., average scene reflectance being gray), our approach predicts the SPD of the illuminant in the spectral domain. It explicitly models the physical interaction between the illuminant, surface reflectance, and sensor response, using prior knowledge of human skin reflectance and sensor sensitivity.

This spectral reflectance is then converted to an illuminant estimate through a physically grounded reflectance-illumination interaction model. Our method does not rely on the assumption of color constancy across the image or on the average reflectance being gray. Instead, it uses domain knowledge about human skin reflectance and sensor response, which is particularly beneficial in scenarios where skin regions are prominent in the scene.

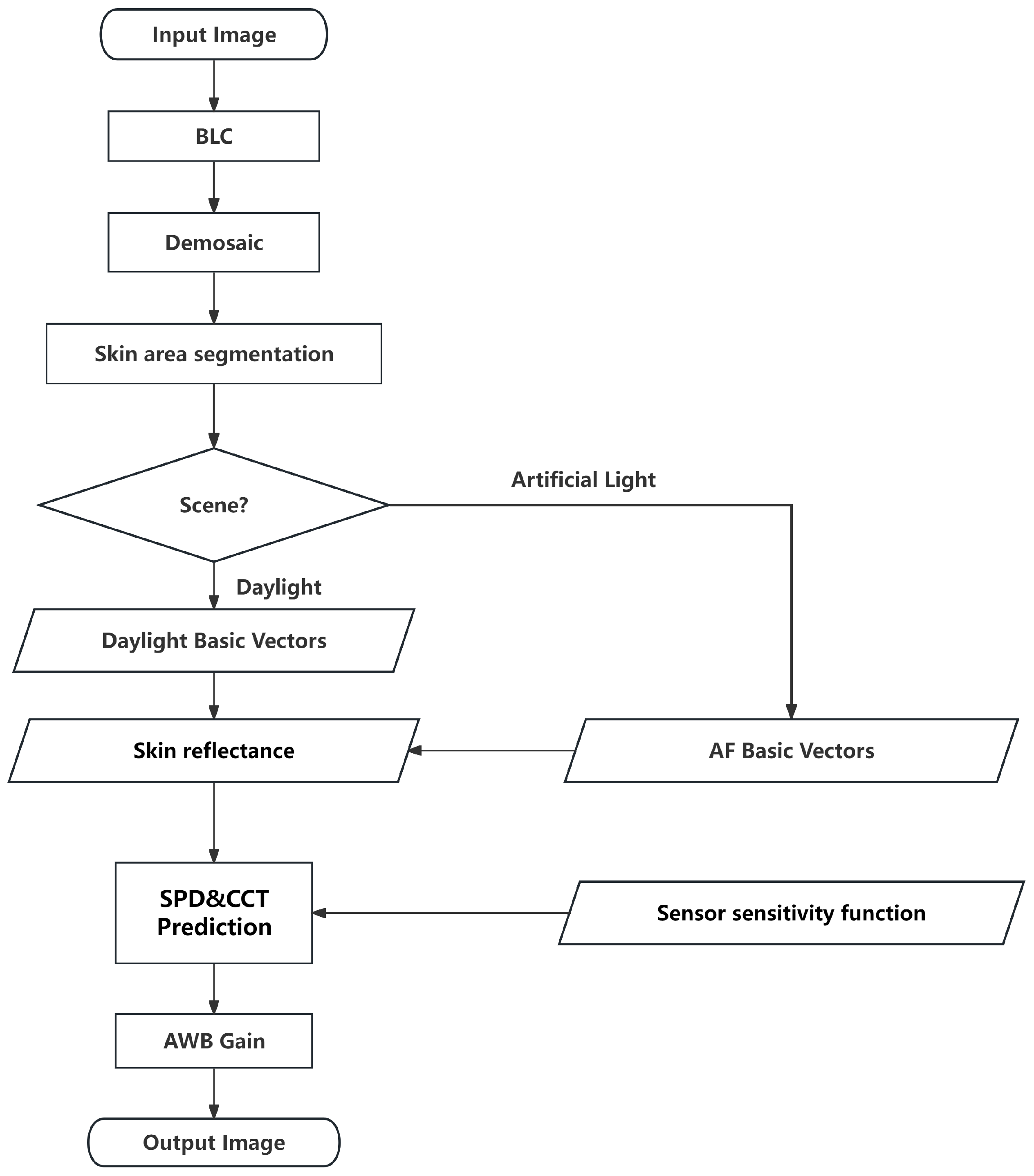
2.1. Theoretical Basis of SCR-AWB Algorithm

2.1.1. Spectral Estimation of Unknown Light Sources

The essential parameters required for the SCR-AWB algorithm include the RGB values of skin color pixels from the raw data, skin reflectance information, sensor sensitivity function data, and the basis vectors used to calculate the spectral power distribution of ambient light [25]. In the calculation, the skin reflectance information, sensor sensitivity function data, and basis vector data for calculating the SPD of ambient light are all prior information, while the RGB values of skin color pixels from the raw data are obtained from the image, and the parameter to be calculated is the light source spectrum.

The underlying principle of the proposed algorithm is derived from fundamental color equations, as outlined in Equations (1)–(3).

Assume that the image scene has the skin region (identified by segmentation techniques). Thus, we have the basic equations for each pixel in the skin region:

$$R=\kappa \int E\left(\lambda \right)r\left(\lambda \right)S_r\left(\lambda \right)d\lambda$$

(1)

$$G=\kappa \int E\left(\lambda \right)r\left(\lambda \right)S_g\left(\lambda \right)d\lambda$$

(2)

$$B=\kappa \int E\left(\lambda \right)r\left(\lambda \right)S_b\left(\lambda \right)d\lambda$$

(3)

Here, $E\left(\lambda \right)$ denotes the unknown SPD of the light source, $r\left(\lambda \right)$ is the skin reflectance spectrum, and $S_r\left(\lambda \right)$, $S_g\left(\lambda \right)$, $S_b\left(\lambda \right)$ represent the camera sensor’s spectral sensitivity functions for the red, green, and blue channels, respectively. $\kappa$ is a scalar representing the overall scene irradiance, which does not affect chromaticity.

Furthermore, we assume $E\left(\lambda \right)$ that need to be calculated can be a combination of three basis vectors, i.e.,:

$$E\left(\lambda \right)={\alpha }_1{E}_1\left(\lambda \right)+{\alpha }_2{E}_2\left(\lambda \right)+{\alpha }_3{E}_3\left(\lambda \right)$$

(4)

Thus, the solution of the unknown light source spectrum $E\left(\lambda \right)$ is converted into the solution of the ${\alpha }_1$,${\alpha }_2$,${\alpha }_3$ parameters. Let ${\lambda }_i$ be the wavelength values sampled uniformly at $\Delta \lambda$ intervals in the wavelength range. We can combine all the prior quantities on the right side of the equal sign in Equations (1)–(3) into $m_{j,p}$ and convert it into the form of numerical integration.

$$m_{j,p}=\kappa \sum _{i=1}^n{E}_p\left({\lambda }_i\right)r\left({\lambda }_i\right)S_j\left({\lambda }_i\right)\Delta \lambda ,j=r,g,b,p=1,2,3$$

(5)

Thus, let M be the 3*3 matrix formed by elements of the set of all prior quantities $m_{j,p}$ defined by Equations (5). The discretized system of algebraic equations of Equations (1)–(4) is given by Equations (6).

$$\left[\begin{array}{c}R\\ G\\ B\end{array}\right]=M\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ {\alpha }_3\end{array}\right]$$

(6)

Substituting all the raw RGB values and the set elements of the prior quantity calculated by Equation (5) into Equation (6), we can calculate ${\alpha }_1$, ${\alpha }_2$ and ${\alpha }_3$. Finally, the calculated ${\alpha }_1$, ${\alpha }_2$ and ${\alpha }_3$ are substituted back into Equation (4) to obtain the predicted SPD of the actual scene.

While early works, such as Barnard et al. [26] have proposed color constancy algorithms that incorporate both surface reflectance information and spatial illumination variation, their methods rely on statistical constraints and assume that reflectance and illumination can be simultaneously disentangled from RGB images through observed variation. In contrast, our method does not estimate surface reflectance from RGBs. Instead, it assumes the spectral reflectance of skin as a known prior and directly solves for the SPD of the illuminant by leveraging sensor sensitivity and a learned basis. This physically constrained inversion avoids the ambiguity typically associated with estimating both reflectance and illuminant from RGBs alone. Thus, although our approach shares the general goal of spectral recovery, it diverges significantly in methodology—offering a deterministic, prior-informed estimation pathway that avoids reliance on global statistical assumptions or spatial reflectance variation.

2.1.2. From Predicted Spectra to CCT

To derive CCT, the predicted SPD is first converted to tristimulus values via CIE 1931 color matching functions. Chromaticity coordinates are computed in the CIE1960 uv space, and CCT is estimated using the Robertson method with Newton-Raphson refinement [27,28].

2.1.3. From Predicted Spectra to Gain

After obtaining the predicted SPD of the light source, it can be substituted into the fundamental Equations (1)–(3) to calculate the RGB values of the white point under the given light source. Before adjusting the white balance, introduce a constant coefficient k that will be eliminated during calculation to represent the light intensity. Set $r\left(\lambda \right)=1$ as the white point reflectance, and then determine the RGB value of the white point by numerically integrating the visible spectrum.

Based on the calculated RGB values of the white point, the gain coefficient is calculated by the ratio between them, including $R_{Gain}=G/R$, $G_{Gain}=G/G$, $B_{Gain}=G/B$. These gain values are subsequently applied to correct the color balance in the image, ensuring accurate reproduction of white under the light source.

2.2. Parameter Acquisition

2.2.1. Prior Information Acquisition

In the algorithm process, the way of obtaining prior information and different parameter choices can significantly impact on both the accuracy and computational efficiency of the algorithm.

Regarding the acquisition of the spectral sensitivity function $S_j\left(\lambda \right),j=r,g,b$, we recommend using a monochromatic light generator to obtain an accurate sensor sensitivity function. However, even without a monochromatic light generator, there are other methods to estimate the spectral sensitivity of mobile device sensors. For example, the sensor can be characterized by capturing an image showing the colors on a display or using a color chart. Zhu et al. proposed a method in Optics Express that uses an orthogonal test design and window filtering, where colors are displayed on a screen and analyzed by camera capture to predict sensor response [29]. Similarly, Huynh and Robles-Kelly in their ICPR conference paper introduced a color chart-based approach (e.g., X-Rite ColorChecker) that uses an optimization algorithm to estimate spectral sensitivity [30].

For skin reflectance data, using the average reflectance calculated for different races can simplify the model and reduce the computational load. Measurements of skin reflectance for different races, collected using the using a spectrophotometer (CM-700d, KONICA MINOLTA, Inc., Osaka, Japan), reveal that skin reflectance varies among individuals due to a variety of factors. However, in most cases, the average reflectance calculated for each race effectively represents the overall skin color characteristics of that group. This approach reduces the deviation caused by outliers from extreme individuals, ensuring the model maintains broad applicability. Consequently, using average race-based skin reflectance can significantly reduce computational complexity and data collection costs while maintaining high algorithmic accuracy, making it particularly suitable for mobile device applications. It is also worth noting that, when computational resources allow, skin reflectance data can account for individual differences. This suggests that future algorithms could be further improved by adopting more personalized approaches tailored to individual skin tones, providing room for advancement in customized solutions.

To reduce computational costs, the basis vectors of the light source can be pre-calculated and stored as fixed values. These basis vectors are obtained by performing singular value decomposition (SVD) on large-scale datasets of similar light sources. For instance, by collecting daylight spectrum data across different time periods and weather conditions, the basis vectors that cover various daylight scenarios can be computed. Similarly, for artificial light sources, basis vectors can be derived from comprehensive artificial light source databases. We derive a set of basis functions for all artificial light sources, from tungsten to daylight fluoresent, via every fluoresent combination, LED combination, high pressure mercury, etc. These pre-calculated vectors can be embedded into the algorithm, significantly reducing the computational load during subsequent processes.

The SVD process can be described as follows: Assume that each piece of spectral information of the spectral data of the light source is taken as a column vector to obtain the spectral matrix A. By applying SVD, we decompose A into Equation (7).

$$A=U\Sigma V^T$$

(7)

where U is an 81*81 orthogonal matrix (assuming the spectral range is set to 380–780 nm with an interval of 5 nm), satisfying Equation (8).

$$U^{T}U=U{U}^T=I$$

(8)

with I being the identity matrix. The column vectors of U, called left singular vectors, are the eigenvectors of the matrix $A{A}^T$. The singular value $\Sigma$, a diagonal matrix, contains the singular values of A, which represent the importance of various features in the spectral data of the light source.

In this algorithm, the basis vectors are composed of the first few column vectors of matrix U, typically selecting the top three left singular vectors to capture the most significant characteristics of the light source. These basis vectors represent the major variation trends of the spectral data under different environmental conditions, eliminating the need for real-time recalculations in each instance.This pre-computation step significantly reduces computational overhead during algorithm execution.

It is worth noting that for specific lighting scenarios in AWB, one only needs to collect the spectral data of the specific scene and calculate the relevant basis vectors using SVD. This allows SCR-AWB to be quickly and accurately applied, ensuring precise color reproduction in those environments.

2.2.2. Image Information Acquisition

Based on the determined prior parameters, the linear RGB information obtained from the image will be a clue to calculate the light source spectrum. If the computing power is sufficient, a light source spectrum can be calculated for each pixel in the facial area.

However, due to the computing power limitations of mobile devices, this article recommends using the median for segmented or selected facial skin color areas when using the SCR-AWB algorithm on mobile devices. The reason for choosing the median is its robustness, as it minimizes the influence of extreme values or outliers—such as highlights or localized overexposure under different lighting conditions—on the algorithm. Additionally, when certain areas of the skin are subjected to varying degrees of illumination, leading to potential errors, the median helps reduce these errors and provides a more stable representation of skin color. Finally, due to the inherent non-uniformity of skin color, using the median avoids excessive smoothing of data, which would otherwise diminish important skin tone details.

3. Experiments

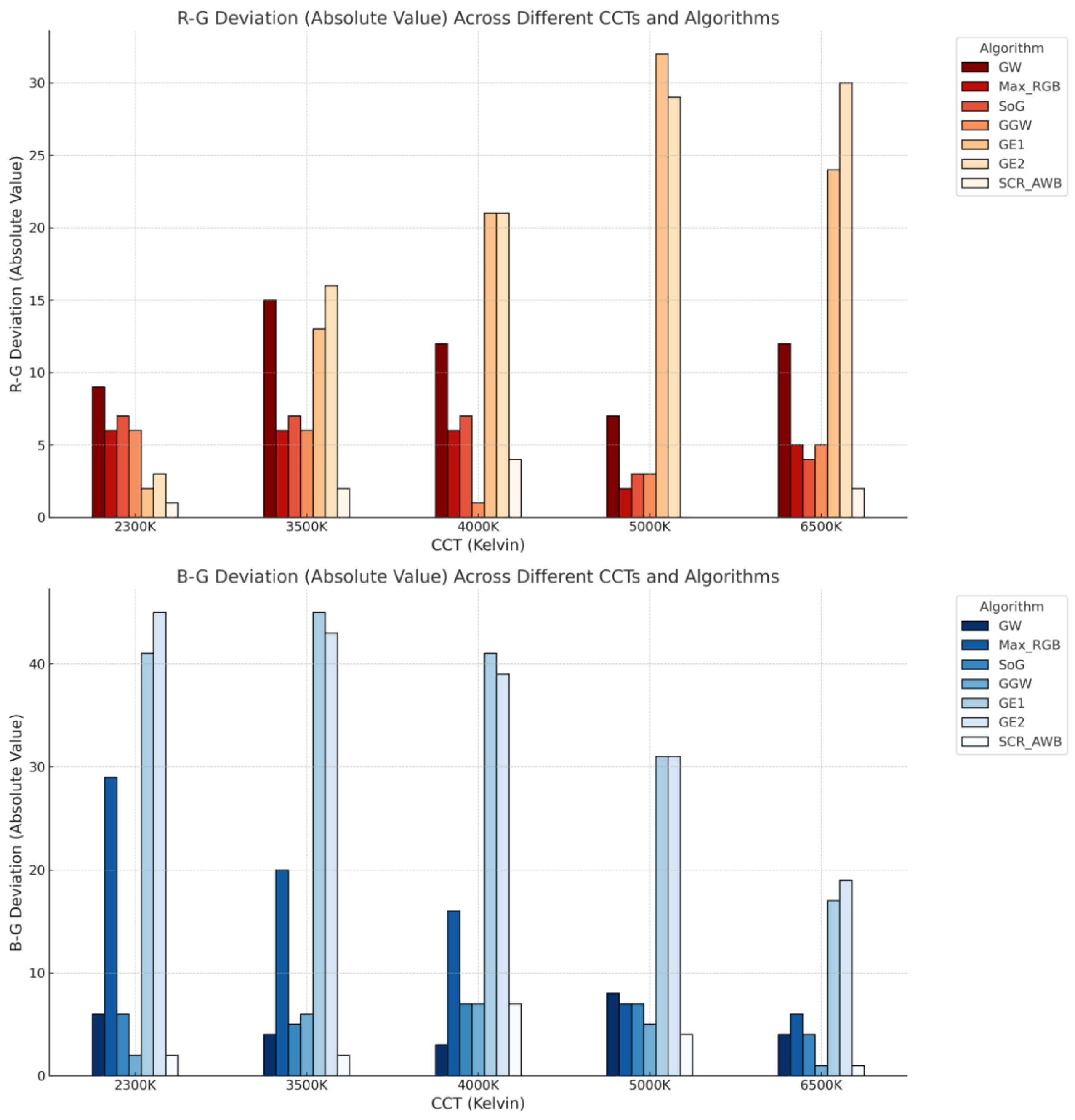
3.1. Experiment 1: Color Chart White Point and Neutral Gray Evaluation Under Different CCT Artificial Light Sources

This experiment aimed to test the white balance effect of SCR-AWB and other AWB algorithms in the color card white point and neutral gray area under artificial light environments with different CCT, and evaluate the basic AWB effect of the algorithm by evaluating whether the values of the R, G, and B channels in these areas are close to equal.

Experimental settings: The experimental location was located in the Lighting Lab, School of Design, University of Leeds, Leeds, UK. The experiments were conducted using the THOUSLITE LEDCube, an advanced spectrally tunable lighting system designed to simulate a wide range of lighting environments. Key features of the LEDCube include its ability to simulate CCT ranging from 2000 K to 20,000 K, offering precise control over the color rendering index (CIE Ra) and Duv values. This flexibility allows for the reproduction of lighting conditions from warm tungsten light to cool daylight, ensuring a controlled and reproducible environment for testing. In our experiments, the LEDCube provided stable, flicker-free lighting with adjustable intensity, ensuring consistency across all test conditions. As Figure 3 shows, a variety of artificial light sources with common CCT values were selected, including a total of 5 light environments from warm light to high color temperature light. The specific CCT settings are: 2300 K, 3500 K, 4000 K, 5000 K, 6500 K. The light environment includes common D50 and D65 light sources to ensure that the spectral distribution of each light source is representative.

The color chart used in this experiment is the Dark Skin Tone Chart, developed by the University of Leeds for Shenzhen Transsion Holdings Co., Ltd. (Shenzhen, China) While the full chart contains multiple patches representing dark skin tones, only achromatic patches (white and neutral gray) were used in this study due to patent and copyright restrictions.

Under standard D65 lighting conditions, the spectral reflectance properties of the white and gray patches on the chart were measured using a calibrated spectrophotometer(CM-700d, KONICA MINOLTA, Inc., Osaka, Japan) to match the reflectance values of an X-Rite ColorChecker, and the reflectance uniformity and calibration accuracy of the achromatic patches were verified in a controlled laboratory environment. The white and gray areas exhibit minimal color differences across the entire visible spectrum, ensuring their reliability as white balance references.

Images of the colour chart were captured under different CCT conditions using the smartphone Tecno AD9. During the experiment, the shooting parameters of the device were kept constant (aperture f/1.8, International Organization for Standardization sensitivity (ISO) 203, exposure time 1/100 s, focal length 7 mm) to ensure consistency and minimize external factors such as exposure variations or sensor noise. In our experiments, we used a single device, and the sensor sensitivity function was specifically matched to the device, so manufacturing tolerances did not affect our experimental results. The images were collected under strictly controlled shooting angles and lighting environments to ensure consistency across all test scenes. Each set of images was initially recorded as Raw (.tiff form) files, without any white balance correction. As Figure 4 shows, Black Level Correction (BLC) will be performed during the algorithm processing, and AWB and demosaic interpolation steps will be performed to obtain basic three-channel AWB output.

The parameter configuration for the SCR-AWB algorithm in this experiment is as follows: The three-channel sensitivity function of the sensor was derived using measurements obtained with a monochromatic light generator.The skin reflectance used in the SCR-AWB algorithm was obtained through direct spectral measurements of the 4J skin color patch on the physical color chart, using a calibrated spectrophotometer (CM-700d, KONICA MINOLTA, Inc., Osaka, Japan) under built-in standardized D65 illumination. This patch was selected for its close match to real dark skin tones and serves as a reliable prior in the spectral prediction process.

Building on the framework proposed by van de Weijer, which utilizes different parameter configurations (Minkowski norm p and standard deviation $\sigma$ [9], the commonly used traditional AWB algorithms and their parameter settings, recommended by researchers for control experiments based on low-level image statistics, are summarized as follows [31,32,33]:

Grey World (GW): p = 1, $\sigma$ = 0

White Point (Max-RGB): p = ∞, $\sigma$ = 0

Shades of Grey (SoG): p = 4, $\sigma$ = 0

General Grey World (GGW): p = 9, $\sigma$ = 9

1st order Grey Edge (GE1): p = 1, $\sigma$ = 6

2nd order Grey Edge (GE2): p = 1, $\sigma$ = 1

In addition to comparing our approach with traditional methods, we incorporated an AWB model that leverages skin color cues. Specifically, Bianco et al. proposed an adaptive color constancy algorithm that utilizes skin color histograms to identify facial regions [20], followed by a Von Kries transform to estimate and correct scene illumination [34]. Furthermore, we included the deep learning-based sRGB color reproduction model introduced by Afifi et al. for comparison [35]. Since this model operates on sRGB images, it was applied to JPG images generated with $R_{Gain}=1$ and $B_{Gain}=1$. In contrast, other models were evaluated using the original Raw images. As a result, the comparison at the $I_{\mathrm{RAW}}$ image level in

Table 1. Comparison of white point reproduction angle errors of $I_{\mathrm{RAW}}$ using different AWB algorithm in experiment 1. $I_{\mathrm{RAW}}$ represents images captured after AWB and demosaic interpolation but without further steps. The asterisk next to the algorithm name represents the p-value of the paired t-test of SCR-AWB (* represents p < 0.05, ** represents p < 0.01).

Algorithm	Mean	Median	Best 25%	Worst 25%	Maximum
GW **	3.20 ± 1.10	3.14	2.58	3.98	4.19
Max-RGB	4.79 ± 4.07	3.75	2.70	6.14	9.82
SoG *	2.41 ± 1.03	2.59	2.17	3.03	3.16
GGW *	1.96 ± 0.50	1.92	1.70	2.00	2.60
GE1 **	10.45 ± 2.92	10.58	9.27	12.04	13.01
GE2 **	10.86 ± 3.15	10.87	8.95	11.36	14.99
Bianco’s [20]	3.45 ± 3.99	2.31	1.73	3.57	8.90
SCR-AWB	0.88 ± 0.55	0.87	0.50	0.98	1.57

does not include this model.

The evaluation of the experimental results consists of two parts. First, following the methodology proposed by Zapryanov et al. [4], the tonal consistency of the AWB algorithm was assessed using different grayscale regions. Second, based on the studies by Li et al. [36] and Tan et al. [37], the recovery angle error and reproduction angle error were calculated using the gray area error and white point error.

The tonal consistency evaluation of the AWB algorithm was to compare the three-channel differences of color blocks with five different grayscale regions (from white to darker gray) in the color chart. For these color blocks, the absolute values of the deviations between the R channel and the G channel, and between the B channel and the G channel were calculated respectively, taking their G channel as the reference, so as to quantitatively obtain the influence of different algorithms on the color reproduction of the B channel and the R channel under different CCT conditions.

In addition to assessing the tonal consistency of the AWB algorithm, this study will calculate angle errors across different color regions to evaluate the color accuracy and reproduction quality of various AWB algorithms. The image data selection includes both linear RGB data (denoted as $I_{RAW}$), captured after AWB and demosaic interpolation but without further steps like CCM and Gamma correction, and the final nonlinear sRGB color data (denoted as $I_{JPG}$), which represents the output after the complete image processing pipeline.

For the grayscale region, due to minimal color difference without brightness adjustments, $I_{RAW}$ only uses the white point to calculate the reproduction angle error. For $I_{JPG}$, grayscale region errors will be calculated using five gradient grayscale values, with the average recorded as the recovery angle error, and the reproduction angle error calculated from the white point. The angle error measurement formula is as follows:

$$\Delta \theta =arccos\left({\displaystyle \frac{e_j·e_e}{\parallel e_j\parallel \parallel e_e\parallel }}\right)$$

(9)

With $e_e$ as the mean RGB value of the estimated light source and $e_j$ as the RGB target AWB value, where the G channel serves as the reference and $e_j$ is set to R = G = B. To evaluate performance, this study uses the mean angle error, median angle error, first quartile (Q1), third quartile (Q3), and maximum angle error—metrics considered suitable for algorithm assessment. Here, the first and third quartiles, Q1 and Q3, represent the 25% and 75% distribution points of the angle error, respectively.

3.2. Experiment 2: Skin Color Reproduction Under Different CCT Artificial Light Sources

The purpose of this experiment is to test the skin color reproduction effect of SCR-AWB under artificial light environments with different CCT and compare it with the mature low-level statistic-based AWB algorithms. The experimental design is as follows:

Experimental settings: The setting of basic experimental environment is the same as that of Experiment 1 expect CCT settings. The specific CCT settings are: 2300 K, 3500 K, 4000 K, 5000 K, 6000 K, 6500 K, 8000 K. A lower color temperature (2300 K) and an extremely high color temperature (8000 K) than the A light source are set to cover the common color temperature range under different lighting conditions. The illuminance of the facial area of the subjects was adjusted to 500 lux, and the light level in this area was measured using a (CS-2000, KONICA MINOLTA, INC., Osaka, Japan) spectroradiometer to ensure that the lighting conditions met the experimental requirements.

Image Acquisition: The image acquisition for this experiment was approved by the AHC Faculty Research Ethics Committee of the University of Leeds (Ethics Approval: LTDESN-189). All collected images containing human faces and skin color data are strictly managed in accordance with ethical standards, and all participants provided written informed consent. A total of 14 participants (3 males and 11 females) with varying skin color characteristics were selected to ensure the generalizability of the experimental results. The subjects were photographed in front of a white wall or a colored curtain. Prior to capturing facial skin color images, it was ensured that the participant’s facial texture is carefully controlled by eliminating potential influencing factors such as makeup and perspiration. This helped to ensure the accuracy of both skin color and skin reflectance measurements. Images of the participants were captured under different CCT conditions using the smartphone Tecno AD9. During the experiment, the shooting parameters of the equipment were the same as those in Experiment 1. Each set of images was initially recorded as Raw (.tiff form) files, without any white balance correction.

In this experiment, the parameters of the SCR-AWB algorithm were set as follows: the RGB information input for predicting the light source comes from the entire facial area of the subject. The facial area was selected by a rectangular box and the median was taken through a Matlab program to avoid the influence of local highlights. For other parameters of the algorithm input, please refer to the parameter setting part in the Method above. The artificial spectral basis vector data used in this study was derived from the SPD dataset collected by KV Houser in 2012, which comprises 401 unique SPD profiles of various light sources [38]. The sensor sensitivity function of Tecno AD9 was used in the experiment. The skin reflectance data came from the real dark skin color data collected at the University of Dar es Salaam, Tanzania using a spectrophotometer (CM-700d, KONICA MINOLTA, INC., Osaka, Japan) spectrophotometer. A five-point sampling method was used for the facial skin color area according to the research of [39,40]: the forehead, right cheek, left cheek, chin, and neck, were collected, which contained a total of 1419 skin reflectance spectra and L*a*b* data. The three-dimensional L*a*b* data is divided into a*b* and L*a* according to the research of [41], and the two-dimensional scatter plot of L*b* is shown in Figure 5. The distribution of these data explains why we use dark skin data for algorithm verification.

The main reason for choosing dark skin people as experimental subjects is that the reflectivity of dark skin is lower, and its color correction task is more challenging than other skin colors. In addition, since the algorithm uses the average skin reflectivity of a specific race, the individual differences of dark skin people are greater than those of other races, so it can be used as an effective test scenario to evaluate the robustness and applicability of the algorithm.

The evaluation of skin color reproduction involves both CCT prediction accuracy and image quality assessment, providing a comprehensive analysis of the algorithm’s capability to deliver accurate and visually pleasing results under diverse lighting conditions. The evaluation is divided into two main components:

1.

Comparison of SCR-AWB Algorithm Predicted CCT with Calibrated Laboratory CCT: As outlined in the methodology, the SCR-AWB algorithm predicts the SPD, which is then converted to CCT. White balance accuracy is assessed by calculating the difference, $\Delta CCT$, between the algorithm-predicted CCT and the actual calibrated CCT, measured using a spectroradiometer (CS-2000, KONICA MINOLTA, Inc., Osaka, Japan). A smaller $\Delta CCT$ indicates a closer match between the predicted ambient light and actual lighting conditions, thereby enhancing white balance performance.

2.

Evaluation of AWB Results on sRGB Output for DCI-P3 Display: The SCR-AWB algorithm outputs both CCT and gain values for the R and B channels. These gain values are applied in the image processing pipeline to adjust white balance, resulting in the final output in sRGB format (JPEG). Other AWB algorithms used for comparison also modify only the R and B channel gains, ensuring that BLC, CCM, Gamma correction, and other processing steps are kept consistent across all algorithms for an accurate evaluation of white balance adjustments.

This dual approach provides a robust evaluation framework for assessing both the technical and visual performance of the SCR-AWB algorithm in reproducing skin color across varied lighting conditions.

We do not employ image similarity metrics such as PSNR, SSIM, or $\Delta$E, as our method operates on RAW data and outputs color-corrected images via a controlled spectral reconstruction process. In contrast, reference JPEGs captured by consumer devices undergo multiple proprietary ISP steps, making fair and reproducible pixel-level comparisons infeasible.

The verification experiment of the SCR-AWB algorithm proposed in this paper was run on a laptop with Matlab 2023a and an AMD Ryzen 7 5800H CPU. The proposed algorithm runs at 0.0718 s per image and uses only 8.36 MB of memory in MATLAB, demonstrating a highly efficient balance between computational cost and correction performance. This suggests feasibility for real-time or near real-time deployment on resource-constrained devices after appropriate optimization.

4. Results

The results of Experiment 1 and Experiment 2 are as follows:

In this study, an analysis of R-G and B-G deviation values across various CCT as shown in Figure 6 demonstrated that the SCR-AWB algorithm significantly outperforms other methods in color reproduction accuracy. SCR-AWB consistently exhibited deviation values near zero between R-G and B-G channel under all tested color temperatures, showcasing superior stability and precision in white balance adaptation. In contrast, other algorithms, including GW, Max-RGB, and SoG, display comparatively larger deviations and greater fluctuation across color temperatures, indicating lower reliability in color correction performance. Although some algorithms show slight improvements at higher CCT 5000 K and 6500 K, their overall performance remains suboptimal compared to SCR-AWB. Therefore, SCR-AWB’s adaptability and accuracy across varying color temperatures highlight its suitability as the preferred method for white balance correction.

Table 1 shows the reproduced angular errors of different AWB algorithms applied to $I_{RAW}$ in experiment 1, using the same original image and BLC, with only $R_{Gain}$ and $B_{Gain}$ vary. The asterisk next to the algorithm name represents the p-value of the paired t-test of SCR-AWB (* represents p < 0.05, ** represents p < 0.01) The Mean with 95% confidence interval and Median values indicate the general accuracy of each algorithm. SCR-AWB achieves the lowest mean (0.88°) and median (0.87°) errors, confirming its precise estimation of white points across diverse lighting conditions. To assess stability, we examine the Worst 25% and Maximum error values. SCR-AWB again outperforms all other methods, with a maximum error of only 1.57°, and worst-case error under 1°, which is significantly lower than all baseline methods. This suggests that SCR-AWB not only performs well on average but also maintains consistent performance under the most challenging CCTs. In contrast, methods like Max-RGB and Bianco’s model, despite acceptable median values, show large maximum errors (up to 9.82° and 8.90° respectively), implying greater performance fluctuation across scenes. GE1 and GE2, with high means and large error spread, clearly struggle with extreme lighting conditions.

Table 2. Comparison of Recovery and Reproduction Angle Errors on $I_{\mathrm{JPG}}$ in experiment 1. $I_{\mathrm{JPG}}$ means the final nonlinear sRGB color data. The asterisk next to the algorithm name represents the p-value of the paired t-test of SCR-AWB (* represents p < 0.05, ** represents p < 0.01).

Algorithm	Recovery Angle Error					Algorithm	Reproduction Angle Error
	Mean	Median	Best 25%	Worst 25%	Maximum		Mean	Median	Best 25%	Worst 25%	Maximum
GW **	2.76 ± 0.65	2.39	1.66	3.18	8.15	GW	1.89 ± 0.89	1.73	1.30	2.39	2.86
Max-RGB **	3.84 ± 1.48	2.65	0.92	5.40	11.77	Max-RGB	3.81 ± 4.95	2.52	0.76	5.40	9.98
SoG **	1.97 ± 0.42	1.76	1.39	2.54	4.63	SoG *	1.62 ± 0.85	1.43	1.35	1.89	2.63
GGW **	1.98 ± 0.50	1.38	1.10	2.53	5.68	GGW	1.85 ± 0.50	1.86	1.27	2.48	2.48
GE1 **	11.07 ± 1.61	10.49	8.38	13.66	19.08	GE1 **	9.73 ± 4.62	8.52	6.61	13.66	13.71
GE2 **	10.94 ± 1.68	10.51	7.13	12.44	18.05	GE2 *	10.21 ± 5.80	10.51	6.18	11.41	17.24
Bianco’s [20] **	1.73 ± 0.40	1.58	1.01	2.31	4.36	Bianco’s [20]	1.93 ± 1.20	1.87	1.84	1.91	3.39
Afifi’s [35] **	8.13 ± 2.99	5.59	2.47	13.66	22.71	Afifi’s [35]	8.84 ± 10.68	5.19	2.47	15.23	20.52
SCR-AWB	1.16 ± 0.23	1.08	0.83	1.29	3.01	SCR-AWB	0.91 ± 0.43	0.95	0.63	1.12	1.35

shows the recovery angle error and reproduced angle error of different AWB algorithms applied to $I_{JPG}$ in experiment1, while the asterisk next to the algorithm name represents the p-value of the paired t-test of SCR-AWB (* represents p < 0.05, ** represents p < 0.01). In the entire image processing pipeline, the same color temperature group uses the same original image, and the process parameters such as BLC, CCM and Gamma correction are set the same, and only $R_{Gain}$ and $B_{Gain}$ are different. According to the evaluation results on JPG images under CCT conditions in Table 2, GW, SoG and Bianco’s method can also show moderate errors on JPG images, while the larger Q3 and Maximum data indicate that Max-RGB algorithms are greatly affected by CCT and are limited in scene use. The deep learning-based method of Afifi et al. showed instability in low color temperature areas such as 2300 K, but showed good results at 6000 K or 6500 K. From the table, SCR-AWB achieves the lowest mean with 95% confidence interval and median angle errors in both recovery and reproduction metrics, clearly indicating its high accuracy across scenes. Furthermore, the SCR-AWB algorithm also exhibits the smallest maximum errors and lowest worst-25% errors among all tested methods, demonstrating strong stability even under challenging CCT conditions. The low spread and minimal peak errors of SCR-AWB shows both its robust generalization across lighting conditions.

In addition, the SCR-AWB algorithm is designed to process images containing scenes with skin tones.

Table 3. The CCT prediction results of the SCR-AWB algorithm on real subject images in artificial light environments with different CCT in experiment 2. $\Delta CCT$ represents the difference between the predicted value and the calibrated value.

Scene	Mean	Median	Best 25%	Worst 25%	Maximum
2300 K	97	93	51	101	252
3500 K	63	60	15	109	132
4000 K	52	35	24	75	114
5000 K	149	147	141	169	215
6000 K	231	138	65	383	560
6500 K	264	213	170	288	542
8000 K	381	299	208	435	1326

highlights the differences between the CCT prediction results of the SCR-AWB algorithm across various artificial light source scenes and the actual calibrated scene CCT. For most scenes with CCT below 6500 K, the SCR-AWB algorithm demonstrates high accuracy, with $\Delta CCT$ values remaining below 300 K. In general, smaller $\Delta CCT$ values indicate better color fidelity, with images exhibiting colors that align closely with real-world conditions. This ensures that skin tones appear natural to the majority of ordinary viewers.

In scenes with 8000 K CCT, the algorithm still achieves a satisfactory median $\Delta CCT$, though some extreme cases exhibit significant deviations ($\Delta CC{T}_{Max}$ = 1326). The impact of these extreme deviations does not cause particularly obvious color differences when observed by the naked eye, as illustrated in Figure 7. This discrepancy is primarily due to the algorithm’s use of the mean reflectance of dark skin tones as a general model for all skin color scenes. Consequently, the prediction does not account for extreme variations in an individual’s skin tone, resulting in very dark skin being reproduced as a chocolate-like color. At present, the implementation focuses solely on accurately estimating the light source spectrum of the primary scene and does not incorporate factors such as color preference or chromatic adaptation.

As demonstrated in Figure 7 and Figure 8, for subjects with substantial differences in skin tone, the SCR-AWB algorithm still delivers visually acceptable skin color reproduction. In contrast, algorithms based on the brightest white point assumption, led by Max-RGB, produce greenish results under high CCT conditions. This issue arises because, in well-illuminated scenes, the maximum values of the green channel, the red and the blue channels are close to 65,535 (16 bit Raw Iamge). Consequently, the algorithm applies lower $R_{Gain}$ and $B_{Gain}$ values and even in extreme cases they approach 1, resulting in green-dominant output. Additionally, in traditional white balance algorithms such as GreyEdge, the parameter p significantly influences overall color reproduction. However, further investigation is required to fully understand the impact of p variations on color accuracy.The skin color reproduction algorithm proposed by Bianco et al. demonstrates limited robustness across varying color temperature conditions [20]. In general, it tends to render skin tones as brighter, without adequate accounting for the characteristics of individuals with darker skin. In contrast, the deep learning-based algorithm by Afifi et al. [35]. produces more stable results, but the images exhibit a slight greenish tint.

5. Discussion and Conclusions

Using skin color information as the basis for image AWB has been considered an effective approach in previous studies, but the simple use of skin color clustering statistics [14,15,16] cannot account for the complexity of real-world SPD. In contrast, we developed the SCR-AWB algorithm, which leverages real measured skin reflectance data. Together with a sensor sensitivity function that matches the device, the spectral characteristics of the light source are accurately captured through basic formulas, providing accurate SPD and CCT predictions. By integrating real skin reflectance data, it achieves more realistic and faithful skin color reproduction.

Experimental results demonstrate that the SCR-AWB algorithm delivers robust color reproduction performance across various CCT scenes, owing to its reliance on measured skin reflectance rather than extensive statistical analyses. Consequently, the algorithm does not require large-scale image databases for training, making it highly adaptable. By simply updating the sensor sensitivity functions, it can be directly transferred to new sensor models without additional training. Compared to other algorithms, SCR-AWB provides additional data beyond the standard $R_{Gain}$ and $B_{Gain}$ values, including predictions of scene SPD and CCT. These predictions can support other stages of the image processing pipeline, such as more accurate CCM applications. However, this aspect of the algorithm’s capabilities falls outside the scope of this article and is not discussed in detail. To be concerned, our input RGB assumption aligns with the parameters in standard ISP pipeline in industrial applications. Our proposed method is based on the assumption of linear RGB responses, which corresponds to white balance processing on raw images. If the RGB responses are nonlinear, the direct correspondence between RGB values, illuminant spectra, skin reflectance, and sensor sensitivity functions (as described in Equations (1)–(3)) no longer holds. Consequently, our method would not be applicable in such cases. Nonlinear RGB responses often indicate that white balance is being performed on JPEG images rather than raw images. While using JPEG images as datasets provides the advantage of large sample sizes, it introduces a more complex mapping between RGB values and illuminant spectra. Many deep learning-based AWB methods adopt this approach; however, they impose significant computational demands, making them challenging to deploy on mobile devices.

In contrast, the SCR-AWB algorithm is computationally lightweight, as it avoids the use of deep neural networks or large-scale iterative optimization. The core computation involves spectral caculation using pre-measured reflectance and sensor sensitivity data, followed by solving a constrained linear system, which can be efficiently implemented on mobile processors. As such, the algorithm is well suited for deployment on edge devices or embedded systems where memory and processing resources are limited. In contrast to deep learning-based AWB methods, which often require substantial computation and memory overhead for inference, SCR-AWB offers a practical and efficient alternative for real-time white balance correction on resource-constrained platforms.

While our evaluation includes several conventional AWB methods and one learning-based baseline, we acknowledge that more extensive comparisons with modern deep learning-based AWB approaches would further contextualize our results. However, many recent deep learning methods operate in the RGB domain and rely on private training datasets, limiting reproducibility and fair benchmarking. Our future work will aim to incorporate such comparisons as reproducible benchmarks become more accessible.

Based on previous research in our laboratory, we have collected skin reflectance data for multiple different ethnic groups, including blacks, whites, white skin, East Asians, Chinese, Saudis, etc. [19]. We acknowledge that the current experiments do not yet include extensive quantitative evaluations across all skin types. In future work, We plan to further expand the dataset and recruit more subjects in future research. And then conduct broader testing with a balanced representation of different ethnicities to more rigorously assess the algorithm’s generalizability across skin tones.

While the proposed method is designed to work under various lighting conditions, the current evaluation focuses on laboratory environments with precisely controlled illumination and known spectral distributions. This allows for rigorous validation of the spectral-based white balance framework. Real-world, uncontrolled scenes (e.g., outdoor daylight, mixed lighting) present additional challenges due to environmental variability and unknown scene content. Extending our evaluation to such scenarios is part of our ongoing research and will be addressed in a future publication.

However, the limitations of the SCR-AWB algorithm are also evident. Its performance depends on the presence of skin color regions in the scene, and it is specifically designed to process images containing human skin tones. For images featuring only natural landscapes or scenes without human skin, the algorithm cannot deliver optimal color reproduction, as its design is fundamentally based on skin reflectance data. Furthermore, while the algorithm ensures authenticity in skin color reproduction, it does not consider subjective color preferences.

Due to intellectual property restrictions and confidentiality agreements with our industrial partner, we are unable to release the full sensor sensitivity data, pre-processing code, or model implementation at this time. However, to support academic exchange, we are willing to share limited portions of the code and data upon reasonable request. Interested researchers may contact the corresponding author via email, and access may be granted on a case-by-case basis, subject to approval.