The Tuning of a CFD Model for External Ballistics, Followed by Analyses of the Principal Influences on the Drag Coefficient of the .223 Rem Caliber

Abstract

This paper presents the subject of external ballistics. The presented research employs a contemporary methodological approach, integrating theoretical analysis, CFD simulations, and experimental measurements. External ballistics is characterized by a wide spectrum of physical phenomena that influence projectile trajectory. This contribution focuses on the analysis of drag force acting on a .223 rem caliber projectile in both subsonic and supersonic regimes. Based on experimental findings, a CFD model was refined and subsequently used to evaluate the drag force and drag coefficient, with a comparative analysis performed against G1 and G7 ballistic coefficient functions. Furthermore, the effect of the barrel length on the resultant outcome was assessed. The validated CFD model was employed to analyze the characteristics of shock waves generated at the projectile’s nose and their impact on the drag force, along with the influence of ambient temperature, particularly within the supersonic domain.

1. Introduction

This paper forms part of an extensive investigation into supersonic flow at low pressures, conducted at the Institute of Scientific Instruments of the Czech Academy of Sciences in collaboration with the Department of Electrical and Electronic Technology, Faculty of Electrical Engineering and Communication, Brno University of Technology. This research focuses on the environmental scanning electron microscope (ESEM), wherein two regions of significant pressure gradients are separated by a small aperture fitted with a nozzle, thereby inducing supersonic flow. This type of electron microscope enables the observation of wet samples, samples in their native state, and under in situ conditions [1,2,3,4].

Since this research is part of the multidisciplinary ESEM problem and concerns the area of supersonic gas flow during pumping of vacuum system chambers, which includes, among other things, flow around the tips of the static Pitot tube probe at supersonic speed, the research has also been extended to the area of external ballistics. This research employs a modern approach that combines the physical theory specific to the problem, computational fluid dynamics (CFD) simulations, and experimental sensing [5,6].

External ballistics, as will be elucidated further, encompasses a wide array of physical influences that affect projectile trajectory [7,8]. Consequently, this article will focus solely on a delimited aspect of this extensive domain, specifically the realm of drag force. This research aims to calibrate a CFD model, specifically for supersonic flow conditions [9], by integrating theoretical frameworks with experimental data. As the focus lies on supersonic projectile flight, a domain inherently complex for experimental investigation, a validated model will enable comprehensive exploration of the subject and accurate characterization of phenomena difficult to analyze experimentally. The calibrated CFD model will be employed herein to analyze the influence of shock waves on drag force, thereby providing a basis for further studies on the effect of projectile shape on drag.

At subsonic velocities, the drag force is primarily attributed to air friction across the projectile’s surface. The geometry of the projectile’s tip and base plays a subordinate role, and the overall projectile form exhibits a diminished influence on drag. Conversely, at supersonic velocities, the projectile’s shape exerts a critical impact on drag, particularly the tip profile, but ultimately encompasses the entire projectile body.

At supersonic velocities, the drag force is composed of wave drag and friction drag. Wave drag is attributed to the compression of air preceding the projectile and the consequent formation of a shock wave. The projectile’s tip geometry exerts a critical influence on the magnitude of this force. Friction drag arises from the tangential interaction between the air and the projectile’s surface. The projectile’s body profile and its longitudinal dimension play a predominant role in this regard.

The drag force experienced by projectiles at supersonic velocities is a complex phenomenon influenced by a multitude of factors, including projectile geometry, velocity, air density, and others. The precise determination of drag force necessitates either sophisticated aerodynamic computations or experimental investigations, both of which are inherently challenging [10,11]. Consequently, the combination of classical research methodologies, encompassing theoretical analysis and experimentation, with CFD analyses proves to be particularly advantageous and efficacious in the study of external flow.

This paper presents an analysis of a .223 rem caliber projectile in supersonic flight, employing ballistic theory, complemented by experimental firing. Velocity decay along the flight path is evaluated using chronograph measurements. Based on the theoretical framework and experimental data, a CFD model is developed, enabling in-depth analysis and mapping of the flow field around the projectile and the resulting drag forces as a function of projectile geometry. This facilitates efficient projectile development. Emphasis is placed on evaluating the characteristics of normal and oblique shock waves and their velocity dependence. The findings will provide a foundation for further research investigating the influence of projectile nose shape on shock wave characteristics.

As will be demonstrated hereinafter, the utilization of CFD simulations markedly improves both the precision and efficacy of delving into the complexities of the presented topic.

This methodology facilitates the calibration of a computational fluid dynamics (CFD) model with a minimal number of demanding experiments to accurately represent the ballistic coefficient for a specific caliber and projectile type. Based on the calibrated model, it becomes feasible to derive results for the given caliber and projectile for comparative analyses under varying climatic conditions, such as alterations in air temperature, pressure variations due to altitude, and changes in air density attributable to humidity, water vapor content, and the like.

2. Methodology

As previously stated, the methodology employed in this paper is predicated upon a synergistic combination of ballistic theory, experimental measurements, and CFD analyses [12,13]. The experimental measurements comprised a series of projectile velocity assessments. CFD analyses were performed using the Ansys Fluent system, employing the finite volume method within the framework of continuum mechanics [14].

2.1. External Ballistics

External ballistics represents a highly complex domain wherein the projectile trajectory is influenced by a comprehensive array of phenomena, encompassing factors intrinsic to the projectile itself, environmental influences encountered during its flight, and other extraneous variables [15]. Projectile-intrinsic factors primarily pertain to its form, dimensions, and mass. Dimensional attributes govern its aerodynamic characteristics and the resistive forces exerted by the surrounding air. The projectile’s mass determines its inertia, thereby affecting its capacity to overcome air resistance and gravitational forces. Environmental influences constitute a multifaceted set of factors, including gravitational acceleration, which imparts a downward curvature to the trajectory. Another significant environmental factor is the drag force, acting in opposition to the projectile’s motion and causing its deceleration. The magnitude of this force is contingent upon the projectile’s shape and size, its velocity, and the ambient air density. This latter factor will be the principal focus of this paper. The air density, as referenced herein, is dependent upon both air temperature and humidity. A further critical environmental influence is wind, which can induce lateral deflection of the projectile’s trajectory and consequently affect its accuracy.

In long-range projectile trajectories, it is imperative to consider additional environmental influences, including the Coriolis effect (due to Earth’s rotation), terrain irregularities, and even the Earth’s curvature [16]. The projectile’s ballistic trajectory, governed by gravity and air resistance, is significantly affected by these factors. Earth’s curvature causes a divergence between the shooter’s horizon and the target’s position. Consequently, for extended-range engagements, an elevated aiming point is necessitated to compensate for the projectile’s descent towards the target location.

Among other influential factors are the projectile’s rotation, which stabilizes its flight [17], thereby enhancing accuracy [18]; the muzzle velocity, which affects both range and kinetic energy; and the point of impact elevation, which influences the trajectory and precision of the projectile.

The comprehension of external ballistics is paramount for long-range shooting, necessitating the consideration of all the aforementioned factors that influence projectile trajectory [19]. Consequently, external ballistics is a subject of study not only for military personnel and hunters, but also for sport shooters and researchers alike.

This paper concentrates solely on a singular aspect within the comprehensive solution of the aforementioned complex, namely the drag force, with particular emphasis on the drag coefficient (C_d) and the ballistic coefficient (B_C) [20,21].

In this specific area, the resultant force acting upon the projectile is resolved into two component forces.

$$F=F_g+F_f$$

(1)

where F_g is the gravitational force vector and F_f is the air resistance vector (drag force).

The following applies to the magnitude of these forces:

$$F_g=m\cdot g$$

(2)

$$F_f={\displaystyle \frac{1}{2}}\cdot C_d\cdot S\cdot \rho \cdot v^2$$

(3)

where m is the mass of the projectile, C_d is the drag coefficient, S is the cross-sectional area of the projectile, ρ is the air density, and v is the projectile velocity.

The aerodynamic drag force exerted by air has a significantly greater influence on a projectile than the gravitational force. In the transition to supersonic flow, the drag force is not directly proportional to velocity; rather, this proportionality increases abruptly due to the formation of a shock wave. This shock wave induces a discontinuous change in pressure magnitudes and, consequently, in density, leading to a sharp rise in the resistance of the medium through which the projectile travels. At subsonic velocities, the drag force is primarily attributed to air friction against the projectile’s surface. The shapes of the projectile’s tip and base play a comparatively minor role, and generally, the projectile shape has a lesser impact on drag force. Conversely, at supersonic velocities, the projectile shape, particularly the morphology of the tip and body, exerts a critical influence on drag force. This constitutes a key consideration within ballistics and forms the central theme of this paper.

At supersonic velocities, the drag force comprises two distinct components: wave drag and frictional drag. Wave drag originates from the compression of air ahead of the projectile and the subsequent formation of a shock wave, with the projectile’s nose geometry exerting a critical influence on the magnitude of this force. Conversely, frictional drag arises from the tangential interaction between the air and the projectile’s surface, wherein the projectile’s body shape and length assume primary importance.

At supersonic velocities, the drag force that is experienced by a projectile is influenced by several aspects of its geometry. Specifically, the projectile’s nose cone morphology exerts a critical influence on the airflow dynamics around the projectile, thereby significantly affecting the drag coefficient. Acute and pointed nose cone configurations serve to minimize shock wave formation, consequently reducing aerodynamic drag. A slender and aerodynamically optimized projectile body diminishes the drag by mitigating turbulence and vortex shedding in the projectile’s wake. Furthermore, the projectile body’s geometry dictates the frictional air resistance across its surface. Elongated and slender projectiles exhibit lower drag characteristics compared to shorter projectiles with larger diameters. A boat’s tail or tapered aft section serves to reduce turbulence and vortex formation, potentially decreasing drag by facilitating the return of the wake flow to a laminar state, thus reducing the overall drag force. A smooth projectile surface minimizes frictional forces between the projectile and the surrounding air, resulting in a reduction in drag. Conversely, rifling or other surface features can modify airflow patterns and, in certain contexts, contribute to a reduction in drag.

The aforementioned considerations primarily address the influence of drag force as investigated within this paper. However, the dynamics of projectile flight, particularly within the supersonic regime, are considerably more complex and extend beyond the scope of this present work. Furthermore, the optimal projectile geometry is subject to variation depending on specific operational parameters, including projectile velocity, air density, and intended projectile application. Consequently, significant attention and ongoing research are dedicated to projectile shape design.

The in-atmosphere flight characteristics of a projectile are quantified by the ballistic coefficient (B_C), a value that indicates the projectile’s ability to overcome air resistance during flight. Generally, a higher B_C value correlates with improved flight performance and reduced susceptibility to air resistance. Consequently, it might be inferred that an elevated B_C signifies a superior projectile. However, this relationship is not unequivocally straightforward. The advantages associated with a higher B_C include a flatter trajectory, which minimizes the projectile’s vertical drop due to gravitational influence, thereby facilitating long-range shooting. Furthermore, projectiles with a higher B_C exhibit reduced wind drift, enhancing shooting accuracy. Additionally, these projectiles retain a greater kinetic energy at extended ranges, which is crucial for impact effectiveness. Conversely, the disadvantages of a higher B_C typically encompass increased projectile mass and dimensions. Nevertheless, it is crucial to acknowledge that B_C values are not universally applicable. Different shooting applications necessitate varying B_C values. For instance, short-range shooting scenarios do not require projectiles with an exceptionally high B_C.

The ballistic coefficient (B_C) may be derived from the following relationship (Equation (4)):

$$B_c={\displaystyle \frac{SD}{i}}$$

(4)

where B_c is the ballistic coefficient of the projectile, SD is the sectional density of a projectile, synonymously, its cross-sectional loading, and i is the form factor of a projectile defined as the ratio of the projectile’s aerodynamic drag to the aerodynamic drag of a standard reference projectile.

The sectional density of a projectile is given by:

$$SD={\displaystyle \frac{m}{d^2}}$$

(5)

where d is the diameter of the projectile (caliber).

$$B_c={\displaystyle \frac{m}{i{d}^2}}{10}^3$$

(6)

Equation (6) demonstrates that the projectile’s ballistic coefficient is directly proportional to its sectional density and inversely proportional to its form factor and the square of its diameter.

A simplified relationship for determining the G1 ballistic coefficient, previously reported in [21], was also employed in this article.

$$G1={\displaystyle \frac{0.0052834\times x}{\sqrt{v_0}-\sqrt{v_x}}}$$

(7)

where v is the velocity of the projectile at a given distance from the barrel, and x is the flight path. The indices for the velocity value indicate the distance of the projectile from the barrel.

The aforementioned relationship (Equation (7)) represents a simplified formulation for the calculation of the ballistic coefficient. While it may provide a reasonable approximation in certain scenarios, it is crucial to acknowledge its limitations and potential inaccuracies. The formula is predicated on several simplifications. It assumes a constant deceleration of the projectile throughout its trajectory, which does not hold true in reality. Air resistance varies with projectile velocity. Consequently, its applicability is primarily confined to instances where the projectile’s velocity within the analyzed flight path remains within a range where the drag force exhibits minimal variation. While the formula may serve as a useful tool for rapid estimation of the ballistic coefficient, the aforementioned methodologies are imperative for more precise calculations.

The ballistic coefficient values will be utilized for comparison against a standard reference projectile. The form factor of the projectile i indicates the degree to which its shape deviates from that of the standard reference projectile. A standard reference projectile is a projectile with defined dimensions, shape, and mass, employed for the purpose of comparing the ballistic properties of other projectiles. The ballistic coefficient of a standard projectile is defined as 1. The most commonly used standard projectile types are G1 and G7 (Figure 1).

The G1 standard projectile is designed for a one-pound mass and a one-inch caliber. For contemporary, aerodynamically efficient .223 rem caliber projectiles featuring a spitzer profile and boat-tail design, frequently employed in medium- to long-range shooting applications, the G7 ballistic coefficient presents a more refined instrument for precise ballistic analysis. This is attributed to its superior form factor agreement and diminished velocity dependence when contrasted with the G1 standard. Consequently, the G7 standard is specifically engineered to more accurately model the behavior of boat-tail projectiles, whereas the G1 standard remains more appropriate for flat-base bullet designs. For the given standard projectiles, the course of the air resistance law was experimentally determined across the entire range of real motion velocity values, and their course is presented in

Table 1. The values of variables G1 and G7 as a function of Mach number.

Mach Number [ ]	G1 [ ]	G7 [ ]
0	0.263	0.12
0.5	0.203	0.119
0.6	0.203	0.119
0.7	0.217	0.12
0.8	0.255	0.124
0.9	0.342	0.146
0.95	0.408	0.205
1	0.481	0.38
1.05	0.543	0.404
1.1	0.588	0.401
1.2	0.639	0.388
1.3	0.659	0.373
1.4	0.663	0.358
1.5	0.657	0.344
1.6	0.647	0.332
1.8	0.621	0.312
2	0.593	0.298
2.2	0.569	0.286
2.5	0.54	0.27
3	0.513	0.242
3.5	0.504	0.215
4	0.501	0.194

and the graphics in Figure 2 [22].

Standard projectiles are utilized in external ballistics as a comparative benchmark for the determination of the drag characteristics of projectiles with other related shapes.

As previously established (Equations (4) and (6)), the projectile form factor, denoted as i, quantifies the deviation of a projectile’s shape from that of a standard reference projectile. A closer resemblance to the reference projectile results in a lower form factor and, consequently, a higher ballistic coefficient. The projectile form factor is defined by the ratio:

$$i={\displaystyle \frac{C_D}{C_{Detalon}}}$$

(8)

The ballistic coefficient and a standard projectile are utilized to calculate ballistic tables, which delineate the trajectory of a projectile as a function of distance, velocity, and other pertinent factors. These tables are employed for precision long-range shooting.

2.2. Experimental Equipment

In the initial phase, an experimental firing of the selected cartridge type was conducted at the War Zone Blansko shooting range (Czech Republic), which features a covered firing range with a 100 m shooting distance. This experiment yielded data regarding the barrel velocity of the projectile and its velocity after traversing 98 m.

For the experiment, an AR-15 V-AR rifle chambered in .223 rem with a 22-inch heavy barrel and a 1:7 twist rate was utilized. The barrel of the test rifle in this experimental measurement was two inches longer than the rifle on which the cartridge in question was originally tested by the manufacturer. All data pertaining to the manufacturer’s cartridge test and the resulting manufacturer-provided data were sourced from Sellier & Bellot [23]. For the purposes of this paper, the .223 rem caliber cartridge manufactured by Sellier & Bellot, specifically the Full Metal Jacket (FMJ) variant with a projectile weight of 69 grains, was selected (Figure 3). The parameters of the selected cartridge are given in

Table 2. .223 rem Full Metal Jacket (FMJ) cartridge parameters manufactured by Sellier & Bellot [23].

Type	FMJ (Full Metal Jacket)	Unit
Projectile Jacket Material	CuZn 10
Projectile weight	69	grs
Projectile diameter	0.224/5.69	inch/mm
Projectile length	0.959/24.37	inch/mm
Sectional Density	0.0195	lb/in2
Ballistic coefficient G1	0.387
Ballistic coefficient G7	0.189
Cartridge length	57.4	mm
Barrel length	20	inch
Velocity v0	880	m·s−1
Energy E0	1742	J

.

The projectile mass was selected, in part, with consideration for the 1:7 twist rate of the rifle employed, wherein lighter projectiles could potentially result in excessive rotation (

Table 3. The correlation between twist rate and projectile mass suitability.

Twist	Projectile Mass [grs]
	No Safety Issue, Just Not the Best for Twist	Fine, Just Not as Good as it Can Be	The Best for the Twist
1:7	40–55	55–69	69 and more
1:8	To 40 and above 87	From 40 to 62 and above 87	From 62 to 77, including
1:9	Above 77 including	Above 62 to 77	To 62 including

).

A pair of Caldwell Chronograph Premium electronic gates (Figure 4) was utilized to measure the projectile velocity. These gates exhibit a measurement deviation of ±0.25%.

2.3. CFD Analyses

Theoretical and experimental foundations were utilized for the refinement and subsequent analysis of the given problem through CFD simulation technology using the Ansys Fluent system.

Given the supersonic nature of the flow, a density-based numerical method was selected for the analysis, as it is inherently appropriate for the prevailing flow regime [24]. This solver concurrently resolves the fundamental conservation laws of mass, momentum, and energy, alongside the transport equations for chemical species, while addressing auxiliary scalar equations in a sequential manner. The intricate flow behavior observed within the nozzle required the implementation of an implicit linearization strategy for the solution of the interconnected governing equations. The fully implicit approach, which determines all variables concurrently at cell interfaces, demonstrated both stability and resilience in managing the complex supersonic flow field and the substantial pressure gradient characteristic of the experimental chamber.

Subsequently, the discretization of convective and compressive flux components was achieved using the Advection Upstream Splitting Method (AUSM). This methodology capitalizes on the eigenvalues inherent within the Jacobian matrices of the fluid flow.

The AUSM discretization approach presents several beneficial attributes, notably:

• Precise resolution of shock and contact discontinuities.
• The capacity to yield solutions that maintain entropy.
• Mitigation of the carbuncle instability, a frequently encountered numerical artifact in schemes designed for low dissipation during shock capture.
• Consistent precision and convergent behavior throughout an extensive spectrum of Mach numbers.

Crucially, the method’s performance is independent of specific eigenvector data, rendering it applicable to systems exhibiting intricate and indeterminate eigenstructures, exemplified by two-fluid multiphase flow models [25].

For the conveyance of data between computational cells, a second-order upwind method, which implemented multivariate linear reconstruction, was implemented [26]. The application of a Taylor series expansion, centered on the cell centroid, to the cell-centered solution resulted in enhanced precision at cell boundaries [27].

Precise computational fluid dynamics simulations demanded a highly optimized mesh.

A structured mesh, incorporating two-dimensional structured quadrilateral cells alongside unstructured triangular cells, was employed. This strategy served to reduce numerical inaccuracies arising from non-orthogonal boundaries and to optimize the computational cell count within predominantly rectangular areas (Figure 5a). Triangular cells were strategically placed in domains where the generation of a regular mesh was infeasible, notably on the projectile’s exterior and within predicted supersonic flow regions characterized by substantial pressure and density gradients. A sufficiently refined boundary layer mesh was created adjacent to the projectile’s surface. Figure 5b presents an enlarged rectangular computational domain (initially shown in Figure 5a), with an embedded close-up illustrating the refined mesh region. Furthermore, user-controlled adaptive mesh refinement, driven by pressure gradient criteria, was executed during the solution process utilizing the Field Variable method. This refinement targeted areas where oblique and normal shock waves were present [28].

Mesh adaptation was performed based on the criteria of maximum pressure gradient, using a cell-derivative scheme and a maximum refinement depth of 4. This procedure yielded a precise discretization of the pressure gradient fields within the supersonic nozzle flow. In the presented case, the computational mesh was refined to the extent that further augmentation exhibited negligible influence upon the resultant drag force. Should future investigations address the complexities of the wake region and its potential impact, for example, on projectile stability, further mesh refinement in the domain downstream of the projectile will likely be necessitated.

Subsequently, to ensure solution stability independent of grid resolution, a manual mesh refinement process was implemented throughout the operational pressure spectrum. A coarse mesh strategy, limited to a refinement level of 2, was applied in areas exhibiting negligible variable gradients. Conversely, a higher refinement level of 4 was employed in regions preceding the aperture, within the nozzle geometry, and in the zone of gas expansion.

The dimension of the first computational cell adjacent to the wall, especially within the boundary layer regions of the aperture and nozzle, was of paramount importance for the creation of the computational mesh. The Shear-Stress Transport k-omega turbulence model was implemented, with the dimensionless wall distance, y+, maintained within the interval of 0 to 1.

In the presented analyses, the accuracy of the computation within the boundary layer is a key factor, encompassing both its precise definition and the generation of a suitable mesh in the boundary layer region. Specifically, this involves the size of the first mesh cell adjacent to the projectile’s wall. For the selected SST k-ω turbulence model [29], the principle of determining the first cell size was adopted to ensure that the y⁺ value remained within the range of 1, and the velocity profile within the boundary layer was resolved through the refinement of the mesh within the boundary layer.

The dimension of the initial wall-adjacent cell is obtained via Equation (9):

$$y={\displaystyle \frac{y^{+}\mu }{U_{\tau }\varrho }}$$

(9)

CFD analyses were conducted to analyze the density gradient distributions in supersonic flow regimes. Here, y⁺ signifies a non-dimensional parameter representing the normalized wall distance within the boundary layer, wherein the scaling is determined by flow properties. Specifically, μ denotes the dynamic viscosity of the fluid, and U_τ represents the wall shear velocity.

For the precise resolution of the boundary layer, adequate mesh refinement within this region is imperative, and the near-wall cell height must be minimized.

The dynamic viscosity, which is a function of the gas temperature T and demonstrates substantial variability within supersonic flow regimes, was determined using Equation (10), as presented in reference [30], with validation performed in accordance with reference [31].

$$\mu ={\displaystyle \frac{{1.38421.T}^{1.5}}{\left(T+103.874\right)}}$$

(10)

Equation (11) provides the means for determining the friction velocity, U_τ:

$$U_{\tau }=\sqrt{{\displaystyle \frac{{\tau }_w}{\varrho }}}$$

(11)

where τ_w is the wall shear stress given by Equation (12):

$${\tau }_w={\displaystyle \frac{1}{2}}{C}_f\varrho U_{max}^2$$

(12)

where U_max is the maximal gas flow velocity in the flow axis, and C_f is the skin friction coefficient.

The skin friction coefficient, a non-dimensional parameter, represents the quotient of the tangential frictional force exerted on a surface and the dynamic pressure of the fluid stream. Its value is calculated according to Equation (13):

$$C_f=0.058{Re}_l^{-0.2}$$

(13)

where Re_l is the Reynolds number derived from Equation (14):

$${Re}_l={\displaystyle \frac{\varrho vL}{\mu }}$$

(14)

where L is the characteristic length of the outer solved space, and v is the flow velocity.

Due to the high flow velocities and considerable temperature reductions observed, it became necessary to further consider Sutherland’s law (Equation (15)), which characterizes the temperature dependence of dynamic viscosity.

$$\eta ={\eta }_0\cdot \left({\displaystyle \frac{a}{b}}\right)\cdot {\left[{\displaystyle \frac{T}{T_0}}\right]}^{{\displaystyle \frac{3}{2}}}$$

(15)

where ${\eta }_0$ is the reference dynamic viscosity at the reference temperature $T_0$, T is the input temperature, a is 0.555T₀ + C, b is 0.555T + C, and C is Sutherland’s constant.

For the analyses described hereafter, the values specified in

Table 4. Parameters requisite for the determination of y⁺.

μ	1.82 × 105	Pa·s
ϱ	1.1965	Kg·m3
L	24.37 × 10−3	m
v	For details on the variations, see Table 5	m·s−1

were adopted.

Based on the aforementioned relations, the initial cell size was evaluated for each planned variant of the CFD simulation. These variants differ in flow velocity to assess the drag force across the entire trajectory of the projectile, within the range of 0 to 4 Mach. The selection of velocities within this range was intentionally non-uniform, with a denser distribution in the regions anticipating velocity gradients near the transition to supersonic speeds. The selected range of velocities for the CFD simulations is presented in

Table 5. The minimal cell size at the projectile wall as a function of flow velocity.

	v [m·s−1]	Mach Number [ ]	Initial Cell Size [mm]
1	100	0.302	0.00294
2	200	0.604	0.00157
3	265.4	0.8	0.00122
4	298.17	0.9	0.0011
5	364.43	1.1	0.0009
6	397.56	1.2	0.00085
7	496.95	1.5	0.00069
8	662.6	2	0.00054
9	880	2.656	0.000414
10	993.9	3	0.00037
11	1325.2	4	0.00029

, which also includes the corresponding initial cell size values for each velocity.

Boundary Conditions

The boundary conditions were defined in the following manner. The computational domain was configured as a 2D axisymmetric model, with the axis of symmetry location depicted in Figure 6 (red line).

The velocity input was set for each variant according to the values presented in Table 5 (Figure 6—blue line). The inlet temperature and static pressure were consistently defined based on the manufacturer’s experimental data, specifically 15 °C and 101, 325 Pa, respectively. These values corresponded to the conditions under which the manufacturer calibrated the ballistic coefficient.

As an OUTPUT, the static pressure and temperature values were selected to align with the manufacturer’s experimental data: a temperature of 15 °C with a pressure of 101.325 Pa (Figure 6—purple line).

The FAIRFIELD boundary condition, defining the ambient environment (Figure 6—green line), was implemented. The flow velocity was set to a Mach number equivalent to the input velocity, consistent with the specific variant. The ambient pressure and temperature were selected in accordance with the prior cases, aligning with the manufacturer’s experimental data.

As a prerequisite for the initial conditions for the computational domain, the precise specification of velocity, pressure, temperature, and composition of the incoming airflow at the inlet was necessary. Any inaccuracies in these conditions would propagate into the simulation results. In the present case, the temperature and pressure were clearly defined, and the turbulence intensity at the inlet was selected as 5%, considering the semicircular geometry of the input domain.

The outlet conditions, such as the outlet pressure and velocity profile, can subsequently influence the upstream propagation of waves and the overall accuracy of the solution. An inappropriately defined outlet condition may lead to spurious wave reflections within the computational domain. In this case, a zero gauge pressure is specified at the outlet, with a reference pressure of 1 atm. No backflow was observed during the computation. To avoid potential issues associated with the boundary condition in the surrounding area, specifically, if a wall boundary were chosen, which could cause the reflection of shock waves, a far-field boundary condition, simulating free space, was implemented, as depicted in Figure 6.

Furthermore, it is necessary to consider unsteady phenomena. In cases where the flow is non-stationary (for instance, due to shock wave oscillations or vortex structures), a steady-state simulation may not provide a comprehensive representation of the physical phenomenon. Consequently, a time-dependent simulation (such as Unsteady Reynolds-Averaged Navier–Stokes (URANS) or Large Eddy Simulation (LES)) must be performed, which is computationally more demanding.

Consequently, a comparison of the results obtained using the RANS and LES turbulence models was undertaken. For the evaluation of drag, the RANS model yielded comparable results. In subsequent research where vortex wake will play a significant role, such as in projectile stabilization, the LES turbulence model will be unequivocally more suitable. The result comparison of the velocity distribution obtained using RANS, LES, with adaptation, and LES without adaptation is shown in Appendix A in Figure A1. The time step was chosen according to Equation (16).

$$∆t\le {\displaystyle \frac{{CFL}_{max}\times {∆x}_{min}}{v_{max}}}$$

(16)

where ∆t is the time step, ∆x is the characteristic mesh cell size, CFL_max is the maximal Courant number, and v_max is the maximal velocity.

The initial time step was derived from Equation (16), resulting in a value of 5 × 10⁻⁷ s. This value was subsequently adjusted to a final temporal step size of 3 × 10⁻⁷ s.

This is also related to the issue of model symmetry. Again, in this case, for the evaluation of drag force, a 2D axisymmetric model can be utilized, providing satisfactory results with a significantly reduced computational time. However, for the evaluation of projectile stability and the influence of the wake, the application of a 3D model is necessary.

3. Results

In the initial phase, experimental measurements were conducted at the velocity measurement gates, wherein a series of thirteen measurements was executed. For each projectile discharge, both the barrel velocity and the velocity upon achieving a flight distance of 98 m were recorded. Utilizing the aforementioned simplified relation (Equation (7)), the G1 ballistic coefficient was determined, and the experimentally measured velocity drop over the specified distance was evaluated in comparison to the manufacturer’s provided values. Additionally, the influence of barrel temperature on the obtained results was assessed.

In the subsequent phase, the form factor i of the specified projectile was assessed for both the G1 and G7 drag functions. Based on the determined form factor, the projected G1 and G7 ballistic coefficient curves were generated for the given projectile.

CFD analyses were performed within the Ansys Fluent environment to evaluate the drag force acting on a 2D axisymmetric projectile model derived from a 3D volumetric representation. The 3D model of the projectile geometry was acquired through 3D scanning technology using a HandyScan BLACK device, which possesses an accuracy specification commencing at ±0.025 mm. The volumetric accuracy is determined by the formula 0.020 mm + 0.040 mm·m⁻¹, thus indicating that the projectile was scanned with an accuracy of 0.04 mm. The scanning procedure was executed at SolidVision Brno (Czech Republic).

CFD analyses were conducted within the Ansys Fluent system for a selected range of velocities, as delineated in Table 5. From these analyses, the drag force acting on the projectile was evaluated for each analyzed velocity. The drag force parameter was subsequently employed to compute the drag coefficient, C_d, utilizing the form factor i and encompassing both G1 and G7 function cases. The results were subjected to analysis and compared with the predicted G1 and G7 functions for the projectile, thereby facilitating the refinement of the Ansys Fluent system for ballistic analysis. Utilizing the refined Ansys Fluent model, further CFD analyses were performed to evaluate the influence of ambient air temperature.

3.1. Experimental Measurements Conducted on Electronic Gates

A series of experimental firings was conducted. The experiments were performed under the following conditions: an indoor firing range temperature of 22 °C, an atmospheric pressure of 101,400 Pa, and a relative humidity of 46%.

Following the removal of outliers, a selection of 12 data points was extracted from the results. These data points represent pairs of velocity measurements: the initial barrel velocity, v₀, and the projectile velocity after traversing 98 m, v₉₈. The results are presented in

Table 6. The determination of the parameter G1 based on experimentally derived data.

	v0 [m·s−1]	v98 [m·s−1]	T [°C]	x [m]	G1 [ ]
1	921	861	22.5	98	0.515105
2	918	865	22.9	98	0.583319
3	935	887	23.9	98	0.651103
4	926	871	24.7	98	0.564306
5	930	864	24.9	98	0.469838
6	933	886	27.2	98	0.664411
7	921	861	27.5	98	0.515105
8	932	868	28.9	98	0.485336
9	917	858	31.1	98	0.522807
10	925	862	34.3	98	0.491257
11	928	872	35.1	98	0.554690
12	925	862	36.1	98	0.491257
Average values	925.9167	868.0833			0.542378

.

Twelve repeated experimental measurements of velocity loss were conducted, and the averaged values were utilized for further analysis. To evaluate the measurement error, the Standard Error of the Mean (SEM) methodology was employed, and the results are given in

Table 7. Evaluation of the Standard Error of the Mean (SEM).

	v0 [m·s−1]	v98 [m·s−1]
Measuring 1	921	861
Measuring 2	918	865
Measuring 3	935	887
Measuring 4	926	871
Measuring 5	930	864
Measuring 6	933	886
Measuring 7	921	861
Measuring 8	932	868
Measuring 9	917	858
Measuring 10	925	862
Measuring 11	928	872
Measuring 12	925	862
Mean value	925.9167	868.0833
σ	5.900	9.558
SEM	1.70	2.76

. The SEM represents the standard deviation of the sampling distribution of the sample mean, derived from data obtained as a random sample from the population. It is a quantity that indicates the extent to which the obtained sample mean is likely to deviate from the true population mean.

The evaluation was performed based on Equation (17):

$$SEM={\displaystyle \frac{\sigma }{\sqrt{n}}}$$

(17)

where σ [Pa] is the standard deviation of the sample, and n is the quantity of data points from which the mean was evaluated.

From the obtained results, the G1 ballistic coefficient was determined for each measurement using the aforementioned simplified methodology.

$$G1={\displaystyle \frac{0.0052834\times 98}{\sqrt{v_0}-\sqrt{v_{98}}}}$$

(18)

The results demonstrate that the experimentally determined G1 value is marginally higher than that specified by the manufacturer (Table 6), indicating an enhanced ability of the projectile to overcome aerodynamic resistance. This discrepancy may be attributed to the experimental firing, which exhibited a slightly elevated barrel velocity, exceeding 900 [m/s], compared to the manufacturer’s stated value (Table 6). This difference likely stems from the fact that the manufacturer’s test firing was conducted using a rifle with a 20-inch barrel, whereas our experiment utilized a 22-inch barrel, thereby facilitating a more complete utilization of the propellant energy.

The experiment demonstrated a relatively consistent velocity deceleration across the examined trajectory in all trials, as illustrated in the graphics (Figure 7). Based on statistical computations, outliers exhibiting extreme deviation from the mean, as determined by the Standard Error of the Mean (SEM), were excluded from the complete dataset of the results (Figure 7a). The occurrence of these anomalies is typically attributed to factors such as inconsistent propellant loading or projectile imbalance. 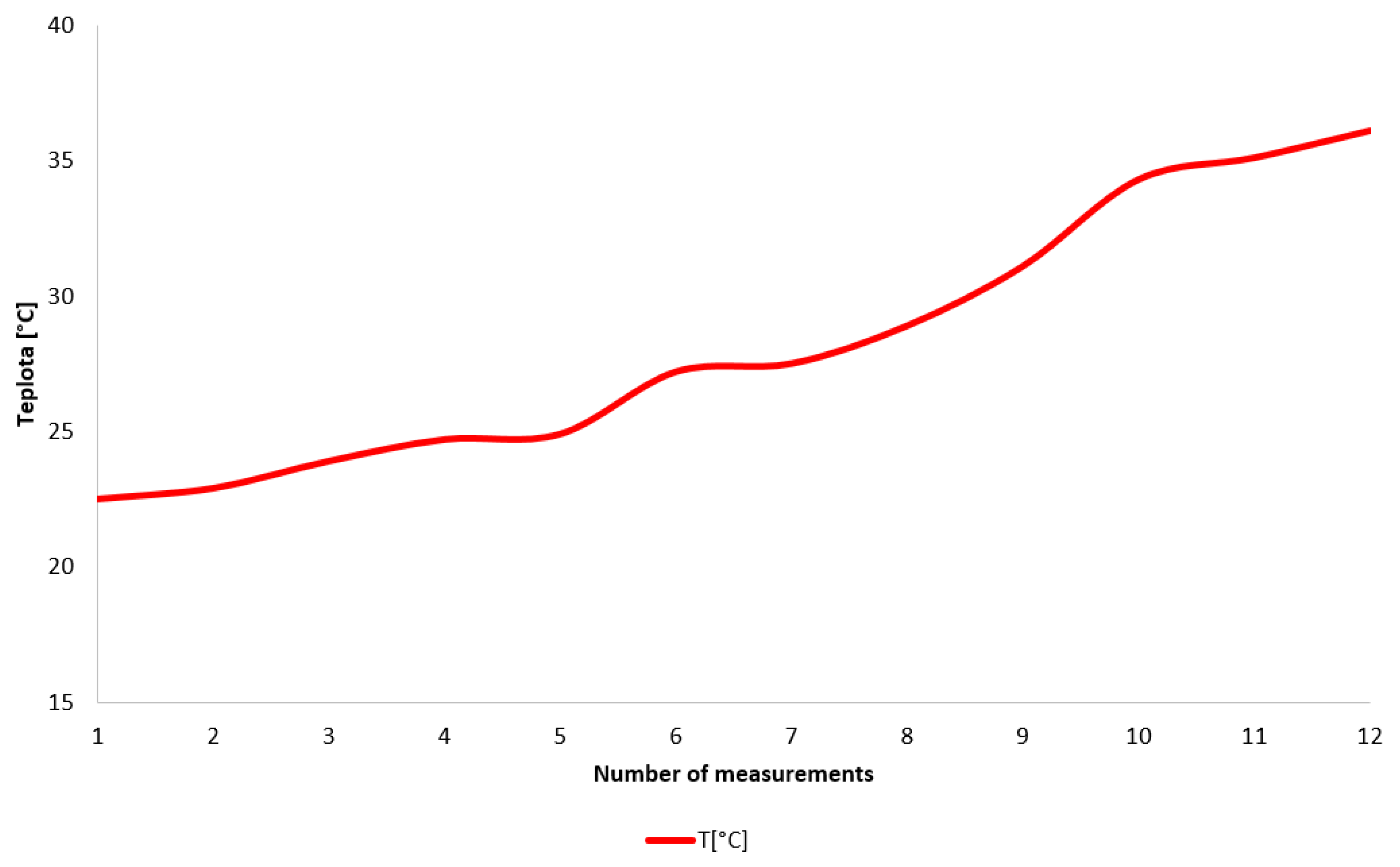Figure 7b illustrates the subset of results that fall within the established deviation criteria. One contributing factor to the observed variations in the results is the increasing temperature, particularly during the experimental measurements. The temperature progression is recorded in Table 6 and presented graphically in Figure 8 for enhanced clarity.

Utilizing the preceding results, it is possible to interpret the disparity in the velocity profiles along the projectile’s trajectory between those provided by the manufacturer and our experimental findings. Figure 9 illustrates the manufacturer’s reported velocity profile [21], depicting a decrease from a muzzle velocity of 800 m·s⁻¹ to 577 m·s⁻¹ upon reaching a trajectory distance of 400 m.

This velocity profile is juxtaposed with the velocity profile obtained from our experiment, wherein average values of muzzle velocities and velocities upon reaching a distance of 98 m were recorded. It is evident from the profiles that the utilization of a rifle with a barrel length extended by 2 inches and the attainment of a higher muzzle velocity, which, in prior results, yielded an elevated ballistic coefficient (B_C), results in a diminished velocity decay over the trajectory.

3.2. The Determination of the Form Factor and the Subsequent Extraction of the G1 and G7 Functions for the Examined Projectile

In the subsequent step, the form factor of the given projectile was evaluated with respect to both the G1 and G7 functions. The form factor was calculated according to Equation (6):

$$i={\displaystyle \frac{m}{B_c{d}^2}}$$

(19)

The input variables listed in Table 1 were utilized to calculate the form factor for the G1 configuration: m = 0.009921 lb, d = 0.224 inch.

The value of G1, taken as 0.387 from Table 1, was adopted for the calculation of B_C. Consequently, the form factor i was calculated to be 0.510905 within the scope of this investigation.

The input parameters specified in Table 1 were again employed for the calculation of the G7 form factor coefficient: m = 0.009921 lb, d = 0.224 inch.

For the B_C parameter, a value of G1, as specified in Table 1, was utilized, resulting in 0.189. In the case of G7, the calculated value for the investigated scenario was determined to be i = 1.046139.

Based on the calculated form factor, the anticipated G1 and G7 ballistic coefficient functions for the specified projectiles were derived and subsequently depicted (

Table 8. The theoretical values of G1 and G7 for the .223 rem caliber.

Mach Number [ ]	G1 .223 rem [ ]	G7 .223 rem [ ]
0	0.134368	0.125537
0.5	0.103714	0.124491
0.6	0.103714	0.124491
0.7	0.110866	0.125537
0.8	0.130281	0.129721
0.9	0.174730	0.152736
0.95	0.208449	0.214458
1	0.245745	0.397533
1.05	0.277421	0.422640
1.1	0.300412	0.419502
1.2	0.326468	0.405902
1.3	0.336686	0.390210
1.4	0.338730	0.374518
1.5	0.335665	0.359872
1.6	0.330556	0.347318
1.8	0.317272	0.326395
2	0.302967	0.311749
2.2	0.290705	0.299196
2.5	0.275889	0.282458
3	0.262094	0.253166
3.5	0.257496	0.224920
4	0.255963	0.202951

and Figure 10).

3.3. CFD Analyses Results

CFD analyses were performed to evaluate the drag force at selected velocities (

Table 9. Determination of the drag coefficient (C_d) from values obtained through CFD analyses.

	v [m·s−1]	Mach Number [ ]	Drag Force [N]	Cd [ ]
1	100	0.302	0.023	0.151638
2	200	0.604	0.087	0.143396
3	265.04	0.8	0.15	0.140782
4	298.17	0.9	0.1855	0.137561
5	364.43	1.1	0.86	0.426923
6	397.56	1.2	1.04	0.433817
7	496.95	1.5	1.47	0.392438
8	662.6	2	2.25	0.337877
9	880	2.656	3.3	0.280949
10	993.9	3	3.88	0.258956
11	1325.2	4	5.71	0.214364

). Subsequently, the drag coefficient was determined using Equation (20) derived from Equation (3). The results are presented in Table 9 and graphically depicted in Figure 11:

$$C_d={\displaystyle \frac{2F_f}{S\cdot \rho \cdot v^2}}$$

(20)

As depicted in Figure 11, three discernible regions are evident on the curve representing the drag force magnitude.

The first region is characterized by subsonic flow, wherein the gas flow surrounding the projectile remains subsonic, and the drag force increases proportionally to the square of the velocity. Within this domain, the augmentation of the drag force is relatively gradual. Specifically, up to 0.3 Mach, negligible compression and localized density increases occur, which would otherwise impede the projectile’s motion.

A second region of interest is the abrupt increase in drag force observed during transonic velocity regimes, specifically at the point of transition across the Mach number boundary. This surge in drag is attributed to the formation of shock waves propagating ahead of the object, generating supplementary resistance due to a localized increase in air density, which can reach an order of magnitude as the projectile traverses the medium.

The third region is characterized by supersonic velocities, wherein the rate of increase in drag force, while still significant relative to subsonic velocities, exhibits a diminished gradient compared to the transonic region.

In the supersonic regime, the drag force exhibits behavior distinct from that observed in subsonic conditions and is composed of wave drag, friction drag, and pressure drag. Wave drag arises from the formation of shock waves propagating ahead of the object and constitutes the dominant component of the drag force within the supersonic regime.

Skin friction drag, arising from the interaction of air with an object’s surface, exhibits diminished significance in the supersonic regime compared to wave drag. Pressure drag, conversely, originates from the compression of air both preceding and following the projectile. Within the supersonic domain, pressure waves propagate at the speed of sound, culminating in the formation of a shock wave.

In the transonic regime, as the projectile velocity approaches the speed of sound, a sharp increase in pressure drag is observed. This phenomenon is attributed to the intensified compression of air ahead of the projectile, resulting in the formation of a shock wave.

However, upon exceeding the speed of sound and entering the supersonic regime, the rate of increase in drag force decelerates. This phenomenon arises from the stabilization of the shock wave, whose form undergoes negligible alteration with further projectile velocity augmentation. Consequently, the pressure drag no longer escalates at the rapid pace observed during the transonic transition.

Furthermore, in the supersonic regime, the influence of frictional drag becomes increasingly evident, exhibiting a gradual rise in magnitude concurrent with the projectile’s velocity. Consequently, the total drag experienced within the supersonic region is a composite of pressure drag and frictional drag, wherein the former no longer demonstrates the steep ascent observed during the transitional flow regime.

Figure 12 presents a comparative analysis of the drag coefficient (C_d) results derived from CFD simulations using Ansys Fluent, juxtaposed with the fundamental G1 and G7 ballistic coefficient curves, as well as the G1 and G7 curves specifically adapted for the .223 rem caliber projectile under investigation. It is evident that, as anticipated, the G7 function exhibits a significantly closer correlation for this slender projectile. This concordance, characterized by minimal deviations, is noteworthy.

As evident in Figure 9, the barrel length indirectly influences the practically observed ballistic coefficient by affecting the projectile’s muzzle velocity. Figure 12 then illustrates that a longer barrel enables a higher muzzle velocity to be achieved. This is attributed to the propellant gases exerting force on the projectile for an extended duration, consequently accelerating it further. The ballistic coefficient of a projectile is not entirely constant and varies as a function of its velocity. This variation arises from the changes in aerodynamic drag across different velocity regimes (subsonic, transonic, and supersonic).

In this case, a longer barrel increases the projectile’s muzzle velocity, such that during its flight along the examined 98 m trajectory, the projectile operates within higher velocity regimes where the condition holds that increased velocity corresponds to a lower ballistic coefficient. Under these circumstances, for the .223 rem caliber, which is generally designed as a lighter, higher-velocity projectile, the barrel length influences the effective ballistic coefficient, which manifests in the projectile’s trajectory [21,32,33].

The coefficients G1 and G7 are the most frequently used drag functions in ballistics for describing the aerodynamic resistance of projectiles. The G1 coefficient represents an older and more traditional standard, predicated on a projectile with a flat base and a short, rounded nose, commonly referred to as a ‘spitzer’. It is particularly suited for older projectile designs and those with lower ballistic coefficients. Conversely, the G7 coefficient represents a more contemporary and precise standard for rifle projectiles, modeling a projectile with a long, slender nose and a tapered boat tail. It is particularly apt for modern projectiles with high ballistic coefficients, employed in long-range shooting, and more accurately reflects the behavior of contemporary projectiles [34].

These observations will become apparent in Section 3.3, where it will be demonstrated that the G7 function is significantly more suitable for the examined caliber.

Also, the G7 model maintains a high degree of generality; Ansys Fluent possesses the capability to capture a broader spectrum of flow phenomena. Subsequently, the fine-tuned model was employed for a detailed analysis of flow dynamics and shock wave character.

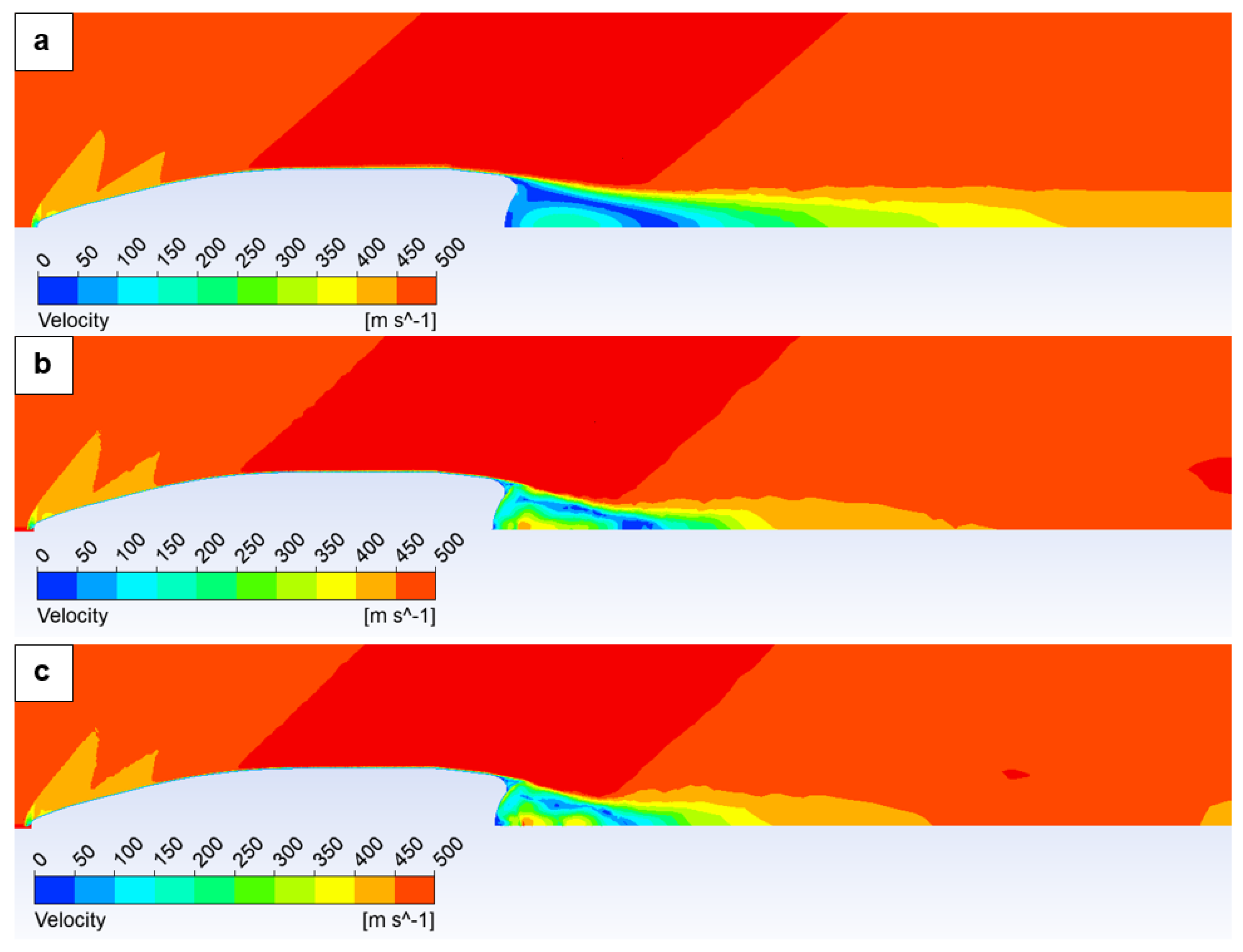
Initially, the character of the shock waves was analyzed. Figure 13 depicts the path along which the static pressure profile, illustrated in Figure 14, was subsequently plotted. Due to the wide range of values, Figure 15, featuring an adjusted static pressure scale, is also provided.

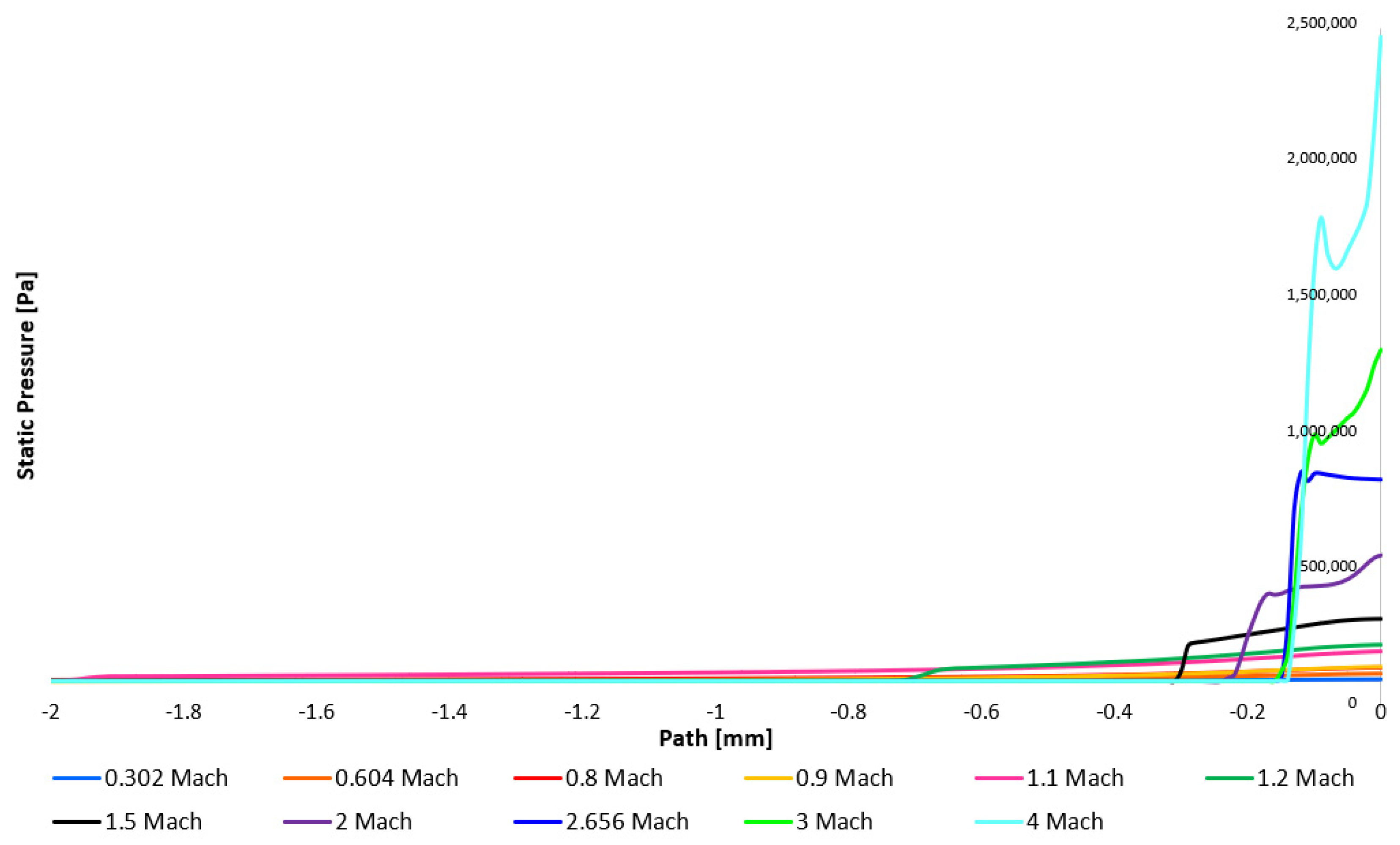
The static pressure profile demonstrates that the air pressure magnitude at the projectile’s leading edge increases with velocity. Consequently, the projectile traverses a denser medium as pressure escalates. The influence of a shock wave, characterized by an abrupt pressure value increase, is evident. As previously stated, this shock wave formation is limited to supersonic velocities, specifically variants exceeding 1 Mach. Figure 14 and Figure 15 reveal a gradual pressure increase within the subsonic regime. This is attributable to the flow’s incompressibility up to approximately 30% of the speed of sound, where the relationship between velocity and pressure is accurately described by Bernoulli’s equation. This domain is not addressed by the majority of the presented variants, with the lowest velocity variant (0.302 Mach) positioned at the threshold. The variants presented and detailed in Table 9 can be categorized into two distinct regimes: subsonic, yet compressible flow (0.302 to 0.9 Mach), and supersonic flow (1.1 to 4 Mach).

For flow velocities exceeding 30% of the speed of sound, the fluid must be treated as compressible. In the theory of compressible flow, it is imperative to account for the fact that the static pressure at the projectile’s leading edge will no longer be equivalent to the ambient static pressure but rather will assume the stagnation value of static pressure, which is greater than the surrounding static pressure. The relationship between static and stagnation pressure can be determined from Equations (21) and (22):

$$v=\sqrt{{\displaystyle \frac{2\gamma }{\gamma -1}}{\displaystyle \frac{p_{stat}}{{\rho }_{stat}}}\left[{\left({\displaystyle \frac{p_{stag}}{p_{stat}}}\right)}^{\left({\displaystyle \frac{\gamma -1}{\gamma }}\right)}-1\right]}$$

(21)

$$\gamma ={\displaystyle \frac{C_p}{C_v}}={\displaystyle \frac{c_p}{c_v}}$$

(22)

where p_stat is the static pressure of the area, through which the projectile traverses, ϱ_stat is the density of the area, through which the projectile traverses, p_stag is the stagnation pressure on the projectiles head, which arises from isentropic deceleration and compression, γ is the Poisson constant, C_p is the heat capacity at constant pressure, C_v is the heat capacity at constant volume, ans c_v and c_p are the respective specific heat capacities.

In the supersonic regime (M > 1), a shock wave forms ahead of the projectile’s leading edge. The gas is initially decelerated non-isentropically to subsonic velocity and subsequently decelerates isentropically to zero velocity at the stagnation point. The relationship between static and stagnation pressure can be discerned from a more complex equation:

$${\displaystyle \frac{P_{stag}}{P_{stat}}}={\displaystyle \frac{{\left[\frac{\gamma +1}{2}\right]}^{\left(\frac{\gamma }{\gamma -1}\right)}}{{\left[\frac{2\gamma }{\gamma +1}{M}^2-\frac{\gamma -1}{\gamma +1}\right]}^{\left(\frac{1}{\gamma -1}\right)}}}={\displaystyle \frac{\gamma +1}{2}}{M}^2{\left[{\displaystyle \frac{{\gamma +1}^2{M}^2}{4\gamma M^2-2\left(\gamma -1\right)}}\right]}^{\left({\displaystyle \frac{1}{\gamma -1}}\right)}$$

(23)

These phenomena demonstrate that within the subsonic, yet in this instance, compressible region preceding the projectile’s leading edge, a gradual and continuous increase in static pressure values occurs. In the supersonic regime, a discrete rise in static pressure is evident at the shock wave, followed by a subsequent increase towards the projectile’s leading edge. As illustrated in Figure 16, the static pressure increase at the projectile’s leading edge is significantly steeper within the supersonic domain. The corresponding values are tabulated in

Table 10. The values of static pressure at the projectile’s nose as a function of flow velocity.

Mach Number [ ]	Shock Wave Distance [mm]	Static Pressure [Pa]
0.302	No shock wave	101,423
0.604	No shock wave	128,856
0.8	No shock wave	151,533
0.9	No shock wave	153,967
1.1	−2	210,644
1.2	−0.75	235,086
1.5	−0.26	330,295
2	−0.23	564,311
2.656	−0.16	842,334
3	−0.15	1,319,337
4	−0.14	2,470,305

. Furthermore, Figure 14 and Figure 15 reveal that the shock wave approaches the projectile’s leading edge with increasing velocity, contributing to the elevated pressure. This proximity contributes to an elevated pressure at the projectile’s front, which the projectile must overcome, thereby influencing the drag force. Concurrently, the shock wave exhibits a more acute angle with increasing velocity, as depicted in Appendix A, Figure A2. An additional observation derived from the results is the occurrence of pulsation at higher velocities, manifested as a pressure fluctuation preceding the shock wave’s leading edge. 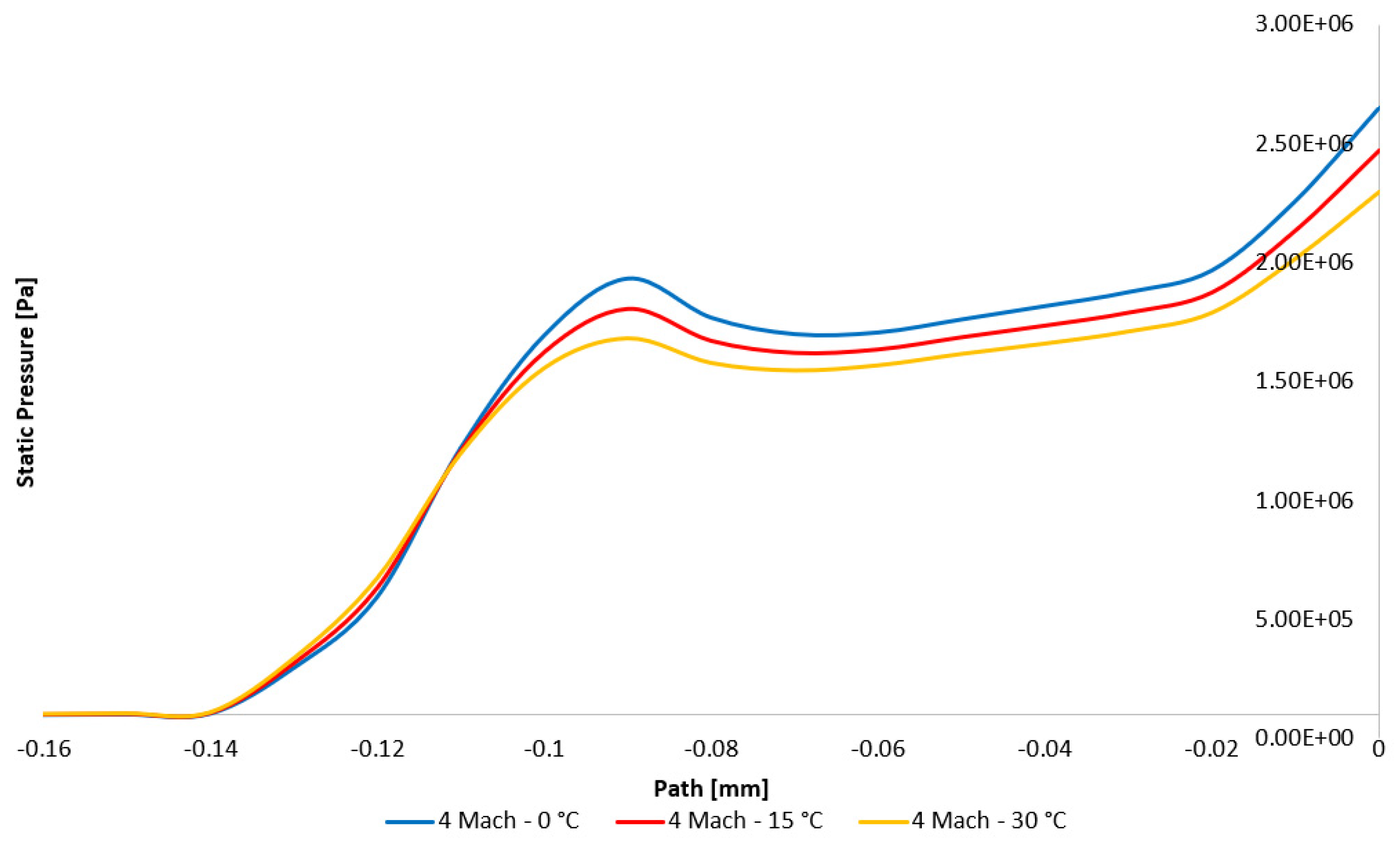This fluctuation becomes more pronounced from 2 Mach onwards, with the pressure distribution in Figure 17 illustrating this effect for the 4 Mach variant.

These findings will enable the future paper to proceed with the analysis of projectiles’ nose shape influences on shock wave characteristics and their consequential impact on stagnation pressure and drag coefficient.

Finally, the fine-tuned system was used for an initial analysis of the influence of ambient temperature on drag force and drag coefficient. In addition to the ambient temperature of 15 °C, under which all previous analyses were conducted and which, as previously stated, was selected based on the temperature at which the manufacturer performed experiments and reported results, comparative analyses were performed with temperatures 15 °C higher and lower, thus for temperatures of 0 °C and 30 °C.

Figure 18 illustrates the drag force profile, from which it is evident that the effect of the temperature variation is primarily manifested in the supersonic regime, subsequently influencing the drag coefficient profile depicted in Figure 19.

This alteration in drag force within the supersonic regime is primarily influenced by variations in the material properties of the medium, notably density. Furthermore, the aforementioned shock wave, characterized by a discontinuous change in density, exerts a significant influence on this alteration. These changes within the supersonic regime can be summarized as follows: A variation in ambient temperature leads to a change in density → A change in density leads to a change in Reynolds number → A change in Reynolds number leads to a change in pressure → A change in pressure leads to a change in drag force → The higher the velocity, the greater the difference in drag force for disparate temperatures, a phenomenon attributable to the relationship defining the Reynolds number as the product of density and flow velocity (Equation (14)).

Furthermore, in this instance, temperature exerts a significant influence upon the determination of the Reynolds number (Equation (14)), as evidenced by Sutherland’s law (Equation (15)).

These variations are observable in the shock wave characteristics depicted in Figure 19 for a velocity of 4 Mach across all three temperature variants. It is evident that a decrease in temperature correlates with an increase in the static pressure value at the projectile’s leading edge.

Figure 20 delineates the velocity ranges over the previously mentioned hundred-meter projectile flight path, comparing both the 20-inch barrel length, as specified by the manufacturer in their experiment, and the 22-inch barrel length utilized in our experiment. The results indicate that both configurations operate within a region of lower drag coefficient values. Furthermore, the data reveal a notable trend: while barrel length variations between 12 and 20 inches appear to exert a significant influence, the impact of length variations beyond 20 inches, up to 24 inches, is considerably diminished. However, the results presented in Figure 20 demonstrate a substantial influence. The V-AR version with a 22-inch barrel exhibits superior drag coefficient conditions throughout the majority of the flight path. This advantage would likely be further amplified at extended ranges, such as 300 m, which is well within the capabilities of this caliber.

4. Conclusions

This paper examined the subject of external ballistics. This research was conducted using a contemporary methodology that integrates theoretical principles, CFD analyses, and experimental measurements. This paper presented an analysis of the drag force and drag coefficient for a .223 rem caliber projectile within both subsonic and supersonic velocity regimes. Based on the experimental findings, the CFD model was tuned, and subsequently, the aforementioned quantities were evaluated and compared with the G1 and G7 ballistic coefficient functions. A high degree of correlation was demonstrated with the G7 function, and the suitability of G7 for this projectile type was proved. Furthermore, a considerable influence of the barrel length differential between 20 inches and 22 inches on the resultant performance of this caliber was evidenced, a factor that typically exhibits diminished effects in rifle calibers exceeding 20 inches in barrel length. The fine-tuned CFD model facilitated the evaluation of the shock wave characteristics at the projectile’s nose, where the normal shock wave exhibited a positional shift towards the nose with increasing velocity, and the oblique shock wave angles underwent a change in sharpness. These findings will be utilized in future research concerning projectile nose geometry optimization. Additionally, the influence of ambient temperature was analyzed using the refined model, and its significant impact, particularly within the supersonic regime, was substantiated. The methodology presented in this paper enables the precise calibration of a CFD model, employing a parsimonious number of resource-intensive experiments, to yield an accurate representation of the ballistic coefficient for a defined caliber and projectile typology. Subsequent to model calibration, it becomes efficacious to derive pertinent results for the specified caliber and projectile, thereby permitting comparative analyses across a spectrum of variable atmospheric conditions, encompassing fluctuations in ambient temperature, barometric pressure variations contingent upon altitudinal displacement, and modifications in atmospheric density ascribable to hygrometric variations, aqueous vapor content, and analogous environmental factors. Subsequent research will extend this calibrated model to analyze an alternative projectile typology of the same caliber, exemplified by the hollow-point boat-tail (HPBT) configuration. The investigation will encompass an analysis of the morphological variations in both the cavity and the projectile body, specifically focusing on the ogive and boat-tail geometries. Analogous analyses will be conducted for additional calibers, and their respective characteristics will be subjected to comparative evaluation.