Exploring the Economic Hypothetical for Downhill Belt Conveyors Equipped with Three-Phase Active Front-End Load Converters

Abstract

This paper integrates empirical assessments of energy recovery in downhill belt conveyor systems with rigorous theoretical modeling and economic analysis. An alternative approach for capturing and transforming the potential energy of a descending conveyor into electrical energy is proposed using an active front-end (AFE) load energy recovery system. Adjusting the drive configuration from a standard direct-on-line (DOL) system to a regenerative AFE converter, the conveyor’s excess kinetic energy can be fed back into the grid. The investigation shows that operating a 300 kW downhill conveyor at full capacity would consume about 142,800 kWh per month in a conventional setup. However, at 90% of the maximum capacity over 17 h per day (~476 h per month), the conveyor with an AFE system produces a regenerative power of 188 kW (negative demand), yielding a net generation of 89,488 kWh per month. The results indicate that integrating a regenerative AFE control system can achieve energy savings of approximately 37% compared to a non-regenerative system. The key economic indicators, including lifecycle cost, payback period, and net present value, confirm the financial viability of the proposed system over a 20-year span.

1. Introduction

Downhill belt conveyors play an essential role in various industries by efficiently transporting materials over great distances. However, the energy dynamics of these conveyors during their descent phase pose significant operational costs and environmental concerns [1]. Escalating electricity tariffs and evolving time-of-use pricing structures have heightened the need for more efficient energy utilization in energy-intensive sectors such as mining, where conveyors moving large quantities of material can consume up to 40% of a facility’s total power usage [2]. In South Africa, for instance, materials handling systems account for about 10% of the nation’s energy consumption [3]. Therefore, optimizing the energy model—including the throughput and operating parameters of belt conveyors—is crucial for reducing costs and improving sustainability [4].

This study focuses on the potential financial and technical benefits of implementing energy recovery systems in downhill conveyors, specifically, three-phase active front-end load (AFEL) converters [5]. Energy recovery systems have garnered considerable attention for capturing kinetic energy that would otherwise be wasted (usually dissipated as heat through mechanical braking) and converting it into useful electrical energy [6]. AFE converters enable efficient bidirectional power flow and grid integration of this regenerated energy [7]. While downhill conveyors (DBCs) inherently can regenerate power due to gravity, traditional setups dissipate this energy as heat, requiring cooling and causing wear on brake systems [8]. The gravitational force on the material descending an incline causes a continuous acceleration tendency and kinetic energy buildup [9]. Without energy recovery, this energy must be absorbed by mechanical brakes and is lost as heat [10]. Major losses also occur due to friction between the belt and rollers and other resistances in the conveyor system [11]. In contrast, an AFE converter-equipped drive can send power back to the electrical grid, essentially using the motor as a generator during descent. Unlike conventional rectifier drives, AFEs use controlled semiconductor switches (IGBTs) instead of diodes, allowing bidirectional power flow and active power factor correction [9,10,11].

Several methods exist to harness the potential energy of downhill conveyors. One approach is regenerative electrical drives that convert excess kinetic energy to electricity and feed it back to the grid or a local intermediate energy storage [12]. Other methods include energy storage devices such as batteries, ultracapacitors, or flywheels to store regenerative energy when generation exceeds the immediate demand [13]. The performance of these energy recovery strategies depends on system parameters such as material mass flow, belt speed, conveyor length and slope, and the efficiency of the conversion equipment. These factors must be carefully analyzed to predict the potential energy output and evaluate the economic feasibility of deploying regenerative systems [13]. AFEL converters, combined with brake choppers in the drive unit, provide dynamic control over the power flow, and they can seamlessly switch the motor drive from the motoring mode (drawing power) to the generating mode (feeding power back) while maintaining stable operation and grid compliance [6]. Real-world case studies have demonstrated substantial improvements in both energy efficiency and operational safety by using regenerative drives in long downhill conveyors [14].

Despite prior research into regenerative conveyors, significant gaps remain. Most studies focus on immediate technological performance or short-term energy savings. There is a scarcity of longitudinal analyses evaluating the long-term economic benefits and lifecycle performance of regenerative conveyor systems [15]. While the environmental advantage, reduced energy consumption, and, thus, lower carbon emissions are often qualitatively mentioned, quantitative assessments of emission reductions are limited. This research aimed to address these gaps by not only analyzing the technical performance of an AFE-based regenerative conveyor system, but also by conducting a comprehensive economic evaluation over the system’s lifespan. The novelty of this work lies in its integrated approach to combining dynamic modeling of a downhill conveyor with AFE converters, control system development for regeneration, and a lifecycle cost–benefit analysis to assess the viability of implementing such technology in practice.

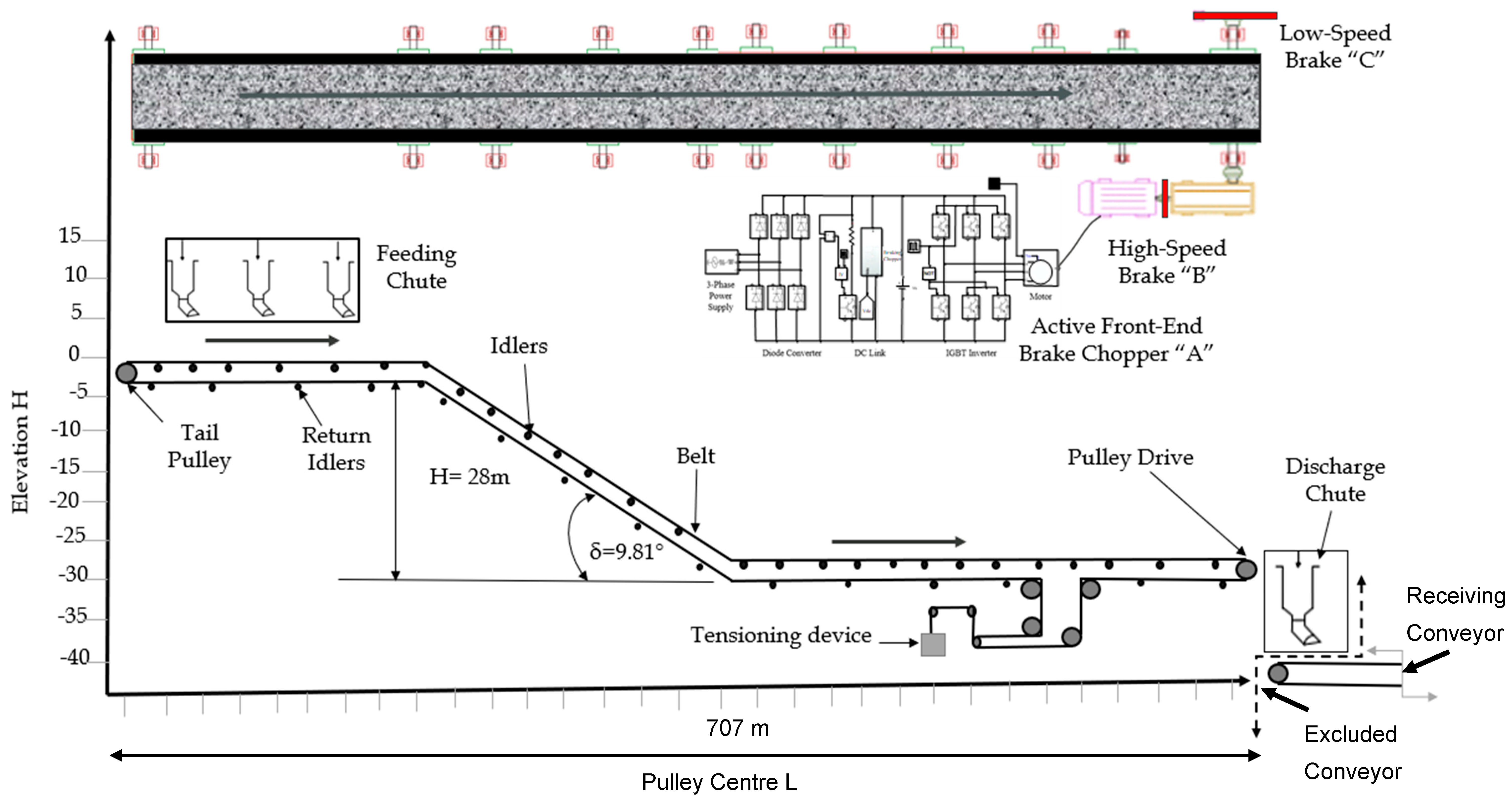
2. Scope of Work Reported

The scope of this paper encompasses an integrated approach that blends theoretical modeling, simulation, and empirical data to investigate energy recovery in a downhill conveyor application. The study advocates for an alternative to traditional drive configurations, such as the fixed-speed or direct-on-line induction motor drives, by introducing a scenario-based braking system and regenerative inverter. A case study of an underground coal mine conveyor is considered, where space constraints and strict safety regulations shape the design of the braking and electrical systems. The proposed integrated system consists of three distinct braking mechanisms working in concert, as illustrated in Figure 1:

-

Brake A: A regenerative brake chopper for regular operation. This dynamic brake can absorb surplus energy and dissipate it to slow the conveyor, bringing it to a stop in about 30 s under normal stop conditions.

-

Brake B: A high-speed disk brake on the drive shaft, serving as an emergency brake. It can stop the conveyor within ~10 s in urgent conditions, handling scenarios where mechanical backup is needed.

-

Brake C: A low-speed drum or disk brake on the pulley shaft, providing a redundant emergency stop, also within ~10 s. This ensures fail-safe operation if both the regenerative and high-speed brakes are unavailable.

These components are evaluated for their ability to convert kinetic energy into electrical energy and safely control the conveyor speed. The regenerative AFE drive Brake A is at the core of energy recovery, while Brakes B and C enhance safety. The study addresses key issues such as limited space and mining safety compliance.

On the modeling and analysis side, a MATLAB/Simulink model of the conveyor and AFE drive was developed to simulate dynamic behavior and design appropriate control algorithms. The conveyor’s mechanical design was performed using the Sidewinder conveyor design software version 9.83, to obtain accurate belt tensions, resistances, and power requirements under various loading conditions. For the economic analysis, detailed calculations of capital expenditures (CAPEX), operational costs (OPEX), lifecycle cost (LCC), and payback period (PBP) were carried out using spreadsheet-based financial models. The model incorporates real tariff structures (time-of-use electricity pricing from Eskom, South Africa’s utility), maintenance schedules, and inflation projections. Metrics such as net present value (NPV) and internal rate of return (IRR) are used to assess the project’s long-term attractiveness.

Figure 1 illustrates the general arrangement of the downhill conveyor system and the integration of these components, providing a visual overview of the setup analyzed in this study.

3. Methodology

The development of a comprehensive mathematical model for the downhill belt conveyor system—incorporating the mechanical dynamics and the AFEL converter’s electrical behavior—is a foundational part of this work. Both mechanical and electrical domains are modeled simultaneously, ensuring that interactions, such as how regenerative torque affects belt speed, are accurately captured [14].

3.1. Key Equations Governing the System’s Operation

Mechanical Dynamics: This includes forces, resistances, and tensions in the conveyor. The total resistive force that the drive must overcome is the sum of various components, such as the idler rotation friction, belt indentation rolling resistance, material sliding resistance, and any force required to accelerate the belt and the material. If we denote the driving force required at the head pulley as $F_d$, the frictional resistance force as $F_f$, and the force due to the acceleration of the material/belt as $F_A$, we have:

$$F_d=F_f+F_A$$

(1)

Equation (1) states that the driving force is the sum of forces needed to overcome frictional resistances and accelerate the conveyor when applicable. To calculate $F_f$, we drew from industry standards as in previous studies [15,16]. The resistive forces are typically scaled with conveyor length, mass of moving parts, and inclination. One formulation for the main resistances is as follows [17]:

$$F_f=CfL\left[{m^{\prime }}_{roll}+\left(2{m^{\prime }}_{belt}+{m^{\prime }}_{bulk}\right)cos\delta \right]\mathrm{g}+\mathrm{H}{m\prime }_{bulk}\mathrm{g}+F_s$$

(2)

In Equation (2):

-

$Cf$ is the artificial friction coefficient accounting for secondary resistances, such as idler misalignment, belt cleaner drag, etc.,

-

L is the conveyor length (m),

-

${m^{\prime }}_{roll}$ is the mass of idler rolls per unit length of the conveyor (kg/m),

-

${m^{\prime }}_{belt}$ is the mass of the belt per unit length (kg/m), multiplied by 2 to account for the top and bottom strands,

-

${m^{\prime }}_{bulk}$ is the bulk material mass per unit length of the conveyor (kg/m), related to the carrying capacity and loading,

-

δ is the angle of inclination of the conveyor (degrees),

-

g is the gravitational acceleration (9.81 m/s²),

-

H is the vertical height difference between the head and tail pulleys (m), and

-

$F_s$ represents any special additional resistances, such as skirtboard friction and hopper drag.

These parameters collectively define the motional resistances acting against the belt movement. Figure 2 provides a mechanical schematic and key design outputs from these calculations. With the resistive force known, the mechanical power that needs to be managed when either supplied or regenerated can be determined. The mechanical power at the drive pulley is as follows [18]:

$$P_m=F_{d}v$$

(3)

where v is the belt speed (m/s). Some of this mechanical power is lost due to inefficiencies, and the rest is either drawn from the motor or sent back to the grid through regeneration. The conversion of mechanical energy to electrical energy by the drive is governed by the drive and motor efficiency. The required electrical power input $P_{e, req}$ to the motor drive, which is positive when motoring and negative when regenerating, given an efficiency η of the drive system, can be calculated as follows [19]:

$$P_{e, req}=F_d.v.{\eta }_{system}$$

(4)

The above equation is basically the mechanical power divided by efficiency. For the motoring mode, this is power drawn from the grid; for the generating mode, this is power returned to the grid; hence, a negative value of $P_{e, req}$ indicates regeneration. Equation (4) is used to estimate how much electrical power the AFE system handles under various load conditions. The illustration in Figure 3 shows the design outputs for a continuous demand power of the DBC operating under constant speed and loaded to its full capacity. The sketch indicates that a positive power demand of 53.22 kW is required at start-up of the conveyor belt, before stabilizing and maintaining the demand power of −188 kW shortly after start-up.

A critical aspect of conveyor design is ensuring the belt tension remains within safe limits during operation, especially under transient conditions during start/stop, or switching between motoring and regenerating. The point of highest tension is typically right before the drive pulley on the carrying side or uphill side for a downhill conveyor [20]. Using standard formulas [21], the belt tension at the drive pulley $T_{1max}$ can be estimated with an exponential function of the wrap angle and friction, or for acceleration scenarios:

$$T_{1max}=T_2^{e\mu \theta }+{(m}_{belt, eq}+m_{load, eq})\times a$$

(5)

where $T_2$ is the tail tension, μ is the belt–pulley friction coefficient, θ is the wrap angle on the drive pulley, and the second term accounts for the additional tension from acceleration, where the equivalent masses are denoted by $m_{belt, eq}$ and $m_{load, eq}$ and a is the belt acceleration. As seen in Figure 4, the point on this conveyor where the belt tension is at its highest is immediately before the driving pulley. The allowable maximum tension $T_{allow}$ is determined by the belt rating and safety factors:

$$T_{1max}={\displaystyle \frac{K_{N}B}{S_{min}}}{T}_2$$

(6)

Managing belt tension is essential for preventing excessive stress and potential failure, ensuring the reliability and longevity of the conveyor system. Figure 5 demonstrates the calculated fluctuation in belt tension. This variation shows that the belt tension stays within the specified system limits of 59.613 kN on both the higher and lower levels throughout the operation of the belt conveyor with the regulated AFE system. This performance mitigates belt damage and minimizes excessive stress during operation.

3.2. Conveyor Belt System: Power Consumption Model

Electrical energy recovery is achieved through regenerative braking, where the mechanical energy recovered is converted into electrical energy. The active front-end load inverter plays a crucial role in this conversion. The primary equations include the following:

$$P_e={P_m \mathrm{\eta }}_{inv}$$

(7)

The power consumption of an individual conveyor belt is defined by the material flow rate and operating speed [19]. This phenomenon occurs specifically when the conveyor belt is functioning at the predetermined nominal speed [15]. The electrical power consumption at the nominal speed ($v_{nom}$) is as follows:

$$P_{e,con}={\displaystyle \frac{CfL[{m^{\prime }}_{roll}+\left(2{m^{\prime }}_{belt}+{m^{\prime }}_{bulk}\right)cos\delta ]\mathrm{g}{v}_{nom}}{{\eta }_{system,con}}}+{\displaystyle \frac{H{m^{\prime }}_{bulk,com}\mathrm{g}{v}_{nom}}{{\eta }_{system,con}}}$$

(8)

When operating at a variable speed $\left(v_{var}\right),$ the electrical power consumption is as follows:

$$P_{e.var}={\displaystyle \frac{CfL[{m^{\prime }}_{roll}+\left(2{m^{\prime }}_{belt}+{m^{\prime }}_{bulk,var}\right)cos\delta ]\mathrm{g}{v}_{var}}{{\eta }_{system,var}}}+{\displaystyle \frac{H{m^{\prime }}_{bulk,var}\mathrm{g}{v}_{var}}{{\eta }_{system,var}}}$$

(9)

Upon conducting a comparative analysis of the two equations, one can ascertain the power savings are achieved through the implementation of speed control [17]. To establish the power conservation achieved through speed control, it is required to compare the electrical power consumption at a consistent speed, denoted as $P_{e,con}$, with the electrical power consumption at a variable speed, denoted as $P_{e,var}$. The concept of power savings can be mathematically represented as follows:

$$\mathsf{\Delta }{P}_e=P_{e,con}-P_{e,var}$$

(10)

The saving ratio, as denoted by the user, is to be noted and examined:

$$R_{pe}=\left(1-{\displaystyle \frac{P_{e,var}}{P_{e,con}}}\right)\times 100\mathrm{\%}$$

(11)

These equations facilitate the assessment of power consumption under different operational conditions and highlight the benefits of speed control in reducing energy usage. Figure 6 illustrates the varying demand power performance of the DBC, where the fully loaded conveyor starts with an initial power of 53.22 kW in 31.87 s from start-up, then drops to –188.87 kW occurring in 212.52 s, and stabilizes at those rates. The incline-only loaded and flat section-only loaded cases start similarly to the fully loaded conveyor; however, they spike down to the regenerative mode for a short span of time, as there is little material transported to keep this case regenerative for longer.

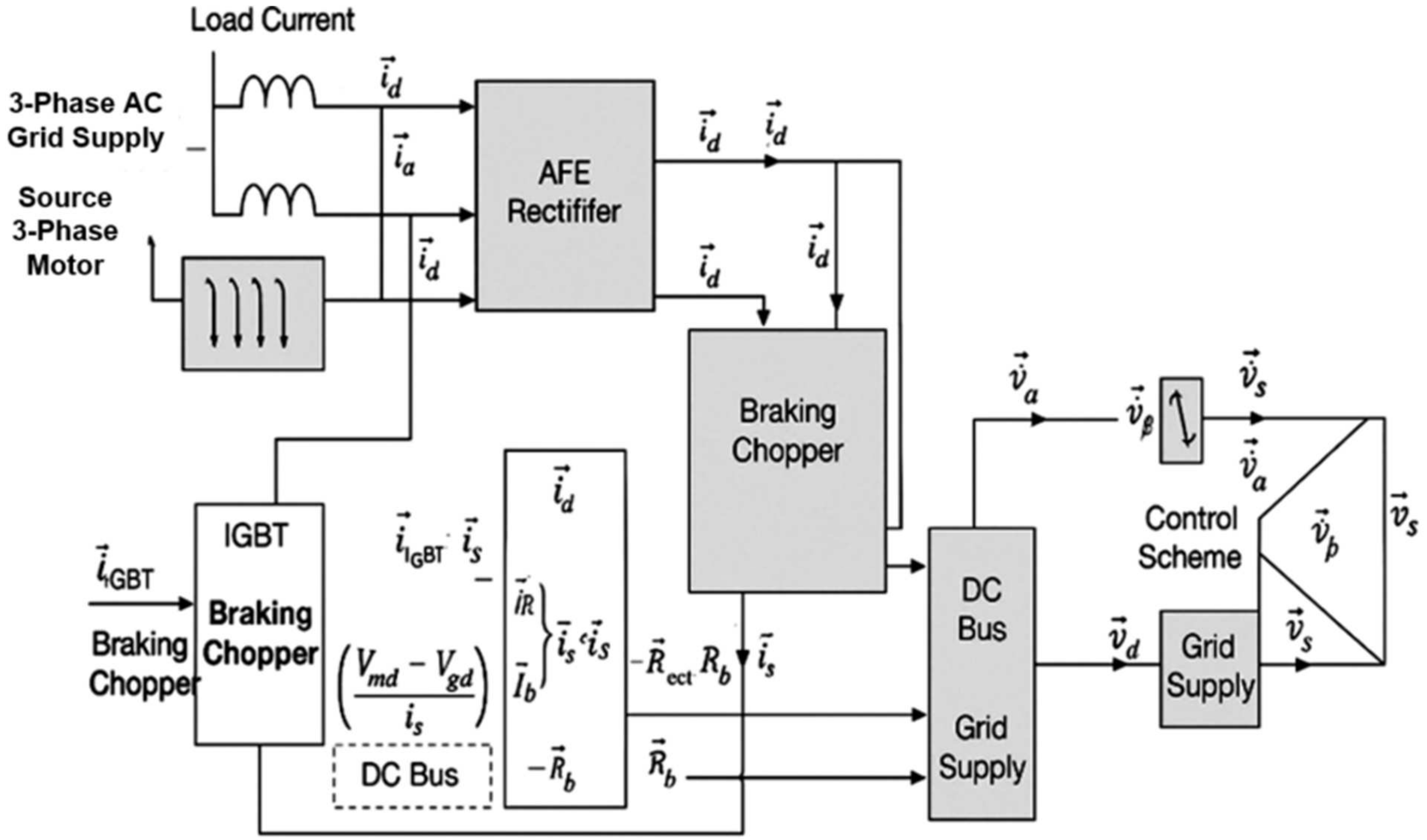
3.3. Active Front End Inverter Principles

To achieve control over the instantaneous active and reactive power supplied to the grid, a synchronization algorithm was employed to estimate the essential grid voltage parameters such as amplitude, frequency, and phase angle, enabling precise control [22,23]. The fundamental operation of an active front-end (AFE) load inverter involves converting AC from the grid into DC and subsequently converting it back to AC to power the load. This process uses insulated gate bipolar transistors (IGBTs) for power factor correction and current waveform modulation [24]. Unlike conventional diode rectifiers, AFE converters use additional IGBTs to actively modulate current waveforms, significantly improving power factor correction [25]. The diagram in Figure 7 illustrates a three-phase AFE rectifier belt conveyor control system, including:

-

A three-phase AC grid supply.

-

Input filter inductors to attenuate switching harmonics.

-

A rectifier utilizing insulated gate bipolar transistors (IGBTs).

-

A braking chopper connected to the DC link for energy dissipation.

-

A bidirectional control system interfacing with the grid and load conditions.

Unlike passive diode-based rectifiers, AFE topologies employ IGBTs to modulate the current waveform actively, thereby enabling dynamic power factor correction and harmonic suppression [24,25].

The bidirectional power flow capability of the AFE permits regenerative braking, an essential feature in downhill belt conveyor systems, where excess mechanical energy from braking is converted into electrical energy and either returned to the grid or dissipated via the braking chopper [26]. The governing equation for the inverter power balance is as follows:

$$P_{in}=P_{out}+P_{loss}$$

(12)

where:

-

$P_{in}$ is the input power from the grid,

-

$P_{out}$ is the output power delivered to the load, and

-

$P_{loss}$ stands for the losses in semiconductors, filters, and passive components.

Compensated signals derived via instantaneous power compensation for active filters involve calculating fluctuating instantaneous power components, subsequently compensating reactive power components [27]. The ABC frame three-phase voltage equations relating phase voltages, currents, inductance $L_s$, and resistance $R_s$ are as follows:

$${\overrightarrow{v}}_{rect}(t)={\overrightarrow{v}}_{grid}\left(t\right)-L_s{\displaystyle \frac{{\overrightarrow{di}}_s\left(t\right)}{dt}}-R_s{\overrightarrow{i}}_s(t)$$

(13)

where:

-

${\overrightarrow{v}}_{rect}(t)$ is the voltage vector at the rectifier input,

-

${\overrightarrow{v}}_{grid}\left(t\right)$ is the grid voltage vector,

-

$L_s$ and $R_s$ are the filter inductances and resistances, respectively, and

-

${\overrightarrow{i}}_s$ represents the three-phase grid currents.

In this instance, the rectifier regulates PWM ${\overrightarrow{v}}_{rect}$ independently of the line voltages [28]. These equations describe current dynamics in response to applied voltages and intrinsic circuit properties [26].

To simplify control analysis, a Clarke transformation from the ABC frame to a two-axis (α, β) stationary frame is used, eliminating zero-sequence components [29]:

$$\left[\begin{array}{c}{i}_{\propto }\\ i_{\beta }\end{array}\right]={\displaystyle \frac{2}{3}} \left[\begin{array}{ccc}1& -\mathrm{½}& -\mathrm{½}\\ 1& {\displaystyle \frac{\sqrt{3}}{2}}& -{\displaystyle \frac{\sqrt{3}}{2}}\end{array}\right] \left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]$$

(14)

where $i_{\propto }$ and $i_{\beta }$ represent the α- and β-axis components of the grid currents.

This transformation is beneficial as it decouples the three-phase system into two orthogonal components, making control strategies easier to implement. The rectifier, in this instance, takes the form of a fully controlled bridge, employing power transistors [26]. These transistors are linked to the three-phase supply voltage through the utilization of filter inductances [30]. The dynamics of the input current can be aptly described within the confines of the stationary αβ frame, wherein the dynamics pertaining to the grid side are eloquently expressed through the utilization of a vector equation [31]:

$$L_s{\displaystyle \frac{{\overrightarrow{di}}_{\alpha \beta }\left(t\right)}{dt}}+R_s{\overrightarrow{i}}_{\alpha \beta }\left(t\right)={\overrightarrow{v}}_{grid,\alpha \beta }\left(t\right)-{\overrightarrow{v}}_{rect,\alpha \beta }\left(t\right)$$

(15)

The relationship between the input current vector and the phase currents can be expressed by the following equation:

$$i_s={\displaystyle \frac{2}{3}}(i_a+{ai}_b+a^2{i}_c)$$

(16)

Consider the scenario where a complex number is denoted as $a=e^{j\left({\displaystyle \frac{2\pi }{3}}\right)}$, which can be expressed as the exponential of the imaginary unit j multiplied by a fraction of 2π divided by 3. In this context, two voltage variables, namely $V_s$ and $V_{afe}$, are defined in a comparable manner to the number [32].

$${\overrightarrow{v}}_{rect}(t)={\displaystyle \frac{2}{3}}(v_{sa}+{av}_{sb}+a^2{v}_{sc})$$

(17)

The voltage denoted as $V_{afe}$ is contingent upon the switching state of the converter as well as the DC link voltage. This relationship can be mathematically represented by the following equation:

$$V_{afe}=S_{afe}{V}_{dc}$$

(18)

The variable $V_{dc}$ represents the voltage of the DC link, while Safe denotes the switching state vector of the rectifier, which is defined as follows [31]:

$$S_{afe}={{\displaystyle \frac{2}{3}}(S}_{\mathrm{a}}+{aS}_{\mathrm{b}}+a^2{S}_{\mathrm{c}})$$

(19)

3.4. Active Front-End Inverter Control Strategy

Proportional–integral controllers are extensively used in control systems to govern diverse process variables. PI controllers are used in three-phase AFE inverters to control the currents in the αβ frame [31]. The αβ frame, sometimes referred to as the fixed reference frame, facilitates the management of three-phase systems by converting the three-phase values into two perpendicular components [22]. PI controllers are used to regulate the currents in the αβ frame. The PI controller for the α component is expressed by the following equation [30]:

$$v_{rect, \propto }\left(\mathrm{t}\right)=K_{p,i}\left(i_{\alpha ,ref }-i_{\alpha }\left(t\right)\right)+K_{i,i}\int \left(i_{\alpha ,ref }-i_{\alpha }\left(t\right)\right)dt$$

(20)

The PI controller for the β component is expressed in the same manner:

$$v_{rect, \beta }\left(\mathrm{t}\right)=K_{p,i}\left(i_{\beta ,ref }-i_{\beta }\left(t\right)\right)+K_{i,i}\int \left(i_{\beta ,ref }-i_{\beta }\left(t\right)\right)dt$$

(21)

PI controllers in the αβ frame are essential for controlling the currents in three-phase AFE inverters. They guarantee the inverter runs effectively and satisfies performance criteria by modifying the control signal in response to the discrepancy between the reference and measured values [28]. Voltage regulators provide a steady DC link voltage, which is important to the correct functioning of the inverter and the linked load [23]. The voltage regulation PI controller works according to the control law [30]:

$$i_{\alpha ,ref }\left(\mathrm{t}\right)=K_{p,v}\left(v_{dc,ref }-v_{dc }\left(t\right)\right)+K_{i,v}\int \left(v_{dc,ref }-v_{dc }\left(t\right)\right)dt$$

(22)

The benefits of voltage regulation can be summarized as follows [27]:

-

Stabilizing voltage regulation enhances the overall performance and reliability of the power system.

-

Protects the system from overvoltage and undervoltage conditions, which can cause damage or inefficiencies.

-

Proper voltage regulation ensures efficient operation of the inverter and connected loads, reducing energy losses.

-

It minimizes voltage fluctuations, providing a consistent power supply to sensitive electronic devices.

3.5. Economic Viability

The economic viability study determination of the model’s capital expenditure is predicated upon a compendium of analogous undertakings, prevailing national benchmarks, and regulatory frameworks within the realm of power generation [32]. The lifecycle cost (LCC) and payback period (PBP) are widely recognized as the key metrics for assessing the desirability and financial feasibility of an investment in an asset [12]. This evaluation largely focuses on the initial investment costs, which encompass the procurement of requisite equipment, subsequent installation, and any indispensable modifications that may need to be made to the existing conveyor system [33]. The calculation of the lifecycle cost associated with the adoption of an AFE system can be delineated in the subsequent manner [34]:

$$LCC(M)=CAPEX+{\sum }_{j=0}^{N_{life}-1}{\displaystyle \frac{{OPEX}_j}{{(1+d)}^j}}-SV$$

(23)

The variables CAPEX, OPEXj, SV, d, and $N_{life}$ represent the capital cost, operating cash flows at the end of the j^th year, disposal cost, discount rate, and the useful lifetime of the asset in years, respectively [35]. The determination of the operating cost incurred from the provision of electricity supply, specifically in relation to the functioning of DBCs, shall be derived through the subsequent methodology:

$${OPEX}_i=365n_c{{\int }_o^T{p}_i\left(t\right)(p_1{u}_1\left(t\right)}_{.}+p_2{u}_2\left(t\right)dt$$

(24)

The calculation of the maintenance cost and the salvage value is performed as follows:

$${MC}_i=mCAPEX$$

(25)

$$SV={\displaystyle \frac{{(1-d)}^{n}CAPEX}{{(1-r)}^n}}$$

(26)

The maintenance ratio, denoted as m, and the annual depreciation ratio of the facilities, denoted as d, are the key variables under consideration. The PBP, in its essence, is a metric that quantifies the temporal duration required to recoup the initial investment expenditure and attain a financial return equivalent to the said outlay [36]. The PBP method, as a means of project monitoring, employs the utilization of the capital cost-to-annual earnings ratio. The mathematical expression for the payback period can be derived from the following equation [34]:

$$PB=n_y+{\displaystyle \frac{{\sum }_{i-1}^{n_y}({LCC}^0\left(i\right)-LCC(i)}{LCC(n_y+1)}}$$

(27)

The Gaussian distribution illustrated in Figure 8 is a continuous probability distribution that is defined in the mathematical framework of probabilities. It is predicated on the assumption that the distribution of data will converge to the normal, particularly within the domain of economics, provided that a significant number of observations are made. Each dataset’s degree of variation or dispersion is quantified by the statistical function “standard deviation,” denoted as σ. A high standard deviation value indicates that the data are dispersed over a wide range, while a low value suggests that most of the data are near the mean [37]. The mean or average price is calculated as follows:

$$\mu ={\displaystyle \frac{{\sum }_{\mathrm{i}-1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}}{\mathrm{n}}}$$

(28)

The standard deviation measures the dispersion or spread of the prices from the mean. It is calculated as the square root of the following variance:

$$\mathsf{\sigma }=\sqrt{{\displaystyle \frac{{\sum }_{\mathrm{i}-1}^{\mathrm{n}}{(\mathrm{x}}_{\mathrm{i}-}{\mu )}^2}{\mathrm{n}}}}$$

(29)

These equations provide the foundation for understanding the variability in pricing and cost estimates, which is crucial for accurate financial modeling and risk assessment. The minimum price is the smallest value in the pricing dataset, and it is given by the following equation:

$$MinPrice=\min {(\mathrm{x}}_1,x_x,x_3,\dots ,x_n)$$

(30)

The maximum price is the highest value in the pricing dataset, and it is given by the following equation:

$$MaxPrice=\max {(\mathrm{x}}_1,x_x,x_3,\dots ,x_n)$$

(31)

These statistical measures are used to analyze the range and distribution of costs associated with the implementation of AFEL converters in DBC systems, providing a comprehensive understanding of the economic implications and aiding in decision-making processes [38].

3.6. Financial Model Sensitivity Analysis

Sensitivity analysis is a method used to determine how the variation in the output of a model can be attributed to different variations in its input parameters. It assesses how sensitive a system is to changes in input variables, helping to identify which inputs have the most significant impact on the output [12]. This analysis not only evaluates the impact of varying electricity costs on energy recovery and financial outcomes, but also aligns with strategic management practices to optimize operational expenditures over time [38].

The baseline nominal monthly electricity cost for an AFEL system is set at R287,758.94. Considering potential annual tariff increases ranging from 3% to 6% based on the inflation rate target, a 20-year forecast period provides a clear picture of how these increments could impact long-term operational costs. The sensitivity analysis uses compound interest to project future electricity costs, factoring in the varying annual increases in tariffs [39]. This approach allows us to evaluate the total financial impact and identify potential cost escalations that could influence investment decisions, such as the possibility for a higher tariff increase of up to 14% [40]. Annual tariff increases ranging from 11% to 14% would be tested to evaluate the sensitivity of the model and observe the variation in PBP and the internal rate of return.

4. Results and Discussion

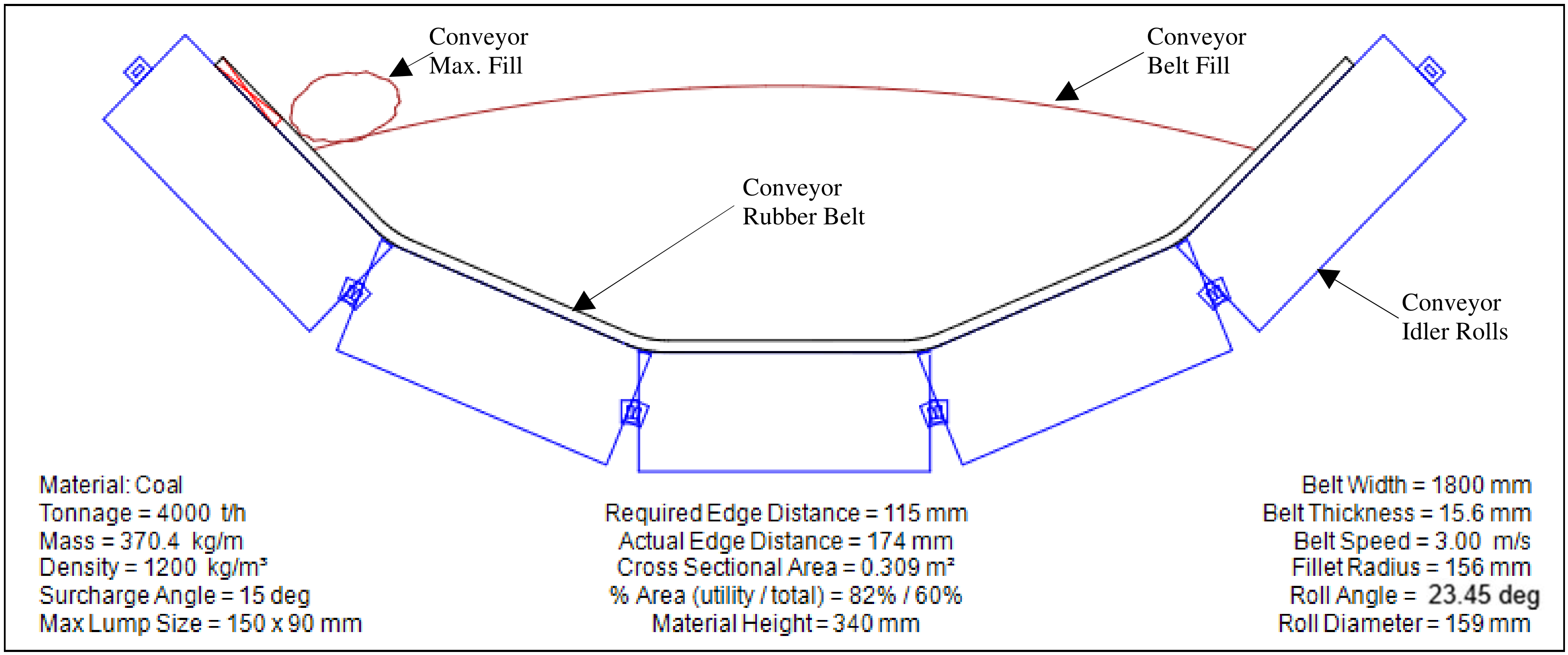
4.1. Conveyor Belt System Design Data Configuration

A case study of a descending belt conveyor was carried out to provide concrete data for the analysis. The conveyor is designed to transport coal at a rate of 4000 t/h. The material has a bulk density of 900 kg/m³ and an angle of surcharge of 15°. The conveyor belt width is 1650 mm, and it operates at a nominal belt velocity of 4.5 m/s. The drive motor nameplate rating is 300 kW, determined using the Sidewinder conveyor design software for the given load and geometry. Depending on loading conditions, the conveyor exhibits different steady-state power requirements, positive for consumption and negative for regeneration: approximately −75 kW when the belt is empty—the weight of the belt itself causes regeneration; −89 kW when only the horizontal (flat) section is loaded; −127 kW when only the inclined section is loaded; and −188 kW when fully loaded (incline-plus-flat-loaded). These values assume a drive efficiency of 95% and 3% slip.

These results show that under all typical operating scenarios, once the conveyor is up to speed, it operates in a regenerative mode, where negative power indicates power being fed back. The initial positive power of about 53 kW is needed at startup to overcome inertia and static friction. After startup, gravity drives the system. With heavier loads, the regenerative power magnitude increases, up to 188 kW for the fully loaded case. The maximum belt tension observed was approximately 59.613 kN, occurring just before the drive pulley during loaded, transient conditions, and it remains within the system’s design limits, as ensured by the combination of mechanical brakes and the AFE drive-controlled deceleration. This is consistent with predictions from Equations (5) and (6) for belt tension limits, and it confirms that the AFE control strategy can maintain safe operating tensions even while allowing energy regeneration.

4.2. Financial Modeling and Assumption

The evaluation of the financial and economic viability of integrating a DBC system with an energy-producing facility is performed by doing calculations within a financial model utilizing the reliable Microsoft Excel program. The factors used to determine the economic viability of the institution were the IRR, NPV of the cash flows, the simple PBP, and the sensitivity consideration based on the Reserve Bank inflation targets. Currently, energy recovery systems have been effectively deployed to capture and convert the excess kinetic energy produced during the descending phase of the conveyor system.

Table 1. Applicable electricity tariff rate 2021/2022 (ESKOM).

Low-Demand Season (1 September to 31 May)				High-Demand Season (1 June to 31 August)
Season	c/kWh	Hours/day	Daily Total	Season	c/kWh	Hours/day	Daily Total
Off-peak	59.07	8	−R888	Off-peak	68.25	8	−R1026
Standard	93.15	1	−R175	Standard	125.68	1	−R236
On-peak	135.37	3	−R763	On-peak	414.91	3	−R2340
Standard	93.15	8	−R1401	Standard	125.68	8	−R1890
On-peak	135.37	2	−R509	On-peak	414.91	2	−R1560
Standard	93.15	2	−R350	Standard	125.68	2	−R473
Daily average	−101.54	24	−R4087	Daily average	−212.52	24	R7526

displays the breakdown of the power pricing for both low- and high-demand seasons [41]. The popularity of demand response initiatives is growing due to electricity supply restrictions in nations such as South Africa. The plant’s functioning is evaluated within the framework of Eskom’s demand-side management initiatives, namely under a time-of-use tariff [12]. All costs associated with energy expenditure and tariffs are shown in South African currency Rand (R).

Critical peak pricing, real-time pricing, and TOU are tariff structures that are frequently implemented, and they are characterized by variable electricity prices. Electricity prices fluctuate frequently in RTP, typically every hour. The CPP provides a compromise between the TOU and RTP. Under the CPP, the discounted TOU prices are typically implemented, and the utility determines the use of relatively higher prices on critical days [42]. The implementation capital cost is determined by the coal plant capacity, which has been estimated to be 22,848 k tons per annum over a 20-year operational period. The financial expenditure associated with the acquisition and implementation of an AFE-equipped conveyor system is included in the estimation, totaling a substantial quantity of R12.9 million in the total capital cost.

The lifecycle operational cost concept encompasses a variety of expenditures that are linked to different aspects of a specific operation. These expenses encompass, but are not restricted to, labor costs, utility expenses, fees for coal sampling services, expenditures associated with mining operations, costs associated with supervision and administration, and any other expenses related to the flow of materials and energy. The comprehensive estimate is equivalent to a substantial sum of R3.5 million. Further, it is imperative to mention that the lifecycle periodic maintenance and service cost, which includes replacement expenditures, is expected to remain consistent at R4.329 million throughout the project’s lifecycle, leading to the comprehensive lifecycle cost of the system, totaling an amount of R20.73 million.

The examination of the data on the range of power costs indicates that the prices conform to a Gaussian distribution, as seen in the histogram in Figure 8. The normal distribution is a fundamental continuous probability distribution in probabilistic mathematics. It assumes that, when many observations are made, the data will tend to follow this distribution. Within economic situations, this assumption is often accurate, and our dataset substantiates this pattern. The standard deviation (σ) of the dataset is measured as R350.28, representing the degree of variance or dispersion in the data. This statistic is essential since it serves as an indicator of the dispersion of the data points.

A larger standard deviation implies that the data points are more widely dispersed throughout a broader range of values, whereas a smaller standard deviation shows that the data points are closer in proximity to the mean. The synopsis of statistical data analysis is as follows:

-

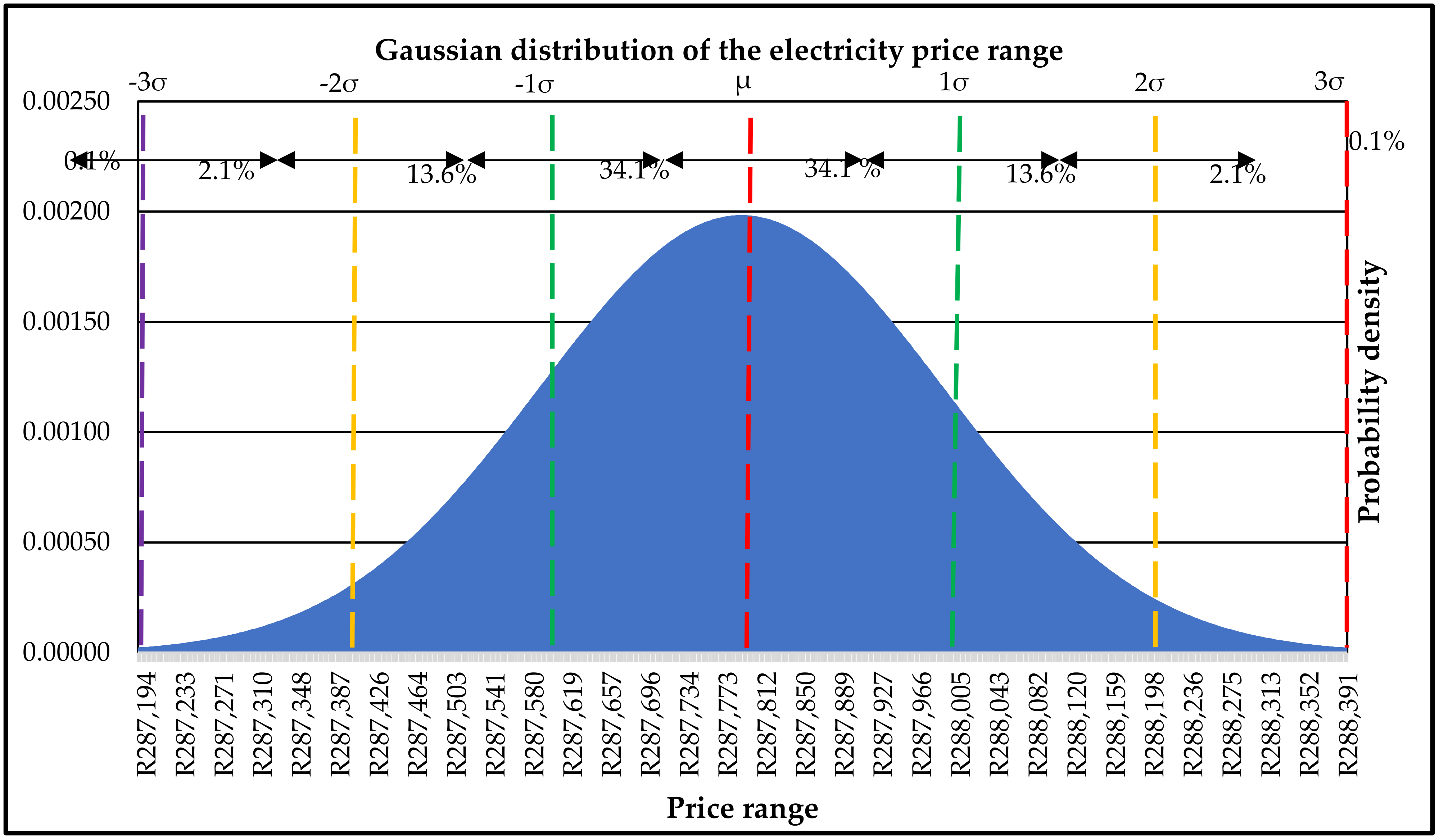
Standard deviation: R350.28

-

Minimum price: R287,200.98

-

Maximum price: R288,410.64

-

Median price: R287,805.11

This visualization provides a clear depiction of the distribution of data points around the mean and the level of their variability, offering a full knowledge of the distribution of energy price ranges. This research provides a fundamental framework for future economic modeling and forecasting in the specific context of energy tariff rates. The present study utilized statistical functions to calculate the nominal tariff rate, which was then applied to estimate the electricity for the duration of the project’s lifespan. The projected nominal tariff rate was R287,758.94. This number was used throughout the research and was raised to account for an expected 3% to 6% rise in power rates. The cost calculations shown here include the power consumption of the DBC, as well as the rates for low- and high-demand power usage. This were achieved by employing statistical sampling approaches and implementing sophisticated mathematical procedures.

Table 2. Energy demand lifecycle: tariff fortitude.

Description	Data	Unit
Total power	−188	kWh
Operating hours	17	Hours/day
Monthly generation	−89,488	kWh
Low-demand cost	R90,869.10	kWh/month
High-demand cost	R190,178.41	kWh/month
Total demand cost	R281,047.50	kWh/month
Lifecycle generation	−R21,477,120.00	kWh
Forecast tariff increase	3% to 6%	Inflation rate target
Minimum cost	R287,173.43	kWh/month
Mean cost	R287,779.52	kWh/month
Maximum cost	R288,385.62	kWh/month
Standard deviation	350.97	kWh/month

provides a succinct summary of the process for determining energy and lifetime tariffs.

The financial feasibility of the project was assessed by analyzing the net present value and internal rate of return of the project’s cash flows. The assumptions were based on an examination of the current market conditions and the price of equipment in the specific context of South Africa. Figure 9 presents a combined visual representation of the cost savings achieved over the whole project duration, together with the total quantity of energy that has been successfully recovered.

The assessment of the financial viability of the DBC system was conducted through the utilization of a comprehensive financial model. Several assumptions were identified as follows:

-

An energy recovery system is used to catch and convert surplus kinetic energy produced while the conveyor moves downhill.

-

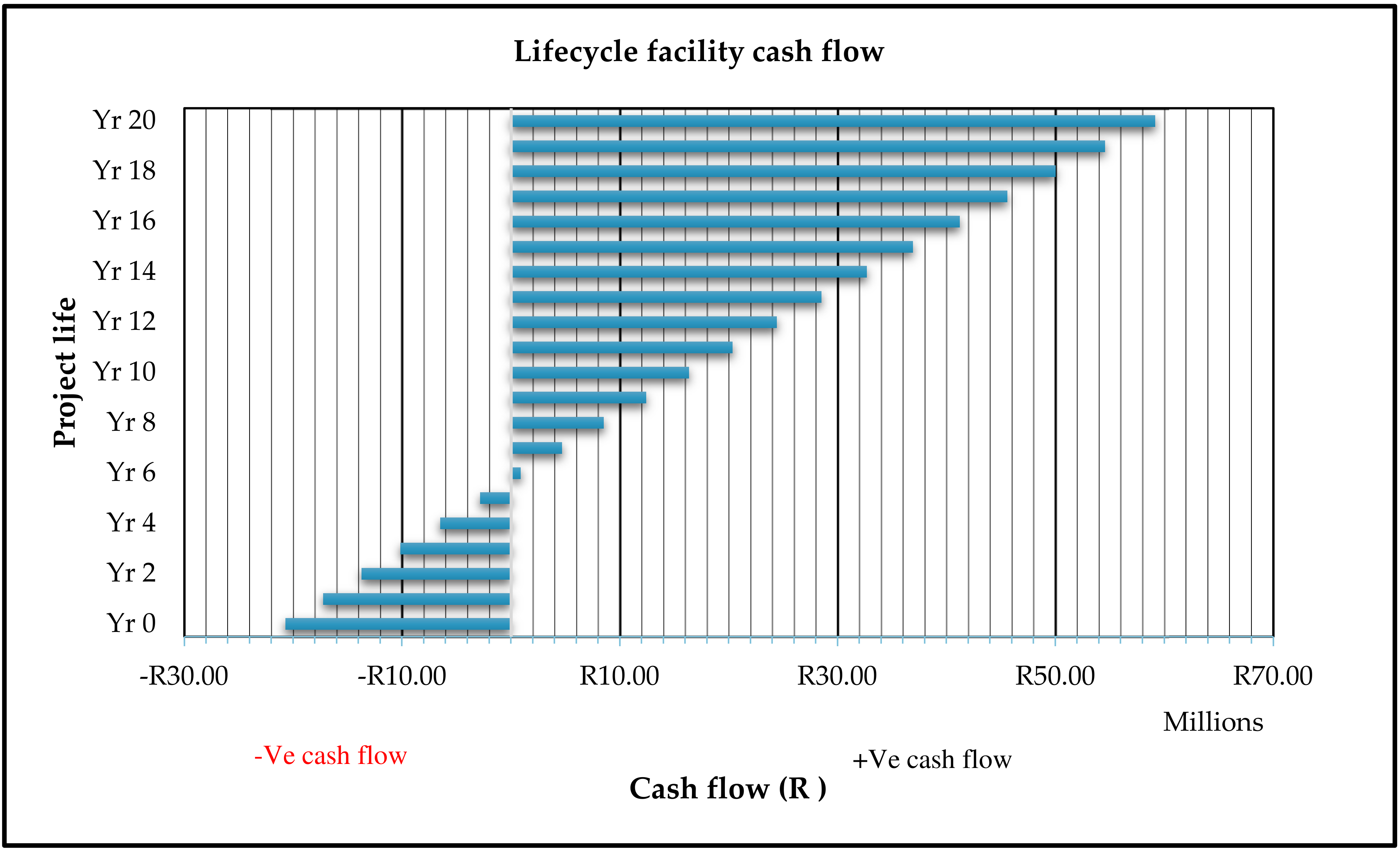
The study considers many characteristics such as payback time, net present value, and return interest rate.

-

The evaluation of electricity tariff rates relies on distinguishing between low- and high-demand times.

This study focused on investigating the energy requirements and the complete lifecycle of energy generation associated with a downhill conveyor belt system. The electricity costs for low and high demand were determined based on the provided data. Evaluating the financial viability of the system involves examining many components such as the net present value, internal rate of return, and payback period. The aggregate cash flows exhibited an initial phase of adverse cash flows, succeeded by a phase of steadiness, and ultimately converting into favorable cash flows in subsequent years. The projected internal rate of return of 15% exceeds the existing return on investment of 6–9% offered by conventional South African banks [43].

The cumulative cash flows in Figure 10 demonstrate that the project will generate negative cash flows during its initial seven years of operation. Nevertheless, it is expected that the project will achieve a break-even repayment period of 6 years, with the value of R971,555.97 attained in that year, and subsequently generate positive income for the remaining 14 years of its existence. The equipment design will generate a total positive cash flow of R60.157 million throughout its 20-year lifecycle, which will be carefully documented. The sensitivity of the financial model is tested in Figure 11, with the inflation target changed to a range of 11–14% as suggested by the literature. The PBP remains at 6 years, with a value of R926,768.33 achieved in the year; however, the total cash flow drops slightly to R59.78 million rand and the IRR remains at 15%. These results prove that the financial model can be used as is regardless of the possible impact of the change in inflation targets in the future.

Economically, the results indicate that the integration of brake choppers and three-phase AFEL inverters in DBCs is feasible. The system efficiently collects and transforms excess potential energy into useful energy, providing a cost-effective approach to energy management. The economic evaluation indicates that the investment returns are prospective, the cash flows are favorable, and the internal rate of return is higher than the typical bank return on investment. The system’s energy-generating capacity makes a substantial contribution to the enhancement of the environmental sustainability of energy. This research illustrates the feasibility of incorporating energy-efficient technology into industrial systems, with a particular focus on DBCs.

4.3. Benefits Comparison: 3-Phase AFEL vs. DOL Induction Motor Technologies

In evaluating the financial and operational implications of integrating three-phase active front-end load converters versus direct on-line induction motor technologies in downhill belt conveyor systems, several studies and industry practices underscore the significant advantages of AFEL systems. Notably, the capacity for energy recovery and conversion of potential energy into electrical energy through AFEL systems provides a substantial reduction in energy costs when compared to traditional DOL systems, which lack such capabilities. These power savings not only reduce operational costs, but also contribute to environmental sustainability by lowering carbon emissions [13]. Typically, DOL systems operate without the capability to regenerate or recover energy. For a 300 kW motor fully utilized, the monthly power consumption would be approximately 142,800 kWh, if operating at 100% capacity for 17 h a day over 476 h per month. Over a 20-year period, the total electricity cost would reach approximately R142,508,330.51 considering the baseline electricity cost aligned to the 300 kW motor. The initial investment includes the purchase of the motor and setup and is R18,831,450, which is relatively lower than those for AFEL systems. However, without energy recovery capabilities, the total cost of ownership, including maintenance and operational costs, remains high as indicated in Figure 12.

AFEL technology allows the transformation of potential energy into electrical energy during the operation of downhill conveyors. With an AFEL system, there’s a potential saving of 39% in energy consumption, which equates to a significant reduction in operational costs. The lifecycle energy generation of 21,477,120 kWh results in a return on investment of R60,457,065 based on an initial capital and operational cost of R20,729,795. Despite a higher upfront cost, the operational savings from reduced energy consumption and the ability to generate electricity significantly offset the initial expenditure. The integration of AFEL results in a cumulative lifecycle cost that is substantially lower when factored over the lifespan of the system. The cash flow is included in Figure 10.

These systems not only offer immediate operational benefits, but also contribute to long-term sustainability and risk management objectives, making them a prudent investment in scenarios where energy recovery is feasible and desirable.

Table 3. Energy demand lifecycle tariff comparison of AFE vs. DOL systems.

Description	AFE data	DOL data	Unit
Total power	−188	300	kWh
Operating hours	17	17	Hours/day
Monthly generation	−89,488	142,800	kWh
Low-demand cost	R90,869.10	−145,003.88	kWh/month
High-demand cost	R190,178.41	−R303,476.18	kWh/month
Total demand cost	R281,047.50	−R448,480.06	kWh/month
Lifecycle generation	−R21,477,120.00	0	kWh
Forecast tariff increase	3% to 6%	11% to 14%	Inflation rate target
Minimum cost	R287,173.43	−R443,593.71	kWh/month
Mean cost	R287,779.52	−R442,629.52	kWh/month
Maximum cost	R288,385.62	−R441,665.34	kWh/month
Standard deviation	350.97	558.34	kWh/month

indicates a system comparison on energy demand and related cost performance for each. The formula for calculating power savings in an AFE-integrated system can be expressed as follows [19]:

$${∆P}_{saving}=P_{DOL}-P_{AFE}=\mathrm{142,800}-\mathrm{89,488}=\mathrm{53,312} \mathrm{k}\mathrm{W}\mathrm{h}/\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}$$

(32)

This represents a significant power saving of 53,312 kWh per month. Furthermore, when considering that the AFE system is designed to recover approximately 39% of the energy, the formula for power saving ratio $R_p$ can be expressed as follows [36]:

$$R_p={\displaystyle \frac{P_{DOL}-P_{AFE}}{P_{DOL}}}. 100={\displaystyle \frac{\mathrm{142,800}-\mathrm{89,488}}{\mathrm{142,800}}}=37.35\%$$

(33)

Energy savings from the AFE system directly correlate to reduced carbon emissions, particularly in regions where electricity generation is dependent on fossil fuels, such as coal. The carbon emission reduction can be calculated based on the energy saved and the CO₂ emission factor for coal-fired electricity, typically around 0.91 to 0.95 kg CO₂ per kWh [44,45]. The carbon emission reduction ${∆CO}_2$ is calculated as follows:

$${∆CO}_2=∆P ({∆CO}_2 Factor)=\mathrm{53,312}\times 0.91=\mathrm{48,514}kg$$

(34)

This results in a carbon emission reduction of approximately 48.51 metric tons of CO₂ per month, which translates to a total of 582.13 tons of carbon over a year. This reduction in carbon emissions aligns with sustainability goals and provides a strong case for the use of AFE converters in energy-intensive operations, such as mining and material handling.

5. Conclusions

This research demonstrated the viability and cost-effectiveness of utilizing an active front-end (AFE) regenerative drive coupled with appropriate braking systems for downhill belt conveyors. From the technical analysis, the AFE system achieved substantial energy savings by efficiently capturing and converting excess potential energy into electrical energy, thereby reducing the overall energy consumption of the conveyor system. The regulated regenerative operation also provided effective speed and tension control, enhancing operational safety and reducing mechanical stress on the conveyor and mitigating risks such as belt over-tension and breakage.

Key Findings and Contributions of the Study

-

The AFE-equipped conveyor showed a ~37–39% reduction in net energy drawn from the grid, as it was able to feed power back during loaded downhill operation. Over the conveyor’s life, this translates to tens of GWh of energy saved, highlighting the significant impact on energy efficiency in mining operations.

-

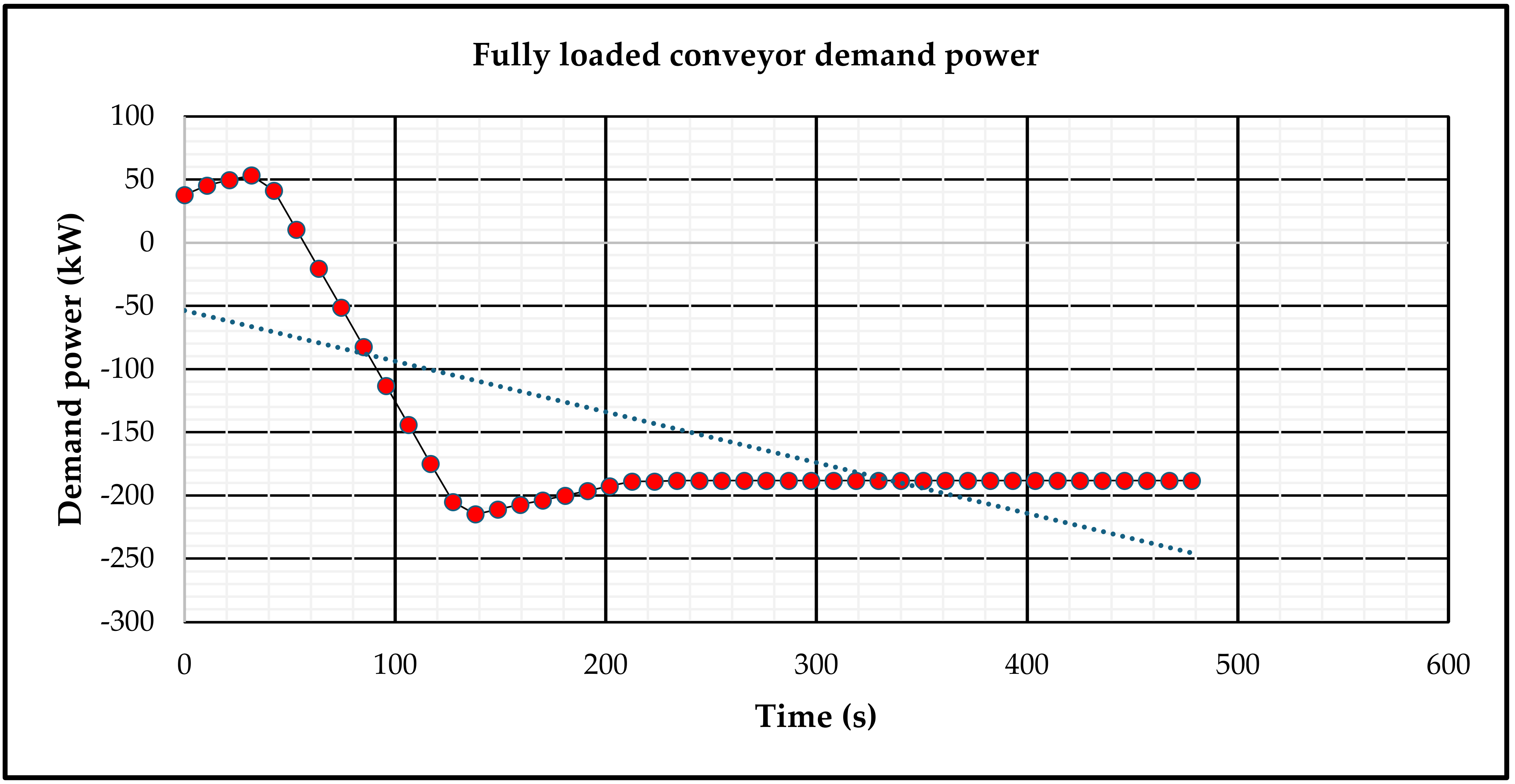
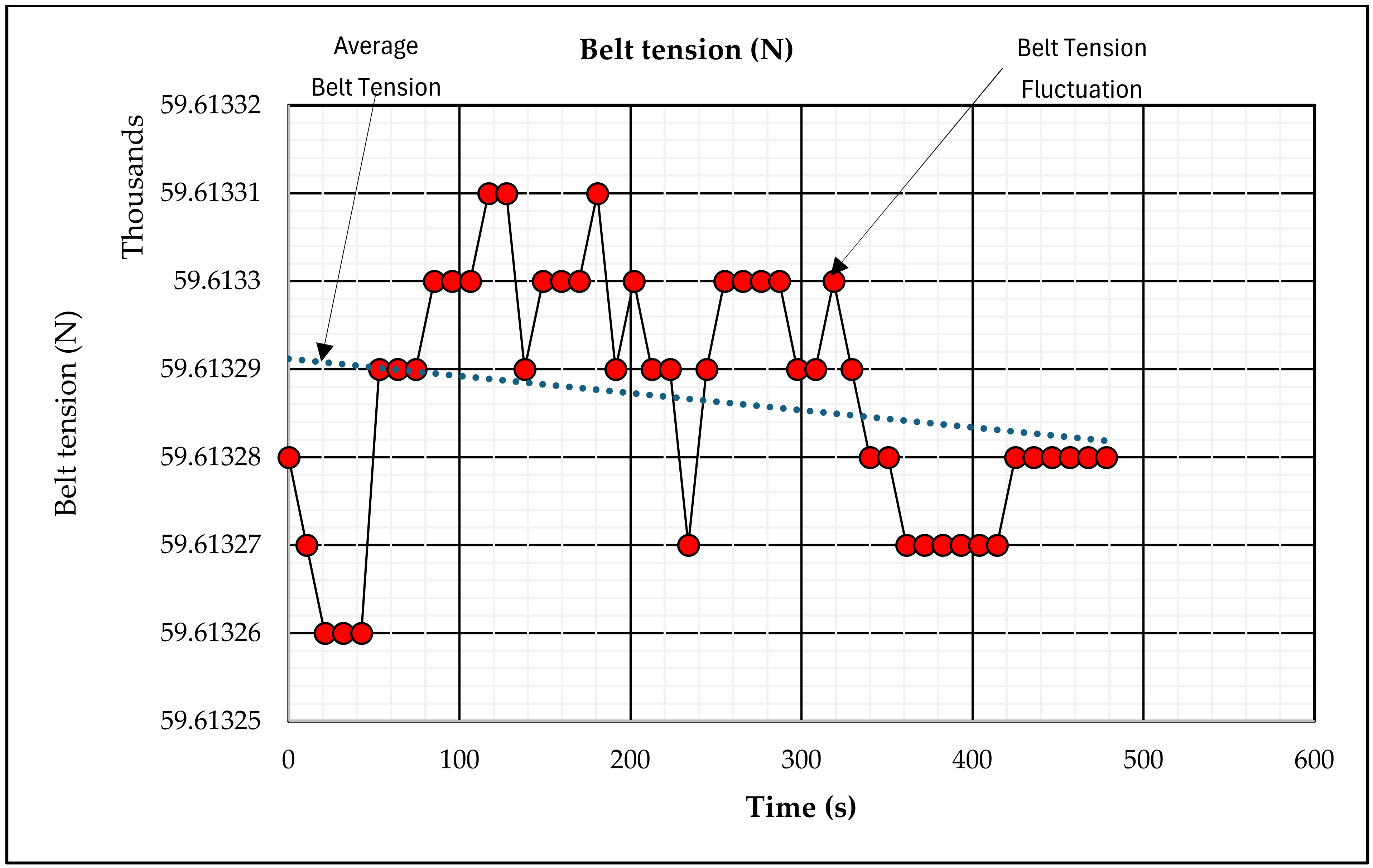
Through dynamic modeling (MATLAB/Simulink) and control design, it was verified that the regenerative drive can maintain stable conveyor speed and acceptable belt tensions during various scenarios, such as the start-up, normal operation, sudden load changes. The system effectively works as a motor when needed and a generator, when possible, seamlessly switches roles. Soft-start capability of the AFE and the coordinated braking system (Brake A, B, C) ensure safe operation under all conditions.

-

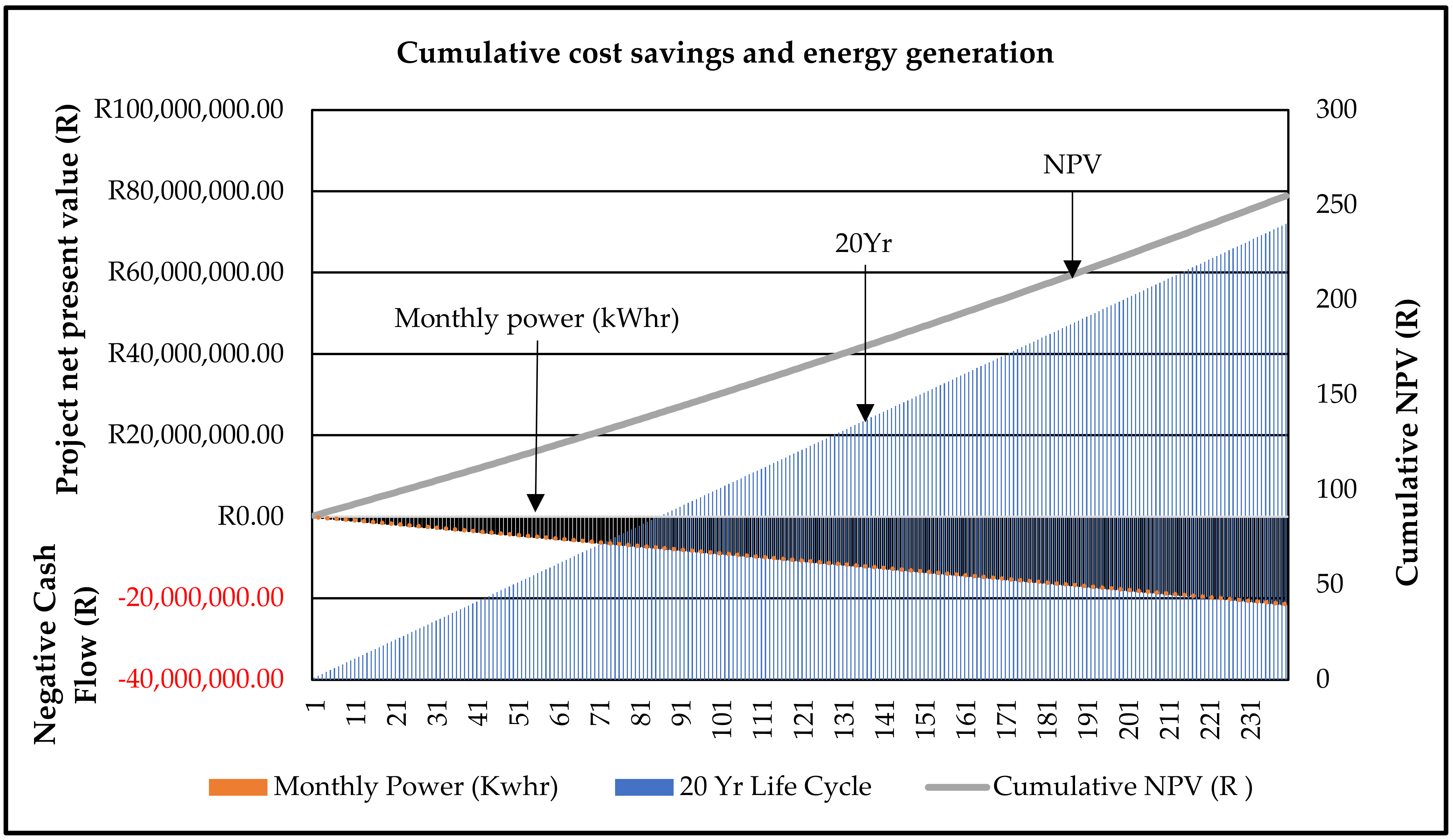
The lifecycle cost analysis and financial modeling confirmed that despite a higher initial investment for the AFE system, the project yields a favorable economic return. As calculated, the payback period is ~6 years and the IRR is ~15%, which is very attractive. The NPV over 20 years was strongly positive, indicating that the investment not only pays for itself, but also generates additional value. These results were robust even under sensitivity scenarios of varying electricity inflation, meaning the regenerative system is a financially sound investment under a range of future conditions. This addresses a gap in the existing research by providing a long-term economic perspective, not just a short-term energy saving estimate.

-

The distinctiveness of this approach lies in the holistic integration of mechanical, electrical, and economic analyses. The study moved beyond a traditional DOL drive paradigm and demonstrated, via modeling and a case study, the advantages of regenerative AFE converters. The investigation utilized dynamic simulation tools to capture transient behaviors and design the control system, engineering design software (Sidewinder) to accurately parameterize the conveyor’s physical characteristics, and financial modeling to evaluate viability. This comprehensive methodology provides a template for evaluating similar systems in other industrial contexts.

-

Through reducing the energy drawn from coal-based power and feeding energy back, the AFE system contributes to lower carbon emissions. For energy-intensive sectors like mining, adopting such technologies can be a significant step toward sustainability and reducing the carbon footprint. The calculations show meaningful CO₂ reductions, aligning the project with broader environmental and regulatory goals.

In conclusion, implementing AFE regenerative drive technology on downhill conveyors is both technically feasible and economically advantageous. It transforms a conveyor from being an energy sink to an energy source, turning what was a cost center into a potential mini power generator for the operation. This not only cuts costs, but also helps in mitigating climate change impacts by conserving energy.