A Novel Three-Dimensional Sliding Pursuit Guidance and Control of Surface-to-Air Missiles
Abstract
1. Introduction
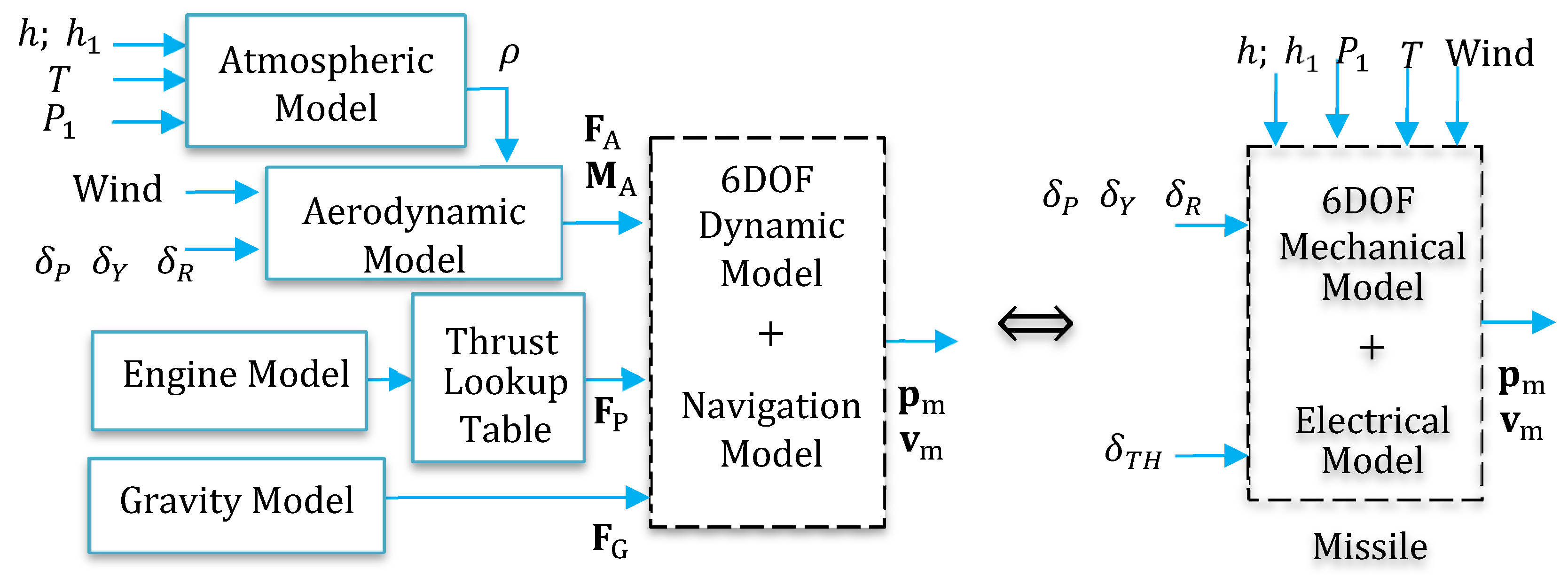
2. Dynamic Models of Generic Missiles
2.1. Six-Degree-of-Freedom Variable Mass Non-Linear Model
2.2. The Euler Angles and the Navigation Model
2.3. Propulsive and Aerodynamic Models
2.4. The Atmospheric Model
2.5. The Missile/Target Motion
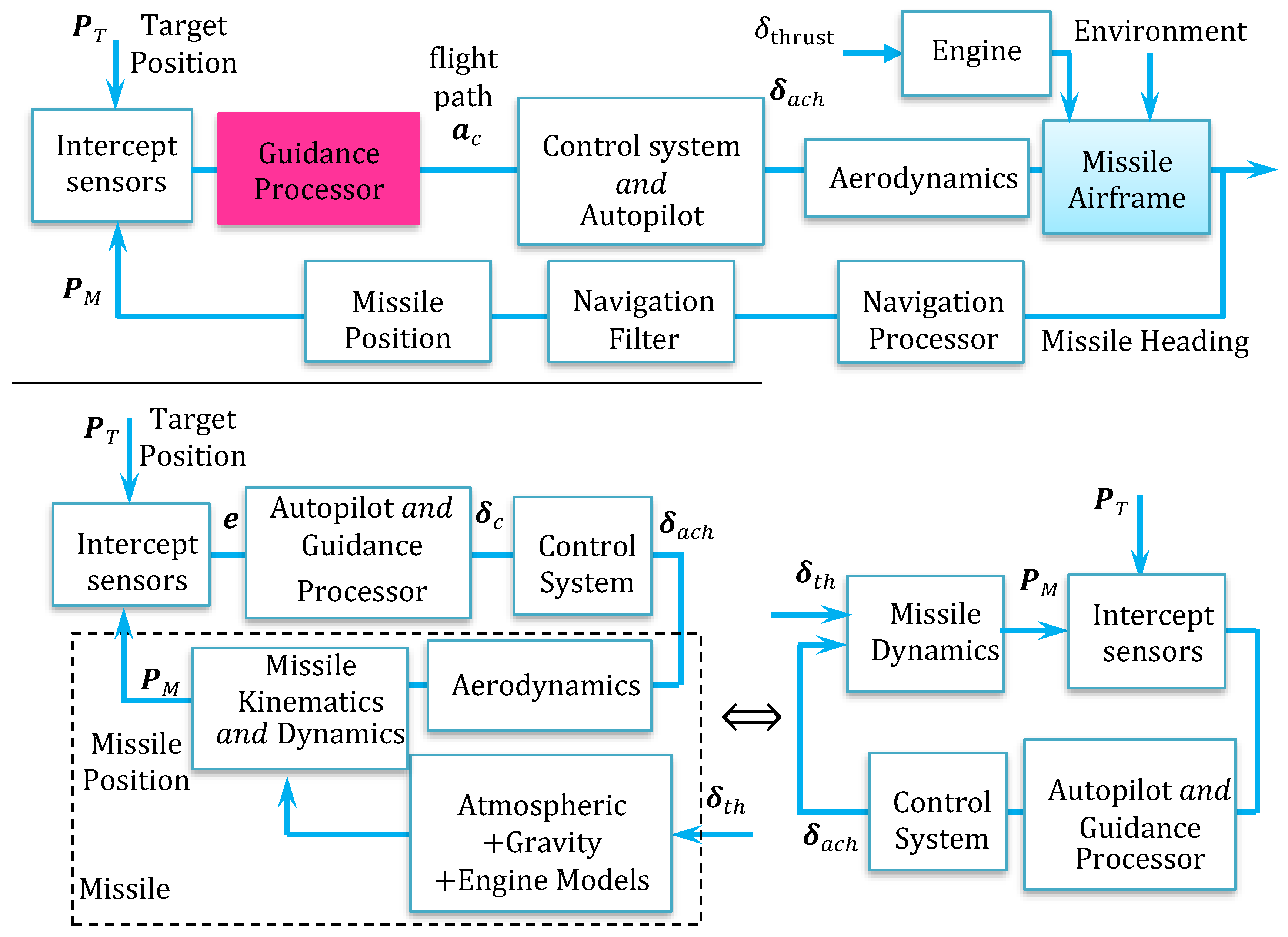
3. Autopilot Model and Control
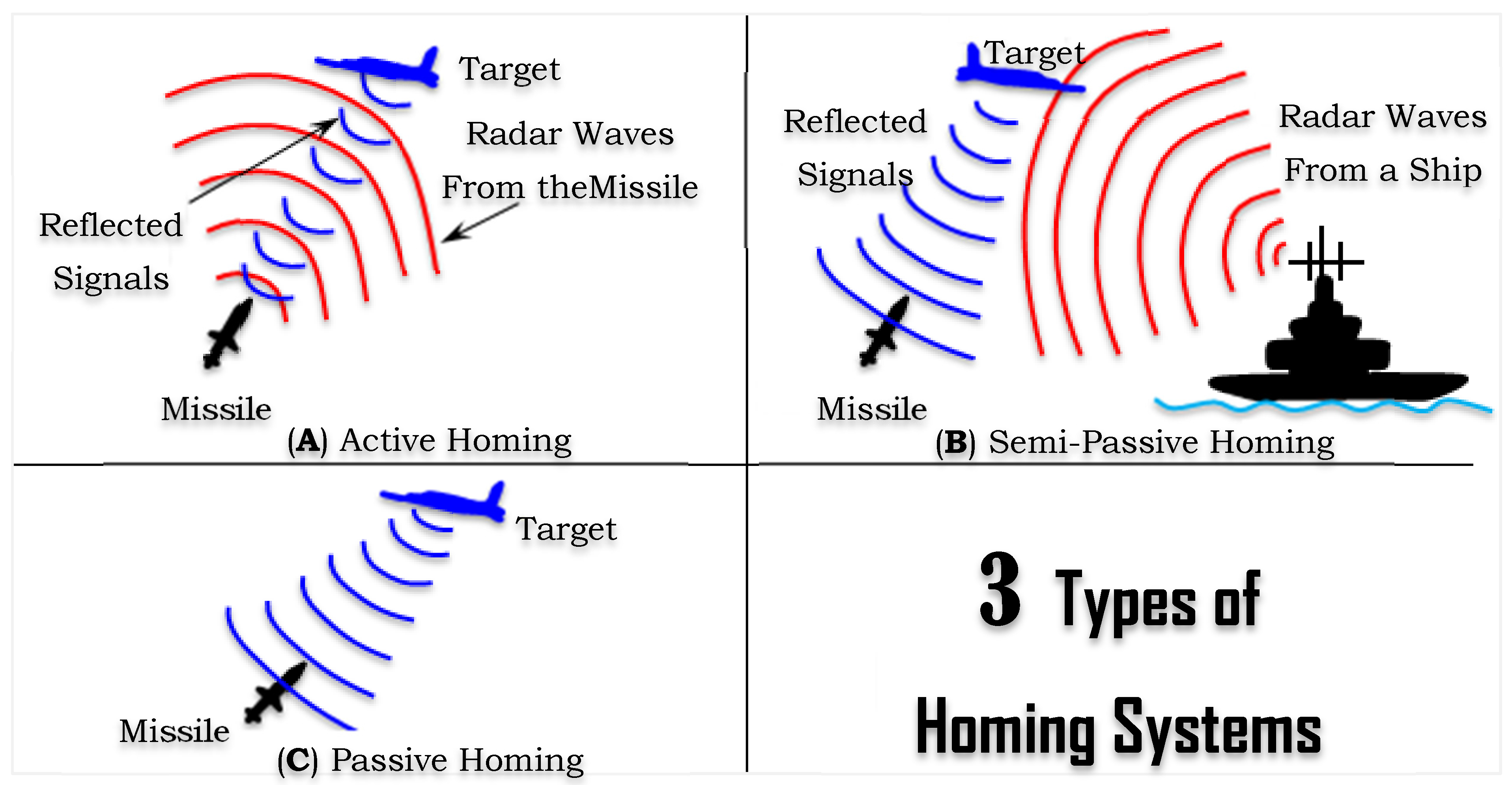
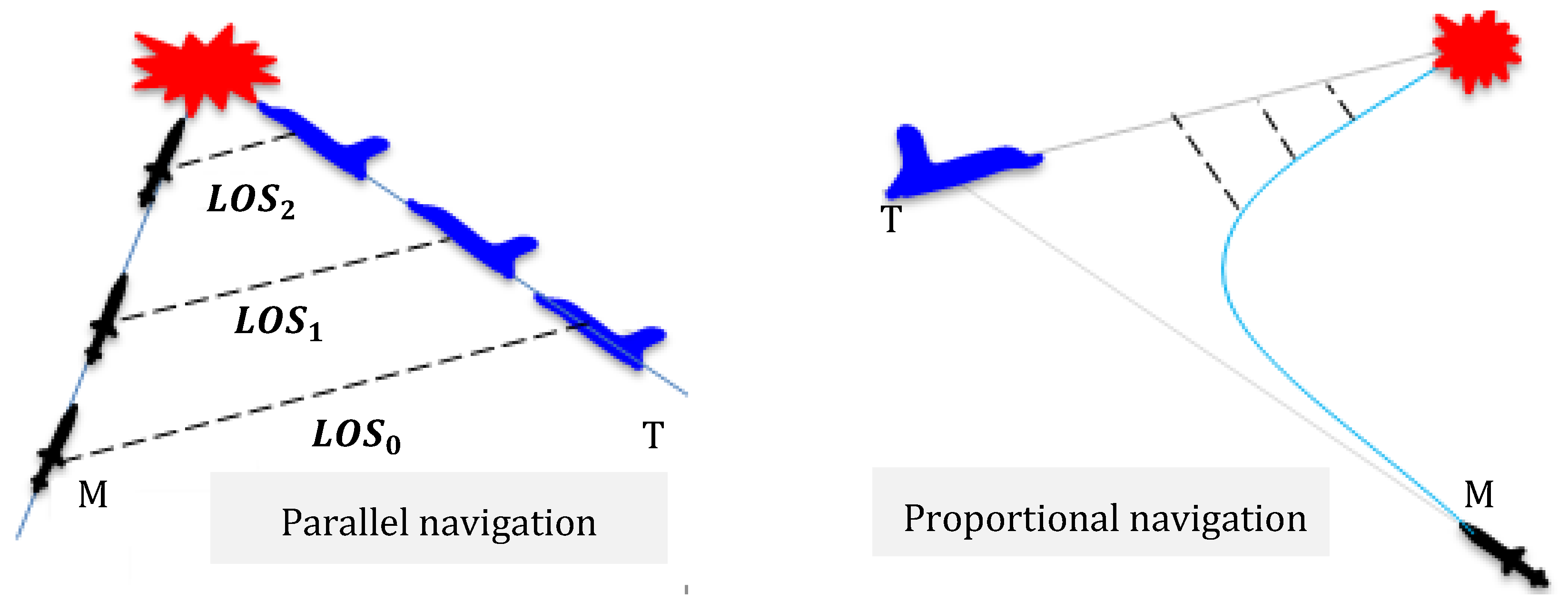
3.1. Different Types of Homing Guidance
3.2. The Autopilot and the Control Systems
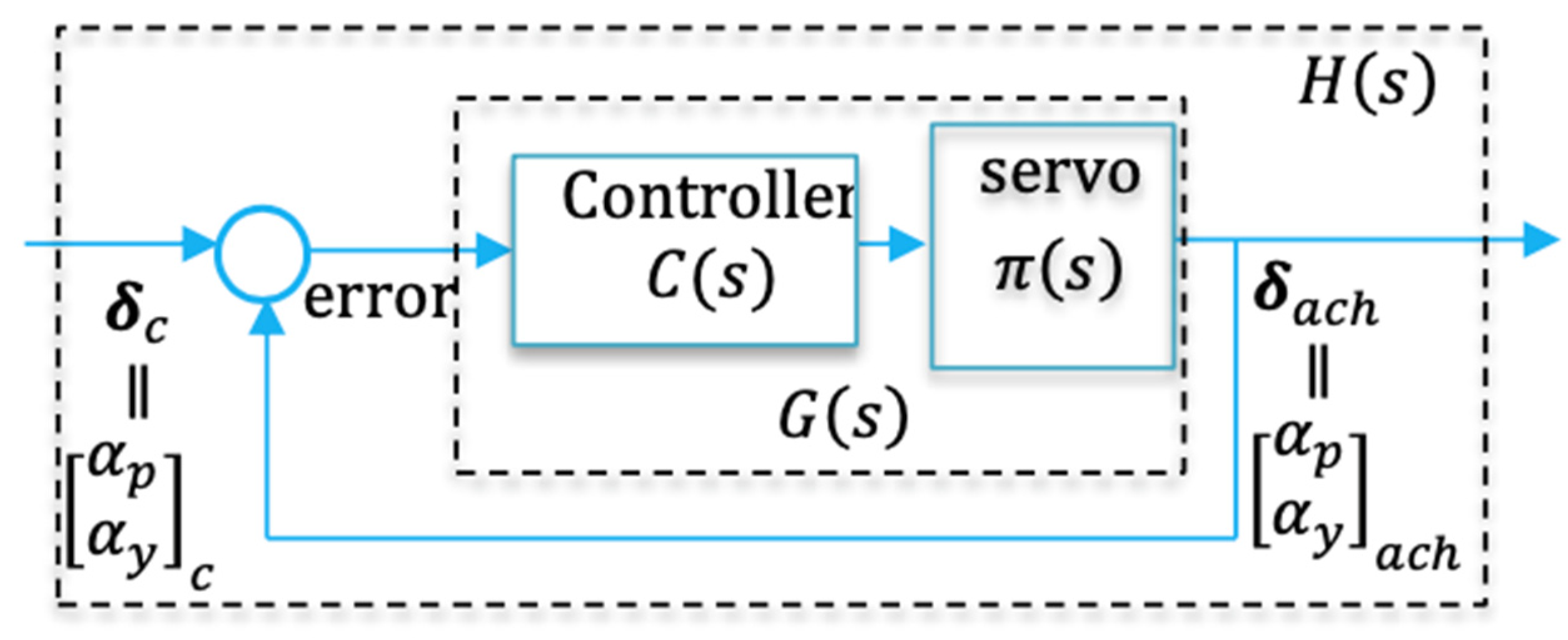
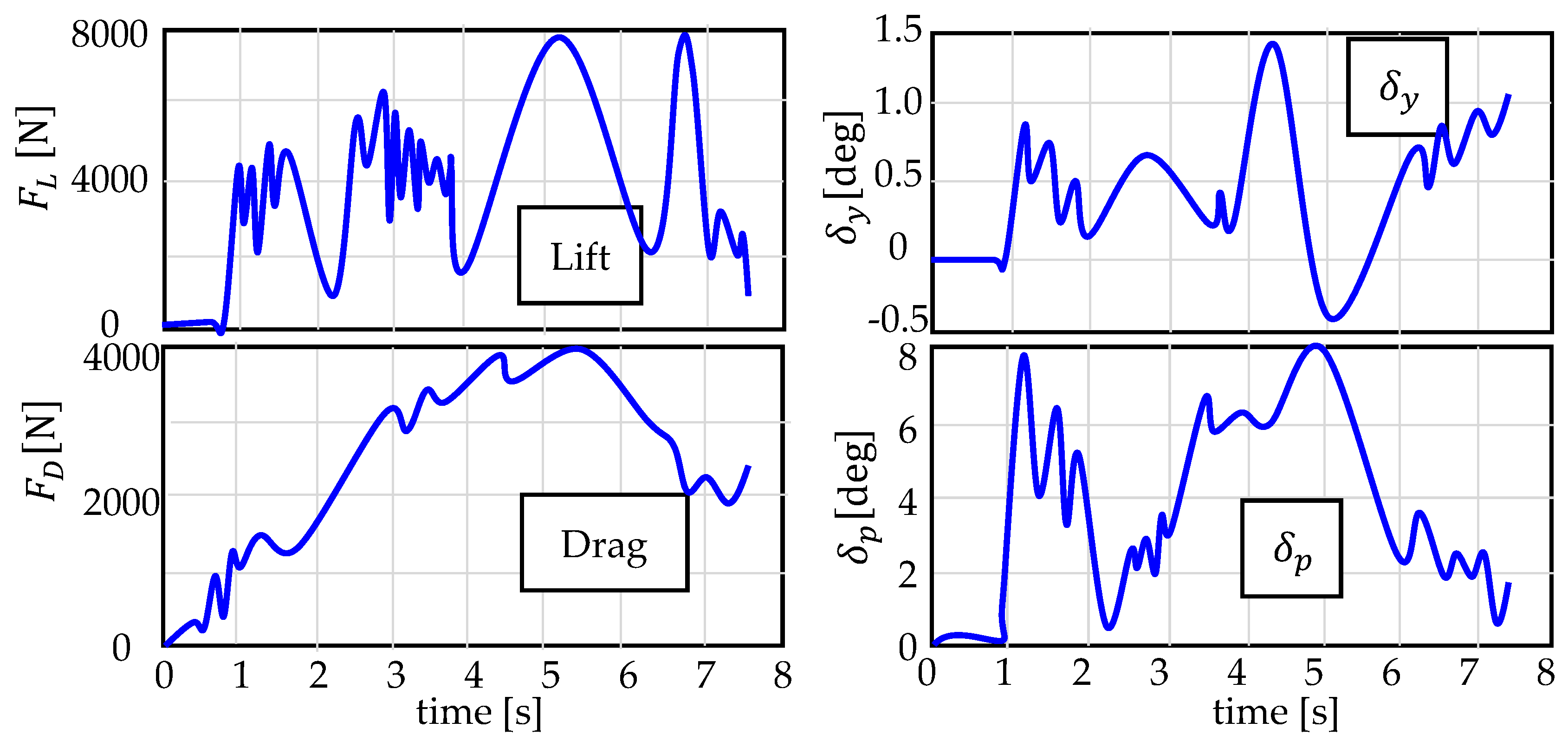
3.3. The Deflection Commands
3.4. Commanded Signals
3.5. Signal Processing and Data Filtering
- is the seeker tracking loop constant.
- is the seeker signal processing time constant.
3.6. Servo System Modeling
4. Overview of the Existing Guidance Laws
- Pure pursuit (and velocity pursuit);
- Proportional navigation and all of its variations;
- Command-to-line-of-sight and beam riding.
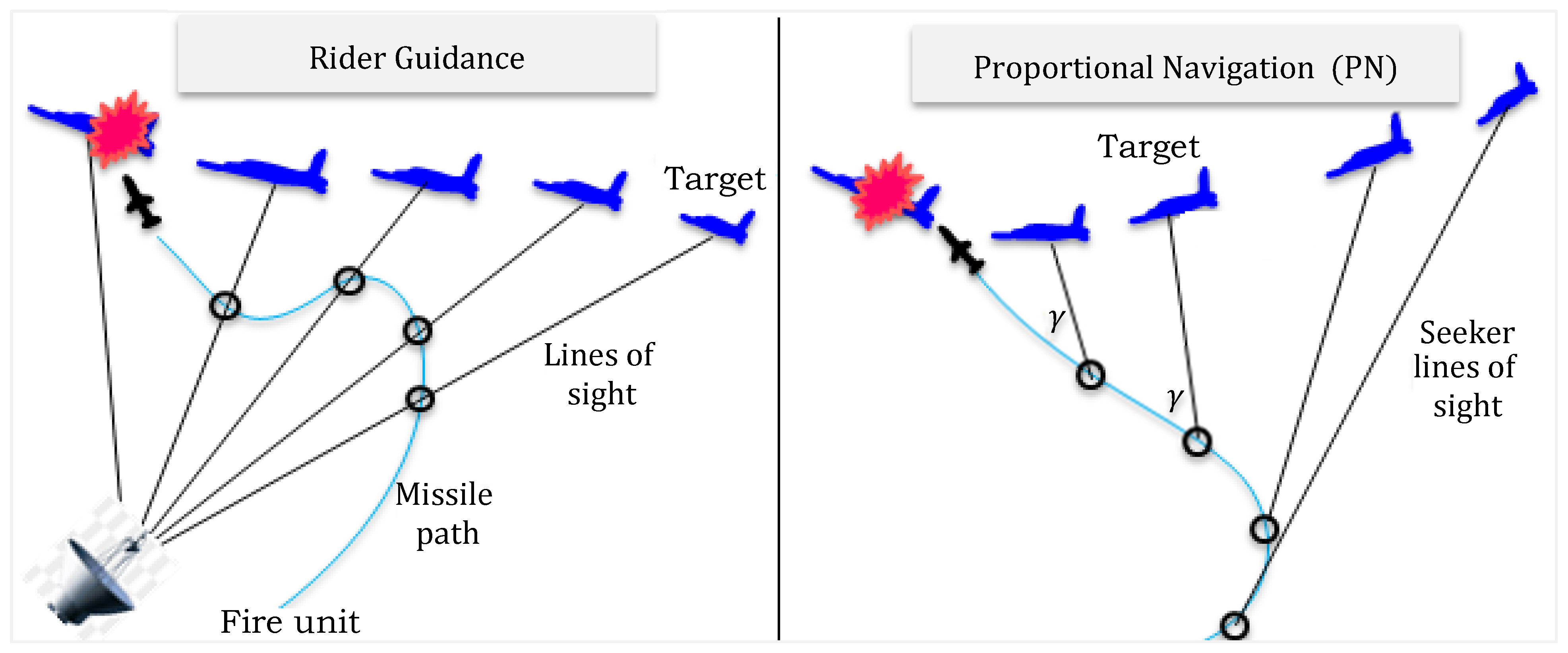
4.1. Proportional Navigation
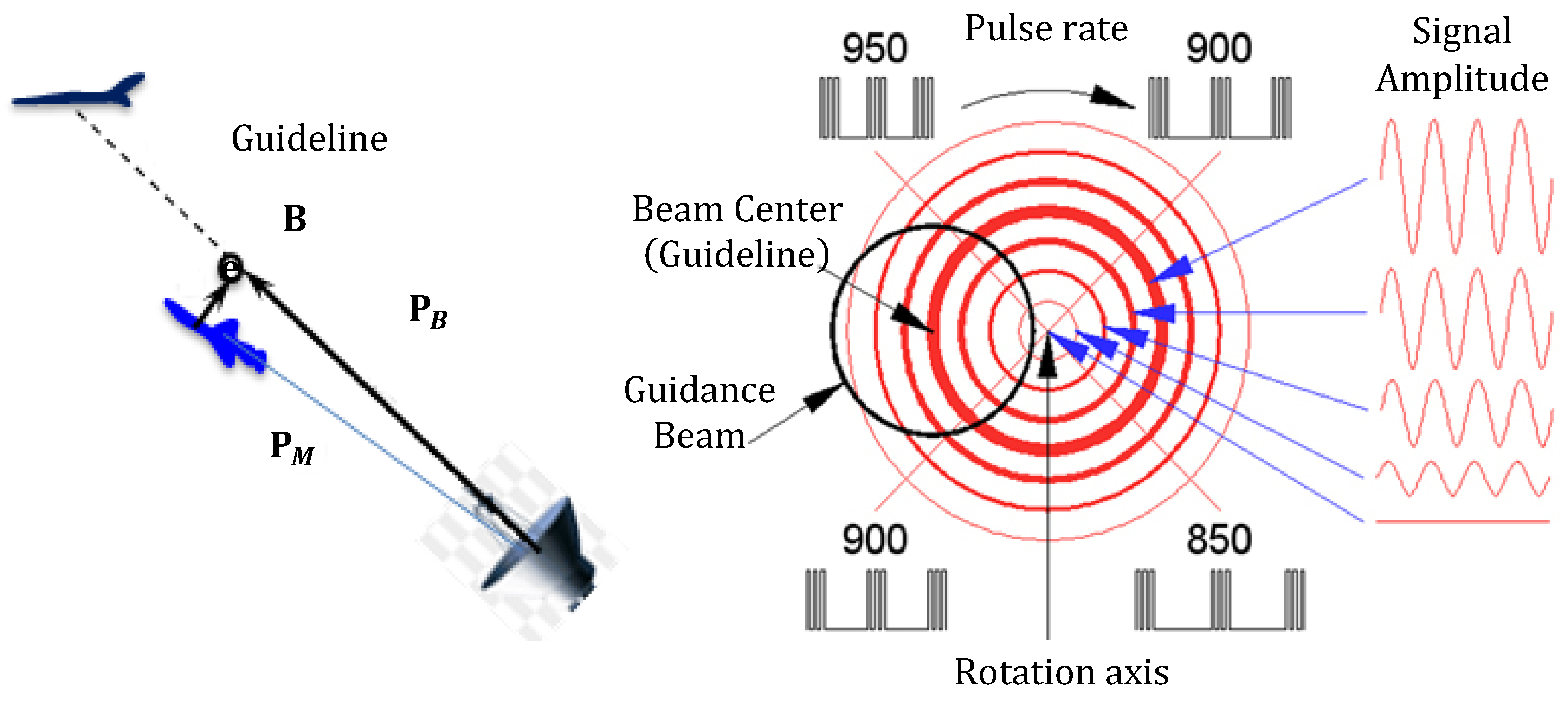
4.2. Line of Sight (and/or Beam Rider) Guidance
4.3. Zero-Effort Miss Guidance Law
| Algorithm 1: Zero-Effort Miss Guidance Law |
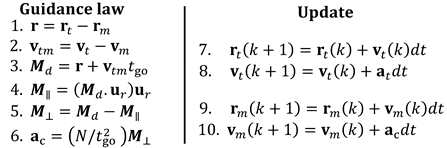 |
5. The Proposed 3D Pure Pursuit Guidance Law
5.1. The Proposed 3D Pure Pursuit Navigation
- Search and track radar (computational techniques);
- Inertial sensors and Kalman filters;
- Artificial intelligence/machine learning techniques.
| Algorithm 2: The Proposed 3D Pure Pursuit Navigation |
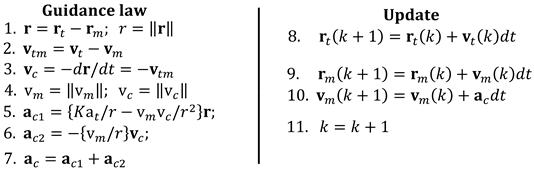 |
5.2. Pure Pursuit Sliding Mode Guidance
| Algorithm 3: The Proposed 3D Pure Pursuit Sliding Guidance |
6. Full Simulation Study
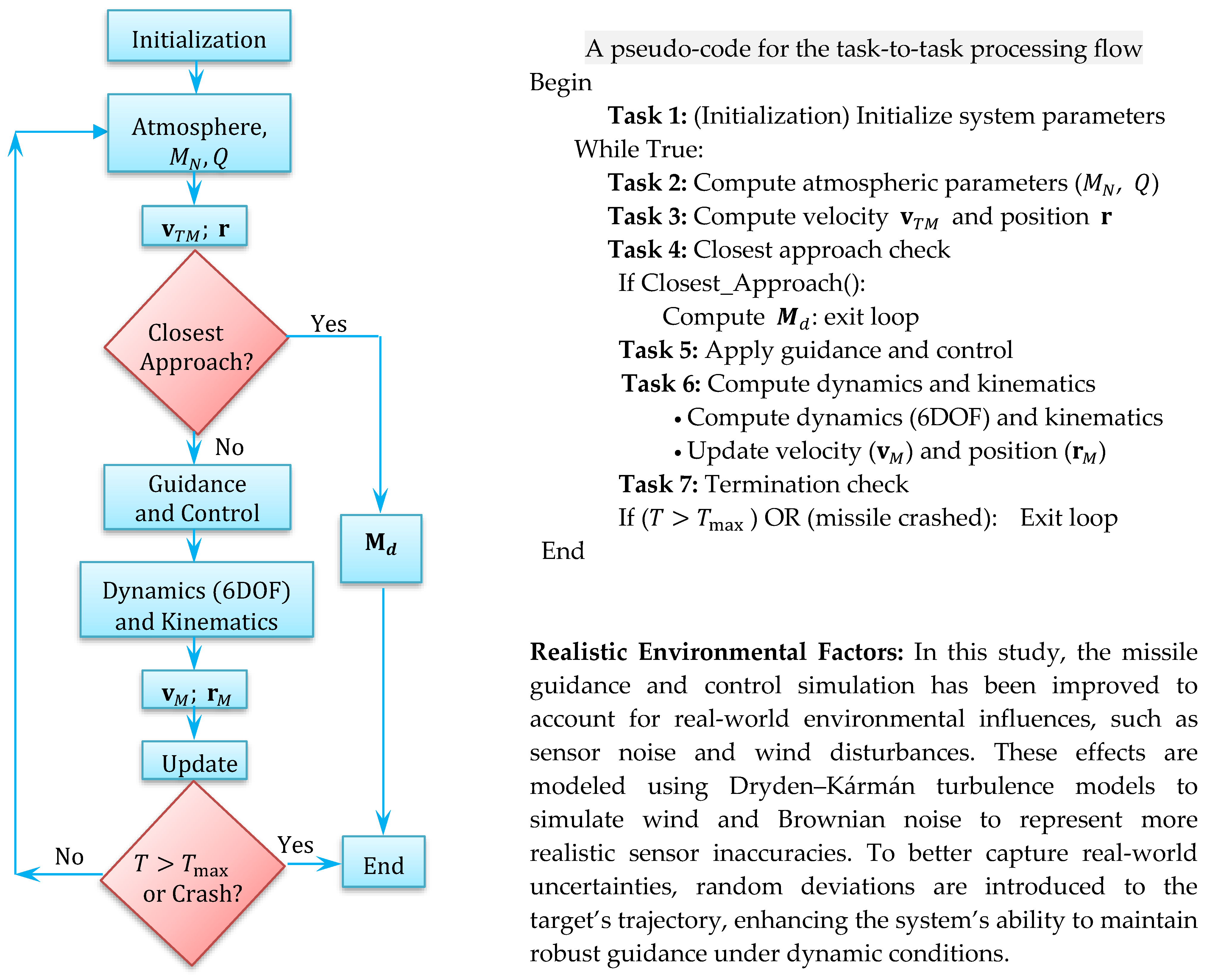
6.1. Overall Program Structure
6.2. The Overall Pseudocode

6.3. Optimization Using the PSO Algorithm
- The velocity vector denotes the increment of the current position. It is given for each agent or (particle) by
- = the current velocity of agent at the iteration;
- = inertia weight, takes a value between 0 and 1;
- = inertia weight factor (learning parameters);
- = random vectors, entries take a value of [0, 1];
- = the current position of agent at the kth iteration;
- = the ith agent’s best position;
- = the group’s best position.
- Inertia weight (Function) is given as follows:The inertia can be taken as a constant, typically . This is equivalent to introducing a virtual mass to stabilize the motion of particles, and thus the algorithm is expected to converge more quickly.
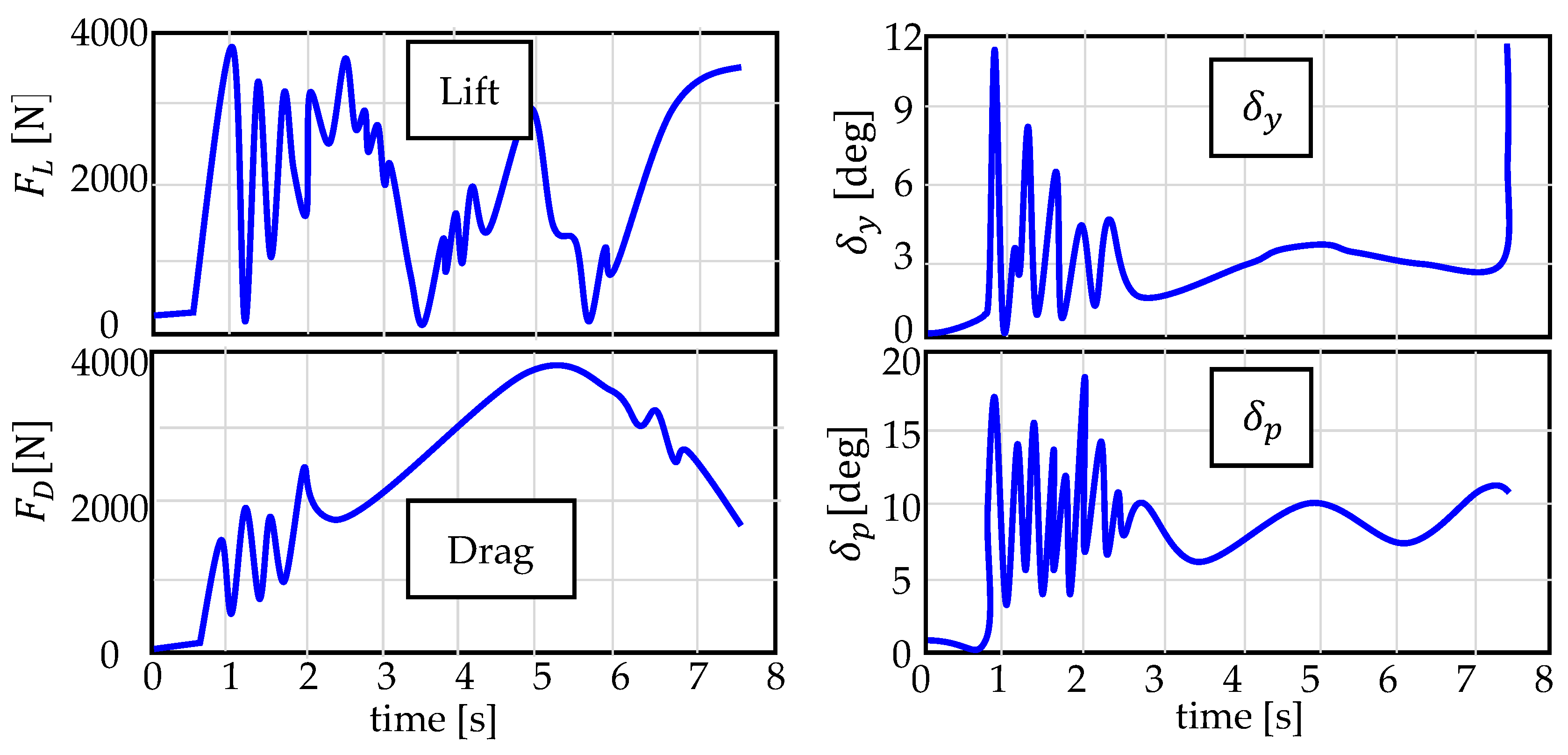
6.4. Example of a Simulation
- is the aerodynamic ref length (Missile’s diameter).
- is the fuselage length (from the tile of the missile to the center of mass).
- is the time of burnout.
- is the ref-ambient pressure.
- is the specific impulse and is the lapse rate.
- is the exit area of rocket nozzle.
- is the sound speed in elastic medium.
- is the gas constant.
- is the missile aerodynamic ref area.
- is the air density at sea level.
- is the temperature at sea level.
- is the
- .
- ,
- ,
- Seeker: time constants , and ,
- Autopilot:
- , ,
- , and
- and
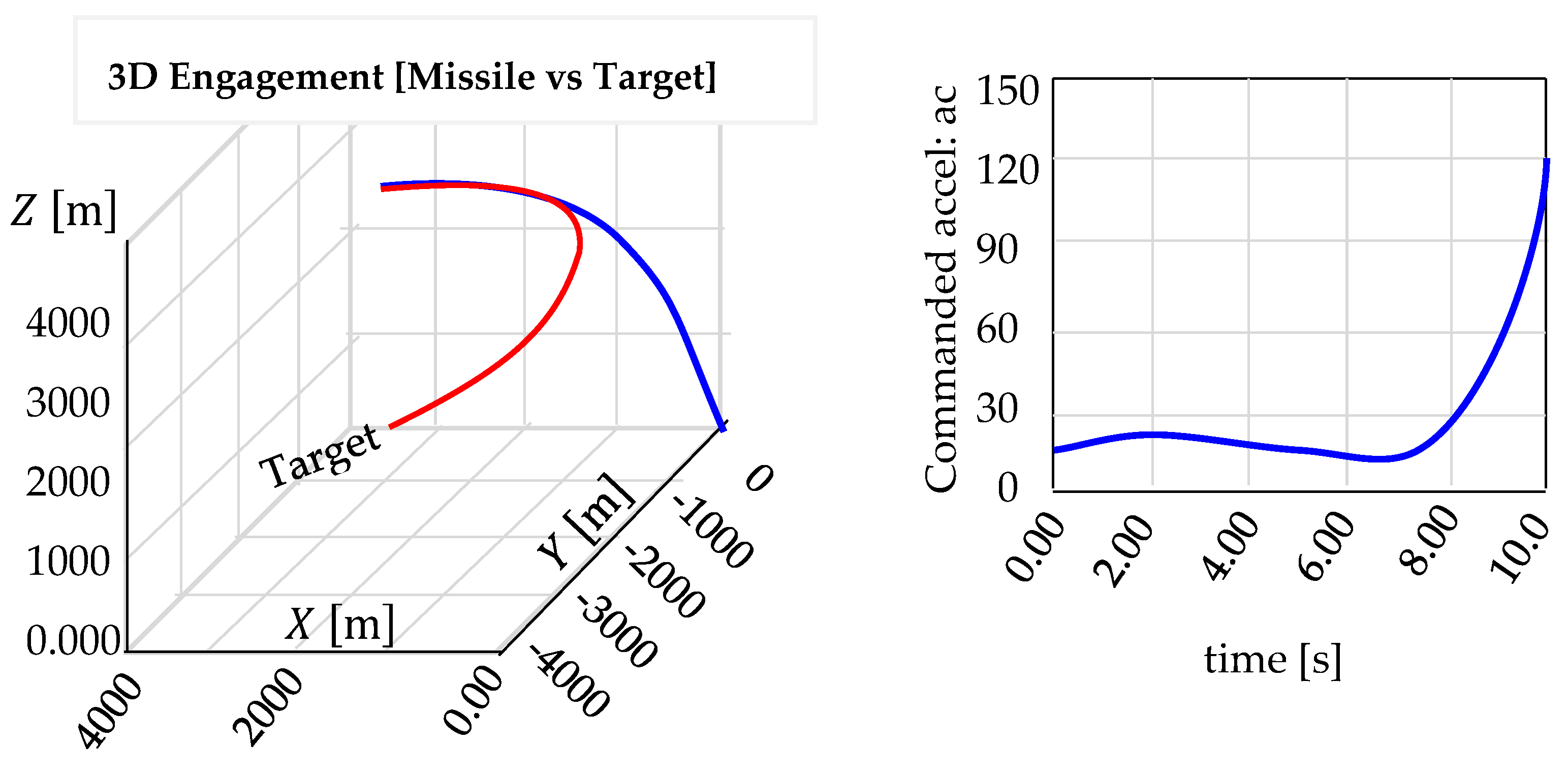
- The Optimal Proportional Navigation by ZEM:
- B.
- The Proposed Optimal 3D Pure Pursuit Guidance:
- C.
- The Proposed Optimal 3D Sliding Pure Pursuit:
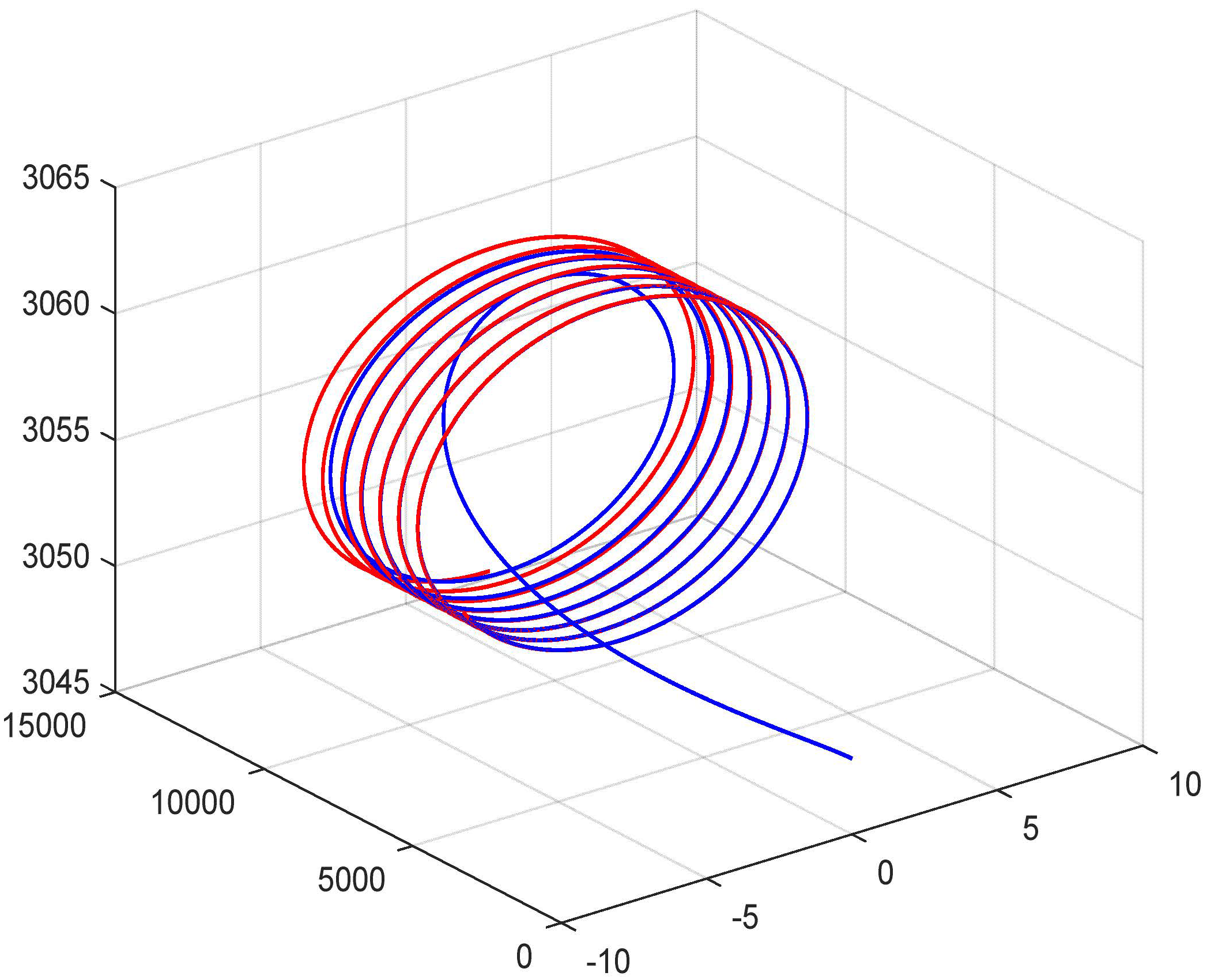
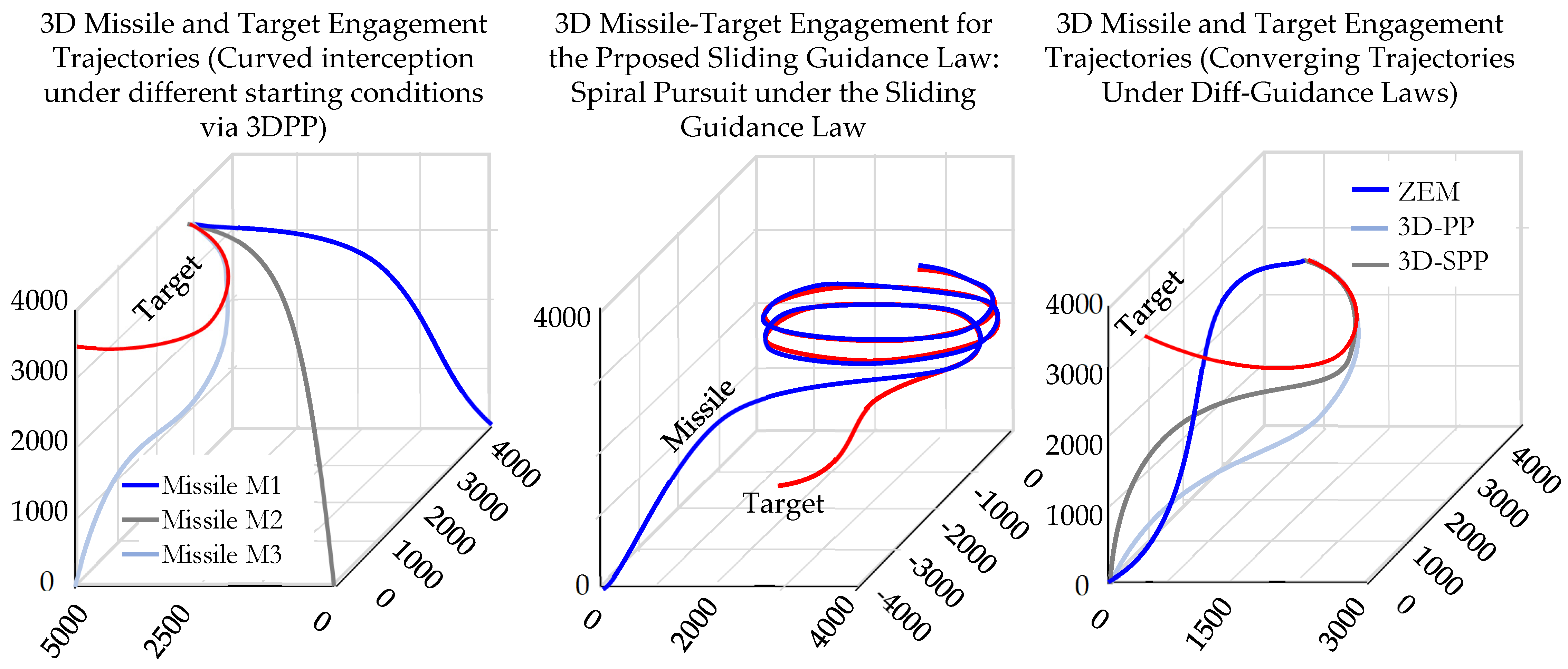
6.5. Simulation of Interception Under Varying Conditions
- A lower ensures precise interception.
- A shorter leads to rapid convergence.
- A higher supports successful interception but requires efficient control.
- A higher acceleration provides maneuverability but adds structural stress.
- The load factor measures the missile’s ability to withstand G-forces.
- The flight path and impact angles affect trajectory efficiency and lethality.
- Control effort impacts actuator demand and precision.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ZEM | Zero-Effort Miss Distance |
| PP | Pure Pursuit |
| PN | Proportional Navigation |
| LOS | Line of Sight |
| CLOS | Command to Line of Sight |
| 3D | Three-Dimensional |
| SAM | Surface-to-Air Missiles |
| PNG | Proportional Navigation Guidance |
| BTT | Bank-to-Turn |
| LQG | Linear Quadratic Gaussian |
| RF | Radio Frequency |
| RTD | Radians To Degrees |
| PSO | Particle Swarm Optimization |
| SI | Swarm Intelligence |
Appendix A
References
- Paul, Z. Tactical and Strategic Missile Guidance. In Progress in Astronautics and Aeronautics AIAA, 4th ed.; American Institute of Aeronautics & Astronautics Inc.: Reston, VR, USA, 2019. [Google Scholar] [CrossRef]
- Farooq, J. Hybrid Deep Neural Network for Data-Driven Missile Guidance with Maneuvering Target. Def. Sci. J. 2023, 73, 602–611. [Google Scholar] [CrossRef]
- He, S. Three-Dimensional Optimal Impact Time Guidance for Antiship Missiles. J. Guid. Control Dyn. 2019, 42, 941–948. [Google Scholar] [CrossRef]
- Wang, C.; Yan, J.; Lyu, R.; Liang, Z.; Chen, Y. Optimal Guidance Law for Critical Safe Miss Distance Evasion. Aerospace 2024, 11, 1041. [Google Scholar] [CrossRef]
- Jeon, I.S. Optimality of P-Navigation based on Nonlinear Formulation. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 2051–2055. [Google Scholar] [CrossRef]
- Cho, N.; Kim, Y. Optimality of Augmented Ideal Proportional Navigation for Maneuvering Target Interception. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 948–954. [Google Scholar] [CrossRef]
- Kim, H.-G. Integrated Autopilot Guidance Based on Zero-Effort-Miss Formulation for Tail-Controlled Missiles. Appl. Sci. 2022, 12, 7120. [Google Scholar] [CrossRef]
- Gutman, S. 3D-Nonlinear Vector Guidance and Exo-Atmospheric Interception. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 4. [Google Scholar] [CrossRef]
- Zhang, G. Structure Synchronized Dynamic Event-Triggered Control for Marine Ranching AMVs via the Multi-Task Switching Guidance. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20295–20308. [Google Scholar] [CrossRef]
- Li, J. Integrating Dynamic Event-Triggered and Sensor-Tolerant Control: Application to USV-UAVs Cooperative Formation System for Maritime Parallel Search. IEEE Trans Intell. Transp. Syst. 2024, 25, 3986–3998. [Google Scholar] [CrossRef]
- Wang, W.; Wu, M.; Chen, Z.; Liu, X. Integrated Guidance-and-Control Design for Three-Dimensional Interception Based on Deep-Reinforcement Learning. Aerospace 2023, 10, 167. [Google Scholar] [CrossRef]
- Yan, T.; Liu, C.; Gao, M.; Jiang, Z.; Li, T. A Deep Reinforcement Learning-Based Intelligent Maneuvering Strategy for the High-Speed UAV Pursuit-Evasion Game. Drones 2024, 8, 309. [Google Scholar] [CrossRef]
- Choi, W.-J.; Lee, J.-S. A Balanced Path-Following Approach to Course Change and Original Course Convergence for Autonomous Vessels. J. Mar. Sci. Eng. 2024, 12, 1831. [Google Scholar] [CrossRef]
- Zhao, J. Cooperative guidance of seeker-less missile considering localization error. Chin. J. Aeronaut. 2019, 32, 1933–1945. [Google Scholar] [CrossRef]
- Chen, C.-H. Design of Midcourse Guidance Laws via a Combination of Fuzzy and SMC Approaches. Int. J. Control Autom. Syst. 2010, 8, 272–278. [Google Scholar] [CrossRef]
- Liu, X. Target Tracking Enhancement by Three-Dimensional Cooperative Guidance Law Imposing Relative Interception Geometry. Aerospace 2021, 8, 6. [Google Scholar] [CrossRef]
- Tahk, M.J.; Shim, S.W.; Hong, S.M.; Choi, H.L.; Lee, C.H. Impact Time Control Based on Time-to-Go Prediction for Sea-Skimming Antiship Missiles. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2043–2052. [Google Scholar] [CrossRef]
- Hodžić, M. Missile Guidance using Proportional Navigation and Machine Learning. J. Eng. Res. Sci. 2024, 3, 19–26. [Google Scholar] [CrossRef]
- Scott, B. Guidance of a homing missile via nonlinear geometric control methods. J. Guid. Control Dyn. 1995, 18, 441–448. [Google Scholar]
- Rusnak, I. Optimal Guidance for High-Order and Acceleration Constrained Missile. J. Guid. Control Dyn. 1991, 14, 383–391. [Google Scholar] [CrossRef]
- Liang, H. Optimal Guidance Laws for a Hypersonic Multiplayer Pursuit-Evasion Game Based on a Differential Game Strategy. Aerospace 2022, 9, 97. [Google Scholar] [CrossRef]
- Yang, C.D. Analytical Solution of Three-Dimensional Realistic True Proportional Navigation. J. Guid. Control Dyn. 1996, 19, 7504–7509. [Google Scholar] [CrossRef]
- Li, Z. Field-to-View Constrained Integrated Guidance and Control for Hypersonic Homing Missiles Intercepting Supersonic Maneuvering Targets. Aerospace 2022, 9, 640. [Google Scholar] [CrossRef]
- Alibani, M. A Fuzzy Guidance System for Rendezvous and Pursuit of Moving Targets. Robotics 2020, 9, 110. [Google Scholar] [CrossRef]
- Shinar, J. Robust pursuit of a hybrid evader. Appl. Math. Comput. 2010, 217, 1231–1245. [Google Scholar] [CrossRef]
- Shinar, J. Three Dimensional Optimal Pursuit and Evasion with Bounded Control. IEEE Trans. Autom. Control 1980, 25, 492–496. [Google Scholar] [CrossRef]
- Shinar, J. Solution Techniques for Realistic Pursuit-Evasion Games. In Advances in Control and Dynamic Systems; Leondes, C.T., Ed.; Academic Press: Amsterdam, The Netherlands, 1981; Volume 17. [Google Scholar]
- Berglund, E. Guidance and Control Technology, Defense Technical Information Center Compilation Part Notice ADP010953; Defense Technical Information Center: Fort Belvoir, VA, USA, 2001. [Google Scholar]
- Oleg, M.; Zhang, K. Pursuit Problem of Unmanned Aerial Vehicles. Mathematics 2023, 11, 4162. [Google Scholar] [CrossRef]
- Sui, Y. A Fuzzy Pure Pursuit for Autonomous UGVs Based on Model Predictive Control and Whole-Body Motion Control. Drones 2024, 8, 554. [Google Scholar] [CrossRef]
- Su, Z. Evade Unknown Pursuer via Pursuit Strategy Identification and Model Reference Policy Adaptation (MRPA) Algorithm. Drones 2024, 8, 655. [Google Scholar] [CrossRef]
- Li, Z. Research on Head Pursuit Interception Strategy for Hypersonic Target. Appl. Sci. 2023, 13, 4772. [Google Scholar] [CrossRef]
- Shima, T. Optimal Cooperative Pursuit and Evasion Strategies Against a Homing Missile. J. Guid. Control. Dyn. 2011, 34, 414–425. [Google Scholar] [CrossRef]
- Shima, T. Head Pursuit Guidance. J. Guid. Control. Dyn. 2007, 30, 1437–1444. [Google Scholar] [CrossRef]
- Yamasaki, T. Sliding mode-based pure pursuit guidance for unmanned aerial vehicle rendezvous and chase with a cooperative aircraft. Proc. IMechE Part G J. Aerosp. Eng. 2010, 224, 1057–1067. [Google Scholar] [CrossRef]
- Kumar, S.R. Finite-Time Impact Time Guidance using Deviated Pursuit against Maneuvering Targets. In Proceedings of the American Control Conference Denver, Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Don, L. Hommertzheim. Training an artificial neural network the pure pursuit maneuver. Comput. Oper. Res. 1991, 18, 343–353. [Google Scholar]
- Jerger, J.J. Systems Preliminary Design; U.S. Naval Air Development Center, Inc.: Patuxent River, MD, USA, 1960. [Google Scholar]
- U.S. Army Missile Command. Military Handbook: Missile Flight Simulation, Part One Surface-To-Air Missiles; MIL-HDBK-1211(MI); U.S. Government Printing Office: Washington, DC, USA, 1995.
- Siouris, G.M. Missile Guidance and Control Systems; Springer: New York, NY, USA, 2004. [Google Scholar]
- Hawley, P.A.; Blauwkamp, R.A. Six-Degree-of-Freedom Digital Simulations for Missile Guidance, Navigation, and Control. Johns Hopkins APL Tech. Dig. 2010, 29, 71–84. [Google Scholar]
- Özkan, B. Modeling of dynamics, guidance, and control systems of air-to-surface missiles. J. Def. Model. Simul. Appl. Methodol. Technol. 2012, 9, 101–112. [Google Scholar] [CrossRef]
- Belkacem, B. Advanced Strategies for Guidance & Control of SAM Missiles; Lambert Academic Publishing: Chisinau, Moldova, 2024. [Google Scholar]
- Yanushevsky, R. Modern Missile Guidance; Kiev Polytechnic Institute: Kyiv, Ukraine; Taylor, Francis: Abingdon, UK, 2019. [Google Scholar]
- Arthur, S.L. Principles of Guided Missile Design; Naval Air Development Center: Warminster Township, PA, USA; D. Van Nostrand Company, Inc.: New York, NY, USA, 1955. [Google Scholar]
- Mohan, R.S. Fundamentals of Guided Missiles; Defense Research and Development Organization: New Delhi, India, 2016. [Google Scholar]
- Palumbo, N.F. Basic Principles of Homing Guidance. Johns Hopkins APL Tech. Digest 2010, 29, 25–41. [Google Scholar]
- Shneydor, N.A. Missile Guidance and Pursuit: Kinematics, Dynamics and Control; Israel Institute of Technology: Chichester, UK, 1998. [Google Scholar]
- Jackson, P.B. Overview of Missile Flight Control Systems. Johns Hopkins APL Tech. Digest 2010, 29, 9–24. [Google Scholar]
- Chen, Y.-W. Dynamic interception point guidance algorithm based on particle swarm optimization. Meas. Control 2022, 55, 983–995. [Google Scholar] [CrossRef]
- Yamasaki, T. Modified Command to Line-of-Sight Intercept Guidance for Aircraft Defense. J. Guid. Control. Dyn. 2013, 36, 898–902. [Google Scholar] [CrossRef]
- Ahi, B. Novel command to line of sight guidance with practical limitations. Asian J. Control 2021, 24, 1426–1436. [Google Scholar] [CrossRef]
- Turetsky, V. Minimum Effort Pursuit Guidance with Delayed Engagement Decision. J. Guid. Control Dyn. 2019, 42, 1310–1319. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Nguyen, N.P.; Pham, D.B.; Dao, N.N.; Nguyen, H.T.; Ha Le Nhu Ngoc, T.; Vu, M.T.; Hong, S.K. Novel gain-tuning for sliding mode control of second-order mechanical systems: Theory and experiments. Sci. Rep. 2023, 13, 10541. [Google Scholar] [CrossRef] [PubMed]










| Coefficient | |||||||
|---|---|---|---|---|---|---|---|
| Mach Number | 0.0 | 0.8 | 38.00 | 180.0 | −6.000 | 0.0225 | −160.00 |
| 0.8 | 0.8 | 39.00 | 250.0 | −13.000 | 0.0305 | −170.00 | |
| 1.14 | 1.2 | 56.00 | 230.0 | −16.000 | 0.0361 | −185.00 | |
| 1.75 | 1.15 | 55.00 | 130.0 | −13.500 | 0.0441 | −235.00 | |
| 2.5 | 1.05 | 40.00 | 80.0 | −10.000 | 0.0540 | −190.00 | |
| 3.5 | 0.94 | 33.00 | 45.0 | −6.000 | 0.0665 | −150.00 | |
| Time | 0 | 0.01 | 0.04 | 0.05 | 0.08 | 0.10 | 0.20 | 0.30 | 0.60 | 1.00 | 1.50 | 2.50 |
| Trust | 0 | 450 | 17,800 | 23,100 | 21,300 | 20,000 | 18,200 | 17,000 | 15,000 | 13,800 | 13,300 | 13,800 |
| Time | 3.50 | 3.80 | 4.00 | 4.10 | 4.30 | 4.50 | 4.70 | 4.90 | 5.20 | 5.60 | 100 | 150 |
| Trust | 14,700 | 14,300 | 12,900 | 11,000 | 7000 | 4500 | 2900 | 1500 | 650 | 0.000 | 0.000 | 0.000 |
| ZEM Guidance | 3D-PP Guidance | 3D-PP Silding Guidance | |
|---|---|---|---|
| ZEM [m] | [s] | Max Commanded Accel | Max Angle of Attack | Max Closing Velocity | Load Factor | Flight Path Angle | |
|---|---|---|---|---|---|---|---|
| ZEM Guidance | 0.145 | 7.814 | 38 | ||||
| 3D-PP Guidance | 0.120 | 7.631 | 59 | ||||
| 3D Sliding PP | 0.162 | 7.293 | 78 |
| ZEM | [s] | Max Commanded Accel | Max Angle of Attack | Max Closing Velocity | Load Factor | Flight Path Angle | |
|---|---|---|---|---|---|---|---|
| 1st starting point | 0.152 | 7.135 | 66 | ||||
| 2nd starting point | 0.158 | 7.324 | 58 | ||||
| 3rd starting point | 0.149 | 7.245 | 76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekhiti, B.; Fragulis, G.F.; Rahmouni, M.; Hariche, K. A Novel Three-Dimensional Sliding Pursuit Guidance and Control of Surface-to-Air Missiles. Technologies 2025, 13, 171. https://doi.org/10.3390/technologies13050171
Bekhiti B, Fragulis GF, Rahmouni M, Hariche K. A Novel Three-Dimensional Sliding Pursuit Guidance and Control of Surface-to-Air Missiles. Technologies. 2025; 13(5):171. https://doi.org/10.3390/technologies13050171
Chicago/Turabian StyleBekhiti, Belkacem, George F. Fragulis, Mohamed Rahmouni, and Kamel Hariche. 2025. "A Novel Three-Dimensional Sliding Pursuit Guidance and Control of Surface-to-Air Missiles" Technologies 13, no. 5: 171. https://doi.org/10.3390/technologies13050171
APA StyleBekhiti, B., Fragulis, G. F., Rahmouni, M., & Hariche, K. (2025). A Novel Three-Dimensional Sliding Pursuit Guidance and Control of Surface-to-Air Missiles. Technologies, 13(5), 171. https://doi.org/10.3390/technologies13050171








