Numerical and Experimental Investigations on Oil Supply Characteristics of a Multi-Passage Lubrication System for a Three-Stage Planetary Transmission in a Tracked Vehicle

Abstract

The multi-passage lubrication system is adopted to meet the demand of the main heat generation parts (gears and bearings) in the three-stage planetary transmission system of a large tracked vehicle. As rotational speed increases, the flow regime inside the passages with multi-oil outlets becomes highly complex. Under high-speed conditions, the flow rate in Zone 2 decreases sharply, and some oil outlets even drop to zero, representing a 100% reduction amplitude, which results in an unstable oil supply for heat generation parts and even potential lubrication cut-off. In the present work, the lubrication characteristics of the oil supply system for the three-stage planetary transmission system are investigated by a combination of CFD (computational fluid dynamics) simulations and experiments. A complete CFD model of the multi-passage lubrication system is established, comprising a stationary oil passage, a main oil passage, and a three-stage variable-speed oil passage. A transient calculation method based on sliding mesh rotation domain control is used to simulate the oil-filling process in the oil passages, and the oil supply characteristics of the variable-speed oil passage are investigated. A test bench for the multi-stage planetary transmission system is designed and constructed to collect oil flow data from outlets of planetary gear sets. The comparison between simulated and experimental results confirms the validity of the proposed numerical method. Additionally, numerical simulations are conducted to investigate the effects of key factors, including input speed, oil supply pressure, and oil temperature, on the oil flow rate of outlets. The results indicate that the rotational speed is the major parameter affecting the oil flow rate at the oil passage outlets. This work provides a practical guidance for optimizing lubrication design in complex multi-stage planetary transmission systems.

1. Introduction

Multi-stage planetary gear transmission systems are widely used in applications such as electric wheels for vehicles and high-speed heavy-duty machinery due to their compact structure, high power density, wide range of gear transmission ratios, and power splitting capabilities. Lubrication conditions of gear and bearing characteristics under a high-speed operation condition would significantly impact the working performance of multi-stage planetary gear transmission systems; to be more specific, this would depend on whether or not the lubricating oil precisely reaches the heat generation parts and work effectively. In such transmission systems, lubrication oil passages are typically integrated within the rotating shaft to ensure comprehensive lubrication efficacy. These oil passages rotate synchronously with the shaft, utilizing centrifugal force to distribute the lubricating oil, thereby enabling its delivery to all necessary components within the system. For multi-stage planetary transmission systems, the lubrication oil supply system not only involves the absolute rotation of the main shaft and each planetary gear set but also the relative rotation between the main shaft and the planetary gears, which would create complex fluid flow behavior in the rotating-stationary interface region. However, under the operational boundaries of the multi-stage planetary gearbox lubrication system, it is critical to determine which factor—lubricant oil temperature, supply pressure, or inter-stage rotational speed—predominantly influences performance. Therefore, studying the flow behaviors and oil supply characteristics in multi-planetary gear systems holds significant practical application value.

Investigations on oil flow supply characteristics of multi-stage planetary transmission systems typically involve liquid flow behaviors inside rotating passages and the lubrication of gears and bearings inside gearboxes (fixed-axle gearboxes and single-stage or multi-stage planetary gearboxes). Aiming at this topic, researchers have carried out a lot of works, which demonstrates the potential of numerical and experimental methods for solving key challenges of the present work.

Some studies have been performed on the fluid flow behaviors inside rotating oil passages. Numerical investigations by Chang et al. [1] of two-phase flow in an axially rotating passage indicated that their model can be considered as an effective tool for simulating the liquid phase motion. However, the structural model is relatively simplistic and does not account for the complex flow regimes within the multi-stage transmission lubrication system. Using large eddy simulation (LES), Abdi et al. [2] found that the centrifugal force induced by rotation would lead to an increase in the average axial velocity of the fluid within a rotating passage. Yet, it does not account for the branched structure of the lubrication passages or the flow field interactions resulting from inter-stage rotational speed differentials in multi-stage transmission systems. Bochkarev et al. [3] studied the stability of fluid motion inside a rotating passage under different rotational speeds and observed that flow velocity was influenced by changes in both the structural size and boundary conditions. Nevertheless, it fails to consider fluid perturbations induced by the lubrication passage boundaries and the dynamic distribution of oil flow within the multi-stage planetary gear sets. Gao [4] employed CFD simulations to examine the lubricant flow characteristics in the passages of a rotating machinery lubrication system. However, it does not account for flow partitioning resulting from differential rotational speeds between stages or the associated flow field inhomogeneities induced by these inter-stage speed differentials within the multi-stage planetary transmission system. Kim et al. [5] investigated the effects of inlet pressure and flow rate variations on the outlet flow characteristics of rotating passages and found that at sufficiently high rotational speeds, the flow developed into an annular pattern. In spite of this, it does not address the flow resistance and perturbations imposed by the branched structure and inter-stage structures on oil distribution within the multi-stage transmission system. Guerrero et al. [6] investigated the causes and effects of backflow in a turbulent passage flow using direct numerical simulations. Ceci et al. [7] employed a direct numerical simulation, demonstrating that the flow characteristics in rotating pipes were governed by complex interactions among rotational speed, inertial forces, and viscous forces.

About the lubrication of gears and bearings inside gearboxes, Shi et al. [8] employed a VOF multi-phase model coupled with the SST k-ω turbulence model to conduct CFD simulations of oil–water two-phase flow in horizontal pipes with high viscosity ratios. Their study analyzed the effects of wall contact angle, initialization methods, and volume fraction discretization schemes on numerical results. Deng et al. [9] studied the effects of parameters including oil viscosity, immersion depth, turbine rotational speed, worm arrangement angle, and oil groove volume on the lubrication performance of a high-precision roller enveloping reducer. Yet, it does not consider the influence of inter-stage rotational speed differentials on oil flow distribution and lubrication performance within the planetary transmission system. Boni et al. [10] investigated the flow characteristics in splash-lubricated planetary gear sets under conditions where an oil ring fails to form. They experimentally examined various oil volumes, temperatures, and input speeds, thereby determining the critical oil quantity required for oil ring formation and characterizing the associated flow regimes. In contrast, the analysis focuses on churning losses and flow regime characterization, without addressing forced lubrication in the multi-branch oil supply passage of multi-stage planetary transmission systems. Liu et al. [11] established an experimental platform for oil–gas two-phase flow to investigate the behavior in vertical vent pipes of aero-engines. Their study analyzed the effects of the oil supply rate, air supply rate, and pipe diameter on flow patterns. Zhou et al. [12] developed a jet lubrication model for a high-speed helical gear to evaluate the lubrication performance based on the oil volume fraction and oil pressure. However, it does not address the combined effects of the multi-branch lubrication passage and inter-stage rotational speed differentials on jet lubrication efficacy, thereby limiting its direct applicability to spray parameter analysis in three-stage planetary transmission systems. Mastrone et al. [13] presented a CFD model of a two-stage industrial reducer within the open-source framework OpenFOAM^®, addressing boundary motion in multi-stage gearboxes. In spite of this, the study focuses on a two-stage industrial gearbox and does not consider the substantial flow field perturbations induced by pronounced inter-stage speed differentials in three-stage systems. Mastrone et al. [14] performed a numerical analysis on the lubrication performance of a planetary gearbox using a finite-volume-based re-meshing strategy implemented in the open-source code OpenFOAM^® to investigate the flow characteristics within the rotating oil passages of a helicopter’s variable-speed transmission. But, the adaptability of its mesh strategy to the complex flow field of the three-stage system has not been verified, and thus it cannot be directly applied to the accurate analysis of the system’s lubrication performance. Hu et al. [15] first established a model of a two-stage system with a single inlet and multiple branched outlets and validated this simulation methodology through experimental measurements. Yet, its oil passage structure is a two-stage transmission mechanism without different inter-stage rotational speeds. Meanwhile, the testing mechanism in its experimental bench has been correspondingly simplified, and the experimental operating conditions are not sufficient. Shao et al. [16] performed a CFD study on a two-stage herringbone gearbox with an idler in a high-speed train to investigate the impacts of gear rotational speed, lubricant volume, and temperature on oil flow, film distribution, and lubrication conditions in the meshing zone. Hildebrand et al. [17] conducted a combined numerical, experimental, and analytical investigation of oil flow in a dip-lubricated single-stage gearbox. In spite of this, its research object is a single-stage gearbox, and it does not involve the complex effects of the multi-branch oil circuits and inter-stage speed differences of the three-stage system on the oil flow. Chen et al. [18] simulated the practical lubrication behavior of planetary gear journal bearings (PGJBs) in high-power wind turbines and performed experiments on a full-scale PGJB test bench. The experimental results demonstrated consistent agreement with numerical predictions. In contrast, the study focuses on the lubrication of planetary gear journal bearings—a single component—and does not address the overall passage design and oil flow distribution in multi-stage planetary transmissions, thereby limiting its direct applicability to the design of integrated lubrication systems for such systems.

Previous studies on liquid flow characteristics in rotating oil passages primarily addressed turbulent flow states within single rotating pipe segments. Moreover, experimental studies in previous research predominantly focused on oil distribution patterns captured by high-speed cameras in splash-lubricated or jet-lubricated gearboxes. However, investigations into the lubricating oil supply volume, which is a critical parameter affecting lubrication performance, are still insufficient. Furthermore, most existing studies pay more attention to single-stage planetary transmission systems. Owing to the limited computational capacity and the complexity of CFD simulation models, few studies have explored lubrication in two-stage planetary transmission systems, let alone more complex planetary transmission systems. The present study investigates a three-stage planetary transmission system of a large tracked vehicle and performs CFD analysis considering both the rotational dynamics of the entire oil passage and the relative motion of planetary gear sets under different gear ratios. The experiments are conducted on a specially made test bench to validate the numerical methods by comparing between numerical and experimental oil supply volumes. Furthermore, the lubrication performance of the overall oil passages of the three-stage planetary transmission is evaluated under varying influential parameters.

2. Numerical Methods

In this research, the effect of oil temperature heating is not considered during experimental validation. Numerical simulations are performed using CFD methods to discretize the flow field and obtain corresponding numerical solutions. The fluid flow is governed by the conservation of mass and momentum, which yields the continuity equation and the Navier–Stokes equations as the governing equations.

The continuity equation, which applies the principle of mass conservation to fluid flow models, serves as a governing equation for fluid motion. It asserts that the mass flow rate entering and exiting a fluid element must be equal, as expressed by the following equation:

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial \left(\rho u\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho v\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho w\right)}{\partial t}}=0$$

(1)

where $\rho$ is the density,$t$ is time, $u$, $v$, and $w$ are the velocity toward the $x$, $y$, and $z$ directions, ($\nabla \rho v)$ is commonly denoted as ${\displaystyle \frac{\partial \left(\rho u\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho v\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho w\right)}{\partial t}}$, and $v$ is the velocity vector field.

The fluid momentum equation conforms to Newton’s second law, whereby the product of a fluid element’s mass and its acceleration equals the total force acting upon it. These forces comprise both body forces and surface forces, as expressed by the following equation:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \left(\rho u\right)}{\partial t}}+\nabla ·\left(\rho uV\right)=-{\displaystyle \frac{\partial p}{\partial x}}+{\displaystyle \frac{\partial {\tau }_{xx}}{\partial x}}+{\displaystyle \frac{\partial {\tau }_{yx}}{\partial y}}{\displaystyle \frac{\partial {\tau }_{zx}}{\partial z}}+\rho f_x=0\\ {\displaystyle \frac{\partial \left(\rho u\right)}{\partial t}}+\nabla ·(\rho vV)=-{\displaystyle \frac{\partial p}{\partial y}}+{\displaystyle \frac{\partial {\tau }_{xy}}{\partial x}}+{\displaystyle \frac{\partial {\tau }_{yy}}{\partial y}}{\displaystyle \frac{\partial {\tau }_{zy}}{\partial z}}+\rho f_y=0\\ {\displaystyle \frac{\partial \left(\rho u\right)}{\partial t}}+\nabla ·(\rho wV)=-{\displaystyle \frac{\partial p}{\partial z}}+{\displaystyle \frac{\partial {\tau }_{xz}}{\partial x}}+{\displaystyle \frac{\partial {\tau }_{yz}}{\partial y}}{\displaystyle \frac{\partial {\tau }_{zz}}{\partial z}}+\rho f_z=0\end{array}\right.$$

(2)

where $p$ is the pressure, ${\tau }_{ij}$ is the stress in the $j$ direction acting on the plane perpendicular to the $i$ axis, and $f$ is the body force per unit mass acting on the fluid element.

In this work, the flow of lubricating oil in the oil passages is categorized as viscous flow. Its flow state typically involves pipeline losses due to frictional resistance and variations in pipe diameter. For the simplification and analysis of the lubricating oil passage, it satisfies the Bernoulli equation [4], which is specifically expressed as follows. Meanwhile, Bernoulli’s equation is used for conceptual illustration only and is not applied in the CFD solver.

$$z_1+{\displaystyle \frac{p_1}{\rho g}}+{\displaystyle \frac{{\alpha }_1{v}_1^2}{2g}}=z_2+{\displaystyle \frac{p_2}{\rho g}}+{\displaystyle \frac{{\alpha }_2{v}_2^2}{2g}}+h_w{,h}_w=h_f+h_j{h}_f=\lambda {\displaystyle \frac{l}{d}}{\displaystyle \frac{v^2}{2g}}{h}_j=\xi {\displaystyle \frac{v^2}{2g}}$$

(3)

where $z$ is the position head, ${\displaystyle \frac{p}{\rho g}}$ is the pressure head, ${\displaystyle \frac{\alpha v^2}{2g}}$ is the velocity head, $h_w$ is the along-the-line loss, $h_f$ is the local loss, $\lambda$ is the friction coefficient, $l$ is the pipe length, $\mathrm{d}$ is the pipe diameter, and $\xi$ is the local resistance coefficient.

2.1. Turbulence Model

This section is organized with subheadings. It should provide a concise and precise description of the experimental results and their interpretation, as well as the experimental conclusions that can be drawn.

The turbulence model employed in this study is the κ-ε model, a two-equation approach based on the Reynolds-averaged Navier–Stokes (RANS) equations, which solves two separate transport equations. The standard κ-ε model is a high-Reynolds-number formulation, valid for fully developed turbulent flows but neglecting molecular viscosity—thus rendering it inapplicable in regions such as near-wall zones where turbulence is not fully developed. To address this limitation, the RNG and realizable κ-ε models were introduced. The SST k–ω model is more accurate and reliable for adverse pressure gradient flows, airfoils, and transonic shock waves in fields such as aerospace, automotive engineering, and turbomachinery, whereas the RNG k–ε model is more appropriate for the turbulent flow of lubricating oil in pipelines. The RNG model incorporates an additional term in the dissipation rate equation, improving accuracy for flows with rapid strain. In the present work, the lubrication oil passage operates at high rotational speeds, where centrifugal forces induced by vortices enhance circumferential turbulence intensity near the wall. Consequently, the RNG κ-ε model is adopted as the turbulence model herein. The corresponding transport equations are given below, where $R_{\epsilon }$ is the correction term for different $R_e$ values.

$${\displaystyle \frac{\partial \left(\rho \kappa \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho \kappa u_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left({\alpha }_{\kappa }{\mu }_{\mathrm{eff}}{\displaystyle \frac{\partial \kappa }{\partial x_j}}\right)+G_{\kappa }+G_b-\rho \epsilon -Y_M+S_{\kappa }$$

(4)

$${\displaystyle \frac{\partial \left(\rho \epsilon \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho \epsilon u_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left({\alpha }_{\epsilon }{\mu }_{\mathrm{eff}}{\displaystyle \frac{\partial \epsilon }{\partial x_j}}\right)+C_{1\epsilon }{\displaystyle \frac{\epsilon }{\kappa }}\left(G_{\kappa }+C_{3\epsilon }{G}_b\right)-C_{2\epsilon }\rho {\displaystyle \frac{{\epsilon }^2}{\kappa }}-R_{\epsilon }+S_{\epsilon }$$

(5)

$$R_{\epsilon }={\displaystyle \frac{C_{\mu }\rho {\eta }^3(1-\eta /{\eta }_0)}{1+\beta {\eta }^3}}{\displaystyle \frac{{\epsilon }^2}{k}}$$

(6)

where $G_K$ is the kinetic energy released during turbulence due to the mean velocity gradients, $G_b$ is the amount of kinetic energy generated by buoyancy effects in turbulence, $Y_M$ is the amount of variable dilatation in compressible turbulence that contributes to the total rate of dissipation, ${\alpha }_{\kappa }$ and ${\alpha }_{\epsilon }$ are the inverse effective Prandtl numbers for turbulence kinetic energy and the turbulence dissipation rate, respectively, $S_{\kappa }$ and $S_{\epsilon }$ are custom source items, $C_{\mu }=0.0845$, $\eta =S_k/\epsilon$, ${\eta }_0=4.38,\mathrm{a}\mathrm{n}\mathrm{d}\beta =0.012$.

2.2. Multi-Phase Flow Model

The lubrication of the multi-stage planetary gear sets, bearings, and other components in a tracked vehicle’s multi-stage planetary transmission involves gas–oil two-phase flow during startup and operation. To track the oil–air interface under dynamic rotating conditions, the Volume-of-Fluid (VOF) method is employed. Within the computational domain, the volume fractions of lubricating oil and air maintain a fixed relative proportion, and their sum remains in unity [8]. The governing equations are expressed as follows:

$${\alpha }_{air}+{\alpha }_{oil}=1$$

(7)

where ${\alpha }_{air}$ and ${\alpha }_{oil}$ are the air and lubricating oil volume portions. If ${\alpha }_{air}$ is 0, it indicates that the unit is filled with lubricating oil; if ${\alpha }_{oil}$ is 0, it indicates that the unit is filled with air; otherwise, it indicates a state where lubricating oil and air coexist.

3. Validation of the Numerical Methods

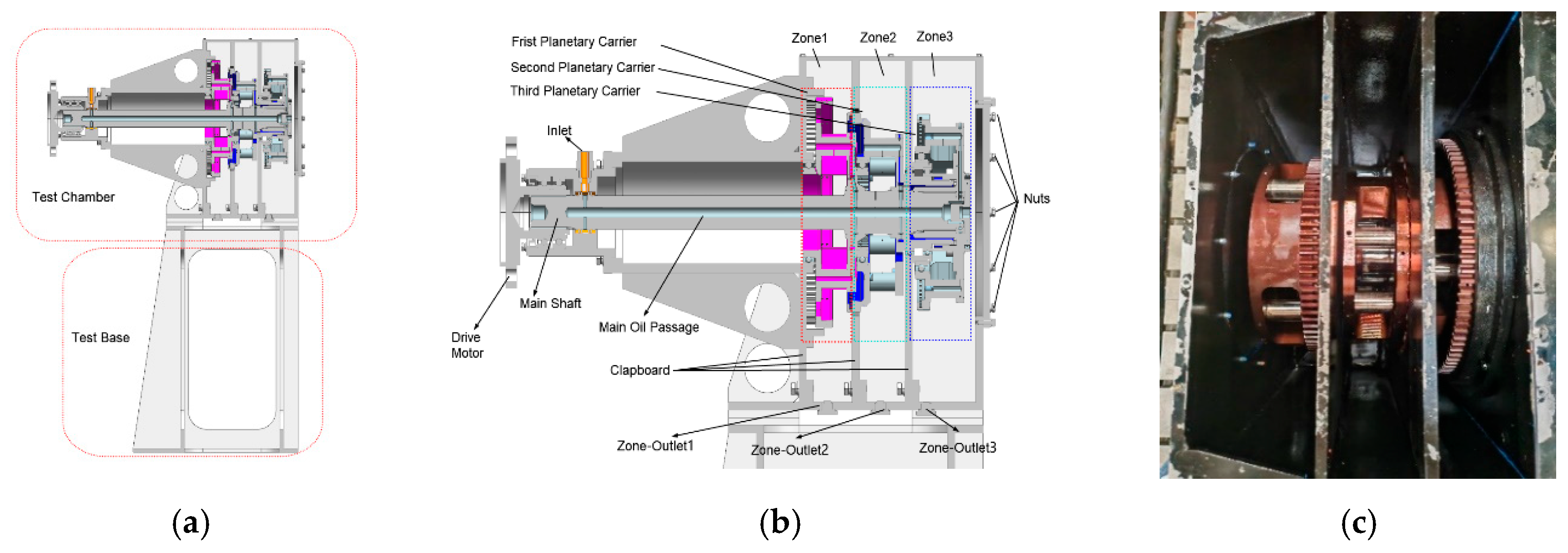
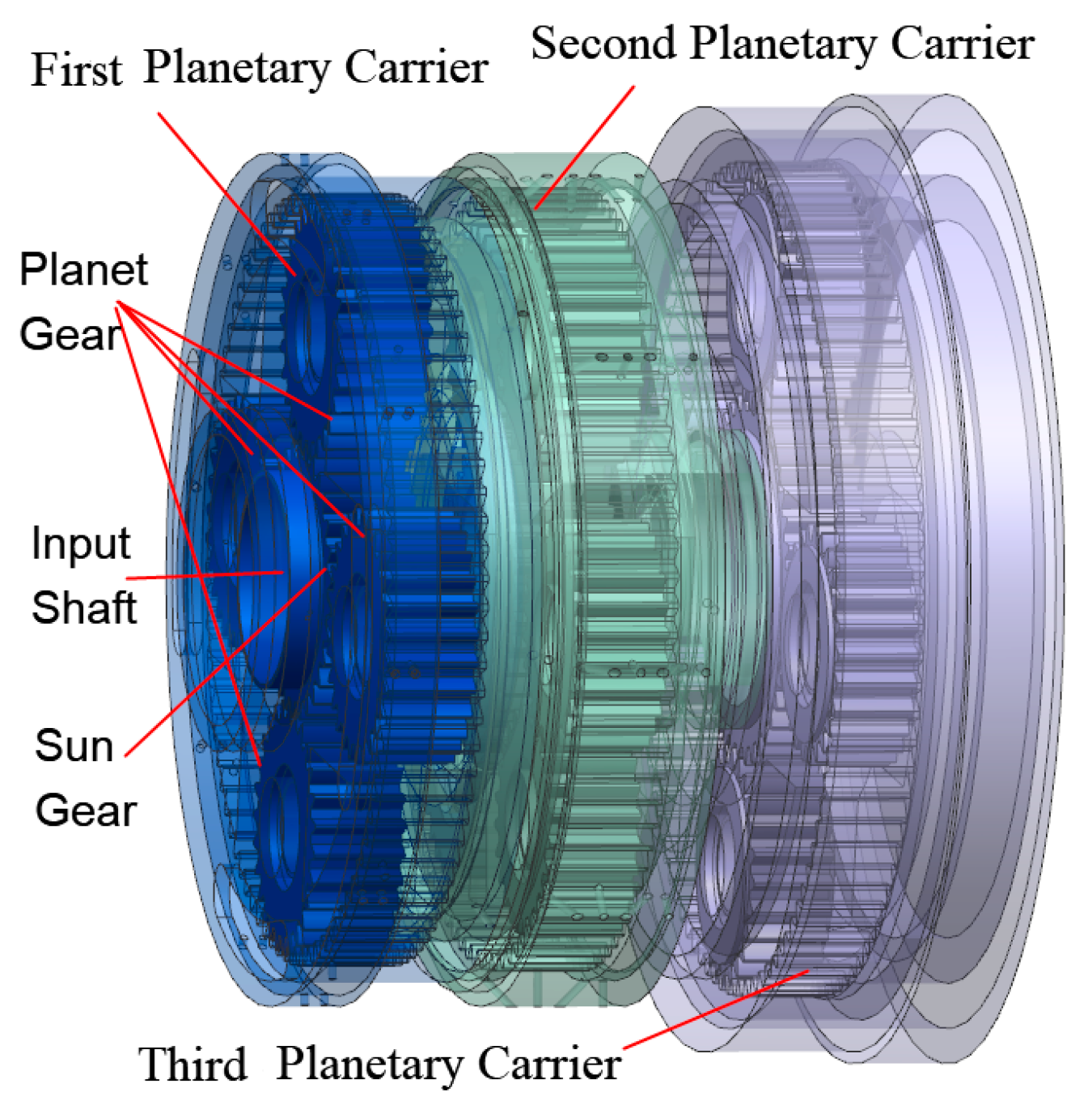
To validate the numerical methods employed for analyzing the oil supply characteristics of the multi-stage planetary transmission system, experiments are conducted on a dedicated test bench, as illustrated in Figure 1. The test bench primarily consists of key components such as an oil reservoir, a motor, oil pumps, filters, flow meters, and pressure-regulating valves. The lubrication pump station adjusts the oil supply pressure and flow rate. Measuring cups are positioned at the outlet ports corresponding to each planetary gear set within the test assembly to collect oil discharge volumes for quantitative comparison. The configuration of the multi-stage planetary gear test assembly is illustrated in Figure 2. The rotational speed of the planetary carriers is controlled by a drive motor connected to the main shaft. The carriers are mounted within three separate compartments in the test gearbox, each partitioned by baffles. A 16 mm diameter oil outlet is located at the bottom of each compartment, and the connected tubing and measuring cups are used to collect and quantify the drained oil. In this experiment, the measuring cup used has a range of 5000 mL with a permissible error of ±10 m. Detailed experimental parameters are provided in

Table 1. Detailed parameters of the validation test.

Parameter	Value
Input rotational speed n1 [rpm]	10,482,096
Inlet pressure P1 [MPa]	0.2, 0.3, 0.4
Oil density at 25 °C ρ1 [Kg/m3]	870
Oil dynamic viscosity at 25 °C μ1 [Kg/m·s]	1.74 × 10−1
Air density ρ2 [Kg/m3]	1.128
Air dynamic viscosity μ2 [Kg/m·s]	1.907 × 10−5

.

To compare the numerical results with experimental ones, first, a grid independence study was conducted to ensure that the computational results were unaffected by mesh discretization, thereby enhancing simulation reliability. Three mesh sizes—0.8 mm, 1.2 mm, and 1.6 mm—were evaluated by comparing the deviation between the inlet and total outlet flow rates. As the mesh was refined, this deviation decreased, with the relative error falling below 0.2%. Considering both computational accuracy and cost, a mesh size of 1.2 mm was selected as the optimal configuration. The grid independence analysis data are presented in

Table 2. Grid independence analysis.

Mesh Size	Mesh Number	Deviation of Flow Rate
0.8 [mm]	3,038,901	0.08%
1.2 [mm]	2,787,983	0.11%
1.6 [mm]	2,440,692	0.23%

. Furthermore, in simulations, the number of fluid domain elements is equal 2,787,983, with an orthogonal quality exceeding 0.2005 and an element quality greater than 0.21648, meeting the requirements for accurate fluid dynamic computations.

The experimental procedure is described as follows: first, the drive motor is activated, and the main shaft begins to rotate. The first-stage planetary carrier remains stationary at 0 rpm, while the second- and third-stage carriers rotate at the same speed as the main shaft. The oil pump is then engaged to circulate lubricant through all planetary stages. Following a 20 s operational period of the drive motor, the test bench underwent oil supply cessation and system shutdown. Oil flow was subsequently collected over a 10 min interval until the volume in the measuring cups stabilized, indicating the attainment of steady-state conditions. After the oil flow reaches a steady state, the discharged lubricant is collected via three measuring cups (called Cup 1, Cup 2, and Cup 3, respectively) connected to the outlet ports at the bottom of the three compartments, as shown in Figure 3. For each oil pressure and rotational speed condition, data are acquired over a 20 s interval, with each measurement repeated three times. After data recording, the oil from the measuring cups is returned to the pump reservoir, and this procedure is repeated until all experimental conditions are tested. 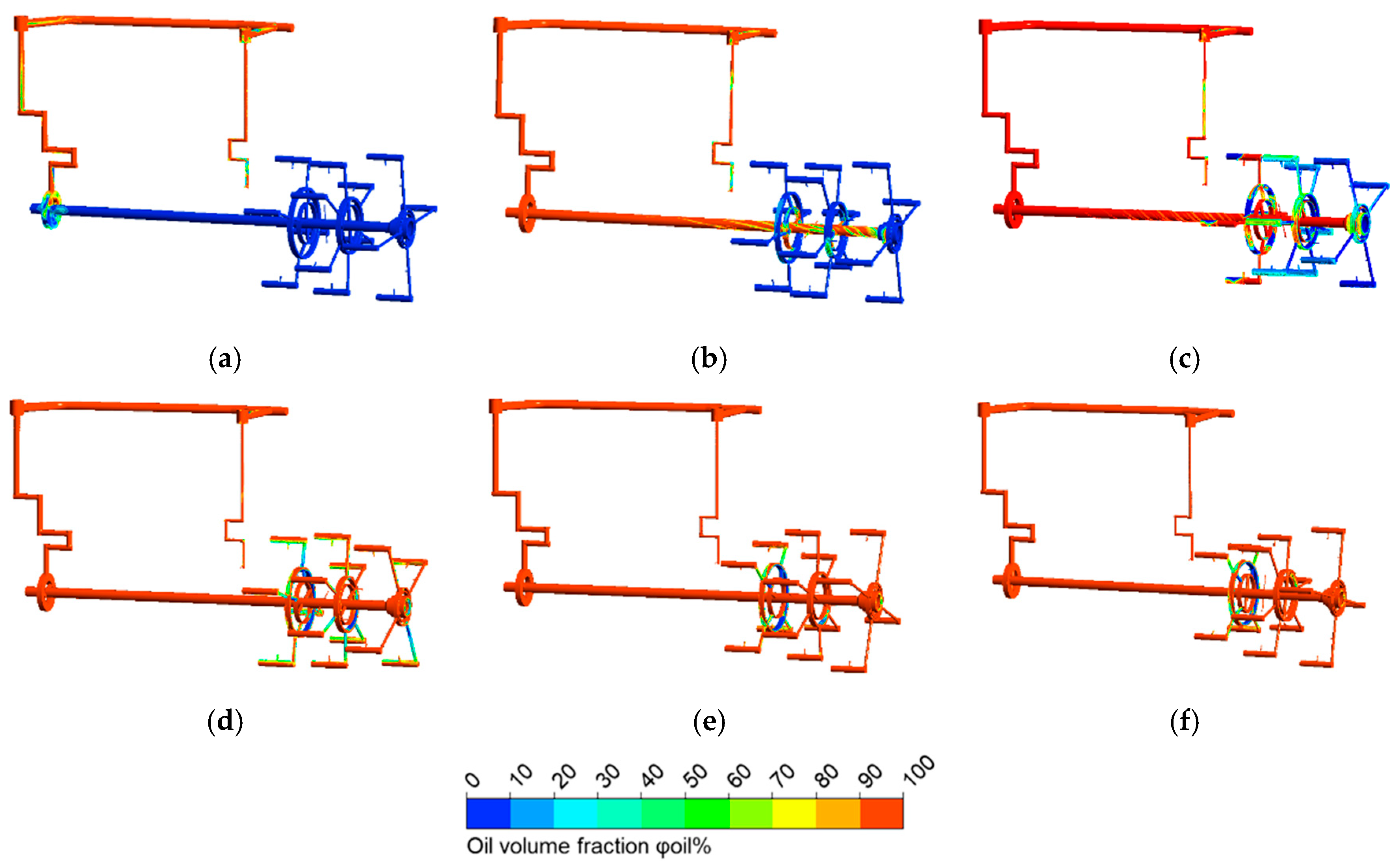As shown in Figure 4, three compartments can be seen and are called Zone 1, Zone 2, and Zone 3, corresponding to the first, second, and third-stage planetary gear set, respectively. Oil splashing behavior resulting from planetary gear rotation can be observed through a transparent window mounted on the top cover. Figure 4 indicates that the oil volume in the second and third planetary stages is greater than in the first stage due to their rotational motion.

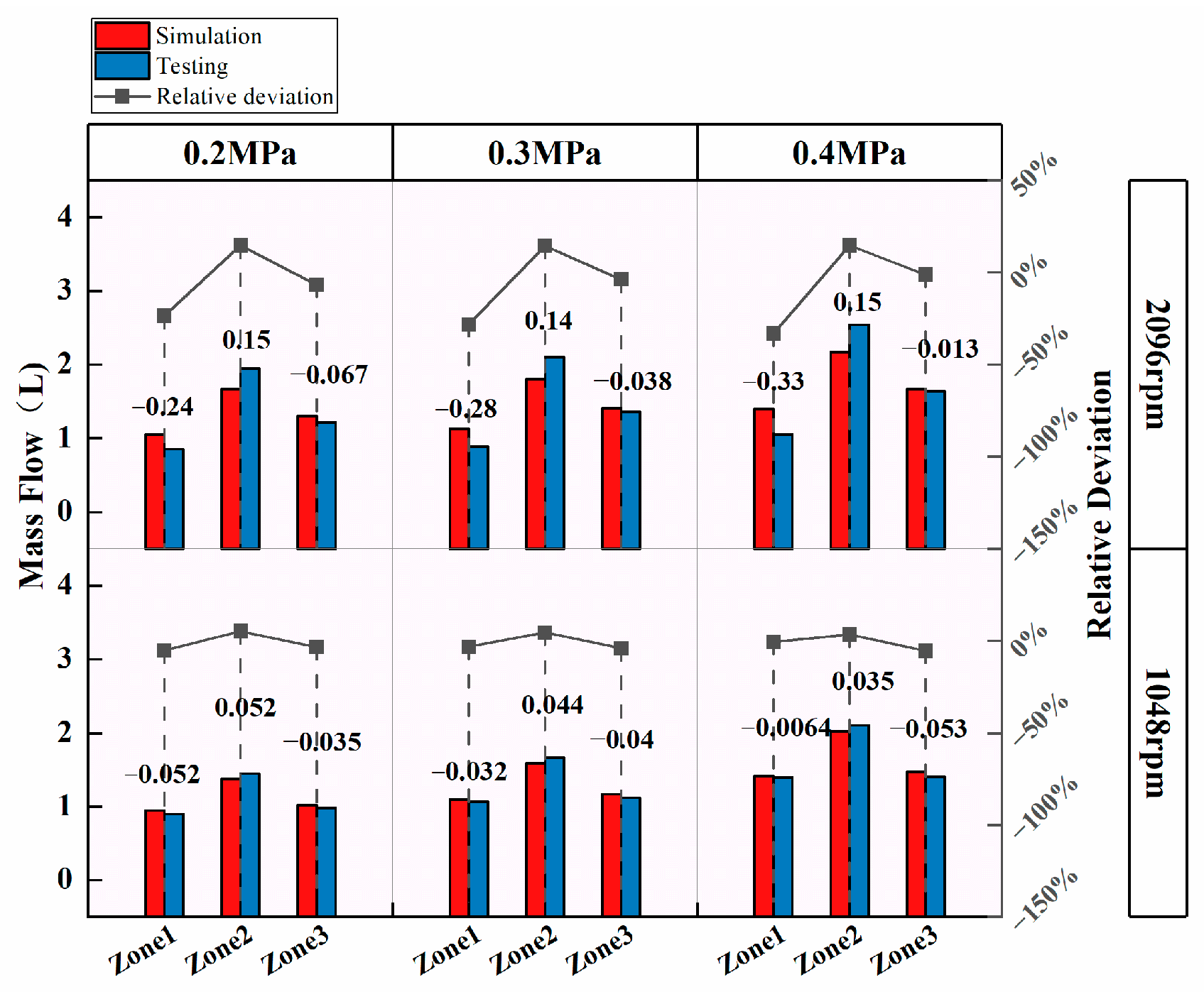
The proposed numerical methods are validated by comparing the simulated oil discharge volumes from each planetary stage with the corresponding experimental measurements. The experiments are conducted under inlet oil pressures of 0.2 MPa, 0.3 MPa, and 0.4 MPa at drive speeds of 1048 rpm and 2096 rpm. The relative deviations of oil volumes between experimental and simulated results are calculated, as illustrated in Figure 5 and Figure 6. As shown in the figures, the simulation results are in good agreement with the experimental data. At 1048 rpm, the maximum observed deviation is 5.3%. At 2096 rpm, larger deviations are observed in Zone 1 and Zone 2, with maximum errors of 33.2% and 14.7%, respectively, and Zone 3 shows a maximum error of 6.8%. This phenomenon can be attributed to the increased centrifugal force resulting from the higher rotational speed and oil pressure, which enhances the oil discharge in Zone 2 and reduces the outflow in Zone 1. Despite these discrepancies, the relative errors remain within an acceptable range for engineering applications; therefore, the proposed numerical methods can be considered suitable for analyzing the lubrication behavior of multi-stage planetary transmission systems under a wide range of operating conditions.

4. Simulation Model

4.1. Geometric and Physical Parameters

The structural model of the multi-stage planetary transmission system is shown in Figure 7. This system comprises two NGW-type planetary gear sets, a dual-star planetary gear set, and multiple cylindrical roller bearings and deep-groove ball bearings. The present work focuses on the oil passages of the multi-stage planetary transmission system; therefore, components such as sun gears, planet gears, and bearings within the transmission system have been simplified. The three-dimensional model of the lubrication oil passages is presented in Figure 8.

A fluid domain model is developed, wherein the lubrication oil passages consist of both stationary and rotating components. Based on their position, the rotating components can be categorized into the main oil passage and the transmission passages for Zones 1–3, as shown in Figure 9. Lubricating oil is delivered by the oil pump into the stationary section of the oil passages, and then it enters the main oil passage after a defined interval and is subsequently distributed to the lubrication passages of the individual planetary stages. Under centrifugal force, the lubricating oil is discharged through various outlets. The three-dimensional model of the complete oil passage is shown in Figure 10.

To facilitate the analysis of oil discharge volumes at different outlets, their positions are illustrated in Figure 11. The key physical parameters used in simulations are provided in

Table 3. Physical parameters of simulations.

Parameter	Value
Input rotational speed n [rpm]	See Table 4
Inlet pressure P1 [MPa]	0.2, 0.3, 0.4
Inlet mass m1 [Kg/s]	0.208
Oil density at 70 °C ρ3 [Kg/m3]	831.7
Oil density at 90 °C ρ3 [Kg/m3]	819.2
Oil density at 90 °C ρ3 [Kg/m3]	808.9
Oil dynamic viscosity at 70 °C μ3 [Kg/m·s]	2.65 × 10−2
Oil dynamic viscosity at 90 °C μ3 [Kg/m·s]	1.51 × 10−2
Oil dynamic viscosity at 110 °C μ3 [Kg/m·s]	0.962 × 10−2
Air density at 70 °C ρ4 [Kg/m3]	1.029
Air density at 90 °C ρ4 [Kg/m3]	0.9733
Air density at 110 °C ρ4 [Kg/m3]	0.9253
Air dynamic viscosity at 70 °C μ4 [Kg/m·s]	2.048 × 10−5
Air dynamic viscosity at 90 °C μ4 [Kg/m·s]	2.138 × 10−5
Air dynamic viscosity at 110 °C μ4 [Kg/m·s]	2.237 × 10−5

.

This research studies the first and second-gear conditions, commonly used at both low and high rotational speeds. Under the first-gear conditions, all three planetary stages rotate. Under second-gear conditions, the first transmission stage remains stationary, while the main oil passage and the second and third transmission stages rotate at the same speed. The rotational speeds for each zone are detailed in

Table 4. Physical parameters of simulations.

Speed	Gear Positions	Main Shaft (rpm)	Zone 1 (rpm)	Zone 2 (rpm)	Zone 3 (rpm)
Low speed	First-gear condition	354	573	354	354
	Second-gear condition	1149	0	1149	1149
High speed	First-gear condition	1416	2292	1416	1416
	Second-gear condition	4596	0	4596	4596

.

4.2. Mesh

The lubrication oil passage of the overall multi-stage planetary transmission system is discretized using unstructured tetrahedral elements. A global mesh size of 1.2 mm is applied, with local refinement at the rotating–stationary interfaces and oil outlets, where the element size is controlled to 0.3 mm. The final mesh consisted of 3,048,324 elements and 635,817 nodes. The mesh exhibited an orthogonal quality above 0.2005, a cell quality greater than 0.21648, a maximum aspect ratio of 10.555, and a maximum skewness of 0.7, fulfilling the criteria for accurate fluid dynamic computations. The transient analysis employs a time step of 1 × 10⁻⁶ s with 20 iterations per time step. Details are provided in Figure 12.

5. Results and Discussion

Under different operating conditions of the multi-stage planetary transmission system, lubrication of bearings and gears is ensured by the oil discharge from various outlets. Thus, the oil discharge volume, time, and velocity at the outlets of each planetary stage are positively correlated with the system’s lubrication performance. Typical outlets in each zone are selected for oil flow monitoring, and the internal lubrication characteristics of the oil passages are analyzed based on these monitoring data under high- and low-speed conditions of the first and second-gear conditions.

5.1. Flow Characteristics at Low-Speed Conditions

As shown in Figure 13, the internal flow performance within the oil passages stabilizes earlier in first gear than in second gear, owing to the distinct rotational speed distributions of the planetary gear sets. In first-gear conditions, the flow rates at outlets 2-1, 5-1, and 7-1 are relatively large, as these outlet positions are farther from the rotating shaft and are subject to stronger centrifugal forces. In second-gear conditions, with Zone 1 stationary (0 rpm), the oil discharge from outlets 2-1 and 3-1 decreases significantly. Conversely, due to the increased rotational speeds in zones 2 and 3, the flow rates from outlets 5-1 and 7-1 rise markedly. Meanwhile, outlets 6-1 and 8-1, characterized by smaller pipe diameters, exhibit minimal changes in flow rate.

To visualize the oil-filling dynamics within the passages, the complete process—from the initial entry to full filling of the passages—is illustrated in Figure 14 and Figure 15. At 0.32 s, the oil reaches Outlet 1 and fills the entire stationary passage. Furthermore, due to the differences in rotational speed distribution, the second-gear condition facilitates a larger amount of oil entering into transmission Zones 2 and 3. This is attributed to the combined effects of flow inertia and the dynamic rotation of these zones. Subsequently, lubricant gradually moves into the stationary passage of Zone 1. Consequently, the oil-filling process under the first-gear condition slightly lags behind that under the second-gear condition. At 1.2 s, oil is discharged from all outlets, and a more uniform distribution is observed under the first-gear condition than under second-gear condition. By 2.56 s, the lubricant distribution within the oil passages has stabilized, and no significant changes are observed up to 3 s.

5.2. Flow Characteristics at High-Speed Conditions

As shown in Figure 16, under high-speed conditions, the oil discharge from outlets 3-1, 4-1, 6-1, and 8-1 decreases significantly compared to that under low-speed conditions, while the flow from outlets 5-1 and 7-1 increases markedly. This discrepancy occurs because outlets 3-1, 4-1, 6-1, and 8-1 have passage diameters about 75% of those of outlets 5-1 and 7-1 and are positioned on branch lines connected to the main regional discharge passages. As centrifugal forces intensify with increasing rotational speed, flow through these smaller outlets is further reduced. An analysis of the flow distribution across the outlets reveals that under the first-gear condition, the oil flow within the passages remains relatively stable. In contrast, under the second-gear condition, outlets 7-1 and 8-1 exhibit significant flow fluctuations. Those observations suggest that higher rotational speeds tend to amplify flow instabilities within the lubrication passages.

Figure 17 illustrates the Reynolds number distribution within the oil passages under high-speed conditions for first and second gears. As defined by $R_e=\rho VD/\mu$, the Reynolds number varies with flow velocity. In Figure 17a, the maximum Reynolds number under first-gear conditions reaches 8080, predominantly localized in the three rotating regions. Figure 17b shows a maximum value of 19,500 under second-gear operation, where the stationary Zone 1 exhibits significantly lower Reynolds numbers, while the rotating Zones 2 and 3 maintain elevated values.

Figure 18 and Figure 19 illustrate the lubricant distribution within the oil passages under high-speed conditions. As observed, the flow velocity of lubricant entering the rotating passages from the stationary zone increases compared with its value under the low-speed operation. Under second-gear conditions, the lubricant exhibits a sequential flow behavior not observed under the low-speed condition: it first enters the stationary Zone 1, followed by Zone 3. Simultaneously, at high speeds, the oil distribution within the passages becomes significantly non-uniform. Under both first and second-gear conditions, the lubricant shows a strong tendency to concentration along the outer wall of the planetary pin bore passages in the radial direction across all transmission zones, and this centrifugal bias flow becomes more pronounced at higher rotational speeds. Finally, under high-speed conditions, the lubricant distribution within the passages stabilizes after 2.56 s.

5.3. The Influence of Different Factors on Oil Passage Outlet Flow

Analysis of the lubrication characteristics under high- and low-speed conditions of first and second-gear conditions reveals variations in oil discharge among different transmission zones. Under the second-gear condition, the differing rotational speeds among the planetary stages further affect the lubrication behavior. Therefore, the influences of key factors—such as rotational speed, supply pressure, and oil temperature—on the flow rates at outlets are systematically investigated for second-gear operation condition.

5.3.1. Effect of Rotational Speed on Flow Rates at Outlets of the Oil Passage

Rotational speed can significantly affect the centrifugal forces and flow regime within the oil passages, leading to notable changes in discharge rates across the outlets under different speed conditions. To investigate the relationship between rotational speed and flow rates through outlets, numerical simulations are performed under a constant oil supply rate of 15 L/min with input speeds of 1149 r/min, 3447 r/min, and 4596 r/min. The computed discharge flow rates for all outlets under these three speed conditions are shown in Figure 20. Outlet 1, located in the stationary section (Zone 1) of the oil passage, exhibits minimal variation in flow rate under different rotational speeds. The flow rates at outlets in Zone 1 and the main oil passage increase with rotational speed, whereas the oil discharge from Zone 2 outlets gradually decreases and even ceases completely under higher speed conditions. For Zone 3, the flow rates at outlets 7-1, 7-3, 8-1, and 8-2 exhibit an increasing trend with rising rotational speed. Although outlets 7-2 and 7-4 are geometrically symmetric to outlets 7-1 and 7-3, their flow rates decrease significantly at higher rotational speeds. This disparity occurs because the branch oil path containing outlets 7-1 and 7-3 also connects outlets 8-1 and 8-2, which reduces flow resistance in that oil pathway. Consequently, more oil is diverted toward outlets 7-1 and 7-3, resulting in relatively lower discharge at outlets 7-2 and 7-4.

5.3.2. Effect of Oil Supply Pressure on Flow Rates at Outlets of the Oil Passage

A comparative analysis of flow rates across outlets under different oil supply pressures (0.2 MPa, 0.3 MPa, and 0.4 MPa) at rotational speeds of 1149 r/min and 4596 r/min is shown in the following pictures respectively. Figure 21 present pressure distribution contours in the rotating regions at different inlet oil pressures under low-speed condition in second-gear. At 1149 r/min, as shown in Figure 22, the flow rates at all outlets increase consistently with higher supply pressures, exhibiting a clear positive correlation under ambient temperature conditions. The flow rates at the planetary pin shaft outlets are generally higher than those at other branched outlets on the carrier. Compared to the stationary section (Zone 1), the outlets in the rotating sections (Zones 2 and 3) display higher discharge oil rates.

Figure 23 present pressure distribution contours in the rotating regions at different inlet oil pressures under high-speed condition in second-gear. Meanwhile, as shown in Figure 24, intensified turbulent flow within the passages results in significantly larger fluctuations in output from outlets located in rotating zones (Zones 2 and 3) in the same condition. At 4596 r/min, as shown in Figure 25, flow rates at all outlets increase with rising supply pressure, while discharges from the stationary section (Zone 1) show only minor variation. For the pin shaft outlets in Zone 2, flow rates slightly increase at 0.4 MPa but remain consistently low overall. The axial outlets 6-1 and 6-2 show negligible discharge at higher supply pressures. Additionally, the flow rates at the main passage outlets 4-1 and 4-2 are largely unaffected by changes in supply pressure and remain nearly constant.

Analysis of the outlet flow data across varying rotational speeds and supply pressures indicates that, under both high- and low-speed conditions, discharge rates at all outlets increase with elevated supply pressure. In Zone 1, which is not affected by rotation, outlet flow rates demonstrate a consistent and predictable relationship with changes in supply pressure. In Zones 2 and 3, flow complexity and unsteady fluctuations of flow rate intensify as the rotational speed increases. Notably, under high-speed conditions in Zone 2, centrifugal forces and flow instabilities lead to reduced reduction of discharge oil rates, with some outlets exhibiting no measurable flow, indicating that centrifugal effects dominate over pressure-driven flow under higher speed conditions.

5.3.3. Effect of Oil Temperature on Flow Rates at Outlets of the Oil Passage

The above work reveals that flow rates of outlets are strongly influenced by rotational speed and oil supply. Yet, as the viscosity of lubricating oil is temperature-dependent, its dynamic viscosity decreases by approximately 60% when the lubricating oil temperature rises from 70 °C to 110 °C. The significant impact of oil temperature variations will be discussed in detail next.

Under an oil supply pressure of 0.2 MPa, the flow rate differences across outlets are analyzed under rotational speeds of 1149 r/min and 4596 r/min for lubricant temperatures of 70 °C, 90 °C, and 110 °C.

As shown in Figure 26, under a rotational speed of 1149 r/min, the flow rates at outlets in Zone 1 initially increase and then decrease as the temperature increases. In Zones 2 and 3, the flow rates at the planetary pin shaft outlets show a slight increase, while axial outlet flows decrease. This behavior is primarily attributed to the reduction in lubricant viscosity with increasing temperature, which enhances fluid mobility. Beyond a certain temperature threshold, the lubricant exhibits a stronger tendency to flow toward the rear sections of the oil passage, thus reducing discharge from outlets located in the forward regions. Overall, flow variations across outlets remain stable without abrupt fluctuations.

As shown in Figure 27, under high-speed conditions, flow rates at the main passage outlets and those in Zone 1 increase with temperature, while the discharge from the stationary outlet (outlet 1) decreases slightly, though the reduction is marginal. In Zone 2, minimal lubricant discharge is observed at 110 °C, while no measurable flow occurs at other temperatures. In Zone 3, although the four pin shaft outlets (7-1, 7-2, 7-3, and 7-4) are uniformly distributed circumferentially, their flow behaviors differ. The flow rates at outlets 7-1 and 7-3 decrease with rising temperature, while those at outlets 7-2 and 7-4 increase. This asymmetry results from the presence of additional outlets along the supply pathways to 7-1 and 7-3, which divert oil and reduce the volume reaching these outlets.

Analysis of outlet flow data across varying rotational speeds and oil temperatures indicates that elevated temperatures reduce lubricant viscosity, thus enhancing the lubricant’s fluidity. This property facilitates oil movement within the passages to a limited extent. However, under high-speed conditions, flow behavior becomes increasingly complex, and rotational speed exerts a more major influence on outlet discharge rates.

6. Conclusions

This research presents a CFD simulation model to investigate the oil supply characteristics of a multi-stage planetary transmission system in a tracked vehicle under different operational conditions. The experimental results validate that the proposed numerical method can effectively predict the oil discharge volumes of the outlets of the three planetary stages. Furthermore, utilizing the developed numerical model, the effects of input rotational speed, supply pressure, and oil temperature on the oil discharge volumes through the outlets have been systematically investigated. However, with the advancement of experimental technologies and the deepening of research, the observation of lubricant flow phenomena between different regions, the influence of phase change and surface tension, and the comparative analysis of different structures in the experiment remain to be carried out in subsequent work. The following conclusions are drawn:

(1)

Under low-speed conditions, oil flow within the passages exhibits minimal fluctuations. In the first-gear condition, oil simultaneously enters the passages of all planetary stages, while in the second-gear condition, it first fills the rotating passages before advancing into the stationary ones. Under high-speed conditions, oil distribution becomes non-uniform and shows significant fluctuations. In the first-gear condition, oil preferentially flows into the passages of planetary stages with higher rotational speeds; in second-gear condition, the flow sequence is reversed relative to that under low-speed conditions. Under all conditions, the oil distribution stabilizes within approximately 2.56 s of operation time.

(2)

Across all outlets of the three-stage planetary system, flow rates from the stationary passage, main passage, and transmission Zone 1 (0 rpm) increase steadily with rising speed. For the rotating transmission Zones 2 and 3, flow rates in Zone 2 decrease sharply with increasing speed, resulting in flow cessation at several outlets, while those in Zone 3 exhibit significant and erratic fluctuations. With increasing supply pressure, outlet flow rates rise uniformly under low-speed conditions but exhibit irregular and disordered variations at high rotational speeds. With rising oil temperature, flow rates at all outlets under low-speed conditions show minimal fluctuations and minor changes, whereas under high-speed conditions, discharge volumes exhibit intense and erratic variations.

(3)

Among the factors influencing oil discharge variations at the planetary stage outlets, under low-speed conditions, increasing the oil supply pressure elevates outlet flow rates by up to 61%, whereas temperature increases cause a maximum variation of only 18%. Thus, supply pressure exerts a greater effect than temperature. At high speeds, the effects of both pressure and temperature diminish, and rotational speed remains the major factor governing outlet flow behavior across all conditions.

The present work can provide guidance for optimizing lubrication passage design and oil supply strategies in multi-stage planetary transmissions.