Model Predictive Load Frequency Control for Virtual Power Plants: A Mixed Time- and Event-Triggered Approach Dependent on Performance Standard

Abstract

To improve the load frequency control (LFC) performance of power systems incorporating virtual power plants (VPPs) while reducing network resource consumption, a model predictive control (MPC) method based on a mixed time/event-triggered mechanism (MTETM) is proposed. This mechanism integrates an event-triggered mechanism (ETM) with a time-triggered mechanism (TTM), where ETM avoids unnecessary signal transmission and TTM ensures fundamental control performance. Subsequently, for the LFC system incorporating VPPs, a state hard constrained MPC problem is formulated and transformed into a “min-max” optimisation problem. Through linear matrix inequalities, the original optimisation problem is equivalently transformed into an auxiliary optimisation problem, with the optimal control law solved via rolling optimisation. Theoretical analysis demonstrates that the proposed auxiliary optimisation problem possesses recursive feasibility, whilst the closed-loop system satisfies input-to-state stability. Finally, validation through case studies of two regional power systems demonstrates that the MPC approach based on MTETM outperforms the ETM-based MPC approach in terms of control performance while maintaining a triggering rate of 33.3%. Compared with the TTM-based MPC algorithm, the MTETM-based MPC method reduces the triggering rate by 66.7%, while maintaining nearly equivalent control performance. Consequently, the results validate the effectiveness of the MTETM-based MPC approach in conserving network resources while maintaining control performance.

1. Introduction

With the rapid transformation of the global energy system, the penetration rate of renewable energy keeps rising. However, due to the intermittency and volatility of renewable energy [1,2], the frequency stability of power systems and the operational regulation function of power grids are significantly affected. Against this background, it is necessary to introduce more adjustable resources to improve the frequency stability of power grids [3]. Currently, the large-scale integration of distributed energy sources such as wind power and photovoltaic power in distribution networks provides a new solution for power system frequency regulation [4]. Considering the limited capacity of such distributed energy sources, the use of virtual power plant (VPP) to aggregate and coordinately dispatch them for system frequency regulation has gradually developed into a new and widely considered solution [5,6]. By integrating distributed energy sources, including electric vehicles (EVs), energy storage systems (ESSs), and other energy, VPP forms a controllable aggregated unit, which provides a new approach for system frequency control.

As the number of connected devices in VPP continues to increase, the use of load frequency control (LFC) to ensure power supply stability and power quality has become an important measure. In LFC systems incorporating VPPs, maintaining the frequency within a stable range is a prerequisite for ensuring the overall safe operation of the system [7]. In existing studies, traditional LFC strategies are mostly based on the proportional–integral control structure. Although simple in structure, they are difficult to cope with the uncertainties and complex dynamic processes caused by the high proportion of renewable energy integration. Some scholars have attempted to introduce robust control [8,9], adaptive control [10,11], or fuzzy logic [12,13] to enhance system robustness. However, these methods usually do not fully consider the state constraints and multi-objective coordination issues in actual systems, and there are limitations such as response delay, especially when dealing with the coordinated regulation of heterogeneous resources in VPP.

Model predictive control (MPC) has shown significant advantages in power system frequency control due to its ability to handle hard constraints, rolling optimisation, and multi-variable coordination [14,15]. Some scholars conducted research on MPC-based LFC involving VPP and achieved certain results. A VPP frequency controller based on centralised MPC was designed in [16], which effectively suppresses the fluctuations of wind and photovoltaic output. For the coordinated frequency regulation among multiple VPPs, Moritz et al. proposed a distributed MPC architecture, thereby realising the collaborative frequency control of multi-VPP systems [17]. However, traditional MPC methods usually relied on periodic control updates and global information interaction, resulting in heavy computational and communication burdens [18,19,20]. In cases where the VPP cluster is large in scale and the equipment is highly heterogeneous, the frequent optimisation calculations and high-speed communication requirements limit its practical application in engineering, making it difficult to meet the frequency control scenarios with limited communication resources.

To reduce computational resources and communication overhead, researchers have introduced event-triggered mechanisms (ETMs) into the MPC framework. This mechanism updates control commands only when the trigger threshold is satisfied, thereby effectively reducing redundant communication and computational overhead [21,22,23]. In the field of power system frequency control, several studies have explored event-triggered MPC strategies. For the LFC problem of systems with wind turbines, Hu et al. proposed a robust event-triggered MPC strategy that is resilient to false data injection attacks, and adopted an enhanced ETM to reduce the computational burden [24]. Wang et al. integrated a periodic ETM with disturbance estimation and prediction capabilities into MPC. This approach not only mitigated network and computational load while compensating for disturbances, but also enhanced control performance and optimised resource utilisation [25]. However, in scenarios with severe disturbances, the aforementioned methods may encounter problems such as excessively frequent triggering or insufficient control response.

Due to the limitations of existing dynamic ETMs in further reducing communication overhead while maintaining control performance, hybrid triggering mechanisms have received significant attention in recent years. Such approaches combine time-triggered and event-triggered modes, ensuring system control performance while reducing computational burden through event mechanisms [26,27]. Saxena et al. proposed an event-triggered LFC strategy based on hybrid trigger logic, optimising update timing through adaptive trigger interval adjustment to enhance coordination efficiency in multi-agent systems [28]. Zhang et al. designed a multi-area LFC hybrid trigger scheme incorporating virtual synchronous generators, integrating trigger conditions with system state variability to effectively balance communication volume and control performance under insecure communication conditions [29]. Within the LFC system domain, alongside reducing communication resource consumption, minimising equipment losses constitutes another key research focus. The core methodology involves adjusting controller gains within LFC schemes by reference to the Control Performance Standards (CPSs) established by the North American Electric Reliability Corporation [30,31,32]. Based on these studies, this paper proposes a CPS-dependent mixed time/event-triggered mechanism (MTETM)-based MPC algorithm. By dynamically adjusting trigger thresholds, the MTETM avoids resource wastage from frequent updates while ensuring control performance during abrupt frequency changes, thereby significantly enhancing the system’s resilience against random disturbances [33].

Based on the aforementioned research status, the existing research questions (RQs) are summarised as follows:

RQ1: When VPPs aggregating renewable energy sources are integrated into the power system, existing models fail to adequately capture the variability of renewable energy, leading to significant deviations in LFC and optimisation results.

RQ2: Most existing single-event triggering mechanisms fail to guarantee system control performance well; single time-triggered mechanisms introduce communication redundancy; and most triggering mechanisms fail to strike a balance between these two aspects.

RQ3: Most existing control strategies fail to adequately account for the physical hard constraints of power systems. Concurrently, analysing the feasibility of the algorithm and system stability remains a challenging issue when considering positively invariant set (PIS) characteristics and the impact of internal dynamic variable (IDV) within the triggering mechanism.

In this paper, a mixed time/event-triggered model predictive LFC method for VPPs is proposed. To balance the overall system performance, we adopt the CPS to switch flexibly between ETM and the time-triggered mechanism (TTM). The key contributions of this study include the following three aspects.

(1) A unified dynamic model for VPP integrating wind power, photovoltaic power, ESSs, and EVs to participate in power system LFC is constructed, which describes the dynamic behaviour of distributed resources during frequency regulation.

(2) Based on CPS, an MTETM is proposed that balances communication resource consumption and system control performance under external disturbances.

(3) A rolling optimisation strategy with constraint-handling capability is designed, ensuring the recursive feasibility of the proposed auxiliary optimisation problem (OP) and the input-to-state stability of the closed-loop system.

The following is the structure of this article. Section 2 introduces the LFC systems incorporating VPP and the design of the MTETM. Section 3 details the solution process for the MPC problem based on the MTETM, providing stability analysis and a recursive feasibility proof. Section 4 validates the effectiveness of the method through a case analysis. Section 5 summarises the paper and outlines future research directions.

2. Problem Formulation

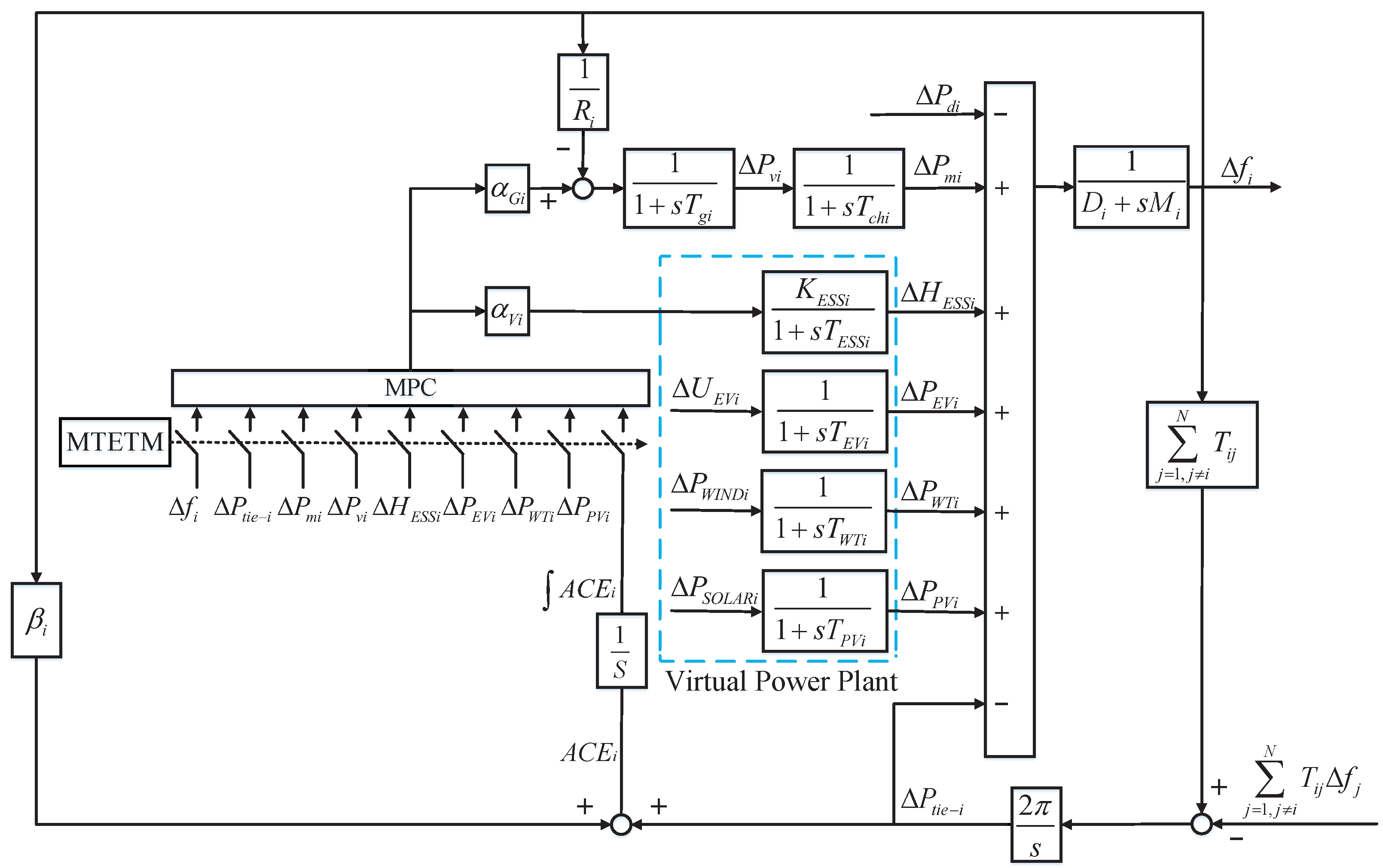
2.1. Overall Structure of Virtual Power Plant

VPPs leverage the internet and advanced information and communication technologies to integrate distributed generation, ESSs, and power loads, while providing grid support services such as peak shaving, valley filling, and frequency regulation. Figure 1 illustrates the model of the ith LFC area incorporating a VPP, which aggregates diverse distributed energy resources, including ESS, EV, wind power, and photovoltaic generation, to participate collaboratively in frequency control within the power system.

In Figure 1, $\Delta f_i$ is the deviation in frequency, $\Delta P_{mi}$ is the deviation in the generator’s mechanical power output, $\Delta P_{\nu i}$ is the deviation in the valve position, $\Delta P_{di}$ is the deviation in the load demand and $\Delta P_{tie-i}$ is the deviation in the tie-line active power. Meanwhile, ${ACE}_i$ is the area control error, $M_i$ is the generator moment of inertia, $R_i$ is the speed droop, $T_{gi}$ is the time constant of the governor, $T_{chi}$ is the turbine time constant, $D_i$ is the generator damping coefficient, ${\beta }_i$ is the frequency bias factor and $T_{ij}$ is the tie-line synchronising coefficient between the ith and jth areas. Furthermore, the parameters ${\alpha }_{Gi}$ and ${\alpha }_{Vi}$ denote the participation factors for the conventional governor-turbine system and the ESS [34], respectively, satisfying ${\alpha }_{Gi}+{\alpha }_{Vi}=1$.

2.2. Energy Storage Systems Modelling

ESSs are critical supporting equipment for power system frequency regulation. Their functions are primarily reflected in two aspects: significantly enhancing the grid’s rapid response capability to frequency fluctuations, and effectively reducing the operational burden on conventional thermal power units during transients. To address frequency regulation challenges in multi-source power systems, this study establishes a first-order lag model to characterise the dynamic behaviour of ESSs, as shown below [35]:

$$\begin{array}{c}\hfill \Delta H_{ESSi}={\displaystyle \frac{K_{ESSi}}{1+s{T}_{ESSi}}}{\alpha }_{Vi}{u}_i\end{array}$$

(1)

where $K_{ESSi}$ denotes gain coefficient of the ESS, $T_{ESSi}$ represents the response time constant of the ESS and $u_i$ denotes the control input of the system.

2.3. Electric Vehicle Modelling

Featuring their flexible and controllable characteristics, EVs can dynamically switch between acting as grid loads and power sources during charging and discharging processes. For aggregated EV clusters, the following frequency regulation model is considered [36].

$$\begin{array}{c}\hfill \Delta P_{EVi}={\displaystyle \frac{\Delta U_{EVi}}{1+s{T}_{EVi}}}\end{array}$$

(2)

where $\Delta U_{EVi}$ is the charge and discharge depth of EV batteries and $T_{EVi}$ is the response time constant of the EV.

2.4. Wind Power Modelling

In LFC, the dynamic characteristics of wind power are represented by a first-order transfer function. This model treats meteorological parameters such as wind speed and direction as disturbance inputs, which significantly influence the power generation performance of wind turbines. This study employs the following wind turbine model [37]:

$$\begin{array}{c}\hfill \Delta P_{WTi}={\displaystyle \frac{\Delta P_{WINDi}}{1+s{T}_{WTi}}}\end{array}$$

(3)

where $\Delta P_{WTi}$ denotes the fluctuation in wind turbine output power relative to its rated value, $T_{WTi}$ represents the inertial time constant of the wind turbine, characterising the unit’s response to wind speed disturbances, and $\Delta P_{WINDi}$ signifies the fluctuation amplitude of the input wind power.

2.5. Photovoltaic Power Modelling

In photovoltaic power generation systems, photovoltaic units operate under maximum power point tracking control, with the objective of the inverters being to ensure a stable power output. The dynamic response properties of the system’s active power can be described as follows [38]:

$$\begin{array}{c}\hfill \Delta P_{PVi}={\displaystyle \frac{\Delta P_{SOLARi}}{1+s{T}_{PVi}}}\end{array}$$

(4)

where $\Delta P_{PVi}$ denotes the active power variation of the photovoltaic inverter, $\Delta P_{SOLARi}$ represents the fluctuation of incident solar radiation energy, and $T_{PVi}$ represents the inertial time constant for the photovoltaic inverter unit.

2.6. Model Predictive LFC Model with Participation of VPP

For LFC areas, each area is interconnected with neighbouring areas via tie-lines. According to Figure 1, the model of the ith control area is described as follows:

$$\left\{\begin{array}{c}\Delta f_i\left(s\right)={\displaystyle \frac{\Delta P\left(s\right)}{s{M}_i+D_i}}\hfill \\ \Delta P_{tie-i}\left(s\right)={\displaystyle \frac{2\pi }{s}}\sum _{j=1,j\ne i}^N{T}_{ij}(\Delta f_i\left(s\right)-\Delta f_j\left(s\right))\hfill \\ \Delta P_{mi}\left(s\right)={\displaystyle \frac{\Delta P_{\nu i}\left(s\right)}{1+s{T}_{chi}}}\hfill \\ \Delta P_{\nu i}\left(s\right)={\displaystyle \frac{1}{1+s{T}_{gi}}}(u_i\left(s\right){\alpha }_{Gi}-{\displaystyle \frac{1}{R_i}}\Delta f_i\left(s\right))\hfill \\ AC{E}_i\left(s\right)=\Delta P_{tie-i}\left(s\right)+{\beta }_i\Delta f_i\left(s\right)\hfill \end{array}\right.$$

(5)

where $\Delta P\left(s\right)=\Delta H_{ESSi}\left(s\right)+\Delta P_{mi}\left(s\right)+\Delta P_{EVi}\left(s\right)+\Delta P_{WTi}\left(s\right)+\Delta P_{PVi}\left(s\right)-\Delta P_{di}\left(s\right)-P_{tie-i}\left(s\right)$.

By applying inverse Laplace transformation and defining the state vector $x_i\left(t\right)={[\Delta f_i\left(t\right),\Delta P_{tie-i}\left(t\right),\Delta P_{mi}\left(t\right),\Delta P_{\nu i}\left(t\right),\int AC{E}_i\left(t\right)dt,\Delta H_{ESSi}\left(t\right),\Delta P_{EVi}\left(t\right),\Delta P_{WTi}\left(t\right),\Delta P_{PVi}\left(t\right)]}^{\mathrm{T}}$, output vector $y_i\left(t\right)={[AC{E}_i\left(t\right),\int AC{E}_i\left(t\right)dt]}^{\mathrm{T}}$, and disturbance vector $w_i\left(t\right)={[\Delta P_{di}\left(t\right),\Delta U_{EVi}\left(t\right),\Delta P_{WINDi}\left(t\right),\Delta P_{SOLARi}\left(t\right)]}^{\mathrm{T}}$, we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_i\left(t\right)={\overline{A}}_{ii}{x}_i\left(t\right)+{\overline{B}}_i{u}_i\left(t\right)+{\overline{F}}_i{w}_i\left(t\right)+\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{\overline{A}}_{ij}{x}_j\left(t\right)\hfill \\ y_i\left(t\right)={\overline{C}}_i{x}_i\left(t\right)\hfill \end{array}\right.\end{array}$$

(6)

where

$${\overline{A}}_{ii}=\left[\begin{array}{ccccccccc}-{\displaystyle \frac{D_i}{M_i}}& -{\displaystyle \frac{1}{M_i}}& {\displaystyle \frac{1}{M_i}}& 0& 0& {\displaystyle \frac{1}{M_i}}& {\displaystyle \frac{1}{M_i}}& {\displaystyle \frac{1}{M_i}}& {\displaystyle \frac{1}{M_i}}\\ 2\pi \sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{T}_{ij}& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& -{\displaystyle \frac{1}{T_{chi}}}& {\displaystyle \frac{1}{T_{chi}}}& 0& 0& 0& 0& 0\\ -{\displaystyle \frac{1}{R_i{T}_{gi}}}& 0& 0& -{\displaystyle \frac{1}{T_{gi}}}& 0& 0& 0& 0& 0\\ {\beta }_i& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -{\displaystyle \frac{1}{T_{ESSi}}}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -{\displaystyle \frac{1}{T_{EVi}}}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& -{\displaystyle \frac{1}{T_{WTi}}}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& -{\displaystyle \frac{1}{T_{PVi}}}\end{array}\right],$$

$${\overline{A}}_{ij}=\left[\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ -2\pi T_{ij}& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right],{\overline{F}}_i=\left[\begin{array}{cccc}-{\displaystyle \frac{1}{M_i}}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& {\displaystyle \frac{1}{T_{EVi}}}& 0& 0\\ 0& 0& {\displaystyle \frac{1}{T_{WTi}}}& 0\\ 0& 0& 0& {\displaystyle \frac{1}{T_{PVi}}}\end{array}\right],$$

$${\overline{B}}_i=\left[\begin{array}{c}0\\ 0\\ 0\\ {\displaystyle \frac{a_{Gi}}{T_{gi}}}\\ 0\\ {\displaystyle \frac{a_{Vi}{K}_{ESSi}}{T_{ESSi}}}\\ 0\\ 0\\ 0\end{array}\right],{\overline{C}}_i={\left[\begin{array}{cc}{\beta }_i& 0\\ 1& 0\\ 0& 0\\ 0& 0\\ 0& 1\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right]}^{\mathrm{T}},T_{ij}=T_{ji}.$$

We obtain the following dynamic model of the LFC system with VPPs:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{x}\left(t\right)=\overline{A}x\left(t\right)+\overline{B}u\left(t\right)+\overline{F}w\left(t\right)\hfill \\ y\left(t\right)=\overline{C}x\left(t\right)\hfill \end{array}\right.\end{array}$$

(7)

where $x\left(t\right)={[x_1\left(t\right),\dots ,x_N\left(t\right)]}^{\mathrm{T}}$, $y\left(t\right)={[y_1\left(t\right),\dots ,y_N\left(t\right)]}^{\mathrm{T}}$, $u\left(t\right)={[u_1\left(t\right),\dots ,u_N\left(t\right)]}^{\mathrm{T}}$, and $w\left(t\right)={[w_1\left(t\right),\dots ,w_N\left(t\right)]}^{\mathrm{T}}$ are the state vector, the measurement output, the control input, and the disturbance, respectively. Accordingly, define the state matrix $\overline{A}={\left[{\overline{A}}_{ij}\right]}_{N\times N}$, input matrix $\overline{B}=\mathrm{diag}\{{\overline{B}}_1,\dots ,{\overline{B}}_N\}$, output matrix $\overline{C}=\mathrm{diag}\{{\overline{C}}_1,\dots ,{\overline{C}}_N\}$, and perturbation matrix $\overline{F}=\mathrm{diag}\{{\overline{F}}_1,\dots ,{\overline{F}}_N\}$.

Note that ${\sum }_{\begin{array}{c}i=1\end{array}}^N\Delta P_{tie-i}=0$. The following is a reduced-order LFC system model in discrete-time setting:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}x(p+1)=Ax\left(p\right)+Bu\left(p\right)+Fw\left(p\right)\hfill \\ y\left(p\right)=Cx\left(p\right).\hfill \end{array}\right.\end{array}$$

(8)

Assume that the load disturbance $w\left(p\right)$ is bounded such that

$$\begin{array}{c}\hfill {\parallel w\left(p\right)\parallel }^2\le \overline{w}\end{array}$$

(9)

where $\overline{w}\ge 0$ is a constant. The following hard constraint is considered for the physical limitations of the VPP and conventional generation units:

$$\begin{array}{c}\hfill {|[\Xi ]}_{o}x\left(p\right)|\le {\left[\overline{x}\right]}_o,o\in \mathcal{O}\triangleq \{1,2,\dots ,n_{\Xi }\}\end{array}$$

(10)

where $\Xi \in {\mathbb{R}}^{n_{\Xi }\times n_x}$ denotes a known matrix, $\overline{x}\in {\mathbb{R}}^{n_{\Xi }}$ represents a predefined vector with all non-negative entries, and ${[·]}_o$ represents the o-th row of a matrix.

In this study, we adopt the CPS function to construct the MTETM. Its expression is given as follows [39]:

$$\begin{array}{c}\hfill \mathrm{CPS}\left(p\right)=(\sum _{i=1}^N|AC{E}_i\left(p\right)\left|\right)-L_{cps}\end{array}$$

(11)

where $L_{cps}=1.65{\eta }_1{\sum }_{i=1}^N\sqrt{(-10{\eta }_2)(-10{\beta }_i)}$ is a CPS-related constant, where ${\beta }_i$ is the frequency bias factor mentioned earlier, ${\eta }_1\ne 0$ represents the targeted frequency bound for CPS and ${\eta }_2>0$ represents the frequency bias summation of all interconnection control areas. When the system maintains effective control over the active power of the interconnection line, CPS(p) was required to be less than or equal to 0.

Remark 1.

The core physical meaning of CPS$\left(p\right)$ is to limit the cumulative magnitude of $ACE$ across all control areas to ensure stable tie-line power exchange and frequency control performance. Determine the overall control effectiveness of the power system by assessing whether the CPS(p) is less than or equal to 0. The critical parameter $L_{cps}$ is calculated as $L_{cps}=1.65{\eta }_1{\sum }_{i=1}^N\sqrt{(-10{\eta }_2)(-10{\beta }_i)}$, whose practical calculation requires predefined parameters (${\eta }_1,{\eta }_2$) and measured data of ${\beta }_i$. During real-time operation, verifying CPS(p) compliance further requires measuring the $AC{E}_i$ of each control area $AC{E}_i\left(p\right)={\beta }_i\Delta f_i\left(p\right)+\Delta P_{tie-i}\left(p\right)$, which relies on real-time data of $\Delta f_i\left(p\right)$ and $\Delta P_{tie-i}\left(p\right)$ from each area.

In this paper, an MTETM is put forward to conserve network resources and attain the desired control performance. The precise form of the MTETM, which incorporates an IDV $\theta \left(p\right)$, is presented as follows.

$$\left\{\begin{array}{cc}\mathrm{If}\hfill & \mathrm{CPS}\left(p\right)>0,s_{m+1}=s_m+1.\hfill \\ \mathrm{If}\hfill & \mathrm{CPS}\left(p\right)\le 0,\hfill \\ \hfill & s_{m+1}=\underset{p\in {\mathbb{N}}^{+}}{min}\{p>s_m|{\rho }_1\theta \left(p\right)\hfill \\ \hfill & +{\xi }_1{x}^{\mathrm{T}}\left(p\right)\mathsf{\Pi }\left(p\right)x\left(p\right)-{\xi }_2{e}^{\mathrm{T}}\left(p\right)\mathsf{\Pi }\left(p\right)e\left(p\right)\le 0\}\hfill \\ \hfill & \theta (p+1)={\rho }_2\theta \left(p\right)+{\xi }_3{x}^{\mathrm{T}}\left(p\right)\mathsf{\Pi }\left(p\right)x\left(p\right)-{\xi }_4{e}^{\mathrm{T}}\left(p\right)\mathsf{\Pi }\left(p\right)e\left(p\right),\hfill \end{array}\right.$$

(12)

where $s_m$ denotes the mth triggering instant, with $s_0=0$ and $\theta \left(0\right)\ge 0$. $\mathsf{\Pi }\left(p\right)\in {\mathbb{R}}^{n_x\times n_x}$ represents a time-varying weighting matrix. It is to be designed by solving the OP at p. Meanwhile, ${\rho }_1\ge 0$, $0\le {\rho }_2\le 1$, ${\xi }_1\ge 0$, ${\xi }_2>0$, ${\xi }_3\ge 0$, and ${\xi }_4>0$ are given scalars and $e\left(p\right)=x\left(p\right)-x\left(s_m\right)$.

Additionally, let

$$\begin{array}{cc}\hfill & \widehat{x}\left(p\right)=x\left(s_m\right),\forall p\in [s_m,s_{m+1}),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & e\left(p\right)=x\left(p\right)-\widehat{x}\left(p\right).\hfill \end{array}$$

(14)

$\forall p\in [0,\infty ),e\left(p\right)=x\left(p\right)-x\left(s_m\right)$ and (13) are satisfied when $m\in [0,+\infty )$.

Remark 2.

We introduce $CPS\left(p\right)$ to effectively enhance the flexibility of MTETM (12). When $CPS\left(p\right)>0$, this indicates poor control performance of the system. In such a case, the TTM is employed to ensure that the controller acquires sufficient system information, thereby safeguarding control performance. Conversely, when $CPS\left(p\right)\le 0$, this signifies good control performance of the system. In this situation, ETM substantially reduces unnecessary packet transmission, thereby lowering communication and computational resource consumption. It should be specifically noted that when employing TTM, $e\left(p\right)=x\left(p\right)-\widehat{x}\left(p\right)$ remains valid, as $e\left(p\right)=0$ at this point.

We give the following feedback control controller under the MPC framework:

$$\begin{array}{c}\hfill u\left(p\right)=K\left(p\right)\widehat{x}\left(p\right).\end{array}$$

(15)

The gain matrix $K\left(p\right)$ requires to be solved. Substituting (14) and (15) into (8) yields the closed-loop system:

$$\begin{array}{c}\hfill x(p+1)=(A+BK(p\left)\right)x\left(p\right)-BK\left(p\right)e\left(p\right)+Fw\left(p\right).\end{array}$$

(16)

We define $x(l,p)$ as the predicted value of the state at the future instant $p+l$ with respect to instant p. We can get the following prediction model:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}x(l+1,p)=(A+BK(p\left)\right)x(l,p)-BK\left(p\right)e(l,p)+Fw(l,p)\hfill \\ \theta (l+1,p)={\rho }_2\theta (l,p)+{\xi }_3{\parallel x(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2-{\xi }_4{\parallel e(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2.\hfill \end{array}\right.\end{array}$$

(17)

In this paper, the following cost function is considered:

$$\begin{array}{c}\hfill J^{\infty }\left(p\right)=\sum _{l=0}^{\infty }\left[{∥x(l,p)∥}_L^2+{∥u(l,p)∥}_P^2-\nu {∥w(l,p)∥}^2\right]\end{array}$$

(18)

with $L>0$, $P>0$ being predefined weighting matrices, and $\nu$ is a constant.

To design a controller for system (16) at p, the following “min-max” OP is formulated:

$$\begin{array}{cc}\hfill & O{P}_1:\underset{u\left(p\right)}{min}\underset{w\left(p\right)}{max}{J}^{\infty }\left(p\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {|[\Xi ]}_{o}x\left(p\right)|\le {\left[\overline{x}\right]}_o,o\in \mathcal{O}\triangleq \{1,2,\dots ,n_{\Xi }\}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & [x^{\mathrm{T}}(l,p),{\theta }^{{\displaystyle \frac{1}{2}}}(l,p){]}^{\mathrm{T}}\in \mathsf{\Gamma },l\in \mathbb{N}\hfill \end{array}$$

(20)

where

$$\begin{array}{c}\hfill \mathsf{\Gamma }\triangleq \{[x^{\mathrm{T}}(l,p),{\theta }^{{\displaystyle \frac{1}{2}}}(l,p){]}^{\mathrm{T}}|x^{\mathrm{T}}(l,p)\mathrm{\Phi }\left(p\right)x(l,p)+\theta (l,p)\le \zeta \}.\end{array}$$

(21)

Here, $\mathrm{\Phi }\left(p\right)>0$ and $\zeta >0$ denote the weighting matrix and the optimisation index to be designed, respectively.

The subsequent definition and lemma are introduced for analytical purposes.

Definition 1.

For the system described by system (8), a set Γ is designated as a PIS provided that $[x^{\mathrm{T}}(l+1,p),{\theta }^{{\displaystyle \frac{1}{2}}}(l+1,p){]}^{\mathrm{T}}\in \mathsf{\Gamma }$ whenever $[x^{\mathrm{T}}(l,p),{\theta }^{{\displaystyle \frac{1}{2}}}(l,p){]}^{\mathrm{T}}\in \mathsf{\Gamma }$ and $w(l,p)$ is an allowable disturbance.

Definition 2.

Letting $\mathfrak{X}\left(p\right)=[x^{\mathrm{T}}\left(p\right),{\theta }^{{\displaystyle \frac{1}{2}}}\left(p\right){]}^{\mathrm{T}}$, system (16) is input-to-state stable (ISS) under MTETM (12) if there exist a positive definite function $V_{ISS}(·)$, a $\mathcal{K}$-function b, and ${\mathcal{K}}_{\infty }$-functions $a_1$, $a_2$ and $a_3$ such that

$$\begin{array}{cc}\hfill & a_1(\parallel \mathfrak{X}\left(p\right)\parallel )\le V_{ISS}\left(\mathfrak{X}\left(p\right)\right)\le a_2(\parallel \mathfrak{X}\left(p\right)\parallel ),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & V_{ISS}\left(\mathfrak{X}(p+1)\right)-V_{ISS}\left(\mathfrak{X}\left(p\right)\right)\le -a_3(\parallel \mathfrak{X}\left(p\right)\parallel )+b(\parallel w\left(p\right)\parallel ).\hfill \end{array}$$

(23)

Lemma 1.

Consider the MTETM given by (12) with initial condition $\theta \left(0\right)\ge 0$. If non-negative constants ${\rho }_1,{\xi }_1,{\xi }_3$, ${\rho }_2\in [0,1]$, and positive constants ${\xi }_2,{\xi }_4$ satisfy the inequalities ${\rho }_1{\xi }_4\le {\rho }_2{\xi }_2$ and ${\xi }_1{\xi }_4\le {\xi }_2{\xi }_3$, then $\theta \left(p\right)\ge 0$ holds for $\forall p\in {\mathbb{N}}^{+}$.

The proof of Lemma 1 can be established using an approach analogous to that presented in [40], and, thus, the detailed derivation is not repeated here.

3. Results

In this section, we first formulate an auxiliary OP to design the matrices $K\left(p\right)$ and $\mathsf{\Pi }\left(p\right)$. Subsequently, we analyse the feasibility of the constructed auxiliary OP and input-to-state stability of system (16).

3.1. Auxiliary OP for $O{P}_1$

Construct the following Lyapunov function:

$$\begin{array}{c}\hfill V(\theta \left(p\right),x\left(p\right))=x^{\mathrm{T}}\left(p\right)\mathrm{\Phi }\left(p\right)x\left(p\right)+\theta \left(p\right).\end{array}$$

(24)

At p, we assume the following inequality holds:

$$\begin{array}{cc}\hfill & V\left(\theta \right(l+1,p),x(l+1,p\left)\right)-V\left(\theta \right(l,p),x(l,p\left)\right)\hfill \\ \hfill \le & -{\parallel x(l,p)\parallel }_L^2-{\parallel u(l,p)\parallel }_P^2+\nu {\parallel w(l,p)\parallel }^2.\hfill \end{array}$$

(25)

By summing both sides of (25) over l from 0 to ∞, we obtain

$$\begin{array}{c}\hfill J^{\infty }\left(p\right)\le J^{\infty }\left(p\right)+V(\theta (\infty ,p),x(\infty ,p))\le V(\theta \left(p\right),x\left(p\right)).\end{array}$$

(26)

Substituting (21) into (26) yields

$$\begin{array}{c}\hfill J^{\infty }\left(p\right)\le V(\theta \left(p\right),x\left(p\right))\le \zeta .\end{array}$$

(27)

It is clear that $\zeta$ is an upper bound on $J^{\infty }\left(p\right)$. Therefore, we give the following auxiliary OP:

$$\begin{array}{cc}\hfill & O{P}_2:\underset{K\left(p\right)}{min}\zeta \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(17\right),\left(19\right),\left(20\right),\left(25\right)\hfill \end{array}$$

(28)

Theorem 1.

Let the scalars ${\rho }_1\ge 0$, $0\le {\rho }_2\le 1$, ${\xi }_1\ge 0$, ${\xi }_2>0$, ${\xi }_3\ge 0$, ${\xi }_4>0$ and $v>0$ that satisfy ${\rho }_1{\xi }_4\le {\rho }_2{\xi }_2$ and ${\xi }_1{\xi }_4\le {\xi }_2{\xi }_3$, and the matrices Ξ, $L>0$ and $P>0$ be presented. If the scalar $\zeta >0$ and matrices $X\left(p\right)>0$, $T>0$, $G\left(p\right)>0$, $S\left(p\right)$, and $Y\left(p\right)$ exist for each $o\in \mathcal{O}$ such that

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}{\mathfrak{M}}_1^{(1,1)}& \ast \\ {\mathfrak{M}}_1^{(2,1)}& {\mathfrak{M}}_1^{(2,2)}\end{array}\right]\le 0,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}T& \ast \\ Y^{\mathrm{T}}\left(p\right){\Xi }^{\mathrm{T}}& Y^{\mathrm{T}}\left(p\right)+Y\left(p\right)-X\left(p\right)\end{array}\right]\ge 0,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & {\left[T\right]}_{oo}\le {\left[\overline{x}\right]}_o^2\hfill \end{array}$$

(31)

where

$$\begin{array}{cc}\hfill & {\mathfrak{M}}_1^{(1,1)}=\mathrm{diag}\{X\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right),{\xi }_4(G\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right)),-\nu \zeta I\},\hfill \\ \hfill & {\mathfrak{M}}_1^{(2,1)}=\left[\begin{array}{ccc}AY\left(p\right)+BS\left(p\right)& -BS\left(p\right)& \zeta F\\ P^{{\displaystyle \frac{1}{2}}}S\left(p\right)& -P^{{\displaystyle \frac{1}{2}}}S\left(p\right)& 0\\ L^{{\displaystyle \frac{1}{2}}}Y\left(p\right)& 0& 0\\ \sqrt{{\xi }_3}Y\left(p\right)& 0& 0\end{array}\right],\hfill \\ \hfill & {\mathfrak{M}}_1^{(2,2)}=\mathrm{diag}\{-X\left(p\right),-\zeta I,-\zeta I,-G\left(p\right)\},\hfill \end{array}$$

then conditions (19) and (25) hold, and the gain matrix $K\left(p\right)$ and weight matrix $\mathsf{\Pi }\left(p\right)$ are constructed as follows:

$$\begin{array}{c}\hfill K\left(p\right)=S\left(p\right)Y^{-1}\left(p\right),\mathsf{\Pi }\left(p\right)=\zeta G^{-1}\left(p\right).\end{array}$$

(32)

Proof. 

According to the predictive model (17) and $0\le {\rho }_2\le 1$, we have

$$\begin{array}{cc}\hfill & \theta (l+1,p)-\theta (l,p)\le {\xi }_3{\parallel x(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2-{\xi }_4{\parallel e(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2.\hfill \end{array}$$

(33)

Combining (24) and (25) yields

$$\begin{array}{cc}\hfill & x^{\mathrm{T}}(l+1,p)\mathrm{\Phi }\left(p\right)x(l+1,p)+\theta (l+1,p)-x^{\mathrm{T}}(l,p)\mathrm{\Phi }\left(p\right)x(l,p)-\theta (l,p)\hfill \\ \hfill & +{\parallel x(l,p)\parallel }_L^2+{\parallel u(l,p)\parallel }_P^2-\nu {\parallel w(l,p)\parallel }^2\le 0.\hfill \end{array}$$

(34)

From (33), it follows that (34) holds when

$$\begin{array}{cc}\hfill & {\parallel (A+BK\left(p\right))x(l,p)-BK\left(p\right)e(l,p)+Fw(l,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2-{\parallel x(l,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2\hfill \\ \hfill & +{\xi }_3{\parallel x(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2-{\xi }_4{\parallel e(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2+{\parallel x(l,p)\parallel }_L^2\hfill \\ \hfill & +{\parallel u(l,p)\parallel }_P^2-\nu {\parallel w(l,p)\parallel }^2\le 0.\hfill \end{array}$$

(35)

Thus, rewrite (35) as

$$\begin{array}{c}\hfill {\delta }_1^{\mathrm{T}}(l,p)({\mathfrak{A}}_{\mathfrak{1}}+{\mathfrak{A}}_{\mathfrak{2}}\mathrm{\Phi }\left(p\right){\mathfrak{A}}_{\mathfrak{2}}^{\mathrm{T}}+{\mathfrak{A}}_{\mathfrak{3}}P{\mathfrak{A}}_{\mathfrak{3}}^{\mathrm{T}}){\delta }_1(l,p)\le 0,\end{array}$$

(36)

where

$$\begin{array}{cc}\hfill & {\delta }_1(l,p)={\left[x^{\mathrm{T}}(l,p)e^{\mathrm{T}}(l,p)w^{\mathrm{T}}(l,p)\right]}^{\mathrm{T}},\hfill \\ \hfill & {\mathfrak{A}}_1=\mathrm{diag}\{L-\mathrm{\Phi }\left(p\right)+{\xi }_3\mathsf{\Pi }\left(p\right),-{\xi }_4\mathsf{\Pi }\left(p\right),-\nu I\},\hfill \\ \hfill & {\mathfrak{A}}_2={[A+BK\left(p\right)-BK\left(p\right)F]}^{\mathrm{T}},\hfill \\ \hfill & {\mathfrak{A}}_3={[K\left(p\right)-K\left(p\right)0]}^{\mathrm{T}}.\hfill \end{array}$$

According to Schur complement, (36) holds when

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}{\mathfrak{M}}_2^{(1,1)}& \ast \\ {\mathfrak{M}}_2^{(2,1)}& {\mathfrak{M}}_2^{(2,2)}\end{array}\right]\le 0,\hfill \end{array}$$

(37)

where

$$\begin{array}{cc}\hfill & {\mathfrak{M}}_2^{(1,1)}=\mathrm{diag}\{-\mathrm{\Phi }\left(p\right),-{\xi }_4\mathsf{\Pi }\left(p\right),-\nu I\},\hfill \\ \hfill & {\mathfrak{M}}_2^{(2,1)}=\left[\begin{array}{ccc}A+BK\left(p\right)& -BK\left(p\right)& F\\ P^{{\displaystyle \frac{1}{2}}}K\left(p\right)& -P^{{\displaystyle \frac{1}{2}}}K\left(p\right)& 0\\ L^{{\displaystyle \frac{1}{2}}}& 0& 0\\ \sqrt{{\xi }_3}I& 0& 0\end{array}\right],\hfill \\ \hfill & {\mathfrak{M}}_2^{(2,2)}=\mathrm{diag}\{-{\mathrm{\Phi }}^{-1}\left(p\right),-I,-I,-{\mathsf{\Pi }}^{-1}\left(p\right)\}.\hfill \end{array}$$

Then, multiply the matrix in (37) by $\mathsf{\Omega }=\mathrm{diag}\{{\zeta }^{-{\displaystyle \frac{1}{2}}}{Y}^{\mathrm{T}}\left(p\right),{\zeta }^{-{\displaystyle \frac{1}{2}}}{Y}^{\mathrm{T}}\left(p\right),{\zeta }^{{\displaystyle \frac{1}{2}}}I,{\zeta }^{{\displaystyle \frac{1}{2}}}I,{\zeta }^{{\displaystyle \frac{1}{2}}}I,{\zeta }^{{\displaystyle \frac{1}{2}}}I,{\zeta }^{{\displaystyle \frac{1}{2}}}I\}$ on the left and by ${\mathsf{\Omega }}^{\mathrm{T}}$ on the right. Meanwhile, set $K\left(p\right)=S\left(p\right)Y^{-1}\left(p\right),\mathsf{\Pi }\left(p\right)=\zeta G^{-1}\left(p\right),\mathrm{\Phi }\left(p\right)=\zeta X^{-1}\left(p\right)$. The following result is obtained:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}{\mathfrak{M}}_3^{(1,1)}& \ast \\ {\mathfrak{M}}_3^{(2,1)}& {\mathfrak{M}}_3^{(2,2)}\end{array}\right]\le 0,\hfill \end{array}$$

(38)

where

$$\begin{array}{cc}\hfill & {\mathfrak{M}}_3^{(1,1)}=\mathrm{diag}\{-Y^{\mathrm{T}}\left(p\right)X^{-1}\left(p\right)Y\left(p\right),-{\xi }_4{Y}^{\mathrm{T}}\left(p\right)G^{-1}\left(p\right)Y\left(p\right),-\nu \zeta I\},\hfill \\ \hfill & {\mathfrak{M}}_3^{(2,1)}=\left[\begin{array}{ccc}AY\left(p\right)+BS\left(p\right)& -BS\left(p\right)& \zeta F\\ P^{{\displaystyle \frac{1}{2}}}S\left(p\right)& -P^{{\displaystyle \frac{1}{2}}}S\left(p\right)& 0\\ L^{{\displaystyle \frac{1}{2}}}Y\left(p\right)& 0& 0\\ \sqrt{{\xi }_3}Y\left(p\right)& 0& 0\end{array}\right],\hfill \\ \hfill & {\mathfrak{M}}_3^{(2,2)}=\mathrm{diag}\{-X\left(p\right),-\zeta I,-\zeta I,-G\left(p\right)\}.\hfill \end{array}$$

Considering that $-Y^{\mathrm{T}}\left(p\right)X^{-1}\left(p\right)Y\left(p\right)\le X\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right)$ and $-Y^{\mathrm{T}}\left(p\right)G^{-1}\left(p\right)Y\left(p\right)\le G\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right)$, we can conclude that when (29) holds, (38) is valid.

Next, we need to prove that (19) holds when (30) and (31) are satisfied. From $X^{-1}\left(p\right)={\zeta }^{-1}\mathrm{\Phi }\left(p\right)$ and (21), it can be deduced that

$$\begin{array}{cc}\hfill & \underset{l\in \mathbb{N}}{max}{\left|{[\Xi ]}_{o}x(l,p)\right|}^2\hfill \\ \hfill & =\underset{l\in \mathbb{N}}{max}|{[\Xi ]}_o{X}^{{\displaystyle \frac{1}{2}}}\left(p\right)X^{-{\displaystyle \frac{1}{2}}}\left(p\right)x(l,p){|}^2\hfill \\ \hfill & \le \underset{l\in \mathbb{N}}{max}\parallel {[\Xi X^{{\displaystyle \frac{1}{2}}}\left(p\right)]}_o{\parallel }^2\parallel X^{-{\displaystyle \frac{1}{2}}}\left(p\right)x(l,p){\parallel }^2\hfill \\ \hfill & \le \underset{l\in \mathbb{N}}{max}\parallel {[\Xi X^{{\displaystyle \frac{1}{2}}}\left(p\right)]}_o{\parallel }^2(1-{\displaystyle \frac{\theta (l,p)}{\zeta }})\hfill \\ \hfill & \le \parallel {[\Xi X^{{\displaystyle \frac{1}{2}}}\left(p\right)]}_o{\parallel }^2\hfill \end{array}$$

(39)

Next, if there exists a matrix $T>0$ such that

$$\begin{array}{c}\hfill T-\Xi X\left(p\right){\Xi }^{\mathrm{T}}\ge 0\end{array}$$

(40)

and (31) hold, then (19) holds. By Schur complement, we can conclude that when

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}T& \Xi \\ \ast & X^{-1}\left(p\right)\end{array}\right]\ge 0\hfill \end{array}$$

(41)

holds, (40) is met.

Multiplying the matrix in (41) by $\mathrm{diag}\{I,Y^{\mathrm{T}}\left(p\right)\}$ on the left and then by its transpose on the right, combined with $Y^{\mathrm{T}}\left(p\right)X^{-1}\left(p\right)Y\left(p\right)\ge -X\left(p\right)+Y\left(p\right)+Y^{\mathrm{T}}\left(p\right)$, shows that (30) ensures (41). Then, (19) holds when (30) and (31) are satisfied. Thus, Theorem 1 is proven.    □

3.2. PIS Guaranteeing Conditions

To guarantee that $\mathsf{\Gamma }$ is a PIS, we will present sufficient conditions and supply the corresponding linear matrix inequalities.

Theorem 2.

Define the scalar ϵ satisfying $0\le ϵ\le 1-{\rho }_2$ and let the scalars ${\rho }_1\ge 0$, $0\le {\rho }_2\le 1$, ${\xi }_1\ge 0$, ${\xi }_2>0$, ${\xi }_3\ge 0$, ${\xi }_4>0$ and $v>0$ that satisfy ${\rho }_1{\xi }_4\le {\rho }_2{\xi }_2$ and ${\xi }_1{\xi }_4\le {\xi }_2{\xi }_3$, and the matrices Ξ, $L>0$ and $P>0$ be presented. If the scalar $\zeta >0$ and matrices $X\left(p\right)>0$, $G\left(p\right)>0$, $S\left(p\right)$, and $Y\left(p\right)$ exist such that

$$\begin{array}{cc}\hfill & \left[\begin{array}{ccc}1& \ast & \ast \\ x\left(p\right)& X\left(p\right)& \ast \\ \sqrt{\theta \left(p\right)}& 0& \zeta \end{array}\right]\ge 0,\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}{\mathfrak{M}}_4^{(1,1)}& \ast \\ {\mathfrak{M}}_4^{(2,1)}& {\mathfrak{M}}_4^{(2,2)}\end{array}\right]\le 0\hfill \end{array}$$

(43)

hold, where

$$\begin{array}{cc}\hfill {\mathfrak{M}}_4^{(1,1)}=& \mathrm{diag}\{(1-ϵ)(X\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right)),\hfill \\ & {\xi }_4(G\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right)),-{\displaystyle \frac{ϵ}{\overline{w}}}I\},\hfill \\ \hfill {\mathfrak{M}}_4^{(2,1)}=& \left[\begin{array}{ccc}AY\left(p\right)+BS\left(p\right)& -BS\left(p\right)& \zeta F\\ \sqrt{{\xi }_3}Y\left(p\right)& 0& 0\end{array}\right],\hfill \\ \hfill {\mathfrak{M}}_4^{(2,2)}=& \mathrm{diag}\{-X(p),-G(p\left)\right\},\hfill \end{array}$$

then the set Γ is a PIS.

Proof. 

Noting $\zeta {\mathrm{\Phi }}^{-1}\left(p\right)=X\left(p\right)$ and using the Schur complement, we obtain from (42) that $[x^{\mathrm{T}}\left(p\right),{\theta }^{{\displaystyle \frac{1}{2}}}\left(p\right){]}^{\mathrm{T}}\in \mathsf{\Gamma }$. Next, we use mathematical induction to conduct the proof. Assuming that $[x^{\mathrm{T}}(l,p),{\theta }^{{\displaystyle \frac{1}{2}}}(l,p){]}^{\mathrm{T}}\in \mathsf{\Gamma }$ holds, we need to prove that $[x^{\mathrm{T}}(l+1,p),{\theta }^{{\displaystyle \frac{1}{2}}}(l+1,p){]}^{\mathrm{T}}\in \mathsf{\Gamma }$.

Then, if the following inequality holds, (20) also holds at prediction time $l+1$.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\zeta }}{\parallel x(l+1,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2+{\displaystyle \frac{1}{\zeta }}\theta (l+1,p)-{\displaystyle \frac{1-ϵ}{\zeta }}{\parallel x(l,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2\hfill \\ \hfill & -{\displaystyle \frac{1-ϵ}{\zeta }}\theta (l,p)-{\displaystyle \frac{ϵ}{\overline{w}}}{w}^{\mathrm{T}}(l,p)w(l,p)\le 0\hfill \end{array}$$

(44)

More specifically, substitute ${\parallel w(l,p)\parallel }^2\le \overline{w}$ into (44), and noting that $x^{\mathrm{T}}(l,p)\mathrm{\Phi }\left(p\right)x(l,p)+\theta (l,p)\le \zeta$, we can get ${\displaystyle \frac{1}{\zeta }}{\parallel x(l+1,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2+{\displaystyle \frac{1}{\zeta }}\theta (l+1,p)\le 1$. As such, ${\parallel x(l+1,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2+\theta (l+1,p)\le \zeta$, which means that $[x^{\mathrm{T}}(l+1,p),{\theta }^{{\displaystyle \frac{1}{2}}}(l+1,p){]}^{\mathrm{T}}\in \mathsf{\Gamma }$.

Noting that $0\le ϵ\le 1-{\rho }_2$, $\zeta >0$ and (17), (44) holds when

$$\begin{array}{cc}\hfill & {\parallel (A+BK\left(p\right))x(l,p)-BK\left(p\right)e(l,p)+Fw(l,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2+({\xi }_3{\parallel x(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2\hfill \\ \hfill & -{\xi }_4{\parallel e(l,p)\parallel }_{\mathsf{\Pi }\left(p\right)}^2{)-(1-ϵ)\parallel x(l,p)\parallel }_{\mathrm{\Phi }\left(p\right)}^2-{\displaystyle \frac{ϵ}{\overline{w}}}\zeta w^{\mathrm{T}}(l,p)w(l,p)\le 0.\hfill \end{array}$$

(45)

Furthermore, rewrite (45) as

$$\begin{array}{c}\hfill {\delta }_2^{\mathrm{T}}(l,p)({\mathfrak{B}}_{\mathfrak{1}}+{\mathfrak{B}}_{\mathfrak{2}}\mathrm{\Phi }\left(p\right){\mathfrak{B}}_{\mathfrak{2}}^{\mathrm{T}}){\delta }_2(l,p)\le 0,\end{array}$$

(46)

where

$$\begin{array}{cc}\hfill & {\delta }_2(l,p)={\left[x^{\mathrm{T}}(l,p)e^{\mathrm{T}}(l,p)w^{\mathrm{T}}(l,p)\right]}^{\mathrm{T}},\hfill \\ \hfill & {\mathfrak{B}}_1=\mathrm{diag}\{{\xi }_3\mathsf{\Pi }\left(p\right)-(1-ϵ)\mathrm{\Phi }\left(p\right),-{\xi }_4\mathsf{\Pi }\left(p\right),-{\displaystyle \frac{ϵ}{\overline{w}}}\zeta I\},\hfill \\ \hfill & {\mathfrak{B}}_2={[A+BK\left(p\right)-BK\left(p\right)F]}^{\mathrm{T}}.\hfill \end{array}$$

Using the Schur complement, (46) holds when

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}{\mathfrak{M}}_5^{(1,1)}& \ast \\ {\mathfrak{M}}_5^{(2,1)}& {\mathfrak{M}}_5^{(2,2)}\end{array}\right]\le 0,\hfill \end{array}$$

(47)

where

$$\begin{array}{cc}\hfill & {\mathfrak{M}}_5^{(1,1)}=\mathrm{diag}\{-(1-ϵ)\mathrm{\Phi }\left(p\right),-{\xi }_4\mathsf{\Pi }\left(p\right),-{\displaystyle \frac{ϵ}{\overline{w}}}\zeta I\},\hfill \\ \hfill & {\mathfrak{M}}_5^{(2,1)}=\left[\begin{array}{ccc}A+BK\left(p\right)& -BK\left(p\right)& F\\ \sqrt{{\xi }_3}I& 0& 0\end{array}\right],\hfill \\ \hfill & {\mathfrak{M}}_5^{(2,2)}=\mathrm{diag}\{-{\mathrm{\Phi }}^{-1}\left(p\right),-{\mathsf{\Pi }}^{-1}\left(p\right)\}.\hfill \end{array}$$

Then, multiply the matrix in (47) by $\mathsf{\Omega }=\mathrm{diag}\{{\zeta }^{-{\displaystyle \frac{1}{2}}}{Y}^{\mathrm{T}}\left(p\right),{\zeta }^{-{\displaystyle \frac{1}{2}}}{Y}^{\mathrm{T}}\left(p\right),{\zeta }^{-{\displaystyle \frac{1}{2}}}I,{\zeta }^{{\displaystyle \frac{1}{2}}}I,{\zeta }^{{\displaystyle \frac{1}{2}}}I\}$ on the left and by ${\mathsf{\Omega }}^{\mathrm{T}}$ on the right. Meanwhile, define $\mathsf{\Pi }\left(p\right)=\zeta G^{-1}\left(p\right)$, $K\left(p\right)=S\left(p\right)Y^{-1}\left(p\right)$ and $\mathrm{\Phi }\left(p\right)=\zeta X^{-1}\left(p\right)$. We can get

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}{\mathfrak{M}}_6^{(1,1)}& \ast \\ {\mathfrak{M}}_6^{(2,1)}& {\mathfrak{M}}_6^{(2,2)}\end{array}\right]\le 0,\hfill \end{array}$$

(48)

where

$$\begin{array}{cc}\hfill & {\mathfrak{M}}_6^{(1,1)}=\mathrm{diag}\{-(1-ϵ)Y^{\mathrm{T}}\left(p\right)X^{-1}\left(p\right)Y\left(p\right),-{\xi }_4{Y}^{\mathrm{T}}\left(p\right)G^{-1}\left(p\right)Y\left(p\right),-{\displaystyle \frac{ϵ}{\overline{w}}}I\},\hfill \\ \hfill & {\mathfrak{M}}_6^{(2,1)}=\left[\begin{array}{ccc}AY\left(p\right)+BS\left(p\right)& -BS\left(p\right)& \zeta F\\ \sqrt{{\xi }_3}Y\left(p\right)& 0& 0\end{array}\right],\hfill \\ \hfill & {\mathfrak{M}}_6^{(2,2)}=\mathrm{diag}\{-X\left(p\right),-G\left(p\right)\}.\hfill \end{array}$$

Noting that $-Y^{\mathrm{T}}\left(p\right)X^{-1}\left(p\right)Y\left(p\right)\le X\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right)$ and $-Y^{\mathrm{T}}\left(p\right)G^{-1}\left(p\right)Y\left(p\right)\le G\left(p\right)-Y\left(p\right)-Y^{\mathrm{T}}\left(p\right)$, we can show that (43) ensures (48). Then, we conclude that (44) is ensured by (43). Finally, (20) is guaranteed by (42) and (43). Theorem 2 is proven.    □

Leveraging Theorems 1 and 2, $O{P}_2$ can be transformed into

$$\begin{array}{cc}\hfill & O{P}_3:\underset{K\left(p\right)}{\min }\zeta \hfill \\ \hfill \mathrm{s}.\mathrm{t}.\left(29\right),& \left(30\right),\left(31\right),\left(42\right),\left(43\right).\hfill \end{array}$$

(49)

Based on $O{P}_3$, we give the following Algorithm 1 to design a CPS-dependent mixed time/event-triggered MPC controller.

Algorithm 1: MTETM-based MPC for system (16)

Step 1. At $p=0$, set the initial state $x_i\left(0\right)$, set the scalars ${\rho }_1,{\rho }_2$, ${\xi }_1$, ${\xi }_2$, ${\overline{\xi }}_3$, ${\xi }_4$, $\nu$, ${\eta }_1,{\eta }_2,\overline{w},$$ϵ,\theta \left(0\right)$ and the matrices L and P. Step 2. If $CPS\left(p\right)\le 0$ and the event-triggered condition in the MTETM (12) is satisfied, update $x\left(s_m\right)$ with $x\left(p\right)$. Conversely, if $CPS\left(p\right)>0$, update $x\left(s_m\right)$ with $x\left(p\right)$. If $CPS\left(p\right)\le 0$ and event-triggered condition in the MTETM (12) is not satisfied, implement $x\left(s_m\right)$ on the controller. Step 3. Solve $O{P}_3$ to obtain the feedback gain matrix $K\left(p\right)$, and the matrix $\mathsf{\Pi }\left(p\right)$, and then calculate $u\left(p\right)$ by (15). Step 4. Apply $u\left(p\right)$ to system (8). Set $p=p+1$ and return to Step 2.

3.3. Recursive Feasibility and Stability Analysis

Theorem 3.

Given the initial state $x\left(0\right)$, scalars ${\rho }_1$, ${\rho }_2$, ${\xi }_1$, ${\xi }_2$, ${\xi }_3$, ${\xi }_4$, ν, $\theta \left(0\right)$ and matrices Ξ, L and P, $O{P}_3$ remains feasible at $t>p$ when it is feasible at p. Moreover, under the designed MPC controller, system (16) is ISS.

Proof. 

(1) The proof of recursive feasibility.

For $O{P}_3$, (42) depends on the time-varying variables $\theta \left(p\right)$ and $x\left(p\right)$. Let us prove that if $O{P}_3$ is feasible at p. It is also feasible at $p+1$. Considering that $\mathsf{\Gamma }$ is a PIS, the vector $[x^{\mathrm{T}}(1,p),{\theta }^{{\displaystyle \frac{1}{2}}}(1,p){]}^{\mathrm{T}}$ is contained within $\mathsf{\Gamma }$. Furthermore, noting that $\zeta \left(p\right){\mathrm{\Phi }}^{-1}\left(p\right)=X\left(p\right)$, it follows from (21) that

$$\begin{array}{c}\hfill x^{\mathrm{T}}(p+1){X^{★}}^{-1}\left(p\right)x(p+1)+{\displaystyle \frac{\theta (p+1)}{{\zeta }^{★}\left(p\right)}}\le 1.\end{array}$$

(50)

Set $X(p+1)=X^{★}\left(p\right)$, $\zeta (p+1)={\zeta }^{★}\left(p\right)$, where the notation with ’★’ denotes the optimal solution to an OP. Then, it is easy to conclude that (42) is feasible at $p+1$.

(2) The proof of stability.

We give the following definition:

$$\begin{array}{c}\hfill V_{ISS}(x\left(p\right),\theta \left(p\right))=x^{\mathrm{T}}\left(p\right){\mathrm{\Phi }}^{★}\left(p\right)x\left(p\right)+\theta \left(p\right).\end{array}$$

(51)

Define $\mathfrak{X}\left(p\right)=[x^{\mathrm{T}}\left(p\right),{\theta }^{{\displaystyle \frac{1}{2}}}\left(p\right){]}^{\mathrm{T}}$ and $\mathcal{Z}\left(p\right)=\mathrm{diag}\{{\mathrm{\Phi }}^{★}\left(p\right),I\}$. Based on (51), it can be deduced that

$$\begin{array}{cc}\hfill & V_{ISS}\left(\mathfrak{X}\left(p\right)\right)={\mathfrak{X}}^{\mathrm{T}}\left(p\right)\mathcal{Z}\left(p\right)\mathfrak{X}\left(p\right),\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill & c_{min}{\left(\mathcal{Z}\left(p\right)\right)\parallel \mathfrak{X}\left(p\right)\parallel }^2\le V_{ISS}\left(\mathfrak{X}\left(p\right)\right)\le c_{max}\left(\mathcal{Z}\left(p\right)\right){\parallel \mathfrak{X}\left(p\right)\parallel }^2.\hfill \end{array}$$

(53)

In (53), $c_{min}\left(\mathcal{Z}\left(p\right)\right)$ and $c_{max}\left(\mathcal{Z}\left(p\right)\right)$ denote the minimum eigenvalue and the maximum eigenvalue of $\mathcal{Z}\left(p\right)$, respectively. By noting (9), we obtain from (29) that

$$\begin{array}{cc}\hfill & x^{\mathrm{T}}(1,p){\mathrm{\Phi }}^{★}\left(p\right)x(1,p)+\theta (1,p)-x^{\mathrm{T}}\left(p\right){\mathrm{\Phi }}^{★}\left(p\right)x\left(p\right)-\theta \left(p\right)\hfill \\ \hfill & \le -{\parallel x\left(p\right)\parallel }_L^2-{\parallel u\left(p\right)\parallel }_P^2+\nu {\parallel w\left(p\right)\parallel }^2\hfill \\ \hfill & \le -{\parallel x\left(p\right)\parallel }_L^2+\nu {\parallel w\left(p\right)\parallel }^2\hfill \end{array}$$

(54)

In (54), ${\mathrm{\Phi }}^{★}\left(p\right)$ is a feasible solution. With $x(p+1)=x(1,p)$, $\mathrm{\Phi }(p+1)={\mathrm{\Phi }}^{★}\left(p\right)$ and $\theta (p+1)=\theta (1,p)$, we can obtain

$$\begin{array}{cc}\hfill & x^{\mathrm{T}}(p+1){\mathrm{\Phi }}^{★}(p+1)x(p+1)+\theta (p+1)-x^{\mathrm{T}}\left(p\right){\mathrm{\Phi }}^{★}\left(p\right)x\left(p\right)-\theta \left(p\right)\hfill \\ \hfill & \le -{\parallel x\left(p\right)\parallel }_L^2+\nu {\parallel w\left(p\right)\parallel }^2.\hfill \end{array}$$

(55)

Setting $\mathfrak{N}=\mathrm{diag}\{L,0\}$, (55) can be rewritten as

$$\begin{array}{cc}\hfill & {\mathfrak{X}}^{\mathrm{T}}(p+1)\mathcal{Z}(p+1)\mathfrak{X}(p+1)-{\mathfrak{X}}^{\mathrm{T}}\left(p\right)\mathcal{Z}\left(p\right)\mathfrak{X}\left(p\right)\hfill \\ \hfill & \le -{\parallel \mathfrak{X}\left(p\right)\parallel }_{\mathfrak{N}}^2+\nu {\parallel w\left(p\right)\parallel }^2.\hfill \end{array}$$

(56)

Noting (52), (56) can be rewritten as

$$\begin{array}{c}\hfill V_{ISS}\left(\mathfrak{X}(p+1)\right)-V_{ISS}\left(\mathfrak{X}\left(p\right)\right)\le -{\parallel \mathfrak{X}\left(p\right)\parallel }_{\mathfrak{N}}^2+\nu {\parallel w\left(p\right)\parallel }^2.\end{array}$$

(57)

Observing that (53) and (57) satisfy the two conditions specified in Definition 2, we have proved that system (16) is ISS under Algorithm 1. □

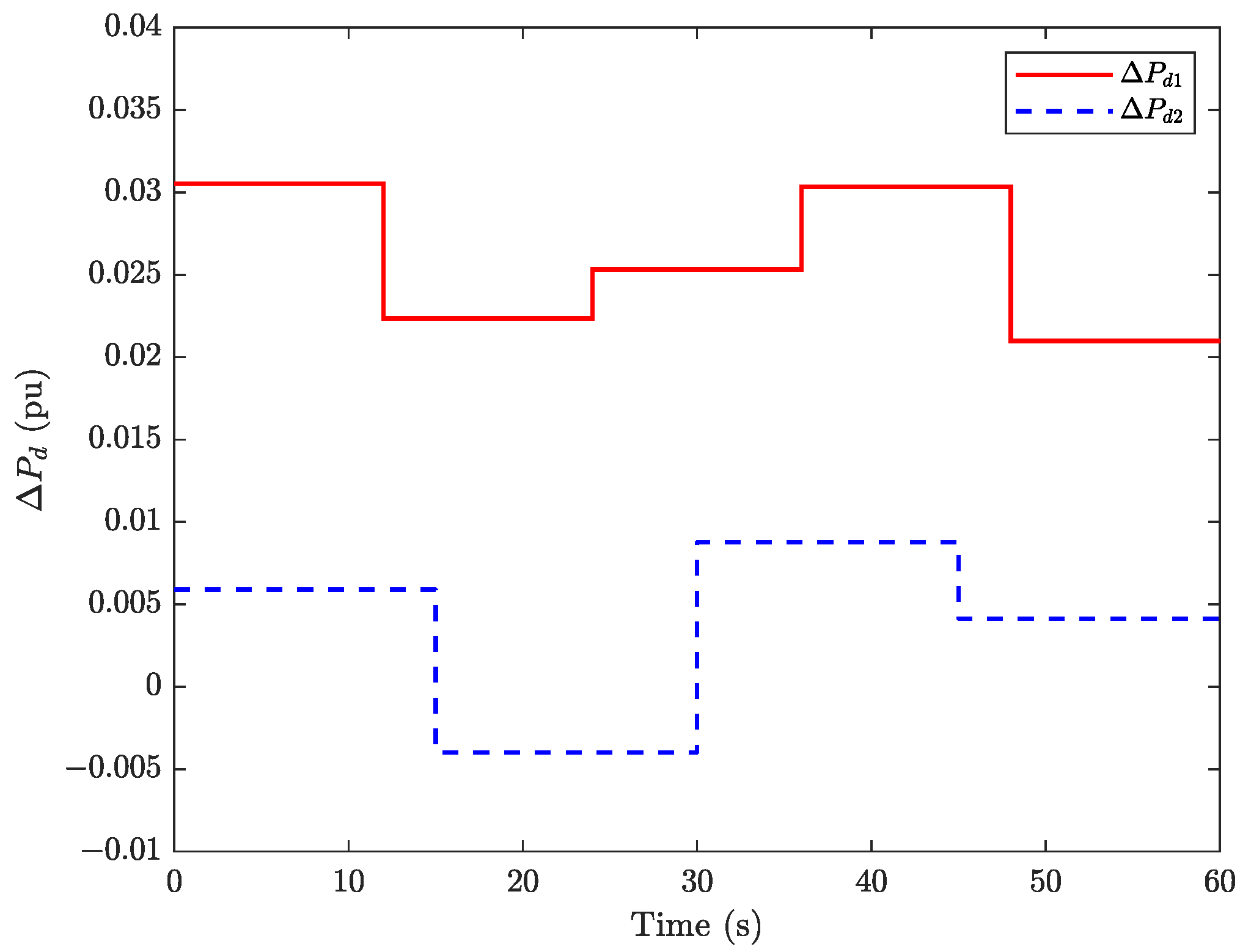
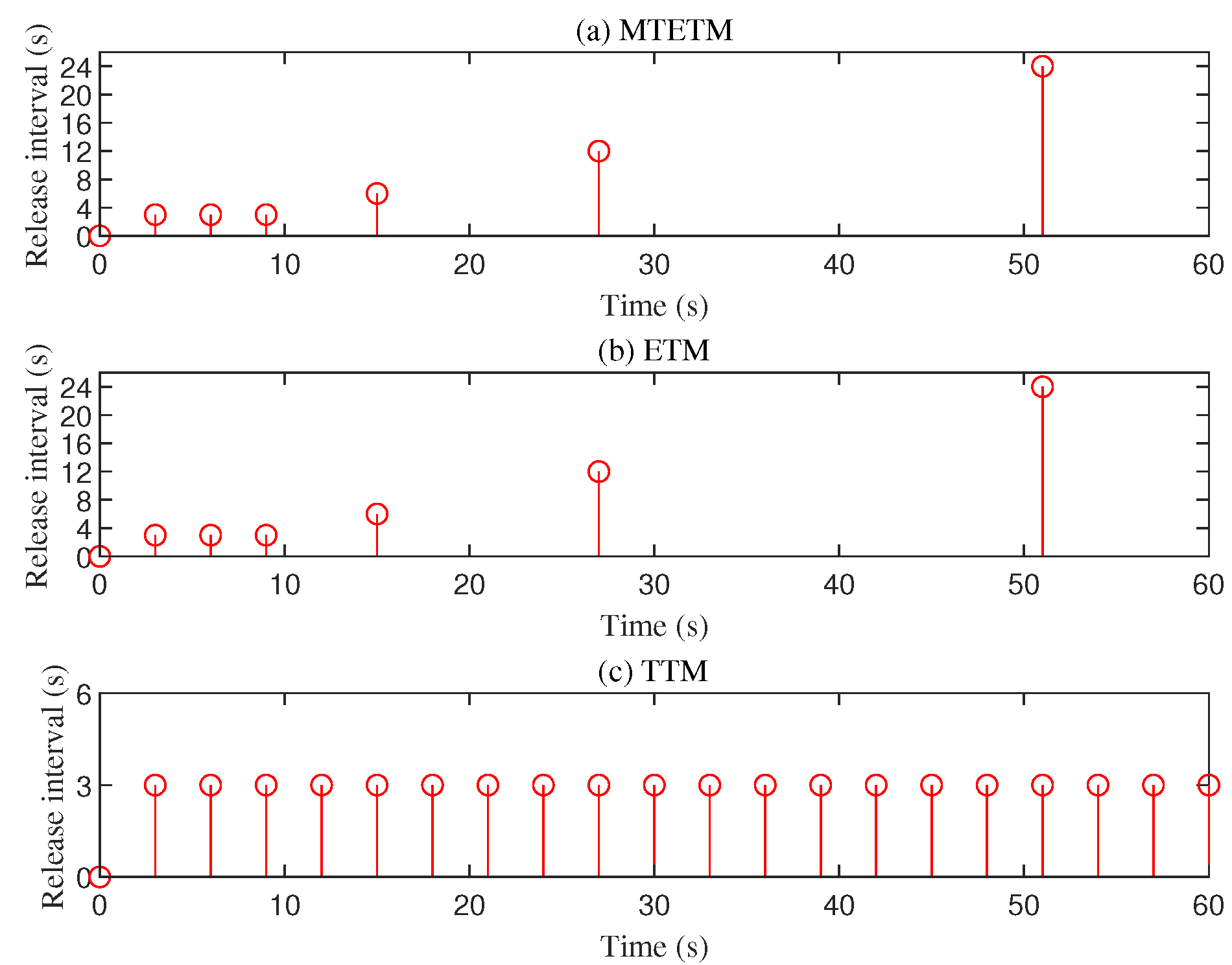
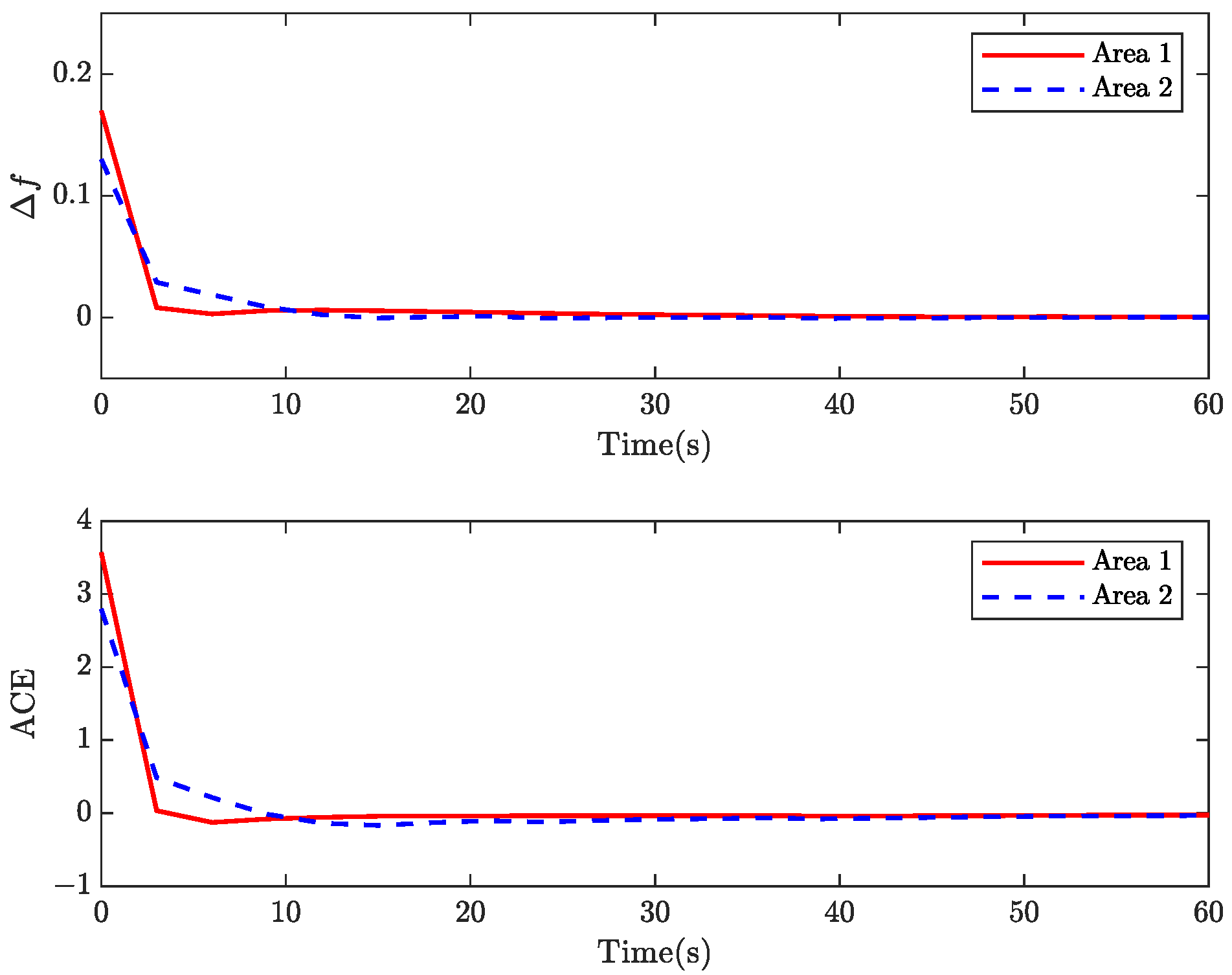
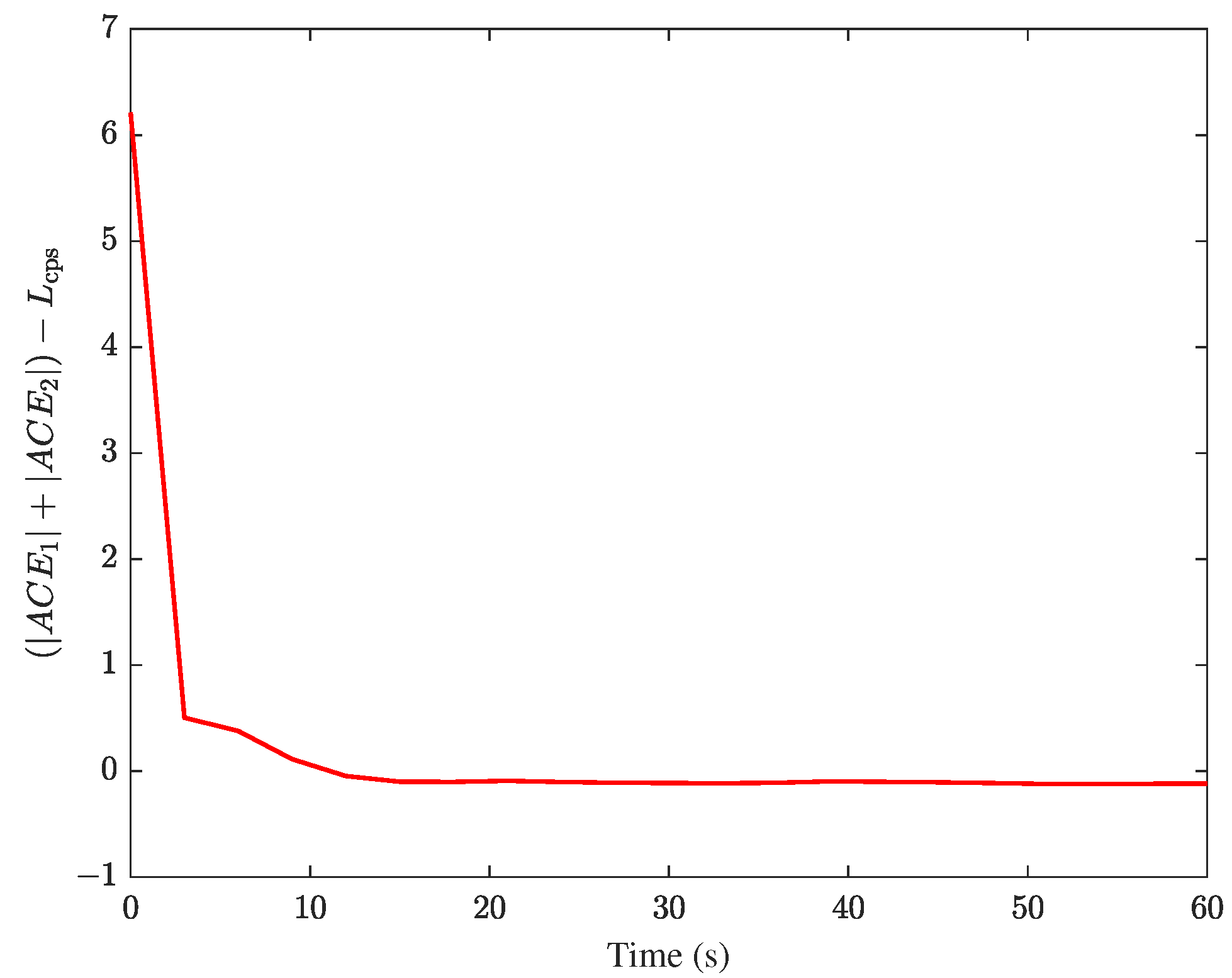
4. Case Analysis

To verify the effectiveness of the MTETM-based MPC method, a two-area LFC system model is built. Each area is provided with a VPP that integrates wind power, ESS, photovoltaic power and EV. The system parameters in

Table 1. Parameters of the two-area LFC scheme.

Parameter	${\mathit{T}}_{\mathbf{chi}}$	${\mathit{T}}_{\mathbf{gi}}$	${\mathit{R}}_{\mathit{i}}$	${\mathit{D}}_{\mathit{i}}$	${\mathit{\beta }}_{\mathit{i}}$	${\mathit{M}}_{\mathit{i}}$
Area 1	0.30	0.37	0.05	1.0	21	10
Area 2	0.17	0.4	0.05	1.5	21.5	12
$T_{12}=T_{21}=0.2$,    ${\alpha }_{Gi}=0.7,{\alpha }_{Vi}=0.3$

are borrowed from [41], and the system parameters in

Table 2. Parameters of the VPP.

VPP	${\mathit{T}}_{\mathbf{ESSi}}$	${\mathit{K}}_{\mathbf{ESSi}}$	${\mathit{T}}_{\mathbf{WTi}}$	${\mathit{T}}_{\mathbf{PVi}}$	${\mathit{T}}_{\mathbf{EVi}}$
Area 1	0.1	0.3	1.5	1.3	1.0
Area 2	0.2	0.3	1.7	1.5	1.1

are partly borrowed from [42].

Set the hard constraint $\overline{x}={[3,2,3,2,5,8,5,4,4,3,3,2,5,8,5,4,4]}^{\mathrm{T}}$, $\overline{w}=0.1$ and $\Xi =I$, the initial state $x_1\left(0\right)={[0.17,0,0,0,0,0.01,0.02,0.01,0.02]}^{\mathrm{T}}$ and $x_2\left(0\right)={[0.13,0,0,0,0,0.01,0.02,0.01,0.02]}^{\mathrm{T}}$, and the parameters ${\rho }_1=1$, ${\rho }_2=0.05$, ${\xi }_1=0.05$, ${\xi }_2=10$, ${\xi }_3=0.1$, ${\xi }_4=0.4$, $\nu =3$, ${\eta }_1=0.01$, ${\eta }_2=0.01$, $ϵ=0.9$, $\theta \left(0\right)=0.5$. Set the discretisation period $T_p=3$ s, the weight matrixes $L=50I$ and $P=0.1I$. For disturbances in VPP, set $\Delta U_{EV1}=\Delta U_{EV2}=\Delta P_{SOLAR1}=\Delta P_{SOLAR2}=0.001$ pu, $\Delta P_{WIND1}=\Delta P_{WIND2}=0.002$ pu.

We assume that random load disturbances occur within the initial 60 s, and $\Delta P_{d1}$ and $\Delta P_{d2}$ in the two areas are illustrated in Figure 2.

Figure 3a presents the triggering instants and release intervals of MTETM and Figure 4 shows the variation trajectories of $\Delta f$ and $ACE$. Figure 3a and Figure 4 indicate that the MPC algorithm based on MTETM saves packet transmissions while achieving desired control performance.

To demonstrate the advantages of the MTETM design, comparative experiments are conducted to evaluate the performance of the MPC algorithm based on this mechanism against MPC algorithms employing pure ETM and pure TTM. When ${\eta }_1$ is set sufficiently large such that $CPS\left(p\right)<0$, an ETM-based MPC algorithm is obtained; when ${\eta }_1$ is set sufficiently small such that $CPS\left(p\right)>0$, a TTM-based MPC algorithm is obtained. Figure 3b,c, respectively, illustrates the release intervals for ETM and TTM.

Table 3. TRs under different triggering mechanisms.

	MTETM (12)	ETM	TTM
TRs	33.3%	33.3%	100%

enumerates the triggering rates (TRs) under different triggering mechanisms. In

Table 4. Performance comparison of different algorithms.

Performance Criteria	SAE	SSE	STSE	STAE
MTETM (12)-based MPC	28.143	63.131	16.462	201.98
ETM-based MPC	34.29	68.736	54.804	244.34
TTM-based MPC	27.958	63.135	16.38	188.47

, the performance criteria of MPC algorithms regarding three triggering mechanisms are given, where $\mathrm{SAE}={\sum }_{k=0}^{T_s/T_p}{T}_p\left(\right|AC{E}_1|+|AC{E}_2\left|\right), \mathrm{SSE}={\sum }_{k=0}^{T_s/T_p}{T}_p\left(\right|AC{E}_1{|}^2+|AC{E}_2{|}^2), \mathrm{STAE}={\sum }_{k=0}^{T_s/T_p}k{T}_p^2\left(\right|AC{E}_1|+|AC{E}_2\left|\right), \mathrm{STSE}={\sum }_{k=0}^{T_s/T_p}k{T}_p^2\left(\right|AC{E}_1{|}^2+|AC{E}_2{|}^2)$ with $T_s=60$ s.

From Table 3 and Table 4 and Figure 3, it can be concluded that MTETM exhibits lower TR compared to TTM. In other words, enabling flexible switching between ETM and pure TTM through the introduction of CPS, the MTETM-based MPC algorithm significantly reduces the TRs while maintaining control performance to some extent. Compared to the MPC algorithm under pure ETM, the CPS-dependent MTETM-based MPC algorithm effectively enhances control performance while maintaining the same low TR. In summary, the proposed MTETM-based MPC algorithm achieves satisfactory control performance while reducing network resource wastage, thereby outperforming the MPC algorithms under the other two triggering mechanisms.

Figure 5 illustrates the evolution of ${\sum }_{i=1}^2\left|AC{E}_i\right|-L_{\mathrm{cps}}$ under the MTETM-based MPC algorithm. Through the MTETM-based MPC algorithm, CPS achieves the target requirement (${\sum }_{i=1}^2\left|AC{E}_i\right|-L_{cps}\le 0$) within 12 s, indicating that the control performance in two areas meets the standard requirements.

5. Model Usability

To fully demonstrate the practical value and application prospects of the proposed LFC system model and the MPC based on MTETM, this section elucidates its applicability in the digitalisation of power system processes and process management, whilst systematically analysing its advantages and limitations.

5.1. Application Analysis

From the perspective of the LFC system model, this study integrates the dynamic characteristics of distributed energy resources such as wind power, photovoltaics, EVs, and ESSs. It characterises the frequency response patterns of different resources through first-order inertia or lag models, adapting the architecture for VVP participation in LFC. Concurrently, this model accommodates the operational characteristics of multi-area interconnected grids, accounting for inter-regional power exchange via interconnectors and coordinated frequency regulation requirements. It is directly applicable to frequency control scenarios within multi-area interconnected power systems. Furthermore, MATLAB R2024b simulations validate its capability to ensure faster frequency stability within two-area systems, effectively countering random load disturbances.

From the perspective of triggering mechanisms, the proposed MTETM achieves flexible switching of triggering mechanisms through CPS$\left(p\right)$. This mechanism is suitable for bandwidth-constrained network environments, effectively reducing redundant communications, alleviating algorithmic computational burdens, and enhancing system robustness under conditions of random load variations and renewable energy fluctuations. Compared to existing triggering mechanisms, it manages packet release more flexibly, effectively lowering the TR. Furthermore, it can be adjusted through parameter tuning to degrade into pure ETM, offering greater versatility. In the context of VPPs utilising information technology to aggregate and synergistically optimise distributed resources, this MTETM effectively resolves network communication congestion issues, thereby safeguarding the real-time operation and reliability of VPPs.

From the perspective of the MPC algorithm, this approach constructs a “min-max” optimisation problem and transforms it into an auxiliary optimisation problem with linear matrix inequality constraints. This problem simultaneously addresses the system’s hard state constraints and input-state stability, achieving effective frequency regulation under random load disturbances. It enables rapid convergence of $\Delta f$ and $ACE$, achieving a low TR at the sacrifice of only a slight reduction in control performance. This approach provides an efficient and reliable LFC strategy for multi-regional VPPs incorporating wind power, ESSs, EVs, and photovoltaic generation. Case analysis indicates that the average computation time for the MPC algorithm at a single sampling instant is $0.688$ s, which is less than the sampling period $T_p=3$ s. This satisfies the requirements for real-time performance and reliability during the digitalisation of industrial systems.

5.2. Advantages and Limitations

The proposed model exhibits the following advantages:

(1) It accurately characterises the dynamic behaviour of power systems incorporating VPPs. By employing MTETM, it excels in balancing active power regulation system control performance with communication resources consumption, maintaining adaptability in simple scenarios while supporting digital transformation.

(2) Compared to conventional single-trigger mechanisms, MTETM reduces communication frequency while maintaining control performance, making it suitable for frequency control scenarios involving large VPP clusters with limited communication resources.

The proposed model has the following limitations:

(1) The designed LFC system model structure is relatively simple, suitable for structurally straightforward LFC systems. While the model does not account for factors such as wind speed and solar irradiance, this leaves scope for future model and algorithm refinement.

(2) The selection of multiple parameters within MTETM relies on system modelling accuracy and expert experience in practical applications. Future developments may explore adaptive parameter tuning schemes based on system requirements.

6. Conclusions

In this study, an MTETM combined with CPS is constructed, and this mechanism reduces the network resource consumption of VPP. To solve the LFC problem with VPP, the LFC system is first modelled, and then the LFC problem is transformed into an MPC problem. The core of the research is to use the OP over an infinite time horizon to explain the MPC problem based on MTETM. To handle this initial optimisation task, an auxiliary OP is proposed. In addition, the original constraints are transformed into the form of linear matrix inequalities, and another auxiliary OP is built. The feasible solution obtained by solving this auxiliary OP enables us to design the corresponding model predictive controller. Moreover, this paper analyses the recursive feasibility of the proposed MTETM-based MPC and the input-to-state stability of the closed-loop system. The case study with random load disturbances shows that the MPC algorithm with MTETM related to CPS has effectiveness and superiority.

The comparison results demonstrate that MTETM can ensure comparable control performance while reducing TR by 66.7% relative to TTM. Additionally, compared to ETM, MTETM achieves superior control performance while maintaining the same TR of 33.3%. These results validate that the MTETM-based MPC algorithm is suitable for addressing the control challenges of VPPs featuring large-scale energy clusters. In the future, we will consider the impact of more fluctuations and cyberattacks on the system to improve the MTETM model and design a new MPC algorithm with high computational efficiency.