Control Methods and AI Application for Grid-Connected PV Inverter: A Review
Abstract
1. Introduction
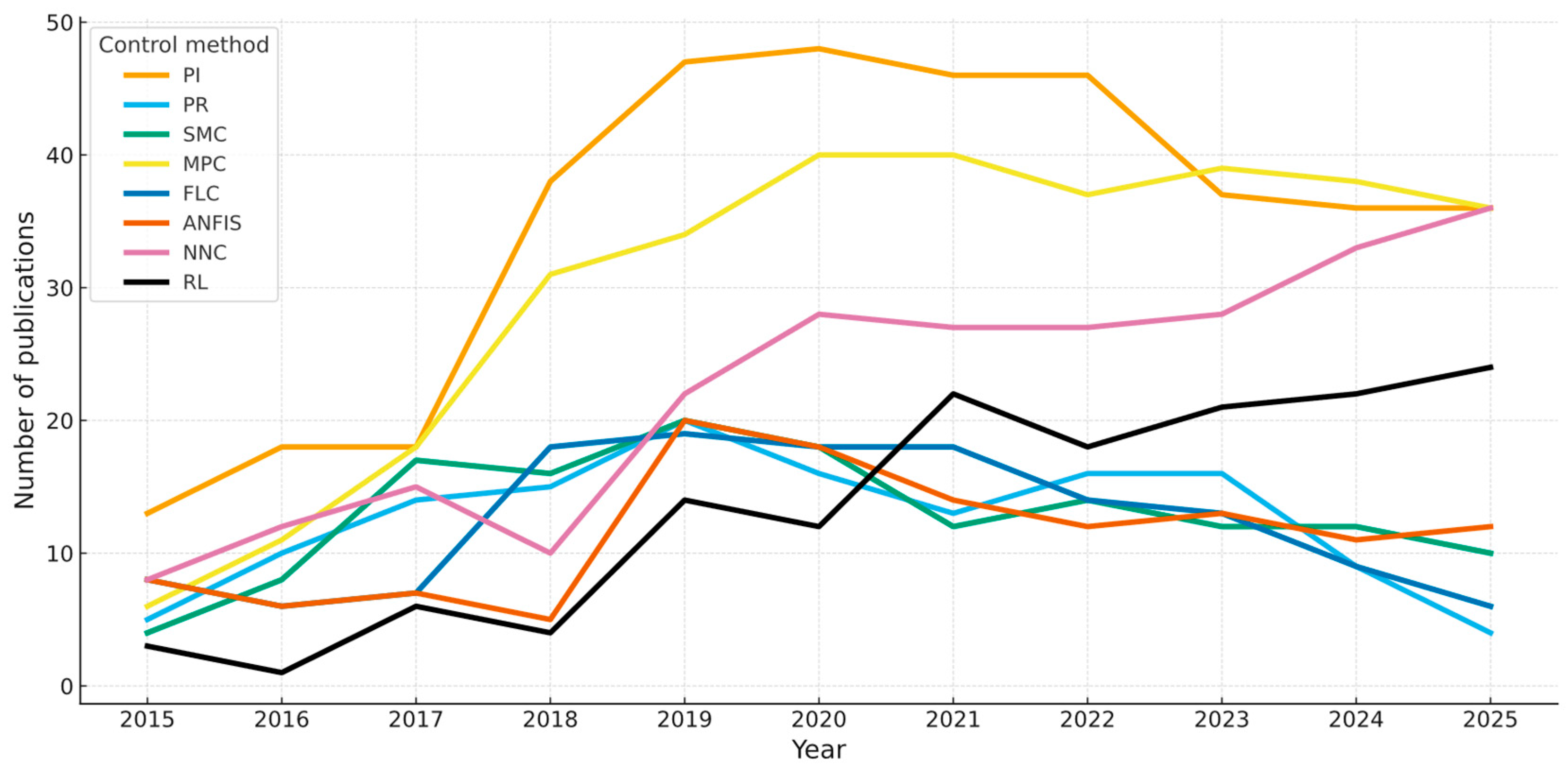
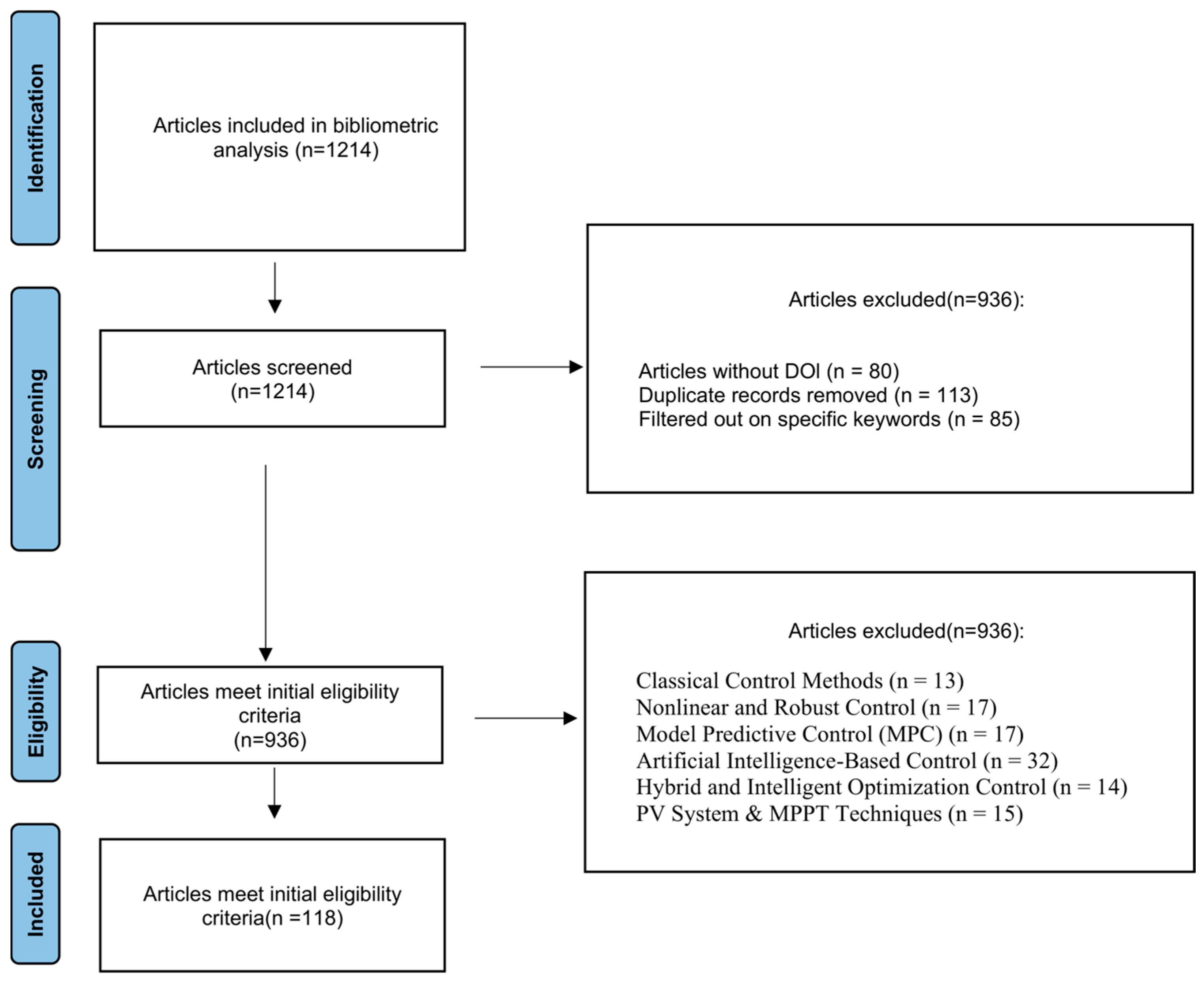
2. Methodology
3. PV Grid-Connected Inverter System
3.1. Photovoltaic System
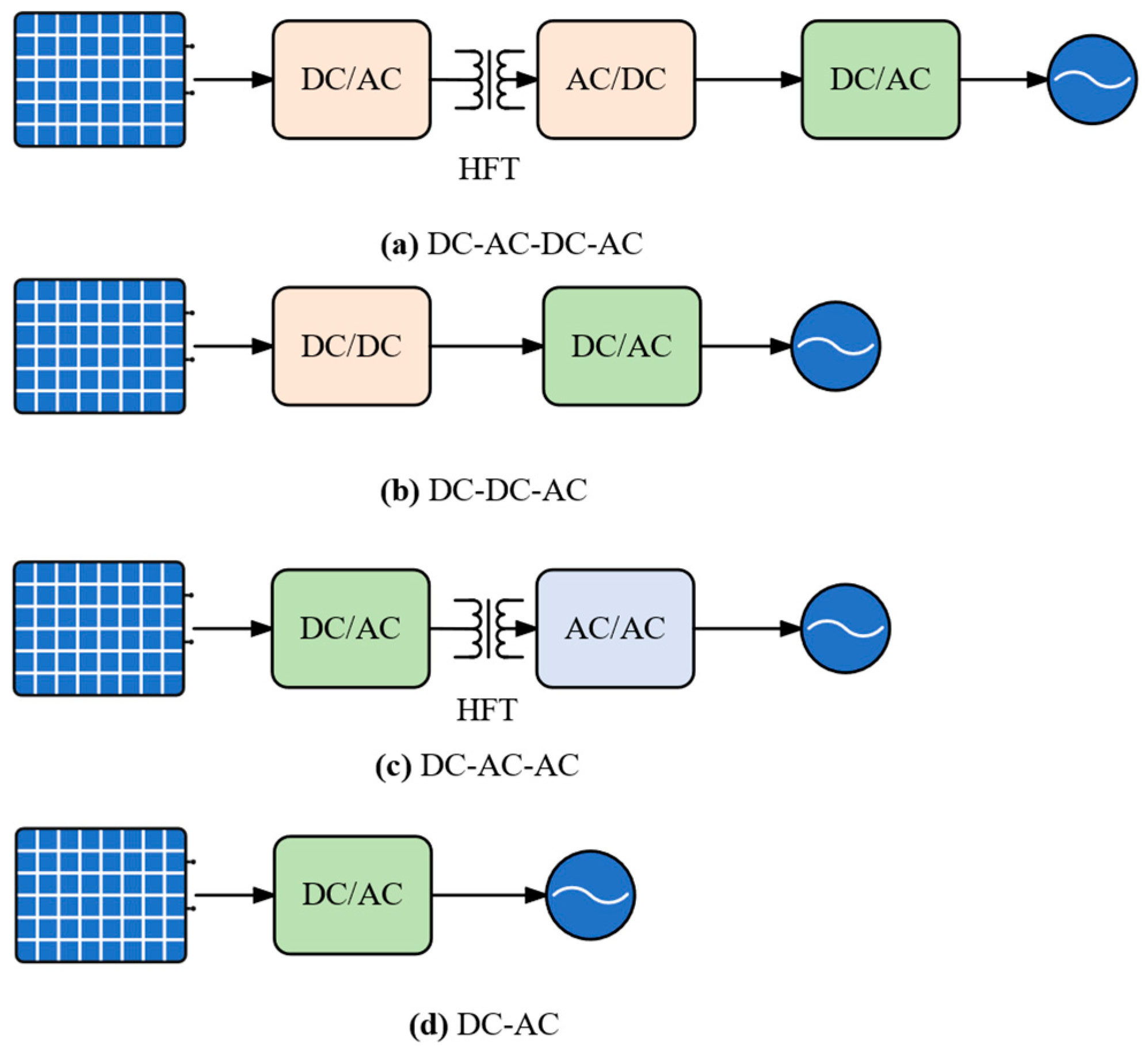
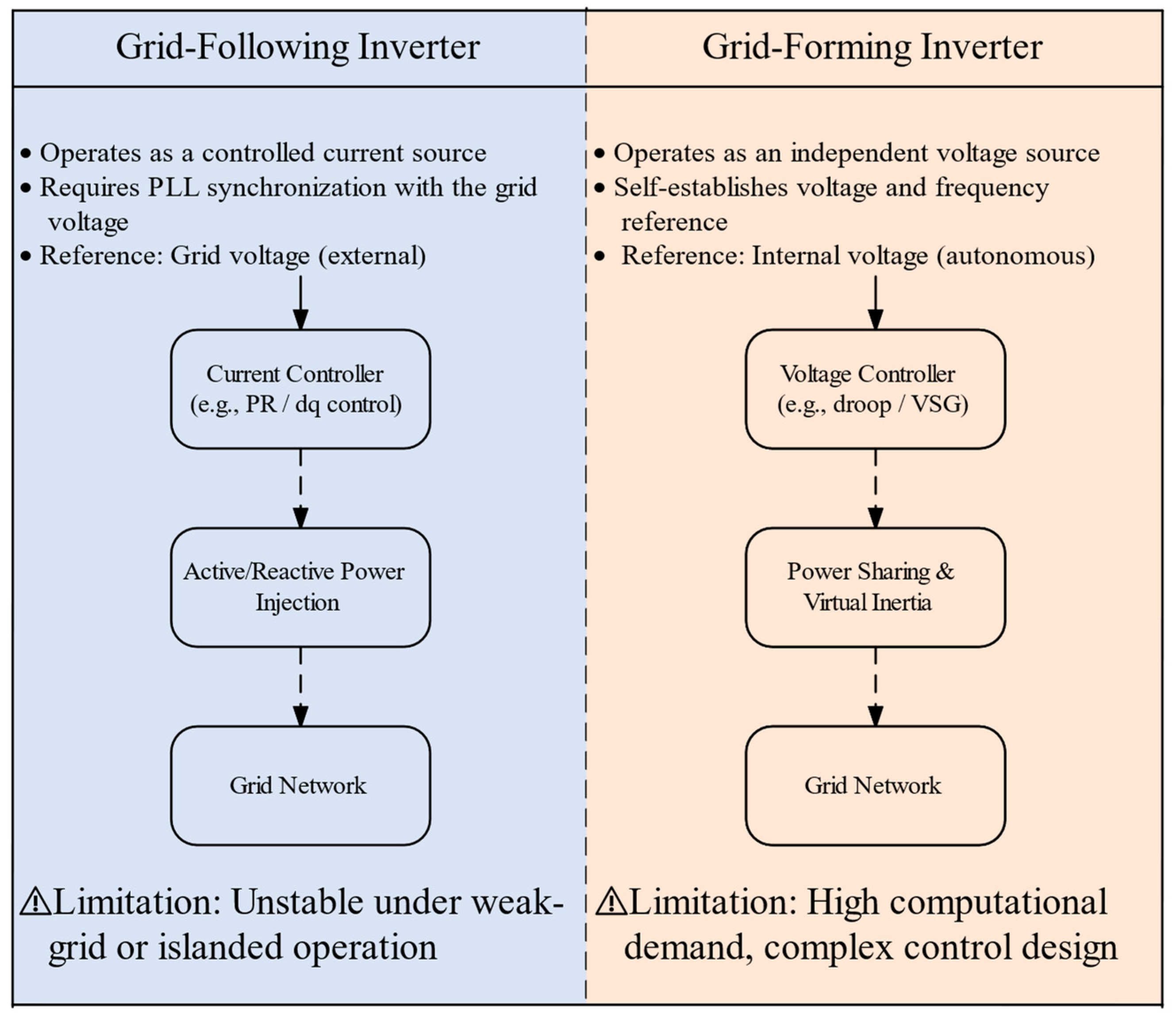
3.2. Grid-Connected Inverter
4. Conventional Control
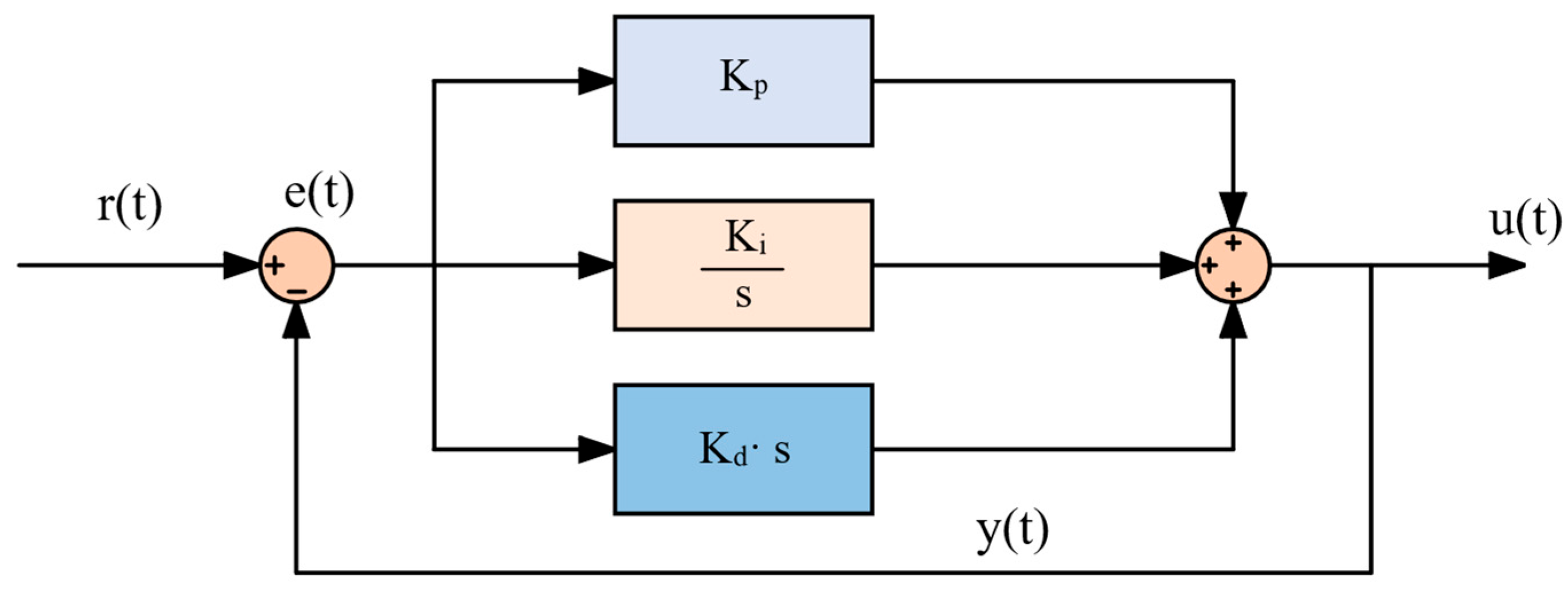
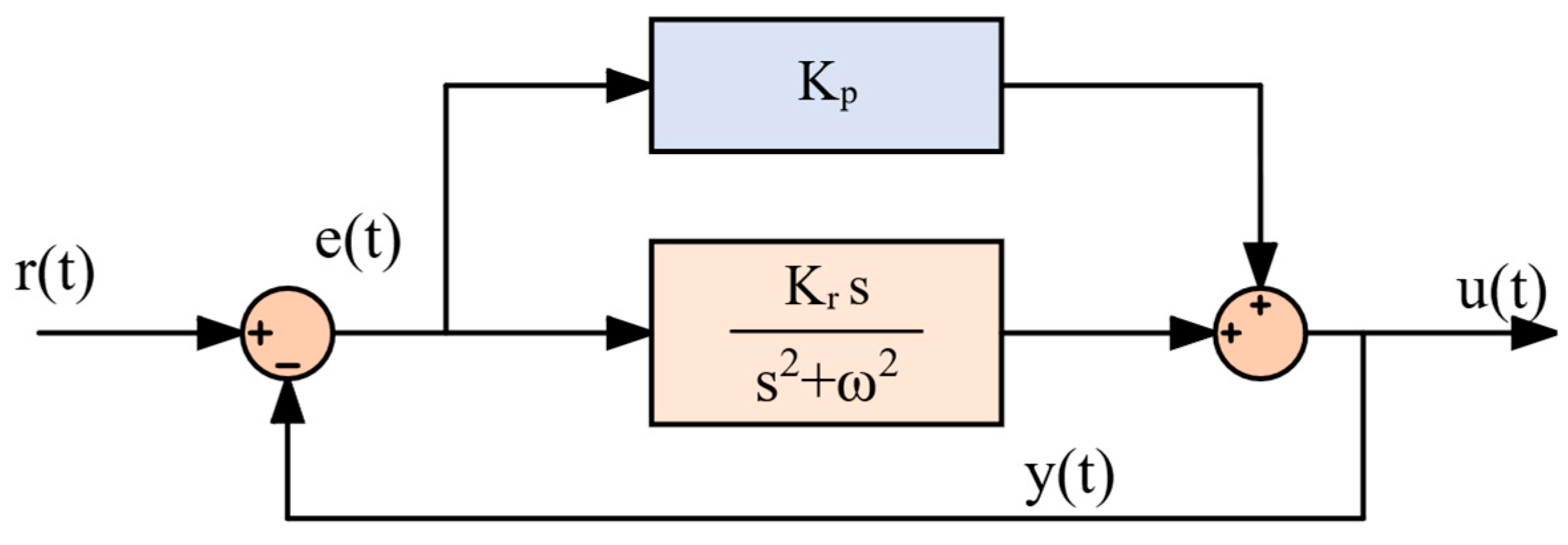
4.1. PID/PR Control
4.2. Sliding Mode Control
4.3. Model Predictive Control
4.4. Comparative Analysis and Technical Limitations of Classic Control Methods
- Robustness, Adaptability, and Model Dependence
- 2.
- Computational and Implementation Constraints
- 3.
- System-Level Performance and Trade-Offs
- PI/PR: High steady-state precision, low cost, but poor dynamic adaptability.
- SMC: Excellent disturbance rejection, good dynamic response, yet chattering-induced energy losses.
- MPC: Optimal transient and harmonic performance, but with high computational burden and model sensitivity.
- 4.
- Collective Technical Limitations
- Limited adaptability: Most require offline tuning and cannot autonomously adjust to real-time grid or load changes.
- High sensitivity to modeling and measurement errors: Even advanced controllers degrade under model mismatch, noise, or communication delay.
- Scalability and computational limits: As PV systems evolve toward multi-inverter, high-bandwidth networks, the computational overhead of model-based or discontinuous control laws becomes a critical bottleneck.
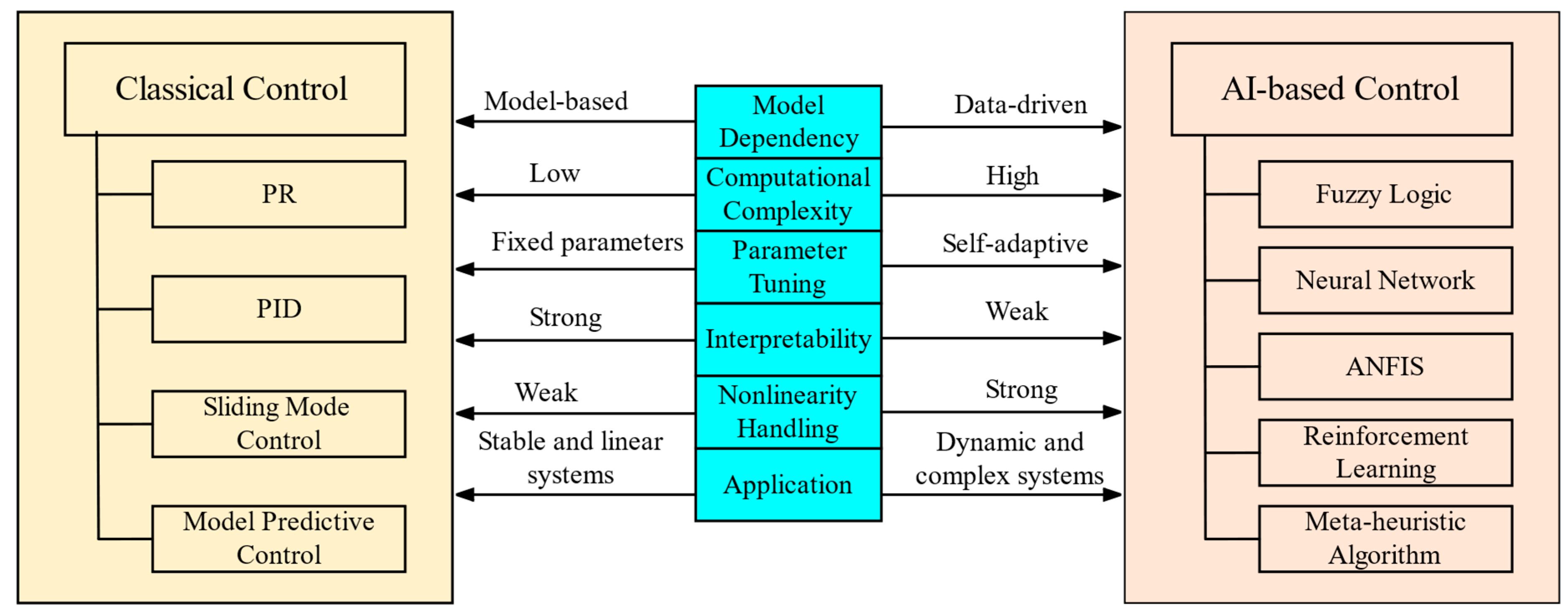
5. AI-Based Control
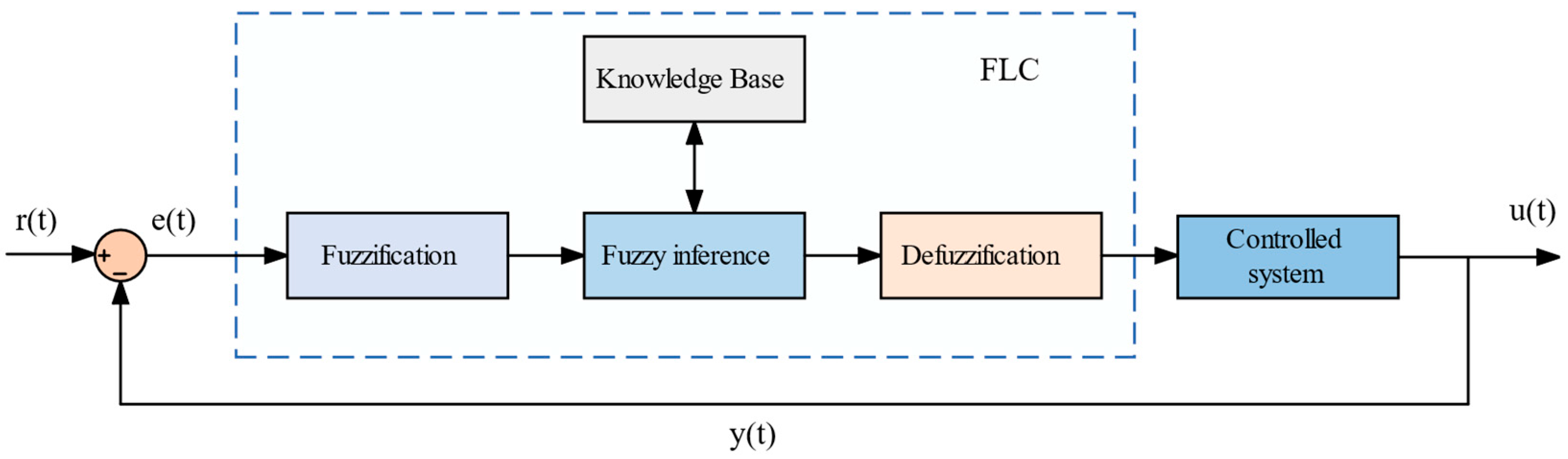
5.1. Fuzzy Logic Control
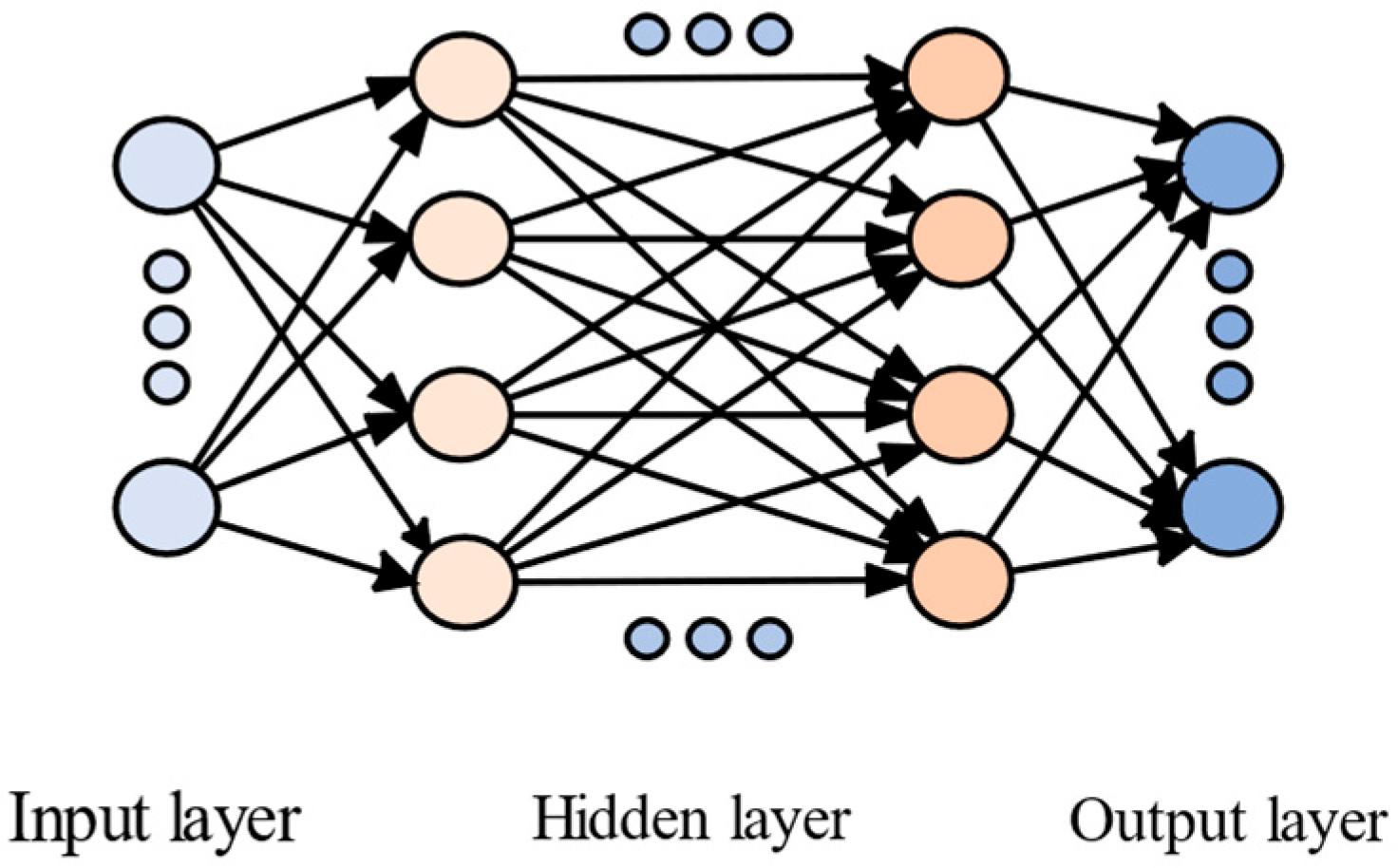
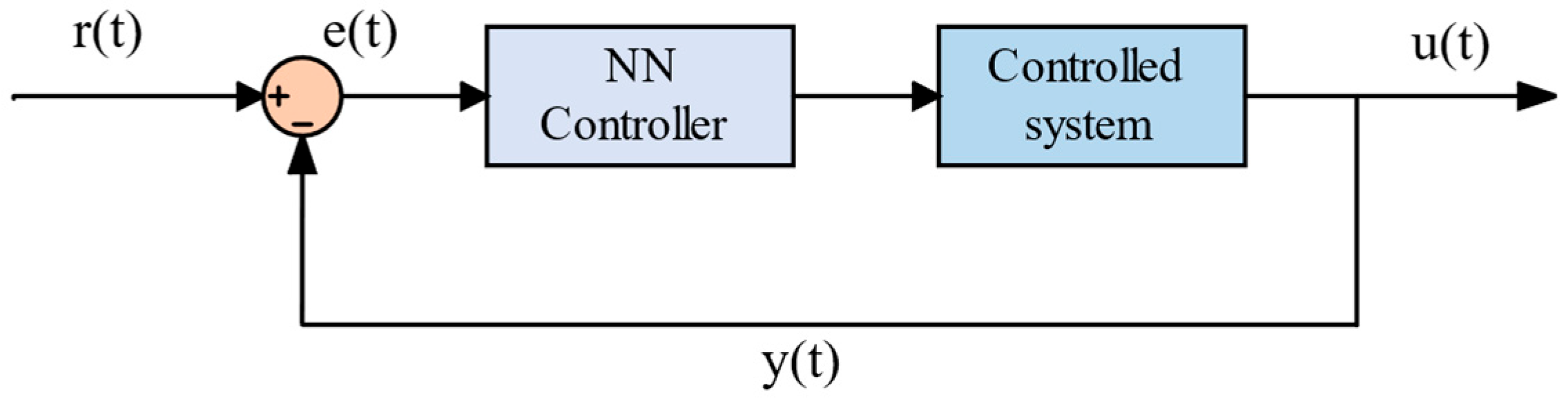
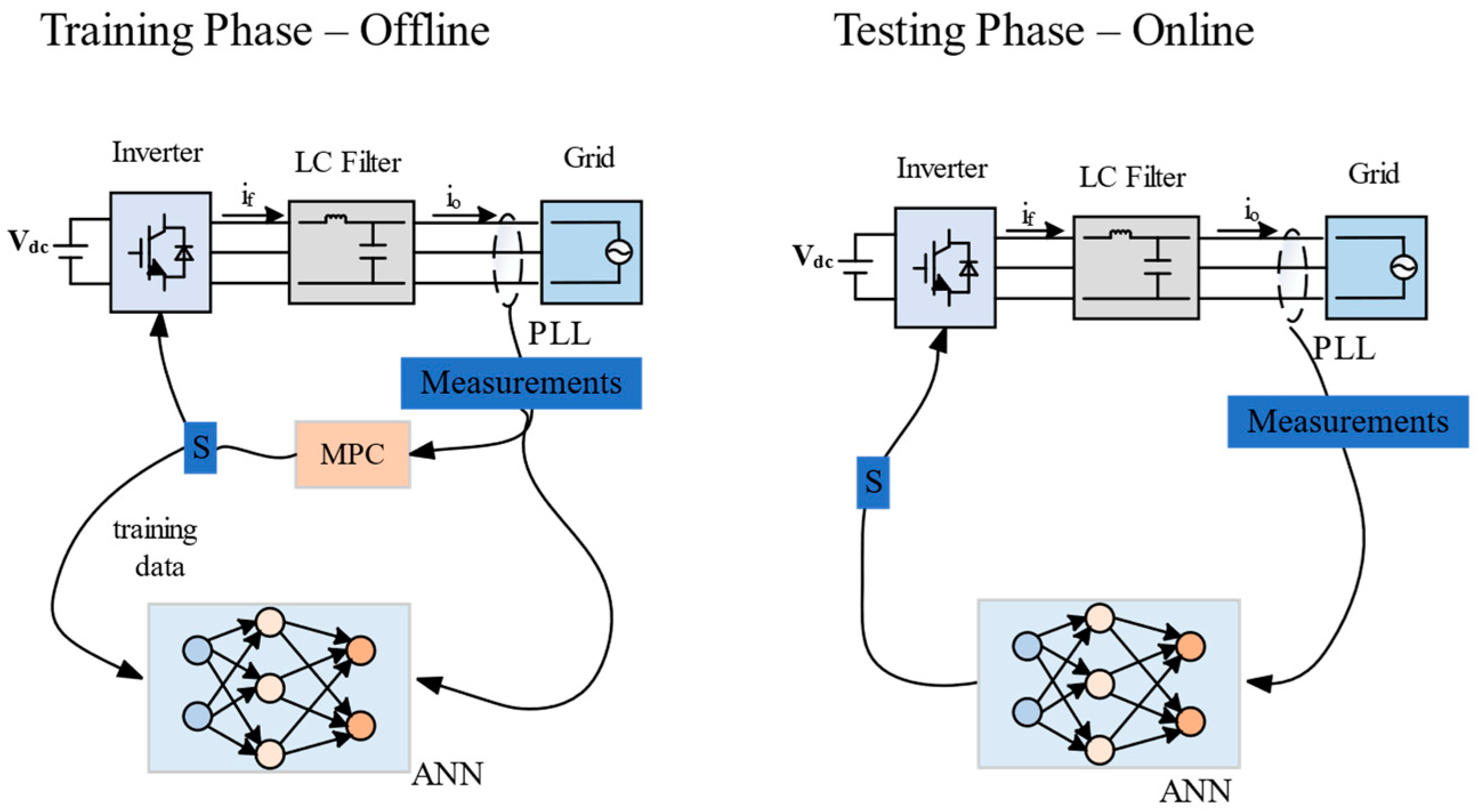
5.2. Neural Network Control
- Data collection—Generate training data using a controller or optimization algorithm to reflect system inputs and corresponding desired outputs.
- Offline training—Train the ANN with the collected data to learn the mapping between inputs and outputs.
- Online testing—Deploy the trained ANN in a real system and evaluate its performance under actual operating conditions.
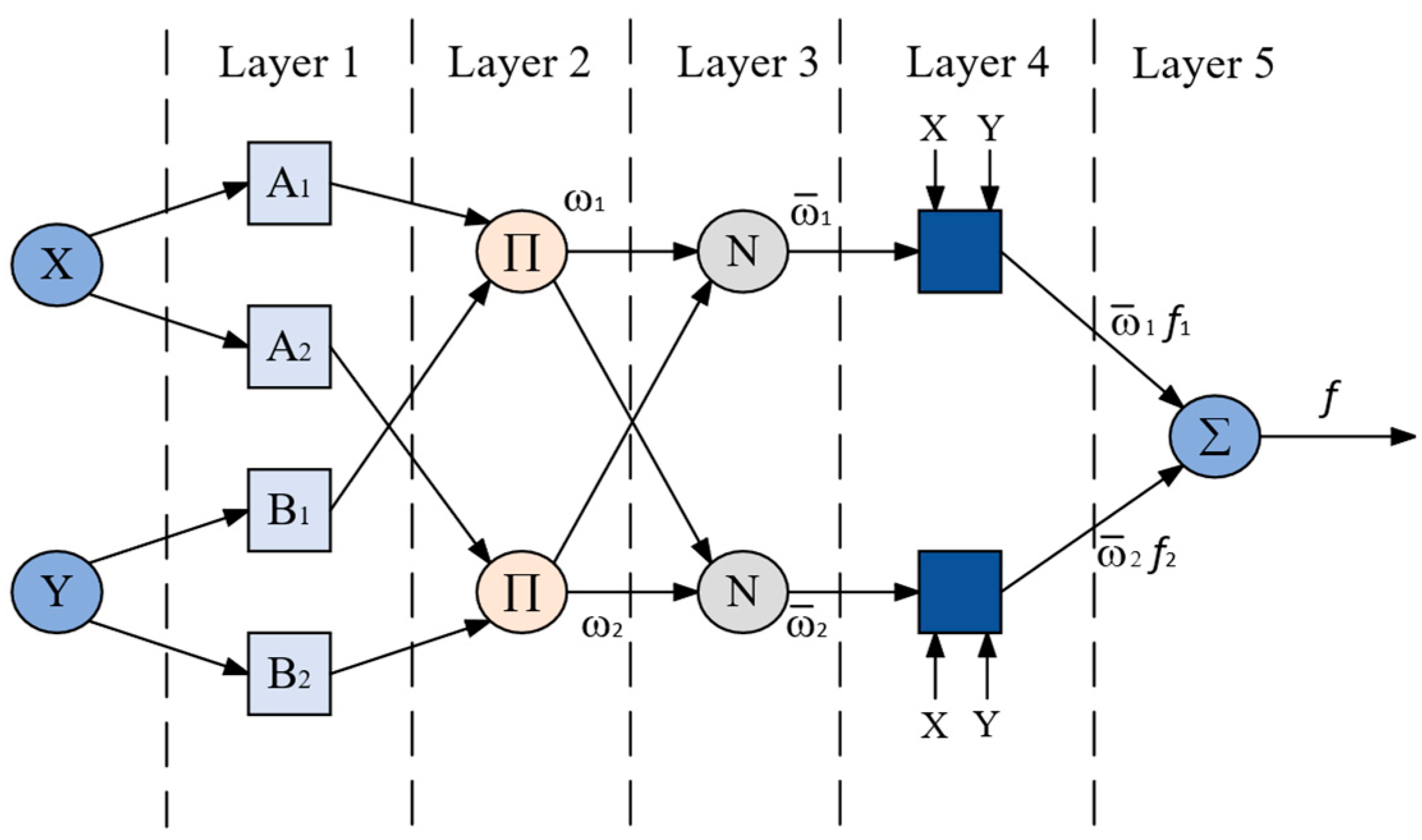
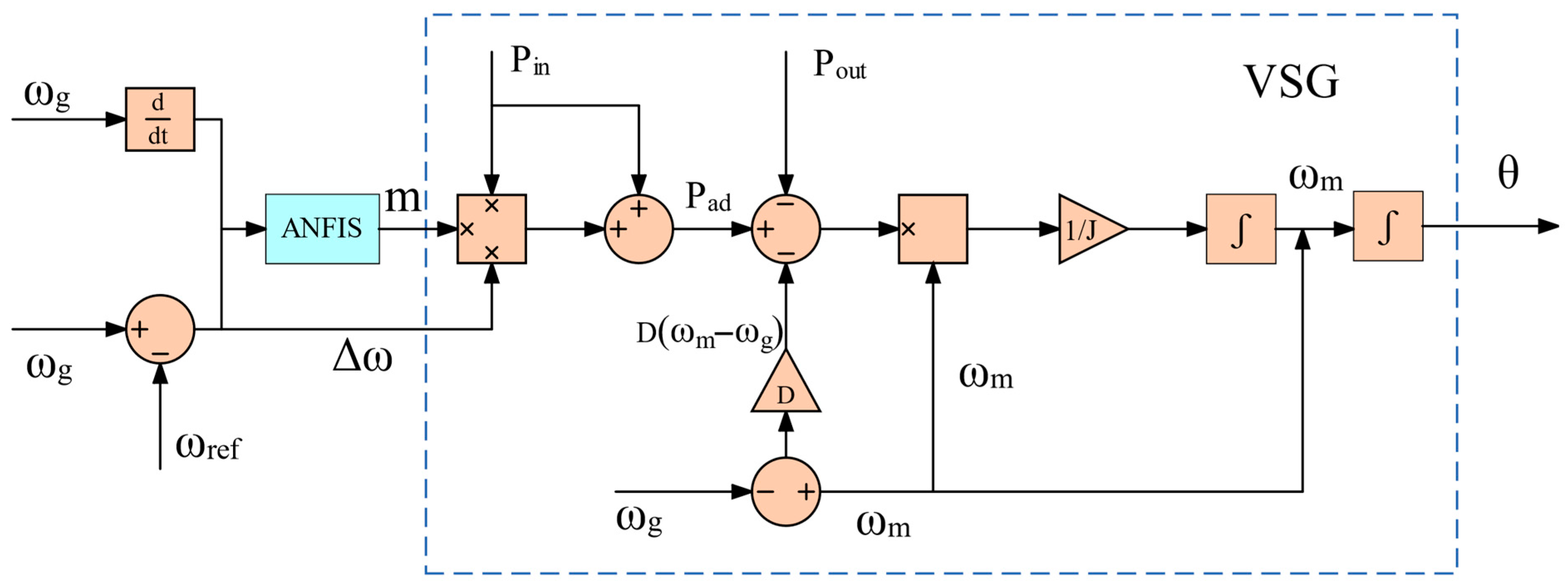
5.3. ANFIS Control
- Input layer: maps input variables to membership degrees.
- Rule layer: computes the firing strength of each rule.
- Normalization layer: normalizes firing strengths to obtain weighting coefficients.
- Consequent layer: produces rule-specific outputs.
- Output layer: aggregates all rule outputs via weighted summation to generate the final system output.
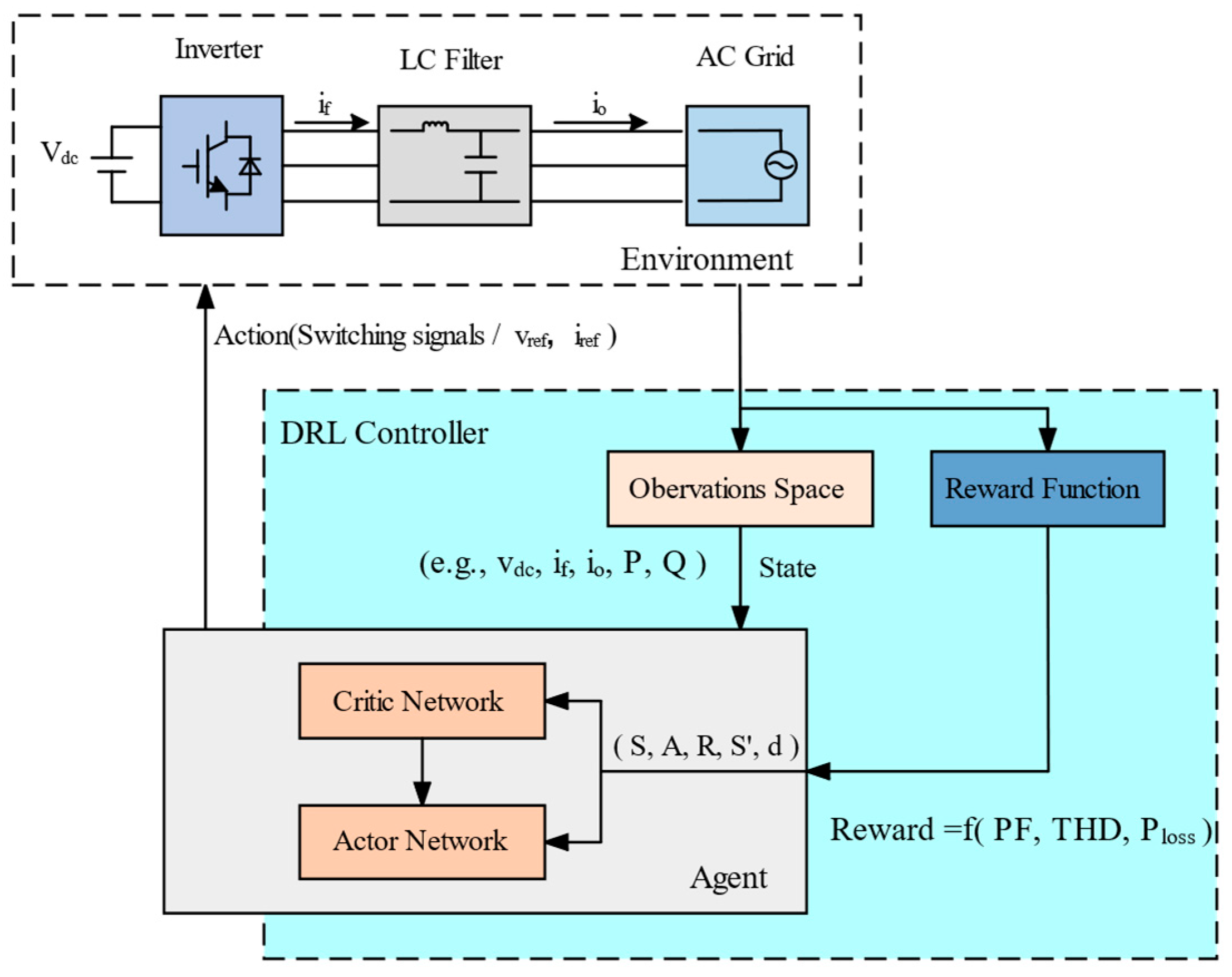
5.4. Reinforcement Learning Control
5.5. Metaheuristic Algorithm Optimization
5.5.1. Particle Swarm Optimization
5.5.2. Genetic Algorithm
5.6. AI-Based Parameter Optimization
5.6.1. Switching-Frequency Optimization
5.6.2. Filter Parameter and Damping Tuning
5.6.3. MPPT Under Partial Shading and Nonuniform Conditions
5.6.4. Power-Quality and Harmonic Regulation
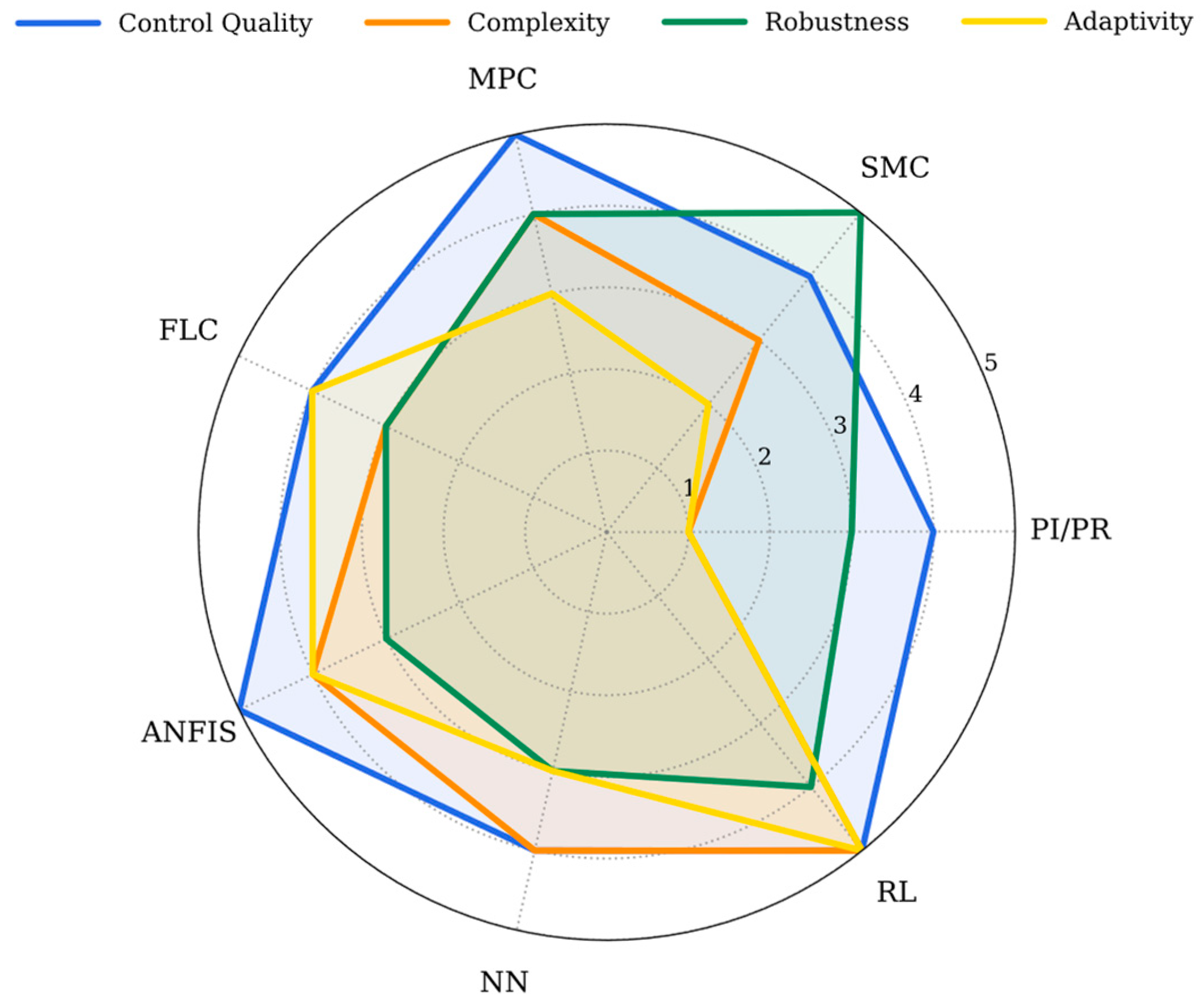
6. Discussion
6.1. Hybrid Control Strategies
6.2. Security and Interpretability of AI-Based Control
- Explainable AI (XAI) for control: Integrating interpretability methods such as sensitivity analysis, feature attribution, and surrogate modeling can reveal how input variables (voltage, current, irradiance) influence AI decisions, enhancing understanding and trust in AI controllers.
- Physics-informed and stability-constrained learning: Embedding physical constraints, Lyapunov functions, or energy-based models into AI training ensures that control actions respect system dynamics and stability boundaries.
- Secure learning and anomaly detection: Implementing adversarial training, fault detection, and cyber-resilient architectures can protect inverter control systems from malicious data injection, communication delays, and false measurements.
- Formal verification frameworks: Applying reachability analysis and formal stability proofs can help certify AI controllers for compliance with grid codes and safety standards.
6.3. Hardware and Real-Time Implementation Requirements
- Computing capability: Many AI controllers need floating-point DSPs, FPGAs, or SoC processors to meet real-time requirements, especially when switching frequencies exceed 10 kHz.
- Sampling time and latency: Stable control requires microsecond-level computation and actuation. AI models must therefore be lightweight, and inference time should be minimized through model simplification or hardware acceleration.
- Memory and storage: Large neural networks and fuzzy systems may exceed the memory capacity of conventional inverter controllers.
- Hardware acceleration and optimization: Quantization, pruning, and compression can reduce computation time and energy use. New edge-AI chips with dedicated neural processing units may help support AI control in commercial inverters.
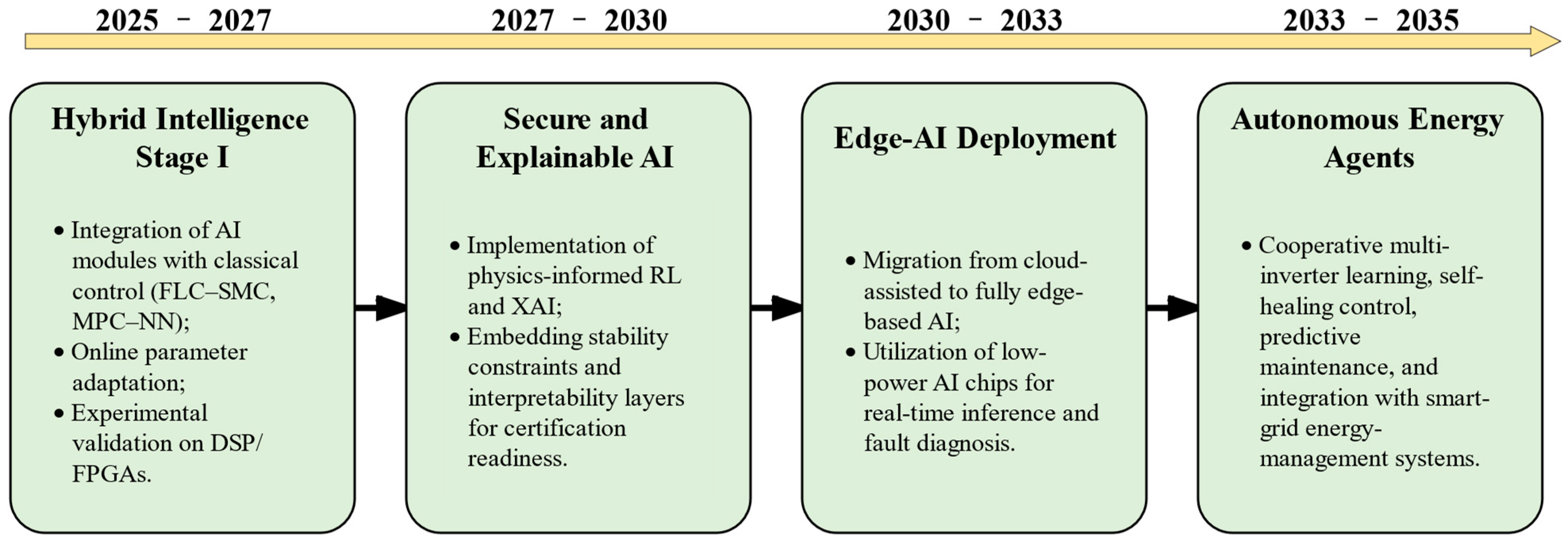
6.4. Emerging and Future Research Trends
- Federated and Collaborative Learning for Distributed PV Systems
- 2.
- Cloud–Edge Cooperative Intelligent Control
- 3.
- Hardware Acceleration and Embedded AI Implementation
- 4.
- Standardization, Safety, and Explainability
- 5.
- Integration with Energy Storage and Multi-Agent Coordination
- 6.
- Cybersecurity and Resilience of Intelligent Inverter Networks
6.5. Summary of Key Insights
- Hybrid control merges physical modeling and data-driven adaptation, achieving both reliability and intelligence.
- Security and interpretability are prerequisites for trusted, grid-compliant AI control.
- Hardware-aware algorithm design ensures real-time implementation on embedded systems.
- Federated and cloud-based architectures will enable large-scale distributed learning and cooperative control among GCPI.
7. Conclusions
- Stable grid environments: Conventional PI/PR and MPC controllers remain the most reliable and cost-effective solutions due to their maturity and simplicity.
- Weak-grid or fluctuating irradiance conditions: AI-based methods, particularly FLC, NN, and ANFIS, offer superior adaptability, improved transient performance, and better harmonic suppression.
- Complex and nonlinear PV system: MPC combined with machine-learning-based weight optimization achieves high accuracy with manageable computational cost.
- Integrated PV–storage and microgrid applications: Hybrid control frameworks (e.g., FLC–SMC, MPC–RL) are the most promising, merging robustness and adaptability for intelligent, autonomous inverter operation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GCPI | Grid-Connected Photovoltaic Inverter |
| PV | Photovoltaic |
| GFLI | Grid-Following Inverter |
| GFMI | Grid-Forming Inverter |
| PID | Proportional–Integral–Derivative |
| PR | Proportional–Resonant |
| SMC | Sliding Mode Control |
| MPC | Model Predictive Control |
| FCS-MPC | Finite Control Set Model Predictive Control |
| CCS-MPC | Continuous Control Set Model Predictive Control |
| FLC | Fuzzy Logic Control |
| NN | Neural Network |
| NNC | Neural Network Control |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| RL | Reinforcement Learning |
| DDPG | Deep Deterministic Policy Gradient |
| TD3 | Twin Delayed Deep Deterministic Policy Gradient |
| PPO | Proximal Policy Optimization |
| MA | Metaheuristic Algorithm |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| PF | Power Factor |
| MPPT | Maximum Power Point Tracking |
| PLL | Phase-Locked Loop |
| VSG | Virtual Synchronous Generator |
| HIL | Hardware-in-the-loop |
References
- Schleussner, C.-F.; Rogelj, J.; Schaeffer, M.; Lissner, T.; Licker, R.; Fischer, E.M.; Knutti, R.; Levermann, A.; Frieler, K.; Hare, W. Science and policy characteristics of the Paris agreement temperature goal. Nat. Clim. Change 2016, 6, 827–835. [Google Scholar] [CrossRef]
- International Energy Agency Net Zero by 2050: A Roadmap for the Global Energy Sector. 2021. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 8 November 2025).
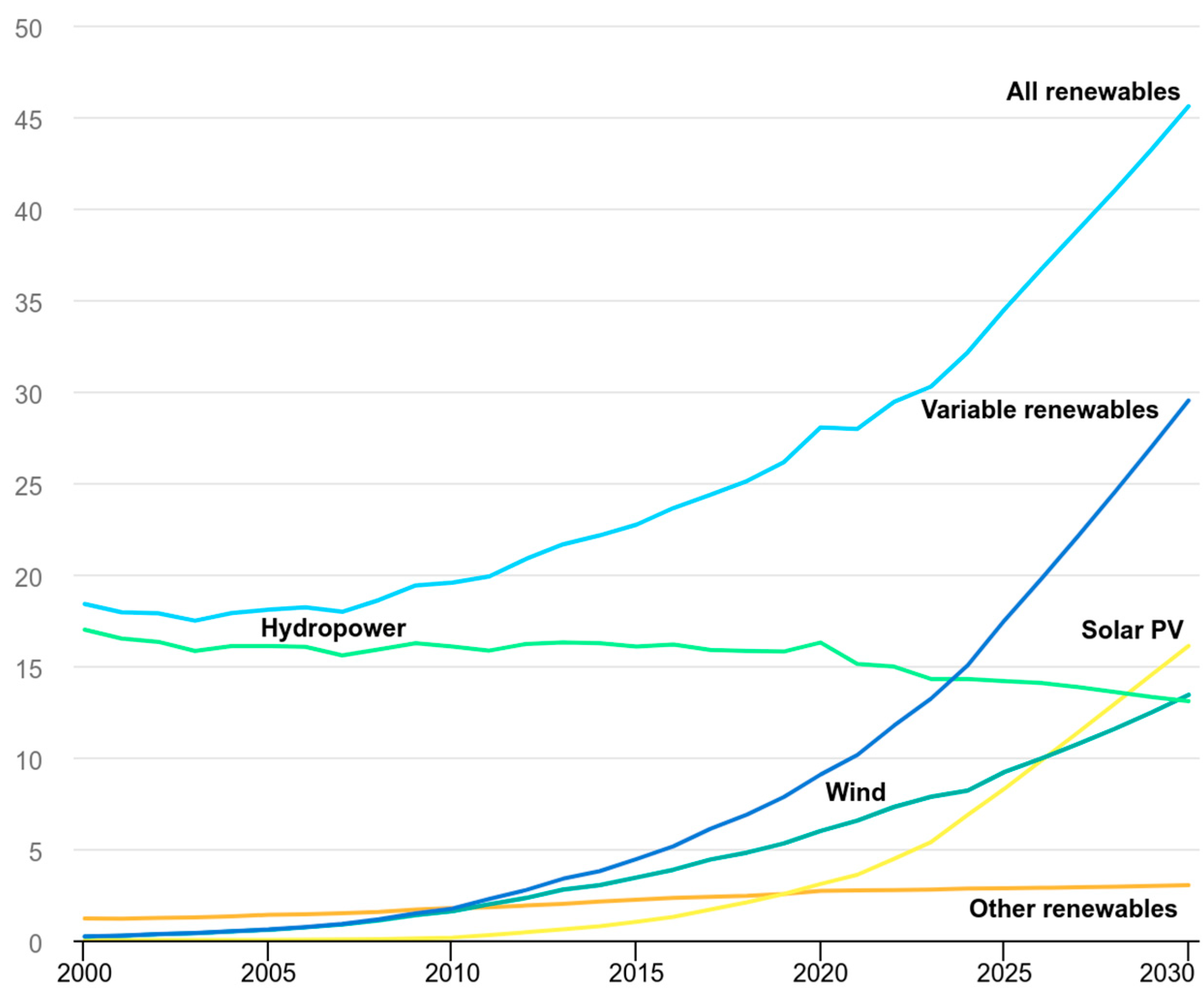
- International Energy Agency. Share of Renewable Electricity Generation by Technology, 2000–2030. 2024. Available online: https://www.iea.org/data-and-statistics/charts/share-of-renewable-electricity-generation-by-technology-2000-2030 (accessed on 26 October 2025).
- Xu, J.; Zhong, J.; Kang, J.; Dong, W.; Xie, S. Stability analysis and robust parameter design of dc-voltage loop for three-phase grid-connected PV inverter under weak grid condition. IEEE Trans. Ind. Electron. 2023, 71, 3776–3787. [Google Scholar] [CrossRef]
- Meegahapola, L.; Sguarezi, A.; Bryant, J.S.; Gu, M.; Conde D, E.R.; Cunha, R.B. Power system stability with power-electronic converter interfaced renewable power generation: Present issues and future trends. Energies 2020, 13, 3441. [Google Scholar] [CrossRef]
- Shair, J.; Li, H.; Hu, J.; Xie, X. Power system stability issues, classifications and research prospects in the context of high-penetration of renewables and power electronics. Renew. Sustain. Energy Rev. 2021, 145, 111111. [Google Scholar] [CrossRef]
- IEEE 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018. Available online: https://standards.ieee.org/standard/1547-2018.html (accessed on 8 November 2025).
- IEC 62116:2014; Utility-Interconnected Photovoltaic Inverters—Test Procedure of Islanding Prevention Measures. BSI Standards Limited: London, UK, 2014. Available online: https://webstore.ansi.org/preview-pages/BSI/preview_30262010.pdf (accessed on 26 October 2025).
- Shelar, S.; Bankar, D.; Bakre, S. Review of Revisions of IEEE 519 Standard on Power System Harmonics (1981 to 2022). In Proceedings of the 2024 21st International Conference on Harmonics and Quality of Power (ICHQP), Chengdu, China, 15–18 October 2024; pp. 415–420. [Google Scholar]
- Boscaino, V.; Ditta, V.; Marsala, G.; Panzavecchia, N.; Tinè, G.; Cosentino, V.; Cataliotti, A.; Di Cara, D. Grid-connected photovoltaic inverters: Grid codes, topologies and control techniques. Renew. Sustain. Energy Rev. 2024, 189, 113903. [Google Scholar] [CrossRef]
- Nagarajan, A.; Thiagarajan, R.; Repins, I.L.; Hacke, P.L. Photovoltaic Inverter Reliability Assessment. 2019. Available online: https://docs.nrel.gov/docs/fy20osti/74462.pdf (accessed on 26 October 2025).
- Deželak, K.; Bracinik, P.; Sredenšek, K.; Seme, S. Proportional-integral controllers performance of a grid-connected solar PV system with particle swarm optimization and ziegler–nichols tuning method. Energies 2021, 14, 2516. [Google Scholar] [CrossRef]
- Pereira, L.F.A.; Bazanella, A.S. Tuning rules for proportional resonant controllers. IEEE Trans. Control Syst. Technol. 2015, 23, 2010–2017. [Google Scholar] [CrossRef]
- Yuan, L.; Xiu, C.; Ma, X. Sliding mode control strategy for microgrid inverter systems. J. Power Electron. 2023, 23, 821–831. [Google Scholar] [CrossRef]
- Sufyan, A.; Jamil, M.; Ghafoor, S.; Awais, Q.; Ahmad, H.A.; Khan, A.A.; Abouobaida, H. A robust nonlinear sliding mode controller for a three-phase grid-connected inverter with an LCL filter. Energies 2022, 15, 9428. [Google Scholar] [CrossRef]
- Merabet, A.; Labib, L.; Ghias, A.M. Robust model predictive control for photovoltaic inverter system with grid fault ride-through capability. IEEE Trans. Smart Grid 2017, 9, 5699–5709. [Google Scholar] [CrossRef]
- Bella, S.; Houari, A.; Djerioui, A.; Chouder, A.; Machmoum, M.; Benkhoris, M.-F.; Ghedamsi, K. Robust model predictive control (MPC) for large-scale PV plant based on paralleled three-phase inverters. Sol. Energy 2020, 202, 409–419. [Google Scholar] [CrossRef]
- Youssef, A.; El-Telbany, M.; Zekry, A. The role of artificial intelligence in photo-voltaic systems design and control: A review. Renew. Sustain. Energy Rev. 2017, 78, 72–79. [Google Scholar] [CrossRef]
- Selvaraj, J.; Rahim, N.A. Multilevel inverter for grid-connected PV system employing digital pi controller. IEEE Trans. Ind. Electron. 2008, 56, 149–158. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Durairaj, S.; Padmavathi, S. A performance evaluation of a fuzzy logic controller-based photovoltaic-fed multi-level inverter for a three-phase induction motor. J. Frankl. Inst. 2021, 358, 7394–7412. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic instability assessment using state-space modeling and participation analysis in inverter-fed power systems. IEEE Trans. Ind. Electron. 2016, 64, 806–816. [Google Scholar] [CrossRef]
- Liao, Z.-X.; Luo, D.; Luo, X.-S.; Li, H.-S.; Xiang, Q.-Q.; Huang, G.-X.; Li, T.-H.; Jiang, P.-Q. Nonlinear model and dynamic behavior of photovoltaic grid-connected inverter. Appl. Sci. 2020, 10, 2120. [Google Scholar] [CrossRef]
- Rehman, A.u.; Ali, M.; Iqbal, S.; Shafiq, A.; Ullah, N.; Otaibi, S.A. Artificial intelligence-based control and coordination of multiple PV inverters for reactive power/voltage control of power distribution networks. Energies 2022, 15, 6297. [Google Scholar] [CrossRef]
- Das, S.R.; Ray, P.K.; Sahoo, A.K.; Singh, K.K.; Dhiman, G.; Singh, A. Artificial intelligence based grid connected inverters for power quality improvement in smart grid applications. Comput. Electr. Eng. 2021, 93, 107208. [Google Scholar] [CrossRef]
- Alharbi, Y.; Darwish, A.; Ma, X. A review of model predictive control for grid-connected PV applications. Electronics 2025, 14, 667. [Google Scholar] [CrossRef]
- Ali Khan, M.Y.; Liu, H.; Yang, Z.; Yuan, X. A comprehensive review on grid connected photovoltaic inverters, their modulation techniques, and control strategies. Energies 2020, 13, 4185. [Google Scholar] [CrossRef]
- Kurukuru, V.S.B.; Haque, A.; Khan, M.A.; Sahoo, S.; Malik, A.; Blaabjerg, F. A review on artificial intelligence applications for grid-connected solar photovoltaic systems. Energies 2021, 14, 4690. [Google Scholar] [CrossRef]
- Kumar, A.; Dubey, A.K.; Segovia Ramírez, I.; Muñoz del Río, A.; García Márquez, F.P. Artificial intelligence techniques for the photovoltaic system: A systematic review and analysis for evaluation and benchmarking. Arch. Comput. Methods Eng. 2024, 31, 4429–4453. [Google Scholar] [CrossRef]
- Clarivate Analytics. Web of Science Core Collection. 2025. Available online: https://www.webofscience.com (accessed on 26 October 2025).
- Lakshmi, M.; Hemamalini, S. Coordinated control of MPPT and voltage regulation using single-stage high gain DC–DC converter in a grid-connected PV system. Electr. Power Syst. Res. 2019, 169, 65–73. [Google Scholar] [CrossRef]
- Jain, S.; Agarwal, V. A single-stage grid connected inverter topology for solar PV systems with maximum power point tracking. IEEE Trans. Power Electron. 2007, 22, 1928–1940. [Google Scholar] [CrossRef]
- Guo, B.; Su, M.; Sun, Y.; Wang, H.; Liu, B.; Zhang, X.; Pou, J.; Yang, Y.; Davari, P. Optimization design and control of single-stage single-phase PV inverters for MPPT improvement. IEEE Trans. Power Electron. 2020, 35, 13000–13016. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, Q.; Ma, Y.; Xie, B. Dc-link voltage research of photovoltaic grid-connected inverter using improved active disturbance rejection control. IEEE Access 2021, 9, 9884–9894. [Google Scholar] [CrossRef]
- Liu, B.; Song, D.; He, D.; Song, S.; Yang, J.; Su, M.; Lu, Y.; Chen, Y.; Liu, H. A modified modulation for single-phase photovoltaic/battery inverter to improve ac power quality with low dc-link capacitance. Int. J. Electr. Power Energy Syst. 2019, 110, 705–712. [Google Scholar] [CrossRef]
- Haitao, W.; Ningning, Z.; Zhixuan, C. Adaptive control of phase-locked loop parameters of the photovoltaic grid-connected system under weak grid. Power Syst. Clean Energy 2024, 40, 52–61. [Google Scholar] [CrossRef]
- Kanagavel, K.; Govindaraju, C. Adaptive single carrier multilevel modulation for grid connected single phase modular multilevel inverter. J. Ambient. Intell. Humaniz. Comput. 2021, 1–9. [Google Scholar] [CrossRef]
- Baeckeland, N.; Chatterjee, D.; Lu, M.; Johnson, B.; Seo, G.-S. Overcurrent limiting in grid-forming inverters: A comprehensive review and discussion. IEEE Trans. Power Electron. 2024, 39, 14493–14517. [Google Scholar] [CrossRef]
- Serban, I.; Ion, C.P. Microgrid control based on a grid-forming inverter operating as virtual synchronous generator with enhanced dynamic response capability. Int. J. Electr. Power Energy Syst. 2017, 89, 94–105. [Google Scholar] [CrossRef]
- Salem, Q.; Aljarrah, R.; Karimi, M.; Al-Quraan, A. Grid-forming inverter control for power sharing in microgrids based on p/f and q/v droop characteristics. Sustainability 2023, 15, 11712. [Google Scholar] [CrossRef]
- Xing, Z.; Xiangdui, Z.; Mengze, W. Review on grid-following/grid-forming hybrid mode control for grid-connected converter in high penetration rate of renewable energy generation. Autom. Electr. Power Syst. 2024, 48, 1–15. [Google Scholar] [CrossRef]
- Alshahrani, S.; Khan, K.; Abido, M.; Khalid, M. Grid-forming converter and stability aspects of renewable-based low-inertia power networks: Modern trends and challenges. Arab. J. Sci. Eng. 2024, 49, 6187–6216. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Buso, S.; Mattavelli, P. Digital Control in Power Electronics; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Zhong, S.; Huang, Y.; Guo, L. A parameter formula connecting PID and ADRC. Sci. China Inf. Sci. 2020, 63, 192203. [Google Scholar] [CrossRef]
- Qing, H.; Zhang, C.; Chai, X.; He, H.; Wang, X. Research on grid-connected harmonic current suppression of three-phase four-wire energy storage inverters. J. Power Electron. 2023, 23, 972–983. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A. Artificial intelligence techniques for photovoltaic applications: A review. Prog. Energy Combust. Sci. 2008, 34, 574–632. [Google Scholar] [CrossRef]
- Errouissi, R.; Al-Durra, A. Decoupled pi current controller for grid-tied inverters with improved transient performances. IET Power Electron. 2019, 12, 245–253. [Google Scholar] [CrossRef]
- Nazeri, A.A.; Zacharias, P.; Ibanez, F.M.; Somkun, S. Design of proportional-resonant controller with zero steady-state error for a single-phase grid-connected voltage source inverter with an LCL output filter. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Xie, C.; Zhao, X.; Li, K.; Zou, J.; Guerrero, J.M. Multirate resonant controllers for grid-connected inverters with harmonic compensation function. IEEE Trans. Ind. Electron. 2018, 66, 8981–8991. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Dang, C.; Tong, X.; Song, W. Sliding-mode control in dq-frame for a three-phase grid-connected inverter with LCL-filter. J. Frankl. Inst. 2020, 357, 10159–10174. [Google Scholar] [CrossRef]
- Teng, Q.; Xu, G.; Zheng, X.; Mai, H.; Ma, X.; Wang, Y. A novel sliding mode observer-based compound sliding mode current control with active damping for single phase grid-tied inverter system in weak grid. Int. J. Electr. Power Energy Syst. 2022, 141, 108117. [Google Scholar] [CrossRef]
- Hu, C.; Chen, H.; Tang, A. Sliding mode control strategy of grid-forming energy storage converter with fast active support of frequency and voltage. Front. Energy Res. 2024, 12, 1416591. [Google Scholar] [CrossRef]
- Mostafa, M.R.; Saad, N.H.; El-sattar, A.A. Tracking the maximum power point of PV array by sliding mode control method. Ain Shams Eng. J. 2020, 11, 119–131. [Google Scholar] [CrossRef]
- Hosseinabadi, P.A.; Mekhilef, S.; Pota, H.R.; Kermadi, M. Chattering-free fixed-time robust sliding mode controller for grid-connected inverters under parameter variations. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 12, 579–592. [Google Scholar] [CrossRef]
- Guo, B.; Su, M.; Sun, Y.; Wang, H.; Dan, H.; Tang, Z.; Cheng, B. A robust second-order sliding mode control for single-phase photovoltaic grid-connected voltage source inverter. IEEE Access 2019, 7, 53202–53212. [Google Scholar] [CrossRef]
- Bagheri, F.; Komurcugil, H. A sliding-mode control with efficient chattering alleviation for single-phase voltage source inverters. Gazi Univ. J. Sci. 2022, 36, 190–206. [Google Scholar] [CrossRef]
- Shen, X.; Liu, J.; Alcaide, A.M.; Yin, Y.; Leon, J.I.; Vazquez, S.; Wu, L.; Franquelo, L.G. Adaptive second-order sliding mode control for grid-connected npc converters with enhanced disturbance rejection. IEEE Trans. Power Electron. 2021, 37, 206–220. [Google Scholar] [CrossRef]
- Afshar, Z.; Zadeh, M.M.; Bathaee, S.T. Sliding mode control of grid-connected inverters using inverter output current. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Oshnoei, A.; Blaabjerg, F. Sliding mode-based model predictive control of grid-forming power converters. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2016, 64, 935–947. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the art of finite control set model predictive control in power electronics. IEEE Trans. Ind. Inform. 2012, 9, 1003–1016. [Google Scholar] [CrossRef]
- Song, Y.; Xu, X.; Yuan, F.; Chang, Y.; Wu, X.; Zhao, R.; Gan, Z.; Lei, W. Research on control strategy of three-level PV grid-connected inverter based on FCS-MPC. In Proceedings of the 2023 4th International Conference on Advanced Electrical and Energy Systems (AEES), Shanghai, China, 1–3 December 2023; pp. 39–44. [Google Scholar]
- Lei, M.; Zhang, Y.; Meng, L.; Wang, Y.; Yang, Z.; Cao, D. A novel adaptive model predictive control based three-phase inverter current control method. Appl. Sci. 2019, 9, 5413. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Z.; Hu, B. Model predictive power control with kalman filter for grid-tied inverter with parameter variation. IET Power Electron. 2022, 15, 621–630. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Guerrero, J.M. A model predictive power control method for PV and energy storage systems with voltage support capability. IEEE Trans. Smart Grid 2019, 11, 1018–1029. [Google Scholar] [CrossRef]
- Aly, M.; de Morais Carnielutti, F.; Grigoletto, F.B.; de Oliveira Silveira, K.; Norambuena, M.; Kouro, S.; Rodriguez, J. Predictive control of common-ground five-level PV inverter without weighting factors and reduced computational burden. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4772–4783. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Liegmann, E.; Makhamreh, H.; Heldwein, M.L.; Novak, M.; Rossi, M.; Abdelrahem, M.; Trabelsi, M.; Ahmed, M. Model-predictive control of multilevel inverters: Challenges, recent advances, and trends. IEEE Trans. Power Electron. 2023, 38, 10845–10868. [Google Scholar] [CrossRef]
- Oyuela-Ocampo, J.-C.; Garcés-Ruiz, A.; Sanchez-Acevedo, S.; Ljøkelsøy, K.; D’Arco, S. Continuous control-set model-predictive control with stability guarantee for the PWM-VSC. Control Eng. Pract. 2025, 157, 106246. [Google Scholar] [CrossRef]
- Pimentel, S.P.; Husev, O.; Vinnikov, D.; Roncero-Clemente, C.; Stepenko, S. An indirect model predictive current control (CCS-MPC) for grid-connected single-phase three-level NPC quasi-z-source PV inverter. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 November 2018; pp. 1–6. [Google Scholar]
- Hannan, M.; Ghani, Z.A.; Mohamed, A.; Uddin, M.N. Real-time testing of a fuzzy-logic-controller-based grid-connected photovoltaic inverter system. IEEE Trans. Ind. Appl. 2015, 51, 4775–4784. [Google Scholar] [CrossRef]
- Ahmad, S.; Mekhilef, S.; Mokhlis, H.; Karimi, M.; Pourdaryaei, A.; Ahmed, T.; Jhuma, U.K.; Afzal, S. Fuzzy logic-based direct power control method for PV inverter of grid-tied ac microgrid without phase-locked loop. Electronics 2021, 10, 3095. [Google Scholar] [CrossRef]
- Alghassab, M.A.; Nour, A.M.; Hatata, A.Y.; Sedhom, B.E. Two-layer hybrid control scheme for distribution network integrated with photovoltaic sources based self-tuning h-infinity and fuzzy logic controller. IET Renew. Power Gener. 2025, 19, e12709. [Google Scholar] [CrossRef]
- Sefa, I.; Altin, N.; Ozdemir, S.; Kaplan, O. Fuzzy pi controlled inverter for grid interactive renewable energy systems. IET Renew. Power Gener. 2015, 9, 729–738. [Google Scholar] [CrossRef]
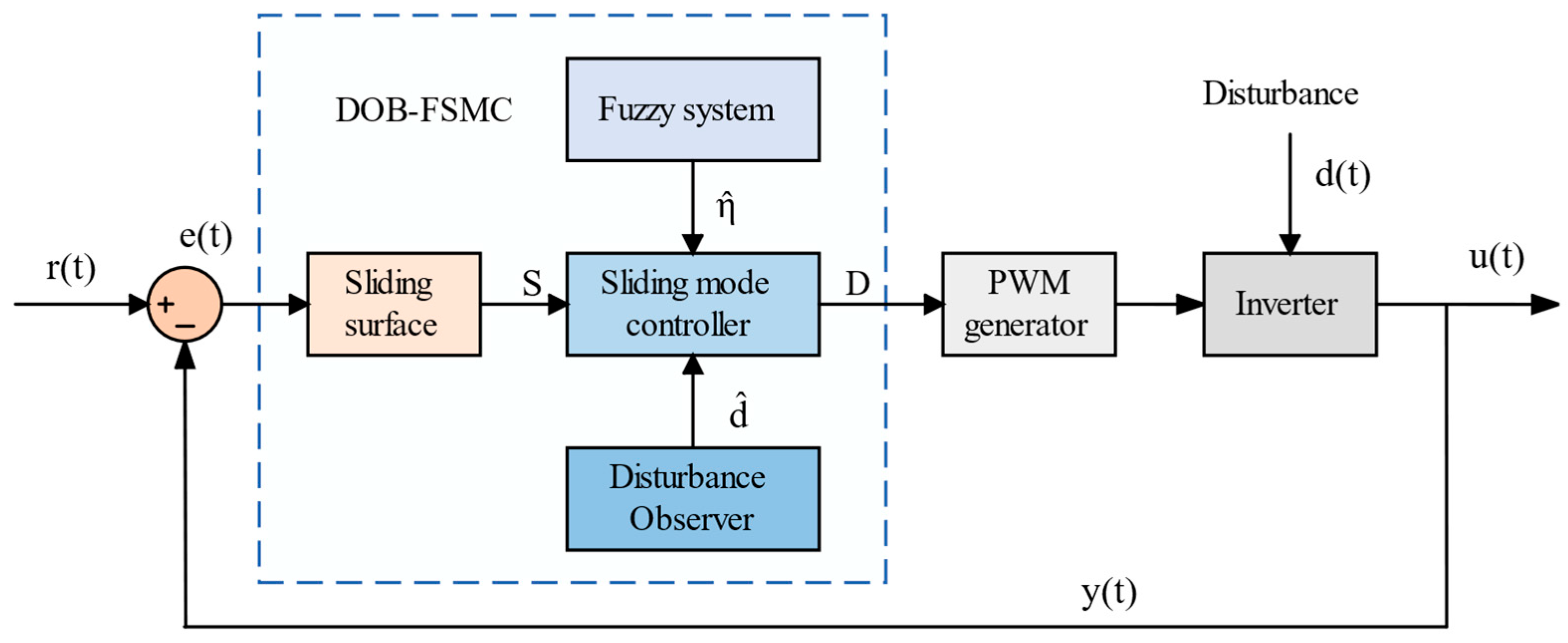
- Zhu, Y.; Fei, J. Disturbance observer based fuzzy sliding mode control of PV grid connected inverter. IEEE Access 2018, 6, 21202–21211. [Google Scholar] [CrossRef]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. Enhancement of frequency regulation in ac microgrid: A fuzzy-MPC controlled virtual synchronous generator. IEEE Trans. Smart Grid 2021, 12, 3138–3149. [Google Scholar] [CrossRef]
- Talbi, B.; Krim, F.; Laib, A.; Sahli, A.; Babes, B. A sugeno-fuzzy tuning approach of weighting factor in model predictive control for PV grid-tied puc7 multi-level inverter. In Proceedings of the 2022 3rd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 20–22 March 2022; pp. 1–6. [Google Scholar]
- Zhou, W.; Wang, B.; Gu, J.; Zhang, Y.; Wang, S.; Wu, Y. Power stability control of wind-PV-battery ac microgrid based on two-parameters fuzzy VSG. Front. Energy Res. 2023, 11, 1298033. [Google Scholar] [CrossRef]
- Jiang, E.; Zhao, J.; Shi, Z.; Mi, Y.; Lin, S.; Muyeen, S. Intelligent virtual impedance based control to enhance the stability of islanded microgrid. J. Electr. Eng. Technol. 2023, 18, 3971–3984. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Sagar Bhaskar, M.; Blaabjerg, F.; Sharma, A. Fuzzy svpwm-based inverter control realisation of grid integrated photovoltaic-wind system with fuzzy particle swarm optimisation maximum power point tracking algorithm for a grid-connected PV/wind power generation system: Hardware implementation. IET Electr. Power Appl. 2018, 12, 962–971. [Google Scholar] [CrossRef]
- Mostafa, S.; Zekry, A.; Youssef, A.; Anis, W.R. Raspberry pi design and hardware implementation of fuzzy-pi controller for three-phase grid-connected inverter. Energies 2022, 15, 843. [Google Scholar] [CrossRef]
- Mamaghani, A.S.; Pedrycz, W. Structural optimization of fuzzy rule-based models: Towards efficient complexity management. Expert Syst. Appl. 2020, 152, 113362. [Google Scholar] [CrossRef]
- Long, B.; Lu, P.; Zhan, D.; Lu, X.; Rodríguez, J.; Guerrero, J.M.; to Chong, K. Adaptive fuzzy fractional-order sliding-mode control of LCL-interfaced grid-connected converter with reduced-order. ISA Trans. 2023, 132, 557–572. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Tariq, M.; Lodi, K.A.; Chakrabortty, R.K.; Ryan, M.J.; Alamri, B.; Bharatiraja, C. Robust ann-based control of modified puc-5 inverter for solar PV applications. IEEE Trans. Ind. Appl. 2021, 57, 3863–3876. [Google Scholar] [CrossRef]
- Fu, X.; Li, S. Control of single-phase grid-connected converters with LCL filters using recurrent neural network and conventional control methods. IEEE Trans. Power Electron. 2015, 31, 5354–5364. [Google Scholar] [CrossRef]
- Babaie, M.; Sharifzadeh, M.; Al-Haddad, K. Three-phase grid-connected NPC inverter based on a robust artificial neural network controller. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2022; pp. 1–5. [Google Scholar]
- Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicević, T.; Diab, A.A.Z. A neural-network-based model predictive control of three-phase inverter with an output LC filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- Bakeer, A.; Mohamed, I.S.; Malidarreh, P.B.; Hattabi, I.; Liu, L. An artificial neural network-based model predictive control for three-phase flying capacitor multilevel inverter. IEEE Access 2022, 10, 70305–70316. [Google Scholar] [CrossRef]
- Bana, P.R.; Amin, M.; Molinas, M. Ann-based surrogate pi and MPC controllers for grid-connected VSC system: Small-signal analysis and comparative evaluation. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 12, 566–578. [Google Scholar] [CrossRef]
- Vazquez, S.; Marino, D.; Zafra, E.; Peña, M.D.V.; Rodríguez-Andina, J.J.; Franquelo, L.G.; Manic, M. An artificial intelligence approach for real-time tuning of weighting factors in FCS-MPC for power converters. IEEE Trans. Ind. Electron. 2021, 69, 11987–11998. [Google Scholar] [CrossRef]
- Sridhar, B.; Shukla, S.P.; Dash, R.; Dwivedi, A.; Biswal, G.; Singh, N.; Chandrakar, M.K.; Reddy, K.J.; Mohapatra, B.; Sahu, B.K. Design and analysis of modular neural network-based pi-controller ensemble with karush-kuhn-tucker conditions for grid-connected photovoltaic systems under ground fault conditions. IEEE Access 2025, 13, 67196–67219. [Google Scholar] [CrossRef]
- Zhu, Y.; Fei, J. Adaptive global fast terminal sliding mode control of grid-connected photovoltaic system using fuzzy neural network approach. IEEE Access 2017, 5, 9476–9484. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Wu, W.; Ma, J.; Fang, Y.; Peng, Z.; Wang, D. Neural predictor-based low switching frequency FCS-MPC for mmc with online weighting factors tuning. IEEE Trans. Power Electron. 2021, 37, 4065–4079. [Google Scholar] [CrossRef]
- Yağan, Y.E.; Vardar, K. Artificial neural networks controllers for three-phase neutral point clamped inverters. Eng. Sci. Technol. Int. J. 2023, 41, 101390. [Google Scholar] [CrossRef]
- Sturtz, J.; Surendranath, K.K.D.; Sam, M.; Fu, X.; Hingu, C.D.; Challoo, R.; Qingge, L. Accelerating the neural network controller embedded implementation on FPGA with novel dropout techniques for a solar inverter. Pervasive Mob. Comput. 2024, 104, 101975. [Google Scholar] [CrossRef]
- Sultana, W.; Jebaseelan, S.D.S. ANFIS controller for photovoltaic inverter transient and voltage stability enhancement. Meas. Sens. 2024, 33, 101154. [Google Scholar] [CrossRef]
- Ahuja, R.K.; Maity, T.; Kakkar, S. Control of active and reactive power of grid connected inverter using adaptive network based fuzzy inference system (ANFIS). In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016; pp. 1–5. [Google Scholar]
- Mahmud, N.; Zahedi, A.; Mahmud, A. A cooperative operation of novel PV inverter control scheme and storage energy management system based on ANFIS for voltage regulation of grid-tied PV system. IEEE Trans. Ind. Inform. 2017, 13, 2657–2668. [Google Scholar] [CrossRef]
- Osheba, D.S.; Osheba, S.; Nazih, A.; Mansour, A.S. Performance enhancement of PV system using VSG with ANFIS controller. Electr. Eng. 2023, 105, 2523–2537. [Google Scholar] [CrossRef]
- Rajamallaiah, A.; Karri, S.P.K.; Alghaythi, M.L.; Alshammari, M.S. Direct current control of grid connected two level inverter with lcl-filter using deep reinforcement learning algorithm. IEEE Access 2024, 12, 119840–119855. [Google Scholar] [CrossRef]
- Rajamallaiah, A.; Karri, S.P.K.; Alghaythi, M.L.; Alshammari, M.S. Deep reinforcement learning based control of a grid connected inverter with LCL-filter for renewable solar applications. IEEE Access 2024, 12, 22278–22295. [Google Scholar] [CrossRef]
- Alquennah, A.N.; Chida, M.; Zamzam, T.; Trabelsi, M. Reinforcement learning based controller for grid-connected PUC PV inverter. In Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Ren, H.; Zhuang, M.; Sun, L.; Ji, H.; Zhang, X.; Su, C.-Y. Two-stage three-phase photovoltaic grid-connected inverter control method based on off-policy integral reinforcement learning. Control Eng. Pract. 2025, 159, 106313. [Google Scholar] [CrossRef]
- Wan, Y.; Xu, Q.; Dragičević, T. Reinforcement learning-based predictive control for power electronic converters. IEEE Trans. Ind. Electron. 2024, 72, 5353–5364. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.-I.; Selișteanu, D. Improvement of the control of a grid connected photovoltaic system based on synergetic and sliding mode controllers using a reinforcement learning deep deterministic policy gradient agent. Energies 2022, 15, 2392. [Google Scholar] [CrossRef]
- Alquennah, A.N.; Saleh, M.A.; Abu-Rub, H.; Ghrayeb, A.; Bayhan, S.; Trabelsi, M. Double deep q networks reinforcement learning-based dynamic weighting factor of FCS-MPC for multilevel inverters. In Proceedings of the 2024 IEEE 18th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Gdynia, Poland, 24–26 June 2024; pp. 1–7. [Google Scholar]
- Rajak, M.K.; Pudur, R. Deep reinforcement learning framework for adaptive power control in grid-forming inverters: A multi-objective optimization approach. J. Renew. Sustain. Energy 2025, 17, 026301. [Google Scholar] [CrossRef]
- Kwon, S.; Yoon, C.; Lee, Y.-I. Practical implementation method of reinforcement learning for power converter. IFAC Pap. OnLine 2022, 55, 437–441. [Google Scholar] [CrossRef]
- Benhmidouch, Z.; Moufid, S.; Ait-Omar, A.; Abbou, A.; Laabassi, H.; Kang, M.; Chatri, C.; Ali, I.H.O.; Bouzekri, H.; Baek, J. A novel reinforcement learning policy optimization based adaptive VSG control technique for improved frequency stabilization in ac microgrids. Electr. Power Syst. Res. 2024, 230, 110269. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J. A novel reinforcement learning algorithm-based control strategy for grid-configured inverters. Energies 2025, 18, 597. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.; Ayob, A.; Mutlag, A.H.; Ustun, T.S. Optimal fuzzy logic controller based PSO for photovoltaic system. Energy Rep. 2023, 9, 427–434. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hannan, M.A.; Hussain, S.M.S.; Ustun, T.S. Optimal pi controller based PSO optimization for PV inverter using spwm techniques. Energy Rep. 2022, 8, 1003–1011. [Google Scholar] [CrossRef]
- Boucheriette, W.; Moussi, A.; Mechgoug, R.; Benguesmia, H. A multilevel inverter for grid-connected photovoltaic systems optimized by genetic algorithm. Eng. Technol. Appl. Sci. Res. 2023, 13, 10249–10254. [Google Scholar] [CrossRef]
- Song, L.; Huang, L.; Long, B.; Li, F. A genetic-algorithm-based dc current minimization scheme for transformless grid-connected photovoltaic inverters. Energies 2020, 13, 746. [Google Scholar] [CrossRef]
- Taran, B.; Mohajeri, H. Designing a fuzzy sliding mode controller for a three-phase inverter via genetic algorithm. Int. J. Dyn. Control 2023, 11, 2452–2465. [Google Scholar] [CrossRef]
- Zheng, C.; Dragicevic, T.; Zhang, Z.; Rodriguez, J.; Blaabjerg, F. Model predictive control of lc-filtered voltage source inverters with optimal switching sequence. IEEE Trans. Power Electron. 2021, 36, 3422–3436. [Google Scholar] [CrossRef]
- Karamanakos, P.; Nahalparvari, M.; Geyer, T. Fixed switching frequency direct model predictive control with continuous and discontinuous modulation for grid-tied converters with lcl filters. IEEE Trans. Control Syst. Technol. 2021, 29, 1503–1518. [Google Scholar] [CrossRef]
- Han, J.; Liu, L.; E., W.; Yao, G.; Wang, Y.; Benbouzid, M.; Tang, T. Double voltage vector model predictive control for grid-connected cascade h-bridge multilevel inverter with fixed switching frequency. ISA Trans. 2023, 142, 653–662. [Google Scholar] [CrossRef]
- Koran, A.; Albatran, S.; Alshorman, D. Adaptive switching frequency selection based on two-step efficiency optimization for grid-connected inverters. IEEE Access 2021, 9, 151741–151752. [Google Scholar] [CrossRef]
- Abbas, H.H.; Shafiee, Q.; Bevrani, H. Optimal passive lcl filter design for grid-connected converters in weak grids. Electr. Power Syst. Res. 2024, 235, 110896. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Diab, A.A.Z.; Rezk, H. Partial shading mitigation of PV systems via different meta-heuristic techniques. Renew. Energy 2019, 130, 1159–1175. [Google Scholar] [CrossRef]
- Xia, K.; Li, Y.; Zhu, B. Improved photovoltaic MPPT algorithm based on ant colony optimization and fuzzy logic under conditions of partial shading. IEEE Access 2024, 12, 44817–44825. [Google Scholar] [CrossRef]
- Sangrody, R.; Taheri, S.; Cretu, A.-M.; Pouresmaeil, E. An improved PSO-based MPPT technique using stability and steady state analyses under partial shading conditions. IEEE Trans. Sustain. Energy 2024, 15, 136–145. [Google Scholar] [CrossRef]
- Chigane, K.; Ouassaid, M. Experimental assessment of integral-type terminal sliding mode control designed for a single-phase grid-interlinked PV system. Control Eng. Pract. 2024, 147, 105903. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, Z.; Guo, M.; Li, K.-J.; Li, Y.-c.; Shen, G.; Li, L.; Cui, C. An enhanced model predictive control method for single-stage three-phase transformerless grid-connected photovoltaic inverter. Int. J. Electr. Power Energy Syst. 2025, 172, 111239. [Google Scholar] [CrossRef]
- Gueye, D.; Ndiaye, A.; Diao, A.; Tankari, M.A.; Traore, M.; Ndiaye, E.H.M.; Ba, A. Experimental validation under dSPACE of the ANN-PID control of the dc link for injection of solar energy to the grid. Int. J. Renew. Energy Res. 2022, 12, 2015–2022. [Google Scholar] [CrossRef]
- Gehbauer, C.; Mueller, J.; Swenson, T.; Vrettos, E. Photovoltaic and Behind-the-Meter Battery Storage: Advanced Smart Inverter Controls and Field Demonstration; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2020; Available online: https://escholarship.org/uc/item/62w660v3 (accessed on 26 October 2025).
- Huawei. Huawei Smart PV Solution White Paper (Special Edition). 2020. Available online: https://solar.huawei.com/en/publications (accessed on 26 October 2025).
- STMicroelectronics. Ai Based Smart Solar Arc Fault Circuit Interrupter (AFCI) Solution. 2023. Available online: https://www.st.com/content/dam/specialevents-assets/industrial-summit-23/pdfs/power-energy/PE2-06_AI%20based%20smart%20solar%20AFCI%20solution_EN.pdf (accessed on 13 November 2025).
- Sungrow. Isolarcloud Datasheet v1. 2023. Available online: https://info-support.sungrowpower.com/application/pdf/2023/03/24/DS_20230323_iSolarCloud_Datasheet_V1.pdf (accessed on 13 November 2025).


| Category | Description |
|---|---|
| Database | Web of Science, IEEE Xplore, and ScienceDirect were used as the main databases. Google Scholar was used for supplementary searches. |
| Search string | TS = ((“photovoltaic inverter” OR “Grid-connected inverter” OR “PV inverter” OR “power converter”) AND (“PI control” OR “proportional integral control” OR “PR control” OR “proportional resonant control” OR “sliding mode control” OR “model predictive control” OR “predictive control” OR “fuzzy logic control” OR “fuzzy controller” OR “fuzzy system” OR “adaptive neuro-fuzzy inference system” OR “ANFIS” OR “neural network” OR “artificial intelligence” OR “machine learning” OR “reinforcement learning” OR “intelligent control” OR “hybrid control” OR “optimization algorithm”)) AND (“photovoltaic” OR “solar energy”) |
| Inclusion criteria | Reviewed and accepted publications. Energy- and engineering-related areas. Academic journals, conference papers, and reviews. Publications between 2015 and mid-2025. |
| Exclusion criteria | Book chapters, technical reports, and articles under review. Publications without full access or DOI. Studies unrelated to inverter control. |
| Method | Robustness | Dynamic Response | Model Dependence | Implementation Complexity | Key Advantages | Technical Limitations | Improvements |
|---|---|---|---|---|---|---|---|
| PI/PR | + | + | Low | Low | Simple, mature, good steady-state accuracy under stable grid. | Fixed gains → poor adaptability under grid disturbances; sensitive to harmonic distortion and frequency variations. | Multi-resonant PR controller for harmonic suppression [50]; PR tuning with zero steady-state error [49]. |
| SMC | +++ | +++ | Medium | Medium | Strong robustness, fast dynamic response. | Chattering problem increases switching losses; performance degrades under noise and sampling delay. | Super-twisting/second-order SMC to reduce chattering [58]; adaptive boundary-layer and gain tuning [59]; observer-assisted disturbance rejection [60]. |
| MPC | ++ | +++ | High | High | Excellent dynamic performance; handles multivariable constraints. | High computational cost; strong dependence on accurate model parameters. | Kalman filter prediction [68]; cascaded objective evaluation [70]; fixed-frequency MPC for low THD [73]. |
| Method | Advantages | Disadvantages | Typical Applications |
|---|---|---|---|
| FLC |
|
|
|
| NNC |
|
| |
| ANFIS |
|
| |
| RL |
|
| |
| PSO/GA |
|
|
| Control Method | THD (%) | Response Time (ms) | Voltage Stability | Computational Complexity | Examples of Industrial Applications |
|---|---|---|---|---|---|
| PI/PR | 2–4 | 5–10 | Moderate | Low (O(1)) | Commonly adopted in commercial GCPI for stable grid conditions |
| SMC | 1.5–3 | 3–6 | High | Medium (O(n)) | Frequently used in research prototypes and laboratory-scale PV systems |
| MPC | 1–2 | 2–5 | High | High (O(n2)) | Demonstrated in academic studies and experimental validation platforms |
| FLC | 1.5–2.5 | 3–7 | High | Medium–High | Widely evaluated in laboratory and pilot-scale hybrid PV systems |
| NNC | 1–2 | 2–4 | High | High | Tested in AI-assisted control simulations and experimental prototypes |
| ANFIS | 1–2 | 2–5 | Very High | High | Reported in the literature for hybrid GCPI simulations and testbeds |
| RL | 0.8–1.5 | 2–3 | Very High | Very High | Applied in recent experimental research on intelligent inverter control |
| PSO/GA | 1–2 | 4–8 | High | High–Very High | Utilized in optimization-based control design studies and simulation environments |
| Method | Strong Grid | Weak Grid | Dynamic Irradiance | Nonlinear Load | Islanded/ Microgrid | Hardware Complexity | Real-Time Feasibility |
|---|---|---|---|---|---|---|---|
| PI/PR | ++++ | ++ | +++ | ++ | ++ | ++++ | +++++ |
| SMC | ++++ | +++ | +++ | +++ | +++ | +++ | ++++ |
| MPC | ++++ | ++++ | +++ | +++ | +++ | ++ | +++ |
| FLC | +++ | ++++ | ++++ | +++ | +++ | +++ | ++++ |
| ANFIS | +++ | ++++ | ++++ | +++ | +++ | ++ | +++ |
| RL | +++ | +++++ | +++++ | +++ | ++++ | + | ++ |
| Year | Control | Key Results | Platform | Reference |
|---|---|---|---|---|
| 2014 | FLC | THD: V 2.48%, I 4.64%; Unity PF; Grid disconnect ≈ 2.65 cycles | dSPACE DS1104 | [74] |
| 2024 | ITTSMC | Current THD 2.1–2.2%; PF 0.998; P ≈ 328 W; Q ≈ 18 VAR | PV + L-filter + Semikron inverter + dSPACE 1104 | [127] |
| 2025 | Enhanced MPC | THD 3.31%; CMV max 127.48 V; Leakage RMS 0.243 A; ΔVcap 10.09 V; Execution time 25.7 μs | OPAL-RT OP5700 + VC707 FPGA | [128] |
| 2022 | ANN-PID | Overshoot 0.54%; THD 2.27%; Response time 0 s; RMSE 0.0466; MAPE 0.0338%; MAE 0.0046 | dSPACE 1202 MicrolabBox; IGBT 10 kHz boost; LV25P/LA25NP sensors | [129] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Tuluhong, A.; Luo, B.; Abudureyimu, A. Control Methods and AI Application for Grid-Connected PV Inverter: A Review. Technologies 2025, 13, 535. https://doi.org/10.3390/technologies13110535
Wang F, Tuluhong A, Luo B, Abudureyimu A. Control Methods and AI Application for Grid-Connected PV Inverter: A Review. Technologies. 2025; 13(11):535. https://doi.org/10.3390/technologies13110535
Chicago/Turabian StyleWang, Feng, Ayiguzhali Tuluhong, Bao Luo, and Ailitabaier Abudureyimu. 2025. "Control Methods and AI Application for Grid-Connected PV Inverter: A Review" Technologies 13, no. 11: 535. https://doi.org/10.3390/technologies13110535
APA StyleWang, F., Tuluhong, A., Luo, B., & Abudureyimu, A. (2025). Control Methods and AI Application for Grid-Connected PV Inverter: A Review. Technologies, 13(11), 535. https://doi.org/10.3390/technologies13110535





