Process Parameter Optimization and Removal Depth Prediction for Robotic Adaptive Hydraulically Controlled Grinding of Aircraft Skin Primer
Abstract
1. Introduction
2. Materials and Methods
3. Results and Analysis
3.1. Results and Analysis of Single-Factor Tests
3.1.1. Influence of Grinding Force on Material Removal Depth and Surface Roughness
3.1.2. Influence of Feed Speed on Material Removal Depth and Surface Roughness
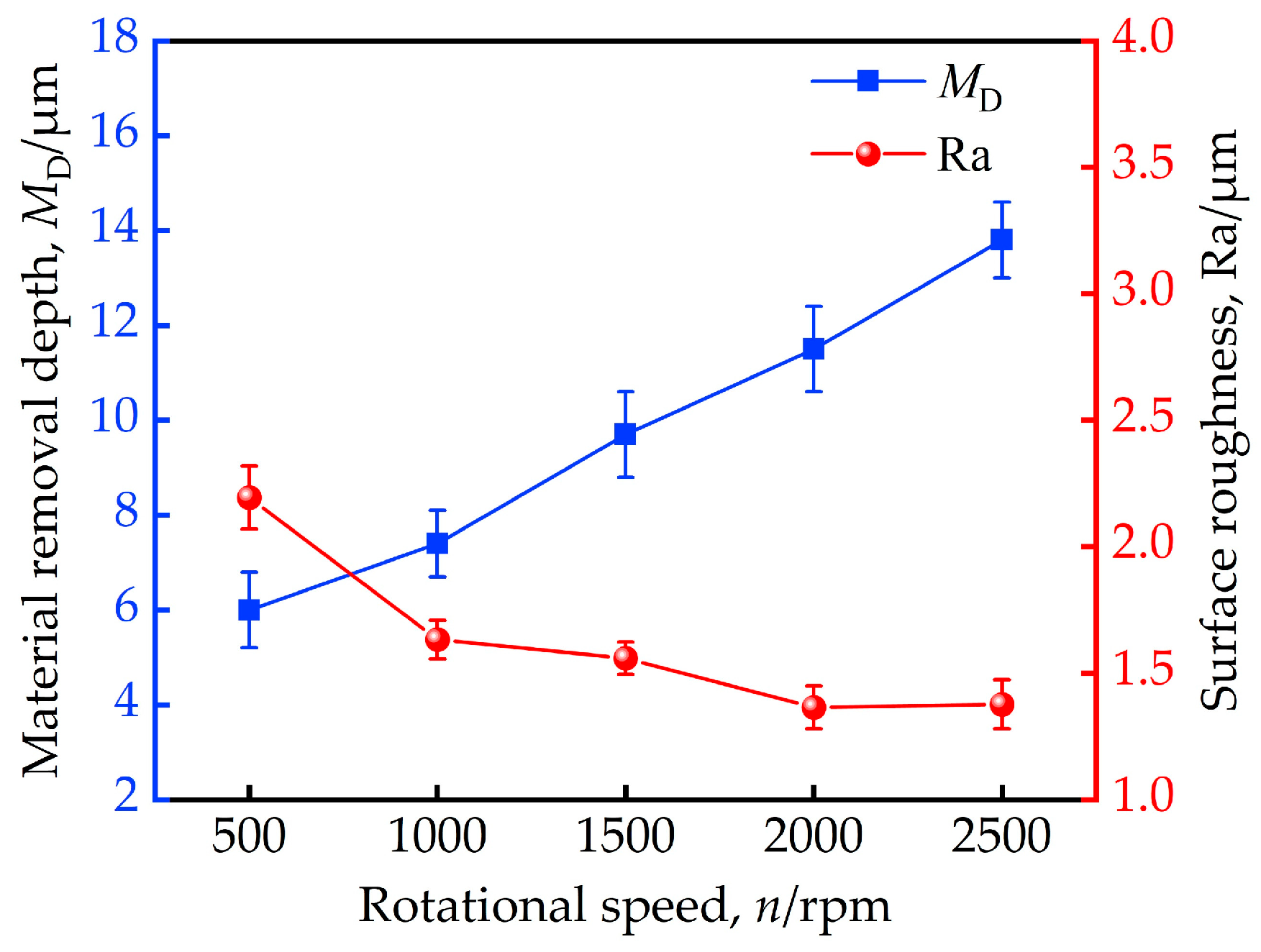
3.1.3. Influence of Rotational Speed on Material Removal Depth and Surface Roughness
3.1.4. Influence of Grit Size on Material Removal Depth and Surface Roughness
3.2. Results and Analysis of Response Surface Methodology
3.3. BP Neural Network Prediction Model for Surface Roughness and Removal Depth
4. Conclusions
- (1)
- The study reveals that the material removal depth of the sample increases with the elevation in grinding force, whereas the surface roughness first decreases and then increases. As the feed speed rises, the material removal depth declines rapidly, with the rate of decrease slowing down significantly when exceeding 60 mm·s−1. In contrast, the surface roughness shows a consistent upward trend. An increase in the rotational speed enhances the material removal depth while gradually reducing surface roughness. Moreover, finer abrasives lead to a pronounced reduction in both material removal depth and surface roughness, highlighting their significant influence on surface quality.
- (2)
- Owing to the inherent adhesiveness of resin materials, the surface quality of the ground workpiece is impaired, and the material removal depth is reduced. The optimal process parameters were identified as F = 20 N, = 40 mm·s−1, n = 2000 rpm, and M = 80. Under these conditions, the maximum material removal depth is 27.5 µm, the maximum material removal depth rate is 5.501 µm·s−1, and the corresponding surface roughness Ra is 1.897 µm.
- (3)
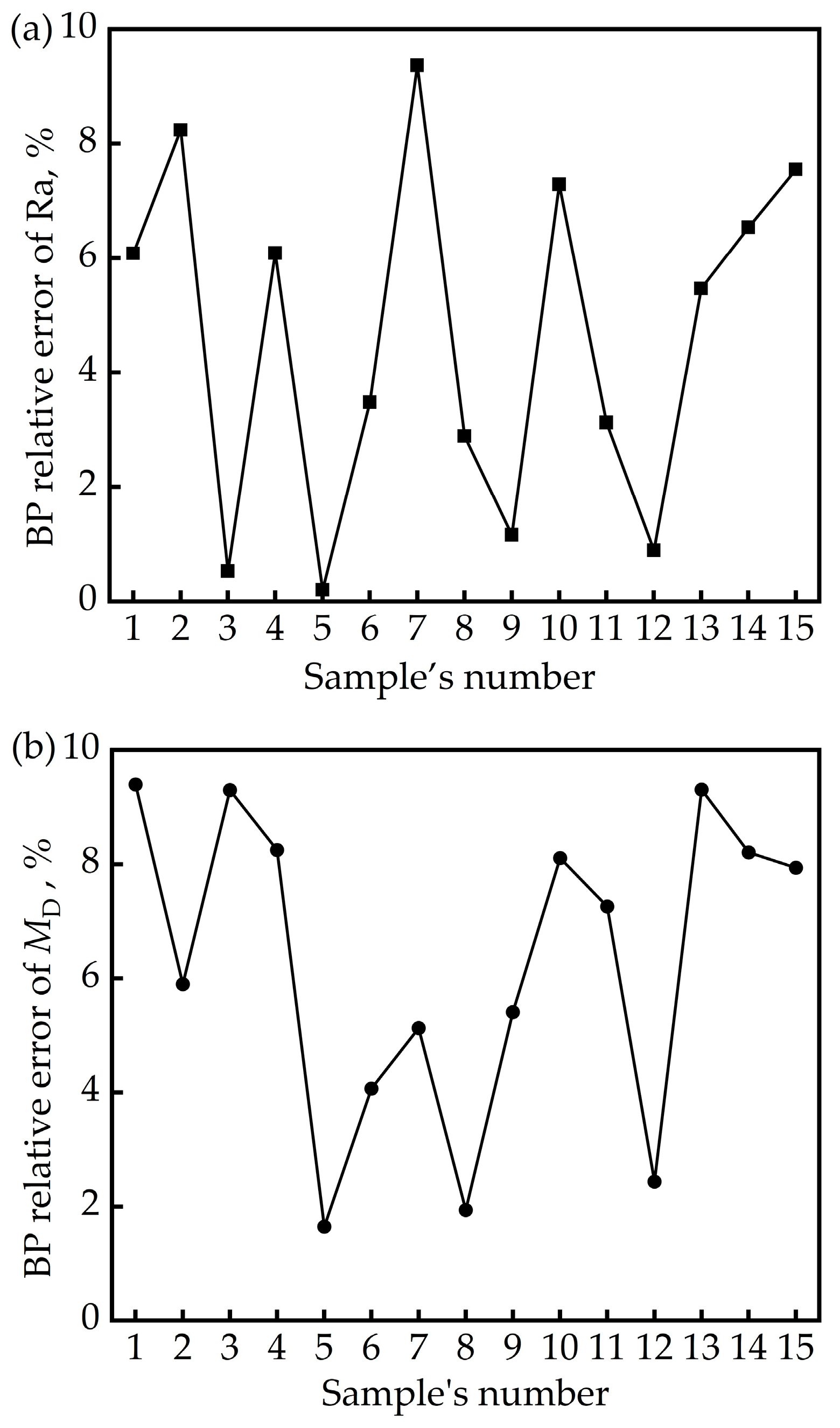
- The maximum relative errors of the material removal depth rate and material removal depth regression models are both below 8%, and the maximum relative error of the surface roughness Ra predicted by the BP neural network model is less than 9.5%. These results indicate that the established models can reliably predict material removal depth rate, material removal depth, and surface roughness. Although the regression model for material removal depth exhibits slightly better accuracy than the BP neural network model, the maximum relative errors of both models remain below 10%, confirming their overall predictive reliability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, G.Y.; Liu, Y.; Liu, L.; Xiong, W.; Deng, L.M.; Zhao, S.N. Mechanism and technology of laser adaptive cleaning for aircraft skin multilayer coatings of Airbus A320. J. Manuf. Process. 2025, 135, 230–239. [Google Scholar] [CrossRef]
- Kurc, K.; Burghardt, A.; Muszyńska, M.; Pietru, P.; Szybicki, D. Measurements of geometrical quantities and selection of parameters in the robotic grinding process of an aircraft engine. Electronics 2024, 13, 4077. [Google Scholar] [CrossRef]
- Cestino, E.; Catapano, J.; Galvano, F.; Felis, A.; Zuccala, S.; Martilla, V.; Sapienza, V.; Chesta, L. Effectiveness of nanotechnology treatments in composite aircraft applications. Appl. Sci. 2024, 14, 1721. [Google Scholar] [CrossRef]
- Sun, X.; Pan, R.; Xu, J.Y.; Zhang, S.Y.; Zhou, T.S.; Shi, Y.; Liu, W.J.; Chen, P.; Chen, S.J. Enhanced superhydrophobicity of acrylic polyurethane coatings by femtosecond laser ablation. Prog. Org. Coat. 2024, 197, 108874. [Google Scholar] [CrossRef]
- Yang, L.C.; Li, Y.; Huan, D.J.; Yang, Y.F.; Wang, J.X.; Zhu, C.L. An icephobic for aircraft anti-icing system. J. Mater. Sci. 2023, 58, 16322–16335. [Google Scholar] [CrossRef]
- Parten, C.; Subeshan, B.; Asmatulu, R. Highly conductive and durable nanocomposite hard coatings of carbon fiber reinforced thermoplastic composites against lightning strikes. Discov. Nano 2024, 19, 97. [Google Scholar] [CrossRef] [PubMed]
- Li, J.X.; Yang, J.J.; Liu, J.X.; Chen, H.; Duan, Y.F.; Pan, X.J. Research on laser cleaning technology for aircraft skin surface paint layer. Materials 2024, 17, 2414. [Google Scholar] [CrossRef]
- Selvan, T.R.; Raja, P.V.; Mangal, P.; Mohan, N.; Bhowmik, S. Recycling technology of epoxy glass fiber and epoxy carbon fiber composites used in aerospace vehicles. J. Compos. Mater. 2021, 55, 3281–3292. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Lu, W.Z.; Zhu, Y.S.; Zuo, D.W. Pretreatment of aircraft carbon fiber-reinforced plastic skin by plastic abrasive jet machining. J. Adhes. Sci. Technol. 2023, 37, 2378–2400. [Google Scholar] [CrossRef]
- Yang, L.C.; Li, Y.; Huan, D.J.; Zhu, C.L. An anti-icing coating with superhydrophobic and photothermal properties for aircraft icing protection system. Colloids Surf. A Physicochem. Eng. Asp. 2025, 709, 136150. [Google Scholar] [CrossRef]
- Membrives, C.Z.; Tamarit, P.; Fernandez, A.L.; Barreneche, C. Chemical procedures for paint removal in used thermoplastics for revalorization as a raw material in the automotive industry. Adv. Polym. Technol. 2025, 11, 8477994. [Google Scholar] [CrossRef]
- Yang, W.F.; Li, G.; Qian, Z.R.; Cao, Y.; Lin, D.H.; Li, S.L.; Zheng, X.; Zhu, D.H.; Xie, M.Y.; Yang, Y.K. Research on online monitoring of aircraft skin laser paint removal thickness using standard curve method and PCA-SVR based on LIBS. Anal. Methods 2024, 44, 2340–2348. [Google Scholar]
- Li, Y.H.; Li, J.Y.; Dong, H.; Zhang, W.; Jin, G.Y. Simulation and experimental study on continuous wave fiber laser removal of epoxy resin paint film on the surface of 6061 aluminum alloy. Photonics 2024, 11, 82. [Google Scholar] [CrossRef]
- Bodrova, I. Models of decision support for aircraft maintenance related to repainting process. Reliab. Stat. Transp. Commun. 2022, 410, 99–109. [Google Scholar]
- Arcari, A.; Anderson, R.M.; Hangarter, C.M.; Leez, E.B.; Policastro, S.A. Tensile properties of aircraft coating systems and applied strain modeling. Coatings 2024, 14, 91. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Q.; Yang, W.F.; Li, S.L.; Tan, D.Q.; Tan, T.; Zhang, H. Influence of laser paint stripping on microstructure and wear performance of 2024-T3 aluminum alloy aircraft skin. Appl. Phys. A 2025, 131, 193. [Google Scholar] [CrossRef]
- Song, H.Y.; Ye, R.F.; Xie, M. Research on complex surface grinding path planning of grinding robot based on NX and Tecnomatix. Int. J. Adv. Manuf. Technol. 2024, 133, 1961–1971. [Google Scholar] [CrossRef]
- Li, R.Z.; Wang, Z.P.; Yan, J.H. Multi-objective optimization of the process parameters of a grinding robot using LSTM-MLP-NSGAII. Machines 2023, 11, 882. [Google Scholar] [CrossRef]
- Vladareanu, V.; Smarandache, F.; Vladareanu, L. Extension hybrid force-position robot control in higher dimensions. Appl. Mech. Mater. 2013, 2466, 260–269. [Google Scholar] [CrossRef]
- Chen, H.Q.; Yang, J.X.; Ding, H. Robotic compliant grinding of curved parts based on a designed active force-controlled end-effector with optimized series elastic component. Robot. Comput. Integr. Manuf. 2024, 86, 102646. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Li, L.; Zhao, J.B.; Zhao, J.C.; Gong, Y.D. Theoretical investigation and implementation of nonlinear material removal depth strategy for robot automatic grinding aviation blade. J. Manuf. Process. 2022, 74, 441–455. [Google Scholar] [CrossRef]
- Xu, D.; Mo, H.J.; Zhong, Z.G.; Yin, L.R. Investigation of a parallel contact force robotic end-effector for thin-Walled parts grinding and deburring with uncertain position. Precis. Eng. 2025, 96, 587–599. [Google Scholar] [CrossRef]
- Senthilkumar, N.; Tamizharasan, T.; Gobikannan, S. Application of response surface methodology and firefly algorithm for optimizing multiple responses in turning AISI 1045 steel. Arab. J. Sci. Eng. 2014, 39, 8015–8030. [Google Scholar] [CrossRef]
- Xie, Y.H.; Chang, G.S.; Yang, J.X.; Zhao, M.Y.; Li, J. Process optimization of robotic polishing for mold steel based on response surface method. Machines 2025, 10, 283. [Google Scholar] [CrossRef]
- Yang, D.P.; Ding, S.G.; Pan, L.F.; Xu, Y. VSG-FC: A combined virtual sample generation and feature construction model for effective prediction of surface roughness in polishing processes. Micromachines 2025, 16, 622. [Google Scholar] [CrossRef]
- Shan, K.; Zhang, L.Y.; Tan, B.; Zhang, Y.S.; Li, W.H.; Li, X.H.; Wen, X.J. Prediction model for material removal rate of TC4 titanium alloy processed by vertical vibratory finishing. Coatings 2025, 15, 286. [Google Scholar] [CrossRef]
- Li, J.; Guan, Y.S.; Bi, H.; He, Z.Y.; Wu, W.Q.; Hu, H.; Li, D.C.; Wu, W.H.; Li, J.; Zhang, T. Predictive surface roughness model for robotic polishing considering initial surface quality. Int. J. Adv. Manuf. Technol. 2025, 137, 2729–2741. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, K.Y.; Zhang, X.J.; Zhang, X. Theoretical modeling and experimental research on the depth of radial material removal for flexible grinding. Int. J. Adv. Manuf. Technol. 2021, 116, 3355–3365. [Google Scholar] [CrossRef]
- Adam, H.; Mateusz, H.; Marcin, L.; Jedrzej, B. The quality of surgical instrument surfaces machined with robotic belt grinding. Materials 2023, 16, 630. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.Q.; Zeng, X.Y.W.; Wang, X.H.; Zhang, H.J. Parameter optimization and surface roughness prediction for the robotic adaptive hydraulic polishing of NAK80 mold steel. Processes 2025, 13, 991. [Google Scholar] [CrossRef]
- Zheng, Q.J.; Xiao, J.L.; Wang, C.; Liu, H.T.; Huang, T. A robotic polishing parameter optimization method considering time-varying wear. Int. J. Adv. Manuf. Technol. 2022, 121, 6723–6738. [Google Scholar] [CrossRef]
- Liu, B.T.; Zhu, G.Y.; Ding, P.J. The research progress of epoxy resin coating in building waterproof. Adv. Mater. Res. 2013, 233, 1779–1782. [Google Scholar] [CrossRef]
- Bucher, C. Metamodels of optimal quality for stochastic structural optimization. Probabilistic Eng. Mech. 2018, 54, 131–137. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Chen, L.; Huang, Y.C. ADAS simulation result dataset processing based on improved BP neural network. Data 2024, 9, 11. [Google Scholar] [CrossRef]
- Abdullah, M.F.; Zulkifli, R.; Moria, H.; Najm, A.S.; Harun, Z.; Abdullah, S.; Ghopa, W.A.W.; Sulaiman, N.H. Assessment of TiO2 nanoconcentration and twin impingement jet of heat transfer enhancement—A statistical approach using response surface methodology. Energies 2021, 14, 595. [Google Scholar] [CrossRef]
- Ji, X.; Wang, Z.F.; Zhang, H.B.; Wang, X.F.; Huo, J.Y.; Zhang, T.H. Optimization design and characterization of slag cementitious composites containing carbide slag and desulfurized gypsum based on response surface methodology. J. Build. Eng. 2023, 77, 107441. [Google Scholar] [CrossRef]
- Chen, J.; Huang, S.J. Evaluation model of green supply chain cooperation credit based on BP neural network. Neural Comput. Appl. 2021, 33, 1007–1015. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, H.H.; Han, S.Y. A merging approach for hole identification with the NMM and WOA-BP cooperative neural network in heat conduction problem. Eng. Anal. Bound. Elem. 2024, 169, 106042. [Google Scholar] [CrossRef]
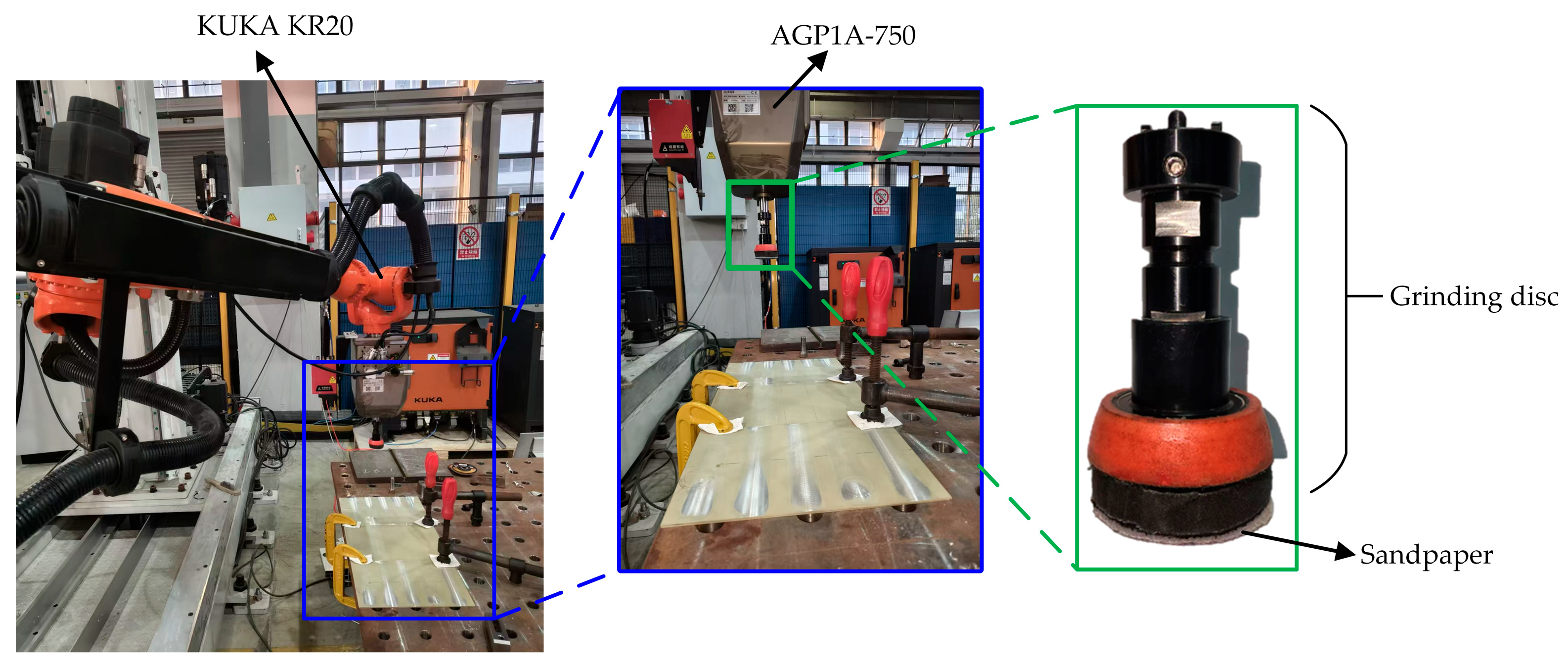




| No. | Grinding Force, F/N | Feed Speed, /mm·s−1 | Rotational Speed, n/rpm | Grit Size, M |
|---|---|---|---|---|
| 1 | 5, 10, 15, 20, 25 | 60 | 1500 | 180 |
| 2 | 15 | 20, 40, 60, 80, 100 | 1500 | 180 |
| 3 | 15 | 60 | 500, 1000, 1500, 2000, 2500 | 180 |
| 4 | 15 | 60 | 1500 | 80, 120, 180, 240, 320 |
| Level | Grinding Force, F (N) | Feed Speed, (mm·s−1) | Rotational Speed, n (rpm) | Grit Size, M |
|---|---|---|---|---|
| A | B | C | D | |
| 2 | 25 | 100 | 2500 | 320 |
| 1 | 20 | 80 | 2000 | 240 |
| 0 | 15 | 60 | 1500 | 180 |
| −1 | 10 | 40 | 1000 | 120 |
| −2 | 5 | 20 | 500 | 80 |
| No. | Grinding Force, F (N) | Feed Speed, (mm·s−1) | Rotational Speed, n (rpm) | Grit Size, M | (µm) | (µm·s−1) | Ra (µm) |
|---|---|---|---|---|---|---|---|
| A | B | C | D | ||||
| 1 | 1 | 1 | 1 | 1 | 12.4 | 4.96 | 1.052 |
| 2 | 1 | 1 | 1 | −1 | 14.0 | 5.60 | 1.571 |
| 3 | 1 | 1 | −1 | 1 | 9.1 | 3.64 | 1.267 |
| 4 | 1 | 1 | −1 | −1 | 8.8 | 3.52 | 2.455 |
| 5 | 1 | −1 | −1 | 1 | 15.5 | 3.10 | 1.023 |
| 6 | 1 | −1 | −1 | −1 | 15.5 | 3.10 | 1.818 |
| 7 | 1 | −1 | 1 | 1 | 22.9 | 4.58 | 0.967 |
| 8 | 1 | −1 | 1 | −1 | 24.7 | 4.94 | 1.361 |
| 9 | −1 | 1 | 1 | 1 | 5.5 | 2.20 | 1.124 |
| 10 | −1 | 1 | 1 | −1 | 8.6 | 3.40 | 1.674 |
| 11 | −1 | 1 | −1 | 1 | 5.5 | 2.20 | 1.036 |
| 12 | −1 | 1 | −1 | −1 | 5.2 | 2.08 | 2.316 |
| 13 | −1 | −1 | −1 | 1 | 11.8 | 2.36 | 1.136 |
| 14 | −1 | −1 | −1 | −1 | 12.4 | 2.48 | 1.886 |
| 15 | −1 | −1 | 1 | 1 | 11.7 | 2.34 | 1.047 |
| 16 | −1 | −1 | 1 | −1 | 15.7 | 3.14 | 1.495 |
| 17 | 2 | 0 | 0 | 0 | 16.9 | 5.07 | 1.541 |
| 18 | −2 | 0 | 0 | 0 | 6.7 | 2.01 | 1.591 |
| 19 | 0 | 2 | 0 | 0 | 7.8 | 3.90 | 1.729 |
| 20 | 0 | −2 | 0 | 0 | 26.0 | 2.60 | 1.203 |
| 21 | 0 | 0 | 2 | 0 | 13.0 | 3.90 | 1.128 |
| 22 | 0 | 0 | −2 | 0 | 6.1 | 1.83 | 2.458 |
| 23 | 0 | 0 | 0 | 2 | 7.7 | 2.31 | 0.954 |
| 24 | 0 | 0 | 0 | −2 | 13.1 | 3.93 | 2.946 |
| 25 | 0 | 0 | 0 | 0 | 9.2 | 2.76 | 1.227 |
| 26 | 0 | 0 | 0 | 0 | 8.5 | 2.55 | 1.562 |
| 27 | 0 | 0 | 0 | 0 | 9.4 | 2.82 | 1.492 |
| 28 | 0 | 0 | 0 | 0 | 9.7 | 2.91 | 1.312 |
| 29 | 0 | 0 | 0 | 0 | 8.8 | 2.64 | 1.363 |
| 30 | 0 | 0 | 0 | 0 | 10.4 | 3.12 | 1.302 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 833.02 | 14 | 59.50 | 56.94 | <0.0001 |
| A | 187.04 | 1 | 187.04 | 179.00 | <0.0001 |
| B | 396.91 | 1 | 396.91 | 379.85 | <0.0001 |
| C | 85.88 | 1 | 85.88 | 82.19 | <0.0001 |
| D | 19.74 | 1 | 19.74 | 18.90 | 0.0006 |
| AB | 3.42 | 1 | 3.42 | 3.28 | 0.0904 |
| AC | 21.62 | 1 | 21.62 | 20.69 | 0.0004 |
| AD | 1.10 | 1 | 1.10 | 1.06 | 0.3206 |
| BC | 4.00 | 1 | 4.00 | 3.83 | 0.0693 |
| BD | 0.36 | 1 | 0.36 | 0.34 | 0.5660 |
| CD | 6.76 | 1 | 6.76 | 6.47 | 0.0225 |
| A2 | 11.13 | 1 | 11.13 | 10.65 | 0.0052 |
| B2 | 100.33 | 1 | 100.33 | 96.02 | <0.0001 |
| C2 | 0.15 | 1 | 0.15 | 0.14 | 0.7091 |
| D2 | 2.04 | 1 | 2.04 | 1.96 | 0.1822 |
| Residual | 15.67 | 15 | 1.04 | — | — |
| Lack of fit | 13.40 | 10 | 1.34 | 2.95 | 0.1222 |
| Pure error | 2.27 | 5 | 0.45 | — | — |
| Cor total | 848.69 | 29 | — | — | — |
| R2 = 0.9815, = 0.9643, = 0.8985 | |||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 28.77 | 14 | 2.06 | 25.42 | <0.0001 |
| A | 15.62 | 1 | 15.62 | 193.19 | <0.0001 |
| B | 0.72 | 1 | 0.72 | 8.92 | 0.0092 |
| C | 6.85 | 1 | 6.85 | 84.71 | <0.0001 |
| D | 1.69 | 1 | 1.69 | 20.91 | 0.0004 |
| AB | 0.37 | 1 | 0.37 | 4.60 | 0.0487 |
| AC | 1.42 | 1 | 1.42 | 17.52 | 0.0008 |
| AD | 0.08 | 1 | 0.08 | 0.97 | 0.3403 |
| BC | 0.04 | 1 | 0.04 | 0.45 | 0.5141 |
| BD | 0.01 | 1 | 0.01 | 0.08 | 0.7823 |
| CD | 0.61 | 1 | 0.61 | 7.53 | 0.0151 |
| A2 | 1.13 | 1 | 1.13 | 13.97 | 0.0020 |
| B2 | 0.47 | 1 | 0.47 | 5.77 | 0.0297 |
| C2 | 0.03 | 1 | 0.03 | 0.39 | 0.5395 |
| D2 | 0.23 | 1 | 0.23 | 2.80 | 0.1147 |
| Residual | 1.21 | 15 | 0.08 | — | — |
| Lack of fit | 1.01 | 10 | 0.10 | 2.46 | 0.1658 |
| Pure error | 0.20 | 5 | 0.04 | — | — |
| Cor total | 29.99 | 29 | — | — | — |
| R2 = 0.9596, = 0.9218, = 0.7626 | |||||
| No. | Grinding Force, F(N) | Feed Speed, (mm·s−1) | Rotational Speed, n (rpm) | Grit Size, M | (µm) | Ra (µm) |
|---|---|---|---|---|---|---|
| 1 | 5 | 20 | 500 | 80 | 6.3 | 4.434 |
| 2 | 5 | 40 | 1500 | 240 | 5.1 | 1.106 |
| 3 | 5 | 60 | 2500 | 120 | 9.7 | 1.539 |
| 4 | 5 | 80 | 1000 | 320 | 2.7 | 1.285 |
| 5 | 5 | 100 | 2000 | 180 | 8.7 | 2.010 |
| 6 | 10 | 20 | 2500 | 240 | 19.2 | 0.718 |
| 7 | 10 | 40 | 1000 | 120 | 12.7 | 1.993 |
| 8 | 10 | 60 | 2000 | 320 | 11.2 | 1.093 |
| 9 | 10 | 80 | 500 | 180 | 8.7 | 2.458 |
| 10 | 10 | 100 | 1500 | 80 | 9.9 | 5.818 |
| 11 | 15 | 20 | 2000 | 120 | 34.1 | 1.725 |
| 12 | 15 | 40 | 500 | 320 | 8.9 | 1.555 |
| 13 | 15 | 60 | 1500 | 180 | 10.2 | 1.245 |
| 14 | 15 | 80 | 2500 | 80 | 12.6 | 3.166 |
| 15 | 15 | 100 | 1000 | 240 | 8.8 | 1.530 |
| 16 | 20 | 20 | 1500 | 320 | 31.8 | 0.714 |
| 17 | 20 | 40 | 2500 | 180 | 25.1 | 1.263 |
| 18 | 20 | 60 | 1000 | 80 | 17.1 | 5.355 |
| 19 | 20 | 80 | 2000 | 240 | 14.8 | 1.052 |
| 20 | 20 | 100 | 500 | 120 | 5.8 | 3.270 |
| 21 | 25 | 20 | 1000 | 180 | 32.3 | 1.471 |
| 22 | 25 | 40 | 2000 | 80 | 35.8 | 4.709 |
| 23 | 25 | 60 | 500 | 240 | 8.3 | 1.719 |
| 24 | 25 | 80 | 1500 | 120 | 13.4 | 1.739 |
| 25 | 25 | 100 | 2500 | 320 | 11.6 | 1.180 |
| No. | Grinding Force, F (N) | Feed Speed, (mm·s−1) | Rotational Speed, n (rpm) | Grit Size, M |
|---|---|---|---|---|
| W1 | 20 | 40 | 2000 | 80 |
| W2 | 16 | 68 | 1742 | 180 |
| W3 | 13 | 42 | 2093 | 240 |
| W4 | 15 | 79 | 1472 | 320 |
| W5 | 7 | 54 | 1064 | 120 |
| No. | (µm·s−1) | Error (%) | (µm) | Reg-Error (%) | BP-Error (%) | Ra (µm) | Error (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | Reg-Pred. | Test | Reg-Pred. | BP-Pred. | Test | BP-Pred. | |||||
| W1 | 5.501 | 5.316 | 3.4 | 27.5 | 25.467 | 29.198 | 7.4 | 6.2 | 1.897 | 1.731 | 8.8 |
| W2 | 3.434 | 3.519 | 2.5 | 10.1 | 9.841 | 9.718 | 2.6 | 3.8 | 1.436 | 1.503 | 4.7 |
| W3 | 2.772 | 2.574 | 7.1 | 13.2 | 14.211 | 12.227 | 7.7 | 7.4 | 1.126 | 1.084 | 3.7 |
| W4 | 2.371 | 2.526 | 6.5 | 6.0 | 6.356 | 6.392 | 5.9 | 6.5 | 1.183 | 1.295 | 9.5 |
| W5 | 2.295 | 2.114 | 7.9 | 8.5 | 8.089 | 9.346 | 4.8 | 10.0 | 2.037 | 2.171 | 6.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, D.; Wang, X.; Yu, W.; Zhang, H. Process Parameter Optimization and Removal Depth Prediction for Robotic Adaptive Hydraulically Controlled Grinding of Aircraft Skin Primer. Technologies 2025, 13, 498. https://doi.org/10.3390/technologies13110498
Shi D, Wang X, Yu W, Zhang H. Process Parameter Optimization and Removal Depth Prediction for Robotic Adaptive Hydraulically Controlled Grinding of Aircraft Skin Primer. Technologies. 2025; 13(11):498. https://doi.org/10.3390/technologies13110498
Chicago/Turabian StyleShi, Dequan, Xuhui Wang, Wenbo Yu, and Huajun Zhang. 2025. "Process Parameter Optimization and Removal Depth Prediction for Robotic Adaptive Hydraulically Controlled Grinding of Aircraft Skin Primer" Technologies 13, no. 11: 498. https://doi.org/10.3390/technologies13110498
APA StyleShi, D., Wang, X., Yu, W., & Zhang, H. (2025). Process Parameter Optimization and Removal Depth Prediction for Robotic Adaptive Hydraulically Controlled Grinding of Aircraft Skin Primer. Technologies, 13(11), 498. https://doi.org/10.3390/technologies13110498






