Construction of Pattern Optimization Model Driven by Fabric Parameters in 3D Garment Development Using Artificial Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Data Acquisition
2.1.1. Fabrics Properties
2.1.2. Preparation of Experimental Garment Samples
2.1.3. Acquisition of Point Cloud Data and Preprocessing
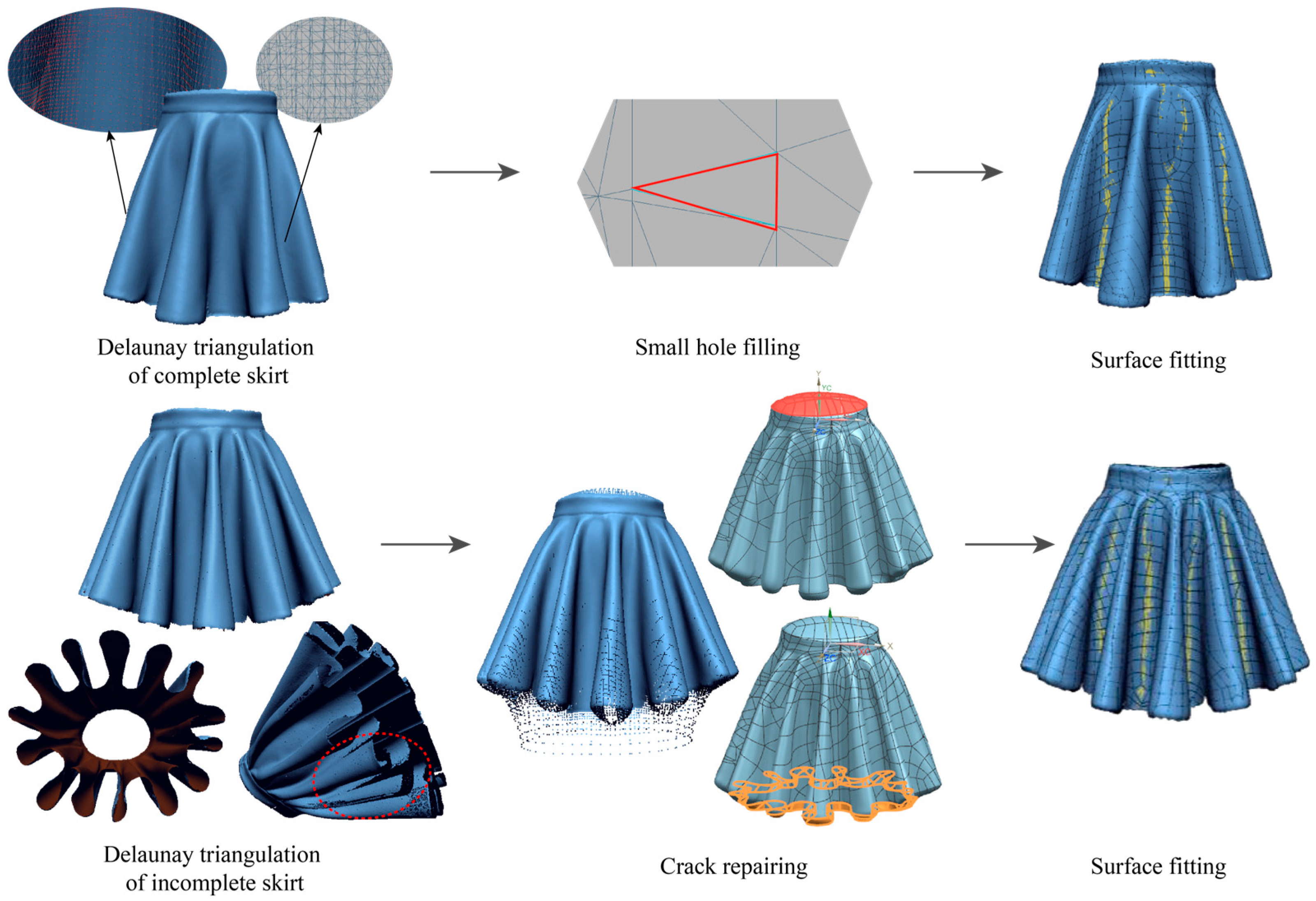
2.2. Surface Reconstruction
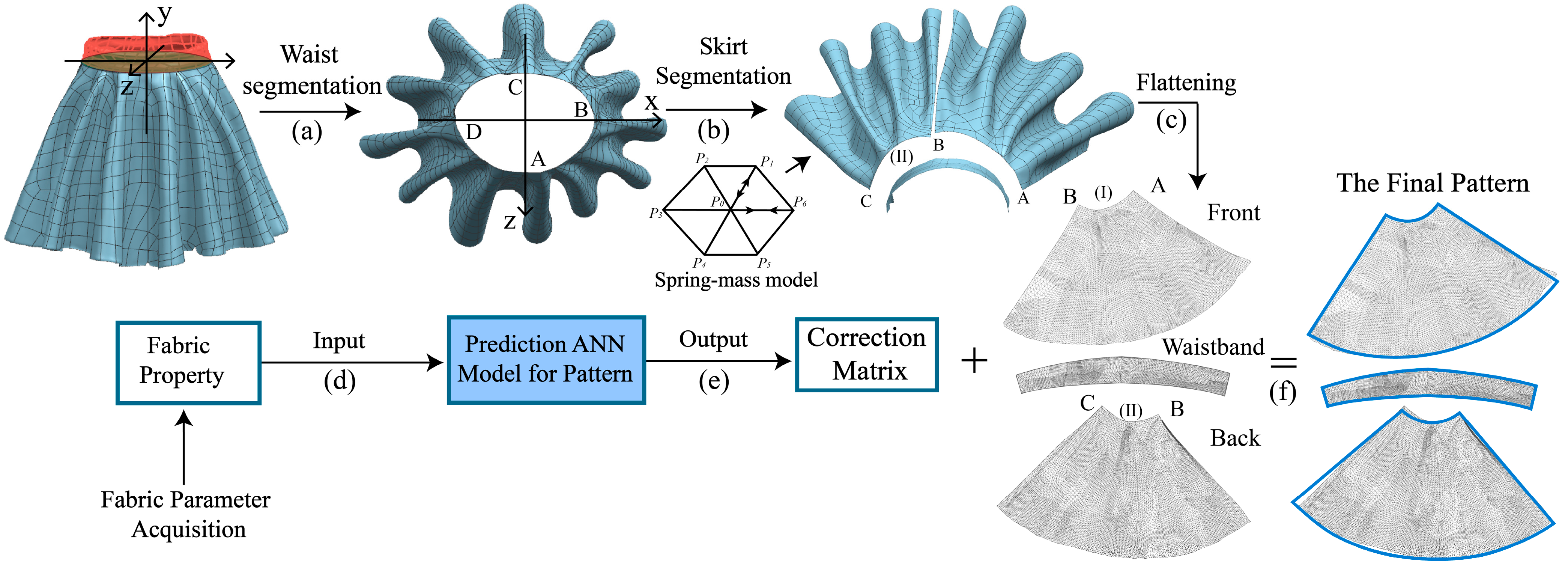
2.3. Surface Flattening to Generate Patterns
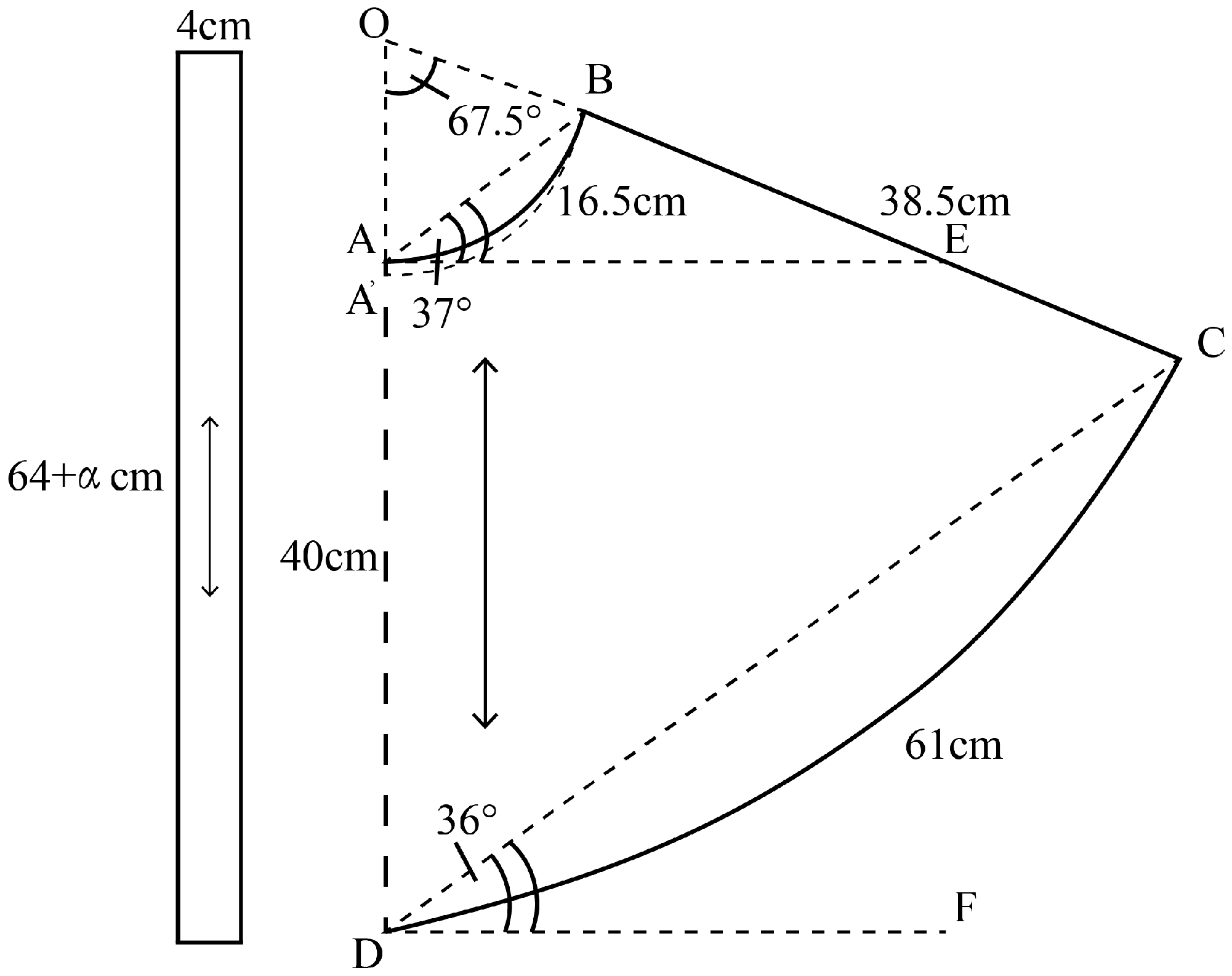
2.4. Key Dimension Obtaining
3. Prediction Model Construction
3.1. Data Preprocessing
3.2. Parameter Dimension Reduction Based on Principal Component Analysis
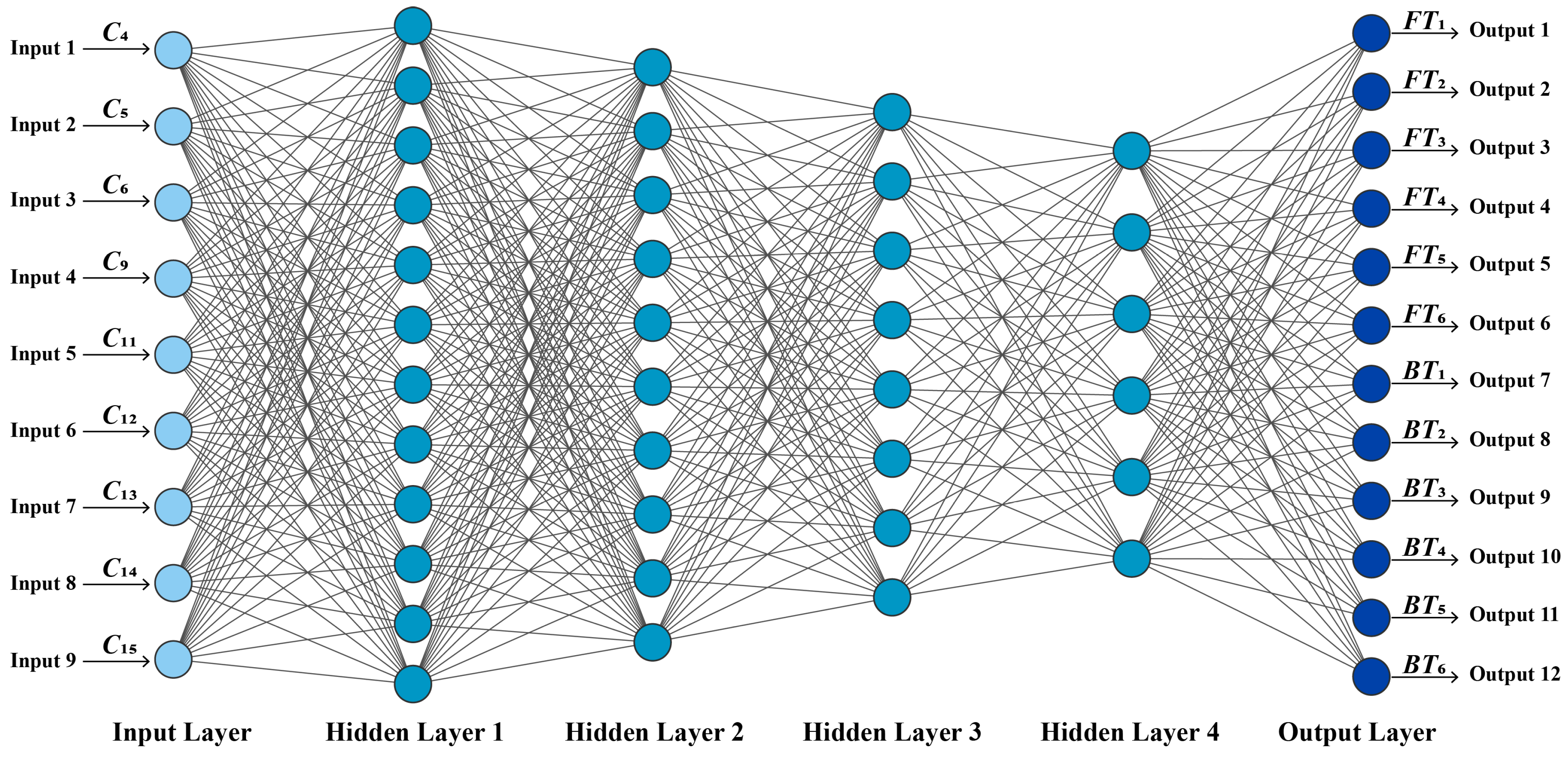
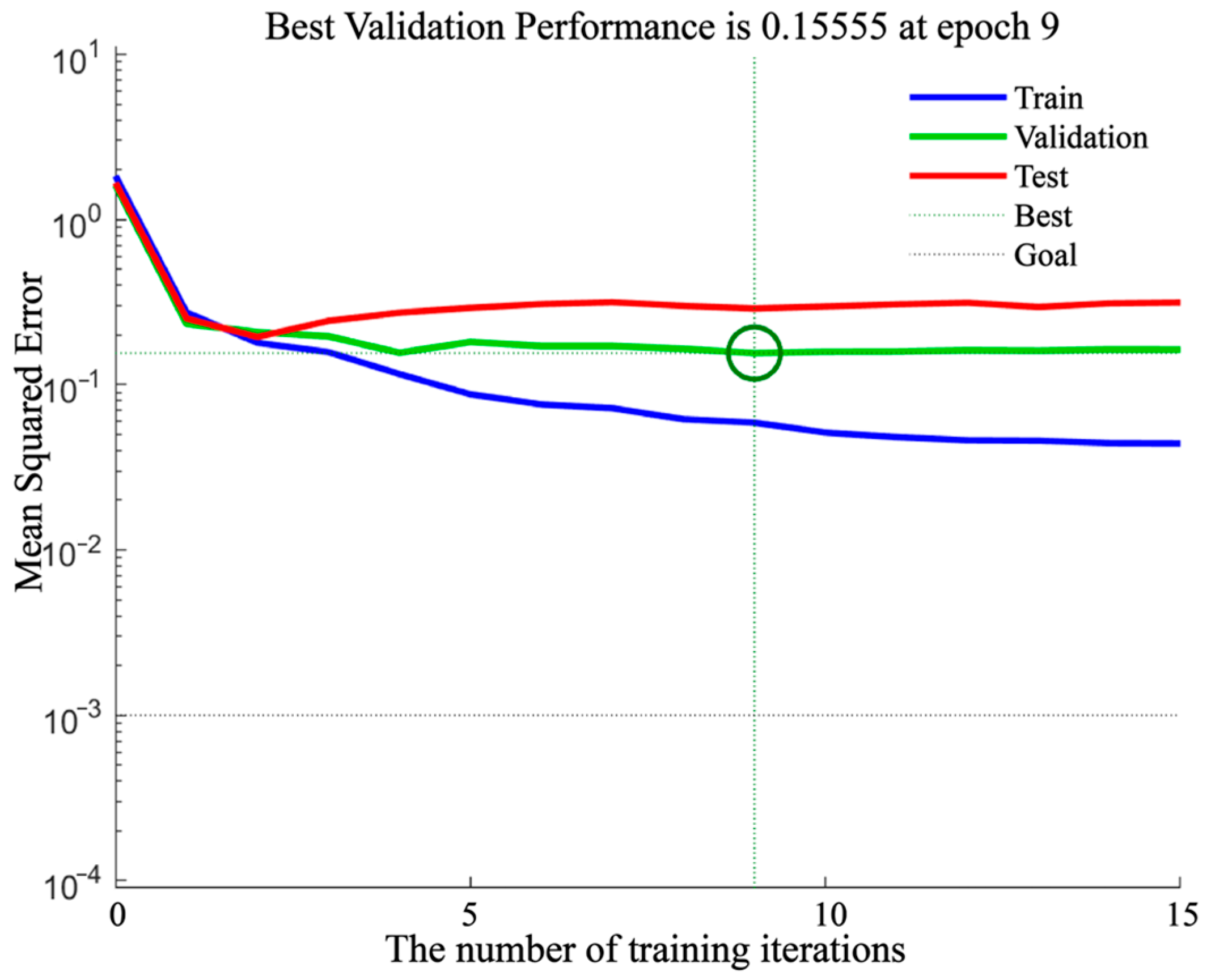
3.3. Prediction of Change Ratio of Pattern Dimension Based on BP Neural Network
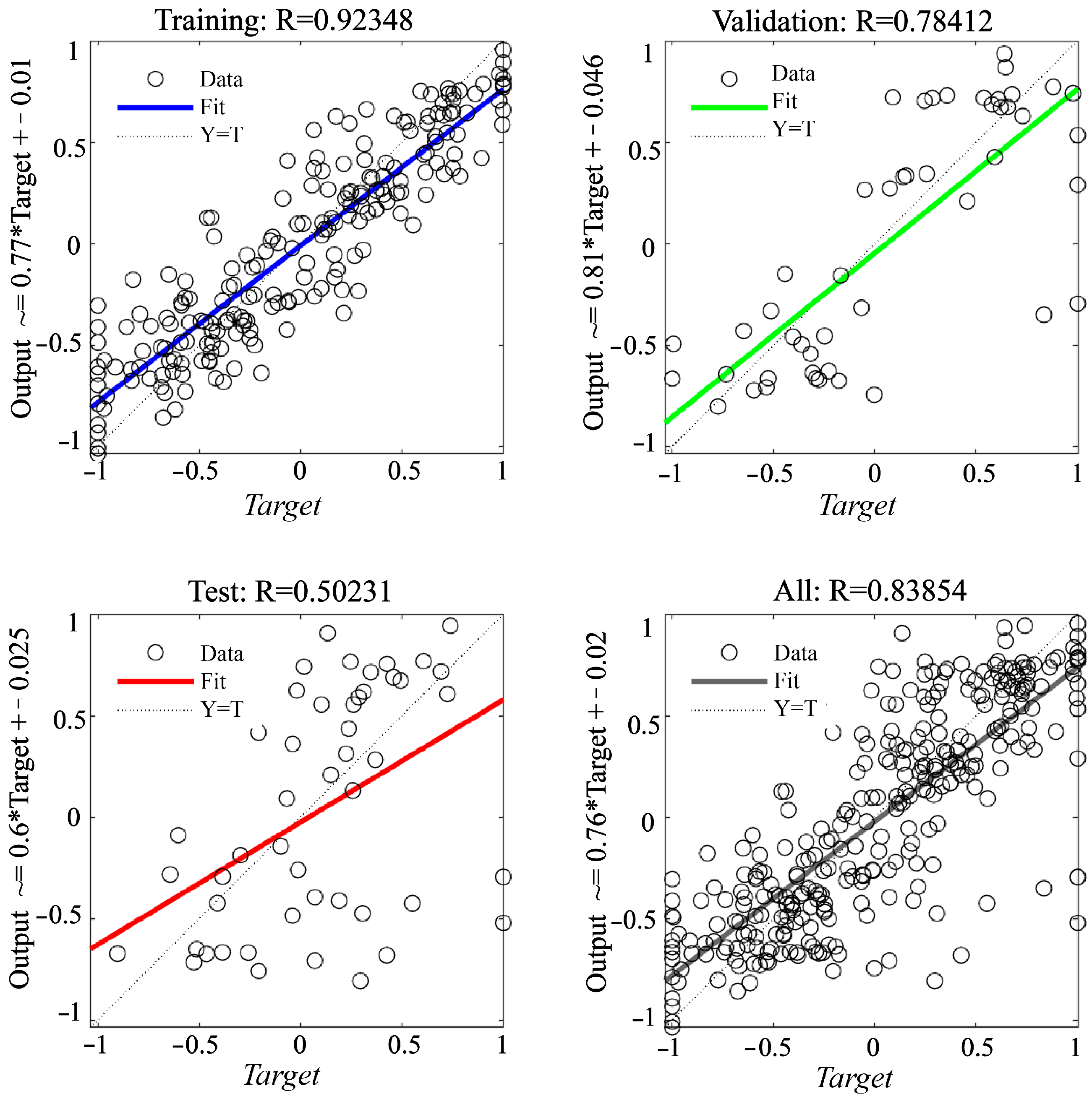
3.4. Evaluation of Predicted Model
4. Results and Discussion
4.1. Dimension Change Ratio Between Original and Developed Pattern
4.2. Correlation Analysis of Dimension Reduction Parameters
4.3. Model Prediction Performance
4.4. Comparison of Prediction Models
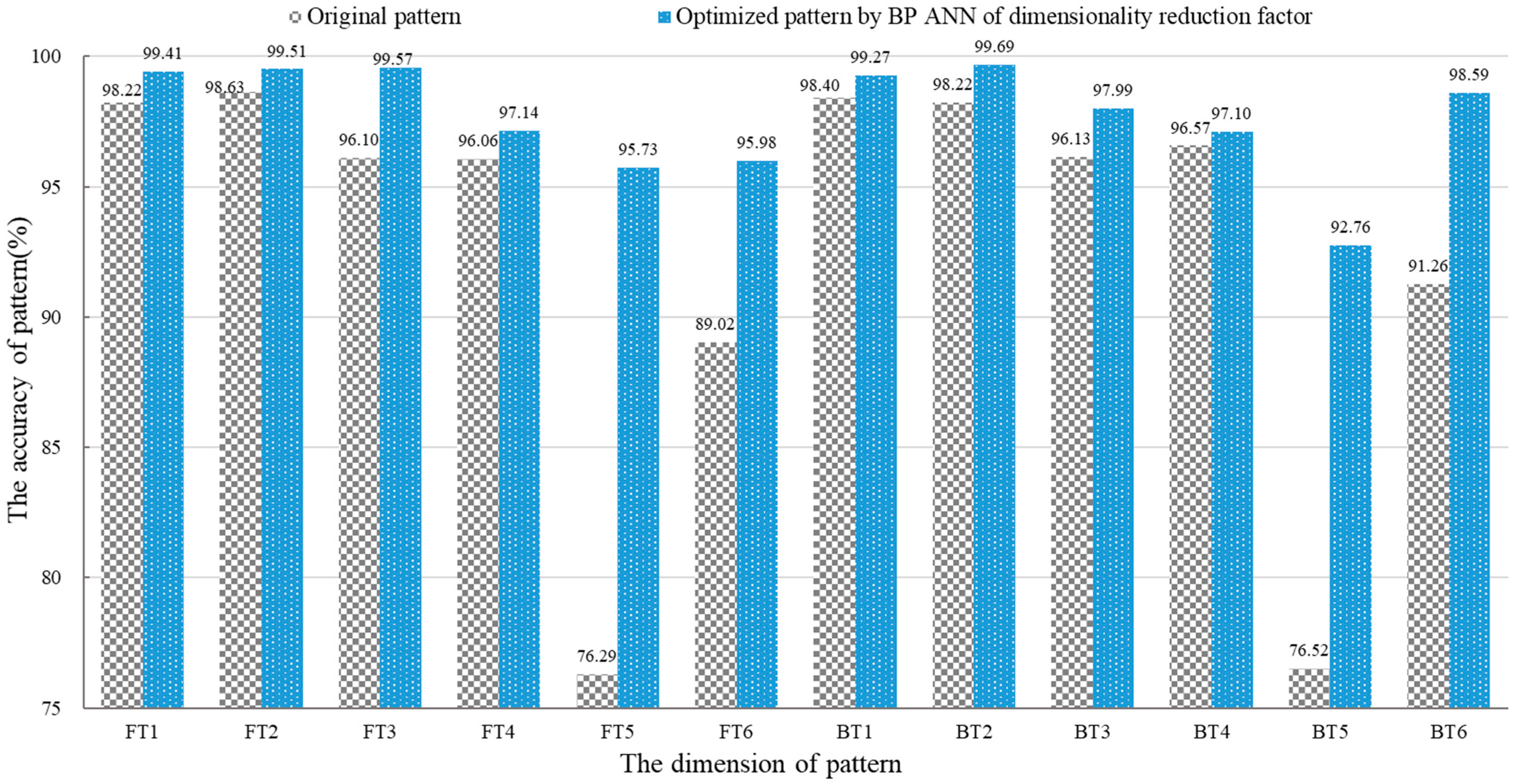
4.5. Improvement of Pattern Accuracy After Optimization
5. Conclusions
- (1)
- Principal component analysis was applied to reduce dimensionality, and correlation analysis was conducted. It was found that the pattern dimension was primarily influenced by parameters such as thickness, bending rigidity, drapability, and shear performance.
- (2)
- Compared with the RBF ANN method, the BP ANN model for the dimension reduction factor achieved an impressive average prediction accuracy of 96.44%. The full-factor BP ANN model demonstrated the most accurate predictions, with an average accuracy of 96.67%. However, the prediction accuracy of the RBF ANN model was comparatively lower, with average accuracies of 90.67% and 88.6% for the full-factor and dimension reduction factor models, respectively. This shows that the dimension reduction factor BP ANN model can replace the full factor due to the minor difference.
- (3)
- After the parameterized correction of the dimension-reducing factor BP ANN prediction model, the pattern accuracy was notably enhanced by 5.11%, reaching 97.73%. It was proven that the prediction model is effective in optimizing the pattern dimensions from scanned garments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BP ANN | Backpropagation Artificial Neural Network |
| RBF ANN | Radial Basis Function Artificial Neural Network |
| PCA | Principal Component Analysis |
| CAD | Computer-Aided Design |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| RMSE | Root Mean Square Error |
| relative RMSE | relative Root Mean Square Error |
| ACR | Average Change Ratio |
Appendix A
| Number | Center Front Length (%) | Side Seam Length (%) | Waistline (%) | Hemline Length (%) | Upwarping Angle of Waistline (%) | Upwarping Angle of Hemline (%) | Center Back Length (%) | Side Seam Length (%) | Waistline (%) | Hemline Length (%) | Upwarping Angle of Waistline (%) | Upwarping Angle of Hemline (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FT1 | FT2 | FT3 | FT4 | FT5 | FT6 | BT1 | BT2 | BT3 | BT4 | BT5 | BT6 | |
| N1 | 1.05 | −0.66 | 4.53 | −2.81 | −15.74 | −8.40 | 1.61 | −0.31 | 1.64 | −0.47 | −12.49 | −3.94 |
| N2 | 0.41 | −0.45 | 0.23 | −0.54 | −19.86 | −9.02 | 0.13 | −0.07 | −1.07 | 1.98 | −12.24 | −4.07 |
| N3 | 0.12 | −1.33 | 4.67 | −3.29 | −12.77 | −6.65 | 0.14 | −2.07 | 1.19 | 0.03 | −14.13 | −9.41 |
| N4 | 4.35 | 5.68 | −5.61 | 0.37 | −16.84 | −13.80 | 0.64 | −1.50 | −5.94 | 4.74 | −11.46 | −7.62 |
| N5 | −0.10 | 0.27 | 0.18 | 0.22 | −11.89 | −4.28 | 2.24 | 2.62 | −0.32 | 0.72 | −20.86 | −8.78 |
| N6 | 3.23 | 4.19 | −7.36 | −1.20 | −24.71 | −10.80 | 1.24 | 2.96 | −3.36 | −4.07 | −22.80 | −10.94 |
| N7 | 0.06 | −0.88 | −3.34 | 0.12 | −14.30 | −1.28 | −0.14 | −1.08 | −2.07 | 0.27 | −12.81 | −0.72 |
| N8 | 3.04 | 0.77 | −3.72 | −0.32 | −17.69 | −5.14 | 0.26 | 1.17 | 0.77 | −0.90 | −12.58 | −5.44 |
| N9 | 0.51 | −0.28 | 3.59 | −0.64 | −9.01 | −3.75 | 0.21 | −1.82 | 6.77 | −0.80 | −13.80 | −6.37 |
| N10 | −0.52 | 0.14 | −4.79 | −0.65 | −8.73 | −3.36 | −0.49 | −1.32 | 1.49 | 3.47 | −12.23 | −3.78 |
| N11 | −0.13 | −2.13 | −4.15 | 2.58 | −13.12 | −2.20 | 0.52 | −2.00 | −0.78 | 2.58 | −16.90 | −1.94 |
| N12 | −0.28 | 0.50 | −1.38 | −0.16 | −11.91 | −5.38 | −0.71 | 0.27 | −0.58 | 0.63 | −9.36 | −2.13 |
| N13 | −1.00 | −0.50 | −2.92 | 0.44 | −8.97 | −3.76 | 0.00 | −0.29 | 0.51 | 0.59 | −10.51 | −6.40 |
| N14 | 1.25 | 2.46 | −8.28 | −4.90 | −32.98 | −16.52 | 2.00 | 4.06 | −5.95 | −5.82 | −32.77 | −17.77 |
| N15 | 1.27 | −1.45 | −4.71 | 0.00 | −16.57 | −5.14 | 1.90 | −2.97 | −3.23 | −0.76 | −26.46 | −7.65 |
| N16 | 0.24 | −1.13 | −3.93 | 1.78 | −13.28 | −3.54 | 0.85 | −0.35 | −2.86 | 0.71 | −15.66 | −2.72 |
| N17 | 2.87 | 4.40 | −3.70 | −0.07 | −16.33 | −8.12 | 0.55 | 0.87 | −0.12 | 2.67 | −17.58 | −3.53 |
| N18 | −1.46 | 0.58 | −5.13 | −0.20 | −14.34 | −6.74 | −0.39 | 0.36 | −0.12 | −0.15 | −13.39 | −7.81 |
| N19 | 1.64 | −0.23 | −5.97 | −0.60 | −19.23 | −5.41 | 0.06 | 0.45 | −3.59 | −1.63 | −16.07 | −7.67 |
| N20 | 0.66 | 2.05 | −5.99 | −1.57 | −10.03 | −5.78 | 1.05 | −0.20 | 1.69 | −2.79 | −17.54 | −7.04 |
| N21 | −0.28 | −0.68 | −0.19 | 0.23 | −11.73 | −3.00 | −0.61 | −1.62 | −3.89 | 0.69 | −11.88 | 0.50 |
| N22 | −0.31 | 0.64 | −3.41 | 0.54 | −13.04 | −4.27 | 0.76 | 1.33 | −2.56 | 0.27 | −14.31 | 0.54 |
| N23 | 2.59 | 4.72 | 2.87 | −1.88 | −23.61 | −14.06 | 2.72 | 4.22 | −1.48 | −2.86 | −26.21 | −17.37 |
| N24 | 0.24 | −1.75 | −1.88 | −1.30 | −17.38 | −3.62 | 3.65 | 5.66 | 1.54 | 0.82 | −17.43 | −6.35 |
| N25 | −1.48 | −1.79 | −7.20 | −2.43 | −20.18 | −6.49 | −1.25 | −1.19 | −6.15 | −2.03 | −18.15 | −7.52 |
| N26 | 0.75 | 1.28 | −5.21 | −0.75 | −14.72 | −6.51 | 1.41 | 0.55 | −4.86 | −0.46 | −14.04 | −5.04 |
| N27 | 0.06 | 0.20 | −7.00 | 2.09 | −16.07 | −4.12 | 1.27 | 0.57 | −3.66 | 0.37 | −17.03 | −3.51 |
| N28 | 3.03 | 2.58 | −0.13 | −1.22 | −20.66 | −7.77 | 0.61 | −1.24 | −1.64 | 0.33 | −16.66 | 0.02 |
| N29 | −2.00 | 1.47 | −5.92 | −3.34 | −18.39 | −11.36 | 2.21 | 0.52 | −7.06 | −3.84 | −26.37 | −9.36 |
| N30 | 3.05 | 1.30 | −1.21 | −12.28 | −48.74 | −25.15 | 2.51 | −1.03 | 2.13 | −12.16 | −43.30 | −25.75 |
| ACR | 1.27 | 1.55 | 3.97 | 1.62 | 17.09 | 7.18 | 1.07 | 1.49 | 2.63 | 1.99 | 17.57 | 6.72 |
References
- Lyu, Y.; Wang, Z.; Ye, Q.; Sun, Y.; Chao, J. Body data-driven garment pattern construction in digital fashion innovations: A review. Text. Res. J. 2025. [CrossRef]
- Zhang, J.; Innami, N.; Kim, K. Upper garment 3D modeling for pattern making. Int. J. Cloth. Sci. Technol. 2015, 27, 852–869. [Google Scholar] [CrossRef]
- Chen, X.W.; Zhou, B.; Lu, F.X.; Wang, L.; Bi, L.; Tan, P. Garment modeling with a depth camera. ACM Trans. Graph. 2015, 34, 1–12. [Google Scholar] [CrossRef]
- Lin, N.; Lin, J.; Lin, N. Reverse 3D garment model reconstruction technology research. Adv. Mater. Res. 2012, 480, 2148–2151. [Google Scholar] [CrossRef]
- Bang, S.; Korosteleva, M.; Lee, S.H. Estimating Garment Patterns from Static Scan Data. Comput. Graph. Forum. 2021, 40, 273–287. [Google Scholar] [CrossRef]
- Chen, J.Z.; Guo, Z.Y.; Li, T.; Du, L.; Zou, F.Y. An undamaged pattern generation method from 3D scanned garment sample based on finite element approach. Ind. Textilă 2023, 74, 35–41. [Google Scholar] [CrossRef]
- Matsudaira, M.; Masuda, T.; Wada, M.; Yokura, H. Shape factor of flared skirts compared with that of circular fabrics. J. Text. Eng. 2015, 61, 69–73. [Google Scholar] [CrossRef]
- Lagė, A.; Ancutienė, K. Virtual try-on technologies in the clothing industry: Basic block pattern modification. Int. J. Cloth. Sci. Technol. 2019, 31, 729–740. [Google Scholar] [CrossRef]
- Magnenat-Thalmann, N.; Volino, P. From early draping to haute couture models: 20 years of research. Vis. Comput. 2005, 21, 506–519. [Google Scholar] [CrossRef][Green Version]
- Porterfield, T.A.; Lamar, M. Examining the effectiveness of virtual fitting with 3D garment simulation. Int. J. Fash. Des. Technol. Ed. 2017, 10, 320–330. [Google Scholar] [CrossRef]
- Rödel, H.; Schenk, A.; Herzberg, C.; Krzywinski, S. Links between design, pattern development and fabric behaviours for clothes and technical textiles. Int. J. Cloth. Sci. Technol. 2001, 13, 217–227. [Google Scholar] [CrossRef]
- Špelic, I. The current status on 3D scanning and CAD/CAM applications in textile research. Int. J. Cloth. Sci. Technol. 2019, 32, 891–907. [Google Scholar] [CrossRef]
- Zhang, D.L.; Li, J.T.; Wang, J. Design patterns of soft products using surface flattening. J. Comput. Inf. Sci. Eng. 2018, 18, 021011. [Google Scholar] [CrossRef]
- Khedher, F.; Jaouachi, B. The principal component analysis method to study mechanical properties and denim manufactured garment shrinkage. Int. J. Cloth. Sci. Technol. 2025, 37, 387–401. [Google Scholar] [CrossRef]
- Hristian, L.; Ostafe, M.M.; Dulgheru, I.; Buhu, L.; Buhu, A.; Negru, D. Identification of influence factors on physical-mechanical properties, using the principal component analysis, in selecting the textile fabrics for the clothing products. Ind. Textilă. 2020, 71, 438–445. [Google Scholar] [CrossRef]
- Peters, J.F. Delaunay Mesh Segmentation. In Foundations of Computer Vision; Springer: Cham, Switzerland, 2017; pp. 199–209. [Google Scholar]
- Wang, C.C.L.; Smith, S.S.F.; Yuen, M.M.F. Surface flattening based on energy model. Comput. Aid Des. 2002, 34, 825–833. [Google Scholar] [CrossRef]
- Liu, Q.S.; Xi, J.T.; Wu, Z.Q. An energy-based surface flattening method for flat pattern development of sheet metal components. Int. J. Adv. Manuf. Technol. 2013, 68, 1155–1166. [Google Scholar] [CrossRef]
- Yang, Y.C.; Zou, F.Y.; Li, Z.; Ji, X.F.; Chen, M.Z. Development of a prototype pattern based on the 3D surface flattening method for MTM garment production. Fibres Text. East. Eur. 2011, 19, 107–111. [Google Scholar]
- Fang, J.J.; Ding, Y. Energy-based optimal darted pattern for garment design. Int. J. Cloth. Sci. Technol. 2014, 26, 164–183. [Google Scholar] [CrossRef]
- Peng, Y.J.; Zhu, Y.X.; Zhang, M.M.; Ma, Y.; Wang, Y.H. Surface flattening based on energy fabric deformation model in garment design. In Proceedings of the 2017 International Conference on Virtual Reality and Visualization (ICVRV), Zhengzhou, China, 21–22 October 2017; pp. 73–78. [Google Scholar]
- Zhuang, M.; Zhang, X.; Fang, J. The optimum flattening for undeveloped 3-D body surface based on energy. In Proceedings of the 2010 International Conference on Electronics and Information Engineering (ICEIE 2010), Kyoto, Japan, 1–3 August 2010. [Google Scholar]
- Thomassey, S.; Zeng, X. Artificial Intelligence for Fashion Industry in the Big Data Era; Springer: Singapore, 2018; pp. 1–6. [Google Scholar]
- Giri, C.; Jain, S.; Zeng, X.; Bruniaux, P. A detailed review of artificial intelligence applied in the fashion and apparel industry. IEEE Access 2019, 7, 1. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Xing, Y.; Yang, Y.; Liu, K. Estimating human body dimensions using RBF artificial neural networks technology and its application in activewear pattern making. Appl. Sci. 2019, 9, 1140. [Google Scholar] [CrossRef]
- Ko, E.; Kim, S. Garment pattern nesting using image analysis and three-dimensional simulation. Fiber Polym. 2013, 14, 860–865. [Google Scholar] [CrossRef]
- Wang, J.; Song, J.Y.; Tang, A.Q. A model construction about predicting the rate of dimensional change after wash of fabric composites. Adv. Mat. Res. 2011, 332–334, 496–499. [Google Scholar] [CrossRef]
- Kalkanci, M.; Sinecen, M.; Kurumer, G. Prediction of dimensional change in finished fabric through artificial neural networks. Text. Appar. 2018, 28, 43–51. [Google Scholar]
- Dowdy, S.; Wearden, S.; Chilko, D. Statistics for Research; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhang, W.B. Apparel Construction Design; China Textile & Apparel Press: Beijing, China, 2006. [Google Scholar]
- Rivara, M.C.; Diaz, J. Terminal triangles centroid algorithms for quality delaunay triangulation. Comput. Aid Des. 2020, 125, 102870. [Google Scholar] [CrossRef]
- Kuzmichev, V.E.; Tislenko, I.V.; Adolphe, D.C. Virtual design of knitted compression garments based on bodyscanning technology and the three-dimensional-to-two-dimensional approach. Text. Res. J. 2018, 89, 2456–2475. [Google Scholar] [CrossRef]
- McCartney, J.; Hinds, B.K.; Chong, K.W. Pattern flattening for orthotropic materials. Comput. Aid Des. 2005, 37, 631–644. [Google Scholar] [CrossRef]
- Olive, D.J. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2017; pp. 189–217. [Google Scholar]
- Kalkanci, M.; Kurumer, G.; Öztürk, H.; Sinecen, M.; Kayacan, Ö. Artificial neural network system for prediction of dimensional properties of cloth in garment manufacturing: Case study on a T-shirt. Fibres Text. East. Eur. 2017, 25, 135–140. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Kamalha, E.; Li, V.; Zeng, X. Construction of a prediction model for body dimensions used in garment pattern making based on anthropometric data learning. J. Text. Inst. 2017, 108, 2107–2114. [Google Scholar] [CrossRef]
- Phellan, R.; Hachem, B.; Clin, J.; Mac-Thiong, J.M.; Duong, L. Real-time biomechanics using the finite element method and machine learning: Review and perspective. Med. Phys. 2021, 48, 7–18. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Liu, Q.; Sun, P.; Fu, X.; Zhang, J.; Yang, H.; Gao, H.; Li, Y. Comparative analysis of BP neural network and RBF neural network in seismic performance evaluation of pier columns. Mech. Syst. Signal Process 2020, 141, 106707. [Google Scholar] [CrossRef]




| Sample | Fabric Content | Weave Structure | Warp Density (Threads/cm) | Weft Density (Threads/cm) | Weight (g/m2) | Fabric Thickness (mm) | Warp Bending Rigidity (N/m) | Weft Bending Rigidity (N/m) | Warp Elastic Modulus (MPa) | Weft Elastic Modulus (MPa) | Static Drape Coefficient (%) | |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | ||||
| N1 | 100% Cotton | 2/1 Left-Hand Twill | 29 | 46 | 176.00 | 0.32 | 20.30 | 22.00 | 394.39 | 411.81 | 0.61 | |
| N2 | 100% Cotton | 2/1 Left-Hand Twill | 57 | 21 | 286.33 | 0.53 | 52.33 | 45.33 | 708.87 | 157.56 | 0.76 | |
| N3 | 100% Cotton | 1/1 Plain | 18 | 13 | 184.67 | 0.52 | 18.33 | 15.33 | 219.95 | 110.13 | 0.65 | |
| N4 | 100% Cotton | 1/1 Plain | 41 | 28 | 108.33 | 0.24 | 2.67 | 2.67 | 790.81 | 361.32 | 0.46 | |
| Warp Shear | Weft Shear | Warp Tensile | Weft Tensile | |||||||||
| Sample | Shear Stiffness (G) (N/cm·deg) | 0.5 Shear Lag Distance (2HG) (N/cm) | 5 Shear Lag Distance (2HG5) (N/cm) | Shear Stiffness (G) (N/cm·deg) | 0.5 Shear Lag Distance (2HG) (N/cm) | 5 Shear Lag Distance (2HG5) (N/cm) | Tensile Linearity (LT) (-) | Drawing Power (WT) (N·cm/cm2) | Response Rate of Stretching Power (RT) (%) | Tensile Linearity (LT) (-) | Drawing Power (WT) (N·cm/cm2) | Response Rate of Stretching Power (RT) (%) |
| C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | C19 | C20 | C21 | |
| N1 | 2.53 | 4.13 | 8.20 | 2.59 | 3.71 | 8.25 | 0.75 | 8.24 | 48.35 | 0.81 | 12.76 | 40.61 |
| N2 | 1.55 | 9.51 | 2.73 | 2.58 | 8.42 | 6.56 | 0.85 | 16.88 | 36.05 | 0.65 | 55.58 | 36.89 |
| N3 | 1.27 | 2.76 | 4.36 | 1.50 | 2.53 | 5.20 | 0.70 | 11.53 | 55.27 | 0.75 | 7.05 | 61.43 |
| N4 | 0.82 | 1.11 | 2.17 | 0.75 | 0.99 | 2.08 | 0.72 | 8.32 | 53.43 | 0.62 | 19.54 | 44.50 |
| Component | Initial Eigenvalues | Rotational Sums of Square Loadings | ||||
|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | |
| 1 | 9.361 | 44.575 | 44.575 | 9.361 | 44.575 | 44.575 |
| 2 | 3.023 | 14.397 | 58.972 | 3.023 | 14.397 | 58.972 |
| 3 | 2.288 | 10.893 | 69.865 | 2.288 | 10.893 | 69.865 |
| 4 | 1.708 | 8.132 | 77.997 | 1.708 | 8.132 | 77.997 |
| 5 | 1.304 | 6.209 | 84.207 | 1.304 | 6.209 | 84.207 |
| 6 | 0.966 | 4.601 | 88.807 | --- | --- | --- |
| Variable Name | Component | Variable Name | Component | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | ||
| C1 | 0.072 | −0.200 | 0.159 | −0.016 | 0.049 | C12 | 0.082 | 0.115 | −0.063 | −0.042 | 0.214 |
| C2 | −0.046 | 0.143 | 0.062 | −0.038 | 0.444 | C13 | 0.095 | 0.111 | −0.064 | −0.051 | 0.091 |
| C3 | 0.076 | −0.136 | 0.206 | 0.017 | 0.105 | C14 | 0.097 | 0.065 | −0.064 | 0.025 | 0.041 |
| C4 | −0.044 | 0.075 | 0.141 | 0.299 | 0.291 | C15 | 0.098 | 0.097 | 0.002 | −0.009 | 0.07 |
| C5 | 0.076 | 0.013 | 0.249 | 0.068 | −0.196 | C16 | 0.026 | 0.183 | 0.041 | −0.015 | −0.437 |
| C6 | 0.083 | 0.003 | 0.257 | 0.067 | −0.037 | C17 | 0.033 | −0.118 | 0.028 | 0.391 | 0.232 |
| C7 | −0.043 | 0.252 | 0.022 | 0.215 | −0.076 | C18 | −0.067 | −0.01 | 0.135 | −0.291 | 0.029 |
| C8 | −0.061 | 0.22 | 0.031 | 0.199 | −0.013 | C19 | 0.044 | 0.127 | 0.019 | −0.299 | 0.204 |
| C9 | 0.08 | 0.103 | 0.166 | 0.075 | −0.211 | C20 | 0.054 | −0.094 | −0.224 | 0.176 | −0.042 |
| C10 | 0.095 | 0.071 | −0.081 | −0.116 | 0.107 | C21 | −0.055 | 0.039 | 0.30 | −0.131 | 0.103 |
| C11 | 0.097 | 0.071 | −0.093 | −0.016 | 0.098 | ||||||
| Number of Hidden Layers | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| R value | 0.5735 | 0.7005 | 0.809 | 0.725 | 0.6984 | 0.664 | 0.5732 |
| Mean absolute error (%) | 6.23 | 4.71 | 3.33 | 5.59 | 5.81 | 5.21 | 5.43 |
| Number | Center Front Length (%) | Side Seam Length (%) | Waistline (%) | Hemline Length (%) | Upwarping Angle of Waistline (%) | Upwarping Angle of Hemline (%) | Center Back Length (%) | Side Seam Length (%) | Waistline (%) | Hemline Length (%) | Upwarping Angle of Waistline (%) | Upwarping Angle of Hemline (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FT1 | FT2 | FT3 | FT4 | FT5 | FT6 | BT1 | BT2 | BT3 | BT4 | BT5 | BT6 | |
| N1 | 1.05 | −0.66 | 4.53 | −2.81 | −15.74 | −8.40 | 1.61 | −0.31 | 1.64 | −0.47 | −12.49 | −3.94 |
| N2 | 0.41 | −0.45 | 0.23 | −0.54 | −19.86 | −9.02 | 0.13 | −0.07 | −1.07 | 1.98 | −12.24 | −4.07 |
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| N29 | −2.00 | 1.47 | −5.92 | −3.34 | −18.39 | −11.36 | 2.21 | 0.52 | −7.06 | −3.84 | −26.37 | −9.36 |
| N30 | 3.05 | 1.30 | −1.21 | −12.28 | −48.74 | −25.15 | 2.51 | −1.03 | 2.13 | −12.16 | −43.30 | −25.75 |
| ACR | 1.27 | 1.55 | 3.97 | 1.62 | 17.09 | 7.18 | 1.07 | 1.49 | 2.63 | 1.99 | 17.57 | 6.72 |
| Ordering | C6 | C9 | C15 | C5 | C12 | C13 | C14 | C4 | C11 |
|---|---|---|---|---|---|---|---|---|---|
| Dimension Reduction Parameters | Weft Bending Rigidity | Static Drape Coefficient | Weft 50 Shear Lag Distance | Warp Bending Rigidity | Warp 50 Shear Lag Distance | Weft Shear Stiffness | Weft 0.5 Shear Lag Distance | Thickness | Warp 0.5 Shear Lag Distance |
| Scores | 0.0814 | 0.0731 | 0.0730 | 0.0668 | 0.0666 | 0.0628 | 0.0596 | 0.0581 | 0.0571 |
| Prediction Methods | BP ANN for Full-Factor Data | BP ANN with Dimensionality Reduction Factor | RBF ANN for Full-Factor Data | RBF ANN with Dimensionality Reduction Factor |
|---|---|---|---|---|
| MAE (%) | 3.33 | 3.56 | 9.33 | 11.40 |
| Variance of error (%) of MAE | 1.31 | 5.05 | 42.36 | 43.29 |
| MAPE (%) | 6.24 | 8.95 | 30.70 | 14.45 |
| RMSE (%) | 4.47 | 6.64 | 16.45 | 16.31 |
| Relative RMSE | 0.39 | 0.58 | 1.55 | 1.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Guo, Z.; Li, T.; Sun, Y.; Yip, J.; Yick, K.-l.; Zou, F. Construction of Pattern Optimization Model Driven by Fabric Parameters in 3D Garment Development Using Artificial Neural Networks. Technologies 2025, 13, 487. https://doi.org/10.3390/technologies13110487
Chen J, Guo Z, Li T, Sun Y, Yip J, Yick K-l, Zou F. Construction of Pattern Optimization Model Driven by Fabric Parameters in 3D Garment Development Using Artificial Neural Networks. Technologies. 2025; 13(11):487. https://doi.org/10.3390/technologies13110487
Chicago/Turabian StyleChen, Jiazhen, Ziyi Guo, Tao Li, Yue Sun, Joanne Yip, Kit-lun Yick, and Fengyuan Zou. 2025. "Construction of Pattern Optimization Model Driven by Fabric Parameters in 3D Garment Development Using Artificial Neural Networks" Technologies 13, no. 11: 487. https://doi.org/10.3390/technologies13110487
APA StyleChen, J., Guo, Z., Li, T., Sun, Y., Yip, J., Yick, K.-l., & Zou, F. (2025). Construction of Pattern Optimization Model Driven by Fabric Parameters in 3D Garment Development Using Artificial Neural Networks. Technologies, 13(11), 487. https://doi.org/10.3390/technologies13110487







