Image-Type Data Security via Dynamic Cipher Composition from Method Libraries

Abstract

In this paper, we propose a novel Dynamic Cipher Composition (DCC) based on multi-algorithm approach using the Library of Image Encryption Methods (LIEM). Unlike conventional static encryption schemes, the proposed DCC randomly selects and applies different encryption algorithms to spatially segmented regions of an image during each execution. To manage this process efficiently, the system employs two lightweight registers: one for configuration management and another for region-specific modality assignment, both indexed for streamlined storage and retrieval. Experimental evaluations conducted on standard test images demonstrate that the DCC achieves a near-optimal Shannon entropy, high values of Net Pixel Change Rate (NPCR) and Unified Average Changing Intensity (UACI), and negligible pixel correlation coefficients. These results confirm the scheme’s strong resistance to statistical, differential, and structural attacks, while preserving computational efficiency suitable for real-time applications such as telemedicine, cloud storage, and video surveillance systems.

1. Introduction

Image-type data are becoming increasingly crucial for many applications, such as cloud storage [1] and medical diagnosis [2]. Protecting image content is, therefore, essential, and encryption remains the most common solution to do so. However, traditional encryption schemes have notable shortcomings when used to protect this type of complex data, which is distinguished by its spatial correlations, its redundancy between pixels in an image, and its multitude of statistical properties [1,2].

In this context, static encryption schemes have a very serious limitation when applied to image-type data because they apply each cryptographic transformation uniformly across all pixels, without it changing during different executions. This uniformity creates weaknesses when utilizing contemporary cryptanalysis techniques, such as frequency analysis, differential attacks, and correlation based pattern recognition [3].

Therefore, the inflexibility of static encryption ignores the specific security needs of image-type data, requiring more variable encryption schemes capable of modifying their cryptographic operations depending on the areas of an image-type data and the execution of uses [4].

In recent years, dynamic image-type data encryption systems have tried to solve all these problems with variable algorithms, but consequently, existing approaches tend to suffer from algorithmic inefficiency or not taking advantage of the full spatial diversity available. This gap informs our design of a new image-type data encryption framework, where we try to achieve three main objectives:

(1)

Dynamic selection of algorithms to utilize;

(2)

Advanced spatial segmentation; and 

(3)

Lightweight performance [5,6,7].

Our proposed encryption DCC embodies a breakthrough in image-type data security, due to its distinct design. Specifically, the system’s innovative structure lies in its dynamic multi-algorithm model, powered by its extensible cryptography repository and ability to accommodate long-standing retention of accommodation with respect to shifting security standards and threats. Algorithmic flexibility is enhanced with a sophisticated spatial segmentation where image-type data are divided into the security domains using customized encryption protocols [8].

This framework’s implementation uses an effective register-based management system that’s designed to keep high security levels while performing well. This is done through indexing and configuration that has been engineered to deliver high-level protection with minimal overhead while still keeping the latency levels low, which is imperative for certain applications [9,10].

The remainder of our article is organized as follows: Section 2 reviews relevant literature to contextualize our research. Section 3 introduces the proposed DCC framework, elaborating on its theoretical foundations and core principles. Section 4 presents the experimental evaluation conducted to validate the effectiveness of DCC. Section 5 offers a comprehensive discussion of the proposed methodology. Section 6 outlines potential directions for future research. Lastly, Section 7 concludes the paper by summarizing the key findings and contributions.

2. Related Work

Recent research has introduced numerous dynamic and multi-algorithm encryption schemes that aim to overcome the limitations of static approaches. For instance, hyperchaotic systems, such as the 6D multistable memristive chaotic framework, have been proposed to enhance diffusion and confusion by exploiting complex dynamical behaviors [11]. These methods achieve high entropy and strong resistance to statistical attacks, but their computational complexity may hinder deployment on lightweight platforms. Similarly, dynamic ciphers, like the novel Hill-based approach for medical IoT, integrate algebraic transformations with adaptive key scheduling to ensure sensitivity to plaintext variations [12]. While effective in constrained environments, such schemes remain bound to single algorithmic structures, limiting long-term adaptability. Other multi-method proposals combine chaotic maps, S-boxes, and DNA-based encodings to increase security diversity [13,14], yet often lack a systematic configuration strategy that balances efficiency with robustness.

Parallel research in image encryption has also diversified into several directions, including chaos-based systems, lightweight ciphers for IoT, and region-specific encryption. Chaos-based systems leverage nonlinear dynamics but often rely on static mapping, leading to predictable patterns and heavy computational overhead [15]. Lightweight ciphers reduce resource usage but usually depend on a single primitive, making them vulnerable to correlation attacks [16]. Region-specific approaches protect perceptually salient regions, particularly in medical contexts, but fail to fully decorrelate global image statistics and often require pre-processing segmentation [17]. Parallel and semantic-aware methods can improve throughput but introduce high metadata overheads or hardware dependencies [18]. Collectively, these approaches contribute valuable insights but highlight a persistent gap: the absence of a unified framework that can dynamically adapt methods, leverage spatial diversity, and remain computationally lightweight.

In our work, the proposed dynamic multi-method encryption strategy directly addresses this gap. It employs randomized selection of multiple algorithms from the LIEM during each encryption round, applied heterogeneously across spatially segmented regions of the image. Each disjoint region is encrypted with a distinct method and modality, ensuring ciphertext diversity across both space and rounds. This combination of dynamism and segmentation achieves strong resistance against statistical, differential, and structural attacks while maintaining lightweight performance suitable for real-time applications.

Compared to the approaches summarized in

Table 1. Comparative summary of related image encryption approaches.

Approach	Strengths	Shortcomings
Chaos-based systems [11,15,19]	Strong diffusion and confusion; resistant to many attacks; high entropy.	Often rely on static mappings; computationally heavy; limited for lightweight platforms.
Dynamic Hill cipher (IoT) [12,16]	Efficient in constrained devices; adaptive key scheduling; good NPCR/UACI.	Bound to single algebraic structure; limited long-term adaptability.
Multi-method hybrids (chaotic maps, S-boxes, DNA) [13,14]	Increase algorithmic diversity; improve security unpredictability.	Lack systematic configuration strategy; may suffer from inefficiency.
Region-specific encryption [17]	Protects sensitive regions; reduces computation.	Does not fully decorrelate global statistics; often requires manual segmentation.
Parallel/semantic-aware methods [18]	Improve throughput; enable content aware protection.	High metadata overhead; depend on hardware or external models.

, the proposed DCC addresses several persistent gaps in existing encryption frameworks. While chaos-based and hybrid methods offer strong confusion and diffusion, they often suffer from computational inefficiency or rigid algorithmic structures. Similarly, region-specific and parallel strategies improve efficiency but fail to ensure global decorrelation or introduce heavy metadata overhead. In contrast, our DCC framework integrates randomized multi-method selection with advanced spatial segmentation, enabling heterogeneous encryption across image regions while maintaining lightweight performance. This unique combination provides both adaptability and robustness, positioning DCC as a more balanced and scalable solution for real-time applications.

3. Proposed DCC

Let IEM denote an Image Encryption Method, and let M-LIEM represent the Library Image Encryption Methods. We define $\Omega (M,N)$ as the set of all possible outcomes when randomly selecting N distinct IEMs from M-LIEM, that is, the complete set of N-IEM configurations that can be formed from a repository of size M.

3.1. Principles of the Proposed DCC

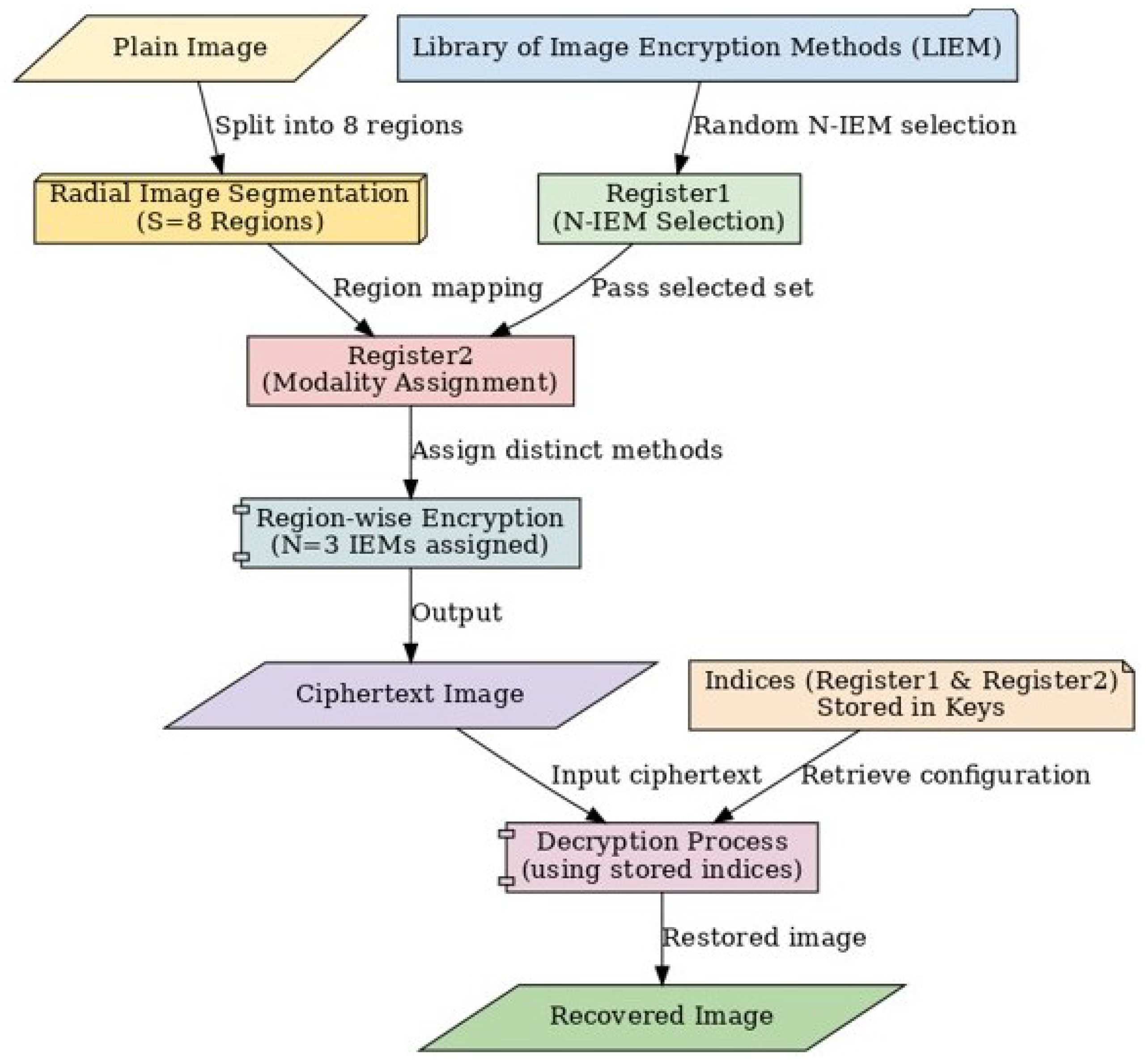
At each encryption round, the DCC initially partitions the plaintext image into multiple regions and determines the precise coordinates of each region before proceeding to encrypt each one distinctly from its neighboring regions [20]. Each region is then encrypted using a specific Image Encryption Method (IEM), resulting in the plaintext image being encoded with N distinct IEMs. These N-IEMs are randomly selected from the M-LIEM. The size of the repository, M, along with the number of methods employed per round, N, are both determined by solving constrained optimization problems to ensure an effective balance between security and computational efficiency [7,20]. The proposed DCC operates through the random utilization of two registers. The first register determines the N-IEM configuration applied during each encryption round, while the second regulates the specific modalities of their application. The fundamental principles underlying the proposed DCC are summarized in

Table 2. Principles of the proposed DCC.

Principle	Function	Innovation Highlight
1. Dynamic Method Provisioning	Provide a set of N-IEM encryption methods	Introduces a randomized, round dependent selection of encryption techniques through controlled interrogation of a Method Definer module «Register1». This promotes heterogeneity and unpredictability in algorithm choice.
2. Optimal Image Segmentation	Partition the plaintext image into SSS regions	Performs a structurally optimized and reversible decomposition of the image, ensuring that the spatial coordinates of each pixel region are precisely defined. This enables region-specific encryption and supports parallel processing.
3. Modal Regulation of Encryption	Govern encryption modalities for each region	Uses a second applicator «Register2» to orchestrate the modal behavior of encryption per region, ensuring that each region is encrypted under distinct rules and constraints, even when using the same method.
4. Round Configuration Memory	Store round specific configuration for decryption	The indexes referencing Register1 and Register2 are securely embedded in two cryptographic keys, each constrained to configurations admissible on 1-byte. This design ensures precise decryption and full reversibility, while preserving the confidentiality of internal DCC parameters and guaranteeing round to round cryptographic consistency.

.

By design and formulation, the proposed Dynamic DCC is inherently extensible, as it leverages a loadable and reloadable LIEM. This repository is populated with a cu-rated set of robust encryption algorithms, carefully chosen from the state-of-the-art advances in contemporary cryptographic research [21].

3.2. Construction of the N-IEM Selection Dictionary (Register1)

Register1 functions as the method definer, acting as an indexed dictionary containing all valid combinations of N distinct IEMs selected from the M-sized space $\Omega (M,N)$. This ensures that only admissible configurations are retained for cryptographic deployment. The generation of Register1 is detailed in the subsequent algorithm.

The detailed steps of the Generator Register (N-IEM Selection Dictionary) are outlined below.

• Initialization Steps:

  (a)

  Initialize Register1 as an empty list.

  (b)

  Set the index counter to zero.

  (c)

  Retrieve the method set containing M distinct image encryption methods.

• Procedure:

  (a)

  Iterate over all possible triplets of methods from the method set.

  (b)

  For each triplet, verify that the three selected methods are distinct.

  (c)

  If the condition is satisfied, create a record including the index and the three methods.

  (d)

  Append the record to Register1.

  (e)

  Increment the index counter by one.

  (f)

  Repeat the process until all valid triplets have been examined.

• Output:

  (a)

  A fully populated Register1 containing all valid and unique triplets of distinct image encryption methods.

  (b)

  Each triplet is associated with an index for efficient lookup during encryption and decryption.

 At this point in the DCC’s design, the parameters M and N need to be carefully optimized so that the total number of possible arrangements, represented by A(M, N), remains within the 1-byte storage limit (allowing 256 indexable entries) while still achieving maximum cryptographic diversity. The next subsection presents a thorough combinatorial analysis of this optimization, highlighting the tradeoff between security and performance.

3.3. Combinatorial Optimization of Selection Parameters

The objective is to jointly optimize M (library size) and N (methods per round), subject to the 1-byte indexing constraint (≤256 values). Rather than an analytical approach, which risks converging towards local optima, we adopt a graphical resolution, allowing us to globally visualize the cryptographic diversity spectrum, defined by the number of ordered arrangements:

$$A(M,N)={\displaystyle \frac{M!}{(M-N)!}}$$

(1)

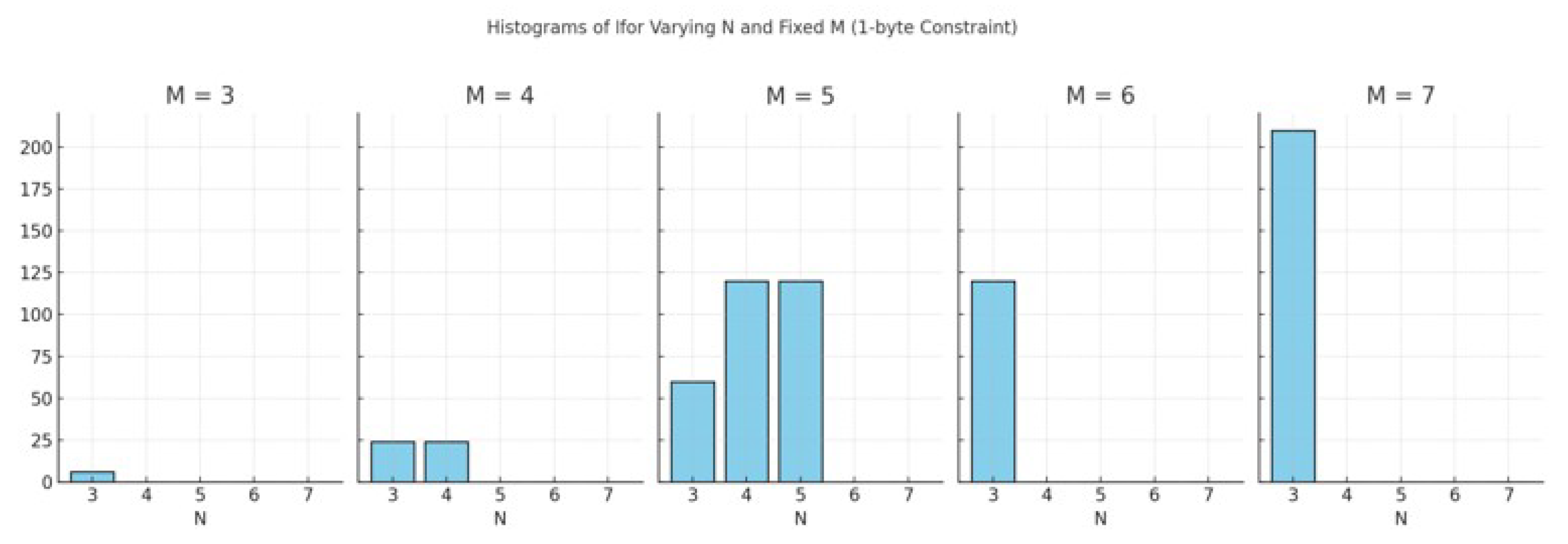
 The cardinality of possible encryption method configurations, depending on the available methods (M) and the number of methods used per encryption round (N), is outlined in Figure 1. This analysis is critical for ensuring that the selected configurations remain within the 1-byte constraint enforced by the system for parameter storage while maximizing the diversity of encryption possibilities. The histogram highlights that choosing M = 7 and N = 3 yields a high cardinality of 210 distinct configurations, providing a rich pool of method combinations. This balance between maximizing configuration diversity and adhering to system constraints is fundamental to the proposed DCC’s design, ensuring adaptability and security.

3.4. Deployment of Register1

According to the combinatorial analysis, selecting M = 7 encryption methods within the library and utilizing N = 3 methods per encryption round results in 210 unique configurations that remain compliant with the system’s 1-byte indexing constraint. The Register1 Method Specifier, illustrated in Figure 2, organizes these configurations within a compact, indexed framework to support efficient storage and quick access during encryption and decryption. This structured indexing not only facilitates lightweight implementation within constrained environments but also ensures that a diverse set of encryption techniques can be dynamically applied across different image regions, thereby enhancing the overall security and adaptability of the proposed encryption DCC.

The 1-byte indexing scheme employed during the encryption and decryption processes enables rapid lookup and retrieval of configurations while maintaining minimal memory overhead.

3.5. Radial Segmentation and Regional Mapping for Encryption

Various segmentation strategies can be employed within the proposed encryption framework to partition the plaintext image into distinct regions for region-specific encryption, as presented in Figure 3. These strategies include both linear segmentation, which divides the image into uniform rectangular or grid-based sections, and non-linear segmentation, which utilizes more complex geometries, such as radial or angular partitions, to disrupt spatial correlations effectively. The selection of the segmentation approach significantly influences the encryption performance, as it determines how the image structure is decomposed to enhance inter-region entropy and resist structural attacks. By employing flexible segmentation methods, the proposed DCC ensures adaptability to diverse application requirements while maintaining high security through increased spatial confusion within the ciphertext.

Radial segmentation [22] was selected for this study, as it divides the image into wedge-shaped regions radiating from a central focal point, effectively disrupting structural patterns and enhancing inter-region entropy. This segmentation approach provides robust resilience against various attacks while preserving visual coherence, making it particularly suitable for applications requiring both high security and perceptual sensitivity. In this work, the image is partitioned into $S^{*}=8$ distinct regions using this method, with the detailed steps of the corresponding algorithm presented below. The $S^{*}=8$ regions are defined by the partitioning. The detailed steps of the second algorithm of the image segmentation into eight regions are outlined below.

• Initialization Steps:

  (a)

  Input: Image I of size $L\times W$ (rows × columns).

  (b)

  Define P as the set of all pixels in I:

  $P=\left\{p(i,j)|0\le i<L,0\le j<W\right\}$

  $P=\left\{p(i,j)|0leqi<L,0leqj<W\}P=\left\{p\right(i,j)\mid 0\le i<L,0\le j<W\right\}.$

  (c)

  Initialize $\mathrm{Regions}[1..8]$ as empty sets to store segmented regions.

• Procedure:

  (a)

  Initialize eight empty regions to store pixel groupings.

  (b)

  Iterate over each pixel in the image.

  (c)

  Check the vertical position of each pixel to determine if it is in the upper or lower half of the image.

  (d)

  Evaluate the horizontal position and relative coordinates of the pixel.

  (e)

  Assign each pixel to one of the eight regions based on its position and predefined geometric rules.

  (f)

  Repeat the process until all pixels have been assigned to a region.

  (g)

  Return the eight segmented regions for subsequent region-wise encryption.

• Output: A list of eight segmented regions $\left(\mathrm{Regions}[1..8]\right)$, each containing a subset of the image’s pixels, ready for region-specific encryption with distinct methods in the proposed DCC.

L and W, respectively, are the length and width of the image, and i and j are the abscissa and ordinate of the pixel.

3.6. Generation and Indexing of Encryption Modalities Applicator in Register2

At this operational phase of the DCC, we have the following:

• An image segmentation into 8 radial regions.
• A random selection of N = 3 IEMs (renewable at each round) (see Algorithm 3) from the LIEM via Register1.

To complete the DCC, we need to perform a constrained assignment of the N = 3 selected methods from the current round to the S = 8 defined image regions, under the constraint that no adjacent regions share the same method. All valid assignments of encryption modalities to the S = 8 segmented regions are reported in the encryption applicator “Register2”, which is generated using the following algorithm.

The detailed steps of the third algorithm of Generator of Register2 (Encryption Modalities Applicator) are outlined below.

• Initialization steps:

  (a)

  Initialize Register2 as an empty list.

  (b)

  Set the index counter to zero.

  (c)

  Define the number of available encryption methods in the round as N (e.g., N=3).

  (d)

  Define the number of regions for encryption as SubblockCount = 8.

• Procedure:

  (a)

  Generate all possible modality configurations for the eight regions using the N methods selected in the round.

  (b)

  Ensure that the same encryption method is not assigned to two adjacent regions (adjacency constraint).

  (c)

  For each valid configuration, assign an index to the configuration.

  (d)

  Store the indexed configuration in Register2.

  (e)

  Increment the index counter and repeat the process until all valid configurations are generated.

• Output:

  (a)

  A fully populated Register2 containing all valid modality configurations for the eight image regions.

  (b)

  Each configuration ensures that adjacent regions are encrypted using different methods, thereby increasing security and local variability.

  (a)

  The index assigned to each configuration allows efficient lookup and restoration during encryption and decryption.

 At the structure of Register2 is presented in Figure 4, which serves as the encryption modalities applicator within the proposed DCC framework. This register ensures that the randomly selected methods from Register1 are systematically assigned to the eight segmented image regions while respecting the adjacency constraint, meaning no two neighboring regions share the same encryption algorithm. By enforcing this constraint, Register2 significantly enhances local variability and disrupts spatial correlations across the ciphertext, thereby strengthening resistance against statistical and differential attacks. The indexed organization also facilitates efficient lookup and retrieval during both encryption and decryption processes, ensuring lightweight implementation without compromising security. Each row is a valid modality configuration:

• It respects the adjacency constraint: ${\mathrm{IEM}}_i\ne {\mathrm{IEM}}_{i+1}$.
• It uses only the $N=3$ methods available from the round’s active Register1 entry.
• The index is used as a reference for reuse or selection during encryption.

If Index $=1$ is drawn for a given encryption round:

• Region 1 → Logistic
• Region 2 → AES
• Region 3 → Hill
• Region 4 → Logistic
• ... etc.

This approach guarantees that different encryption algorithms are systematically applied across the spatial regions of the image, thereby enhancing the entropy and introducing localized confusion within the ciphertext. By ensuring that adjacent regions are encrypted using distinct methods, the proposed DCC disrupts spatial correlations and increases the unpredictability of the encrypted image, which significantly improves resistance against statistical and differential attacks.

3.7. Indexing and Restoration Protocol in the Encryption DCC

The encryption DCC utilizes two 1-byte indices to retrieve the selected N-IEM combination (Register1) and its application modality across the S = 8 image regions (Register2). This design ensures that each configuration remains within a 1-byte constraint, thereby enabling maximum storage efficiency for backup and restoration purposes [22,23,24]. An overview of the process is presented in Figure 5.

Conversely, in the decryption phase, through the extraction of the indexes stored in the two 256-pixel keys, by exploring the two Registers “Register1”/“Register2”, we can determine the 3*-IEM used and also the modality of its application to the encryption of the $S^{*}=8$ regions of the clear image.

3.8. Register Security Assessment and Scalability Strategy

The DCC, which relies on dynamic non-persistence for its security, uses two 1-byte indexed registers, allowing for 65,536 configurations (256 × 256). As a result, if a compromise is detected, it becomes obsolete because the indices are randomly generated at each cycle.

However, the DCC was designed to be extensible, offering the possibility of increasing the register size to 2, 4, or even 16 bytes, thereby expanding the key space to over $2^{128}$ configurations. This extensibility allows for the security–performance balance to be calibrated according to the usage context, without undermining the dynamic and unpredictable nature of the cryptographic processes.

4. Experimental Study

4.1. Experimental Setup

4.1.1. LIEM Cryptographic Library

To operate the DCC system, we define the LIEM library with the following cryptographic methods:

• AES: A symmetric block cipher known for its high security and efficiency [25].
• Hill Cipher: A linear algebra based cipher that uses matrix multiplication for transformation [26].
• RC4: A fast-stream cipher commonly used for secure data transmission [27].
• Logistic Map Permutation: A chaos-based method that permutes pixel positions to enhance diffusion [28].
• S-box Substitution: A nonlinear substitution technique that introduces confusion by replacing input bits with output bits via a predefined box [29].
• SPN (Substitution–Permutation Network): A structured block cipher design combining substitution and permutation layers for strong diffusion and confusion [30].
• DNA Encoding Schemes: Cryptographic transformations inspired by biological DNA structures, allowing for the complex encoding of pixel data [31].

These methods are provided for illustrative purposes; in a practical deployment, they should be replaced with robust, standardized alternatives.

4.1.2. Test Image Dataset

The image dataset employed in this study consists of standard grayscale and RGB test images, which are commonly used in cryptographic benchmarking, as shown in Figure 6.

4.1.3. Evaluation Metrics

To validate the effectiveness of the proposed DCC, we took into account several cryptographic and statistical metrics.

• Histogram Uniformity: This evaluates the resistance to histogram attacks.
• Entropy (H): This quantifies randomness in the pixel intensity distribution. For 8-bit images, ideal value = 8 bits, the entropy is calculated as follows:

  $$H=-\sum _{i=0}^{255}p\left(i\right){log}_{2}p\left(i\right)$$

  (2)

  where p(i) represents the probability of occurrence of intensity value i in the image.
• NPCR (Number of Pixel Change Rate): This measures the percentage of pixels that differ between two encrypted images when only a single pixel in the original image is slightly modified. A value close to 100% indicates that the encryption scheme is highly sensitive to small input changes, which is desirable for resisting differential attacks [32]. It is formally defined as follows:

  $$NPCR={\displaystyle \frac{1}{W\times H}}\sum _{i=1}^W\sum _{j=1}^{H}D(i,j)\times 100\%$$

  (3)

  where W and H are the dimensions of the image, and D(i,j) = 1, if the pixel values at position (i,j) in the two encrypted images are different, and 0 otherwise. A value close to 100% indicates high sensitivity to small changes in the plaintext, which is desirable for resisting differential attacks.
• UACI (Unified Average Changing Intensity): This evaluates the average intensity difference between two encrypted images corresponding to almost identical original images. Values around 33% (for 8-bit images) reflect strong diffusion properties and uniform spreading of small changes across the entire ciphertext [33,34]:

  $$UACI={\displaystyle \frac{1}{W\times H}}\sum _{i=1}^W\sum _{j=1}^H{\displaystyle \frac{|C_1(i,j)-C_2(i,j)|}{255}}\times 100\%$$

  (4)

  where $C_1$ and $C_2$ are the two encrypted images, and the denominator 255 corresponds to the maximum pixel intensity in 8-bit images. A UACI value around 33% reflects strong diffusion properties and uniform propagation of small changes throughout the ciphertext.
• Correlation Coefficients: These measure the spatial dependence between adjacent pixels in horizontal, vertical, and diagonal directions using Pearson’s correlation coefficient:

  $$r={\displaystyle \frac{{\sum }_{k=1}^N(x_k-\overline{x})(y_k-\overline{y})}{\sqrt{{\sum }_{k=1}^N{(x_k-\overline{x})}^2}·\sqrt{{\sum }_{k=1}^N{(y_k-\overline{y})}^2}}}$$

  (5)

  where $(x_k,y_k)$: adjacent pixel intensities;
  $(\overline{x},\overline{y})$: their means;
  N: pair number. Near-zero r indicates broken spatial correlation (resisting statistical attacks).
• Execution Time: Encryption/decryption times (ms) per image measured for fair comparison.

4.2. Results and Analysis

The set of images displayed demonstrates the plaintext samples alongside their encrypted counterparts generated by the proposed DCC. The encrypted outputs show no visible similarity to the originals, proving that the method effectively conceals structural and perceptual details, as shown in Figure 7. This visual evidence highlights the reliability of the scheme in protecting both grayscale and RGB images, making it suitable for diverse application contexts in secure data transmission.

The statistical evaluation confirms the robustness of the proposed encryption. As outlined in Figure 8, the histograms of the ciphertexts appear uniformly distributed, which eliminates statistical redundancies and strengthens resistance against histogram-based analysis. In addition, the correlation diagrams reveal that strong dependencies among adjacent pixels in plaintext images are thoroughly broken after encryption, ensuring effective protection against statistical and differential attacks.

4.2.1. Key Sensitivity Analysis

We evaluated DCC’s response to minimal key perturbations by altering configuration indices:

• $id{x}_1^{\prime }=id{x}_{1}1mod210$.
• $id{x}_2^{\prime }=id{x}_{2}mod89$.

The results of the key sensitivity analysis conducted on different test images are summarized in

Table 3. Key sensivity results.

Image	NPCR (%)	UACI (%)	NPCR Range (%)	UACI Range (%)
Lena	99.6142	33.4721	99.59–99.63	33.45–33.50
Peppers	99.6029	33.4917	99.58–99.62	33.46–33.51
Baboon	99.6098	33.4778	99.57–99.61	33.44–33.49
Male	99.6171	33.5092	99.59–99.64	33.47–33.52
Avg	99.6110	33.4877	99.58–99.63	33.45–33.51

. The values of NPCR consistently exceed 99.60%, while UACI remains close to the ideal benchmark of 33%. These results demonstrate that even a minimal change in the encryption key produces a completely different ciphertext, highlighting the high sensitivity and robustness of the proposed DCC against differential attacks. The narrow variation ranges for NPCR and UACI further confirm the stability and reliability of the encryption scheme.

4.2.2. Noise Resistance

Regional confinement: The independent encryption of segmented regions isolates noise artifacts. Data corruption remains strictly localized without cross-region propagation—a critical advantage over monolithic encryption schemes.

4.2.3. Resistance to Known/Chosen Plaintext Attacks

Security stems from dynamic composition of known algorithms (Kerckhoffs’s principle), not their secrecy. Randomized per-round selection of methods and spatial applications ensures security

4.2.4. Histogram Analysis

All ciphertext images exhibited near-uniform histograms, indicating successful masking of original pixel distributions. The visual results confirm the absence of residual structures.

4.2.5. Entropy Results

The entropy results for both plaintext and encrypted images are presented in

Table 4. Entropy results.

Image	Plaintext Entropy	Encrypted Entropy
Lena	7.46	7.9992
Peppers	7.29	7.9988
Baboon	7.54	7.9973
Male (1024 × 1024)	7.11	7.9983

. While the entropy values of the original images range between 7.11 and 7.54, the encrypted versions achieve values very close to the ideal of 8. This demonstrates that the proposed DCC successfully increases randomness in the ciphertext, thereby eliminating predictable statistical patterns. The consistently high entropy across all test images confirms the ability of the system to resist entropy-based cryptanalysis and reinforces its robustness in securing image data.

4.2.6. NPCR and UACI Results

We performed differential analysis by altering a single pixel in the plaintext image.

The NPCR and UACI values obtained from the differential analysis are illustrated in

Table 5. NPCR and UACI results.

Image	NPCR (%)	UACI (%)
Lena	99.6142	33.4721
Peppers	99.6029	33.4917
Baboon	99.6098	33.4778
Male	99.6171	33.5092

, where a single pixel change in the plaintext image is evaluated for its impact on the ciphertext. Across all tested images, NPCR values are consistently above 99.60%, and UACI values are around 33.5%, both of which meet or exceed standard cryptographic benchmarks. These results highlight the strong sensitivity of the proposed DCC to minor input variations, ensuring effective resistance against differential attacks. Compared to existing approaches, which often trade sensitivity for efficiency, our framework demonstrates that high levels of security can be achieved without compromising lightweight performance, thereby underscoring the practical advantage of the proposed DCC.

4.2.7. Correlation Analysis

The correlation coefficients between adjacent pixels (in plaintext and ciphertext images) are shown below:

The correlation coefficients of adjacent pixels in plaintext and ciphertext images are presented in

Table 6. Correlation results.

Direction	Plaintext				Encrypted
	Lena	Peppers	Baboon	Male	Lena	Peppers	Baboon	Male
Horizontal	0.9186	0.9562	0.8677	0.9294	0.0014	0.0008	−0.0056	−0.0027
Vertical	0.9588	0.9691	0.8356	0.9636	0.0012	0.0027	−0.0081	0.0029
Diagonal	0.8855	0.9244	0.7883	0.9038	-0.0011	−0.0008	0.0021	0.0002

, across horizontal, vertical, and diagonal directions. The plaintext images exhibit strong correlations ranging from 0.79 to 0.96, which reflects the inherent redundancy of natural images. After encryption with the proposed DCC, these correlations drop to values close to zero or slightly negative, indicating that spatial dependencies are effectively disrupted. This sharp reduction confirms that the ciphertext does not preserve structural information from the original images, thereby resisting statistical correlation attacks. Unlike many existing schemes that only partially reduce pixel correlation, our approach achieves near-complete decorrelation while maintaining real-time efficiency, further demonstrating the strength of the proposed DCC.

4.2.8. Execution Time and Efficiency

Despite its structural complexity, the proposed DCC achieves real-time encryption performance suitable for secure cloud transmission and lightweight systems. Effectively, encryption and decryption times remain under 90 ms for large images and under 45 ms for smaller ones, confirming the lightweight nature of the proposed DCC, as shown in

Table 7. Execution time and efficiency.

Image	Encryption Time (ms)	Decryption Time (ms)
Lena	84.1	83.5
Peppers	86.3	85.6
Baboon	89.9	88.2
Male	44.7	44.2

. Despite its structural complexity, the system achieves a real-time performance suitable for practical applications, such as telemedicine, cloud storage, and surveillance.

4.3. Comparative Evaluation

In addition to comparisons with mono-method encryption schemes (e.g., AES-only, Hill-only), we also considered more recent contributions in image encryption. For instance, the work on a 6D multistable memristive chaotic system demonstrated strong hyperchaotic properties that enhanced image confusion and diffusion [11]. Their reported entropy values approached 7.99 with NPCR above 99.60%, which are comparable to our DCC results. However, their approach relies heavily on complex chaotic dynamics, which may introduce implementation overhead on lightweight devices. In contrast, our DCC achieves similar or superior statistical strength while maintaining lightweight performance through register-based indexing.

Similarly, the dynamic Hill cipher proposed for medical IoT applications provided an efficient matrix-based transformation with dynamic key scheduling [12], yielding NPCR and UACI close to theoretical benchmarks. While their design excels in resource-constrained medical scenarios, it remains limited by the algebraic structure of Hill transformations, which may reduce long-term adaptability. Our proposed DCC improves upon this by combining multiple heterogeneous methods dynamically, thus avoiding single-algorithm weaknesses while preserving execution speed suitable for real-time applications.

Overall, these comparisons confirm that the DCC not only achieves state of the art statistical robustness but also introduces practical advantages in terms of modularity, adaptability, and lightweight performance.

5. Discussion

As summarized in

Table 8. Comparative summary of related image encryption approaches with our DCC.

Approach	Framework Type	Algorithmic Diversity	Topological Processing	Overhead (Bytes)	Key Limitations
Chaos-Based Systems [11,15]	Hyperchaotic/nonlinear dynamics	Low/Fixed (chaotic maps)	Fixed/static region mapping	16–32	Static mappings, high computational overhead; limited for lightweight use
Dynamic Hill Cipher (IoT) [12,16]	Matrix-based dynamic cipher	Single (algebraic primitive)	Uniform block processing	4–8	Bound to linear structure; limited adaptability
Multi-Method Hybrids (Chaotic + S-box + DNA) [13,14]	Combined multi-method schemes	Moderate (few hybridized methods)	Partial spatial/bit-level ops	12–24	Lack systematic configuration; potential inefficiency
Region-Specific Encryption  [17]	ROI-based selective framework	Single (ROI focus)	Content-aware segmentation	12–24	Requires preprocessing; fails to decorrelate global statistics
Parallel/ Semantic-Aware  [18]	Hardware/content-aware schemes	Model-dependent	Semantic segmentation	≥64	High metadata overhead; hardware/model dependency
Proposed DCC (This Work)	Dynamic multi-method, register-based engine	High (randomized LIEM selection)	Angular partitioning/ region-wise heterogeneous encryption	2	N/A

, existing encryption frameworks exhibit trade-offs between security strength, algorithmic flexibility, and implementation feasibility. Chaos-based systems achieve strong diffusion and confusion but are constrained by high computational complexity, which limits their use in lightweight platforms [11,15]. Dynamic Hill ciphers perform efficiently in IoT scenarios but remain structurally tied to a single algebraic primitive, reducing their adaptability [12,16]. Hybrid methods that combine chaotic maps, S-boxes, or DNA encoding increase algorithmic diversity but often lack systematic coordination strategies, which may compromise efficiency [13,14]. Region-specific encryption reduces processing costs by focusing on salient areas, yet fails to fully disrupt global statistical dependencies [17], while parallel and semantic-aware approaches benefit from throughput and content sensitivity but introduce significant overhead and hardware dependencies [18]. In contrast, the proposed DCC framework demonstrates a more balanced design: its register-based configuration enables lightweight operation, while randomized multi-method selection and spatial segmentation provide high algorithmic diversity and region-wise heterogeneity. This combination allows DCC to maintain robust resistance against statistical, differential, and structural attacks while ensuring efficiency suitable for real-time applications (Table 8).

The proposed image encryption DCC demonstrates a robust framework for enhancing image-type data security by leveraging a dynamic, multi-method encryption strategy combined with spatial segmentation [35]. The experimental results confirm the DCC’s effectiveness in achieving near-optimal entropy, high NPCR and UACI values, and low correlation between adjacent pixels in the encrypted images, indicating strong resistance to statistical and differential attacks. The modular design, utilizing a cryptographic repository (LIEM) with dynamically selected subsets of methods, ensures adaptability and scalability, while the lightweight 1-byte indexing system enables efficient implementation even in resource-constrained environments.

Radial segmentation, as applied in this study, contributes to the robustness of the DCC by increasing the inter-region entropy and reducing structural correlations in the ciphertext, which is crucial for resisting pattern-based attacks. The effective management of encryption modalities via Register2 further diversifies the encryption process, ensuring that adjacent regions are encrypted with different algorithms from the active subset, enhancing local confusion and overall security.

Despite these strengths, the current implementation is primarily tested on standard grayscale and RGB images under controlled conditions, and the execution times, while suitable for many real-time applications, may require further optimization for ultra-low-latency environments, such as live streaming and IoT edge devices [36].

The proposed DCC has broad application potential in domains that require secure, efficient, and real-time protection of image data. It can be applied to cloud-based image storage and transmission, where confidentiality of sensitive data must be preserved; telemedicine and medical imaging, to protect patient records and diagnostic visuals; video surveillance and defense systems, ensuring integrity and privacy of critical footage; and biometric data protection, safeguarding identifiers such as fingerprints and facial scans. Furthermore, due to its lightweight and modular design, the DCC is well-suited for IoT and edge devices with limited computational resources while also being adaptable for privacy-preserving analytics in AI pipelines, enabling secure computation on encrypted images without prior decryption.

6. Future Work

This study presents a flexible and extensible image encryption framework that leverages dynamic method selection [37], optimized region segmentation [38], and lightweight register-based configuration [39]. By systematically combining multiple cryptographic methods within a single encryption round and applying them across disjoint image regions, the proposed DCC enhances security without sacrificing efficiency.

Future work will focus on several key directions. First, extending the proposed approach to secure real-time video streams will be investigated, which will require additional strategies for maintaining synchronization and minimizing latency [40,41]. Second, adaptive method selection using intelligent decision models could further optimize the choice of encryption techniques based on image characteristics or context-specific constraints [42]. Third, integrating quantum-resistant cryptographic algorithms into LIEM would strengthen the DCC’s resilience against emerging quantum computing threats [43]. Moreover, hardware acceleration on FPGA or GPU platforms will be explored to improve the performance of embedded systems and IoT applications [44]. Finally, future studies will examine the integration of the proposed DCC with privacy-preserving analytics to enable secure computation on encrypted images without requiring decryption [6,41], thus expanding its applicability in secure cloud-based storage, medical imaging, and other sensitive domains.

In addition, recent advances in image encryption highlight new directions that could further enrich our framework. Multi-image encryption schemes, such as batch image encryption using cross-image permutation and diffusion, demonstrate the potential of extending protection to sets of correlated images simultaneously [3,20]. Parallelized encryption approaches, including intra-bitplane scrambling methods, exploit hardware-level acceleration to reduce latency and improve throughput [18]. Furthermore, semantically enhanced selective encryption techniques leverage image content understanding to balance security with computational efficiency [39]. In future work, the proposed DCC engine can be extended to integrate such advanced paradigms by incorporating multi-image handling, parallel computing strategies, and semantic-aware encryption modules within the LIEM repository. This would enable the framework to remain adaptable to emerging requirements in high-performance and intelligent security systems.

7. Conclusions

This study presents a modular and extensible image encryption DCC that employs diverse cryptographic techniques as a core security strategy. Unlike conventional mono-algorithmic approaches, the proposed DCC integrates a curated LIEM, from which a subset of N algorithms is selected in each encryption round and systematically applied across segmented image regions. By combining segmentation, multi-method selection, and indexed modality assignment, the DCC can generate highly variable, region-wise heterogeneous ciphertexts even when encrypting the same image multiple times.

The design achieves an effective balance between implementation efficiency and cryptographic flexibility through lightweight 1-byte indexing and register-based configuration management. Combinatorial analysis and experimental validation identified optimal parameters, supporting up to 210 distinct method combinations.

Overall, the proposed DCC enables encryption to become a dynamic and structurally adaptable process. Its ability to disrupt spatial redundancies, prevent ciphertext uniformity, and incorporate randomness in both technique and modality positions it as a promising solution for secure image transmission in cloud environments, biometric protection, and resource-constrained systems.

The proposed encryption engine can be applied in several domains requiring robust image security. Typical use cases include cloud-based image storage and transmission, telemedicine and medical imaging, video surveillance and defense systems, biometric data protection, and IoT or edge devices where lightweight yet strong encryption is essential. Furthermore, its modular design makes it suitable for privacy-preserving analytics in secure cloud-based AI pipelines.