1. Introduction
The mining industry has witnessed an increased adoption of automation systems across various stages of mineral processing, driven by the need to enhance safety and reduce operational costs. A critical task in this process is secondary reduction, which involves the use of heavy-duty manipulators equipped with hydraulic hammers to reduce the size of oversized rocks.
Figure 1 illustrates rock-breaker hammers, which are utilized to break down large rocks that are unable to pass through grizzly systems or primary crushers. This process, when performed efficiently, ensures a continuous and uninterrupted flow in the processing line, thereby minimizing downtime and enhancing both operational efficiency and productivity [
1].
Research in this field has explored various approaches, including the operation of robotic systems through teleoperation. For instance, ref. [
2] describes the design of a haptic teleoperation system for underground mines. The effective automation of rock reduction requires the implementation of intelligent robotic systems with advanced visual perception capabilities. Initial efforts to automate or modernize rock-breaking systems can be traced back to 1998, when image processing techniques were employed to detect rocks on grizzly systems [
3]. While effective at the time, these early processes had several limitations, including a high sensitivity to environmental conditions, computational intensity, a lack of generalizability, and inefficiency compared to modern deep learning methods.
A comparative analysis of machine learning and deep learning algorithms for rock detection in complex mining environments revealed that the You Only Look Once (YOLO) v4 algorithm offers the highest accuracy, while the Single-Shot Detector (SSD) provides the fastest processing speed [
4]. Further advancements in this field include the development of a deep reinforcement learning scheme for rock breaking using an impact hammer, as presented in [
5]. This approach formulates the problem as a Partially Observable Markov Decision Process and employs Deep Double Deep-Q Networks (DDDQN) for its solution.
Real-time three-dimensional (3D) rock detection has emerged as an effective approach for information processing in mining environments. Numerous studies have explored and leveraged these technologies in various mining contexts. For instance, ref. [
6] evaluated the performance and robustness of clustering methods for object recognition during the secondary breaking phase in mining, utilizing Low-Cost Time-of-Flight (ToF) cameras. This research proposed an algorithmic method to efficiently utilize existing clustering and segmentation techniques in the detection loop, determining optimal contact points and approach angles for hydraulic hammers. An autonomous rock-breaking system featuring a Visual Perception System (VPS) capable of real-time detection of multiple irregularly shaped rocks was presented in [
1]. Employing a stereo camera and an industrial manipulator, the system achieved an average success rate of 34% and a breaking rate of 3.3 attempts per minute in a real experimental environment. Furthermore, ref. [
7] introduced a system for automatically determining target poses for rock breaking in underground mines, utilizing sensor data comprising point clouds and images to segment rocks and generate and evaluate candidate target poses.
Advancements in multimodal fusion techniques were demonstrated in [
8], which presented a system for object identification in point clouds with varying density and coverage. By integrating Light Detection and Ranging (LiDAR) sensors and a ToF camera, the system implemented preprocessing, registration, and data fusion techniques to create a coherent and detailed representation of objects in a controlled environment, thereby optimizing rock-crushing operations in the mining industry.
A visual perception system for rock-breaking robots utilizing sensor fusion, specifically combining cameras and LiDAR, was proposed in [
9]. The system employed the PP-YOLO algorithm for 2D detection and 3D reconstruction from point cloud data, achieving a detection speed of 13.8 ms, a mean Average Precision (mAP) of 91.2%, and a segmentation accuracy of 75.46% for rock-breaking surfaces.
While these studies focus directly on rock detection and localization in mining environments, it is also valuable to consider recent applications of deep learning in related fields, which could offer insights applicable to mining automation. Recent advancements include the automatic classification of road tunnel defects using Ground Penetrating Radar (GPR) images, as presented in [
10]. This study evaluated four models, with the Vision Transformer (ViT) demonstrating superior performance, achieving an average accuracy of 98.1%. Additionally, ref. [
11] employed the YOLO algorithm for the automatic detection of steel ribs in GPR images of tunnels. The study’s evaluation of performance on original and augmented datasets yielded miss rates of 7.18% and 0.38%, respectively. When combined with data augmentation, this technique shows considerable potential for enhancing automation in tunnel maintenance and inspection processes.
Although these investigations have laid important foundations in the detection and localization of rocks in mining environments, it is crucial to recognize that point cloud processing and conversion to Bird’s Eye View (BEV) are techniques that have seen significant advances in other fields. These innovations offer promising opportunities to improve the accuracy and efficiency in rock centroid localization. Recent studies have demonstrated the effectiveness of BEV representations in various tasks. In [
12], a BEV-based loop closure detection method for LiDAR point clouds is presented. The method proves to be robust to rotations and computationally efficient, achieving a mAP of up to 71.81% on the Waymo dataset.
In [
13], a multi-view fusion approach is proposed that combines range (RV) and BEV representations to improve semantic segmentation of point clouds. It also uses a geometric fusion module to align and combine features from both views. It achieves an mIoU of 76.1% on the nuScenes dataset. In [
14], a geometric flow network for semantic segmentation of point clouds is proposed, using BEV and RV projections. It achieves an mIoU of 65.4% on SemanticKITTI. These advances underscore the potential of BEV representations to efficiently compress 3D data and leverage well-established 2D convolutional network architectures.
In addition to these data processing techniques, recent advances in neural network architectures, particularly those based on modular or block structures, present new possibilities for addressing the specific challenges of rock localization in mining. For example, in [
15], an efficient Multi-scale Attention Module (EMA) is proposed that divides channel dimensions into multiple sub-features, retaining information per channel and decreasing computational overhead. Their method achieved a mAP of 57.8% in object detection on COCO. In [
16], a Block-Combined Neural Network (BCNN) is introduced for predicting sediment transport rates, dividing tasks into modular sub-networks, achieving a correct classification rate of 89.77%. Finally, in [
17], the researchers propose a block-based convolutional neural network for image forgery detection, incorporating attention mechanisms, with an accuracy of up to 97.97% on the CASIA v2.0 database.
The aforementioned technologies for 3D detection enable precise and efficient material identification, thereby facilitating the automation of critical tasks in mining operations. However, the processing of such data presents significant challenges due to the diverse shapes, sizes, and textures of rocks. To fully harness the advantages of 3D technology and optimize operational accuracy and efficiency in mining, advanced data analysis methods are essential.
In response to these challenges, this research focuses on the development of a rock centroid localization system characterized by both accuracy and speed, making it suitable for application in mining robotic systems such as rock-breaking hammers. The primary contributions of this study are as follows:
The development and validation of an optimized algorithmic pipeline: This study presents a novel approach combining point cloud preprocessing, BEV conversion, and segmentation using YOLO v8x-Seg, complemented by a postprocessing method employing two variants for rock centroid determination. The developed pipeline demonstrates high-precision centroid localization, achieving a Euclidean distance in the XY plane () of up to 0.0128 m and a normalized error () in the X and Y axes not exceeding 2.3%. These results indicate the successful mitigation of the specific challenges associated with rock localization in mining environments;
Enhanced adaptability and robustness in varied mining conditions: The developed system exhibits consistent performance across diverse lighting conditions and in the presence of suspended particles, a crucial factor for its practical application in dynamic mining environments. This adaptability was achieved through the optimization of system parameters and the incorporation of real mine data in the training set;
Comprehensive experimental validation in real and simulated scenarios: The system underwent rigorous testing using a stationary rock breaker and other industrial equipment in both controlled environments and actual mining conditions. The validation process incorporated tests with 100 point clouds obtained directly from the “La Patagua” mine under a range of operational conditions. This extensive testing protocol ensures the transferability of laboratory results to real-world applications in the mining industry.
The structure of this paper is as follows:
Section 2 provides an overview of the fundamental theoretical aspects underlying point cloud processing, BEV representation, and the YOLO v8 detection algorithm.
Section 3 details the design of the rock centroid localization system.
Section 4 presents and analyzes the results of the study. Finally,
Section 5 concludes the paper and outlines future research directions.
3. System Design
This section provides an in-depth exploration of the design of the rock centroid localization system.
3.1. System Architecture
The rock centroid localization system was implemented in three distinct phases: assembly, data acquisition, and data processing.
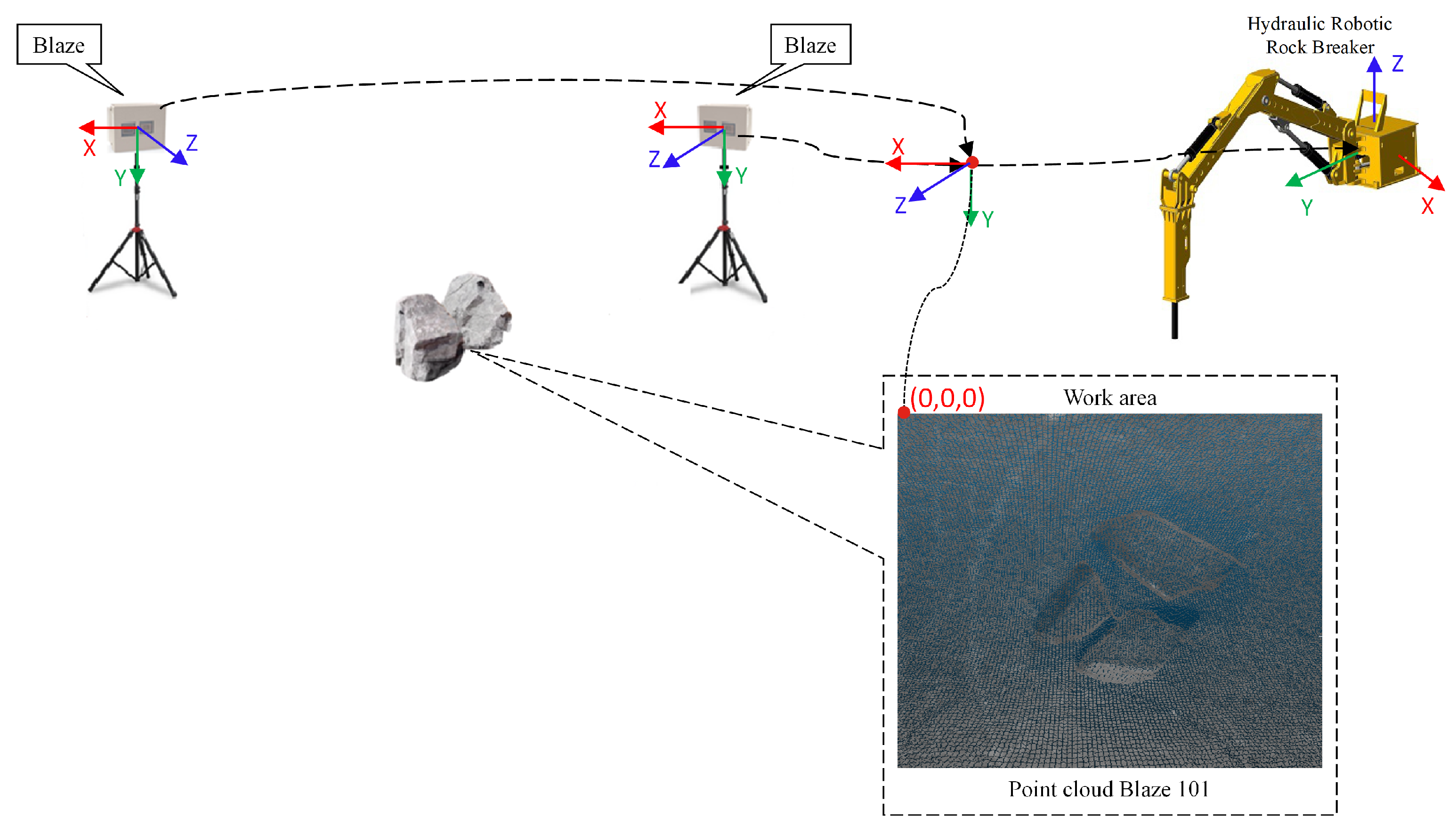
Figure 3 depicts the system’s architecture.
Sensor placement plays a critical role in achieving accurate rock centroid localization.
Figure 4 demonstrates the effects of various sensor positions on the resulting point clouds. To capture the maximum amount of information from the target object, sensors must be strategically positioned, as shown in
Figure 4b. In this study, the sensors were positioned approximately facing the objects of interest. Additionally, to optimize data collection, the objects were positioned near the center of the point cloud.
3.2. Hardware Architecture
This study utilized a Basler Blaze-101 3D ToF camera [
40] (Basler AG, Ahrensburg, Ger many), which provides 3D images with millimeter precision. Operating at a wavelength of 940 nm, this camera is suitable for both outdoor and indoor applications. It features a frame rate of 30 frames per second (fps), a GigE network interface, and a resolution of 640 × 480 pixels. The camera’s field of view is 67 × 51°, with a working range of 0.3 to 10 m. It maintains an accuracy of ±0.005 m within the 0.5 to 5.5 m range and demonstrates efficacy against sunlight of 12.8 W/m
2.
Network connectivity was ensured by a CISCO SG110D-08 switchCISCO SG110D-08 switch (Cisco Systems, Inc., San Jose, CA, USA), equipped with eight RJ-45 ports supporting 10BASE-T/100BASE-TX/1000BASE-T. Data processing was carried out on a laptop Hewellt Packard (HP) Victus featuring a Intel-Core i7-11800H CPU @ 64-bit 2.30 GHz, 16 GB of RAM, and an NVIDIA GeForce RTX 3060 graphics card.
To validate the experiment and facilitate future research, a RHINO model XDi3000 stationary rock breaker from the Canadian company ROCK-TECH (Lively, ON, Canada) was employed. This device represents a four Degree-of-Freedom (DoF) anthropomorphic robot with an end-effector diameter of 0.107 m.
Table 3 shows the parameters of the stationary rock breaker system.
The limitations of LiDAR in this work primarily relate to spatial resolution and the amount of information available for precise rock detection. Although LiDAR is a popular technology in many 3D perception applications, for our specific case of rock detection in mining environments, it presents several disadvantages:
Resolution and point density: The LiDAR sensors considered, such as the SICK MRS 6000 and MRS 1000, and the Ouster OS0, provide a relatively low number of points (between 4000 and tens of thousands). This point density is insufficient to capture the necessary details of rocks, especially in scenarios with stacked or overlapping rocks;
Data structuring: point clouds are unstructured, making them less suitable for direct processing with generic Convolutional Neural Networks (CNNs), which are the state-of-the-art in object detection;
Detail in small objects: the relative scarcity of LiDAR points makes it difficult to evaluate detailed scenes with piles of small, irregular, overlapping rocks;
Quality of additional data: the additional data provided by LiDAR sensors, such as intensity images and depth maps, are of inferior quality compared to those obtained from the Blaze 101 3D ToF camera.
In contrast, the Blaze 101 3D ToF stereo camera we selected offers several advantages:
A higher point density, allowing for a more detailed representation of rocks;
It provides images of adequate resolution with rich texture information, useful for distinguishing objects from the background;
It generates higher quality depth maps and other additional data, which could be valuable for future data fusion implementations;
It offers a better relationship between spatial resolution and the amount of available information, crucial for accurate rock detection in our specific context. These characteristics make the 3D ToF camera more suitable for our specific application of rock detection in mining environments.
To address potential sensor data interruptions, the system incorporates several robust features. The Basler Blaze-101 3D ToF camera was selected partly for its reliability in industrial environments, reducing the likelihood of data interruptions. The system’s real-time processing approach, where each frame is processed independently, mitigates the impact of momentary interruptions. Furthermore, the system’s flexibility to operate with either one or two cameras provides redundancy, allowing continuous operation even if one camera experiences data loss. These design choices collectively enhance the system’s resilience to potential data interruptions, ensuring consistent performance in challenging mining environments.
3.3. Software Architecture
Data analysis and processing were conducted using Python 3.9.18, leveraging several specialized libraries. For training the deep learning networks, PyTorch 2.2.1 with CUDA 11.8 and Ultralytics YOLO v8 (version 8.2.28) were employed. Point cloud processing was handled by Open3D 0.18.0, while Harvester 1.4.3 facilitated connection to and data acquisition from the Blaze 101 sensors. Additionally, CloudCompare 2.13.0 [
41] was utilized for initial point cloud processing, database analysis, and ground truth verification. Database labeling was accomplished using the Roboflow application [
42].
3.4. Mineralogical and Morphological Characteristics Present in Chilean Mining Deposits
The “La Patagua” mine, illustrated in
Figure 5a, is a strata-bound copper and silver deposit situated within volcano-sedimentary sequences. The deposit comprises two mines characterized by heterogeneous materials in terms of mineral composition. The key characteristics include:
Lithology: the predominant rock type is a volcanoclastic breccia tuff of volcanic origin;
Mineralization: Sulfides, including pyrite, chalcopyrite, bornite, and chalcocite, are disseminated throughout clasts and matrix, and in some veinlets. The presence of slight magnetism suggests the occurrence of magnetite and pyrrhotite;
Structure: rock fragments exhibit fracture systems, some of which are subparallel to stratification planes, while others are filled with calcite, as shown in
Figure 5b;
Physical properties: the matrix demonstrates high hardness (R4), corresponding to a compressive strength between 50–100 MPa.
Figure 5.
Mineralogical and morphological characteristics. (a) “La Patagua” mine. (b) Rock fragment displaying fractures and calcite veinlets.
Figure 5.
Mineralogical and morphological characteristics. (a) “La Patagua” mine. (b) Rock fragment displaying fractures and calcite veinlets.
The developed system, based on point clouds obtained from ToF cameras, primarily focuses on the precise localization of rocks rather than identifying their internal composition or lithology. However, it is acknowledged that depth information alone is insufficient for determining the specific lithological characteristics of the mineral under analysis. This limitation presents an opportunity for future research, integrating complementary technologies to enable a more comprehensive characterization of rock material in mining environments.
3.5. Dataset
The dataset for the rock centroid localization system was meticulously designed to capture the complexity and variability of real mining environments. It consists of 627 point clouds, which include samples of eight rocks from the “La Patagua” mine. Of these, 100 were collected directly in the mining environment: 50 under high illumination conditions and 50 under low illumination conditions with suspended particles, simulating typical adverse mining conditions. Additionally, 315 point clouds featured overlapping rocks, while 312 did not. The remaining samples were obtained in a controlled environment, incorporating variations in lighting, rock overlapping, and sensor positioning to enhance dataset diversity. The following considerations guided dataset creation:
Data were collected over several days under varying conditions, including low lighting, high lighting, and low levels of suspended particles;
Two object positioning variants were created: one without overlap between objects, and another with partial object overlap;
Variations in sensor mounting, including translations and rotations of the target objects, were implemented to increase database variability.
Figure 6 illustrates the created database and the different conditions analyzed.
The dataset was randomly divided: 80% (502 point clouds, 259 with overlap and 243 without) for training, 10% (63 point clouds, 29 with overlap and 34 without) for validation, and 10% (62 point clouds, 27 with overlap and 35 without) for testing. Ground truth was established by measuring distances along the X, Y, Z axes between a reference point and each object centroid, verified using the CloudCompare software. All point clouds were subsequently converted to BEV, resulting in 2575 × 2575 pixel images.
The Roboflow application was employed for labeling, which offers tools for computer vision model development, including data acquisition, annotation, processing, and augmentation.
Figure 7 displays the label distribution in the created database. Objects were positioned approximately in the center of the point cloud to ensure full visibility in the BEV image.
The current study employed a static database, meticulously constructed with representative samples from the intended implementation site. This database’s efficacy is evidenced by the results presented in
Section 4.1,
Section 4.2 and
Section 4.3. To enhance model generalization, data augmentation techniques were applied, as described earlier. These techniques included adjustments in brightness (±15%), exposure (±10%), and blur (up to four pixels), as illustrated in
Figure 8, resulting in an expanded training set of 1506 images. It should be noted that these techniques expanded the diversity of the static dataset rather than created a dynamic database. Despite not implementing a dynamic database, the system demonstrated adaptability to various conditions, as shown in
Figure 6. The dataset’s diversity, encompassing various lighting conditions, rock overlaps, and sensor positions, effectively simulates the variability encountered in dynamic mining environments. This approach significantly expands dataset diversity.
While standardized benchmarks are valuable in AI research, our approach prioritizes practical applicability in the specific context of the FONDEF IDeA I + D ID21I10087 project, which aims to provide autonomy to a rock-breaking robotic system. Our database composition, combining images from both the actual mine and a controlled environment, allows for a dataset that is representative of operational conditions while enabling controlled parameter variation to enhance model robustness.
The validity of our approach is demonstrated through the results obtained when applying our algorithms, as detailed in
Section 4.1,
Section 4.2 and
Section 4.3. Furthermore, the transferability of computer vision models to new environments has been demonstrated in previous studies. In our earlier work [
4], we showed that models like YOLO, trained on databases created in different locations, successfully detected rocks in our samples. This suggests that our current model could also perform well if applied to similar, though not identical, data.
3.6. Performance Metrics
To validate the system’s performance, several metrics were employed, categorized into two groups: those evaluating the segmentation [
43,
44] performed by the YOLO v8x-Seg algorithm, and those assessing the localization [
22,
45] of rock centroids. Segmentation quality was analyzed using the Intersection over Union (IoU), also known as the Jaccard similarity coefficient. The IoU quantifies the rate of correctly classified pixels relative to the total pixels of the class. This metric serves as a statistical precision measure that penalizes false positives (
). The IoU score is defined by Equation (
8).
where
,
, and
represent true positives, false positives, and false negatives, respectively.
To ensure a comprehensive and robust evaluation of our segmentation model, we employed MATLAB’s “evaluateSemanticSegmentation” function. This function automatically calculates the confusion matrix and derives various metrics from it, including , , , and . Our evaluation process involved creating two separate datastores: one for the prediction images generated by the YOLO v8x-Seg algorithm, and another for the ground truth images obtained through manual labeling using the Roboflow app. Both sets of images were represented as binary masks, with white pixels denoting rocks and black pixels representing the background. This binary representation allowed for a clear, pixel-wise comparison between predictions and ground truth. The “evaluateSemanticSegmentation” function provided us with a range of metrics, including the confusion matrix, Normalized Confusion Matrix, Class Metrics (such as accuracy, IoU, and MeanBFScore), and Global Metrics (including GlobalAccuracy, MeanAccuracy, MeanIoU, WeightedIoU, and MeanBFScore). This comprehensive set of metrics allowed us to assess our model’s performance from multiple perspectives, providing a thorough understanding of its strengths and potential areas for improvement.
The accuracy of rock centroid localization was evaluated using the Mean Absolute Error (
), normalized error (
), Euclidean distance in the X,Y axes (
), and the coefficient of determination (
). The
,
, and
metrics were calculated individually for each X, Y, Z axis.
,
,
, and
are defined by Equations (
9)–(
12), respectively.
where
denotes the absolute error in a given axis,
represents the size of the rock in a given axis,
and
indicate the ground truth and predicted positions in the
plane, respectively,
are the observed values,
are the predicted values, and
is the mean of the observed values.
3.7. Description of the Centroid Location Algorithm
Figure 9 shows the rock centroid localization algorithm. The following subsections explore this functionality in depth.
3.7.1. Preprocessing
The preprocessing of the point clouds is illustrated in
Figure 10. As previously discussed, we utilized the Harvester library for point cloud acquisition. The initial sensor connection time was approximately 1 s.
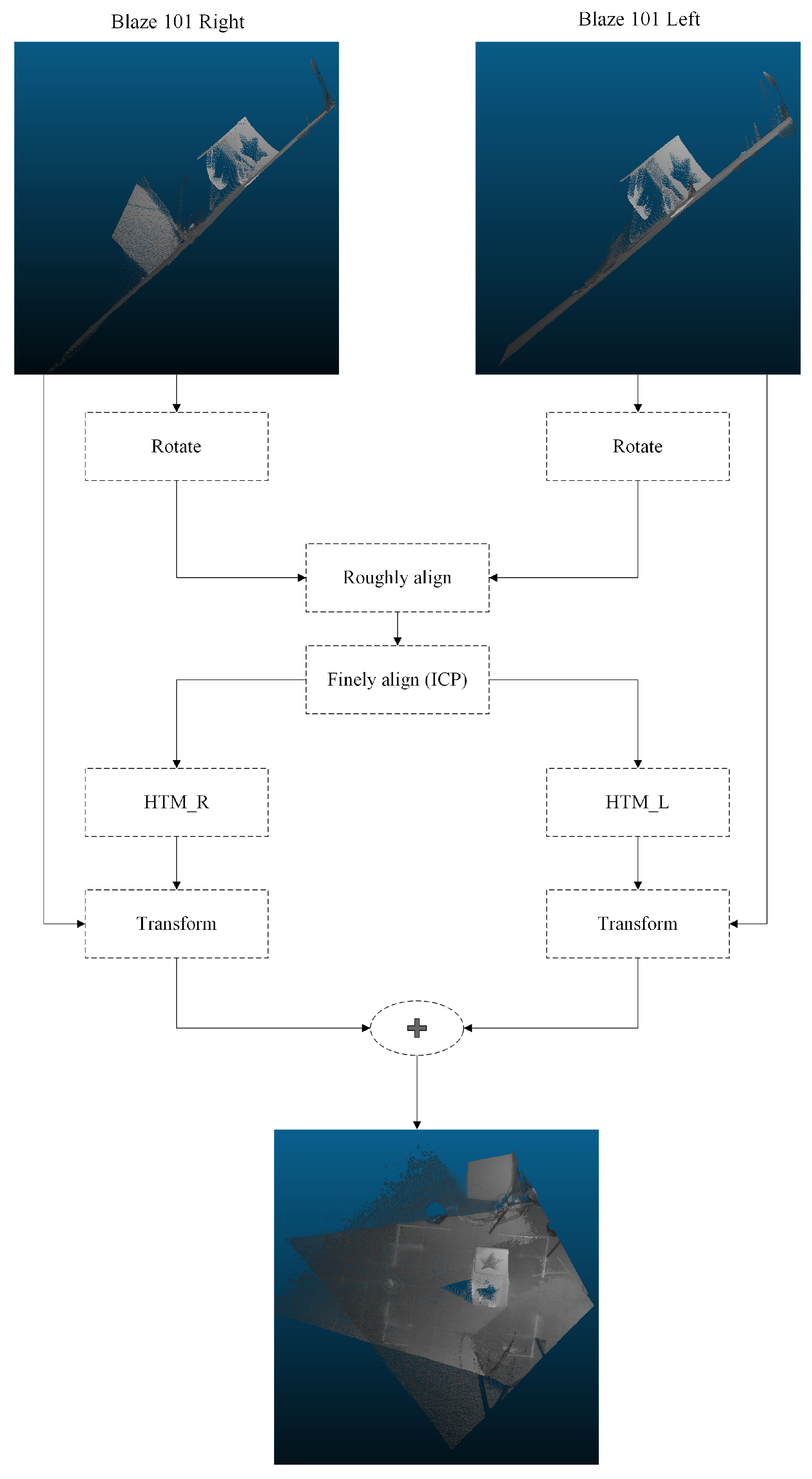
As discussed in the methodology, registration is defined as the alignment of point clouds. The CloudCompare software was employed to obtain an
for each sensor. This software offers two methods for point cloud alignment: rough and fine. Typically, an easily identifiable object is used for proper rough alignment by selecting common points. In this study, a rough alignment was first performed by selecting matching points in both point clouds, followed by a fine alignment using the ICP algorithm. The ultimate goal was to obtain a point cloud with fused information from two Blaze 101 sensors. A cube with stars on its faces was utilized as the object to obtain the necessary matrices for registration. Each point cloud from the Blaze 101 sensor contains approximately 300,000 points, resulting in a fused cloud of approximately 600,000 points.
Figure 11 illustrates the procedure followed.
In the zero adjustment process, a point of interest is defined as the new
and the previously obtained point cloud is transformed using an
. The point clouds from the Blaze 101 sensor are in the millimeter range; therefore, the point cloud was normalized to meters. Finally, the major plane (floor) was segmented using the RANSAC algorithm. The essential parameters for this algorithm are as follows: distance_threshold (which defines the maximum distance a point can have from a plane to be considered an inlier), ransac_n (which defines the number of points randomly sampled to estimate a plane), and num_iterations (which defines how often a random plane is sampled and verified). The most critical parameter that can significantly affect major plane detection is distance_threshold; therefore, the minimum average distance between the points of the final point cloud was calculated, obtaining a value of 0.01 m. After conducting several tests, it was found that a value of 0.03 m yielded the best results. The goal of this process is to remove the major plane and reduce the dimensions of the point cloud, which is crucial for decreasing the computational cost in subsequent steps.
Figure 12 illustrates the RANSAC procedure.
Our system incorporates several strategies to address the challenge of partial occlusions, which are common in mining environments. Firstly, we utilize multiple Basler Blaze-101 3D ToF sensors positioned at different angles. This multi-sensor configuration allows us to capture information from various perspectives, significantly mitigating partial occlusion problems. Secondly, our point cloud processing method enables us to work with complete three-dimensional information, which is particularly useful for inferring the complete shape of partially occluded objects. We can use depth information to distinguish between overlapping objects, enhancing our ability to accurately localize rock centroids even in complex scenes. Furthermore, the use of the YOLO v8x-Seg algorithm for instance segmentation allows us to detect and segment objects even when they are partially occluded. This algorithm has been trained to recognize partial features of objects and can infer the complete shape based on visible parts. By combining these approaches, our system demonstrates robust performance in handling partial occlusions, a critical capability for effective rock centroid localization in real-world mining scenarios.
3.7.2. Statistical Outlier Removal
Outlier points can appear in sensors such as 3D ToF cameras and LiDAR due to their internal functioning, potentially affecting algorithm performance. Therefore, the influence of SOR on the rock centroid localization algorithm was analyzed. In SOR, the average distances of each point to its nearest neighbors are calculated and used to identify outliers based on a standard deviation threshold. The key parameters include the following:
nb_neighbors specifies the number of neighbors considered when calculating the average distance for a given point;
std_ratio sets the threshold level based on the standard deviation of the average distances; a lower value results in more aggressive filtering.
Selecting these parameters is challenging, as they can affect point clouds with different configurations in various ways. In this study, after conducting several tests, configurations with an std_ratio of 1 and nb_neighbors of 16 were selected. It is important to note that this selection may not be optimal, and further research in this area is warranted.
The SOR method was implemented as an experimental variant to examine its efficacy in point cloud outlier removal. The system demonstrated robust performance both with and without SOR, indicating resilience to different data processing approaches. In this study, which focuses on spatial localization of rock centroids in static images, temporal heterogeneity was not considered a critical factor. The system was designed to process individual images or sequences without reliance on strict temporal coherence.
3.7.3. Bird’s-Eye View and Mapping
Given that image-based deep learning techniques are more established than point-cloud-based techniques, the decision was made to convert the point cloud into a BEV pseudo-image. This conversion requires defining several parameters: side_range (left and right limits), fwd_range (back and front limits), res (desired resolution in meters, where each output pixel represents a square region of res × res ), and height (min_height, max_height). Based on the setup and characteristics of the Blaze 101 sensors, the following parameters were defined for this research: side_range (−5.5, 0.02), fwd_range (−0.02, 5.5), res (0.002), and height (−0.1, 2). Mapping was performed to preserve the positions of the X, Y, Z axes in the image form.
The algorithm for converting the point cloud to BEV and performing the mapping is presented below (Algorithm 4).
Figure 13 illustrates the point clouds converted to BEV images.
| Algorithm 4 Point cloud to BEV conversion and mapping |
Require: Point cloud P, side_range, fwd_range, res, height_range
Ensure: BEV image I, X_map, Y_map, Z_map
- 1:
x = P[:, 0] - 2:
y = P[:, 1] - 3:
z = P[:, 2] - 4:
f_filt = np.logical_and((x > fwd_range[0]), (x < fwd_range[1])) - 5:
s_filt = np.logical_and((y > side_range[0]), (y < side_range[1])) - 6:
filter = np.logical_and(f_filt, s_filt) - 7:
indices = np.argwhere(filter).flatten() - 8:
x = x[indices] - 9:
y = y[indices] - 10:
z = z[indices] - 11:
x_img = (-y - side_range[0]) / res - 12:
y_img = (-x - fwd_range[0]) / res - 13:
x_img = x_img.astype(np.int32) - 14:
y_img = y_img.astype(np.int32) - 15:
pixel_values = np.clip(a=z, a_min=height_range[0], a_max=height_range[1]) - 16:
pixel_values = pixel_values - height_range[0] - 17:
I = np.zeros((int((side_range[1] - side_range[0]) / res), int((fwd_range[1] - fwd_range[0]) / res), 3), dtype=np.uint8) - 18:
I[y_img, x_img, 0] = pixel_values - 19:
X_map = np.zeros_like(I[:,:,0]) - 20:
Y_map = np.zeros_like(I[:,:,0]) - 21:
Z_map = np.zeros_like(I[:,:,0]) - 22:
X_map[y_img, x_img] = x - 23:
Y_map[y_img, x_img] = y - 24:
Z_map[y_img, x_img] = z - 25:
return I, X_map, Y_map, Z_map
|
The input that would cause maximum activation in our system is a BEV image that clearly represents rocks distinguishable from the background. Ideal characteristics include rocks represented as high-density point regions, clearly contrasted with a low-density background, and well-defined, separated shapes, preferably circular or elliptical in top view. A uniform point density distribution within rock regions is also crucial. Several constraints must be imposed on this input to ensure optimal performance. Rock shapes must be consistent with typical geometries viewed from above, based on geological data collected from mining environments. The point density distribution should reflect realistic rock surface reflection characteristics, as observed in our dataset, with particular attention to the realistic density transition at rock edges, mimicking natural rock-background interfaces. Furthermore, the BEV image scale and perspective must align with our Basler Blaze-101 3D ToF sensor configuration to maintain consistency with our data acquisition setup. These characteristics and constraints ensure that our system responds optimally to inputs that closely resemble real-world mining scenarios while maintaining the high level of detail necessary for accurate rock centroid localization. Our model’s design and training process, detailed in previous sections, ensure its functionality with complex, real-world data, often more varied than these ideal conditions. This approach balances optimal activation with practical applicability in dynamic mining environments.
3.7.4. Rock Segmentation
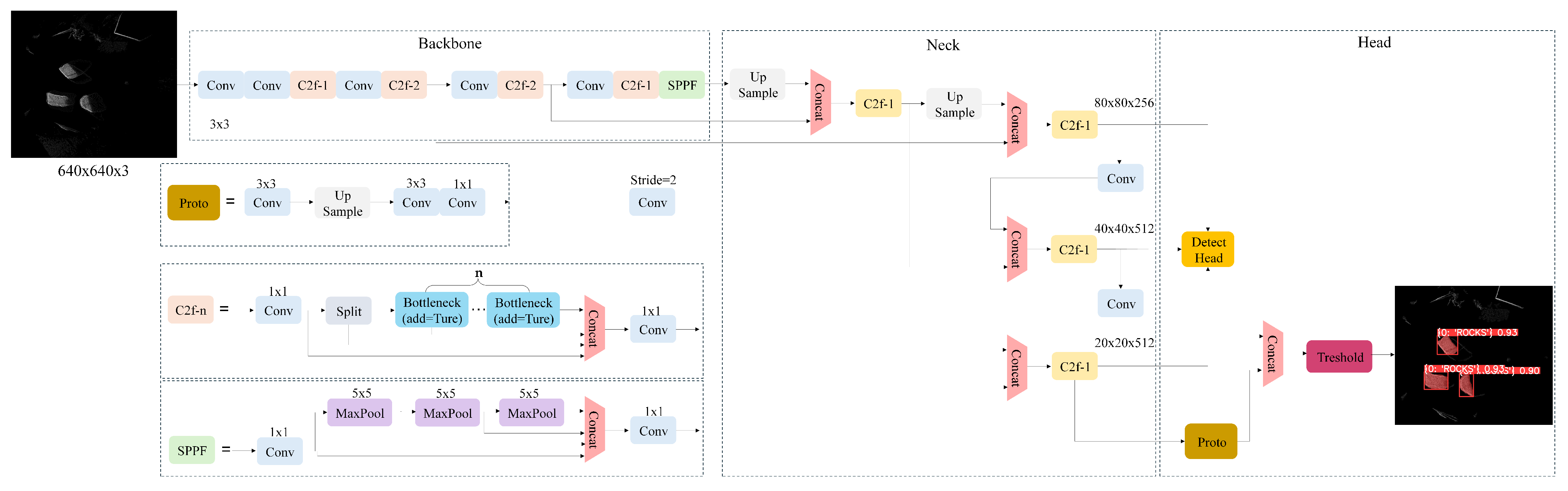
After obtaining the BEV pseudo-image, the next step in the localization system is rock segmentation. The speed of this process is critical due to the requirements of mining robotic systems. Therefore, Ultralytics YOLO v8 was selected for its speed, accuracy, and ease of use. Additionally, it can perform various tasks such as object detection, tracking, instance segmentation, and pose estimation.
The rock segmentation process employs a two-stage approach to feature selection and learning. Initially, the conversion of 3D point clouds to BEV images serves as a form of feature engineering, preserving crucial spatial information while reducing computational complexity compared to direct 3D point cloud processing. This transformation allows for the leveraging of powerful CNN architectures such as YOLO v8x-Seg. Subsequently, YOLO v8x-Seg performs automated feature learning on these BEV images, extracting hierarchical features relevant to rock detection and localization. This approach enables joint optimization of the BEV representation and the network-learned features, resulting in an efficient end-to-end system. The combination of engineered features (BEV representation) and learned features (via YOLO v8x-Seg) constitutes a robust method for selecting and learning relevant features for the specific task of rock detection in mining environments.
The YOLO v8x-Seg segmentation model was used as the basis for training.
Table 4 lists the hyperparameters used.
The results of training the YOLO v8x-Seg model on the BEV image dataset are illustrated in
Figure 14. The training results demonstrate excellent performance. The obtained labels were saved with a .txt extension for further analysis and postprocessing.
The hyperparameters for the YOLO v8x-Seg model were selected based on recommendations from the literature and preliminary experiments. While an exhaustive hyperparameter optimization was not conducted due to computational resource limitations, our results demonstrate that these parameters perform well for our specific application. The high IoU values and accuracy in centroid localization achieved with these settings validate their effectiveness. It is worth noting that the current configuration has proven robust across various testing conditions, indicating a good level of generalization. However, we acknowledge that further optimization could potentially enhance the model’s performance. Future work will include a more comprehensive study of hyperparameter optimization, potentially employing techniques such as a grid search or Bayesian optimization to further refine our model’s performance and adaptability to different mining scenarios.
The system’s ability to handle various input resolutions is facilitated by the inherent flexibility of the YOLO v8 model and our preprocessing pipeline. A key feature of the Ultralytics implementation is that image size is a configurable parameter during both training and inference. While the YOLO v8x-Seg model was pre-trained on 640 × 640 × 3 pixel RGB images, this parameter allows for training and inference on images of different dimensions. Images with sizes different from the selected parameter are automatically resized, enabling the processing of inputs with various initial dimensions.
In this study, BEV images with a resolution of 2575 × 2575 pixels in grayscale were utilized, a deliberate choice to preserve critical details such as rock edges during the BEV conversion process. This high-resolution approach is fundamental for accurate centroid detection and localization. The preprocessing pipeline maintains data integrity by preserving spatial information during the conversion from high-resolution input to the model’s required resolution.
Although the main experiments were conducted with this specific high resolution, the flexibility provided by the configurable image size parameter ensures that the system can adapt to different resolutions during both training and inference. Additional tests with varying input resolutions confirmed the system’s adaptability, demonstrating consistent performance across different resolutions. The system’s only constraint is that input images must have a sufficient resolution to capture relevant rock characteristics, providing flexibility while ensuring accuracy.
This approach effectively handles different input resolutions without compromising integrity or precision, ensuring adaptability to various input scenarios while maintaining accurate centroid localization. The ability to adjust the image size parameter in both training and inference stages allows for fine-tuning the model’s performance for specific application requirements or hardware constraints.
Regarding the storage and retrieval of the optimal weight database, these are managed internally within the YOLO v8x-Seg architecture and can be accessed and updated through the training and model loading functions provided by the Ultralytics library.
3.7.5. Postprocessing
The final stage involved comparing two variants for processing the predictions obtained from the YOLO v8x-Seg algorithm.
Figure 15a depicts variant 1, where predictions were analyzed collectively, while
Figure 15b illustrates variant 2, which considered segmentations individually.
The YOLO v8x-Seg algorithm provides a segmented image and a .txt file containing predictions. This .txt file was utilized to generate mask images. For variant 1, a single mask image incorporating all predictions was created, whereas variant 2 generated individual mask images for each prediction. Random colors were assigned to each prediction in both cases. This color assignment is crucial for the subsequent stages of variant 1 but does not impact variant 2. Inverse mapping was then performed to obtain the point clouds. Variant 1 resulted in a single point cloud containing all rock predictions, while variant 2 produced separate point clouds for each prediction.
For variant 1, given the prior knowledge of the number of predictions, the K-means clustering algorithm was applied. This algorithm is efficient and particularly suitable when the number of clusters is known a priori. The parameters number_cluster, n_init, and max_iter were employed in K-means. The value of number_cluster was obtained directly from the YOLO v8x-Seg algorithm predictions, while the other parameters were determined empirically. Finally, for variant 1, the centroids of each resulting K-means cluster were calculated, whereas for variant 2, the centroids of each individual point cloud were computed.
4. Results and Discussion
This section analyzes and discusses the results of rock centroid localization. The analysis begins with the segmentation results using the YOLO v8x-Seg algorithm, followed by the presentation of rock localization results, a graphical analysis of segmentation and centroid localization, and concludes with a discussion of relevant research aspects. As outlined in the localization system design, several experiments were conducted. Evaluations were performed both with and without overlap. Two experiments in the segmentation section analyzed the influence of Statistical Outlier Removal (SOR) filtering. The variants analyzed in this study are as follows:
N-S-N-O. Without SOR and without overlap;
S-N-O. With SOR and without overlap;
N-S-O. Without SOR and with overlap;
S-O. With SOR and with overlap.
Additionally, in the localization phase, two variants were analyzed to obtain the rock centroid:
N-S-N-O-V1. Without SOR, without overlap, using variant 1;
N-S-N-O-V2. Without SOR, without overlap, using variant 2;
S-N-O-V1. With SOR, without overlap, using variant 1;
S-N-O-V2. With SOR, without overlap, using variant 2;
N-S-O-V1. Without SOR, with overlap, using variant 1;
N-S-O-V2. Without SOR, with overlap, using variant 2;
S-O-V1. With SOR, with overlap, using variant 1;
S-O-V2. With SOR, with overlap, using variant 2.
4.1. Results of BEV Image Segmentation
The correct and rapid segmentation of objects in images represents an area of continuous advancement and development. In this context, the YOLO v8x-Seg algorithm is of great importance due to its efficiency, speed, and ease of use.
Table 5 presents the segmentation results achieved with the YOLO v8x-Seg algorithm under various conditions: with and without overlap, and with or without SOR.
As is evident from the table, rock segmentation proved adequate in both overlapping and non-overlapping environments, achieving IoU values above 93%. This high performance is crucial for the subsequent phases of the localization system.
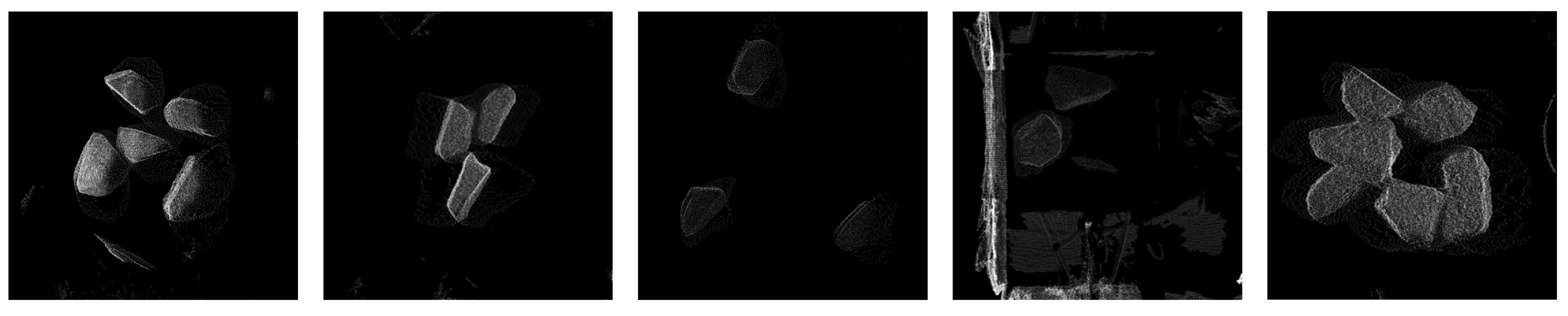
The analysis of the IoU metric per image across the investigated scenarios is illustrated in
Figure 16.
It is worth noting that in the non-overlapping scenario, all rocks were successfully detected and segmented in both analyzed variants. In the overlapping scenario, the SOR variant resulted in the detection and segmentation of seven additional rocks not present in the ground truth. Similarly, the No SOR variant led to the detection and segmentation of 12 additional rocks beyond the ground truth.
4.2. Sensitivity Analysis and Model Robustness
The sensitivity analysis conducted in our study, with results presented in
Table 6, demonstrates the robustness of the YOLO v8x-Seg model against various perturbations in input images. The results indicate that the model maintains consistent performance when faced with changes in brightness and contrast, with minimal variations in Mean IoU. For instance, in the S-N-O variant, the Mean IoU ranges between 92.88% and 94.48% for these perturbations, while for N-S-O, it varies between 95.33% and 96.10%.
Notably, the model exhibits greater sensitivity to rotations, with a significant decrease in Mean IoU for ±5° rotations, dropping to 74.46% and 74.33% for S-N-O, and to 72.26% for both rotations in N-S-O. This information is crucial for understanding the model’s strengths and limitations under different operational conditions, enabling specific adjustments to enhance its performance in real mining scenarios.
4.3. Results of Rock Centroid Localization in Point Clouds
Precision in rock centroid localization is crucial for increasing rock-breaking efficiency.
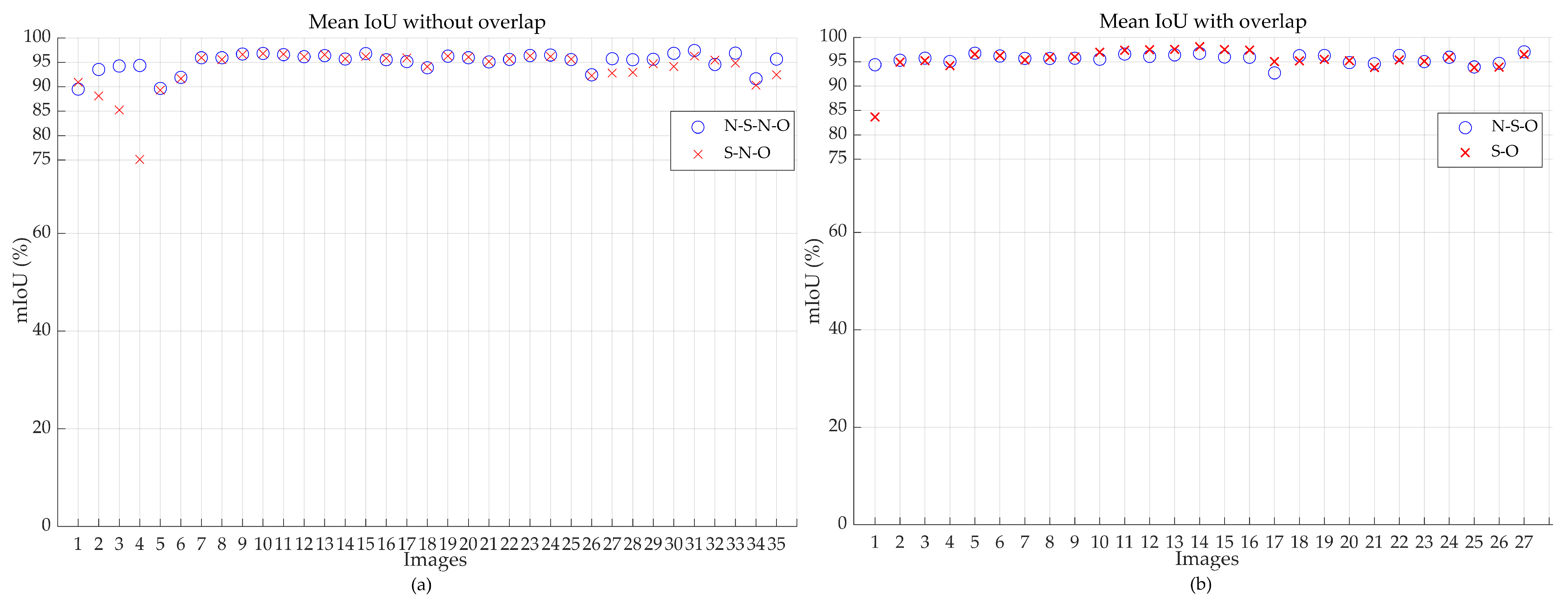
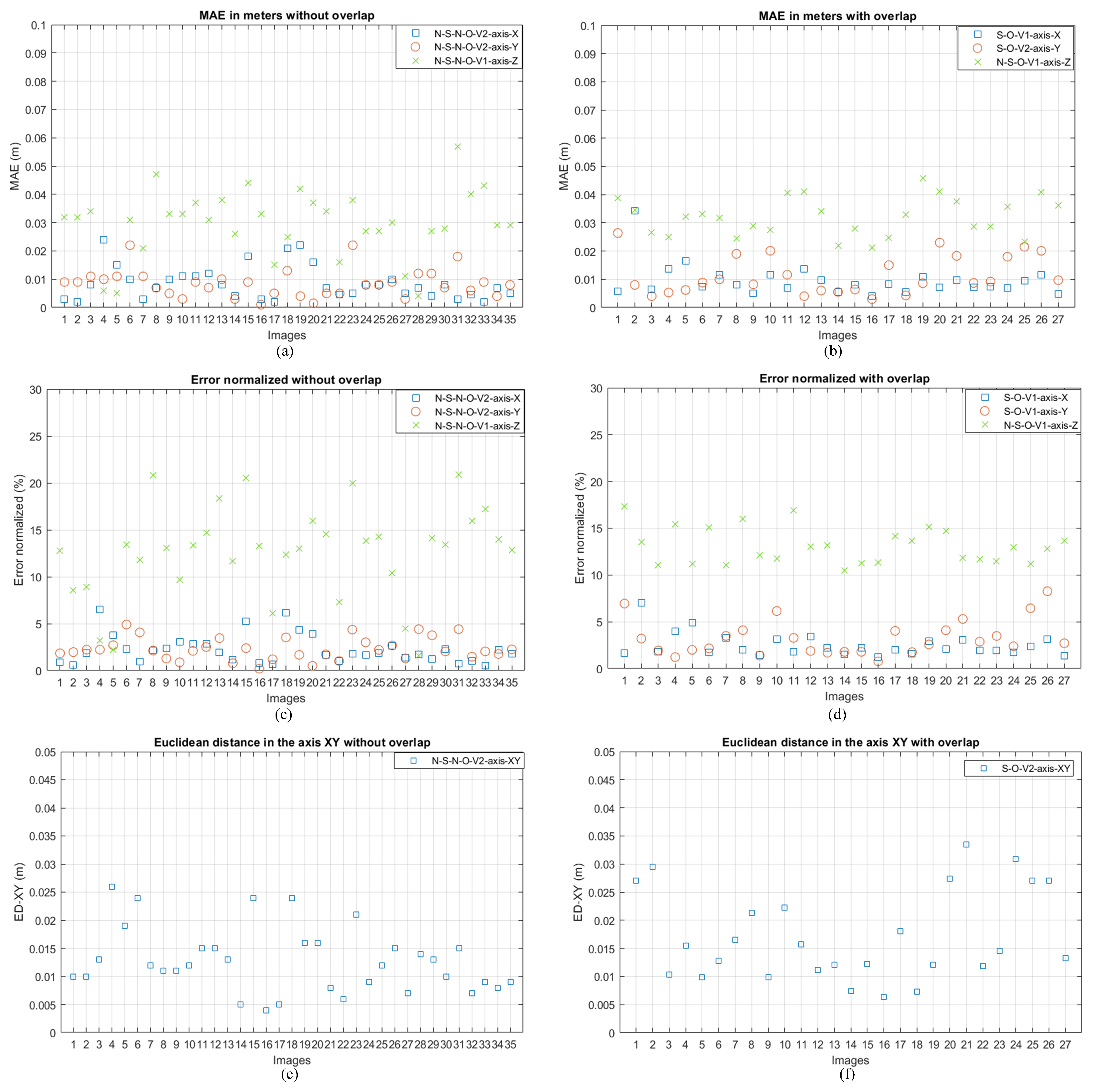
Table 7 presents the results of the metrics used to evaluate the quality of rock centroid localization. The data reveal favorable outcomes across all variants and scenarios analyzed. The most significant results include:
Euclidean Distance Error (): The maximum of 0.0196 m was observed in the N-S-O-V1 experiment (without SOR, with overlapping, variant 1). This result indicates high precision in centroid localization in the XY plane, considering that the typical diameter of rock breaker end effectors ranges between 0.07 m and 0.11 m;
Normalized error (): The in the X and Y axes did not exceed 3.8% in any case, which is an excellent result. The highest was observed in the Z axis, reaching a maximum of 13.6196% in the S-O-V2 experiment (with SOR, overlapping, variant 2);
Coefficient of determination (): values close to 1 were achieved for all experiments’ X and Y axes, indicating a high correlation between predicted and actual values. For the Z axis, values were lower, ranging between 0.334 and 0.843, which is consistent with the higher error observed in this axis due to the use of BEV mapping;
Mean Absolute Error (): Consistently low values were obtained for the X and Y axes, with a maximum of 0.0149 m. The in the Z axis was slightly higher, with a maximum of 0.0333 m.
Table 7.
Results of the metrics used to evaluate the location of rocks in the point cloud dataset.
Table 7.
Results of the metrics used to evaluate the location of rocks in the point cloud dataset.
| Metrics | Experiments |
|---|
| | N_S_N_O_V1 | N_S_N_O_V2 | S_N_O_V1 | S_N_O_V2 | N_S_O_V1 | N_S_O_V2 | S_O_V1 | S_O_V2 |
|---|
| 0.0092 | 0.0085 | 0.0088 | 0.0089 | 0.0105 | 0.0106 | 0.0095 | 0.0100 |
| 0.0095 | 0.0084 | 0.0098 | 0.0089 | 0.0135 | 0.0149 | 0.0120 | 0.0114 |
| 0.0297 | 0.0307 | 0.0301 | 0.0310 | 0.0320 | 0.0322 | 0.0331 | 0.0333 |
| 2.4000 | 2.2263 | 2.3288 | 2.3183 | 2.7712 | 2.8300 | 2.5112 | 2.6873 |
| 2.5240 | 2.3151 | 2.6052 | 2.4181 | 3.7826 | 3.3895 | 3.2508 | 3.0954 |
| 12.5305 | 12.8894 | 12.6450 | 12.9817 | 13.1099 | 13.2652 | 13.4980 | 13.6196 |
| 0.999 | 1.000 | 0.999 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 0.394 | 0.360 | 0.376 | 0.334 | 0.841 | 0.843 | 0.827 | 0.822 |
| 0.0144 | 0.0128 | 0.0149 | 0.0134 | 0.0196 | 0.0184 | 0.0173 | 0.0171 |
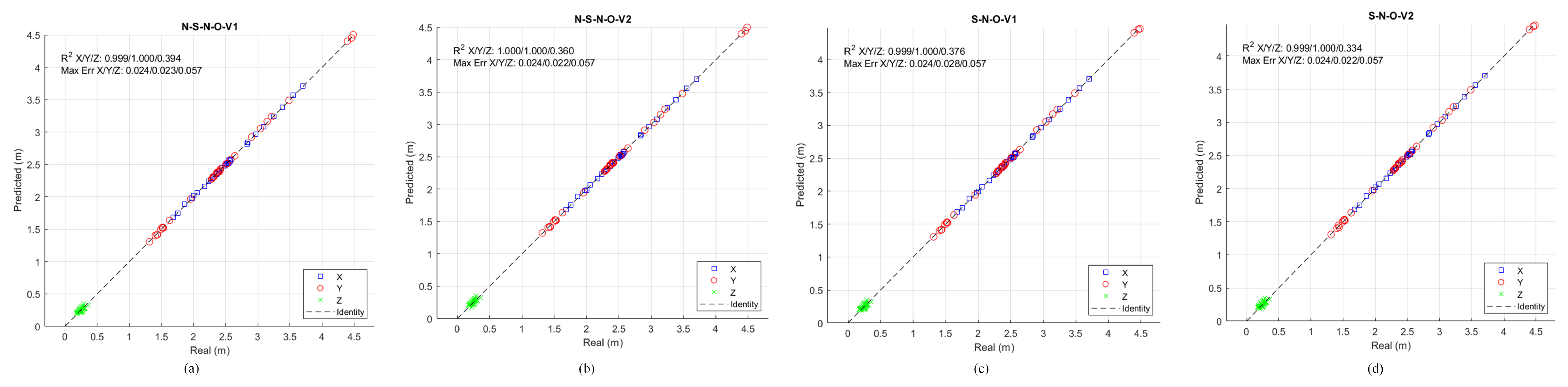
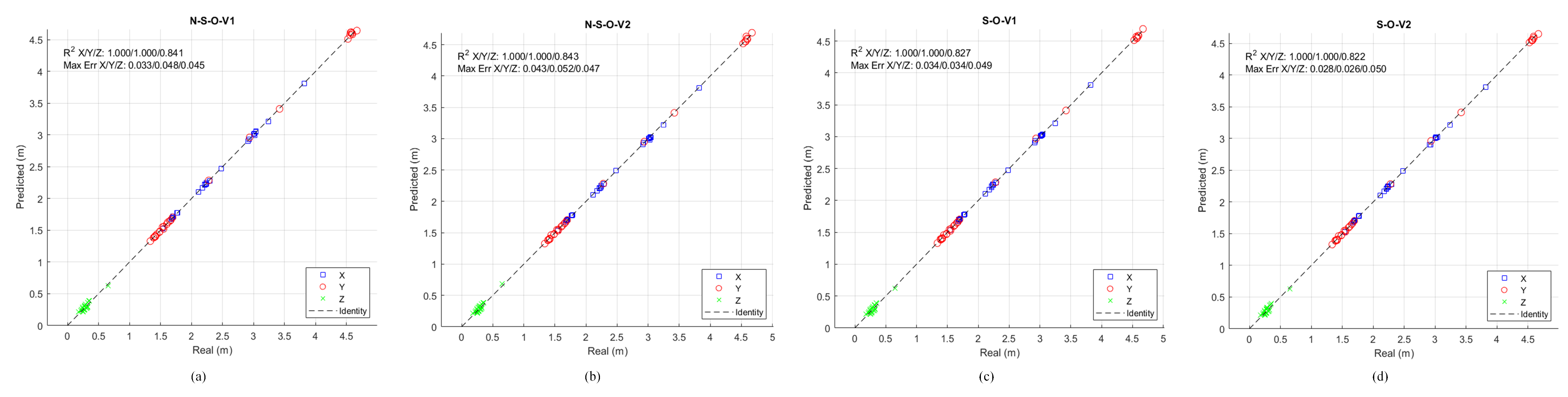
A visual representation of the
results and maximum error for cases without overlapping and with overlapping is provided in
Figure 17 and
Figure 18, respectively.
Figure 17 illustrates the
results and maximum error for cases without overlapping. The
values for the X and Y axes are consistently high (close to 1), while they are lower for the Z axis. Maximum errors are generally higher in the Z axis, consistent with the inherent challenges of using BEV mapping for depth estimation.
Figure 18 reveals a slight performance degradation compared to the cases without overlapping, especially in the Z axis. However, the results remain robust, with
values for X and Y close to 1 and relatively low maximum errors.
Figure 19 provides a detailed analysis of the
,
, and
metrics per image in the investigated scenarios. The most significant errors consistently occur in the
Z axis, attributable to BEV mapping. However, due to the operation of the analyzed robotic system, these errors do not significantly impair the overall performance. Notably, the extreme cases of
did not exceed 22%, as shown in
Figure 19c,d. This demonstrates the system’s robustness even in challenging situations.
Overall, these results demonstrate the high precision and reliability of the developed rock centroid localization system, both in scenarios with and without overlapping and with or without the use of SOR. The consistency of good results across different configurations underscores the system’s robustness and adaptability to diverse operating conditions in mining environments.
4.4. Graphical Analysis of the Segmentation in the BEV Image and of the Rock Location in the Point Cloud
The graphical analysis of rock segmentation and localization results provides a valuable qualitative evaluation of the developed system.
Figure 20 presents several examples of point clouds, with the first two exhibiting top-to-bottom overlap, while the last one does not.
In all the illustrated examples, the system successfully detected and localized the rocks in the scene. This performance is particularly noteworthy given the challenges posed by overlapping, suspended particles, and varying lighting conditions, which typically complicate localization tasks. It was observed that localization errors tended to increase in cases of overlap.
4.5. Relevant Aspects
The rock centroid localization system achieved excellent results, as discussed in the previous sections. This section analyzes some relevant aspects found in the research: mining robotic systems with rock-breaking hammers, as mentioned, have four DoF. The first three are used for positioning in the 3D Cartesian space, and the last provides the attack angle of the end effector. Analyses of their operation in various mining operations in Chile suggests that the end effector should always be vertical concerning the major plane or the floor, as this requires less effort when breaking rocks. This implies that the last DoF of the rock-breaking hammer should be at 90° to the floor. This allows for obtaining the necessary joint angles to perform the rock-breaking task autonomously using the robot’s inverse kinematics and the proposed system. The error obtained on the Z axis, despite being close to 22%, has little influence because the value given for the hammer’s positioning on this axis will always be approximately twice the centroid value, as in [
1]. Another significant aspect is that the
on the X,Y axes is not substantial when considering that the diameters of the analyzed robotic system and similar ones vary between approximately 0.07 m and 0.11 m.
The implemented system required approximately 5 s, making it suitable for mining operations. The initial connection with the Blaze 101 sensors using the Harvester library required 1 s, and then it maintained streaming. This reduced the data acquisition time, reaching 0.03 s per sensor. The BEV image conversion required approximately 1 s, mainly because of the resolution used for its creation. Preprocessing allowed a better scene representation and reduced the point cloud size, which is vital for lowering subsequent computational costs. Depending on whether the SOR was used, the preprocessing time ranged from 1 to 1.5 s. The speed of the YOLO v8x-Seg algorithm allowed an inference time ranging from 1 to 1.5 s, despite having an input image of 2575 × 2575 pixels.
Correct sensor positioning is a vital aspect, as it greatly influences the accuracy of rock centroid localization. Poor sensor placement can result in an object’s shape not being captured, thereby increasing the occurrence of unwanted points or areas lacking object information.
The same methodology for point cloud registration as in [
8] was used, which allowed for better scene representation. However, further improvements or incorporation of other methods are needed, as small differences between objects in the final point cloud were observed, affecting proper segmentation and subsequent rock localization.
Using ROL, SOR, and other filters to remove unwanted points is a common technique in point cloud processing; however, a more in-depth analysis of this procedure is required because its parameters can influence the final result of rock centroid localization differently. In some cases, applying SOR removed not only unwanted points but also points belonging to the object to be detected, reducing the accuracy of the IoU as shown in the non-overlapping scenarios.
The analyses and results obtained at La Patagua Mining Company, thanks to the FONDEF IDeA I + D ID21I10087 project, concluded that rock-breaking hammer operators first checked whether the rocks were stacked or overlapping; if so, they use the hammer to unstack them before starting to break them. This demonstrates that implementing the rock centroid localization system would provide excellent results for rock-breaking hammers used in mining operations. The objective of the dataset was to pose a challenge for the developed algorithms, as the overlapping scenario, despite being present in mining operations, always involves unstacking rocks as the first step.
Specifically, it was identified that in environments with high concentrations of suspended particles, the quality of point clouds significantly deteriorates due to the internal functioning of ToF technology-based sensors, such as LiDAR and 3D ToF cameras. This degradation can lead to system malfunction under these particular conditions. To address this challenge, future work will focus on implementing a combination of 3D ToF cameras and thermal cameras. This sensor fusion could mitigate the drawbacks of ToF technologies in environments with high particle concentrations, thereby improving the system’s robustness and reliability across the full spectrum of mining conditions.
In designing the system, its applicability to other types of 3D sensors was considered, keeping in mind some key considerations, such as the following:
Method Generality. The system is based on 3D point cloud processing, making it adaptable to various 3D sensor technologies. The main algorithms (preprocessing, BEV conversion, and YOLO v8x-Seg) were designed to work with point cloud data regardless of the specific sensor;
Requirements and adaptability. (a) Point density. For adequate characterization of objects such as rocks in BEV images, point clouds must have sufficient points. For example, LiDAR sensors like MRS1000 and MRS6000 were initially considered, but their 4000 and 20,000 points proved insufficient for this specific use case. (b) Parameter adjustment. Some system parameters from the utilized sensor are closely related to the characteristics of the point clouds. These parameters directly influence algorithms such as RANSAC and SOR. It is important to note that these adjustments are made only once during the initial setup, and they do not affect the subsequent operation of the system. (c) YOLO retraining. Depending on the characteristics of BEV images generated by different sensors, it might be necessary to retrain or adjust the YOLO v8x-Seg model. This would ensure optimal performance with the specific data from the new sensor;
Ensuring universality. (a) The method was validated with data from controlled environments and real mining conditions. (b) The dataset includes variations in lighting, rock sizes, and environmental factors. (c) Deep learning techniques allow adaptation to new types of data through retraining.
5. Conclusions and Future Work
This study presents a robust and efficient rock centroid localization system for mining robotic applications, particularly rock-breaking hammers, demonstrating significant advancements in addressing the challenges of rock localization in dynamic mining environments. The system achieved exceptional localization accuracy, with a Euclidean distance in the XY plane () of up to 0.0128 m and a normalized error () on the X and Y axes not exceeding 2.3%, surpassing the precision requirements for typical rock-breaking end effectors. Notably, the system exhibited consistent performance under diverse lighting conditions and in the presence of suspended particles, crucial factors in real-world mining operations.
Rigorous testing, including a sensitivity analysis, validated the system’s efficacy and transferability to real-world scenarios. The YOLO v8x-Seg model demonstrated robust performance against various image perturbations, maintaining high Mean IoU scores (92.88% to 96.10%) for changes in brightness and contrast. However, a notable sensitivity to rotations was observed, with Mean IoU dropping to around 74% for ±5° rotations, highlighting areas for future improvement. The innovative combination of point cloud preprocessing, BEV conversion, and segmentation using YOLO v8x-Seg proved highly effective for precise rock centroid localization, addressing specific challenges in mining environments. With an average processing time of approximately 5 s, the system demonstrates its suitability for real-time applications in mining operations.
While limitations such as sensitivity to high concentrations of suspended particles and interference from intense light were identified, the overall performance suggests that this system could significantly enhance the efficiency and safety of rock-breaking operations in mining. This successful implementation, backed by a comprehensive sensitivity analysis and robustness testing, represents a crucial step towards fully autonomous mining operations. It has the potential to increase productivity, reduce operational costs, and improve worker safety in hazardous mining environments, while also providing a solid foundation for future research in 3D perception and object localization in complex, unstructured environments beyond the mining industry.
Future work will focus on several key areas to further enhance the system’s performance and versatility:
While the current preprocessing pipeline effectively handles various input resolutions, more advanced techniques will be developed to optimize this process. This includes refining the adaptive preprocessing module to more efficiently normalize input images across an even wider range of resolutions and sensor types, ensuring consistent performance across different sensor inputs;
Cutting-edge super-resolution techniques will be explored to potentially improve the quality of lower-resolution inputs, expanding the system’s applicability to scenarios where high-resolution sensors are not available or practical. This research will focus on adapting concepts from the Swift Parameter-free Attention Network (SPAN), as presented in the NTIRE 2024 Efficient Super-Resolution Challenge [
46], to the YOLO architecture. The incorporation of Swift Parameter-free Attention Blocks (SPAB) and parameter-free attention generation techniques aims to enhance spatial dependency capture and improve object detection efficiency across various scales. Additionally, the use of strategic residual connections will be investigated to optimize information flow through the network. This direction of research seeks to push the boundaries of what is possible with lower-quality input data, potentially broadening the system’s utility in challenging mining environments while maintaining the computational efficiency crucial for real-time applications;
Advanced image fusion methods for combining data from Basler Blaze-101 3D ToF and thermal cameras will be investigated to enhance system robustness in diverse mining environments. A fusion approach based on ResNet and zero-phase component analysis (ZCA), as proposed in [
47], will be adapted to the existing YOLO architecture. Modifications to the YOLO backbone will be implemented to process multimodal inputs, with ZCA being applied to project features into a sparse subspace. Within the YOLO framework, a fusion strategy utilizing local average l1-norm and soft-max operations will be developed to effectively merge depth and thermal information. These enhancements are expected to improve rock detection and localization accuracy, particularly in environments with suspended particles, while preserving YOLO’s real-time performance capabilities. The proposed improvements aim to increase system versatility and applicability across a wider range of mining operations;
The robustness of the model will be enhanced through the implementation of advanced sensitivity analysis techniques, drawing inspiration from uncertainty quantification (UQ) methods for deep neural networks, as demonstrated in [
48]. Their automated randomly deactivating process (ARDCW) will be adapted to the YOLO architecture employed in this study. This process involves the selective deactivation of network components to assess their influence on centroid localization accuracy. Three-dimensional visualizations of uncertainty intervals will be developed to facilitate spatial sensitivity analysis. The results will be compared with traditional sensitivity methods to provide a comprehensive evaluation of the model’s sensitivity. These findings will be utilized to optimize the YOLO architecture specifically for rock centroid localization, with potential incorporation of adaptive structures suited to mining environments;
To validate these improvements, extensive testing will be conducted with various camera configurations and resolutions, ensuring that the system not only maintains but potentially exceeds its current high performance across different hardware setups.