A Comparative Evaluation of Conveyor Belt Disc Brakes and Drum Brakes: Integrating Structural Topology Optimization and Weight Reduction

Abstract

Topology optimization is a well known and sophisticated method for designing structures. Through a finite element analysis, this method optimizes the design and material distribution to obtain an ideal strength-to-weight ratio and improved strain-to-weight ratio. This study involves the development of a comprehensive model for a brake using the ANSYS Parametric Design Language. The purpose of the model is to accurately characterize the geometry of the disc or drum. The technique of a complex eigenvalue analysis is used to identify the presence of unstable modes occurring at distinct frequencies, indicating instability. A braking force of 17,492 kN was exerted at a rotational velocity of 55 rad/s for 10 s. The optimization process resulted in significant mass reduction while maintaining structural integrity. In the drum brake, the mass was reduced from 114.01 kg to 104.07 kg, while the disc brake’s mass decreased from 68.81 kg to 56.68 kg.

1. Introduction

This journal paper examines the sophisticated engineering of conveyor belt braking systems. The subject utilizes topology, an essential element of geometry, which has played a key role in various fields such as structural engineering and computer science [1]. The research utilizes topology optimization and finite element analyses to improve the performance characteristics of braking systems in bulk material handling conveyor belt systems. This study aims to optimize the arrangement of materials inside a given design area to obtain the most efficient distribution of materials and mass reduction under a defined set of loads, torque, and boundary conditions [2]. Using this technology is essential for the creation of structures that are lightweight and durable, resulting in a major improvement in the energy efficiency and operational expenses of conveyor belt braking systems [3].

FEA, being a powerful computational technique, allows for accurate models of intricate physical phenomena under various torques applied on the brake circumstances. This methodology enables an in-depth analysis of stress distribution, vibration, and deformation in brake components, resulting in the development of brakes that are both lightweight and durable when subjected to the demanding operational circumstances of conveyor systems [2]. This study enhances its scientific and practical value by conducting a comparative contrast evaluation between disc and drum brakes. Drum brakes are recognized for their durability and excellent heat dispersion, although disc brakes are frequently preferred due to their cost-effectiveness and easier servicing [4]. This comparative methodology guarantees that the research findings are both theoretically sound and practically applicable in different industrial environments. Moreover, this research exemplifies the application of engineering to address and eliminate the obstacles in attaining enhanced and environmentally friendly industrial systems [5].

Traditionally, conveyor belt braking systems mostly relied on mechanical components, which were characterized by simple materials and designs that prioritized basic performance rather than its effectiveness or dependability [6]. Early systems, which were frequently operated manually and required a lot of physical effort, faced complications with inconsistency and had limited control [7]. The adoption of computerized braking systems, specifically with the use of drum brakes, marked a substantial advancement, offering enhanced control and dependability [8]. This investigational text consolidates information from multiple investigations, documenting the evolution of brake technology from conventional designs to modern approaches such as topology optimization and a finite element analysis [9]. Thoroughly analyzing these various sources, this literature study aims to establish an in-depth understanding of the present condition of conveyor belt braking technology and pinpoint promising areas for future research and development [4].

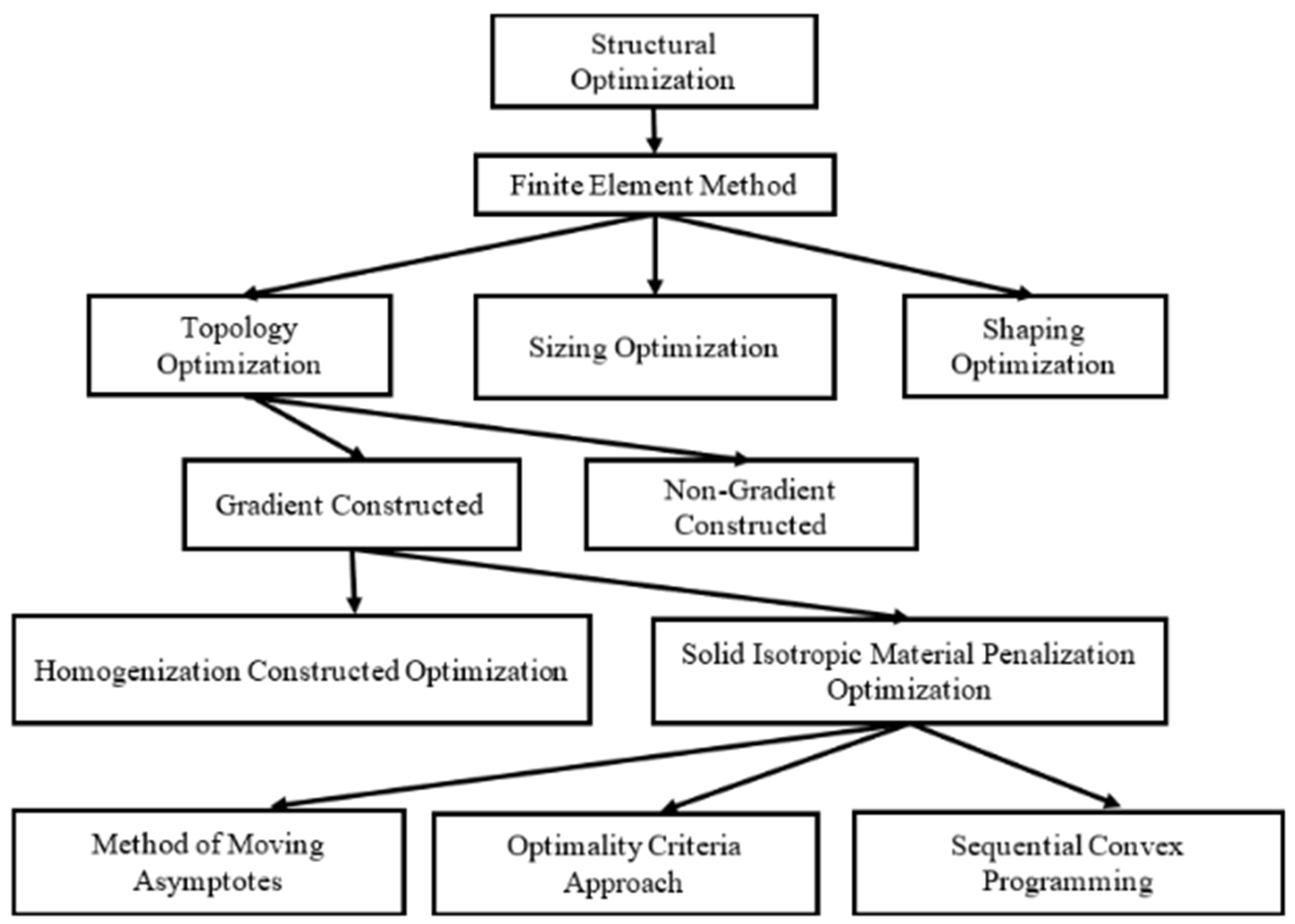
The optimality criterion method in structural optimization has proven to be quite effective in tackling topology optimization challenges. This study enhances its scientific and practical value by conducting a comparative contrast evaluation between disc and drum brakes [4]. Figure 1 depicts the arrangement of structural optimization, highlighting the utilization of Solid Isotropic Material Penalization (SIMP) as a gradient-based method for density distribution. These demonstrate the application of the optimality criterion, a mathematical model that operates through SIMP interpolation [10].

FEA is employed for topology optimization as the initial step in the process of meshing of the component, followed by the analysis of total deformation and equivalent stress. The quantity of stress or deformation operating on the section of the component in the software is visible in a variety of sections. Although certain sections will have optimal material distribution, others may necessitate the pruning process. 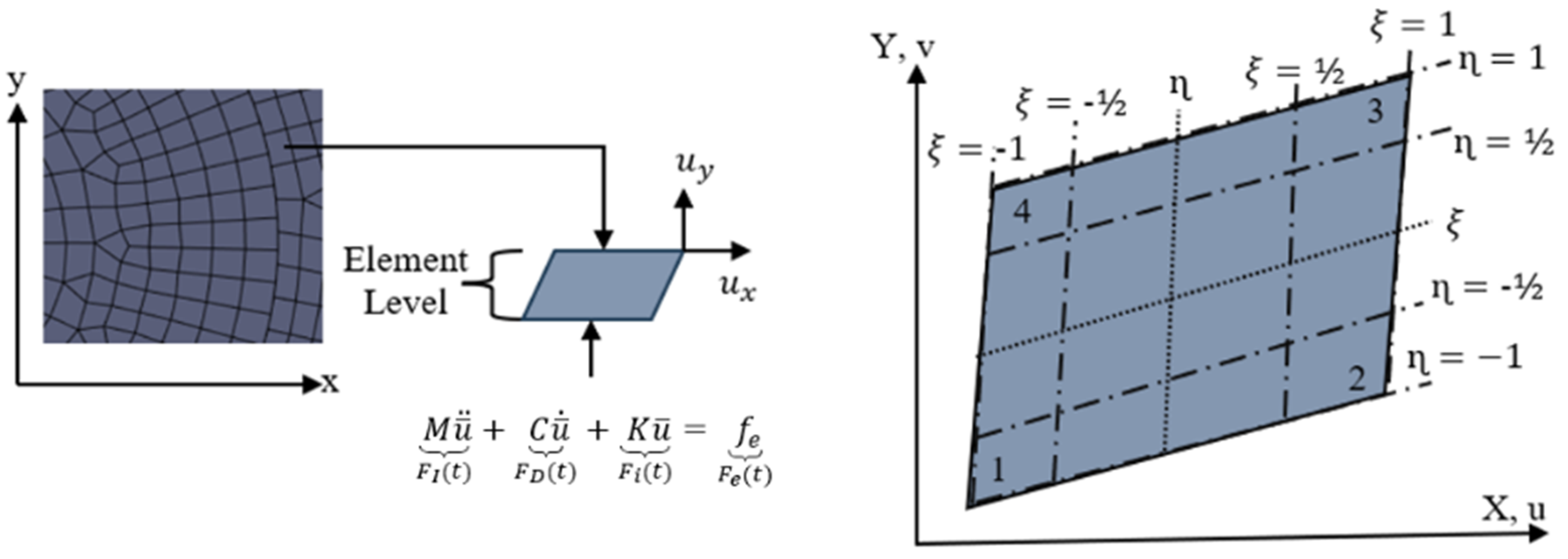Sections with minimal stress and deformation levels are identified using the finite element method [11]. The current study developed an analysis of the finite element model mechanical geometry, in Figure 2, which included explicit LS-Dyna meshing physics with linear element order. LS-DYNA is an advanced software programme that uses a finite element analysis to tackle complex problems involving nonlinear, time-dependent dynamics. It has the capability to use both explicit and implicit solvers. The explicit solution is efficient for situations that include dynamic problems with the presence of mass acceleration [12].

The governing equation that captures the dynamic behaviour for this situation is given as

$${ma}_n+{cv}_n+{kd}_n=f_n$$

The integer “n” represents the time step, whereas the term ${\mathrm{k}\mathrm{d}}_{\mathrm{n}}$ is referred to as the internal force inside the structure. The main challenge is to predict the movement at a future time step ${\mathrm{d}}_{\mathrm{n}+1}$ that occurs at time ${\mathrm{t}}_{\mathrm{n}+1}.$ The explicit dynamic solution is formulated in the following manner:

$$a_{n+1}=f(d_n, v_n, a_n, d_{n+1}, v_{n+1}, \dots )$$

At present, in step “n,” all elements in this equation are known, which allows for a direct solution. This implies that the solution advances in time regardless of element deformation, contact behaviour, or other nonlinearities. It is imperative to include “mass” in the explicit dynamic analysis solution to advance the simulation. The nodal acceleration is determined by dividing the force at the nodal mass, which is the result of the combination of external and internal forces at each node. The maximal time step size is restricted by the Courant–Friedrichs–Lewy criterion, and the solution is developed by integrating this acceleration over time [13]. When conducting precise analyses, the quality of the elements remains an essential factor, as a normalized random area within a coordinate system that spans from “−1” to “+1” becomes the starting point of the investigation [14]. The interior coordinates and displacements are determined by the two-dimensional linear quadrilateral formulation, which employs shape functions. In the following manner, the formulation is presented:

$$u(\xi , ɳ)=\sum N_{ij}\overline{u}k=\sum _{i=1}^n.\sum _{j=1}^m{N}_j\left(\xi \right)N_i(ɳ)\overline{u}k$$

In this context, the equation $k=\left(i-1\right)m+j$ represents a mathematical relationship. The symbol $N_i$ represents the shape function, which acts as an interpolation function for both coordinates (x) and displacements (u). This form function is what gives the term “iso-parametric” its meaning, as seen in Figure 3 [14]. The right part of the figure shows a two-dimensional quadrilateral element in a parametric space defined by the natural coordinates $\xi$ and η. The nodes are numbered 1 to 4, with their positions specified in the $(\xi , ɳ)$ coordinate system. The shape functions $N_i$ for a quadrilateral element are defined as follows:

$$\begin{gathered} {\mathrm{N}}_1\left(\mathsf{\xi },\mathrm{ɳ}\right)={\displaystyle \frac{1}{4}}(1-\mathsf{\xi })(1-\mathrm{ɳ}) \\ {\mathrm{N}}_2\left(\mathsf{\xi },\mathrm{ɳ}\right)={\displaystyle \frac{1}{4}}(1+\mathsf{\xi })(1-\mathrm{ɳ}) \\ {\mathrm{N}}_3\left(\mathsf{\xi },\mathrm{ɳ}\right)={\displaystyle \frac{1}{4}}(1+\mathsf{\xi })(1+\mathrm{ɳ}) \\ {\mathrm{N}}_4\left(\mathsf{\xi },\mathrm{ɳ}\right)={\displaystyle \frac{1}{4}}(1-\mathsf{\xi })(1+\mathrm{ɳ}) \end{gathered}$$

For the explicit time integration, we first modify the differential equation to include the damping effects [14].

The LS-Dyna dynamic analysis employs an explicit formulation, as depicted above. In this formulation, the mass matrix “M”, damping matrix “C”, and stiffness matrix “K” are utilized. Additionally, the external load vector “$f_e”$ and the acceleration “$\ddot{\overline{u}}$”, velocity “$\dot{\overline{u}}$”, and displacement (u) vectors of the finite element assemblage are considered. Another approach to analyse this equation involves studying the equation of statics at time “t”, where $F_I\left(t\right)$, $F_D\left(t\right)$, $F_i\left(t\right)$, and $F_e\left(t\right)$ represent the inertia, damping, internal, and external elastic forces, respectively.

The calibre of the finite element mesh significantly impacts the precision and consistency of explicit dynamic analyses. The research study mesh is presented in Figure 2, which illustrates the interlocking mechanism of both the drum brake and disc brake. The mesh in both instances exhibits a significant density, particularly in the vicinity of the central aperture and the supporting flange region. This demonstrates a purposeful effort to precisely portray the concentration of stress and complicated conduct in these locations. If the integrity of the material is disrupted during the removal process, the operation is stopped and the material in that place is kept [11].

A sequential zero-order optimization method is used for the model to optimize a specified objective function, either by increasing or decreasing it, while considering any imposed constraints. The main challenge is optimizing the frequency differentiation between certain eigenmodes of the braking structure.

In the second scenario, the weight or volume of drum brakes and disc brakes is reduced by considering their performance under the same applied forces and torque ratings that are created during the braking activity [15]. Figure 4 illustrates the proposed process flow diagram for the optimization of brake structural components. This study is motivated by the need to bridge gaps found in research completed in automotive industries by applying advanced FEA techniques for a structural analysis as an approach for comparative evaluation and optimization [16]. The target is to establish a multidimensional framework that not only improves the design and material distribution for weight reduction but also ensures robust performance tailored to the unique demands of bulk material handling systems [4]. The scope of the work presented in this paper will address aspects such as heat dissipation, reliability, and challenges associated with each type of brake system [17].

2. Methodology

The challenge is characterized by the known applied loads, potential support conditions, volume of the structure to be built, and potentially some extra design constraints, such as the specified placement and size of holes or solid portions [18]. In the broader structural optimization problem, the objective function of a structure, f($x$), which includes factors like manufacturing cost, strain energy, stress, and displacement, among others, needs to be minimized or maximized based on the specified boundary conditions, a-state-of-equilibrium constraints, behavioural restrictions, and limitations of design [19]. Hence, the optimization problem is described as

$$\left(SO\right)\left\{\begin{array}{c}max or min f\left(x,y\right) with regards to x and y \\ such that\left\{\begin{array}{c}behavioral restriction on y\\ limitations of design on x\\ equilibrium constraints\end{array}\right.\end{array}\right.$$

The objective of the multi-phase topology optimization issue is to identify the minimal value of the objective function by achieving an optimal arrangement of materials inside a two-dimensional or three-dimensional design domain represented as the symbol omega (Ω) [20]. Let us assume a mechanical component that exists within a specific area called ${\Omega }^m$. This area is a subset of a larger reference area called Ω in the two-dimensional space $R^2$. To the benchmark domain Ω, the optimal shape design issue can be defined as the issue associated with selecting the optimal elasticity tensor $E_{ijkl}\left(x\right)$, which is an attribute throughout the domain, and has the following structure [21]:

$$E_{ijkl}\left(x\right)={X\left(x\right)\overline{E}}_{ijkl}$$

The character ${\overline{E}}_{ijkl}$ represents the constant stiffness tensor of the material used to build the mechanical component. The function $X\left(x\right)$ serves as an indicator for the specific region ${\Omega }^m$ within Ω that is filled with the material:

$$X\left(x\right)=\left\{\begin{array}{c}1\\ 0\end{array} \right. {\displaystyle \genfrac{}{}{0pt}{}{if}{if}} {\displaystyle \genfrac{}{}{0pt}{}{x\in {\Omega }^m}{ x\in \Omega \backslash {\Omega }^m}}$$

The SIMP methodology employs a penalization factor to assign lower stiffness values, hence penalizing intermediate density to enhance the binary topological patterns. This involves examining constructions composed of a singular substance and empty space. The link between the stiffness tensor $E_{ijkl}\left(x^e\right)$ and the relative density of the element $x^e$ is assumed to be fundamental [22]:

$$E_{ijkl}\left(x^e\right)={(x}^e{)}^p{E}_{ijkl}^0, p>1$$

The stiffness tensor of a solid element is denoted as ${E^0}_{ijkl}\left(x^e\right)$ and the penalty factor, $p,$ is a key component of the SIMP technique. The challenge of topology optimization, utilizing the SIMP technique, is aiming to minimize compliance and can be expressed as follows [22]:

$${\displaystyle \genfrac{}{}{0pt}{}{min}{x}} :c\left(x\right)=U^{T}KU=\sum _{e=1}^N(x^e{)}^p U_e^T{k}_0{U}_e$$

$$such that.:\left\{\begin{array}{c}KU=F\\ {\displaystyle \frac{V\left(x\right)}{V_0}}=f\\ 0<X_{min}\le x\le 1\end{array}\right.$$

The variables in the equation are defined as follows: $“x”$ represents the vector of design variables. U and F represent the global displacement and force vectors. K represents the global stiffness matrix, $k_0$ represents the element displacement vector and the element stiffness matrix, and “N” represents the number of elements. The function $V\left(x\right)$ represents the volume of the material, while $V_0$ represents the volume of the design domain, and the volume fraction $“f”$ is a predetermined value.

2.1. Optimality Criteria Approach

The process of locating the brake structure that is the most rigid and conceivable is characterized by the highest possible global stiffness, which offers a minimum for the external forces that are experienced through the actual displacement field, known as the minimum mean compliance. This issue may be formulated as follows, written for the case of the SIMP interpolation below [23]:

$$\begin{gathered} {}_{u\in \cup ,\rho }{}^{min}l\left(u\right) \\ s.t. { a}_E\left(u,v\right)=l\left(v\right), for all v \in U \\ { E}_{ijkl}\left(x\right)={\rho {\left(x\right)}^{p}E}_{ijkl}^0 \\ {\int }_{\Omega }^{.}\rho \left(x\right)d\Omega \le V; 0<{\rho }_{min}\le \rho \le 1 \end{gathered}$$

A mathematical method known as the Lagrangian technique is used to determine the optimal value of the goal function after the dual function has been identified [24]. This means that the Lagrangian parameter estimators and the penalty term are updated after the current subproblem has been solved, and then they are utilized to solve the subsequent subproblem [25]. The stationarity requirements for the Lagrange function are stated as the following equation, where the essential criteria for optimality for the sizing variable “ρ” are a subset of the stationarity conditions:

$$\begin{gathered} \mathcal{L}=l\left(u\right)-\left\{a_E\left(u,\overline{u}\right)-l\left(\overline{u}\right)\}+ʌ({\int }_{\Omega }^{.}\rho \left(x\right)d\Omega -V)\right. \\ +{\int }_{\Omega }^{.}{\lambda }^{+}\left(x\right)\left( \rho \left(x\right)-1\right)d\Omega +{\int }_{\Omega }^{.}{\lambda }^{-}\left(x\right)\left( {\rho }_{min}-\rho \left(x\right)\right)d\Omega \end{gathered}$$

The Lagrange multiplier for the equilibrium constraint is denoted as “u” and the Lagrange multipliers for the constraints of the required conditions for optimality are denoted as ${ʌ, \lambda }^{-}\left(x\right)$, and ${\lambda }^{+}\left(x\right)$. When determining whether to apply a certain method in the current scenario, it is necessary to take into consideration the fact that a discretization mesh of a very tiny size will be required to achieve the desired level of prediction for the finer aspects of the form [26].

2.2. Complex Eigenvalue Optimization

A complex eigenvalue analysis, often known as CEA, has been used by researchers as the friction causes the stiffness matrix to be asymmetric; it deals with the calculation of system eigenvalues. To offer data support for a further dynamic analysis and structural design optimization, the objective of a modal analysis is to obtain the modal parameters of the system structure [27]. In general, it is possible to assume that the mass matrix and the stiffness matrix of engineering structures are symmetric, respectively, neutral specific and semi-positive definite [28]. The connection between the eigen-solutions of structures and the vibration of such systems is the utilization of a single finite element package for a big degree-of-freedom model of brakes. This is because many vibrating systems need more complex models than a single-degree-of-freedom system does [29]. With the application of Newton’s second law for each of the “n” masses $m_i$ (where i ranges from 1 to n), the equations of motion may be stated as follows:

$$\begin{gathered} F_i\left(t\right)={m_i \ddot{x}}_i\left(t\right)+\sum _{j=1}^n{c}_{ij}\dot{x_j}\left(t\right)+\sum _{j=1}^n{k}_{ij}{x}_j\left(t\right) \\ i=\mathrm{1,2},\dots ,n \end{gathered}$$

where $x_i\left(t\right)$ represents the displacement of mass $m_i; F_i\left(t\right)$ represents the force that is acting on $m_i$; and $c_{ij}$ and $k_{ij}$ represent the damping and stiffness coefficients, respectively, within the context of this equation. It is necessary to go through several precise modeling procedures to consider all the consequences that are brought about by the application of the braking pressure, and therefore by the normal and friction forces [30]. To carry out the complicated eigenvalue analysis using ANYSY, there are four primary stages that must be considered, which are outlined below [29,30]:

• To apply brake-line pressure by means of the nonlinear static analysis;
• To impose rotational speed on the disc or drum by means of the nonlinear static analysis;
• To extract the natural frequency of an undamped system by means of the normal mode analysis;
• To consider the influence of friction coupling by means of the complex eigenvalue analysis.

The nonlinear dynamic issue surrounding the braking system may be expressed in the following way [31]:

$$M\ddot{x}\left(t\right)+C\dot{x}\left(t\right)+Kx\left(t\right)=F\left(t\right)$$

The mass, damping, and stiffness matrices of the system are denoted as the letters M, C, and K, respectively, and are obtained in the following manner [32]:

$$\begin{gathered} M=\left(\begin{array}{ccccc}{m}_{bp}& 0& 0& 0& 0\\ 0& m_{bp}& 0& 0& 0\\ 0& 0& m_w& 0& 0\\ 0& 0& 0& 3J_d& 0\\ 0& 0& 0& 0& J_w\end{array}\right) \\ C=\left(\begin{array}{ccccc}{c}_n& 0& 0& 0& 0\\ 0& c_i& 0& 0& 0\\ 0& 0& 2c_{ps}& 0& 0\\ 0& 0& 0& C_w& -C_w\\ 0& 0& 0& -C_w& C_w\end{array}\right) \\ K=\left(\begin{array}{ccccc}{k}_n+ksi{n}^2\delta & -ksin\delta cos\delta & 0& 0& 0\\ -ksin\delta cos\delta & k_n+kco{s}^2\delta & 0& 0& 0\\ 0& 0& 2k_{ps}& 0& 0\\ 0& 0& 0& K_w& -K_w\\ 0& 0& 0& -K_w& k_w\end{array}\right) \\ X=\left[\begin{array}{c}{y}_{bp}\\ Z_{bp}\\ Z_w\\ {\theta }_w\\ {\theta }_w\end{array}\right] and F=\left[\begin{array}{c}-F_{bp}\\ F_f\\ 6F_f+P_0-P\\ -6T_f\\ T_w\end{array}\right] \end{gathered}$$

A combination of the external force, the contact force, and the friction force are included in the forcing term $F\left(t\right).$ The vector of displacement that is unknown is denoted by the symbol $x\left(t\right)$ and the dot represents differentiation concerning the time “t”. This equation may be reduced to the free-vibration equation when dampening and where external forces are not available [33]:

$$M\ddot{x}\left(t\right)+Kx\left(t\right)=0$$

The equation that represents the shape of the free vibration displacement solution for the linear system is as follows:

$$x\left(t\right)=u\cos (\omega t-\varphi )$$

In this equation, “u” represents a constant vector, “ω” represents the frequency of oscillation, and “ϕ” represents the phase angle. The equation is obtained by dividing the result by the cosine of the difference between “ω.t” and “ϕ”:

$$Ku={\omega }^2\left(Mu\right)$$

A collection of “n” simultaneous algebraic equations is referred to as the eigenvalue problem. It is necessary to make the following additional assumptions to apply this theory to a practical system, such as in disc or drum brakes. The subsequent assumptions are established as follows [34]:

• The material properties are linear, elastic, and homogeneous;
• The friction coefficient “p” between the disc and the lining pad surfaces is assumed to be constant;
• The speed of the rotor surface is assumed to be significantly lower than the speed of the travelling vibration wave;
• It is assumed that there is complete contact between the rotor and the lining planes.

2.3. Sequential Convex Programming

The process of generating and solving a series of approximation subproblems is a frequent method that is used in the process of addressing structural optimization problems that include continuous variables. This strategy is involved in a wide variety of optimization techniques, including sequential linear computing, sequential convex computing, and sequential quadratic computing, among others [35]. Whenever the goal and/or constraint functions involved in the problem are difficult to assess, sequential approximation optimization (SAO) may be used to find a solution to the nonlinear optimization issue [36].

This phenomenon is a property of the local model of the Method of Moving Asymptotes (MMA) and the Sequential Convex Programming (SCP) itself. This property allows for the availability of effective subproblem solution techniques. A mathematical programming issue is presented here for your consideration [35]:

$$\min \mathrm{f}\left(\mathrm{x}\right),\mathrm{x}\mathsf{ϵ}{\mathrm{R}}^{\mathrm{n}},$$

$$\mathrm{s}.\mathrm{t}.{\mathrm{g}}_{\mathrm{j}}\left(\mathrm{x}\right)=0,\mathrm{j}=1,\dots ,{\mathrm{m}}_{\mathrm{e}\mathrm{q}},$$

$${\mathrm{h}}_{\mathrm{j}}\left(\mathrm{x}\right)\le 0,\mathrm{j}=1,\dots ,{\mathrm{m}}_{\mathrm{e}\mathrm{q}},$$

$$\underset{\_}{{\mathrm{x}}_{\mathrm{i}}}\le {\mathrm{x}}_{\mathrm{i}}\le \overline{{\mathrm{x}}_{\mathrm{i}}},\mathrm{i}=1,\dots ,\mathrm{n}$$

The functions

$$\mathrm{f},{\mathrm{g}}_{\mathrm{j}}(\mathrm{j}=1,\dots ,{\mathrm{m}}_{\mathrm{e}\mathrm{q}}) \mathrm{and} {\mathrm{h}}_{\mathrm{j}}(\mathrm{j}=1,\dots ,{\mathrm{m}}_{\mathrm{e}\mathrm{q}})$$

are to be defined as

$$\mathrm{X}:=\{\mathrm{ǀ}\underset{\_}{{\mathrm{x}}_{\mathrm{i}}}\le {\mathrm{x}}_{\mathrm{i}}\le \overline{{\mathrm{x}}_{\mathrm{i}}},\mathrm{i}=1,\dots ,\mathrm{n}\}$$

The two functions are expected to be continuous across the set “X” and have at least two continuous derivatives inside the interior of “X”. The function “$\underset{\_}{x_i}\le x_i\le \overline{x_i},i=1,\dots ,n$” will be estimated using convex subproblems, where the objective function will be substituted with a strictly convex approximation, and inequality constraints will be approximated using convex functions. Equalities will be linearized, and the box constraints will be allowed to contract in the local model relative to the original box constraints. In this case, the usual objective functions are the mass or shape of a construction, or the compliance, which is a measure of the stiffness of a structure [37]. The primary limitations are the stresses in the components or the displacements of the nodes; however, there are no inherent limits on these factors. While equality restrictions are of lesser significance in this case, they may still be effectively managed [38]. The problem’s objective function is estimated using

$$\begin{array}{r}\overline{f}\left(x\right)≔f\left(x^k\right)+{\displaystyle \sum _{i,+}}\left[{\displaystyle \frac{\partial f\left(x^k\right)}{\partial x_i}}\left({\displaystyle \frac{{(U}_i^k-x_i^k{)}^2}{U_i^k-x_i}}-\left(U_i^k-x_i^k\right)\right)+{\tau }_i{\displaystyle \frac{(x_i-x_i^k{)}^2}{U_i^k-x_i}}\right]\\ -{\displaystyle \sum _{i,-}}\left[{\displaystyle \frac{\partial f\left(x^k\right)}{\partial x_i}}\left({\displaystyle \frac{{(x}_i^k-L_i^k{)}^2}{x_i-L_i^k}}-(x_i^k-L_i^k)\right)-{\tau }_i{\displaystyle \frac{(x_i-x_i^k{)}^2}{x_i-L_i^k}}\right]\end{array}$$

The approximation of the goal must exhibit strict convexity to satisfy an assumption related to the evidence of convergence. Nevertheless, it is advantageous in practical situations to prevent sluggish convergence.

The symbol “$\overline{f}$” represents the mathematical concept of an approximation:

$$\overline{D}:=\left\{x\mathrm{ǀ}{L}_i^k<U_i^k,i=1,\dots ,n\right\}$$

$L_i^k$ and $U_i^k$ are parameters that need to be selected, with $L_i^k$ being less than $x_i^k$ and $U_i^k$ being more than $U_i^k$. Moreover, ${\tau }_i$ are positive parameters, with “i” ranging from 1 to “n”. There are many qualities that are associated with this kind of approximation. Firstly, $\overline{f}$ is a first-order approximation in $x^k$. Additionally, $\overline{f}$ is strictly convex and separable. It is possible for the moving asymptotes, which are the move limits for the approximation, to change from one iteration to the next. The parameters $L_i^k$ and $U_i^k$ constitute the move limits. Approximating inequality restrictions is as follows:

$$\begin{array}{r}\overline{h_j}\left(x\right)≔h_j\left(x^k\right)+{\displaystyle \sum _{i,+}}\left[{\displaystyle \frac{\partial h_j\left(x^k\right)}{\partial x_i}}\left({\displaystyle \frac{{(U}_i^k-x_i^k{)}^2}{U_i^k-x_i}}-\left(U_i^k-x_i^k\right)\right)\right]\\ -{\displaystyle \sum _{i,-}}\left[{\displaystyle \frac{\partial h_j\left(x^k\right)}{\partial x_i}}\left({\displaystyle \frac{{(x}_i^k-L_i^k{)}^2}{x_i-L_i^k}}-(x_i^k-L_i^k)\right)\right]\end{array}$$

A sign of the component of the gradient of the original function and $h_j (j=1,\dots ,m_{eq})$ are taken into consideration while performing the summation. Inequalities have a convex approximation, although it is not always convex in every sense of the word. About transformed variables, equality requirements and the objective function are linearized in this context.

2.4. System Design and Modelling

The design of brake systems for conveyor belts in bulk material handling requires a multifaceted approach, focusing on efficiency, safety, and adaptability. This section outlines the key components and considerations in designing both drum brakes and disc brakes, integrating advanced technologies and optimization strategies as included in

Table 1. Brake design considerations’ data.

Brake Description Data	Value	Brake Description Data	Value
Brake Type	Disc	Material Properties’ Data	Drum/Disc
Brake angular velocity	55 rad/s	Steel density (kg/m³)	7850
Brake torque (N.m.)	8100	Young’s modulus (GPa)	200
Brake disc diameter (mm)	630	Thermal conductivity (W/m.°C)	60.5
Disk thickness (mm)	30	Tensile yield strength (MPa)	250
Force applied to disc (N)	34,858	Tensile ultimate strength (MPa)	460
Brake Type	Drum	Poisson’s ratio	0.3
Brake angular velocity	55 rad/s	Shear modulus (MPa)	76,923
Brake torque (N.m.)	8100	Bulk modulus (GPa)	166.67
Brake drum diameter (mm)	630 mm	Compressive yield strength (MPa)	250
Drum thickness (mm)	20	Ambient temperature	22°
Force applied to disc (N)	34,858	Maximum temperature	200°

. The design of a 707 m downhill conveyor includes incorporating a drop height differential of −26.6 m, and was facilitated through the utilization of the sidewinder v9.62, conveyor design software. The mechanical brake system has been specifically engineered to include a high-speed brake mechanism, characterized by an outer diameter of 630 mm. This brake system can exert a maximum clamping force of 34,858 KN and generate a maximum brake torque of 8.1 KNm. It is strategically positioned between the motor and gearbox, ensuring effective braking functionality within the overall system. The specified braking systems are designed to decelerate the conveyor within a 10 s timeframe during emergency braking situations. These brakes are used alternately to uphold the prescribed maximum temperature limit of 200 degrees Celsius for equipment exposed in deep mining operations.

3. Results and Discussion

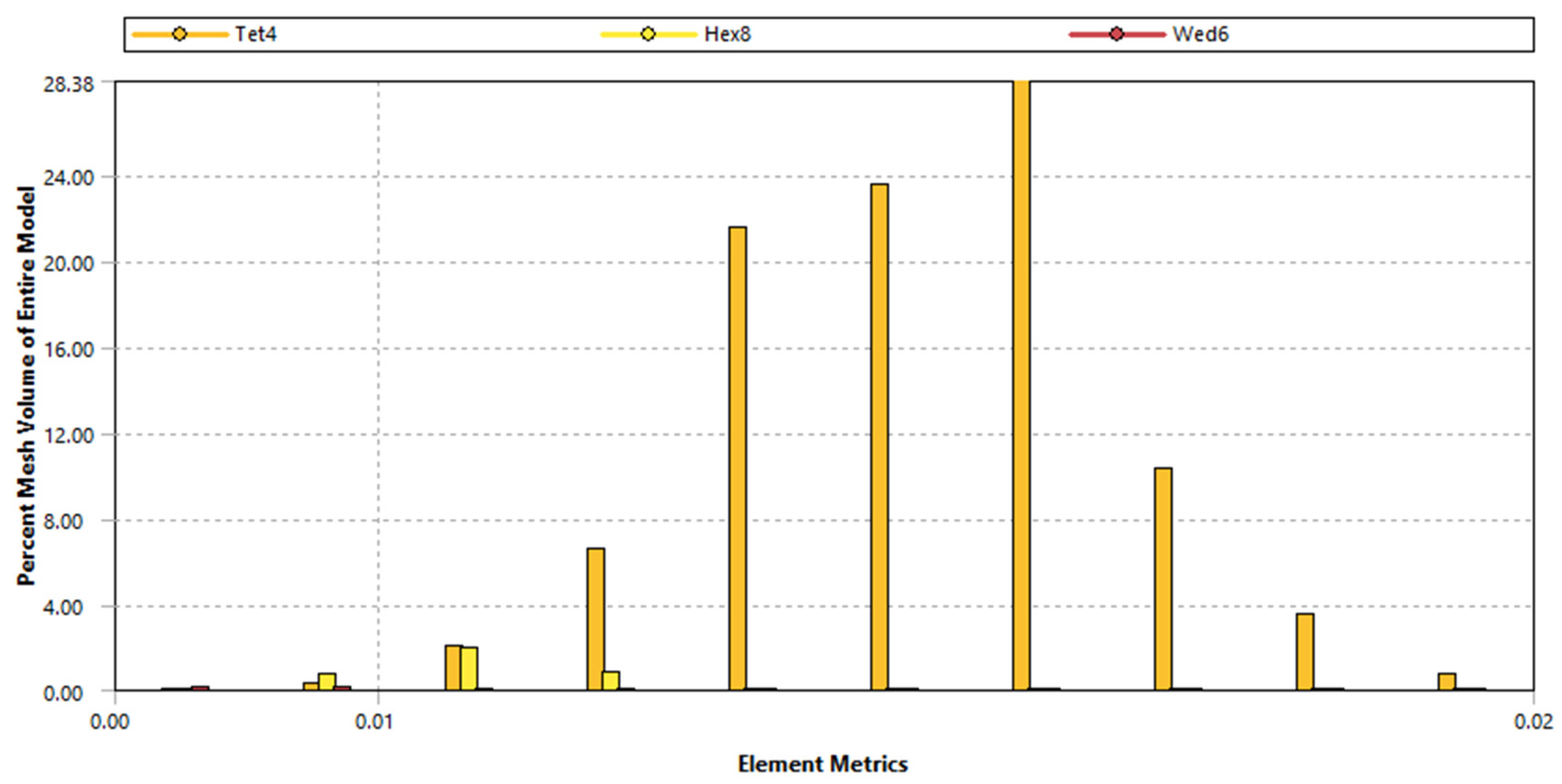
This research study case was initiated by first establishing an FEA model. The results showing the distribution of the element metrics across various quality metrics are illustrated in the histogram in Figure 5. The histogram indicates that Tetrahedral elements comprise the highest percentage of mesh volume at 28.38%, Hexahedral elements contribute approximately 1.91%, and Wedge elements account for a minimal 0.00492%. The model is composed of 18,786 elements and 6190 nodes, with element metrics ranging from 0.00 to 0.02. The aspect ratio, skewness, and element geometry are used to evaluate the mesh’s quality. Aspect ratios that are nearly equilateral are indicative of high-quality elements. This fine mesh can capture detailed physical behaviour, as evidenced by the dense distribution of elements in the lower range of metrics (0.00 to 0.02) in the histogram data. The analysis indicates that Tet4 elements are the most prevalent in the mesh, followed by Hex8 elements, which are more high-quality due to their regular shape, and Wed6 elements, which are used sparingly. Most elements have acceptable aspect ratios; however, some high-aspect-ratio elements may necessitate refinement to enhance accuracy. The typical dimension of the elements’ faces is indicated by the average surface area of 0.0046577 m² and the bounding box diagonal of 0.92168 m.

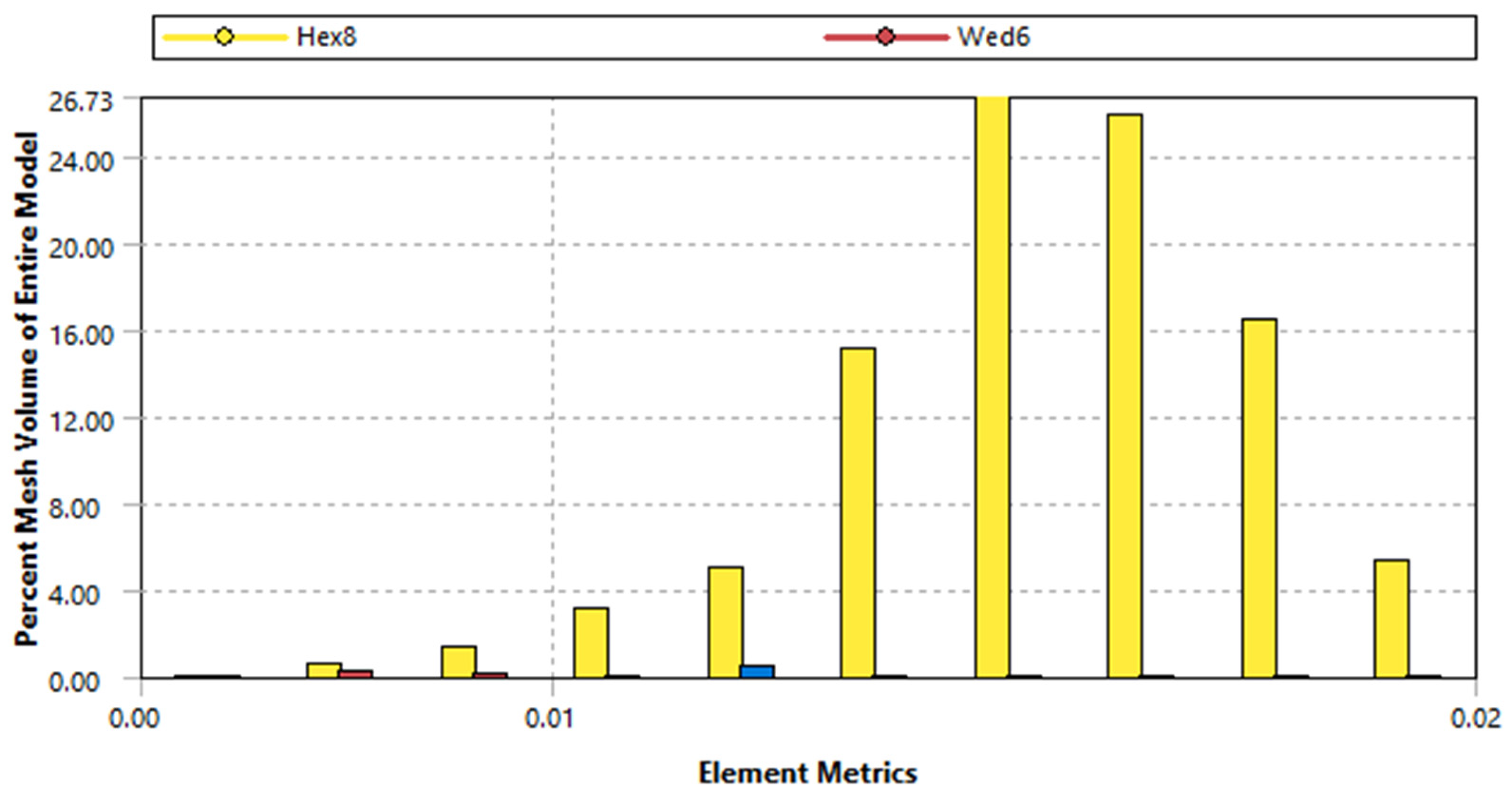
The disc brake analysis follows a similar methodology to that of the drum brake. It involves generating a finite element mesh for a disc brake with an external diameter of 630 mm, which is used in a conveyor belt system. The mesh consists of two sorts of elements: Hex8 and Wed6. The histogram illustration in Figure 6 shows that Hex8 components make up the largest portion, accounting for a high of 26.73% of the mesh volume. In contrast, Wed6 pieces are much less common, with a maximum of just 0.453%. The model is generated from 2528 nodes and 1157 elements, with element metrics ranging from 0.00 to 0.02. The diagonal of the bounding box is established at a length of 0.89146 m, serving as a point of reference for the overall dimensions of the model. The mean surface area of the elements is 0.0030323 m², which represents the normal magnitude of the elements’ faces.

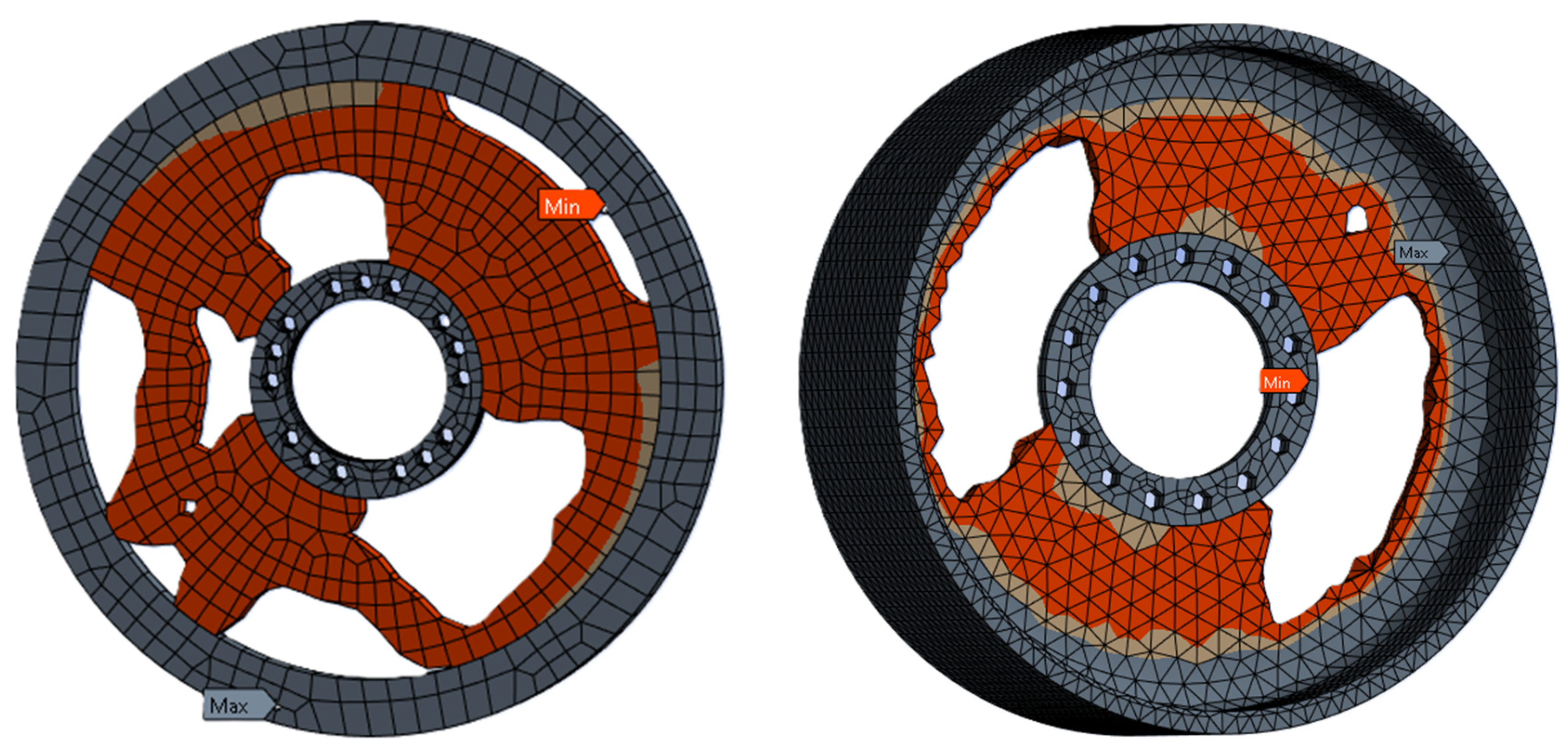
The application of SCP in ANSYS facilitated a nuanced approach to reducing the weight of both drum and disc brakes while maintaining their structural integrity. This technique allowed for the systematic reduction in material volume without compromising performance under normal duty conditions. The optimization process effectively incorporated load conditions and structural constraints, ensuring that all designs remained compliant with predetermined support conditions and specific design requirements, such as the strategic placement and sizing of holes or solid parts within the brake structure [17]. The methodology involved in structural optimization started with parameterization model creation in the ANSYS APDL. The baseline model was formed based on brake design calculations and FEA element sizes, as verified by convergence checks. The model retained 50% of the possible material volume with a retainment threshold of 0.13 as the starting point. The optimization results showed a potential mass reduction from 68.814 kg to 57.287 kg for disc brakes, achieving 83.25% of the original volume. Similarly, for drum brakes, the mass reduction was from 114.01 kg to 101.73 kg, achieving 89.22% of the original volume as illustrated by Figure 7.

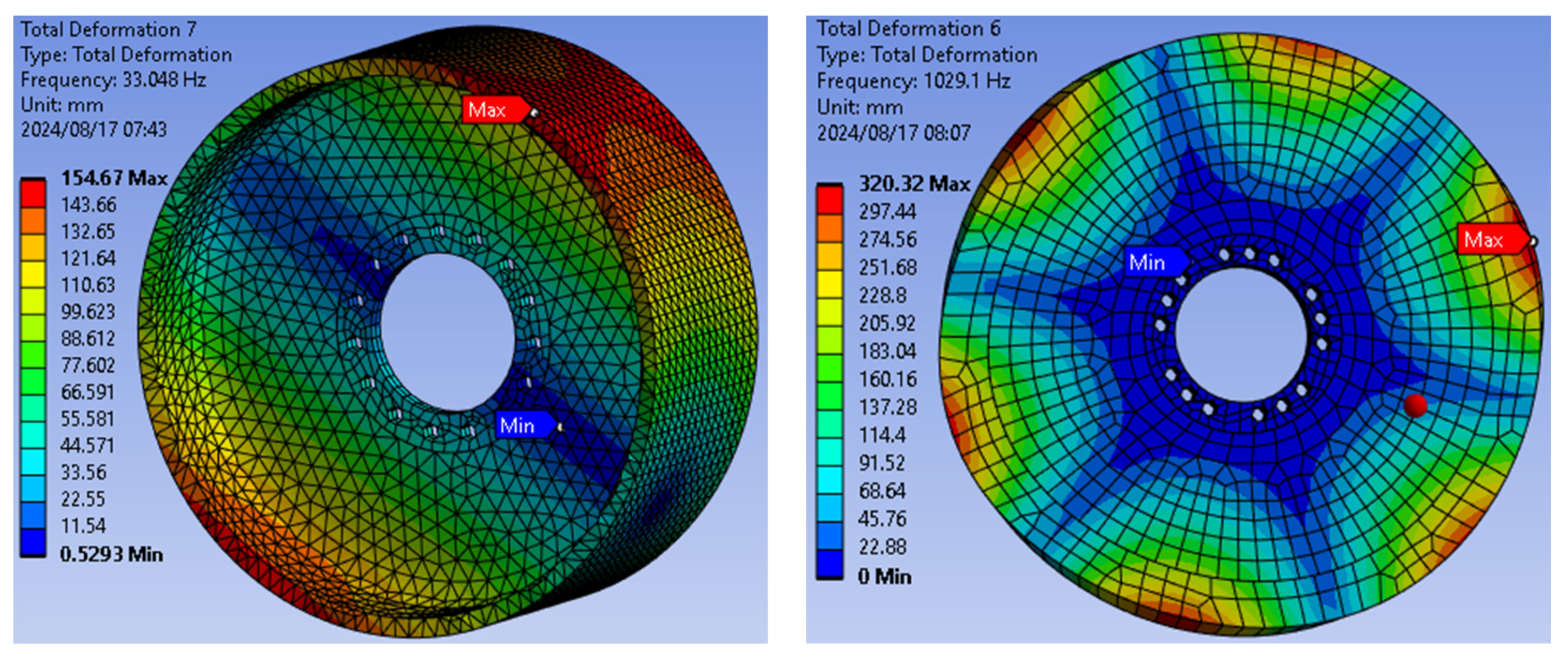
Prior to the optimization procedure, both disc and drum brakes were subjected to a modal analysis and static structural analysis to compare their respective performance levels. According to the modal analysis performed on the drum brake at a natural frequency of 33.08 Hz, the inner radius experienced the least deformation at 0.5293 mm, while the outer circumference experienced the most at 154.67 mm. In contrast, the disc brake, examined at a higher natural frequency of 1029.10 Hz, exhibited a minimum deformation of 22.8813 mm at the support region and a maximum deformation of 320.23 mm at the outermost section. These results are illustrated in Figure 8. These findings suggest that the disc brake, despite having a higher natural frequency and stiffness, is subject to more deformations compared to the drum brake.

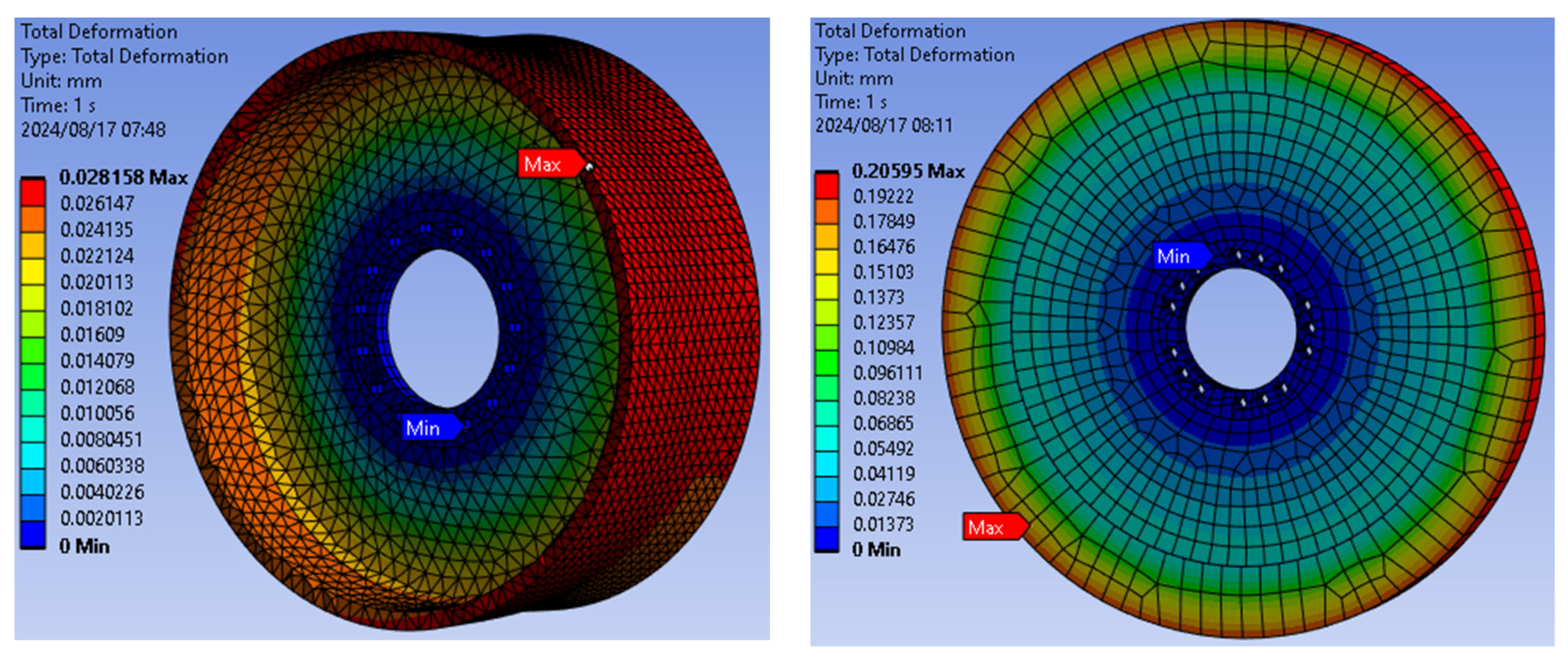
When the drum brake was subjected to an applied force of 34,858 N, the static structural analysis revealed that the inner radius experienced a minimum total deformation of 0.0020 mm, while the outermost section had a maximum total deformation of 0.02815 mm. Conversely, the disc brake exhibited much larger overall deformations, with a minimum of 0.01373 mm at the inner section and a maximum of 0.2059 mm at the outermost tip as indicated in Figure 9.

The von Mises stress analysis illustrated in Figure 10 further corroborates these findings such that regarding the drum brake, it exhibited a minimum of 0.00051263 MPa and a maximum of 11.1977 MPa. The disc brake, on the other hand, produced significantly higher von Mises stress levels, with the lowest of 35.617 MPa and the highest value of 498.63 MPa. These results highlight the inherent differences in the structural responses of drum and disc brakes under similar loading conditions.

Significant improvements in the performance parameters of the disc and drum brakes have been discovered via post-optimization research. These gains are especially noticeable in the areas of deformation and stress distribution. These enhancements were accomplished by means of a methodical optimization procedure that made use of the Optimality Criteria methodology and SIMP interpolation. This part will concentrate on natural frequency, modal deformation, static structural deformation, and von Mises stress distribution as it compares the outcomes of the post-optimization process to the findings of the pre-optimization process. A simulation of the first density optimization was the first step in the optimization process being implemented. With dimensions of 630 mm in diameter and a web thickness of 20 mm, the drum brake had an initial mass of 114.01 kg during its construction. In the end, the mass was reduced to 104.07 kg by cutting eight holes measuring 90 mm in diameter at equal distances around the circumference of the drum brake. They were cut with a pitch circle diameter of 410 mm, which resulted in a final mass reduction of 9.94 kg. This was accomplished through optimization, which allowed for the retention of sufficient mass to perform similar drum brake duties.

Similarly to the last specimen, a topological density optimization was performed on a disc brake that had beginning dimensions of 630 mm by 30 mm and weighed 68.81 kg. The final mass was brought down to 56.68 kg by cutting eight holes with a diameter of 90 mm each at equal intervals and a PCD of 360 mm.

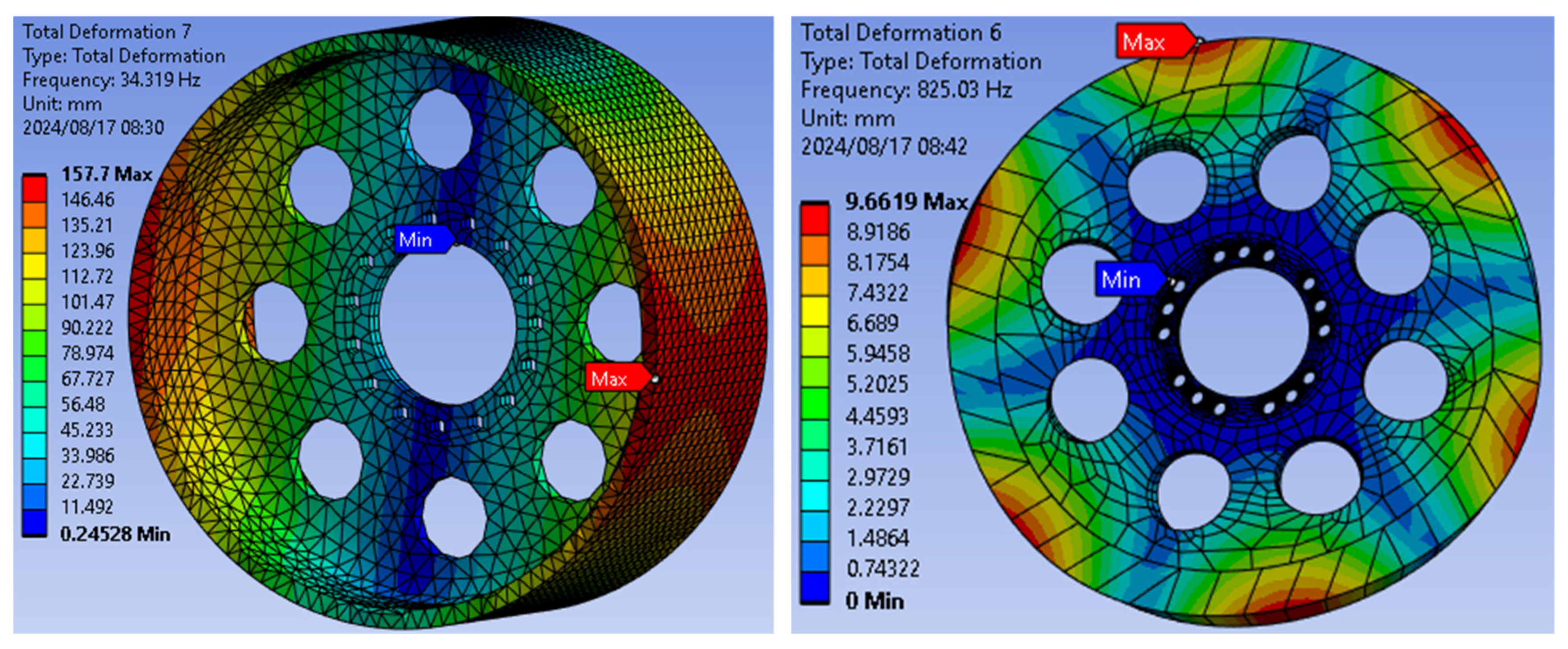
According to the results shown in Figure 11 of the modal analysis performed on the drum brake at a natural frequency of 34.319 Hz, the inner radius experiences the least amount of deformation, which is 0.24528 mm, while the outer circumference experiences the most amount of deformation, which is 157.7 mm. A disc brake, on the other hand, displays a minimum deformation of 0.743 mm at the support region and a maximum deformation of 9.66 mm at the outermost section when it is examined at a natural frequency of 825.03 Hz. A substantial reduction in deformation is indicated by the post-optimization results, which suggests a more efficient material distribution and enhanced structural stiffness. This contrasts with the pre-optimization values, which showed that the disc brake had a maximum deformation of 0.320232 mm at a natural frequency of 1029.10 Hz.

A static structural illustration in Figure 12 reveals that the optimized drum brake exhibits total deformations of 0.0037 mm at the inner radius and 0.00524 mm at the outermost region of the structure. Higher overall deformations of 0.00205 mm at the inner section of the optimized disc brake and 288.29 mm at the outermost tip are experienced by the component of the brake that is optimized. Although these values are greater than those for the drum brake, they represent a substantial improvement over the maximum deformation of 0.205 mm that existed before the optimization process. According to these findings, the optimization procedure was successful in reducing overall deformation, which resulted in a more uniform and efficient distribution of the material that was able to bear the force of 34,858 N that was applied.

The von Mises stress distribution for the optimized drum brake records a value of 2.0802 MPa at the innermost radius, and it rises to a value of 49.992 MPa at the region where the torque is applied. With a minimum of 29.034 MPa and a maximum of 403.77 MPa, the optimized disc brake, on the other hand, exhibits von Mises stress levels that are somewhat greater than the average, as shown in Figure 13. Although the von Mises stress levels of the disc brake are greater than those of the drum brake, the post-optimization data demonstrate a significant improvement in comparison to the highest von Mises stress measurement of 498.63 MPa that was recorded before optimization. The indication of improved structural integrity and the capacity to distribute von Mises stress more effectively throughout the braking surface is visible in the results.

4. Conclusions and Future Research Directions

Reflecting on the research aim, this study successfully establishes a multidimensional framework that not only optimizes weight distribution and material utilization but also enhances the overall design of braking systems tailored to the unique demands of conveyor belt systems. The optimized disc brake now operates at a level that is comparable to, or even superior to, the drum brake, ensuring increased longevity and dependability. The significant weight reduction achieved through topological density optimization further demonstrates the effectiveness of the applied technology in creating a more efficient and reliable brake system [39].

The comparative analysis of drum and disc brakes, before and after optimization, provides valuable insights into their structural and performance attributes. Pre-optimization evaluations revealed that disc brakes, despite their superior natural frequencies and stiffness, experienced more significant deformations and stress concentrations compared to drum brakes. The application of the Optimality Criteria technique and SIMP interpolation method resulted in substantial mass reductions without compromising structural integrity [40]. The drum brake mass was reduced from 114.01 kg to 104.07 kg, while the disc brake mass decreased from 68.81 kg to 56.68 kg. Post-optimization findings showed significant performance improvements for both braking systems. The drum brake exhibited enhanced performance with a natural frequency of 34.319 Hz and notable reductions in deformations. Conversely, the disc brake, with a natural frequency of 825.03 Hz, displayed a considerable decrease in maximum deformation. The post-optimization static structural analysis indicated decreased total deformations and improved stress distribution for both brakes, suggesting a successful optimization outcome [41]. These results indicate that while drum brakes inherently have greater stiffness, their structural performance can be significantly improved through optimization, resulting in more efficient material distribution and enhanced structural stiffness [42].

Considering these discoveries, future research should concentrate on examining the use of sophisticated composite materials and alloys to further reduce weight and enhance structural soundness. Additionally, implementing and comparing different optimization algorithms might identify the most efficient techniques for improving performance [43]. The promising findings of this study open several future research avenues that could enhance conveyor belt braking systems. The introduction of innovative composite materials or new metal alloys may increase the strength-to-weight ratio and heat dissipation capabilities of braking systems, a direction that has been explored in automotive applications but less so in conveyor belt systems [44]. Future work must include experimental validation in a laboratory setting to verify the findings of this research. This involves testing the performance of both drum and disc brakes before and after structural topology optimization under controlled conditions. Such experiments will provide empirical evidence to support the simulation results and further refine the optimization process [45]. Experimental work could incorporate advanced composite materials and high-performance alloys to reduce weight and enhance the structural integrity of the brakes. These materials, known for their superior strength-to-weight ratios and thermal properties, could significantly improve brake performance in demanding operational environments [46]. Implementing and comparing various optimization algorithms, including genetic algorithms, particle swarm optimization, and gradient-based methods, may help identify the most effective techniques for structural optimization. Comparing these algorithms can lead to more efficient designs and better performance outcomes [47]. Conducting dynamic performance tests under different operational scenarios, such as emergency braking, high-speed braking, and power failure braking, will provide a comprehensive understanding of how these brakes perform in real-world conditions. This will ensure that the optimized designs meet all necessary safety and performance standards [48].