Technologies for Increasing the Control Efficiency of Small Spacecraft with Solar Panels by Taking into Account Temperature Shock
Abstract
1. Introduction
2. Materials and Methods
- Situation analysis (analysis of disturbing factors, analysis of motion parameters and their evolution, analysis of the capabilities of the motion control system, and analysis of the capabilities of the information and measurement control system).
- Information preparation (quantitative assessment of factors affecting control, assessment of the need and feasibility of control, and formation of the target values of motion parameters).
- Formation of control laws.
- Implementation of control by actuators of the motion control system.
- Supervision of control efficiency using an information and measurement control system.
3. Mathematical Formulation of the Problem and Its Approximate Solution
3.1. Analysis of the Problem and Simplifications
- The characteristic time of a temperature shock is significantly lower than the period of oscillations of solar panels. This allows the use of a static formulation of the initial/boundary value problem for heat conduction [42,52]. The solar panel over a short period of time (the characteristic time of a temperature shock) moves only under the influence of a temperature shock within the framework of such a formulation. In this case, the oscillations are taken into account through the initial deflection. The shape of the solar panel at the moment of a temperature shock is curved and not flat as in the one-dimensional heat conduction problem [41].
- The solar panel can be represented as a rectangular homogeneous plate as a first approximation. It is rigidly fixed at one edge. Its three other edges are free. This simplification is often used in the literature [11,12,22,24,25]. It does not introduce significant errors in the assessment of disturbances from solar panel vibrations or a temperature shock.
3.2. Analysis of Two-Dimensional Heat Conduction Problem
3.3. Analysis of the Thermoelasticity Problem
3.4. Obtaining an Approximate Solution of the Thermoelasticity Problem
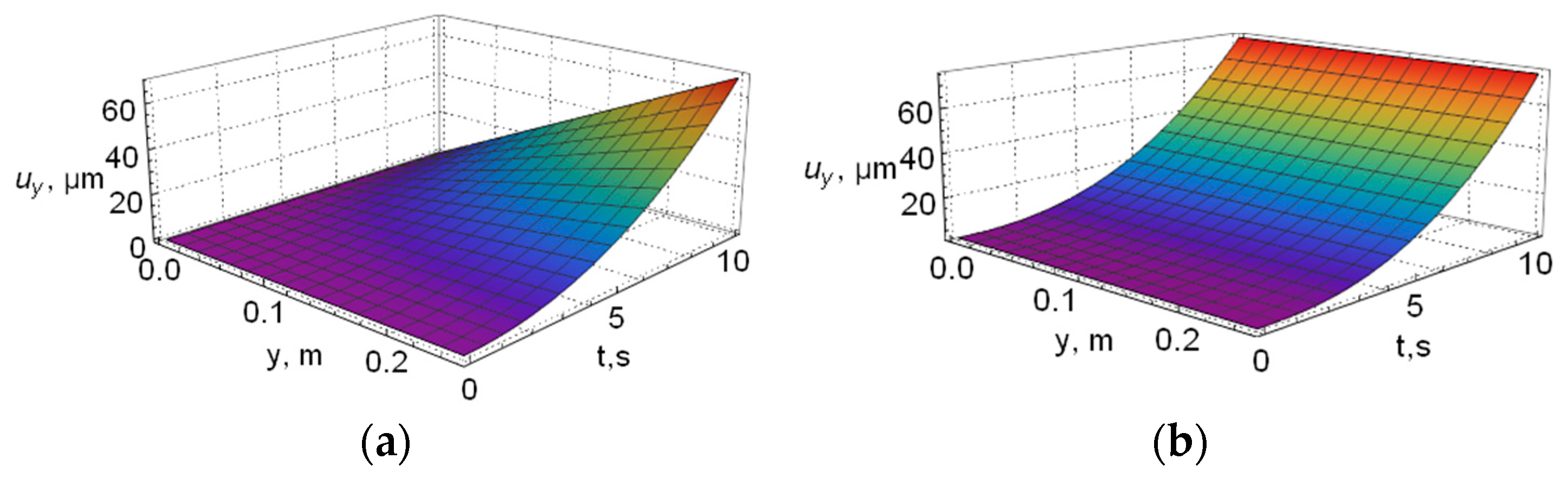
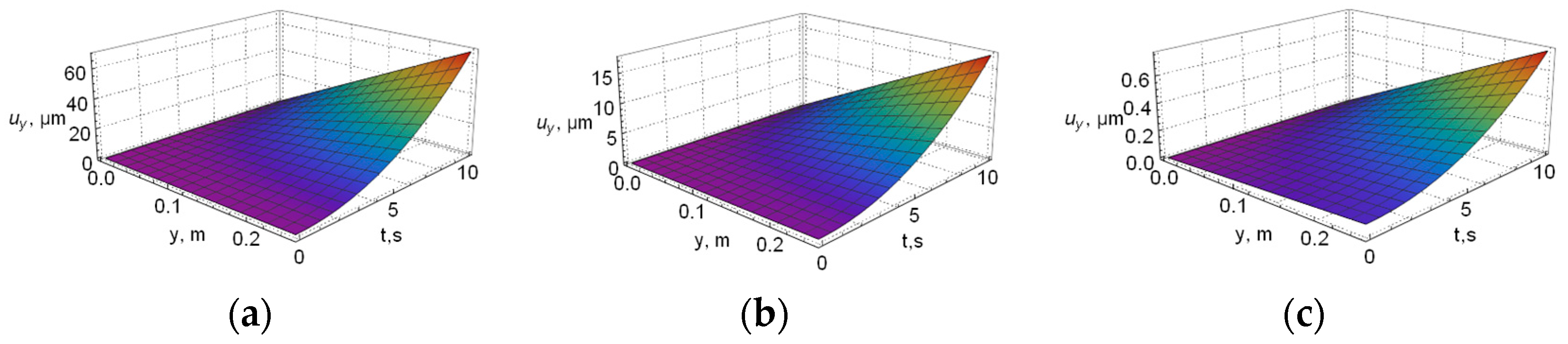
4. Results of Numerical Simulation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perkins, F.M. Flight Mechanics of Low-Thrust Spacecraft. J. Aerosp. Sci. 1959, 26, 291–297. [Google Scholar] [CrossRef]
- Stern, A. Chasing New Horizons. Inside the Epic Fiest Mission to Pluto; Picador: New York, NY, USA, 2018; ISBN 978-1-250-09897-9. [Google Scholar]
- Sedelnikov, A.V. Fast Analysis of Onboard Measurements of the Earth Magnetic Field for the Purpose of Microaccelerations Decrement on Board of the “AIST” Small Spacecraft During its Uncontrolled Orbital Flight. Int. Rev. Aerosp. Eng. 2018, 11, 76–83. [Google Scholar] [CrossRef]
- Khramov, D.; Volosheniuk, O.L. Analysis of the state of the art and the trends in the development of the target characteristics of orbital constellations of small agriculture-oriented Earth re-mote sensing spacecraft. Tech. Mech. 2023, 4, 31–39. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Eskina, E.V.; Taneeva, A.S.; Khnyryova, E.S.; Bratkova, M.E. The problem of ensuring and controlling microaccelerations in the internal environment of a small technological spacecraft. J. Curr. Sci. Technol. 2023, 13, 1–11. [Google Scholar]
- Taneeva, A.S. Analysis of the requirements for microaccelerations and the design appearance of a small spacecraft for technological purposes. E3S Web Conf. 2023, 458, 03006. [Google Scholar] [CrossRef]
- Jin, Y.; Yao, C.; Li, L.; Pan, D.; Li, J. Magnetic Characterization of Spacecraft Equipment in a Magnetic Shielded Room. IEEE Trans. Instrum. Meas. 2024, 73, 6006409. [Google Scholar] [CrossRef]
- Anshakov, G.P.; Belousov, A.I.; Sedelnikov, A.V.; Puzin, Y.Y. Effect of the Mission and Supporting Equipment on Operation of the Magnetometer Sensors of the Foton-M No. 2 Spacecraft. Russ. Aeronaut. 2019, 62, 571–576. [Google Scholar] [CrossRef]
- Hoffmann, A.P.; Moldwin, M.B.; Strabel, B.P.; Ojeda, L.V. Enabling Boomless CubeSat Magnetic Field Measurements with the Quad-Mag Magnetometer and an Improved Underdetermined Blind Source Separation Algorithm. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031662. [Google Scholar] [CrossRef]
- Roldugin, D.; Okhitina, A.; Monakhova, U.; Ovchinnikov, M. Comparison of Feedback Three-Axis Magnetic Attitude Control Strategies. Aerospace 2023, 10, 975. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Orlov, D.I.; Serdakova, V.V.; Nikolaeva, A.S. The Symmetric Formulation of the Temperature Shock Problem for a Small Spacecraft with Two Elastic Elements. Symmetry 2023, 15, 172. [Google Scholar] [CrossRef]
- Shen, Z.; Li, H.; Liu, X.; Hu, G. Thermal shock induced dynamics of a spacecraft with a flexible deploying boom. Acta Astronaut. 2017, 141, 123–131. [Google Scholar] [CrossRef]
- Vailati, A.; Šeta, B.; Bou-Ali, M.M.; Shevtsova, V. Perspective of research on diffusion: From microgravity to space exploration. Int. J. Heat Mass Transf. 2024, 229, 125705. [Google Scholar] [CrossRef]
- Belousov, A.I.; Sedelnikov, A.V. The problems of formation and control of the required level of microacceleration during testing and operation of spacecraft. Russ. Aeronaut. 2014, 57, 111–117. [Google Scholar] [CrossRef]
- Ivliev, N.; Podlipnov, V.; Petrov, M.; Tkachenko, I.; Ivanushkin, M.; Fomchenkov, S.; Markushin, M.; Skidanov, R.; Khanenko, Y.; Nikonorov, A.; et al. 3U CubeSat-Based Hyperspectral Remote Sensing by Offner Imaging Hyperspectrometer with Radially-Fastened Primary Elements. Sensors 2024, 24, 2885. [Google Scholar] [CrossRef]
- Akhmetov, R.; Filatov, A.; Khalilov, R.; Raube, S.; Borisov, M.; Salmin, V.; Tkachenko, I.; Safronov, S.; Ivanushkin, M. “AIST-2D”: Results of flight tests and application of earth remote sensing data for solving thematic problems. Egypt. J. Remote Sens. Space Sci. 2023, 26, 427–454. [Google Scholar] [CrossRef]
- Firsov, N.A.; Podlipnov, V.V.; Ivliev, N.A.; Ryskova, D.D.; Pirogov, A.V.; Muzyka, A.A.; Makarov, A.R.; Lobanov, V.E.; Platonov, V.I.; Babichev, A.N.; et al. Ensembles of spectral-spatial convolutional neural network models for classifying soil types in hyperspectral images. Comput. Opt. 2023, 47, 795–805. [Google Scholar] [CrossRef]
- Wu, X. Neural network big data fusion in remote sensing image processing technology. J. Intell. Syst. 2024, 33, 0147. [Google Scholar] [CrossRef]
- Sedelnikov, A.V. The Assessment Problem of Microaccelerations at the Experimental Sample of the Small Spacecraft “AIST” after the Battery Degradation and the Method of its Solution. Microgravity Sci. Technol. 2020, 32, 673–679. [Google Scholar] [CrossRef]
- Shen, Z.; Hao, S.; Li, H. Comparison of various thin-walled composite beam models for thermally induced vibrations of spacecraft boom. Compos. Struct. 2023, 320, 117163. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Wang, J.; Lin, Y. Integrated design and operation management for enterprise systems. Enterp. Inf. Syst. 2019, 13, 424–429. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, Y.; Zhang, Y.; Li, L.; Zhang, D.; Chen, S.; Eltaher, M.A. Thermally Induced Vibration of a Flexible Plate with Enhanced Active Constrained Layer Damping. Aerospace 2024, 11, 504. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Orlov, D.I. Analysis of the significance of the influence of various components of the disturbance from a temperature shock on the level of microaccelerations in the internal environment of a small spacecraft. Microgravity Sci. Technol. 2021, 33, 22. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Q.-Z.; Fan, G.-W.; Lv, X.-Y.; Gao, Y.; Xiao, Y. Observer-based Attitude Maneuver Control of Flexible Spacecraft: A Parametric Approach. Int. J. Control. Autom. Syst. 2024, 22, 2095–2107. [Google Scholar] [CrossRef]
- Chamberlain, M.K.; Kiefer, S.H.; La Pointe, M.; La Corte, P. On-orbit flight testing of the Roll-Out Solar Array. Acta Astronaut. 2021, 179, 407–414. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, L.; Chen, W. A nonlinear algorithm for large deformations of multi-stepped variable-section flexible solar arrays. Acta Astronaut. 2024, 217, 333–348. [Google Scholar] [CrossRef]
- Crofton, M.; Schoeffler, D.; Young, J.A.; Patterson, M.J. Erosion Rate Measurements for DART Spacecraft Ion Propulsion System. Appl. Sci. 2022, 12, 7831. [Google Scholar] [CrossRef]
- Spence, B.R.; White, S.F.; Sorenson, P. Space Solar Array Architecture for Ultra-High Power Applications. U.S. Patent 9120583, 1 September 2015. [Google Scholar]
- Kuru, K.; Yetgin, H. Transformation to Advanced Mechatronics Systems Within New Industrial Revolution: A Novel Framework in Automation of Everything (AoE). IEEE Access 2019, 7, 41395–41415. [Google Scholar] [CrossRef]
- Csencsics, E.; Schitter, G. Exploring the Pareto Fronts of Actuation Technologies for High Performance Mechatronic Systems. IEEE/ASME Trans. Mechatron. 2021, 26, 1053–1063. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, C.; Zhang, J.; Luo, J.; Guo, Z.; Li, Z.; Liu, R.; Liu, W.-D.; Ding, J.; Chen, Y.; et al. Twin Boundary Induced by High Temperature Shock Boosts Li-rich Layered-oxide Structural Stability. J. Mater. Chem. A 2023, 12, 23712–23722. [Google Scholar] [CrossRef]
- Rakhmanov, A.; Wiseman, Y. Compression of GNSS Data with the Aim of Speeding up Communication to Autonomous Vehicles. Remote Sens. 2023, 15, 2165. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Orlov, D.I.; Bratkova, M.E.; Khnyryova, E.S. Estimating the Inertia Tensor Components of an Asymmetrical Spacecraft When Removing It from the Operational Orbit at the End of Its Active Life. Sensors 2023, 23, 9615. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Choi, D.-G.; Oh, H.-S. Inertia Estimation of Spacecraft Based on Modified Law of Conservation of Angular Momentum. J. Astron. Space Sci. 2010, 27, 353–357. [Google Scholar] [CrossRef]
- Feng, Z.; Chang, J.; Hu, Y.; Liu, Z.; Cui, Y. Micro-vibration Modeling and Suppression Technology and Prospects for High Resolution Remote Sensing Satellite. Springer Proc. Phys. 2022, 295, 535–546. [Google Scholar]
- Li, D.; Wang, M.; Jiang, J. China’s high-resolution optical remote sensing satellites and their mapping applications. Geo-Spat. Inf. Sci. 2021, 24, 85–94. [Google Scholar] [CrossRef]
- Ali, M.A.; Eltohamy, F.; Abd-Elrazek, A.; Hanafy, M. Assessment of micro-vibrations effect on the quality of remote sensing satellites images. Int. J. Image Data Fusion 2023, 14, 243–260. [Google Scholar] [CrossRef]
- Yu, D.; Wang, G.; Zhao, Y. On-Orbit Measurement and Analysis of the Micro-vibration in a Remote-Sensing Satellite. Adv. Astronaut. Sci. Technol. 2019, 1, 191–195. [Google Scholar] [CrossRef]
- Huang, J.; Xi, J.; Yu, Z. Study on Micro-vibration Isolation System Design and Validation for the SDLT-1 Satellite of China. J. Vib. Eng. Technol. 2023, 11, 3879–3891. [Google Scholar] [CrossRef]
- Gao, X.; Wang, G.; Wu, Y.; Wang, Y.; Zhao, Y. Micro-vibration Attenuation Design, Analysis and Verification for Agile Remote Sensing Satellite. Lect. Notes Electr. Eng. 2022, 917, 913–920. [Google Scholar]
- Sedelnikov, A.V.; Orlov, D.I.; Serdakova, V.V.; Nikolaeva, A.S. Investigation of the stress-strain state of a rectangular plate after a temperature shock. Mathematics 2023, 11, 638. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Serdakova, V.V.; Orlov, D.I.; Nikolaeva, A.S. Investigating the Temperature Shock of a Plate in the Framework of a Static Two-Dimensional Formulation of the Thermoelasticity Problem. Aerospace 2023, 10, 445. [Google Scholar] [CrossRef]
- Menchtchikov, B.V. Monte Carlo method for solving boundary value problems for a diffusion equation with complex parameter. The Fourier transform in boundary value problems for a heat conduction equation. Russ. J. Numer. Anal. Math. Model. 2000, 15, 489–506. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Chang, J.-R.; Weng, C.-Y.; Huang, C.-J. An Analytic Solution for 2D Heat Conduction Problems with Space–Time-Dependent Dirichlet Boundary Conditions and Heat Sources. Axioms 2023, 12, 708. [Google Scholar] [CrossRef]
- Kot, V. Integral methods of solving boundary-value problems of nonstationary heat conduction and their comparative analysis. J. Phys. Conf. Ser. 2017, 891, 012356. [Google Scholar] [CrossRef]
- Quarta, A.A. Optimal Guidance for Heliocentric Orbit Cranking with E-Sail-Propelled Spacecraft. Aerospace 2024, 11, 490. [Google Scholar] [CrossRef]
- Hao, A.; Jin, L.; Tianzhe, W.; Jie, Z.; Xianliang, Z.; Yong, H. Mechanism and Application of Attitude and Orbit Coupling Dynamics for Spacecraft Proximity Relative Motion. Int. J. Aerosp. Eng. 2024, 2024, 6636084. [Google Scholar] [CrossRef]
- Russkikh, S.V.; Shklyurchuk, F.N. Nonlinear Oscillations of Elastic Solar Panels of a Spacecraft at Finite Turn by Roll. Mech. Solids 2018, 53, 147–155. [Google Scholar] [CrossRef]
- Li, D.; Liu, W. Vibration control for the solar panels of spacecraft: Innovation methods and potential approaches. Int. J. Mech. Syst. Dyn. 2023, 3, 300–330. [Google Scholar] [CrossRef]
- Ignatov, A.I.; Ivanov, G.; Kolomietz, E.; Martynenkova, E. Implementation of a Spacecraft Solar-Orientation Model Using a Reaction-Wheel System. Cosm. Res. 2023, 60, 154–166. [Google Scholar] [CrossRef]
- Kazantsev, Z.A.; Eroshenko, A.M.; Babkina, L.A.; Lopatin, A.V. Analysis of design of spacecraft solar arrays. Spacecr. Technol. 2021, 5, 121–136. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Serdakova, V.V.; Nikolaeva, A.S.; Evtushenko, M.A. Numerical Simulation of the Stress-Strain State of a Thin Plate in the ANSYS Package as a Two-Dimensional Formulation of the Thermo-Elasticity. Appl. Model. Simul. 2023, 7, 156–167. [Google Scholar]
- Lee, B.H.; Yamasaki, M.; Murozono, M. Experimental Verification of Thermal Structural Responses of a Flexible Rolled-Up Solar Array. Trans. Jpn. Soc. Aeronaut. Space Sci. 2013, 56, 197–204. [Google Scholar] [CrossRef][Green Version]
- Abrashkin, V.I.; Voronov, K.E.; Dorofeev, A.S.; Piyakov, A.V.; Puzin, Y.Y.; Sazonov, V.V.; Semkin, N.D.; Filippov, A.S.; Chebukov, S.Y. Detection of the Rotational Motion of the AIST-2D Small Spacecraft by Magnetic Measurements. Cosm. Res. 2019, 57, 48–60. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Salmin, V.V. Modeling the disturbing effect on the Aist small spacecraft based on the measurements data. Sci. Rep. 2022, 12, 1300. [Google Scholar] [CrossRef] [PubMed]
- Kirilin, A.N. Small Spacecrafts of a AIST Series (Design, Tests, Operation, Development); Publishing House of the Samara Scientific Center: Samara Oblast, Russia, 2017; 348p. [Google Scholar]



| Parameter | Designation | Value | Dimension |
|---|---|---|---|
| Solar panel length | l | 1 | m |
| Solar panel width | b | 0.5 | m |
| Solar panel frame thickness | h | 1 | mm |
| Young’s modulus | E | 4 × 1010 | Pa |
| Lamé coefficient | μ | 7.5 × 1011 | Pa |
| Cylindrical bending stiffness | D | 3.66 | N·m |
| Density | ρ | 1780 | kg/m3 |
| Coefficient of linear expansion | α | 1.35 × 10−5 | K−1 |
| Poisson’s ratio | ν | 0.3 | – |
| Coefficient of thermal diffusivity | a | 4.786 × 10−5 | m2/s |
| Thermal conductivity coefficient | λ | 16.3 | W/(m·K) |
| Degree of blackness | e | 0.2 | – |
| Model parameters: | C1 | 200 | K/m |
| β | 1 | s | |
| M | 3 | K/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sedelinkov, A.; Nikolaeva, A.; Serdakova, V.; Khnyryova, E. Technologies for Increasing the Control Efficiency of Small Spacecraft with Solar Panels by Taking into Account Temperature Shock. Technologies 2024, 12, 207. https://doi.org/10.3390/technologies12100207
Sedelinkov A, Nikolaeva A, Serdakova V, Khnyryova E. Technologies for Increasing the Control Efficiency of Small Spacecraft with Solar Panels by Taking into Account Temperature Shock. Technologies. 2024; 12(10):207. https://doi.org/10.3390/technologies12100207
Chicago/Turabian StyleSedelinkov, Andrey, Alexandra Nikolaeva, Valeria Serdakova, and Ekaterina Khnyryova. 2024. "Technologies for Increasing the Control Efficiency of Small Spacecraft with Solar Panels by Taking into Account Temperature Shock" Technologies 12, no. 10: 207. https://doi.org/10.3390/technologies12100207
APA StyleSedelinkov, A., Nikolaeva, A., Serdakova, V., & Khnyryova, E. (2024). Technologies for Increasing the Control Efficiency of Small Spacecraft with Solar Panels by Taking into Account Temperature Shock. Technologies, 12(10), 207. https://doi.org/10.3390/technologies12100207









