Abstract
As urbanization and industrial activities accelerate globally, air quality has become a pressing concern, particularly due to the harmful effects of particulate matter (PM), notably PM2.5 and PM10. This review paper presents a comprehensive systematic assessment of machine learning (ML) techniques for estimating PM concentrations, drawing on studies published from 2018 to 2024. Traditional statistical methods often fail to account for the complex dynamics of air pollution, leading to inaccurate predictions, especially during peak pollution events. In contrast, ML approaches have emerged as powerful tools that leverage large datasets to capture nonlinear, intricate relationships among various environmental, meteorological, and anthropogenic factors. This review synthesizes findings from 32 studies, demonstrating that ML techniques, particularly ensemble learning models, significantly enhance estimation accuracy. However, challenges remain, including data quality, the need for diverse and balanced datasets, issues related to feature selection, and spatial discontinuity. This paper identifies critical research gaps and proposes future directions to improve model robustness and applicability. By advancing the understanding of ML applications in air quality monitoring, this review seeks to contribute to developing effective strategies for mitigating air pollution and protecting public health.
1. Introduction
Rapid industrialization and urban development have led to a substantial deterioration in air quality globally [1]. This is primarily due to the increased release of diverse air pollutants into the atmosphere. Air pollutants are any substance present in the atmosphere, including particulate matter and gaseous pollutants like nitrogen oxides, sulfur oxides, and volatile organic compounds [2,3,4,5,6,7,8].
Particulate matter (PM) is a key air pollutant that can be classified based on particle size. , , , and refer to particles with an aerodynamic diameter of 1, 2.5, 4, and 10 m or less, respectively [9,10]. Smaller particles, such as and , are considered to be more dangerous, as they can penetrate deeper into the lungs and stay there longer, posing a greater threat to human health [11,12,13]. This is because the smaller the particle size, the more easily it can be inhaled and deposited in the respiratory system, causing various adverse health effects, including cardiovascular and respiratory diseases. PM is generated from both primary sources, including direct emissions from combustion and natural events, as well as secondary sources formed through atmospheric chemical reactions involving gases like sulfur dioxide () and nitrogen oxides () [14].
The World Health Organization has established air quality guidelines recommending that concentrations should not exceed an annual average of 5 or a daily average of 15 to mitigate health risks associated with prolonged exposure. This underscores the importance of monitoring PM levels to protect public health and the environment [2,15].
Accurately estimating the concentrations of PM, particularly and , is crucial for understanding the impacts of air pollution [15,16,17]. While direct measurements from air quality monitoring stations provide high-precision data, the limited spatial coverage of these stations has led to the development of alternative methods such as Chemical Transport Models (CTMs) and satellite remote sensing for estimating PM concentrations. CTMs simulate pollutant movement and transformation by integrating meteorological data with chemical processes [18,19]. In contrast, satellite remote sensing detects aerosol concentrations by analyzing electromagnetic radiation from the Earth’s surface [20,21]. While combining these methods with ground-based measurements helps fill spatial data gaps and offers a more comprehensive view of regional and global air quality, each approach presents challenges [22]. CTMs require significant computational resources, and satellite remote sensing faces limitations in spatial and temporal resolution and cloud interference that can obscure satellite observations.
Traditional statistical models, such as Linear Mixed Effect (LME) models, are commonly used to estimate concentrations. LME models can include random intercepts for various monitoring sites to address site-specific variations in PM levels, which can fluctuate significantly due to local factors such as urbanization, industrial activity, and seasonal changes. While LME models are effective at estimating average PM concentrations across different locations and conditions, they often struggle to accurately estimate extreme values during high pollution events. For example, a comparison of a LME model and a random forest ensemble machine learning (ML) model found that the LME model tended to underestimate ground-level on highly polluted days ( > 100 ) and had less accuracy compared to the random forest model [23].
Recent advancements in traditional Machine Learning (ML) and Deep Learning (DL) techniques have demonstrated their potential to improve the accuracy of PM concentration estimation [24,25,26]. ML models, including random forests and support vector regression, have outperformed traditional statistical approaches in capturing the complex relationships between PM and various factors [23,27]. This is because ML models can identify intricate patterns and nonlinear interactions between meteorological conditions, emission sources, and other variables that influence PM concentrations. Moreover, DL models, such as convolutional neural networks and long short-term memory networks, can provide more robust and comprehensive estimates by handling high-dimensional datasets and learning intricate spatio-temporal patterns in PM pollution data [28,29,30,31]. These advanced ML and DL techniques have the potential to significantly improve the accuracy and spatial resolution of PM estimation compared to traditional methods, which is crucial for informing policy decisions and mitigating the impacts of air pollution [32].
The ongoing research efforts to enhance the accuracy of PM estimation models, including the use of ensemble learning techniques that combine multiple models, are crucial for informing policy decisions and mitigating the impacts of PM pollution on public health and the environment [22,33]. Ensemble learning approaches, which integrate the strengths of different model architectures, can often provide more accurate and reliable PM estimates than individual models by leveraging the complementary information and reducing the biases inherent in each model [22,33]. As the annual death toll attributed to air pollution continues to rise, the need for swift global action to reduce particulate matter levels has become increasingly urgent [34]. Accurate and up-to-date information on PM concentrations is essential to developing and implementing effective strategies to improve air quality and protect public health.
To identify, analyze, and evaluate the capabilities of various ML models in providing more accurate estimates of PM concentrations compared to traditional statistical models, the following questions have to be answered:
- RQ1: What are the benefits of using ML-based models to estimate PM concentrations?
- RQ2: What are the current solutions that employ ML-based models for estimating PM concentrations?
- RQ3: What are the research gaps and future directions for estimating PM concentrations using ML-based models?
By answering these relevant questions, this paper provides a comprehensive assessment of the state-of-the-art in leveraging traditional ML and DL for improved air quality monitoring and estimation.
The following are the main contributions of the current study:
- We propose a Systematic Literature Review (SLR) of the recent advancements in applying ML models to enhance the accuracy of estimating and concentrations. This review covers studies published from 2018 to 2024, ranging from those focused on individual ML models to those exploring ensemble learning models.
- We explore the primary challenges of using a specific type of training dataset in ML-based PM estimation models.
- We provide a comprehensive assessment of the state-of-the-art in leveraging ML for improved air quality monitoring and estimation of and , utilizing key metrics such as feature importance analysis, residual analysis, temporal and spatial consistency, and cross-validation.
- We outline future directions that could enhance the accuracy of and estimation.
2. Background
2.1. Air Pollution Modeling
Accurately estimating PM pollution is a crucial issue for public health and environmental management. Several methods are used to estimate PM concentration: (1) The traditional method uses ground-based air quality monitoring stations, which provide high accuracy but have low spatial coverage and are expensive [18]. (2) The chemical transport model explains the dynamics, sources of PM, and depositions, but it requires high computing power and takes a long time to simulate PM data [35]. (3) ML-based models show good accuracy, are easy to train, and offer high spatial coverage by leveraging data patterns to estimate concentrations at unmonitored locations [36]. However, they need data from ground-based monitoring stations for training. The model’s accuracy is heavily influenced by the choice of input features, such as meteorological variables, land-use data, or traffic patterns, and it requires careful preprocessing to produce accurate PM estimates.
2.1.1. Traditional Statistical Models
Different traditional statistical models were used to estimate pollutant concentrations, such as:
- Linear Mixed-Effect (LME) models: The ability of LME models to handle complex hierarchical data structures and account for both fixed and random effects makes them an effective tool for estimating PM concentrations. LME models incorporate fixed effects, which represent systematic influences of predictors such as geographical features or meteorological variables, along with random effects that capture variability at different levels of the data hierarchy, such as temporal or spatial variations. This approach enhances estimation accuracy by capturing the inherent variability and correlation structures within the data [23,37,38].
- Generalized Additive Models (GAMs): GAMs are a semi-parametric extension of generalized linear models (GLMs). They are particularly effective at capturing intricate, nonlinear, and non-monotonic relationships among variables. Specifically, GAMs are highly useful for estimating concentrations, modeling spatial patterns, and identifying key drivers of air pollution. Their ability to accommodate nonlinear dynamics helps address the intricacies of pollutant dispersion and chemical interactions that influence air quality. Typically, GAMs use an identity link function with a Gaussian error distribution, offering greater flexibility in modeling the relationships between predictors and levels, thereby improving interpretability [39,40]. Additionally, GAMs apply to both cross-sectional and longitudinal data, providing a comprehensive understanding of spatial and temporal variations. For example, cross-sectional data capture concentrations across various locations at a single point in time, while longitudinal data track levels at the same location over an extended period, allowing for the analysis of temporal trends and long-term changes.
- Spatio-Temporal Mixed Effect Model (STMEM): STMEMs are designed for data that vary across both space and time, making them highly effective for estimating PM concentrations. These models incorporate spatial and temporal correlations to account for geographic variability and time-based changes, such as seasonal patterns and pollution events. By using random effects to capture these dynamics, STMEMs offer a robust framework for analyzing complex environmental patterns and improving the accuracy of estimates, which supports public health and air quality management. However, their complexity can make implementation and interpretation challenging [41].
Most statistical models assume a linear relationship between variables when estimating PM concentrations, even though this relationship is non-linear. These models are based on specific assumptions, and to achieve accurate estimates, the data and variables must align with these assumptions. When these conditions are not met, the accuracy of the model can be significantly reduced. This limitation has prompted researchers to turn to ML models for estimating PM concentrations. Although both statistical and machine learning models use similar input data, they handle and process it differently. Unlike statistical models, ML models make fewer assumptions and capture more complex, non-linear relationships in the data, allowing them to achieve higher accuracy [23,42].
2.1.2. Machine Learning (ML)-Based Models
ML emerges as a powerful tool for estimating PM concentrations. ML-based models, when trained on diverse datasets that integrate meteorological and land-use information, can capture complex relationships and provide spatially extensive, low-cost, and accurate estimations of PM concentrations [9,23]. Accurate estimates allow for better tracking of air pollution levels, helping authorities to identify high-risk areas and reduce exposure to protect public health [43,44]. Several ML-based models have achieved good results in improving estimation accuracy, for example:
- Traditional Machine Learning (ML)-based Models:Different models offer an effective basis for air quality estimation. The effectiveness of these models depends on the quality of the input features. Some commonly used models include the following:
- –
- Support Vector Machines (SVMs) model: SVMs effectively estimates PM levels by leveraging their ability to find optimal hyperplanes in high-dimensional spaces. The process begins with collecting relevant input features that influence PM concentrations, such as meteorological data (temperature, humidity, wind speed), geographical information, and PM measurements. These features then transform into a higher-dimensional space using kernel functions, such as linear, polynomial, or radial basis function (RBF) kernels, which capture the underlying patterns in the data. The SVM algorithm minimizes estimation error while maximizing the margin between estimated values and actual PM concentrations by finding a hyperplane that fits the training data. The final output from an SVM model is a continuous numerical value that represents the estimated concentration of PM in the air [10,27,45] (See Figure 1).
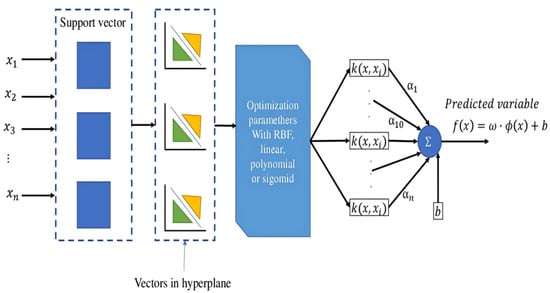 Figure 1. General architecture of a SVM model [46].
Figure 1. General architecture of a SVM model [46]. - –
- Decision Tree (DT) model: The DT algorithm aims to model PM concentrations using various independent variables (e.g., meteorological data and satellite observations). It follows a recursive partitioning process where the tree is made up of decision nodes and terminal leaves. For PM estimation, the algorithm uses standard deviation reduction to determine optimal splits, starting at the root node, based on the most significant variable affecting PM levels. Each split minimizes the sum of squared errors (SSE) to reduce estimation errors. This splitting continues until a termination criterion is met. The final nodes, known as leaf nodes, provide the estimated values for PM concentrations, allowing for effective air quality assessments [9,26,47,48,49]. Figure 2 illustrates the general structure of a standard DT.
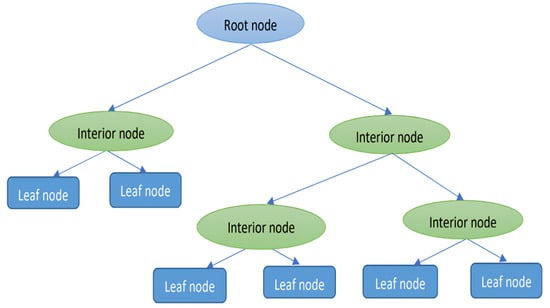 Figure 2. General architecture of DT model [48].
Figure 2. General architecture of DT model [48]. - –
- K-Nearest Neighbor (KNN) model: The KNN model is widely used for estimating PM concentrations. It works by measuring the distance between data points using metrics such as Euclidean or Mahalanobis distance to identify the closest neighbors in the dataset. The choice of k, representing the number of nearest neighbors to consider, is crucial. Selecting the optimal k value helps mitigate overfitting while improving the model’s generalization capabilities. Common methods to determine the optimal value of k include cross-validation, grid search, and using the square root of N (where N is the total number of samples) [50]. When a new data point is introduced, KNN calculates its distance to all training data points to find the k nearest neighbors. The estimated PM concentration for the new point is then determined by averaging the concentrations of these neighbors. This approach effectively captures patterns in environmental data, enabling reliable PM level estimations based on historical observations and spatial relationships among data points [26,32,51,52,53]. Figure 3 illustrates the general structure of a KNN model.
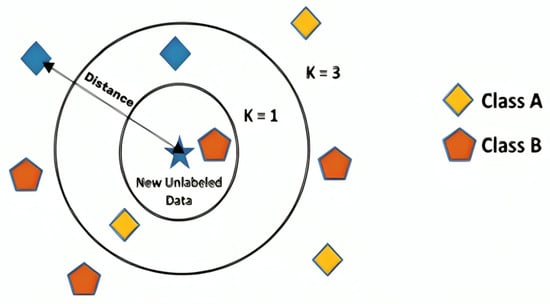 Figure 3. General architecture of KNN model [53].
Figure 3. General architecture of KNN model [53]. - –
- Artificial Neural Networks (ANNs) model: ANNs provide a robust framework for estimating PM concentrations, effectively capturing the complex, non-linear relationships inherent in air quality data. ANNs consist of an input layer that collects data from various sources, including meteorological variables and pollutant concentrations. These data pass through one or more hidden layers, where the model learns complex relationships between the inputs and the target output. The output layer generates a single value that indicates the estimated PM concentration for a given time and location (See Figure 4).
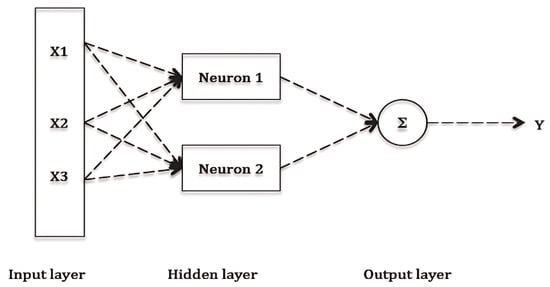 Figure 4. Basic structure of an ANN [54].
Figure 4. Basic structure of an ANN [54].
- DL-based Models:DL algorithms are well-suited for capturing complex, non-linear relationships. They are particularly effective for developing estimation models for PM concentrations. They can effectively analyze and interpret the relationships between meteorological data and PM levels as follows:
- –
- Multi-layer Perceptron (MLP) Neural Network model: The MLP model is effective in estimating PM concentrations. It has a layered structure, consisting of multiple interconnected layers of neurons (See Figure 5). Each node processes input data via weighted connections and uses activation functions to introduce non-linearity. The structure contains an input layer that receives temporal variables (date and time) and meteorological variables (temperature, humidity, and wind speed) that act as explanatory variables. The hidden layers enable the model to learn complex patterns and relationships within the data, and the output layer produces the estimated PM concentration [49,55].
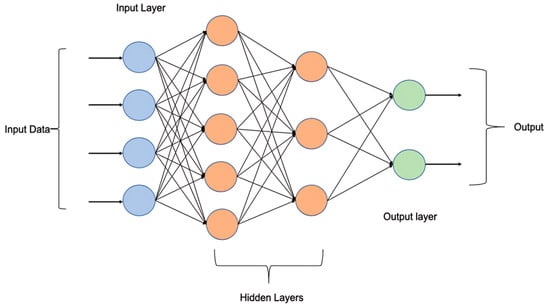 Figure 5. General architecture of MLP model [55].
Figure 5. General architecture of MLP model [55]. - –
- Convolutional Neural Network (CNN) model: Convolutional neural networks have been widely used in image data processing [56,57]. This model enhances the estimation accuracy of PM concentrations in different cities such as the United States [28] and Kaohsiung [9]. They use a structured approach, alternating between convolutional and pooling layers (See Figure 6). The convolutional layers extract spatial features from input data, including air quality measurements and meteorological variables. These layers apply filters or kernels to perform convolution operations, which produce feature maps that highlight important patterns associated with PM levels. The pooling layers reduce the size of the convolved features, decreasing the computational resources needed to process the data. This integration of convolutional and pooling layers enables CNNs to effectively learn and estimate PM concentrations from intricate environmental datasets [9,28,58].
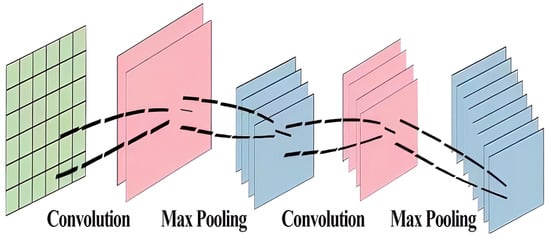 Figure 6. General architecture of CNN model [53].
Figure 6. General architecture of CNN model [53]. - –
- Deep belief-Back Propagation Network model: The prediction model, leveraging a deep belief neural network integrated with a Back Propagation (BP) neural network, represents a sophisticated hybrid approach that combines the strengths of multiple unsupervised Restricted Boltzmann Machines (RBMs) and supervised BP networks to effectively predict pollutant concentrations, specifically and . As illustrated in Figure 7, this architecture comprises an input layer with 29 nodes dedicated to capturing relevant features of the PM, while the output layer consists of a single node that predicts concentration values. The total number of layers in the network is variable, denoted as n, allowing for flexibility in model complexity; each layer is formed by stacking RBMs followed by BP networks, which enhances the model’s ability to learn intricate patterns in the data [59].
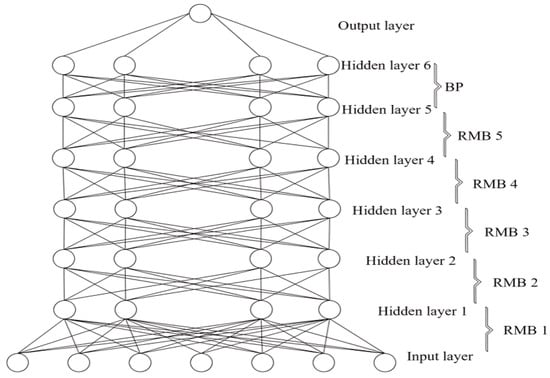 Figure 7. Architecture of deep belief-BP network model [59].
Figure 7. Architecture of deep belief-BP network model [59].
- Ensemble Learning-based ModelsEnsemble learning is an ML approach that combines multiple models to improve accuracy and reduces overfitting in estimating PM concentrations [42]. It includes techniques like bagging, boosting, and stacking. Bagging trains several models on different subsets of data and averages their estimations [60]. Boosting trains multiple models sequentially, with each new model correcting the errors of its predecessor [61]. Stacking uses different models and combines their outputs through a meta-learner for final estimations [62]. Examples of these models include the following:
- –
- Random Forest (RF) model: RF is an effective ensemble learning model for estimating PM concentrations. This model generates multiple decision trees to improve the estimation accuracy. The input variables are usually meteorological and environmental parameters like temperature, humidity, wind speed, atmospheric pressure, and PM levels. Each decision tree is built using a bootstrap sample from the training dataset. This allows each tree to be trained on a unique subset of data. The remaining data are then used to estimate the error for that tree. At each node of the decision trees, it selects a random subset of independent variables to determine the best split, promoting tree diversity and reducing overfitting. The final PM concentration is estimated by averaging the outputs of all trees, providing a robust estimate that captures complex environmental interactions [23,49,53,63,64]. Figure 8 shows the general structure of a random forest regressor.
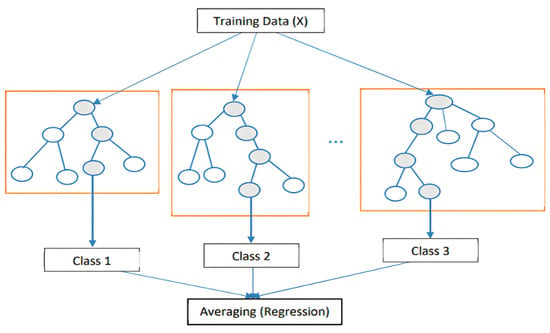 Figure 8. Architecture of RF model [53].
Figure 8. Architecture of RF model [53]. - –
- Extreme Gradient Boosting (XGBoost) model: The XGBoost model is highly effective for estimating PM concentrations. The process begins by training an initial decision tree on a randomly chosen subset of data to estimate PM levels. The model then calculates the residuals, which represent the differences between the estimated and actual PM concentrations. These residuals are used to train the subsequent trees, with each new tree aiming to correct the errors of the previous ones. This iterative approach continues by updating the model parameters to enhance the objective function. The objective function is divided into two parts: the loss function (L), which measures estimation error, and a regularization term that penalizes complexity to prevent overfitting. By incorporating various input features, such as atmospheric data (temperature, humidity, and wind speed) and aerosol optical depth (AOD), XGBoost effectively captures the complex relationships and interactions influencing PM concentrations. The final PM estimation in XGBoost is calculated by summing the estimations from all individual trees in the ensemble [42,45,65,66,67]. This results in enhanced accuracy of estimations across different spatial and temporal contexts (See Figure 9).
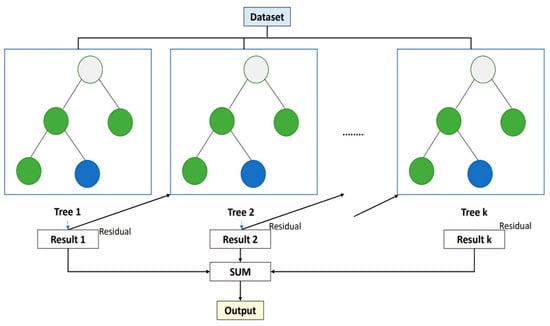 Figure 9. General structure of XGBoost model [67].
Figure 9. General structure of XGBoost model [67]. - –
- Light Gradient Boosting Machine (LightGBM) model: This model performs exceptionally well at modeling complex, non-linear relationships between PM concentrations and various environmental variables. The algorithm constructs a decision tree using input features such as traffic patterns, meteorological data, and PM measurements. It uses a gradient boosting approach, where each subsequent tree corrects the errors of the previous ones. LightGBM speeds up training by applying a histogram-based method that bins continuous features into discrete intervals to efficiently calculate potential split points. The splitting in LightGBM follows a leaf-wise approach, selecting the leaf node with the maximum gain to grow and prioritizing the most informative splits to reduce estimation error. This process continues until a stopping criterion, such as a set number of trees or achieving a sufficient level of accuracy, is reached. The final estimation for PM is calculated as the sum of the estimations from all the individual trees in the model [67,68,69]. Figure 10 shows the structure of the LightGBM model.
 Figure 10. General structure of LightGBM general [67].
Figure 10. General structure of LightGBM general [67].
2.2. Model Evaluation Metrics
The accurate and reliable estimation of the models is crucial to ensuring the robustness of their findings and to mitigate the risk of overfitting. Consequently, in this section, a comprehensive evaluation of the performance of these models using a set of metrics is presented (See Table 1).

Table 1.
Model evaluation metrics.
3. Methodology
To answer the research questions, a comprehensive and systematic review of recent ML models used for estimating PM concentrations is rigorously conducted. Specifically, we followed the systematic methodology introduced by Kitchenham and Charters [70], which encompasses three primary phases: planning, reviewing, and reporting (see Figure 11). This structured approach allowed us to assess all relevant research related to PM estimation in a thorough and organized manner.
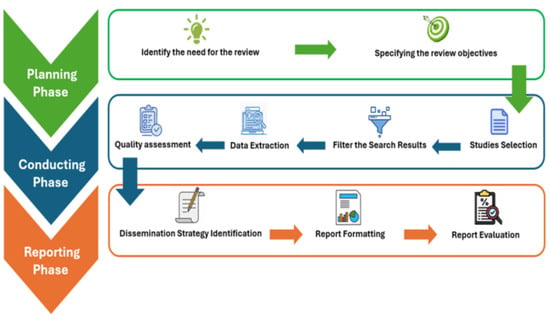
Figure 11.
Systematic literature review phases.
3.1. Planning Phase
This section thoroughly explains the planning phase components, including the following: (1) identify the need for the review; and (2) specify the review objectives.
- Identify the need for the review
This paper examines recent research from 2018 to 2024 that utilized ML to estimate and concentrations. Through the systematic review, we investigate how other researchers have applied ML techniques for this purpose. We then explore the proposed solutions and evaluate the studies to determine effective approaches for estimating and using ML models.
- Specifying the review objectives
We provide a comprehensive understanding of the current state of research on the use of ML for PM estimation and highlight opportunities for future advancements in this field. Table 2 clearly outlining the research questions and corresponding objectives.

Table 2.
The research questions and objectives.
3.2. Conducting Phase
This section presents a comprehensive overview of the methodology utilized for conducting a systematic literature review. This includes determining and refining search terms based on keywords relevant to our research scope and ending with an assessment of the selected studies. The process of the conducting phase encompasses the following steps:
- Step 1: Study selection:In the initial step, a search strategy was implemented to identify all relevant studies aligned with our research objectives. Specifically, a two-step procedure outlining the methodology for sourcing relevant literature using search terms was executed.
- Initially, three keyword groups were identified by taking into account alternative spellings of the terms using the following approach:
- –
- Defining the keywords relevant to the expansive scope of the research, such as air pollutants, particulate matter estimation, , and .
- –
- Specifying the keywords about enhancing the accuracy of and estimation using alternative technologies: artificial intelligence and machine learning.
- –
- Narrowing down the research scope by selecting terms associated with the proposed solution type, such as Random Forest (RF), XGBoost, Convolutional Neural Networks (CNNs), Deep Learning (DL), Artificial Neural Networks (ANNs), and Support Vector Machines (SVsM).
- Second, ten digital libraries were chosen: Springer, MDPI, Elsevier, Aerosol and Air Quality Research, IOP Science, ACS Publication, Nature Environment and Pollution Technology (NEPT), Europe PMC, and Earth System Science Data (ESSD). Subsequently, the Boolean operators OR and AND were utilized to apply the keywords to these libraries. OR was employed between terms within each group, while AND connected keywords across different groups.
- Step 2: Filter the search results:During this step, the papers were refined from the search results to pinpoint thematically relevant studies essential for addressing the research questions of this SLR. Inclusion and exclusion criteria were established (see Table 3). The steps taken in the selection and filtration of this SLR are as follows:
 Table 3. Paper selection criteria.
Table 3. Paper selection criteria.- –
- Implementing our inclusion and exclusion criteria.
- –
- Eliminating any duplicate articles that have been found across multiple libraries.
- –
- Looking up more similar articles by searching the article’s references.
Thirty-two studies were chosen through the selection process. Duplicate studies and publications released before 2018 were eliminated. Table 4 depicts the results of the search process.

Table 4.
Study selection by library.
- Step 3: Data extraction:

Table 5.
Data extracted from the selected studies.
Table 5.
Data extracted from the selected studies.
| Study No. | Ref. | Year | Study Period | Study Location | Measured Parameter |
|---|---|---|---|---|---|
| S1 | [35] | 2018 | 2005–2015 | United States | |
| S2 | [71] | 2018 | 2000–2015 | Butler, Hamilton, Warren, Clermont, Campbell, Kenton, Boone | |
| S3 | [42] | 2018 | 2008–2017 | China | |
| S4 | [72] | 2018 | 2014–2016 | China | |
| S5 | [22] | 2019 | 2000–2015 | United States | |
| S6 | [73] | 2019 | 2013–2015 | Italy | , |
| S7 | [23] | 2020 | 1 July–30 June 2018 | Indo-Gangetic Plain | |
| S8 | [28] | 2020 | 2011 | conterminous United States | |
| S9 | [26] | 2020 | 2015–2017 | Beijing–Tianjin–Hebei (BTH) region | |
| S10 | [74] | 2020 | 2005–2016 | Sweden | , , PM2.5–10 |
| S11 | [75] | 2021 | 2008–2016 | Coastal site in the Eastern Mediterranean | |
| S12 | [27] | 2021 | 2018–2019 | Malaysia | |
| S13 | [76] | 2021 | 2016–2020 | Beijing | |
| S14 | [1] | 2021 | 2018 | Thailand | |
| S15 | [68] | 2021 | 2018 | China | |
| S16 | [63] | 2021 | 2014–2018 | Texas | |
| S17 | [43] | 2021 | 24 March–31 May 2020 | Kolkata metropolitan city | |
| S18 | [77] | 2021 | 2014–2018 | Malaysia | , |
| S19 | [10] | 2021 | February–May 2019 | Algiers | , , , and |
| S20 | [78] | 2022 | 2018–2020 | Guanzhong Urban Agglomeration, China | |
| S21 | [32] | 2022 | 2018 | Continental United States | |
| S22 | [44] | 2022 | 2018–2019 | China | |
| S23 | [79] | 2022 | 2018–2019 | China | |
| S24 | [9] | 2023 | 2021 | Taiwan | |
| S25 | [66] | 2023 | 2011–2020 | Thailand | |
| S26 | [18] | 2023 | 2019 | India | |
| S27 | [51] | 2024 | 2019–2021 | Tuzla Canton, Bosnia and Herzegovina (BiH) | |
| S28 | [60] | 2024 | 2020 | Mexico City | |
| S29 | [47] | 2024 | 2000–2019 | South Coast Air Basin of California | |
| S30 | [80] | 2024 | 2014–2021 | China | |
| S31 | [81] | 2024 | 2013–2021 | China | |
| S32 | [82] | 2024 | 2020 | China |

Table 6.
Data related to ML-based solutions.
Table 6.
Data related to ML-based solutions.
| Study No. | Methods | Evaluation Metrics | Estimation Target | Data |
|---|---|---|---|---|
| S1 | RF | OOB | Ground measurements of constituents, GEOS-Chem simulated constituents, meteorological data, land use and population data, spatial and temporal indicators. | |
| S2 | RF | CV , RMSE, MAE | measurements, aerosol optical depth data, meteorological data, land use data, spatiotemporal features. | |
| S3 | RF, generalized additive model and extreme gradient boosting, generalized additive ensemble model | CV , RMSE, MAE | measurements, MODIS AOD, meteorological data, land use data, Modern Era-Retrospective Analysis for Research and Analysis version 2 (MERRA-2) reanalysis data, visibility data. | |
| S4 | RF | adjusted , RMSE, regression slope, coefficients | In situ measurements of , satellite-retrieved AOD data, meteorological data, land cover data, MODIS active fire data, high-resolution elevation data. | |
| S5 | Ensemble learning model | 10-fold CV , RMSE, bias, slope | monitoring data, AOD measurements and related satellite data, meteorological conditions, land use variables, chemical transport model predictions. | |
| S6 | RF | 10-fold CV , Root Mean Squared Percentage Error (RMSPE), intercepts, slope | , | PM monitored data, AOD data, meteorological parameters |
| S7 | LME model, RF model | , RMSE, Relative Prediction Error (RPE), Mean Prediction Error (MPE), slope (b), and intercept (a) | Ground-based Measurements, MODIS MAIAC products, auxiliary data, meteorological data. | |
| S8 | CNN | , RMSPE, MPE, slope | Ground-truth measurement data, MODIS AOD and GEOS-Chem AOD. | |
| S9 | Decision tree, RF, bagging, GBRT, KNN, and Support Vector Regression (SVR) | Correlation coefficient (R), RMSE | Ground-level concentration, Himawari-8 AOD, AERONET AOD, GEOS-Chem AOD. | |
| S10 | RF | CV | Satellite data, atmospheric composition variables, land use terms, meteorological parameters, population density | |
| S11 | Pattern recognition neural network (PRNN) model | R, RMSE, relative mean bias (RMB), expected error (EE) envelope, mean square error (MSE), mean absolute percentage error (MAPE), mean absolute error (MAE) | Different gap-filled AOD datasets, observations, auxiliary data. | |
| S12 | RF, SVR | , RMSE, MBE, Nash–Sutcliffe Efficiency (NSE) | Ground measured air pollutants, satellite AOD observations, meteorological parameters | |
| S13 | Multilayer perceptron (MLP) neural network analysis | , | gaseous air pollutants, meteorological parameters, daily ambient data | |
| S14 | Machine learning algorithm (MLA) | R, slope, intercept, bias, RMSE | MERRA-2 Reanalysis data, Surface data, meteorological parameters. | |
| S15 | LightGBM model | , RMSE, MAE | Ground monitoring data, meteorological data | |
| S16 | RF algorithm, multiple linear regression (MLR), mixed effects model (MEM) | CV R, mean absolute bias (MAB), mean bias (MB) | EPA surface data, Satellite AOD, meteorological data, MERRA-2 reanalysis data, elevation data, normalized difference vegetation Index (NDVI) 16-day data, land use variables | |
| S17 | MLR, artificial neural network (ANN) models | , RMSE, MAE | concentration of data, daily meteorological data | |
| S18 | Multiple linear regression (MLR), random forest regression (RFR), extra tree regression (ETR), decision tree regression with AdaBoost (BTR) | , RMSE | , | concentration, concentration, meteorological data. |
| S19 | Hybrid dragonfly-SVM algorithm | , RMSE, MAE, MSE, NRMSE, MAPE % | , , , | The hourly data of conventional fractions (, , , and ), weather factors (temperature, pressure, and relative humidity) |
| S20 | RF-XGBoost | , RMSE, MAE | Ground measurements, MODIS AOD, auxiliary data, meteorological conditions. | |
| S21 | Regression models, stochastic gradient descent, k-nearest neighbor (KNN), adaptive boosting (AdaBoost), Gradient Boost (GB), Extreme Gradient Boost (XGB), SVM, RF) | SR, RMSE, MB | MERRA-2 data, ground station data, meteorological and aerosol parameters | |
| S22 | Deep Forest (DF) | CV , RMSE, MAE, EE | FY-4A TOAR data, hourly atmospheric observation data, meteorological parameters, geographic information, time variables. | |
| S23 | DF | CV , RMSE, MAE, bias | and AOD data, auxiliary data | |
| S24 | CNN–RF | , RMSE, MAE, MSE, are error (MSE) | Five meteorological parameters, four spatiotemporal elements, eight air pollution factors (CO, , NO, , , , ) | |
| S25 | Multiple Linear Regression (MLR), RF, XGBoost, SVM | , RMSE | data, satellite data | |
| S26 | Individual and stacking models (XGB, RF, LGBM, ridge, lasso) | , RMSE, MB, MAE | Ground data, MERRA-2 reanalysis data | |
| S27 | XGBoost, KNN, and Naive Bayes (NB) | Accuracy, precision, and Area Under the ROC Curve (AUC) | concentration data, remote sensing data (USGS landsat 8 collection 2 tier 1 and real-time data raw scenes). | |
| S28 | RF | Air pollutant concentration data, meteorological data | ||
| S29 | Decision tree, RF, SVM, SVR, k-nearest neighbor, neural network, Gaussian process regression | , RMSE, cross-validation | meteorological factors, estimated emissions, large-scale climate indices | |
| S30 | LSTM neural networks, RF regression models | , RMSE, MAE | data, MODIS AOD product, auxiliary data, meteorological variables, land use-related variables | |
| S31 | ResNet model | , RMSE | Testbed dataset | |
| S32 | Categorical Boosting (CatBoost) model | , RMSE | Geographical data, nighttime light data, meteorological data, aerosol optical depth products, ground-based measurements. |
- Step 4: Quality assessment:To evaluate the chosen studies based on the research questions, we selected a set of quality assessment metrics for the ML-based models to estimate and concentrations. These metrics ensure the models are accurate, reliable, and suitable for practical applications, such as air quality monitoring and environmental management. Four quality assessment metrics are chosen as follows:
- –
- Feature importance analysis: determine which features—such as meteorological data, geographic information, and temporal factors—contribute most significantly to estimating and levels. Accuracy and model refinement can be achieved by understanding of the features’ importance.
- –
- Residual analysis: examine the residuals (differences between estimated and actual values) to determine patterns or biases in the estimations made by the model. This analysis can help identify areas where the model may be underperforming or where improvements can be made.
- –
- Temporal and spatial consistency: verify that the model estimations match the data that have been observed in terms of both timing and space.
- –
- Cross-validation: offers insights into the model’s resilience and aids in assessing its performance across several dataset subsets.
A scoring system is used, where 0 indicates that the metric is not fulfilled and 1 indicates that it is fulfilled. The results in Table 7 showed that thirty-two studies scored highly, with an average score of 3.6 out of 4. These studies demonstrated strong performance across all the assessed metrics. In contrast, nine studies did not cover the cross-validation aspect in their evaluation, and one study lacked both temporal and spatial consistency as well as cross-validation. These findings prove the effectiveness of using ML-based models for enhancing the accuracy of PM concentration estimation, as the majority of the evaluated studies exhibited a comprehensive approach to quality assessment.

Table 7.
Quality assessment (fulfilled = 1, not fulfilled = 0).
3.3. Reporting Phase
The reporting process in this phase consists of three distinct steps:
- Dissemination strategy identification: determining the most suitable approach to share the outcomes of our review with the relevant audience. This involves strategizing the best methods and channels for effectively disseminating the review findings.
- Report formatting: focusing on formatting the report to present our review findings in a clear, concise, and organized manner. This ensures the information is conveyed in a reader-friendly and easily understandable format.
- Report evaluation: to ensure the quality and effectiveness of the report, the evaluation process is conducted. This involves critically reviewing the content, coherence, and adherence to the objectives of the review. The goal is to validate the integrity and impact of the reported findings.
4. Analysis and Discussion
This section provides a comprehensive analysis of the results, aligning them with the research questions that have driven this investigation. The goal is to thoroughly examine the findings and derive meaningful insights that address the core objectives of this study.
4.1. RQ1: What Are the Benefits of Using ML-Based Models to Estimate PM Concentrations?
Traditionally, environmental monitoring and management programs have relied on statistical models such as the GAMs model [39], multiple linear regression [83], the Geographically Weighted Regression (GWR) model [84,85], and the LME model [23] to measure pollution levels. These traditional statistical models have been widely used to estimate ground-level from AOD and other predictors [23,85]. However, these statistical models have failed to achieve high accuracy in estimating concentrations. The shortcomings of these traditional approaches limit their effectiveness in air quality scenarios [86]. Key drawbacks of these models include the following: (1) these models are constrained by assumptions such as the independence of observations and the distribution of monitored data; (2) they may not fully capture the complex relationships between and various spatial and temporal predictors; (3) they suffer from a low accuracy due to their inability to estimate extreme values, such as the highest and lowest pollution levels [86]; (4) they have challenges in handling a large number of predictors, especially when these predictors are interdependent due to their increasing complexity; and (5) they incur high computing costs and a long time to simulate PM data [23,87,88]. These limitations have led to a growing interest in using ML-based models as an alternative for estimating ground-level PM [89,90].
Researchers have increasingly turned to a variety of advanced ML-based models to estimate pollutant concentrations. These include ML models such as Support Vector Machines (SVMs), deep learning models like Artificial Neural Networks (ANNs), and ensemble techniques including Random Forests (RFs) and gradient boosting [64]. These sophisticated ML-based models have gained prominence due to their exceptional ability to capture complex, nonlinear, and interactive relationships between predictor variables and PM concentrations, and they are easy to train.
Unlike traditional statistical models, ML-based models can adjust to new information and optimize their estimation performance in response to evolving environmental conditions. The capacity of ML-based models to adapt is particularly valuable given the complex and multifaceted nature of air quality. Air quality is influenced by an intricate interplay of meteorological, geographic, and anthropogenic factors that can fluctuate considerably across space and time. The strong estimation capabilities of these ML-based approaches have proven instrumental in enhancing the accuracy of and concentration estimations and predictions [88,91].
The flexibility and adaptability of ML-based models allow them to effectively track evolving data patterns and handle diverse input variables. This makes them uniquely suited for the dynamic realm of air quality data, where environmental conditions and influential factors are subject to continuous change [9,91,92,93]. By harnessing the power of these advanced ML models, researchers can develop effective tools that account for such complexities and provide more accurate and reliable estimates of and concentrations. This is crucial for evaluating the effectiveness of air quality management strategies and assessing the potential health impacts of PM exposure.
Recently, neural networks, RF, and XGBoost algorithms have been increasingly deployed to produce estimation models leveraging satellite-derived Aerosol Optical Depth (AOD) data [42,94]. These ML-based models have demonstrated superior accuracy, with cross-validation R-squared (CV ) values exceeding 0.8, outperforming traditional statistical approaches such as GAM, LME models, and Geographically Weighted Regression (GWR). The LME model, for instance, has been used to estimate concentrations across the IndoGangetic Plain (IGP) region, but it tended to underestimate ground-level and exhibited poor accuracy, with an of 0.78, compared to the RF model [23].
Another investigation compared an RF model with a two-stage statistical model. The first stage of the statistical model used an LME model fueled by meteorological and AOD variables, while the second stage employed a GAM model driven by land use data. The same clusters and predictors were used in the LME+GAM model. The RF model outperformed the two-stage statistical model. However, the LME+GAM model still achieved a reasonable accuracy, with an of 0.80 when fitted using data from 2013 only. The model’s accuracy significantly dropped to an of 0.64 when fitted using data from 2013–2016. This decline in performance occurred because the statistical model relied on specific daily adjustments tailored to the 2013 data. Although the same adjustments applied to a different period, under the assumption that the conditions affected but remained unchanged, led to a decrease in accuracy and a poor overall performance [42]. This shows that statistical models, though effective with smaller datasets, often struggle to accommodate the non-linearities inherent in air pollution data, significantly limiting their performance and applicability. Figure 12 presents a comparison between ML-based models and traditional statistical models.
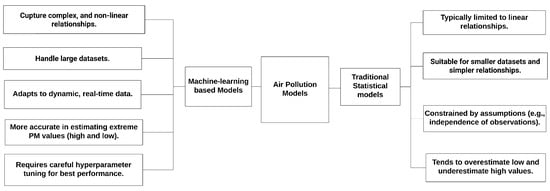
Figure 12.
Comparison between ML-based and traditional statistical models.
By harnessing the power of these advanced ML models, researchers can develop effective tools that account for such complexities and provide more accurate and reliable estimates of and concentrations. This is crucial for evaluating the effectiveness of air quality management strategies and assessing the potential health impacts of PM exposure. ML-based solutions highlight their potential to revolutionize air pollution estimation, making researchers interested in applying them to estimate pollutants in multiple regions for different scenarios.
4.2. RQ2: What Are the Existing Solutions to Estimate PM Concentrations Using ML-Based Models?
In recent years, researchers have extensively explored the use of various ML-based models to improve the accuracy of particulate matter (PM) concentration estimates. These ML-based approaches aim to address the limitations of traditional statistical models by capturing the non-linear relationships between air pollution concentrations and their contributing factors, such as emission sources, dispersion patterns, and meteorological conditions [32]. ML-based models have the potential to overcome the drawbacks of traditional statistical models and provide more accurate, bias-corrected estimates of and levels.
Our comprehensive review of the current literature on ML-based solutions for estimating PM concentrations spans three main categories: traditional Machine Learning (ML)-based models, Deep Learning (DL)-based models, and Ensemble Learning (EL)-based models.
4.2.1. Traditional Machine Learning (ML)-Based Models
This category covers studies that used traditional ML algorithms to develop models for estimating PM concentrations. ML models can learn patterns from training data rather than simply memorizing them. The studies belonging to this category used various ML models to enhance the estimation accuracy of and . These ML models were trained and assessed using several statistical metrics, such as coefficient of determination () and correlation coefficient (R), to identify the best-performing model.
- Decision Tree (DT) model: the decision tree (DT) models offer several benefits for estimating PM concentrations, including:
- Ranking the influencing variables based on their importance.
- Capturing complex interactions among the variables.
- Demonstrating good estimating ability.
- Maintaining low bias [9,26].
The study by Zuo et al. [26] compared the performance of the DT model against five other ML techniques (bagging, gradient boosting regression trees, k-nearest neighbors, and support vector machines) in estimating concentrations in the Beijing–Tianjin–Hebei (BTH) region using AOD data. The models were evaluated under four distinct weather conditions to assess their robustness. The results showed that the DT model performed well, achieving an R of 0.854 in estimating levels. This indicates the DT model’s ability to capture the complex relationships between AOD and in the BTH region. However, the authors acknowledged that the findings from the BTH region may not be directly generalizable to other areas or cities, as air pollution characteristics and their contributing factors can vary significantly across different locations. Moreover, the reliance on AOD data in the training process poses limitations, particularly in heavily polluted areas where haze is often mistaken for clouds, making it challenging to obtain accurate estimates. These caveats highlight the need for further research to evaluate the transferability and robustness of the DT model, as well as the potential benefits of incorporating additional data sources beyond AOD to enhance the accuracy of estimation, especially in diverse urban environments.
- Support Vector Machine (SVM) model: The algorithms of SVMs have also been utilized to build models for estimating regions with high levels of PM concentration. SVMs are a useful technique for classification, pattern recognition, and functional regression problems [95]. SVMs are an excellent choice for modeling the complexities involved in PM concentrations because they can effectively handle variables with nonlinear relationships, such as geographic features, emissions, and weather conditions [47].
SVM models have been applied in various locations, such as Algeria [10] and the Beijing–Tianjin–Hebei (BTH) region [26], to estimate PM concentrations. The performance of SVM models can vary depending on weather conditions and other influential factors. For instance, a study in Algiers employed a hybrid dragonfly–SVM algorithm to estimate concentrations. The authors used the dragonfly algorithm to optimize the hyperparameters of a Support Vector Machine Regression (SVMr) model, aiming to improve the accuracy of PM estimation compared to using SVMr alone. The results showed that the hybrid model achieved a high performance, with an of 0.98. This model is useful to help authorities anticipate critical air quality episodes in the absence of continuous monitoring. However, the study did not explore the impact of other factors, such as land use patterns and seasonal effects, on PM concentrations, which could provide a more comprehensive understanding of air quality dynamics. Additionally, the high performance reported for the model may suggest potential overfitting to the training data [10].
In contrast, a study in the BTH region applied an SVM model to estimate daily concentrations under different weather conditions. In this case, the model had a poor accuracy, with an R value of only 0.32. This was likely due to the lack of uniformity in the training data and the use of various data sources [26]. These contrasting results highlight the importance of considering the influence of various contextual factors, such as location, weather conditions, and data quality, when developing and evaluating SVM models for PM concentration estimation.
- Support Vector Regression (SVR) model: Recent studies on air quality have shown the promise of SVR models in accurately estimating PM concentrations and their temporal evolution across different cities [27,47].
A study in Malaysia developed SVR and Random Forest (RF) models, trained on satellite-derived, ground-based, and meteorological data, to estimate levels. Overfitting was minimized by relying on the kernel function during model training. The SVR model achieved an of 0.69, despite some biases and underestimation of peak values. However, the limited geographical coverage may restrict the findings’ applicability to other regions [27].
Similarly, a study in the South Coast Air Basin of California used various ML and DL algorithms, including SVR, to estimate daily average levels and exceedances. The SVR model had the highest accuracy, with an of 0.94, and low computational requirements [47]. However, It did not accurately predict the extreme values in some regions.
- Artificial Neural Networks (ANNs) model: ANNs are non-linear computational algorithms that simulate the natural neural network of the human nervous system to make decisions and arrive at conclusions [96]. Researchers have leveraged ANN algorithms as cost-effective methods in constructing models for estimating levels, striving to calculate concentrations based on easily sensed data [97,98].
In a study conducted during the COVID-19 lockdowns in Kolkata, India, researchers concentrated on predicting concentrations. They conducted two modeling approaches, multiple linear regression (MLR) and artificial neural networks (ANN), and they trained the models by obtaining data from the state pollution control board and meteorological data from online sources. The results indicated that the non-linear ANN model was a rational model that outperformed the linear MLR model, achieving an value of 0.91 during training and 0.69 during testing. However, the model lacks comprehensive data sources detailing spatial or temporal coverage. To improve the model, expanding the range of data sources and exploring the potential applications of the findings in Kolkata could greatly enhance the accuracy of concentration estimations [43].
Table 8 provides a summary of the findings from the studies discussed above. While these studies demonstrate the potential of ML for PM estimations, their narrow geographic focus may limit the transferability of the findings. Effective PM modeling also requires high-quality data and the selection of relevant features [Data Science Central]. Researchers have increasingly turned to DL models, as they can capture complex patterns in the data, making them well-suited for PM estimation.

Table 8.
Summary of traditional ML-based models results.
4.2.2. Deep Learning (DL)-Based Models
This category includes recent work that has explored the benefits of applying DL algorithms for constructing estimation models for and . The studies falling within this category utilized a diverse range of DL models to refine the accuracy of and estimations.
- Convolutional Neural Networks (CNNs) model: CNNs are designed to process grid-like data patterns. They excel in tasks like image classification and segmentation and can also handle time-series data, such as air quality measurements. Therefore, CNN algorithms are ideal for constructing estimation models [9,99].
Park et al. [28] applied a Convolutional Neural Network (CNN) model to estimate 24 h average ground-level in the conterminous United States. AOD data, meteorological variables, and land use data were used to train the model. The CNN achieved a relatively accurate estimation, with an of 0.84, and produced a smooth annual prediction map of . However, the model has defects, including its limited temporal scope. The model focuses on 2011 and may not reflect the most recent changes in concentrations.
- Pattern Recognition Neural Network (PRNN) model: The PRNN algorithm is a type of neural network that learns to find patterns in data and link those patterns to particular outcomes. When a PRNN is used to build a PM estimation model, it can identify patterns that correlate with PM levels by analyzing input data such as environmental and meteorological parameters. With the help of fresh data inputs, the network can estimate PM concentrations after learning these patterns during training, which makes it valuable for monitoring air quality [75].
Tuygun et al. [75] conducted an artificial neural network model based on the pattern recognition algorithm (PRNN) to estimate in the Eastern Mediterranean region—Turkey. They used a combination of satellite-derived aerosol optical depth (AOD) data and other datasets to address the limitations of using satellite-based AOD data only. The results showed that the model performed better (R = 0.74) on the concentration estimation when combining MODIS and MERRA-2 AOD than the MODIS AOD alone (R = 0.62). It was capable of handling random variations. However, the model focused on a single coastal site in the Eastern Mediterranean region, which limited the generalizability of the findings to other locations. Additionally, the model’s CV R was poor, which negatively affected the evaluation of the estimative accuracy and reliability of the model.
- Residual Neural Network (ResNet) model: The ResNet model was capable of handling the inherent nonlinearity in atmospheric processes and demonstrated strong capabilities in estimating concentrations [100]. Its architecture, which utilized residual connections, allowed for improved feature extraction and adaptability to complex atmospheric data.
Li et al. [81] developed Random Forest (RF) and ResNet models to estimate concentrations across China. They found that the RF model overestimated levels in downwind areas due to an imbalance in training samples. To address this issue, they: (1) implemented a novel testbed using a chemical transport model (CTM) to generate real data beyond traditional monitoring sites; (2) utilized the concentrations simulated by the CTM as training labels for the ML models; and (3) incorporated spatiotemporal-neighborhood features into the training to enhance estimation accuracy. As a result, the ResNet model achieved a high accuracy, with an value of 0.61, compared to the RF model. However, the numerical model-based testbed may have uncertainties in emissions and chemical mechanisms, leading to discrepancies with real observations. Table 9 summarizes the results of the DL models mentioned earlier.

Table 9.
Summary of Dl-based models findings.
Challenges such as the need for extensive data for training, model interpretability, and potential overfitting remain prevalent, highlighting the importance of addressing these issues to further enhance the reliability and applicability of DL-based approaches in air quality analysis. Therefore, the researchers tend to leverage ensemble learning models to obtain accurate PM concentration estimates.
4.2.3. Ensemble Learning (EL)-Based Models
EL-based models gained popularity for estimating PM concentrations due to their ability to combine multiple base models, improving accuracy and reducing bias in air quality monitoring and estimation. This category includes studies that employed EL-based models to estimate PM concentrations, such as the following:
- Deep Forest (DF) model: DF models use decision trees to make independent estimations, which are then aggregated. These models also can identify the most influential features, aiding in understanding data relationships and improving the overall estimation of the model [101].
A study was conducted in China, employing a novel DF model. The authors used satellite data to estimate ground-level PM concentrations (). The model’s results indicated that the the optimal hourly of CV was 0.85, while the values for daily, monthly, seasonal, and annual averages were 0.82, 0.97, 0.98, and 0.99, respectively. Additionally, the model’s performance was notably better in the Yangtze River Delta (0.86), Beijing–Tianjin–Hebei (0.86), and Central China (0.87) regions. However, potential biases from incomplete or missing satellite data coverage could have affected the accuracy of the PM estimates. Moreover, the DF model was influenced by topography, the strength of pollution sources, and high surface pressure contributions, exhibiting distinct regional and seasonal performance variations, with notably lower performance during summer and autumn [44].
Another Chinese study presented an interpretable DF model to estimate concentrations of hourly . This model combined the strengths of deep neural networks and tree-based models. The DF model was trained using Himawari-8 AOD data at a 0.05° × 0.05° spatial resolution. The model, evaluated with a 10-fold CV, demonstrated strong performance, with values ranging from 0.82 to 0.88 for hourly estimates. The DF model had limited predictors and excluded some aerosol precursors and land use factors. This led to a need for further improvements in model performance by incorporating additional variables. Additionally, the DF model struggled in areas significantly affected by surface pressure. High pressure can cause atmospheric stagnation, which complicates PM concentration modeling and results in less accurate estimates [79].
- Random Forest (RF) model: RF is an ensemble learning algorithm that builds multiple decision trees. This algorithm is used to build the estimation model. It enhances performance by introducing feature randomness and aggregating the outputs from each tree, leveraging their strengths while minimizing their shortcomings [66].
Across the contiguous United States, Meng et al. [35] applied the RF algorithm to develop daily, monthly, and annual estimation models. These models estimated constituents, including sulfate, nitrate, organic carbon, and elemental carbon. The RF achieved a high estimation performance, with values ranging from 0.71 to 0.86 for the different constituents. However, the spatial resolution of the estimation maps was 0.250 × 0.31250. This resolution might not have been sufficient to capture the spatial variability of constituents.
Furthermore, Sayeed et al. [32] built an ML model to estimate concentrations in the USA. The data used to train the model were collected from 13 regions. They tested ten different ML algorithms, including Ordinary Least Squares (OLS), ridge and lasso regression, Stochastic Gradient Descent (SGD), KNN, Adaptive Boosting (AdaBoost), Gradient Boosting (GB), Extreme Gradient Boosting (XGB), and SVM. The results showed that the 10-fold CV RF model outperformed the other models. The RF achieved the highest accuracy, with an SR of 0.96 for training and 0.65 for testing. However, the model had limitations due to uncertainties in MERRA-2 data emissions, which covered a 50 × 50 area. Additionally, insufficient satellite data posed challenges, such as detecting heavy aerosol layers, retrieving data in snowy regions, and scanning complex surfaces. Brokamp et al. [71] developed an RF model to estimate daily concentrations at a 1 × 1 km resolution across a seven-county urban area around Cincinnati and Ohio. The model was trained using various data sources, including satellite-derived AOD, meteorological data, atmospheric composition data, and land use characteristics. The RF model performed well, achieving a CV of 0.91. However, the model had limited generalizability to other regions, specifically Cincinnati and Ohio.
In Sweden, Stafoggia et al. [74] developed an RF model for estimating daily concentrations of PM, including , , and PM2.5–10. The air pollution monitoring and satellite data were collected at a high spatial resolution (1 ). The model achieved an accuracy with a CV ranging from 0.64 to 0.77 for OOB samples. However, the key defects and weaknesses included the following: (1) limitations due to the spatial resolution of cloud cover data (1 ) compared to ground-based measurements; (2) data processing and feature engineering were insufficient; and (3) model performance was inadequate.
Chen et al. [72] constructed an RF model to estimate historical exposures to in China. The model was trained using AOD data at an approximately 10 km resolution. The RF model was able to estimate 78% of the daily concentrations with a low bias. However, the model lacked ground monitoring data for validating the estimates, which may have affected the accuracy of long-term trends. Missing AOD values also posed a challenge for satellite-based PM estimations. Additionally, there was insufficient data processing and feature engineering. In another Chinese study, Yang et al. [80] developed an RF regression model to estimate levels. They employed remote sensing technologies to acquire information quickly. The RF model achieved a high accuracy, with an value of 0.93. Nevertheless, the models had lower precision in temporal and spatial CV due to variability.
In another study from China, Xiao et al. [42] combined an RF algorithm with the generalized additive model and XGBoost to build an ensemble ML model. The model was trained on satellite data to estimate historical concentrations. They divided China into seven regions using spatial clustering to address spatial heterogeneity. The ensemble ML models, trained for each region, achieved a CV of 0.79. The models were able to characterize daily and monthly levels. However, the models had several limitations: (1) limitations on cloud cover compared to ground-based measurements; (2) incomplete satellite data coverage, which might have affected the accuracy of the PM estimates; and (3) the model performance was insufficient.
In Italy, Stafoggia et al. [73] utilized a five-stage RF model to estimate daily and concentrations. The model captured variability in and using satellite data. It achieved an estimation accuracy with CV values ranging from 0.75 to 0.86. However, the model had some potential defects and weaknesses: (1) it had limited geographical scope, as it focused only on Italy, which may have limited the generalizability of the findings to other regions or countries; (2) potential biases were observed in model estimation, particularly during the summer months and in southern Italy; and (3) incomplete data coverage occurred, as satellite-derived AOD data had missing values, which might have affected the accuracy of the PM estimates.
Zaman et al. [27] estimated concentrations in Malaysia across urban, industrial, suburban, and rural sites. They employed seven estimation models using RF and SVR. The models combined AOD, meteorological parameters, and ground-measured air pollutants. The RF model performed slightly better than SVR, with accuracies ranging from 0.46 to 0.76. The model had an effective representation of values and temporal changes. Nevertheless, the model had limitations: (1) limited geographical coverage within Malaysia, which may have restricted the applicability of the findings to other regions, so expanding the analysis to a broader Southeast Asian context could have provided more accuracy; and (2) reliance on satellite data, which had limitations in spatial coverage.
Over Thailand, Gupta et al. [1] presented a 10-fold supervised RF model to estimate hourly and daily concentrations. They collocated one year of hourly data from 51 ground monitoring stations. NASA’s MERRA-2 reanalysis data on aerosols and meteorological data were also collected. The model was able to estimate with nearly zero mean bias and achieved a high correlation (R = 0.95) between the observed and estimated values. However, the model had some limitations: (1) limited geographical coverage, as it focused on Thailand, which limited the generalizability of the findings; and (2) short-term trend analysis, as it only focused on one year and did not explore the model’s ability to capture long-term trends in concentrations.
Another Thai study conducted by Buya et al. [66] utilized a 1 km satellite data resolution and multiple ML models, including RF, MLR, XGBoost, and SVM, to estimate daily concentrations. The results showed that the RF model outperformed the MLR, XGBoost, and SVM models. It achieved a high accuracy, with values of 0.95 for the training, 0.78 for the validation, and 0.71 for the testing datasets. However, the model reported a high accuracy, which may have led to potential overfitting of the training data. Additionally, the study focused on concentrations in Thailand, without exploring the model’s applicability to other regions or countries. Finally, the 1 km satellite data used had limitations, including issues with cloud cover, scanning complex surfaces, and missing values.
In the IGP region, Mhawish et al. [23] compared LME and RF models to estimate daily ground-level concentrations. They used satellite data. The RF model outperformed the LME model across daily, weekly, monthly, seasonal, and annual time scales, achieving a higher accuracy, with a CV of 0.87. However, the RF model’s performance in the northwestern IGP was affected by limited observations and the lack of historical data, which prevented an accurate assessment of year-to-year variability.
In an investigation conducted over Texas, Ghahremanloo [63] applied an RF model with CV to estimate . AOD data were used to train the model. The RF model achieved a high estimation accuracy, with R values ranging from 0.83 to 0.90, and low MAB. However, the limited spatial coverage in estimating concentrations only in Texas may have restricted the generalizability of the findings to other regions. Valencia et al. [60] applied an RF model to estimate particle levels in Mexico City and the State of Mexico. Data were obtained from 29 environmental monitoring stations. The RF model achieved an estimation accuracy of 80.40%. However, the study had limitations: (1) it focused on Mexico City, which may have limited the generalizability of the findings; (2) The accuracy of the model was influenced by the quality of the data used.
Chen et al. [9] demonstrated the benefits of combining the RF algorithm with another algorithm to enhance the estimation accuracy of concentrations in Kaohsiung, Taiwan. They developed a novel estimation model that combined CNN and RF algorithms. They used observational data from 13 monitoring stations. The CNN algorithm was used to extract key features from the meteorological and pollution data, after which they employed the RF algorithm to train the model. The CNN-RF model outperformed the single CNN and RF models, achieving an accuracy with an of 0.93. However, the authors relied on data from the 13 monitoring stations in Kaohsiung and the specific period of 2021 for the analysis, leading to limited geographical coverage and short-term trend analysis.
Similarly, across the contiguous United States, Di et al. [22] integrated RF, gradient boosting, and neural networks to develop an estimation model. They used different data sources to train the model. The ensemble-based model was trained to estimate concentrations at a 1 km × 1 km resolution. The model achieved a high performance, with a CV of 0.86 for daily estimation and 0.89 for annual estimates. Although the model provided a solid foundation for modeling, it focused on a 1 km × 1 km spatial resolution, which may not have been sufficiently fine-grained for epidemiological applications requiring higher spatial resolution.
- Extreme Gradient Boosting (XGBoost) model: XGBoost algorithms are known for their superior data mining capabilities and high performance. Due to these strengths, they have been increasingly used to construct PM concentration estimation models. This has led to enhanced accuracy and reliability in these estimates [18].
For instance, Ayinde et al. [51] constructed several models to estimate seasonal concentrations in Tuzla Canton, Bosnia, and Herzegovina. These models included XGBoost, K-Nearest Neighbor (KNN), and naive Bayes. The models were trained using Landsat-8 satellite data. The results showed that the XGBoost model outperformed the other models and achieved a high accuracy in summer, with an R value of 0.85 and 0.98 in winter. However, the models had limitations: (1) the limited geographic scope, which focused only on Tuzla Canton, may have restricted the applicability of the findings to other regions within or beyond the country; (2) potential bias due to data limitations, which may have affected the accuracy; (3) the uneven distribution of monitoring stations; and (4) not considering important predictors like meteorological parameters, traffic factors, and industrial emission data.
Another application of the XGBoost model was in the Guanzhong Urban Agglomeration in China to estimate daily levels. XGBoost was combined with RF to develop a new model. The RF-XGBoost model used satellite-derived AOD data. The model achieved a high accuracy, with an of 0.93. However, the model underestimated on high-pollution days. In addition, it overestimated the on low-pollution days due to the limited number of data samples used for training [78].
Finally, Dhandapani et al. [18] applied the XGBoost, Random Forest (RF), and LightGBM (LGBM) models across India to estimate concentrations. The models were trained using data from 106 monitoring stations and MERRA-2 data. The XGBoost model was considered the most effective individual estimation model, achieving a high accuracy, with an of 0.73. Additionally, the authors developed a stacking model that used the XGBoost model as a meta-regressor alongside the RF and LGBM models. This improved the estimation accuracy to an of 0.77. The stacking model was then applied regionally, dividing India into five regions. The model provided the best hourly estimates in the eastern region, with an of 0.80. However, the analysis was limited by its focus on a single year, restricting its ability to estimate long-term patterns and trends in concentrations.
- Light Gradient Boosting Machine (LightGBM) model: The LightGBM model employed a leaf-by-leaf growth method with deep constraints. It accelerated training by using a histogram-based algorithm, which reduced both training time and memory consumption. As a result, the researchers used the LightGBM algorithm to develop the estimation model [69].
To estimate hourly concentrations in China, Zeng et al. [68] applied a LightGBM model, using ground-based monitoring and meteorological data to build the model. It demonstrated a relatively high performance, with an of 0.86. However, the sparse distribution of ground-based monitoring sites in China impeded the investigation of spatial and sub-daily variation patterns in . Additionally, the lack of hourly estimations across space prevented further investigations. Finally, the study focused solely on the year 2018, introducing potential temporal limitations in assessing concentrations.
- Categorical Boosting (CatBoost) model: The CatBoost algorithm gained popularity in environmental research for building PM estimation models. Its strength lied in handling regression problems with complex, periodic, non-stationary, and non-linear characteristics. These models also took into account numerous features and noisy data, which helped achieve high accuracy [82,102].
For instance, Ding et al. [82] estimated levels in China using a novel estimation strategy based on ML and wavelet decomposition, referred to as the Wavelet-CatBoost model. This strategy was designed to produce a seamless hourly dataset, addressing the issue of spatial discontinuity when using latitude and longitude as input features. The improved AOD dataset, with a resolution of 0.01°× 0.01° and 1 h intervals, was incorporated into the model. The wavelet-based model (without time and geolocation), achieved highly accurate seamless hourly estimation, with a spatial CV- of 0.84. Additionally, it enhanced spatiotemporal connectivity compared to the non-wavelet (with time and geolocation) model. Table 10 provides the results of previously discussed EL-based models.

Table 10.
Summary of El-based model findings.
EL-based models are effective in estimating PM concentrations. However, several factors affect their effectiveness:
- Noise, missing values, or inaccurate data could negatively impact model performance. Therefore, the model must be trained on high-quality, well-labeled, balanced data to generate accurate estimates.
- Important meteorological parameters were neglected when training EL-based models for precise PM concentration estimations, such as temperature, humidity, wind speed, and air pressure.
- Using latitude and longitude as input features in models for estimating PM concentrations produced spatial discontinuity.
4.2.4. Comparison of ML-Based Solutions for PM Estimation
As shown in Figure 13, the majority of the studies included in our review utilized ensemble learning models to enhance the accuracy of PM concentration estimates. Ensemble learning approaches combine multiple individual models, such as ML or DL algorithms, to leverage their complementary strengths and improve the overall predictive performance.
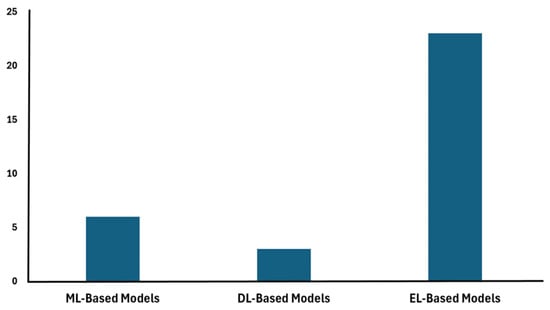
Figure 13.
Number of publications in each category.
The prevalence of ensemble learning models in the literature reflects the recognition that integrating diverse ML-based techniques can lead to more robust and accurate estimates of PM levels. By combining the capabilities of different modeling approaches, ensemble models are able to capture the complex relationships between PM concentrations and their influencing factors more effectively than a single standalone model. In contrast, the use of pure ML-based and DL-based models appears to be less prominent in the current research landscape, suggesting that the integration of multiple AI techniques through ensemble learning has been a preferred strategy for advancing the state-of-the-art in PM estimation.
This observation highlights the potential benefits of ensemble learning in addressing the inherent challenges of PM estimation, such as non-linearity, temporal and spatial variability, and data availability. The systematic review of these three main categories of ML-based solutions will provide valuable insights into the strengths, limitations, and future directions for enhancing the accuracy and reliability of PM concentration estimates.
4.3. RQ3: What Are the Research Gaps and Future Directions for Estimating PM2.5 and PM10 Concentrations Using ML-Based Models?
This section outlines the research gap in recent ML-based and estimation models. Then, the future directions for research in the field are identified.
4.3.1. The Research Gap
Accurately estimating PM concentrations presents significant challenges, primarily due to the limitations of ground monitoring stations. These stations often have limited spatial coverage and face resource constraints, making it difficult to provide comprehensive monitoring in expansive regions with diverse pollution sources. The establishment and maintenance of a widespread network of ground monitoring stations is costly and logistically challenging, resulting in notable gaps in coverage [32].
As a result, many nations and regions struggle to monitor and continuously, given the intricate spatiotemporal variations of these pollutants. Consequently, satellite-based remote sensing has emerged as a popular technique for monitoring PM contaminants, utilizing data derived from spectral Aerosol Optical Depth (AOD) measurements. However, relying solely on satellite AOD data presents its own challenges, including issues with cloud cover and difficulties in aerosol-type detection [103].
Moreover, MERRA-2 data has proven valuable for estimating PM concentrations, offering global spatial coverage, high temporal resolution, and long-term data availability. Its cost-effectiveness makes it particularly useful in resource-limited regions. However, MERRA-2 data often fail to capture fine-scale variations in PM concentrations, especially in urban areas characterized by high spatial heterogeneity. Additionally, reliance on model assumptions introduces uncertainties and biases, preventing the data from effectively capturing short-term changes due to events such as wildfires or industrial activities [18].
In this context, ML-based models have outperformed traditional statistical models by capturing complex nonlinear relationships between AOD data and concentrations, thus reducing bias in MERRA-2 data and improving pollutant estimation accuracy. However, a key limitation of many current ML models is their reliance on the specific characteristics of the training data. While they may perform well in the regions or periods in the original dataset, their transferability to other contexts can be limited. Moreover, sampling imbalance impacts model accuracy where data that focus on certain areas ignore differences in different areas, leading to poor generalization performance and high bias in estimation. This lack of generalizability is concerning, as air quality and the factors influencing concentrations can vary significantly across different geographic areas, urban–rural gradients, and climatic regimes.
Traditional models such as tree models can face challenges related to spatial discontinuity when estimating concentrations. This is because they use satellite AOD data with spatial gaps and geolocation and time information that are not directly physically related to ground-level as inputs. This discontinuity occurs because the tree models can create abrupt changes in estimation based on small differences in geographic coordinates, leading to spatial mapping inaccuracies.
To address these challenges, it is essential to enhance the diversity of training data by incorporating a wide range of conditions. Implementing cross-validation techniques can assess model performance across various contexts, while domain adaptation methods can improve transferability. Additionally, utilizing ensemble learning can capture broader patterns, and continuous learning approaches will enable the model to adapt over time. Utilizing a numerically model-informed testbed can mitigate sample imbalance-induced biases. Applying a semi-Lagrangian model can enhance estimation accuracy and reduce the risks associated with spatial discontinuities. Establishing monitoring protocols will ensure that the model remains accurate and relevant in diverse settings, allowing for timely updates and adjustments based on emerging data.
To conclude, the strengths and weaknesses of each ML-based model will be summarized. Table 11 presents the strengths and limitations of traditional ML-based models, while Table 12 and Table 13 outline the strengths and limitations of current deep learning (DL) and ensemble learning models, respectively.

Table 11.
Traditional ML-based solution review summary.

Table 12.
DL-based solution review summary.

Table 13.
Ensemble learning-based solution review summary.
4.3.2. Future Directions
This section highlights critical areas requiring further investigation to validate the efficacy of estimating PM concentrations using ML-based models (See Figure 14). Consequently, by exploring future research directions, the knowledge gained from these previous studies can be further expanded, ultimately leading to more accurate estimation models that can inform evidence-based policymaking and contribute to air quality and public health outcome improvements. Potential future directions are as follows:
Figure 14.
Future directions of PM concentration estimation.
- Balanced long-term historical PM dataset:The short-term datasets spanning minutes, hours, or days often caused overfitting, which decreased model accuracy. Additionally, they minimized the consistency of PM concentration estimates across periods and environmental conditions. Long-term trends were not captured, making it difficult to determine whether the state of the air was improving or worsening. These short datasets were also unsuitable for evaluating chronic PM exposure, which could have led to an underestimation of the long-term health risks associated with air pollution. Therefore, the development of an extensive dataset containing historical information on PM concentrations over several years or even decades is essential, since it records long-term changes in PM levels as well as trends and seasonal variations. Balanced long-term databases are necessary for epidemiological studies to evaluate population exposure to PM over an extended period. This is because imbalanced samples cause ML-based models to fail to provide accurate estimations of PM across the entire spatial domain. Furthermore, the inclusion of a comprehensive set of meteorological parameters, along with land use and land cover variables, is crucial for understanding PM concentration dynamics and enhancing the performance and applicability of the ML-based models. Meteorological factors such as boundary layer height can significantly influence PM concentrations by trapping pollutants near the surface during low-ventilation and inversion conditions. Similarly, changes in land use, such as urbanization or drought in arid and semi-arid regions, can enhance PM emissions. Addressing the limitations of existing datasets and developing comprehensive, balanced, long-term databases should be a high priority for the research community.
- Spatiotemporal modeling:Spatiotemporal modeling techniques will offer valuable insights into the patterns and trends of and concentrations. These techniques will reveal how PM levels vary across different locations and times. By incorporating spatial elements, the model will better account for regional differences in PM concentrations, such as higher levels near highways or industrial zones and lower levels in rural or forested areas. Additionally, including temporal features will enable the model to capture how PM concentrations change over time. This will account for factors such as daily cycles, seasonal variations, and long-term trends. Furthermore, it is important to use climate similarity to address issues of spatial discontinuity when using latitude and longitude as input features when training the model for enhancing and describing the spatial proximity of samples.
- Hybrid ML-based model:In heavily polluted metropolitan regions, PM concentration estimation solutions that use hybrid ML models are becoming more crucial. Hybrid models allow for an improved comprehension of difficulties in metropolitan contexts, where pollution can fluctuate dramatically due to traffic congestion, industrial activity, and shifting weather patterns. These models provide a strong instrument for monitoring air quality, supporting efficient pollution control plans, and safeguarding public health.For instance, the Hybrid dragonfly–SVM–RF model may potentially revolutionize air quality monitoring and estimate PM concentration. The dragonfly algorithm will be used for optimization tasks such as feature selection or parameter tuning. By combining it with the estimation power of SVM and the ensemble capabilities of RF, the hybrid dragonfly–SVM–RF model may achieve superior accuracy in estimating PM concentrations compared to individual models. This combination may allows the model to capture non-linear relationships within the data, providing a more comprehensive analysis.
- Site-based Ttme-based cross validations:In site-based cross validation, a model will be trained using data from several monitoring stations and tested using data from additional, unseen stations. This technique will promote the assessment of the model’s generalizability to new contexts. In time-based cross validation, we will train the model on data from specific years and test it on data from different years. This will ensure that the model estimates remain consistent over time and can accurately estimate future trends based on historical data.Based upon the directions, future research can further enhance the understanding and estimation of air pollution, ultimately supporting more effective air quality management.
5. Conclusions
Machine Learning (ML) advancements offer a promising solution to enhance PM concentration estimation by capturing complex relationships among factors. Our research focusing on ML in air quality monitoring and PM estimation provides a comprehensive analysis of the field. This systematic review, spanning studies from 2018 to 2024, evaluates the benefits of ML, identifies research gaps, and outlines future directions, aiming to improve models for PM concentration estimation.
By developing ML-based estimation models for and , researchers and policymakers can gain valuable insights into the sources, transport mechanisms, and impacts of PM pollution. This will ultimately contribute to efforts to mitigate air pollution and safeguard human health and the environment. Our study successfully addresses several research questions. Furthermore, we examine the strengths and limitations associated with each category. Moreover, our contribution emphasizes the significance of estimating PM using ML-based models and leveraging diverse datasets that incorporate meteorological information to enhance accuracy.
Our research has effectively tackled a range of research inquiries, meticulously assessing the strengths and limitations within each model category. Moreover, our contribution emphasizes how critical it is to apply machine learning (ML) models for PM estimation and leverage various balanced datasets that incorporate meteorological data to improve accuracy. Our systematic literature review (SLR) results will impact the creation of more robust models for estimating PM concentrations, which will advance initiatives to strengthen environmental and public health via ML-guided air quality monitoring.
Finally, this paper suggests future directions for researchers to enhance air monitoring systems. Future research should focus on leveraging balanced long-term datasets and spatiotemporal modeling for accurate PM concentration estimation, as well as implementing site-based and time-based cross validation techniques to improve air pollution estimation models. Additionally, optimizing hybrid ML models like the hybrid dragonfly–SVM–RF model in polluted metropolitan areas can boost air quality monitoring and pollution control strategies.
Author Contributions
Conceptualization, A.A. (Amjad Alkhodaidi), A.H., A.A. (Afraa Attiah) and A.M.; methodology, A.A. (Amjad Alkhodaidi); formal analysis, A.A. (Amjad Alkhodaidi); investigation, A.A. (Amjad Alkhodaidi); resources, A.A. (Amjad Alkhodaidi); data curation, A.A. (Amjad Alkhodaidi); writing—original draft preparation, A.A. (Amjad Alkhodaidi), A.H., A.M. and A.A. (Afraa Attiah); writing—review and editing, A.A. (Amjad Alkhodaidi), A.H. and A.A. (Afraa Attiah); visualization, A.A. (Amjad Alkhodaidi); supervision, A.A. (Afraa Attiah) and A.H.; project administration, A.A. (Afraa Attiah), A.H. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We would like to express our sincere gratitude to Abdullah Amoudi for his invaluable assistance in facilitating communication with the Sand and Dust Storm Warning Regional Center. His efforts in highlighting critical problems that need to be addressed were essential to the development of this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gupta, P.; Zhan, S.; Mishra, V.; Aekakkararungroj, A.; Markert, A.; Paibong, S.; Chishtie, F. Machine learning algorithm for estimating surface PM2.5 in Thailand. Aerosol Air Qual. Res. 2021, 21, 210105. [Google Scholar] [CrossRef]
- Air Pulltion. 2024. Available online: https://www.who.int/health-topics/air-pollution#tab=tab_1 (accessed on 13 July 2024).
- Alamoudi, M.; Taylan, O.; Keshtegar, B.; Abusurrah, M.; Balubaid, M. Modeling sulphur dioxide (SO2) quality levels of Jeddah City using machine learning approaches with meteorological and chemical factors. Sustainability 2022, 14, 16291. [Google Scholar] [CrossRef]
- Kampa, M.; Castanas, E. Human health effects of air pollution. Environ. Pollut. 2008, 151, 362–367. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Chen, Z.; Zhou, L.F.; Huang, S.X. Air pollutants and early origins of respiratory diseases. Chronic Dis. Transl. Med. 2018, 4, 75–94. [Google Scholar] [CrossRef]
- Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar] [CrossRef]
- Cohen, A.J.; Ross Anderson, H.; Ostro, B.; Pandey, K.D.; Krzyzanowski, M.; Künzli, N.; Gutschmidt, K.; Pope, A.; Romieu, I.; Samet, J.M.; et al. The global burden of disease due to outdoor air pollution. J. Toxicol. Environ. Health Part A 2005, 68, 1301–1307. [Google Scholar] [CrossRef]
- Künzli, N.; Tager, I.B. Air pollution: From lung to heart. Swiss Med. Wkly. 2005, 135, 697–702. [Google Scholar]
- Chen, M.H.; Chen, Y.C.; Chou, T.Y.; Ning, F.S. PM2.5 Concentration Prediction Model: A CNN–RF Ensemble Framework. Int. J. Environ. Res. Public Health 2023, 20, 4077. [Google Scholar] [CrossRef]
- Ibrir, A.; Kerchich, Y.; Hadidi, N.; Merabet, H.; Hentabli, M. Prediction of the concentrations of PM1, PM2.5, PM4, and PM10 by using the hybrid dragonfly-SVM algorithm. Air Qual. Atmos. Health 2021, 14, 313–323. [Google Scholar] [CrossRef]
- Valavanidis, A.; Fiotakis, K.; Vlachogianni, T. Airborne particulate matter and human health: Toxicological assessment and importance of size and composition of particles for oxidative damage and carcinogenic mechanisms. J. Environ. Sci. Health Part C 2008, 26, 339–362. [Google Scholar] [CrossRef]
- Shaltout, A.A.; Boman, J.; Shehadeh, Z.F.; Dhaif-Allah, R.; Hemeda, O.; Morsy, M.M. Spectroscopic investigation of PM2.5 collected at industrial, residential and traffic sites in Taif, Saudi Arabia. J. Aerosol Sci. 2015, 79, 97–108. [Google Scholar] [CrossRef]
- Aina, Y.A.; Van der Merwe, J.H.; Alshuwaikhat, H.M. Spatial and temporal variations of satellite-derived multi-year particulate data of Saudi Arabia: An exploratory analysis. Int. J. Environ. Res. Public Health 2014, 11, 11152–11166. [Google Scholar] [CrossRef] [PubMed]
- Heisler, S.L.; Friedlander, S. Gas-to-particle conversion in photochemical smog: Aerosol growth laws and mechanisms for organics. Atmos. Environ. 1977, 11, 157–168. [Google Scholar] [CrossRef]
- Carvalho, H. New WHO global air quality guidelines: More pressure on nations to reduce air pollution levels. Lancet Planet. Health 2021, 5, e760–e761. [Google Scholar] [CrossRef]
- Sprigg, W.; Nickovic, S.; Galgiani, J.; Pejanovic, G.; Petkovic, S.; Vujadinovic, M.; Vukovic, A.; Dacic, M.; DiBiase, S.; Prasad, A.; et al. Regional dust storm modeling for health services: The case of valley fever. Aeolian Res. 2014, 14, 53–73. [Google Scholar] [CrossRef]
- Haq, M.A. SMOTEDNN: A novel model for air pollution forecasting and AQI classification. Comput. Mater. Contin. 2022, 71, 1403–1425. [Google Scholar]
- Dhandapani, A.; Iqbal, J.; Kumar, R.N. Application of machine learning (individual vs stacking) models on MERRA-2 data to predict surface PM2.5 concentrations over India. Chemosphere 2023, 340, 139966. [Google Scholar] [CrossRef]
- Mircea, M.; Calori, G.; Pirovano, G.; Belis, C. European Guide on Air Pollution Source Apportionment for Particulate Matter with Source Oriented Models and Their Combined Use with Receptor Models; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Johnson, T.M.; Guttikunda, S.; Wells, G.J.; Artaxo, P.; Bond, T.C.; Russell, A.G.; Watson, J.G.; West, J. Tools for Improving Air Quality Management: A Review of Top-Down Source Apportionment Techniques and Their Application in Developing Countries; World Bank: Washington, DC, USA, 2011. [Google Scholar]
- Li, Y.; Yuan, S.; Fan, S.; Song, Y.; Wang, Z.; Yu, Z.; Yu, Q.; Liu, Y. Satellite remote sensing for estimating PM2.5 and its components. Curr. Pollut. Rep. 2021, 7, 72–87. [Google Scholar] [CrossRef]
- Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef]
- Mhawish, A.; Banerjee, T.; Sorek-Hamer, M.; Bilal, M.; Lyapustin, A.I.; Chatfield, R.; Broday, D.M. Estimation of high-resolution PM2.5 over the Indo-Gangetic Plain by fusion of satellite data, meteorology, and land use variables. Environ. Sci. Technol. 2020, 54, 7891–7900. [Google Scholar] [CrossRef]
- Kaginalkar, A.; Kumar, S.; Gargava, P.; Niyogi, D. Review of urban computing in air quality management as smart city service: An integrated IoT, AI, and cloud technology perspective. Urban Clim. 2021, 39, 100972. [Google Scholar] [CrossRef]
- Essamlali, I.; Nhaila, H.; El Khaili, M. Supervised Machine Learning Approaches for Predicting Key Pollutants and for the Sustainable Enhancement of Urban Air Quality: A Systematic Review. Sustainability 2024, 16, 976. [Google Scholar] [CrossRef]
- Zuo, X.; Guo, H.; Shi, S.; Zhang, X. Comparison of six machine learning methods for estimating PM2.5 concentration using the Himawari-8 aerosol optical depth. J. Indian Soc. Remote Sens. 2020, 48, 1277–1287. [Google Scholar] [CrossRef]
- Zaman, N.A.F.K.; Kanniah, K.D.; Kaskaoutis, D.G.; Latif, M.T. Evaluation of machine learning models for estimating PM2.5 concentrations across malaysia. Appl. Sci. 2021, 11, 7326. [Google Scholar] [CrossRef]
- Park, Y.; Kwon, B.; Heo, J.; Hu, X.; Liu, Y.; Moon, T. Estimating PM2.5 concentration of the conterminous United States via interpretable convolutional neural networks. Environ. Pollut. 2020, 256, 113395. [Google Scholar] [CrossRef]
- Chakma, A.; Vizena, B.; Cao, T.; Lin, J.; Zhang, J. Image-based air quality analysis using deep convolutional neural network. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3949–3952. [Google Scholar]
- Li, J.; Jin, M.; Li, H. Exploring spatial influence of remotely sensed PM2.5 concentration using a developed deep convolutional neural network model. Int. J. Environ. Res. Public Health 2019, 16, 454. [Google Scholar] [CrossRef]
- Qadeer, K.; Rehman, W.U.; Sheri, A.M.; Park, I.; Kim, H.K.; Jeon, M. A long short-term memory (LSTM) network for hourly estimation of PM2.5 concentration in two cities of South Korea. Appl. Sci. 2020, 10, 3984. [Google Scholar] [CrossRef]
- Sayeed, A.; Lin, P.; Gupta, P.; Tran, N.N.M.; Buchard, V.; Christopher, S. Hourly and Daily PM2.5 Estimations Using MERRA-2: A Machine Learning Approach. Earth Space Sci. 2022, 9, e2022EA002375. [Google Scholar] [CrossRef]
- Shtein, A.; Kloog, I.; Schwartz, J.; Silibello, C.; Michelozzi, P.; Gariazzo, C.; Viegi, G.; Forastiere, F.; Karnieli, A.; Just, A.C.; et al. Estimating daily PM2.5 and PM10 over Italy using an ensemble model. Environ. Sci. Technol. 2019, 54, 120–128. [Google Scholar] [CrossRef]
- Gu, Y. Estimating PM2.5 Concentrations Using 3 km MODIS AOD Products: A Case Study in British Columbia, Canada. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2019. [Google Scholar]
- Meng, X.; Hand, J.L.; Schichtel, B.A.; Liu, Y. Space-time trends of PM2.5 constituents in the conterminous United States estimated by a machine learning approach, 2005–2015. Environ. Int. 2018, 121, 1137–1147. [Google Scholar] [CrossRef]
- Yu, W.; Li, S.; Ye, T.; Xu, R.; Song, J.; Guo, Y. Deep ensemble machine learning framework for the estimation of PM2.5 concentrations. Environ. Health Perspect. 2022, 130, 037004. [Google Scholar] [CrossRef] [PubMed]
- LME. 2024. Available online: https://www.geeksforgeeks.org/linear-mixed-effects-models-lme-in-r/ (accessed on 13 July 2024).
- Lee, H.; Liu, Y.; Coull, B.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef]
- Yu, H.; Fotheringham, A.S.; Li, Z.; Oshan, T.; Kang, W.; Wolf, L.J. Inference in multiscale geographically weighted regression. Geogr. Anal. 2020, 52, 87–106. [Google Scholar] [CrossRef]
- Zou, B.; Chen, J.; Zhai, L.; Fang, X.; Zheng, Z. Satellite based mapping of ground PM2.5 concentration using generalized additive modeling. Remote Sens. 2016, 9, 1. [Google Scholar] [CrossRef]
- Unnithan, S.K.; Gnanappazham, L. Spatiotemporal mixed effects modeling for the estimation of PM2.5 from MODIS AOD over the Indian subcontinent. GISci. Remote Sens. 2020, 57, 159–173. [Google Scholar] [CrossRef]
- Xiao, Q.; Chang, H.H.; Geng, G.; Liu, Y. An ensemble machine-learning model to predict historical PM2.5 concentrations in China from satellite data. Environ. Sci. Technol. 2018, 52, 13260–13269. [Google Scholar] [CrossRef]
- Bera, B.; Bhattacharjee, S.; Sengupta, N.; Saha, S. PM2.5 concentration prediction during COVID-19 lockdown over Kolkata metropolitan city, India using MLR and ANN models. Environ. Chall. 2021, 4, 100155. [Google Scholar] [CrossRef]
- Chen, B.; Song, Z.; Huang, J.; Zhang, P.; Hu, X.; Zhang, X.; Guan, X.; Ge, J.; Zhou, X. Estimation of atmospheric PM10 concentration in China using an interpretable deep learning model and top-of-the-atmosphere reflectance data from China’s new generation geostationary meteorological satellite, FY-4A. J. Geophys. Res. Atmos. 2022, 127, e2021JD036393. [Google Scholar] [CrossRef]
- Maltare, N.N.; Vahora, S. Air Quality Index prediction using machine learning for Ahmedabad city. Digit. Chem. Eng. 2023, 7, 100093. [Google Scholar] [CrossRef]
- Deo, R.C.; Wen, X.; Qi, F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]
- Gao, Z.; Do, K.; Li, Z.; Jiang, X.; Maji, K.J.; Ivey, C.E.; Russell, A.G. Predicting PM2.5 levels and exceedance days using machine learning methods. Atmos. Environ. 2024, 323, 120396. [Google Scholar] [CrossRef]
- Balogun, A.L.; Tella, A. Modelling and investigating the impacts of climatic variables on ozone concentration in Malaysia using correlation analysis with random forest, decision tree regression, linear regression, and support vector regression. Chemosphere 2022, 299, 134250. [Google Scholar] [CrossRef] [PubMed]
- Méndez, M.; Merayo, M.G.; Núñez, M. Machine learning algorithms to forecast air quality: A survey. Artif. Intell. Rev. 2023, 56, 10031–10066. [Google Scholar] [CrossRef] [PubMed]
- The Optimal Value of K in KNN. 2024. Available online: https://www.geeksforgeeks.org/how-to-find-the-optimal-value-of-k-in-knn/ (accessed on 4 October 2024).
- Ayinde, B.O.; Musa, M.R.; Ayinde, A.A.O. Application of machine learning models and landsat 8 data for estimating seasonal PM2.5 concentrations. Environ. Anal. Health Toxicol. 2024, 39, e2024011. [Google Scholar] [CrossRef]
- Xiong, L.; Yao, Y. Study on an adaptive thermal comfort model with K-nearest-neighbors (KNN) algorithm. Build. Environ. 2021, 202, 108026. [Google Scholar] [CrossRef]
- Balogun, A.L.; Tella, A.; Baloo, L.; Adebisi, N. A review of the inter-correlation of climate change, air pollution and urban sustainability using novel machine learning algorithms and spatial information science. Urban Clim. 2021, 40, 100989. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, F.J.; Hernandez, E.A.; Terrones-Salgado, J.; Quiroz, L.J.F. Evolutionary artificial neural network for temperature control in a batch polymerization reactor. Ingenius 2023, 79–89. [Google Scholar] [CrossRef]
- Afan, H.A.; Ibrahem Ahmed Osman, A.; Essam, Y.; Ahmed, A.N.; Huang, Y.F.; Kisi, O.; Sherif, M.; Sefelnasr, A.; Chau, K.w.; El-Shafie, A. Modeling the fluctuations of groundwater level by employing ensemble deep learning techniques. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1420–1439. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 1995, 3361, 1995. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Ayturan, Y.A.; Ayturan, Z.C.; Altun, H.O. Air pollution modelling with deep learning: A review. Int. J. Environ. Pollut. Environ. Model. 2018, 1, 58–62. [Google Scholar]
- Tian, J.; Liu, Y.; Zheng, W.; Yin, L. Smog prediction based on the deep belief-BP neural network model (DBN-BP). Urban Clim. 2022, 41, 101078. [Google Scholar] [CrossRef]
- Valencia, A.R.Z.; Rosales, A.A.R. Application of Random Forest in a Predictive Model of PM10 Particles in Mexico City. Nat. Environ. Pollut. Technol. 2024, 23, 711–724. [Google Scholar] [CrossRef]
- Gui, K.; Che, H.; Zeng, Z.; Wang, Y.; Zhai, S.; Wang, Z.; Luo, M.; Zhang, L.; Liao, T.; Zhao, H.; et al. Construction of a virtual PM2.5 observation network in China based on high-density surface meteorological observations using the Extreme Gradient Boosting model. Environ. Int. 2020, 141, 105801. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.J.; Hua, Y.J.; Lin, Z.; Zhang, T.; Di, Z.M. Stacking machine learning model for estimating hourly PM2.5 in China based on Himawari 8 aerosol optical depth data. Sci. Total Environ. 2019, 697, 134021. [Google Scholar] [CrossRef] [PubMed]
- Ghahremanloo, M.; Choi, Y.; Sayeed, A.; Salman, A.K.; Pan, S.; Amani, M. Estimating daily high-resolution PM2.5 concentrations over Texas: Machine Learning approach. Atmos. Environ. 2021, 247, 118209. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhang, T.H.; Zhang, R.; Zhu, Z.M.; Yang, J.; Chen, P.Y.; Ou, C.Q.; Guo, Y. Extreme gradient boosting model to estimate PM2.5 concentrations with missing-filled satellite data in China. Atmos. Environ. 2019, 202, 180–189. [Google Scholar] [CrossRef]
- Mohammadi, A.; Karimzadeh, S.; Banimahd, S.A.; Ozsarac, V.; Lourenço, P.B. The potential of region-specific machine-learning-based ground motion models: Application to Turkey. Soil Dyn. Earthq. Eng. 2023, 172, 108008. [Google Scholar] [CrossRef]
- Buya, S.; Usanavasin, S.; Gokon, H.; Karnjana, J. An Estimation of Daily PM2.5 Concentration in Thailand Using Satellite Data at 1-Kilometer Resolution. Sustainability 2023, 15, 10024. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Jeong, S.H.; Mansouri, E.; Shamass, R.; Tsavdaridis, K.; Martins, C.H.; De Nardin, S. Five Machine Learning Models Predicting the Global Shear Capacity of Composite Cellular Beams with Hollow-Core Units. Buildings 2024, 14, 2256. [Google Scholar] [CrossRef]
- Zeng, Z.; Gui, K.; Wang, Z.; Luo, M.; Geng, H.; Ge, E.; An, J.; Song, X.; Ning, G.; Zhai, S.; et al. Estimating hourly surface PM2.5 concentrations across China from high-density meteorological observations by machine learning. Atmos. Res. 2021, 254, 105516. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 52. [Google Scholar]
- Keele, S. Guidelines for Performing Systematic Literature Reviews in Software Engineering; Keele University: Keele, UK, 2007. [Google Scholar]
- Brokamp, C.; Jandarov, R.; Hossain, M.; Ryan, P. Predicting daily urban fine particulate matter concentrations using a random forest model. Environ. Sci. Technol. 2018, 52, 4173–4179. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Wang, Y.; Li, S.; Cao, W.; Ren, H.; Knibbs, L.D.; Abramson, M.J.; Guo, Y. Spatiotemporal patterns of PM10 concentrations over China during 2005–2016: A satellite-based estimation using the random forests approach. Environ. Pollut. 2018, 242, 605–613. [Google Scholar] [CrossRef]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; De Hoogh, K.; De’Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013–2015, using a spatiotemporal land-use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef]
- Stafoggia, M.; Johansson, C.; Glantz, P.; Renzi, M.; Shtein, A.; de Hoogh, K.; Kloog, I.; Davoli, M.; Michelozzi, P.; Bellander, T. A random forest approach to estimate daily particulate matter, nitrogen dioxide, and ozone at fine spatial resolution in Sweden. Atmosphere 2020, 11, 239. [Google Scholar] [CrossRef]
- Tuygun, G.T.; Gündoğdu, S.; Elbir, T. Estimation of ground-level particulate matter concentrations based on synergistic use of MODIS, MERRA-2 and AERONET AODs over a coastal site in the Eastern Mediterranean. Atmos. Environ. 2021, 261, 118562. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Z.; Liu, Q. Estimations of ambient fine particle and ozone level at a suburban site of Beijing in winter. Environ. Res. Commun. 2021, 3, 081008. [Google Scholar] [CrossRef]
- Djarum, D.H.; Ahmad, Z.; Zhang, J. Comparing Different Pre-processing Techniques and Machine Learning Models to Predict PM10 and PM2.5 Concentration in Malaysia. In Proceedings of the 3rd International Conference on Separation Technology: Sustainable Design in Construction, Materials and Processes, Johor, Malaysia, 15–16 August 2020; Springer: Singapore, 2021; pp. 353–374. [Google Scholar]
- Lin, L.; Liang, Y.; Liu, L.; Zhang, Y.; Xie, D.; Yin, F.; Ashraf, T. Estimating PM2.5 concentrations using the machine learning RF-XGBoost model in guanzhong urban agglomeration, China. Remote Sens. 2022, 14, 5239. [Google Scholar] [CrossRef]
- Chen, B.; Song, Z.; Shi, B.; Li, M. An interpretable deep forest model for estimating hourly PM10 concentration in China using Himawari-8 data. Atmos. Environ. 2022, 268, 118827. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Cao, C.; Xu, M.; Yang, X.; Wang, K.; Guo, H.; Gao, X.; Li, J.; Shi, Z. Estimation of PM2.5 concentration across china based on multi-source remote sensing data and machine learning methods. Remote Sens. 2024, 16, 467. [Google Scholar] [CrossRef]
- Li, S.; Ding, Y.; Xing, J.; Fu, J.S. Retrieving Ground-Level PM2.5 Concentrations in China (2013–2021) with a Numerical Model-Informed Testbed to Mitigate Sample Imbalance-Induced Biases. Earth Syst. Sci. Data Discuss. 2024, 16, 3781–3793. [Google Scholar] [CrossRef]
- Ding, Y.; Li, S.; Xing, J.; Li, X.; Ma, X.; Song, G.; Teng, M.; Yang, J.; Dong, J.; Meng, S. Retrieving hourly seamless PM2.5 concentration across China with physically informed spatiotemporal connection. Remote Sens. Environ. 2024, 301, 113901. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach. J. Geophys. Res. Atmos. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, G.; Zhu, Z.; Gong, W.; Ji, Y.; Huang, Y. Real-time estimation of satellite-derived PM2.5 based on a semi-physical geographically weighted regression model. Int. J. Environ. Res. Public Health 2016, 13, 974. [Google Scholar] [CrossRef]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886–892. [Google Scholar] [CrossRef]
- Rao, P.; Niharika, V. A survey on air quality forecasting techniques. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 812–816. [Google Scholar]
- Bilal, M.; Nichol, J.E.; Spak, S.N. A new approach for estimation of fine particulate concentrations using satellite aerosol optical depth and binning of meteorological variables. Aerosol Air Qual. Res. 2017, 17, 356–367. [Google Scholar] [CrossRef]
- Chen, M.J.; Yang, P.H.; Hsieh, M.T.; Yeh, C.H.; Huang, C.H.; Yang, C.M.; Lin, G.M. Machine learning to relate PM2.5 and PM10 concentrations to outpatient visits for upper respiratory tract infections in Taiwan: A nationwide analysis. World J. Clin. Cases 2018, 6, 200. [Google Scholar] [CrossRef]
- Azid, A.; Juahir, H.; Toriman, M.E.; Kamarudin, M.K.A.; Saudi, A.S.M.; Hasnam, C.N.C.; Aziz, N.A.A.; Azaman, F.; Latif, M.T.; Zainuddin, S.F.M.; et al. Prediction of the level of air pollution using principal component analysis and artificial neural network techniques: A case study in Malaysia. Water Air Soil Pollut. 2014, 225, 1–14. [Google Scholar] [CrossRef]
- Zang, L.; Mao, F.; Guo, J.; Wang, W.; Pan, Z.; Shen, H.; Zhu, B.; Wang, Z. Estimation of spatiotemporal PM1.0 distributions in China by combining PM2.5 observations with satellite aerosol optical depth. Sci. Total Environ. 2019, 658, 1256–1264. [Google Scholar] [CrossRef]
- Kujawska, J.; Kulisz, M.; Oleszczuk, P.; Cel, W. Machine learning methods to forecast the concentration of PM10 in Lublin, Poland. Energies 2022, 15, 6428. [Google Scholar] [CrossRef]
- Kumar, S.; Mishra, S.; Singh, S.K. A machine learning-based model to estimate PM2.5 concentration levels in Delhi’s atmosphere. Heliyon 2020, 6, e05618. [Google Scholar] [CrossRef] [PubMed]
- Liao, K.; Huang, X.; Dang, H.; Ren, Y.; Zuo, S.; Duan, C. Statistical approaches for forecasting primary air pollutants: A review. Atmosphere 2021, 12, 686. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 concentrations in the conterminous United States using the random forest approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef] [PubMed]
- Unik, M.; Sitanggang, I.S.; Syaufina, L.; Jaya, I.N.S. PM2.5 estimation using machine learning models and satellite data: A literature review. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 359–370. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, H.; Bai, Z.; Han, B.; Xu, J.; Zhao, R.; Zhang, N.; Chen, L.; Lei, X.; Shi, W.; et al. Combined use of principal component analysis and artificial neural network approach to improve estimates of PM2.5 personal exposure: A case study on older adults. Sci. Total Environ. 2020, 726, 138533. [Google Scholar] [CrossRef]
- Haiming, Z.; Xiaoxiao, S. Study on prediction of atmospheric PM2.5 based on RBF neural network. In Proceedings of the 2013 Fourth International Conference on Digital Manufacturing & Automation, Qingdao, China, 29–30 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1287–1289. [Google Scholar]
- Zheng, Y.; Liu, F.; Hsieh, H.P. U-air: When urban air quality inference meets big data. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago IL, USA, 11–14 August 2013; pp. 1436–1444. [Google Scholar]
- Kaushik, R.; Kumar, S.; Pooling, M. Image segmentation using convolutional neural network. Int. J. Sci. Technol. Res 2019, 8, 667–675. [Google Scholar]
- Tao, H.; Xing, J.; Zhou, H.; Pleim, J.; Ran, L.; Chang, X.; Wang, S.; Chen, F.; Zheng, H.; Li, J. Impacts of improved modeling resolution on the simulation of meteorology, air quality, and human exposure to PM2.5, O3 in Beijing, China. J. Clean. Prod. 2020, 243, 118574. [Google Scholar] [CrossRef]
- Yan, X.; Zang, Z.; Jiang, Y.; Shi, W.; Guo, Y.; Li, D.; Zhao, C.; Husi, L. A Spatial-Temporal Interpretable Deep Learning Model for improving interpretability and predictive accuracy of satellite-based PM2.5. Environ. Pollut. 2021, 273, 116459. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Levy, R.C. The dark-land MODIS collection 5 aerosol retrieval: Algorithm development and product evaluation. In Satellite Aerosol Remote Sensing over Land; Springer: Berlin/Heidelberg, Germany, 2009; pp. 19–68. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).