Abstract
Electronic circuits/systems operating in harsh environments such as space are likely to experience faults or failures due to the impact of high-energy radiation. Given this, to overcome any faults or failures, redundancy is usually employed as a hardening-by-design approach. Moreover, low power and a small silicon footprint are also important considerations for space electronics since these translate into better energy efficiency, less system weight, and less cost. Therefore, the fault-tolerant design of electronic circuits and systems should go hand in hand with the optimization of design metrics, especially for resource-constrained electronics such as those used in space systems. A single circuit or system (also called a simplex implementation) is not fault-tolerant as it may become a single point of failure and is not used for a space application. As an alternative, a triple modular redundancy (TMR) implementation, which uses three identical copies of a circuit or system and a voter to perform majority voting of the circuits and systems outputs, may be used. However, in comparison with a simplex implementation, a TMR implementation consumes about 200% more area and dissipates 200% more power when circuits or systems are triplicated. To mitigate the area and power overheads of a TMR implementation compared to a simplex implementation, researchers have suggested alternative redundancy approaches such as selective TMR (STMR) insertion, partially approximate TMR (PATMR), fully approximate TMR (FATMR), and majority voting-based reduced precision redundancy (VRPR). Among these, VRPR appears to be promising, especially for inherently error-tolerant applications such as digital image/video/audio processing, which is relevant to space systems. However, the alternative redundancy approaches mentioned are unlikely to be suitable for the implementation of control logic. In this work, we analyze various redundancy approaches and evaluate the performance of TMR and VRPR for a digital image processing application. We provide MATLAB-based image processing results corresponding to TMR and VRPR and physical implementation results of functional units based on TMR and VRPR using a 28-nm CMOS technology.
1. Introduction
For a safety-critical system such as a spacecraft, satellite, etc., fault tolerance and design optimization are two important considerations. Fault tolerance is important because when electronic functional units such as circuits or systems operate in a harsh environment such as space, they could be impacted by high-energy radiation such as solar flares, solar particle events, cosmic rays, Van Allen radiation belts, electromagnetic pulses, etc. Solar flares are sudden bursts of high-energy radiation from the sun, including X-rays and gamma rays, which can interfere with or damage electronic systems on spacecraft and satellites and even affect communication systems on Earth. Cosmic rays are highly energetic charged particles, primarily protons and atomic nuclei, that originate from outside the solar system and can penetrate spacecraft and satellites, causing glitches, bit-flips in computer memory, and even hardware damage. Van Allen radiation belts are regions of intense radiation trapped by Earth’s magnetic field, which contains charged particles such as electrons and protons that can affect spacecraft and satellites passing through them and can cause temporary or permanent damage to electronic components. Electromagnetic pulses are short bursts of electromagnetic radiation that can be generated by intense solar activity, which can induce high-voltage surges in electronic systems and may damage or disrupt their functionality. Galactic cosmic rays are high-energy particles mostly originating from outside of our solar system, such as supernovae, which are a continuous source of radiation in space and can cause single-event upsets (SEUs) or other forms of radiation-induced errors in electronic systems. Solar particle events are bursts of energetic particles, primarily protons and ions, ejected from the sun during solar flares or coronal mass ejections, which can interfere with or damage electronic components in space systems. To mitigate the effects of high-energy radiation, space systems are designed with protective measures such as shielding, redundancy in critical systems, error-correcting codes, etc. to minimize the impact on electronic circuits/systems.
This paper analyzes different redundancy techniques that may be used at the functional unit level for a resource-constrained electronics design, such as those applicable to space systems where fault tolerance, weight, cost, and design metrics are given important consideration. The rest of this paper is organized into three sections. Section 2 surveys the existing literature on different redundancy schemes and discusses their pros and cons. Section 3 provides a comparative evaluation of the performance of conventional TMR and VRPR when used for an example practical application, viz., digital image processing (DIP). MATLAB-based image processing results obtained using TMR and VRPR are provided, and the physical design metrics of example TMR and VRPR implementations using a 28-nm CMOS technology are also provided. Section 4 makes the concluding remarks.
2. Survey of Redundancy Schemes
With reductions in transistor size, electronic circuits or systems (henceforth, generically called ‘functional units’) are becoming more susceptible to faults or failures during normal operation [1,2] or as a result of aging [3]. The situation worsens when these circuits and systems are exposed to challenging conditions such as radiation [4,5]. Consequently, it is crucial to safeguard circuits and systems used in safety-critical applications such as space against the risk of faults or failures. In such scenarios, redundancy is commonly utilized to address the occurrence of faults or failures within a predetermined limit.
N-Modular Redundancy (NMR) is a widely recognized approach in which N identical functional units are used, and their outputs are combined through majority voting to generate the final output. In NMR, where N is an odd number, the correct operation of NMR is ensured when (N + 1)/2 functional units are operating correctly, assuming the majority voter is also operating correctly. According to NMR, faults or failures occurring in (N − 1)/2 functional units can be tolerated, meaning they are effectively concealed without impacting the output.
TMR, or Triple Modular Redundancy, which is a popular and widely used version of NMR, involves the use of three identical functional units whose outputs are majority-voted to produce the final output. TMR can successfully mask any single fault or failure. To mask multiple faults or failures, higher order NMR such as quintuple modular redundancy, septuple modular redundancy, etc. may be used, or some versions of the majority and minority voted redundancy (MMR) scheme [6] may be used. Although increasing the redundancy would lead to improved fault tolerance, it would be at the expense of an increase in the number of resources (such as functional units), which would increase the cost and design metrics. Nevertheless, as suggested in [7], redundancy may be employed progressively, whereby TMR is used widely and higher-order NMR or MMR is used selectively in a redundant design.
In a practical study [8] that exposed different Virtex FPGAs to proton and heavy-ion-induced radiation, it was observed that single-bit upsets accounted for 96% to 99% of the total upsets and multiple-bit upsets accounted for a small remainder, making TMR a suitable choice to realize a redundant functional unit for safety-critical applications. Reference [9] discusses different ways of implementing TMR at the register level and/or block (i.e., functional unit) level and/or voter level, etc., depending upon an application requirement. When TMR is implemented at the functional unit level, it requires two additional (and identical) functional units and a majority voting logic, resulting in over 200% area and power overheads compared to a single functional unit, i.e., a simplex implementation. Additionally, a TMR implementation may have a slightly increased delay compared to a simplex implementation because of the introduction of the majority voter in the critical data path. Despite these limitations, TMR can fully tolerate the fault or failure of an arbitrary functional unit. Nonetheless, researchers have proposed trade-off approaches to reduce the area and power overhead of a TMR implementation at the expense of a compromise on fault tolerance, and these are discussed next.
In [10], selective TMR (STMR) insertion is presented, whereby TMR is applied only to the critical sections of a functional unit, while the non-critical sections are retained as a simplex implementation. This approach reduces the area and power overhead of a redundant implementation compared to the blanket use of TMR. However, there are two potential problems with STMR. Firstly, distinguishing the critical and non-critical parts of a functional unit may not be straightforward for practical applications, and this differentiation may not remain valid during the operational life of a functional unit. Secondly, if the non-critical part of a functional unit, which is not protected, is affected, there is no guarantee that the output of the functional unit will remain unchanged.
Reference [11] proposed a method called partially approximate TMR (PATMR) in which one accurate functional unit and two distinct approximate functional units with reduced logic are used, and their corresponding outputs are majority-voted to produce the final output. PATMR can reduce area and power overheads compared to conventional TMR, which uses three accurate functional units. For a PATMR implementation, the basic requirement is that the outputs of any two functional units should match, in contrast to a TMR implementation where the outputs of three identical functional units match. This might cause some issues with PATMR. First, if there is a fault in one of the outputs of the accurate or approximate functional units, the corresponding output of a PATMR implementation could become incorrect because the basic requirement is violated. Second, if the accurate functional unit fails, the outputs of the approximate functional units may not match, causing a failure of PATMR. These scenarios indicate that PATMR may not be able to completely mask a single fault or failure of a functional unit, which violates the fundamental property of TMR.
To reduce the design overheads (delay, area, and power) of conventional TMR, researchers introduced Fully Approximate TMR (FATMR) [12]. FATMR utilizes three distinct approximate versions of an original accurate functional unit, and their corresponding outputs are combined using precise majority voters. Like PATMR, in FATMR, the corresponding outputs of any two of the approximate functional units are matched. Consequently, if an output of an approximate functional unit becomes faulty, the corresponding output of FATMR would be affected. Moreover, if one of the approximate functional units were to fail, the entire FATMR implementation might become corrupted because the outputs of the other two approximate functional units may not match, resulting in erroneous outputs. Therefore, FATMR is less reliable compared to ATMR. Nonetheless, both ATMR and FATMR are unlikely to be adopted for safety-critical applications due to the uncertainty surrounding their output in the presence of a single fault or failure. Furthermore, there is a lack of demonstrated practical applications showcasing the utility of ATMR and FATMR.
In [13], a majority voting-based reduced precision redundancy (VRPR) adder was presented. Nevertheless, VRPR can be generalized as an alternative redundancy technique to TMR. We note that VRPR, when carefully used, is suitable for redundant implementation of functional units specifically for inherently error-tolerant applications such as digital signal processing, e.g., digital image/video/audio processing. These applications exploit natural limitations in human perception, allowing for minor distortions in images, video frames, or faint noise in audio to be tolerated. Since digital imaging, video, and audio systems are commonly used in space systems, small errors in their outputs can be tolerated if they help improve design metrics and increase energy efficiency.
According to VRPR, an original functional unit is partitioned into two parts, viz., a significantly accurate part and a less significant accurate part, although the parts remain connected. This method of dividing a functional unit into two parts based on their significance is feasible for both arithmetic and logic circuits. Concerning arithmetic circuits, one of the parts would be inherently significant while the other part would be less significant, depending on the weighted impact of the corresponding part’s output on the primary output. According to VRPR, TMR is applied to the significant part, while the less significant part is retained as a simplex implementation. Thus, in a VRPR implementation, the less significant part of a functional unit is left unprotected. VRPR, therefore, offers only moderate fault tolerance capability compared to TMR. Consequently, if the less significant part is affected by bit upset(s), it may have an undesirable impact on the overall output, although this issue was not properly analyzed in [13]. The usefulness of VRPR for a practical application was also not demonstrated in [13].
3. Comparative Analysis of TMR and VRPR for a Practical Application
This section provides a comparative analysis of the performance of TMR and VRPR for a practical application, viz., DIP. However, before that, the architectures of TMR and VRPR will be discussed for better understanding. Representative architectures of TMR and VRPR are shown in Figure 1a and Figure 1b respectively.
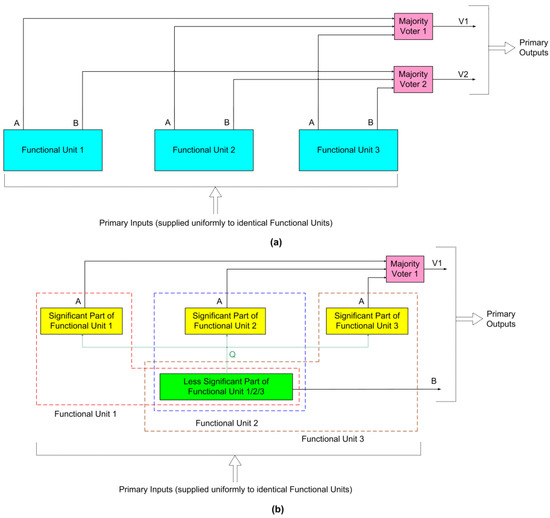
Figure 1.
Block diagram representations of (a) TMR architecture, and (b) VRPR architecture.
According to the TMR architecture shown in Figure 1a, three identical functional units 1, 2, and 3 are used. Each functional unit is assumed to produce two outputs, namely A and B, and all the functional units are supplied with the same primary inputs. It is also assumed that A is more significant than B. This assumption would not be difficult to comprehend for an arithmetic circuit. For example, a binary full adder adds two input bits along with any carry input and produces a sum bit and any carry overflow bit, where the carry overflow bit is deemed more significant than the sum bit.
The functional units’ corresponding outputs A and B are voted on using majority voters 1 and 2 in Figure 1a. Assuming X, Y, and Z are inputs to a majority voter, its output is expressed by the Boolean relation V = XY + YZ + XZ. Different majority voter designs are given in [14]. In Figure 1a, V1 and V2 not only denote the outputs of majority voters 1 and 2 but also the primary outputs of the TMR implementation.
Figure 1b shows the architecture of VRPR. According to VRPR, the significant part of a functional unit is implemented alone in triplicate, while the less significant part of the functional unit is implemented in a simplex fashion. The less significant part may be connected to the triplicated significant parts, and these connections are shown in dotted lines in green in Figure 1b. The connection between the significant parts and the less significant part is dependent upon how a functional unit is divided, but more importantly, the integrity of the original functional unit should be maintained. Assuming there is a connection between the significant parts and the less significant part of a functional unit, the intermediate output Q produced by the less significant part of the functional unit is given to all the triplicated significant parts. The composition of functional units 1, 2, and 3 is shown within the red, blue, and brown dashed boxes in Figure 1b, respectively. Since the significant part of a functional unit is alone triplicated, output A is alone voted using majority voter 1, and V1 and B (which is the output of the less significant simplex part) together represent the primary outputs of the VRPR implementation. Since the less significant part of a functional unit has not been triplicated, and given the absence of majority voter 2, VRPR would consume less area and dissipate less power than a TMR implementation.
In [13], an adder was implemented according to the VRPR scheme. Hence, though we consider DIP as an example application in this paper, to comparatively evaluate the performance of TMR and VRPR, we exclusively focus on the adder functionality. We also consider the adder a functional unit for the physical implementation of TMR and VRPR. Reference [13] suggests dividing an adder (which represents the functional unit) into two equal parts, with one part being significant and the other part being less significant. However, the carry input from the less significant adder part is given to the significant adder part to maintain the integrity of the adder. Hence, according to VRPR, concerning Figure 1b, a 32-bit adder with inputs, say, X[31:0] and Y[31:0] is split into a significant part having inputs X[31:16] and Y[31:16], and a less significant part having inputs X[15:0] and Y[15:0], and the significant part is alone triplicated. Thus, in Figure 1b, output A would represent SUM[32:16], which is the sum output by the significant adder part that is majority voted (requiring 17 majority voters), and output B would represent SUM[15:0], which is the sum output by the less significant adder part. Q represents the carry output of the less significant adder part that is forwarded as the carry input to the significant adder part.
Reference [13] hypothesized that if Q experiences a single-bit upset (SBU), that would not affect the output of the significant adder part much, as the sum output of the significant adder part would be less accurate by just an integer 1 if Q is affected. However, Ref. [13] did not consider the impact on the overall sum output when Q is affected, particularly when small to medium-sized inputs are added. To give an example, let us consider an addition where 018Fh is added to 018Fh. According to VRPR, in the significant adder part, 01h is added to 01h, and in the less significant adder part, 8Fh is added to 8Fh. The carry output of the less significant adder part would be 1, which represents the value of Q in Figure 1b. Supposing Q is affected due to radiation, resulting in Q becoming 0 instead of 1 (representing an SBU), the final sum output of the VRPR adder would be 021Eh (542 in decimal), whereas the actual sum output of the adder should be 031Eh (798 in decimal), resulting in a difference of 256 in decimal, thus causing an error in the total sum by 32%, which is considerable. We noted that for the addition of large numbers, any impact on Q may not affect the total sum much, but when small to medium-sized numbers are added, an impact on Q due to an SBU might substantially affect the sum output. This issue with VRPR was not analyzed in [13], and the impact of this issue on a practical application was also not studied.
To validate our insights, we considered DIP a practical application that utilizes fast Fourier transform (FFT) and inverse FFT (IFFT). For experimentation, we considered many 8-bit grayscale images with a spatial resolution of 512 × 512 [15]. Each original image was converted into a matrix and subsequently subjected to FFT computation. The image was then reconstructed by performing an IFFT computation. Throughout the process of FFT and IFFT computations, precise integer calculations were executed, and a constant scaling factor was used to up-scale the inputs given to the FFT operation and down-scale the inputs given to the IFFT operation to maintain data integrity and ensure that no data loss or overflow occurred in the computations. Accurate multiplication was employed for FFT and IFFT computations, while the addition was carried out using a precise 32-bit adder for both TMR and VRPR architectures. In implementing VRPR, the impact of the carry input to the significant adder part getting affected due to radiation (representing an SBU) has been captured. The results of MATLAB-based DIP corresponding to VRPR with the internal carry input not affected and the internal carry input affected either way are shown in Figure 2, with the adder split into two equal parts, as suggested in [13].

Figure 2.
Example digital images processed using a VRPR adder. In each image, “(a) Accurate” corresponds to a VRPR adder with no SBU of the internal carry input, and “(b) Half split carry 0” and “(c) Half split carry 1” imply that a 32-bit VRPR adder was split into two equal parts as suggested in [13] (implying ‘half split’), with the carry input to the significant 16-bit adder part stuck at 0 and 1, respectively, due to a radiation impact representing an SBU. Thus, if the internal carry input of an equally partitioned VRPR adder is affected either way due to an SBU, it is found to result in the corruption of images.
Peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) were used to quantify the quality of processed images. PSNR is a general metric used in digital signal processing [16], while SSIM is a specific metric used for digital image processing [17]. Both PSNR and SSIM are computed for all the images. The ideal value of PSNR is ∞, and the ideal value of SSIM is decimal 1—these are achieved for a TMR implementation regardless of any SBU and for a VRPR implementation when the internal carry input does not experience an SBU. PSNR and SSIM for the images corresponding to VRPR when the internal carry input is affected either way (i.e., becoming binary 0 when it should be binary 1, and becoming binary 1 when it should be binary 0 due to a radiation impact representing an SBU) are also provided in Figure 2.
From Figure 2, it is evident that the splitting up of a VRPR adder into two equal parts, as suggested in [13], is not universally suitable for practical applications, as demonstrated here in the case of DIP. Therefore, a functional unit, according to VRPR, must be split commensurate with a target application. To substantiate this observation, we considered splitting up a VRPR adder into two adder parts of different sizes and then repeating the DIP discussed previously. The results of the repeated experimentation are shown in Figure 3 for an example image (cameraman).

Figure 3.
Example digital image (cameraman) processed using VRPR adders containing different sizes of significant and less significant adder parts, with the carry input to the significant adder part provided by the less significant adder part. (a) and (b) correspond to a 32-bit VRPR adder having a 26-bit significant part and a 6-bit less significant part with the internal carry input stuck at binary 0 and 1, respectively, due to an SBU. (c) and (d) correspond to a 32-bit VRPR adder having a 24-bit significant part and an 8-bit less significant part with the internal carry input stuck at binary 0 and 1, respectively, due to an SBU. (e) and (f) correspond to a 32-bit VRPR adder having a 22-bit significant part and a 10-bit less significant part with the internal carry input stuck at binary 0 and 1, respectively, due to an SBU. (g) and (h) correspond to a 32-bit VRPR adder having a 16-bit significant part and a 16-bit less significant part with the internal carry input stuck at binary 0 and 1, respectively, due to an SBU; (g,h) were also shown in Figure 2.
From Figure 3, it is seen that a 32-bit VRPR adder split into a 26-bit significant part and a 6-bit less significant part or into a 24-bit significant part and an 8-bit less significant part enables the production of images with acceptable quality, as evident from Figure 3a–d, despite the internal carry input experiencing an SBU either way. When the VRPR adder features a 22-bit significant part and a 10-bit less significant part, an SBU of the internal carry input is found to affect the resulting images, as seen in Figure 3e,f, rendering the images unacceptable due to degradation of quality. According to VRPR [13], after splitting up a functional unit into two parts, the significant part is triplicated while the less significant part is retained as simplex. Therefore, it is desirable to have a maximum acceptable size for the less significant part so that the savings in hardware and design metrics can be maximized for a VRPR implementation. In addition, as suggested in [13], an arbitrary partitioning of a functional unit into two halves is unlikely to suit a practical application. Rather, it would be pragmatic to determine the optimum partition suitable for a practical application. For the DIP application considered here, splitting a 32-bit VRPR adder into a 24-bit significant adder part and an 8-bit less significant adder part was found to achieve an acceptable tradeoff between the resulting image quality (as seen in Figure 3c,d) and the savings in hardware for a physical implementation. The results of DIP utilizing a 32-bit VRPR adder split into a 24-bit significant sub-adder and an 8-bit less significant sub-adder are shown in Figure 4 for many images, which confirms our finding.

Figure 4.
Example images processed using a 32-bit VRPR adder comprising a 24-bit significant part and an 8-bit less significant part. In each image, “(a) Accurate” corresponds to a VRPR adder with no SBU of the internal carry input, which would be the same obtained using a TMR adder (regardless of any SBU), and “(b) Eight bit split carry 0” and “(c) Eight bit split carry 1” indicate that the internal carry input to the significant adder part is stuck at 0 and 1, respectively, due to a radiation impact representing an SBU; nevertheless, the resultant images are of acceptable quality.
Given the acceptable quality of images presented in Figure 4, for a hardware implementation, we considered a 32-bit adder, a 32-bit TMR adder, and a 32-bit VRPR adder featuring a 24-bit significant adder part and an 8-bit less significant adder part. All these adders were structurally described in Verilog HDL based on a carry look-ahead adder (CLA) topology [18] and synthesized for high speed using a 28-nm CMOS standard cell library [19] using Synopsys Design Compiler. The total area of the adders, including the area of the cells and interconnect area, was estimated using Design Compiler. To verify the functionality of the synthesized adders, simulations were performed using Synopsys VCS by supplying a test bench containing about 1000 random inputs, supplied at a latency of 2ns, i.e., at an input frequency of 500 MHz. A typical low-leakage, high Vt library specification with a supply voltage of 1.05 V and an operating temperature of 25 °C was considered for synthesis. The switching activity of the adders recorded from the functional simulations was subsequently used for power estimation. The total power dissipation of the adders was estimated using Synopsys PrimePower, and the critical path delay of the adders was estimated using Synopsys PrimeTime. A default wire-load model was considered for the synthesis and estimation of the design metrics. A fan-out-of-4 drive strength was associated with all the sum bits of the adders. The design metrics estimated are given in Table 1.

Table 1.
Design metrics of simplex and redundant 32-bit adders, realized using a 28-nm CMOS standard digital cell library.
From Table 1, it is seen that compared to the redundant adders, the simplex adder (i.e., CLA) has reduced delay, area, and power, which is understandable due to no redundancy; however, the simplex adder is not fault-tolerant. Compared to the simplex adder, the TMR adder has a higher delay, and this is due to the introduction of the majority voter in the critical data path, which is absent in the simplex adder. Since the simplex adder is triplicated and combined with majority voters to realize the TMR adder, the TMR adder occupies 232% more area and dissipates 218% more power than the simplex adder. The VRPR adder considered for implementation has a 24-bit significant part, which is triplicated, and an 8-bit less significant part, which is implemented as simplex. Since the latter part is not triplicated in contrast to TMR, the VRPR adder requires 15% less area and dissipates 15% less power than the TMR adder. The delay of the VRPR adder is slightly greater than that of the TMR adder, and this is owing to the loading effect on the internal carry output (i.e., the carry output produced by the less significant adder part, which is provided as the carry input to the triplicated more significant adder parts). Compared to the simplex adder, the VRPR adder has 44.6% more delay, requires 183% more area, and dissipates 170% more power.
The product of power and delay, also called the power-delay product (PDP), is a well-known low-power figure-of-merit for digital logic designs. Since power and delay are desirable to minimize, PDP is also best minimized. Since it is welcome to achieve less area occupancy, the product of power, delay, and area, also called the power-delay-area product (PDAP), is best minimized. We calculated PDP and PDAP for the different adders and normalized these figures of merit by dividing the PDP and PDAP values of each adder with the highest corresponding PDP and PDAP values of the TMR adder since the TMR adder has the highest PDP and PDAP compared to its counterparts. The normalized figures of merit are plotted in Figure 5, where the normalized PDP is highlighted by the blue bars and the normalized PDAP is highlighted by the orange bars. PDP and PDAP values of 1 denote an inferior design in terms of the design metrics.
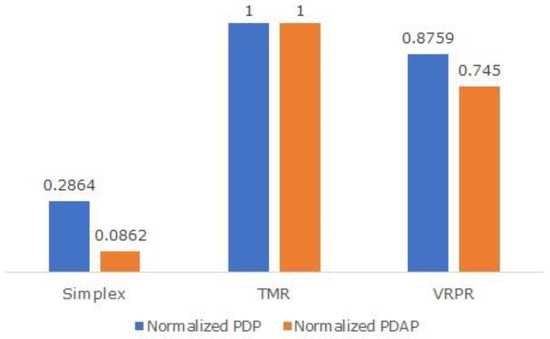
Figure 5.
Normalized figures of merit corresponding to simplex and redundant adders.
From Figure 5, it is seen that the simplex adder (CLA) has the least PDP and PDAP, which is understandable since it is non-redundant, but the simplex adder is not fault-tolerant. Compared to the TMR adder, the VRPR adder has a 12.4% reduced PDP and a 25.5% reduced PDAP. From the image processing results shown in Figure 4, the design metrics given in Table 1, and the normalized figures of merit plotted in Figure 5, it is concluded that the VRPR adder is preferable to the TMR adder. Hence, VRPR could be a potential alternative to TMR for naturally error-tolerant applications.
4. Conclusions
Electronic functional units used in safety-critical applications such as space, aerospace, etc. usually incorporate redundancy in their designs to overcome likely faults or failures. In mission-critical applications such as space, the functional units are subjected to a harsh environment, and therefore they are highly likely to be impacted by radiation, which underlines the need for fault tolerance. At the same time, the functional units are expected to be compact, i.e., requiring less area, as that would augur well for optimizing the cost and design metrics. Conventionally, TMR, which is a subset of NMR, is a popular and widely used redundancy technique that guarantees complete tolerance for a single fault or failure of a functional unit. However, at the functional unit level, TMR requires two extra functional units and a majority voting logic, which results in an increase in the area and power overheads of a redundant implementation by over 200% compared to a simplex implementation. To decrease the design overheads of TMR, alternative redundancy approaches such as STMR, PATMR, and FATMR were put forward in the literature, but they do not guarantee the same assured fault tolerance as the TMR scheme for the entire functionality. VRPR is another alternative redundancy scheme that promises only moderate fault tolerance compared to TMR but is suitable for naturally error-tolerant applications such as digital signal processing, which is commonly used in space systems. However, the limitations of VRPR were not ascertained, and the usefulness of VRPR was not validated for a practical application in the literature.
In this paper, we have analyzed various alternative redundancy schemes to TMR. Among the alternatives to TMR, we found VRPR to be promising, especially for naturally error-tolerant applications. Nevertheless, we found the suggestion of equally splitting a functional unit into two halves for a VRPR implementation to be rather naïve. Going further, we carefully and extensively analyzed the suitability of a VRPR implementation for a practical application, viz., DIP. VRPR could be a potential alternative to TMR in terms of yielding an acceptable image quality while reducing the design metrics. For the DIP application considered, VRPR enabled approximately 15% savings in area and power compared to TMR, but VRPR does not guarantee 100% tolerance to a single fault such as TMR. Furthermore, VRPR may not be suitable for error-intolerant application(s), or the implementation of control logic. The insights and experimental results provided in this work could serve as a useful reference for a researcher/practitioner in fault-tolerant design.
Funding
This research received no external funding.
Data Availability Statement
Acknowledgments
The author wishes to thank Raunaq Nayar for his assistance in obtaining the image processing results.
Conflicts of Interest
The author declares no conflict of interest.
References
- Miskov-Zivanov, N.; Marculescu, D. Multiple transient faults in combinational and sequential circuits: A systematic approach. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2010, 29, 1614–1627. [Google Scholar] [CrossRef]
- Baumann, R.C. Radiation-induced soft errors in advanced semiconductor technologies. IEEE Trans. Device Mater. Reliab. 2005, 5, 305–316. [Google Scholar] [CrossRef]
- Rossi, D.; Omaña, M.; Metra, C.; Paccagnella, A. Impact of aging phenomena on soft error susceptibility. In Proceedings of the IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems, Vancouver, BC, Canada, 3–5 October 2011. [Google Scholar]
- Seifert, N.; Slankard, P.; Kirsch, M.; Narasimham, B.; Zia, V.; Brookreson, C.; Vo, A.; Mitra, S.; Gill, B.; Maiz, J. Radiation-induced soft error rates of advanced CMOS bulk devices. In Proceedings of the IEEE International Reliability Physics Symposium, San Jose, CA, USA, 26–30 March 2006. [Google Scholar]
- Mahatme, N.N.; Bhuva, B.; Gaspard, N.; Assis, T.; Xu, Y.; Marcoux, P.; Vilchis, M.; Narasimham, B.; Shih, A.; Wen, S.-J.; et al. Terrestrial SER characterization for nanoscale technologies: A comparative study. In Proceedings of the IEEE International Reliability Physics Symposium, Monterey, CA, USA, 19–23 April 2015. [Google Scholar]
- Balasubramanian, P.; Maskell, D.L.; Mastorakis, N.E. Majority and minority voted redundancy for safety-critical applications. In Proceedings of the 61st IEEE International Midwest Symposium on Circuits and Systems, Windsor, ON, Canada, 5–8 August 2018. [Google Scholar]
- Ban, T.; Naviner, L. Progressive module redundancy for fault-tolerant designs in nanoelectronics. Microelectron. Reliab. 2011, 51, 1489–1492. [Google Scholar] [CrossRef]
- Quinn, H.; Graham, P.; Krone, J.; Caffrey, M.; Rezgui, S. Radiation-induced multi-bit upsets in SRAM-based FPGAs. IEEE Trans. Nucl. Sci. 2005, 52, 2455–2461. [Google Scholar] [CrossRef]
- Sielewicz, K.M. Mitigation Methods Increasing Radiation Hardness of the FPGA-Based Readout of the ALICE Inner Tracking System. Ph.D. Thesis, Faculty of Electronics and Information Technology, Warsaw University of Technology, Warszawa, Poland, 2018. Available online: https://cds.cern.ch/record/2643800/files/CERN-THESIS-2018-193.pdf (accessed on 26 May 2023).
- Ruano, O.; Maestro, J.A.; Reviriego, P. A methodology for automatic insertion of selective TMR in digital circuits affected by SEUs. IEEE Trans. Nucl. Sci. 2009, 56, 2091–2102. [Google Scholar] [CrossRef]
- Gomes, I.A.C.; Martins, M.G.A.; Reis, A.I.; Kastensmidt, F.L. Exploring the use of approximate TMR to mask transient faults in logic with low area overhead. Microelectron. Reliab. 2015, 55, 2072–2076. [Google Scholar] [CrossRef]
- Arifeen, T.; Hassan, A.S.; Moradian, H.; Lee, J.A. Input vulnerability-aware approximate triple modular redundancy: Higher fault coverage, improved search space, and reduced area overhead. Electron. Lett. 2019, 54, 934–936. [Google Scholar] [CrossRef]
- Ullah, A.; Reviriego, P.; Pontarelli, S.; Maestro, J.A. Majority voting-based reduced precision redundancy adders. IEEE Trans. Device Mater. Reliab. 2018, 18, 122–124. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Mastorakis, N.E. Power, delay and area comparisons of majority voters relevant to TMR architectures. In Proceedings of the 10th International Conference on Circuits, Systems, Signal and Telecommunications, Barcelona, Spain, 13–15 February 2016. [Google Scholar]
- Available online: https://imageprocessingplace.com/root_files_V3/image_databases.htm (accessed on 13 February 2023).
- Bovik, A.C. Handbook of Image and Video Processing, 2nd ed.; Academic Press: Orlando, FL, USA, 2005. [Google Scholar]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar]
- Balasubramanian, P.; Mastorakis, N.E. High-speed and energy-efficient carry look-ahead adder. J. Low Power Electron. Appl. 2022, 12, 46. [Google Scholar] [CrossRef]
- Synopsys SAED_EDK32/28_CORE Databook. Revision 1.0.0. January 2012. Available online: https://www.synopsys.com/academic-research/university.html (accessed on 4 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).