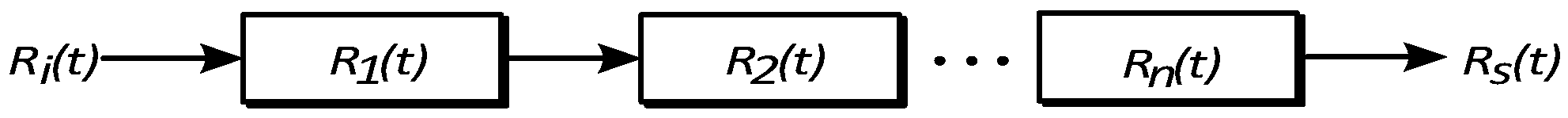Photovoltaic Inverter Reliability Study through SiC Switches Redundant Structures

Abstract

Reliability is a very important issue in power electronics; however, sometimes it is not considered, studied, or analyzed. At present, renewables have become more popular, and more complex setups are required to drive this type of system. In the specific case of inverters in photovoltaic systems, the user’s safety, quality, reliability, and the system’s useful life must be guaranteed. In this paper, the reliability of a full bridge inverter is predicted by calculating metrics such as failure rates and Mean Time Between Failures. Reliability is obtained using different types of structures for SiC MOSFETs: serial systems, active parallel redundant systems, and passive parallel redundant systems. Finally, the reliability study shows that a system with a passive parallel redundant structure is more reliable and has a higher useful life compared to the other structures.

1. Introduction

Nowadays, it is of vital importance to have systems with high reliability. Systems with higher tolerances to failures caused by internal or external interferences to the system are required. These should comply with the characteristics of reliability. Safety is focused on the operational aspect, and the system needs to be in continuous operation and to have a good response in case of unstable conditions. Quality refers to the service provided to the user, and it must satisfy the appropriate electrical characteristics [1].

It is very usual to listen to the adverse effects on the environment caused by the generation and use of conventional energies, such as fossil fuels and nuclear energy. In recent years, alternative energy sources have been significantly developed, such as wind energy and solar energy, contributing to reducing CO₂ emissions and the greenhouse effect [1,2].

At present, photovoltaic solar energy is one of the most popular. There are geographic areas with a high solar concentration. In addition, it presents the best relation to the cost of energy produced [3].

Photovoltaic systems include arrays of panel modules, a Maximum Power Point Tracking (MPPT) stage, the DC–AC power conversion stage (inverter), and the filtering/coupling to the grid stage [4].

Transformerless photovoltaic inverters are complex power electronic converters. These are of critical importance because they must supply the appropriate electrical characteristics to deliver active power to the grid. They can present reliability problems and a decreased useful life. An adequate component-level operation would improve the reliability of each component while improving the inverter and the photovoltaic system’s overall reliability [2].

Recent studies reported that MOSFETs are among the most critical devices in inverters. MOSFETs are devices that are characterized by presenting higher failure rates and lower reliability. Previous studies have shown that thermal and electrical stress during switching results in higher losses, provoking a higher failure rate and a reliability reduction in the system in general [5,6].

Different methodologies for the reliability analysis of systems have been studied, based on the evaluation of qualitative characteristics and quantitative parameters. Reliability tests can be classified into different types, some of them measuring and demonstration techniques, based on estimated and statistical data, to approximate the degree of reliability. Parameter variation measurement evaluates the degree of stresses affecting or deteriorating the different components, potentially causing a failure. Additionally, failure mechanisms are evaluated to identify the causes of the physical degradation of components [6,7,8].

Methods that use techniques, tools, and physical/mathematical models with the assistance of computer analysis enable the evaluator to validate a product [7]. The most common employed standards for reliability analysis are from MIL-HDBK-217F [6,8]. They are performance tests to determine if a system operates adequately under specific operating conditions. Stress and environmental tests also exist for the analysis of electronic systems, such as inverters.

The MIL HDBK-217F standards are used, which contain statistical data on failure rates and models for different electronic components [9,10,11,12]. These standards consider a method traditionally used in electronics for measurement and reliability demonstration, was published by the Department of Defense of the United States of America, and it originated after the Second World War to analyze the failures of military electronic equipment [9].

The papers dealing with reliability usually make studies for specific topologies reported in the literature [10,11,12,13,14], but they do not consider the different configuration that a power device should have.

Other standards that are regularly used are from the IEC TR 62380, which is based on the mission profile. This defines the phases and operating environments in which an equipment or system regularly operates. Other studies based on this standard determine which traditional single-phase inverter topologies are the most reliable. The two standards are characterized by using the same metrics and a component stress model for the reliability calculation [14].

According to the literature, the use of coupled systems in structures for different purposes has been proposed. In [5], the authors created hybrid modules with different types of power transistors. Other authors in [15] proposed series connection MOSFETs in order to increase the voltage and support more voltage than any device alone. Other authors in [16] used parallel coupling to increase the nominal current and support more power. However, the reliability of different coupling structures is ignored.

These structures can cause triggering problems, thermal and electrical unbalances, inadequate current and voltage distributions, etc. These factors would cause degradation; the reliability and useful life of devices and systems is reduced.

In another reliability study [17], authors developed a high-reliability photovoltaic inverter with a hybrid power module formed by a Si-IGBT with a SiC anti-parallel diode. They considered an annual mission profile of ambient temperature and solar irradiation at two different locations, giving positive results. To calculate reliability, they used the Monte Carlo simulation method, Weibull distribution, and Miner’s rule.

In [18], the authors analyzed a methodology for calculating reliability, a modular multilevel ANPC inverter, and a fault-tolerant control strategy. The system presented redundancy in the inverters, and, in this way, a failure does not globally affect the performance of the system; the reliability of the system depends on the load. A mission profile and Markov model were used, and the failure rate and the junction temperature were related using the MIL HDBK-217F standard.

All these studies also do not analyze the different redundant structures that can be used in switching devices. The redundancy of systems is more economically expensive than the redundancy in specific devices. In this case, the most critical are the MOSFETs. Due to this, the reliability study of different structures can be made to give an approach that is the most appropriate in photovoltaic systems.

In this paper, a comparative analysis of the reliability of the full-bridge inverter is presented, using different structures in the MOSFET device, such as the serial system, active parallel redundant system, or passive parallel redundant system; this is made to determine the best option based on reliability. The analysis is based on the calculation of the failure rate and in the Mean Time Between Failure (MBTF) indicators for each component, which are adjusted using the component stress model of the MIL HDBK-217F standard. This study can be summarized into:

• The reliability analysis of the full bridge inverter with different structures showed that the system presented the best reliability and useful life using a passive parallel redundant structure.
• The redundancy of the switching components in the system with a passive parallel structure allowed a substantial increase of up to 75% in the reliability of the system.
• The use of SiC switches contributed to increased system reliability due to the material’s performance, such as lower internal resistance and better thermal conductivity. This contributed to reducing switching problems, losses, and, therefore, allows a better thermal balance, higher reliability, and longer useful life.

2. Reliability Theory

Reliability analysis and prediction is a topic concerning modern electronics. Manufacturers and researchers of equipment focus on the economic and technical effects of equipment failures. A reliability study is based on the analysis of failure rates in components or equipment.

Recently, the reliability problem has been increasing due to the technical complexity of electronic systems. In modern systems, the origin of failures is due to several reasons, e.g., systems include n components, the operating conditions are more extreme, and access to maintenance is more complicated, among many others.

Reliability analysis terms and methodologies are important considerations, which are described below.

2.1. Reliability

Reliability is defined as the probability that an electronic system or component will satisfactorily perform the function that has been designed for during a determined period under specific experimental conditions and survive [10,12,19,20]. It is represented as R(t), which is given by (1), and signifies the values reached by a random variable R at t ϵ [0, ∞]. Where λ is the risk of failure of a component in operation.

$$R\left(t\right)=1-F\left(t\right)=\underset{0}{\overset{t}{\int }}f\left(t\right)dt,$$

(1)

where f(t) is a failure density function. t is the time when the component will fail. Finally, F(t) is the cumulative distribution function.

When an electronic component or system presents a risk of failure, it is called a failure rate. This variable is defined by:

$$\lambda \left(t\right)=\frac{f\left(t\right)}{1-F\left(t\right)}=\frac{f\left(t\right)}{R\left(t\right)}$$

(2)

Consequently, the time elapsed before the first failure occurs, given it has survived for a time t ϵ [0, ∞], is called the Mean Time Between Failures (MTBF) and is denoted by [10,12,19,20]:

$$MTBF=\underset{0}{\overset{t}{\int }}R(t)dt$$

(3)

The exponential probability distribution is used in electronic components in devices that have overcome the initial useful life t > 0. The density function of the exponential distribution is:

$$f(t)=\lambda e^{-\lambda t}$$

(4)

An electronic component has its own λ = constant.

The reliability function for electronic devices is given in (5). It is obtained by substituting (4) into (1) and integrating from t ϵ [0, ∞].

$$R\left(t\right)=e^{-\lambda t}$$

(5)

The MTBF for the exponential distribution is shown in (6). It is obtained by substituting (5) into (3) and integrating from t ϵ [0, ∞].

$$MTBF=\frac{1}{\lambda }$$

(6)

2.2. Reliability Structures

Reliability is considered a stochastic process since it is not considered deterministic; however, it is a random phenomenon, where the later predicted result depends on past conditions.

Electronic systems are composed of a great number of internal components; they are interrelated through different structures. For the reliability analysis of the system, these are divided into subsystems and can be depicted as block diagrams as follows.

The structures to be analyzed are the series system, active parallel redundant system, and passive parallel redundant system. Each block represents a unit or component.

For a serial system to properly operate, as shown in Figure 1, all blocks must work properly; if a single component fails, the complete system will fail.

A system presents a catastrophic failure when any one of the subsystems fails before the process is completed [6,19]:

The reliability of an electronic system is represented by (5), and a serial coupled system is represented as the product of the individual reliabilities in good conditions (7) or the union of the probability of n blocks in good conditions [6,7,10,19].

$$R_S\left(t\right)=R_1(t)\cdot R_2(t)\dots \dots R_n(t)$$

(7)

For an n component electronic system, substituting (5) into (7) results in (8).

$$R_S\left(t\right)=e^{-\left({\lambda }_1+{\lambda }_2+\dots +{\lambda }_n\right)t}$$

(8)

MTBF is represented by (9). It is obtained by substituting the total reliability of the serial system (8) in (3) and integrating

$$MTBF=\frac{1}{\lambda }=\frac{1}{{\displaystyle \sum _{i=1}^n\lambda }}$$

(9)

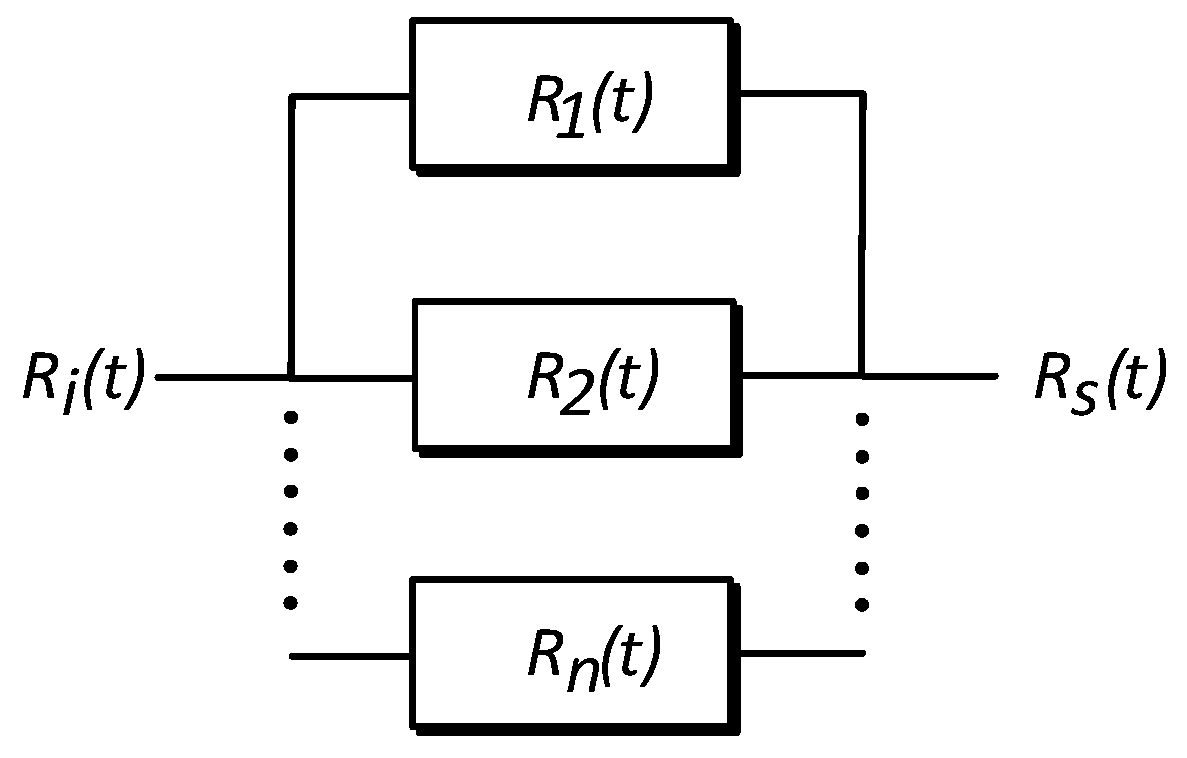
In an active parallel redundant system, as illustrated in Figure 2, one block must be operating properly for the system to succeed; the failure of a block does not imply the catastrophic failure of the system [6,19]:

Therefore, the reliability of a parallel system is the product of n blocks in bad conditions. Reliability is obtained by substituting (1) in (10) and solving, which can be observed in (11).

$$1-R_p\left(t\right)=\left(1-R_1\left(t\right)\right)\cdot \left(1-R_2\left(t\right)\right)\dots \dots \left(1-R_n\left(t\right)\right)$$

(10)

$$R_p\left(t\right)=1-\left(1-R_1\left(t\right)\right)\cdot \left(1-R_2\left(t\right)\right)\dots \dots \left(1-R_n\left(t\right)\right)$$

(11)

Substituting (11) in (2) obtains the failure rate of the system, supposing that each block of the system is equal and identical.

$${\lambda }_i\left(t\right)=1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}$$

(12)

Finally, the MTBF of this system is obtained by substituting (11) in (3), resulting in:

$$MTBF=\frac{1}{\lambda }\left(1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}\right)$$

(13)

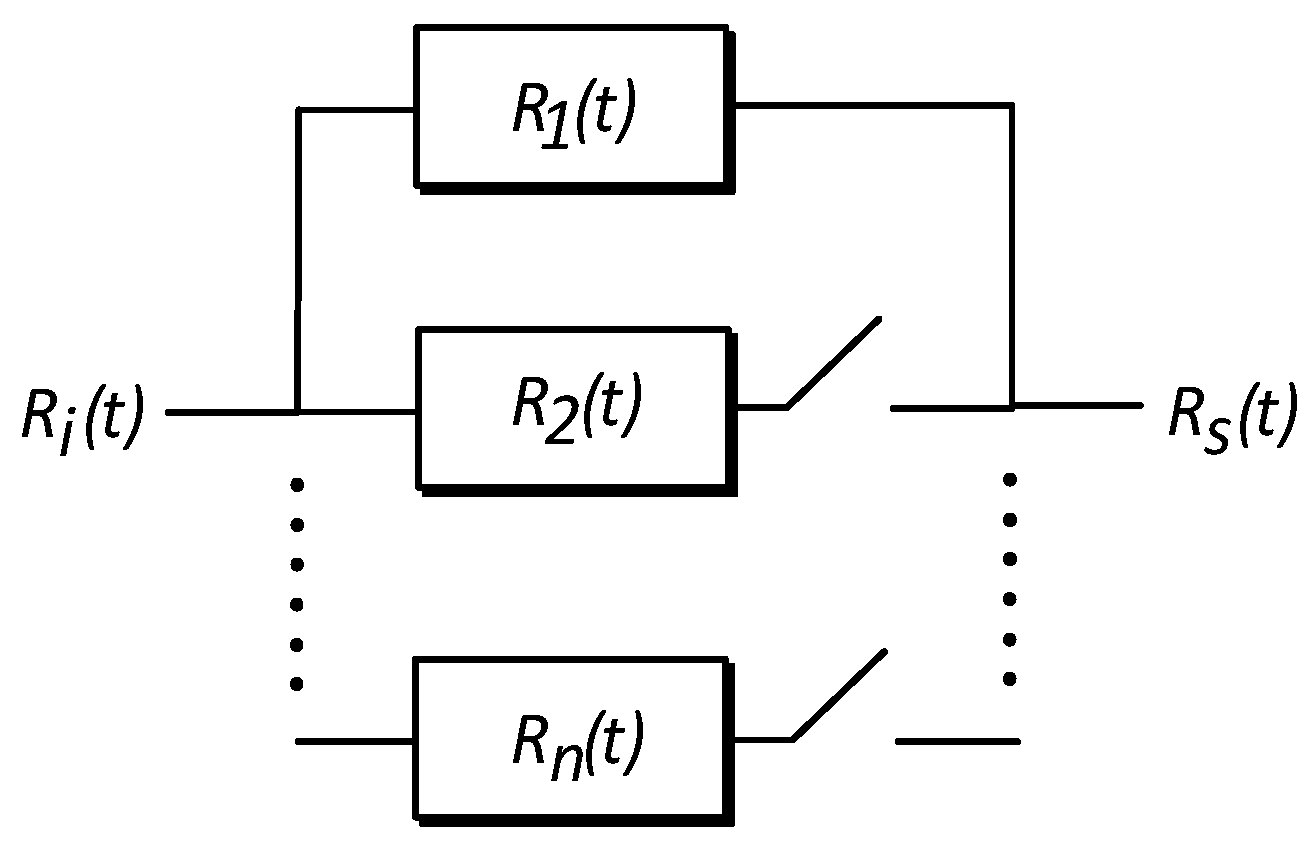
The unrepairable passive redundant parallel system, shown in Figure 3, is similar to the active parallel system. In this case, one block is in operation, while the others are waiting for the first block to fail to start its operation [6,19]:

The reliability of the passive redundant system depends on the Poisson distribution. Where the probability that an event occurs in a given time is determined according to λ, which represents the frequency of occurrence of that event. According to Poisson distribution, the reliability of an n unit system, where (n − 1) units are on standby, is represented by:

$$R\left(t\right)=e^{-\lambda t}{\displaystyle \sum _{r=0}^{n-1}\frac{{\left(\lambda t\right)}^r}{r!}},$$

(14)

where r = 1, 2,…, and n equals the number of components.

By expanding (14), we obtained:

$$R\left(t\right)=e^{-\lambda t}\left[1+\lambda t+\frac{{\left(\lambda t\right)}^2}{2!}\dots \dots \frac{{\left(\lambda t\right)}^{(n-1)}}{(n-1)!}\right]$$

(15)

MTBF of the passive parallel redundant system can be obtained by substituting (15) in (3), giving the result:

$$MTBF=\frac{1}{\lambda }+\lambda \frac{1}{{\lambda }^2}+{\lambda }^2\frac{1}{{\lambda }^3}+\dots +\frac{n}{\lambda }$$

(16)

2.3. Standard MIL HDBK-217F

It is a traditional standard, and the most commonly used is based on the experience and observation of events. It includes databases about failure rate models for different components such as transistors, diodes, etc. Other factors affecting reliability are included based on the operating environments for the telecommunications industry, such as Ground Benign (GB), Ground Fixed (GF), Ground Mobile (GM), etc. It uses the component stress calculation method [6,7,8,9,10,11,12]:

$${\lambda }_p={\lambda }_b\left({\pi }_T,{\pi }_S,{\pi }_C,{\pi }_Q,{\pi }_E,{\pi }_A,{\pi }_{CV}\right),$$

(17)

where λ_P is the adjusted component failure rate, λ_b is the component base failure rate, π_T is the encapsulation temperature factor, π_S is the electrical stress factor, π_C is the construction factor, π_Q is the quality factor, π_E is the environmental factor, π_A is the application factor, and π_CV is the capacitance factor.

Table 1. Mathematical stress model for each component.

Device	Failure Rate Equation
Diode	${\lambda }_p={\lambda }_b\left({\pi }_T.{\pi }_S.{\pi }_C.{\pi }_Q.{\pi }_E\right)$
Transistor	${\lambda }_p={\lambda }_b\left({\pi }_T.{\pi }_A.{\pi }_Q.{\pi }_E\right)$
Inductor	${\lambda }_p={\lambda }_b\left({\pi }_Q.{\pi }_E.{\pi }_T\right)$
Capacitor	${\lambda }_p={\lambda }_b\left({\pi }_Q.{\pi }_E.{\pi }_{CV}\right)$

shows the equations for the adjustment of the failure rate λ_P for each component.

In most components, the factor with the greatest effect on the failure rate is the temperature factor π_T, as shown in the table previously described.

The temperature factor π_T, which has a considerable weight in the failure rate, is presented in (18) based on the Arrhenius model, which indicates the temperature acceleration in the component [6,9,10,11,12,14]:

$${\pi }_T=\exp \left(-\frac{Ea}{k}\left(\frac{1}{T_U+273}-\frac{1}{298}\right)\right),$$

(18)

where E_a is the activation energy in _eV; k is Boltzmann’s constant, equal to 8.617 × 10⁻⁵ _eV/^oK; K is the absolute temperature in Kelvin; and T_U will be the temperature in use.

Table 2. Arrhenius model for each component.

Device	Arrhenius Model
Diode	${\pi }_T=\exp \left(-3091\left(\frac{1}{T_j+273}-\frac{1}{298}\right)\right)$
Transistor	${\pi }_T=\exp \left(-1925\left(\frac{1}{T_j+273}-\frac{1}{298}\right)\right)$
Inductor	${\pi }_T=\exp \left(-\frac{0.11}{0.00008617}\left(\frac{1}{T_{{}^{HS}}+273}-\frac{1}{298}\right)\right)$
Capacitor	${\pi }_T=\exp \left(-\frac{0.15}{0.00008617}\left(\frac{1}{T_a+273}-\frac{1}{298}\right)\right)$

presents the Arrhenius model of MIL HDBK-217F, used for the temperature adjustment of each component, based on environmental conditions.

The temperature factor is directly related to P_loss in the components (8) [5,9,10,11,12,14]. It depends on the junction temperature T_j for MOSFETs, and T_U can be replaced by T_j.

$$T_j=\left(T_C+{\theta }_{jc}\right).p_{loss}$$

(19)

$$P_{loss(static)}=R_{DSon}.I_{rms}^2$$

(20)

$$P_{loss(dynamic)}=V_{avg}.I_{avg}.(t_{on}+t_{off}).f_{SW}$$

(21)

$$P_{loss}=P_{loss(static)}+P_{loss(dynamic)}$$

(22)

where Tc is the case temperature. P_loss is the sum of the static P_loss(static) and dynamic losses P_{loss(dynamic)}. θ_jc is the junction thermal resistance of the package. R_DSon is the internal resistance at the moment of ignition. I_rms represents the effective current. I_avg and V_avg are the average current and voltage values, respectively.

Certain elements such as diodes are directly dependent on the electrical stress factor π_S, and it is a function of V_S in (23). It also depends on the voltage stress ratio in which the component is stressed, which is the ratio of V_a, the applied operating voltage, and the nominal voltage V_n [9,10,12].

$$V_S=\frac{V_a}{V_n}$$

(23)

Therefore, the value that π_S will assume is a function of the following conditions.

π_S = 0.054 if the condition is satisfied: V_S ≤ 0.3.

π_S = $V_S^{2.43}$ if the condition is satisfied: 0.3 < V_S ≤ 0.3.

Adjustment of λ_b on the inductor should be made using (24); it is directly dependent on the temperature T_HS. Therefore, the hot spot temperature T_HS (25) is obtained according to the temperature change in the component ΔT_d, resulting in an average increase in T_a. T_U can be replaced by T_HS and T_a, according to the component to be analyzed [9,10,12].

$${\lambda }_b=0.0016e^{{\left(\frac{T_{HS}+273}{329}\right)}^{15.6}}$$

(24)

$$T_{HS}=T_a+1.1\Delta T_d$$

(25)

The S parameter, shown in (26), corresponds to the capacitor operating voltage ratio [9,10,12] and is directly dependent on the applied voltage V_o and the nominal operating voltage V_n. Substituting S and T_a, the base failure rate for the capacitor, shown in (27), is calculated.

$$S=\frac{V_o}{V_n}$$

(26)

$${\lambda }_b=0.00254\left[{\left(\frac{S}{0.5}\right)}^3+1\right].e^{\left[5.09{\left(\frac{T_a+273}{358}\right)}^5\right]}$$

(27)

The capacitance factor π_CV for the capacitor depends directly on the capacitor value C and is expressed as follows [6,9,10,11,12].

$${\pi }_{CV}=0.34\left(C^{0.18}\right)$$

(28)

Reliability is evaluated with MTBF and failure rate (λ) metrics in units of failures by the unit of time. The MIL-HDBK-217F standards express them as 10⁶ h [9,10,21].

As it is a classical standard based on count and component stress, an average ambient temperature, to which the component is exposed during the operating cycle, is considered. The junction temperature in this case depends on the package temperature and this, in turn, on the average ambient temperature around the equipment. This can be seen in (19) and Table 2. There are other types of accelerated tests that are based on a more controlled environment and a specific mission profile. Power cycles and thermal cycles are defined, and different end-of-life criteria are used. However, an accelerated life test model is presented, based on a junction temperature estimation method similar to the standard, which depends on temperature and changes in ambient temperature. It is still complex to have an accurate estimation of the temperature, which, in turn, would have a higher cost, since it requires the monitoring of several variables [22].

3. Power and Reliability Design

Reliability is a great challenge in power electronics, where it is necessary to consider the effects that failures in the components affect the general system.

For this reason, it is important to have a good design and analysis prior to the manufacturing process, based on technical background and experience, to reduce costs and risks.

Complying with reliability, quality, and durability, it contributes to the continuous improvement and better evaluation of these electronic components and systems.

The reliability design and design of the power stage of the system are realized in the following.

3.1. Reliability Design

Reliability is estimated for a full bridge inverter, considered to be one of the most popular inverters. The advantages are high efficiency, low cost, small size, and low weight. They consist of four switches organized in two legs, one composed of S₁ and S₂ and the other of S₃ and S₄. These can generate four operating states and three different output voltage levels [10,13,14,23].

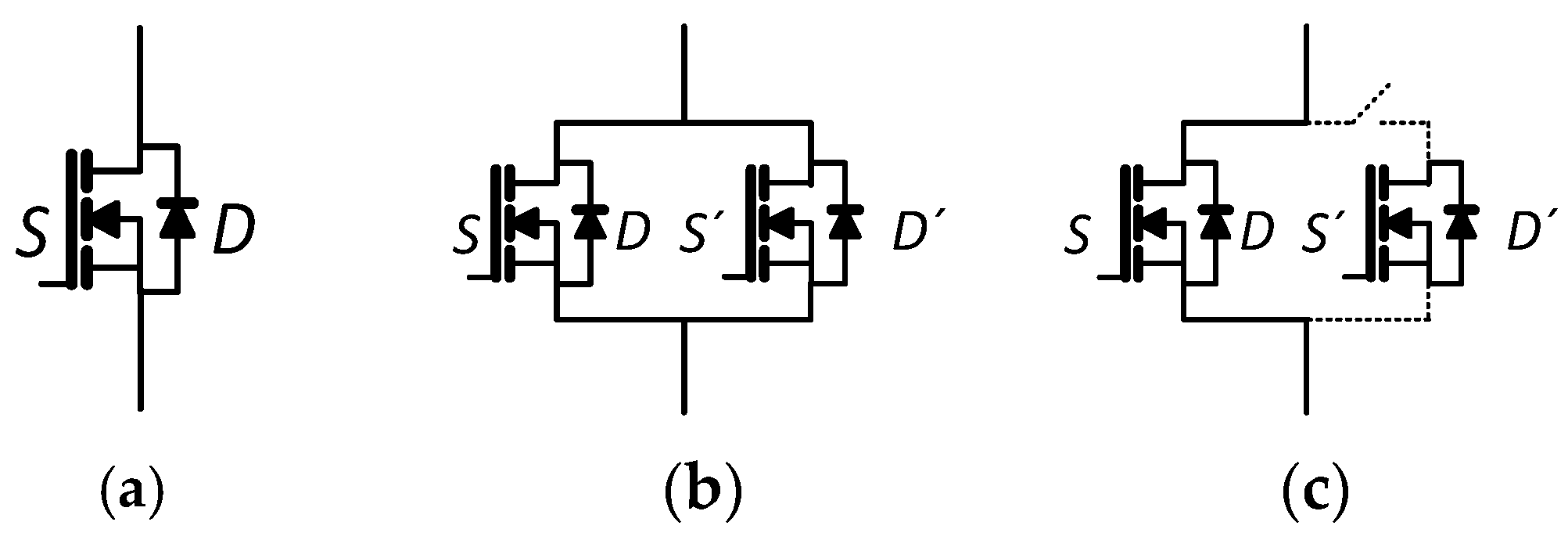
The reliability design was performed using the reliability structures in Figure 1, Figure 2 and Figure 3, where each MOSFET in Figure 4 was equivalent to a block. The analysis with a parallel active structure in Figure 2 is presented as a demonstration of the reliability calculation [6,9,10,11,14]. First, the reliability R_SW1 of the two MOSFETs in parallel is obtained as a single module that includes the reliability of R_S1 y R’_S1, which is similarly performed for each of the MOSFET structures. Following this, the serial model should be used to estimate the overall reliability R_S(t) of the inverter.

Figure 5 presents the full bridge inverter topology considered for an active power injection system to the grid.

Inverter reliability analysis is realized in different steps. The first step consists of the obtaining of the reliability of the module R_Sw1 of two parallel active switches presenting an equal failure rate of λ_S1 = λ’_S1 = λ₁.

From (11), the two-block parallel (29) is applied, and it is reduced algebraically, resulting in (30). Substituting (4) directly in (30) results in (31).

$$R_p\left(t\right)=1-\left[\left(1-R_1\left(t\right)\right)\cdot \left(1-R_2\left(t\right)\right)\right]$$

(29)

$$R_p\left(t\right)=R_1\left(t\right)+R_2\left(t\right)-R_1\left(t\right)R_2\left(t\right)$$

(30)

$$R_p\left(t\right)=1-\left[\left(1-e^{-{\lambda }_{1}t}\right)\cdot \left(1-e^{-{\lambda }_{1}t}\right)\right]$$

(31)

The reliability of two parallel switches is shown in

$$R_p\left(t\right)=2e^{-{\lambda }_{1}t}+e^{-2{\lambda }_{1}t}-\left(e^{-{\lambda }_{1}t}\right)\cdot \left(e^{-{\lambda }_{1}t}\right)=2e^{-{\lambda }_{1}t}+e^{-2{\lambda }_{1}t}$$

(32)

The Mean Time Between Failure of a parallel system is obtained by substituting R_P(t) from (32) in R(t) from (3) and integrating from 0 to t when t = ∞ to obtain (34).

$$MTBF={\displaystyle \underset{0}{\overset{t}{\int }}2e^{-{\lambda }_{1}t}}dt-{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-2{\lambda }_{1}t}}dt$$

(33)

$$MTBF={\left[\frac{2e^{-{\lambda }_{1}t}}{-{\lambda }_1}-\frac{e^{-2{\lambda }_{1}t}}{-2{\lambda }_1}\right]}_0^{\infty }=\frac{2}{{\lambda }_1}-\frac{1}{2{\lambda }_1}$$

(34)

Following the parallel reliability of each module, the global reliability of the inverter is obtained.

The serial block diagram in Figure 1 is used, performing the reliability product of the four switch modules R_SW1(t) = R_SW2(t) = R_SW3(t) = R_SW4(t) = R₁(t), the two inductors R_Lf1(t) = R₂(t) and R_Lf2(t) = R₃(t), and, finally, the capacitor R_Cf(t) = R₄(t). The following assumption is considered. Parallel switch modules R₁(t) are equal and have an equal failure rate, λ_SW1 = λ_SW2 = λ_SW3 = λ_SW4 = λ₁. The inductor failure rate λ_Lf1 is λ_Lf1 = λ₂ for the inductor λ_Lf2 will be λ_Lf2 = λ_3. Finally, the capacitor λ_Cf = λ₄. The block diagram is simplified, and (35) is obtained.

$$R_S\left(t\right)=R_1(t)\cdot R_2(t)\cdot R_3(t)\cdot R_4(t)$$

(35)

$$R_S\left(t\right)={\left(-e^{-2{\lambda }_{1}t}\right)}^4\cdot e^{-{\lambda }_{2}t}\cdot e^{-{\lambda }_{3}t}\cdot e^{-{\lambda }_{4}t}$$

(36)

The global MTBF of the inverter is calculated by replacing the global inverter reliability (36) in (3).

$$\begin{array}{ll}MTBF=& \frac{16}{4{\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4}-\frac{32}{5{\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4}+\frac{24}{6{\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4}\\ & -\frac{8}{7{\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4}+\frac{1}{8{\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4}\end{array},$$

(37)

3.2. Power Stage Design and Simulation

A numerical simulation of the full bridge inverter with an LCL filter, shown in Figure 6, was designed with the parameters of

Table 3. Design parameters.

Parameter	Value
PO	1 kW
Vg	127 Vrms
VPV	200 V
α	3
Lf1	425 µH
Lf2	141 µH
Cf	6.6 nF

as follows. The LCL filter was selected according to previous studies for a ratio of inductances α = 3, resulting in a smaller size and demonstrating higher reliability for that transformation ratio [10].

Silicon carbide MOSFET C3M0065090D parameters were used. They had low on-resistance, permitting higher current flow with a faster switching response. In addition, the thermal balance of the MOSFET reduced the conduction losses [14,24].

The LCL filter design was performed using the methodology proposed in [10,14,23,25].

The following was considered in the design of the filter: 10f₀ ≤ f_res ≤ f_sw. The resonant frequency f_res was between 10 times higher than the grid frequency f₀ and 10 times lower than the switching frequency f_sw.

In the LCL filter design, the two inductors L_f1 and L_f2 and the capacitor C_f are considered. The output voltage V_g in (38) is a function of the supply voltage V_PV and the modulation index m of the inverter.

$$V_g=V_{pv}m$$

(38)

The inductor voltage L_f1 is given by:

$$L_{f1}=\frac{V_{pv}\left(1-m\right)m}{{\Delta }_{iLf1}{f}_{sw}},$$

(39)

where ∆iL_f1 is the inductor’s current ripple.

To obtain L_f2, it is necessary to use the following relation:

$$L_{f1}=\alpha L_{f2},$$

(40)

where α is the inductance ratio for the LCL filter, and α = 3 was selected.

The filter capacitor was selected according to (41), considering ωres as the resonant frequency.

$$C_f=\frac{L_{f1}+L_{f2}}{L_{f1}{L}_{f2}{\omega }_{res}}$$

(41)

The system was simulated in PSIM^® using a unipolar modulation [5,10,26] and silicon carbide MOSFETs C3M0065090D (Manufacturer CREE) [5,14,24].

In this modulation type, the inverter legs switched at a high frequency, permitting high efficiency and small output filter sizes, in addition to producing three voltage levels at the output [5,10,26].

Parameters according to the manufacturer’s technical data sheet were also considered.

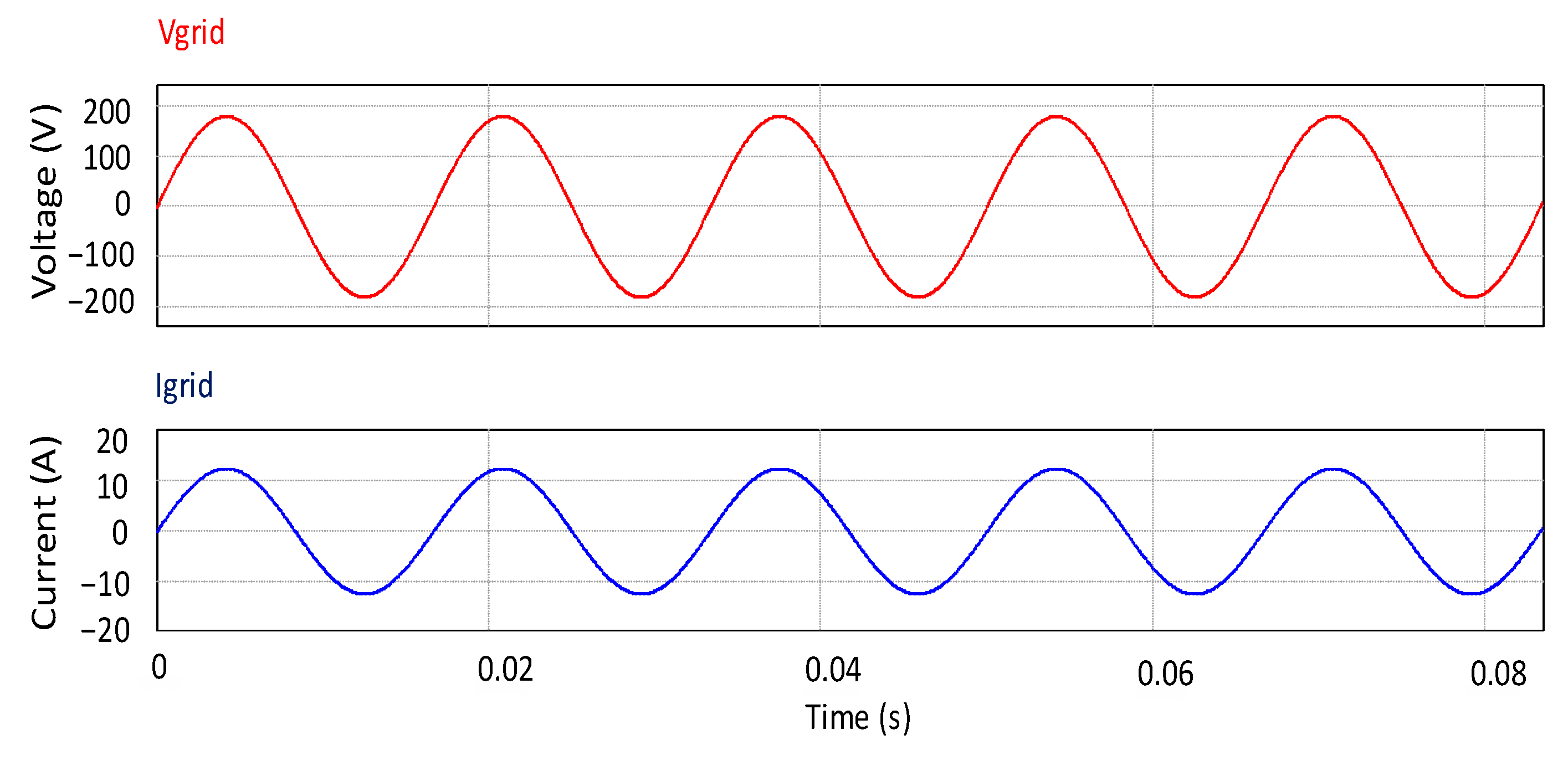
The results showed that the supply of active power to the grid was ensured, given that the voltage of 120 Vrms and a current supplied to the grid of 8.3 Arms were in phase, complying and ensuring the injection of 1 kW of active power to the grid.

4. Reliability Results

The traditional MIL HDBK-217F standard is used for reliability analysis and prediction. Adjustment factors are considered, including the base failure rate, which will result in a component failure rate being adjusted later.

According to the simulation of Section 3.2, the values of average and effective current and voltage are obtained. These values are used for the calculation of the losses and then the junction temperature calculation. This allows us to adjust the temperature factor using the Arrhenius model and, finally, the failure rate in the case of the MOSFET. As a demonstration, the equation used in the calculation of the effective current, which will be used in (20) to calculate the losses, is included.

$$I_{rms}=\sqrt{\frac{1}{T}{\int }_0^{T}i{(t)}^{2}dt}=I_{\max }\sqrt{D},$$

(42)

where i(t) is the instantaneous current and I_max are the maximum current values. T is the signal period. D is the duty cycle.

The system global λ_S(t), MTBF, and R_S(t) were calculated using the traditional standard MIL HDBK-217F. An ambient temperature of 35 °C and an environmental factor (GB) were considered.

Equations (19)–(22) were used to calculate the losses and average values of the voltage and current flows through the switch during switching.

Adjustment factors for the reliability computation of the four full-bridge inverter switches and the LCL filter components are shown in

Table 4. Adjustment factors (MIL HDBK-217F standard).

Device	λb	πT	πA	πQ	πE	πC	πV
Transistor (MOSFET)	0.012	3.6	5.5	8	6	-	-
Inductor	0.00003	1.82	-	3	6	-	-
Capacitor	0.00037	1.209	-	10	10	0.35449	26.17

.

As shown in

Table 5. Reliability of the different structures.

Failure/106 h	Serial	Active Parallel	Passive Parallel
λPM(Each module)	12.34900000	5.962000000	3.087250000
λPI(Ls)	0.000983550	0.000983550	0.000983550
λPC(C)	0.014092541	0.014092541	0.014092541
λSystem(Total)	49.41100000	23.86400000	12.36500000
MTBF	0.020238000	0.041904000	0.080873000

, the analysis presents the total failure rate and the MTBF of the system using the three structures, expressed in failure/10⁶ h.

They were calculated according to the models in Equations (17) to (27) and Table 1, Table 2, and Table 4.

Case 1 (Serial): The MOSFET S₁ was on, the flowing current was 6.26 A_rms, and the failure rate would be 12.349 failure/10⁶ h for the single MOSFET. Case 2 (Active parallel redundant): MOSFETs S₁ and S’₁ in parallel were simultaneously active, the total current flowing was equal to Case 1, but this was divided between the two MOSFETs. As a result, 3.13 A_rms will flow into each switch, causing the losses and failure rate in each MOSFET to be reduced, giving 5.962 failure/10⁶ h for each pair of active switches. Case 3 (passive parallel redundant): S₁ and S’₁ were in parallel. State 0: Only S₁ was active, and S’₁ was on standby. State 1: S₁ failed and, consequently, was deactivated, and S’₁ was activated. Now, the equivalent failure rate of the pair of MOSFETs in passive parallel redundancy was equal to 3.08725 failure/10⁶ h. This was because it presented a double redundancy.

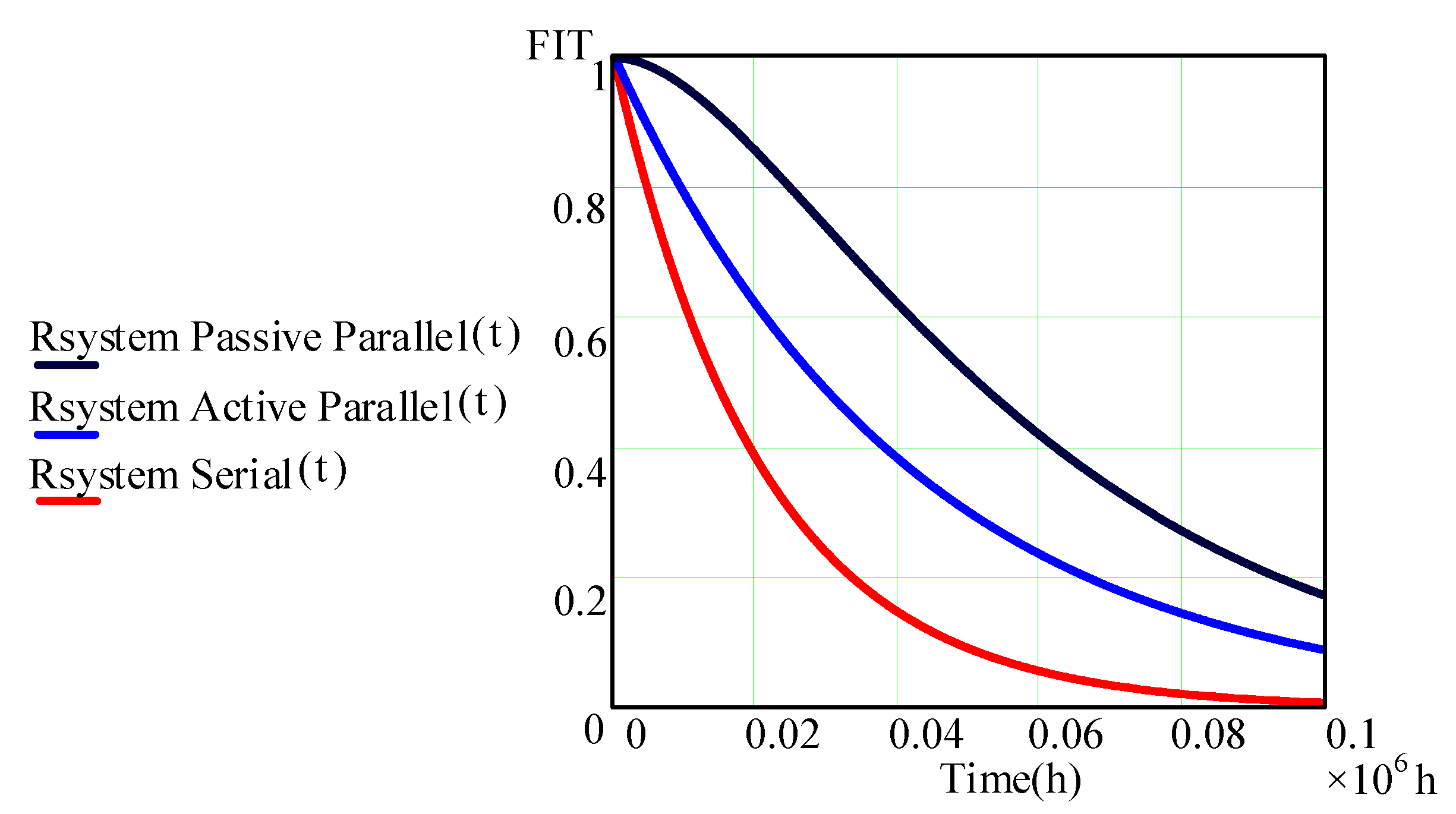
The global failure rate of the system included the four MOSFETs or four pairs of MOSFETs as the situation required, the failure rate of the two inductors, and the failure rate of the capacitor. The passive parallel redundant system presented the best reliability and MTBF. The disadvantage of this system was the increase in cost and volume, given that the number of MOSFETs increased from four to eight. The analysis with passive parallel structure increased the total system reliability by 75%, and the analysis with active parallel structure improved the reliability by 48.29% in comparison with the reliability of the system with one MOSFET. The parallel active redundant structure, as well as the passive, had the same characteristics in terms of weight, cost, and size, since they had the same number of elements. The advantage of the parallel passive redundant structure was the higher reliability.

Figure 7 shows how the passive parallel system presents higher reliability compared to the other two structures, showing the passive parallel system had a higher MTBF, which represented a longer operating time before a first failure occurred. Additionally, it can be observed that the worst reliability and MTBF occurred in the system with one MOSFET.

Figure 8 shows the contribution of the failure rate of each component to the inverter’s global rate. For each structure, it can be observed that the higher contributions are from the MOSFETs with over 99% of the total, the capacitor follows, and, finally, the inductor with the lower contribution. Silicon Carbide devices with a good heatsink design and forced cooling are recommended, reducing losses, and resulting in a lower failure rate and higher reliability. It is demonstrated in the parallel configuration, since the MOSFETs, being under lower current, would reduce the thermal stress during switching.

5. Conclusions

In this paper, the reliability prediction of a full bridge inverter with different MOSFET-redundant structures was presented. The reliability calculation was performed based on the MIL HDBK 217F standards, used for calculating the failure rate and the Mean Time Between Failures for the different components and then to obtain the global reliability parameters. The reliability study shows that the best-performing structure was the parallel passive structure, followed by the parallel active structure, and, finally, the serial structure with a single component. As reported in the literature, it was also confirmed that the components that are more susceptible to failure are the MOSFETs with a percentage higher than 99%, followed by the capacitors, and, finally, the inductors.