On the Sliding Mode Control Applied to a DC-DC Buck Converter
Abstract
1. Introduction
2. DC–DC Buck Converter and Its Smc
2.1. Case A Given in [4]
- : In this work, is given in (13), where K is a control gain and it can take values to guarantee stability conditions. In the following sections, some values of this gain are given.
2.2. Case B Given in [14]
- : Considering that is given in (29), and by replacing (28) and (29) into (9), the control law function is given in (30). Again, as for case A, u is the signal error that governs a comparator with a threshold equal to zero, thus providing a logic 1 or logic 0 to close or to open the switch of the DC–DC buck converter shown in Figure 1, respectively.
2.3. Case C: Proposed Sliding Surface
3. Stability Analysis
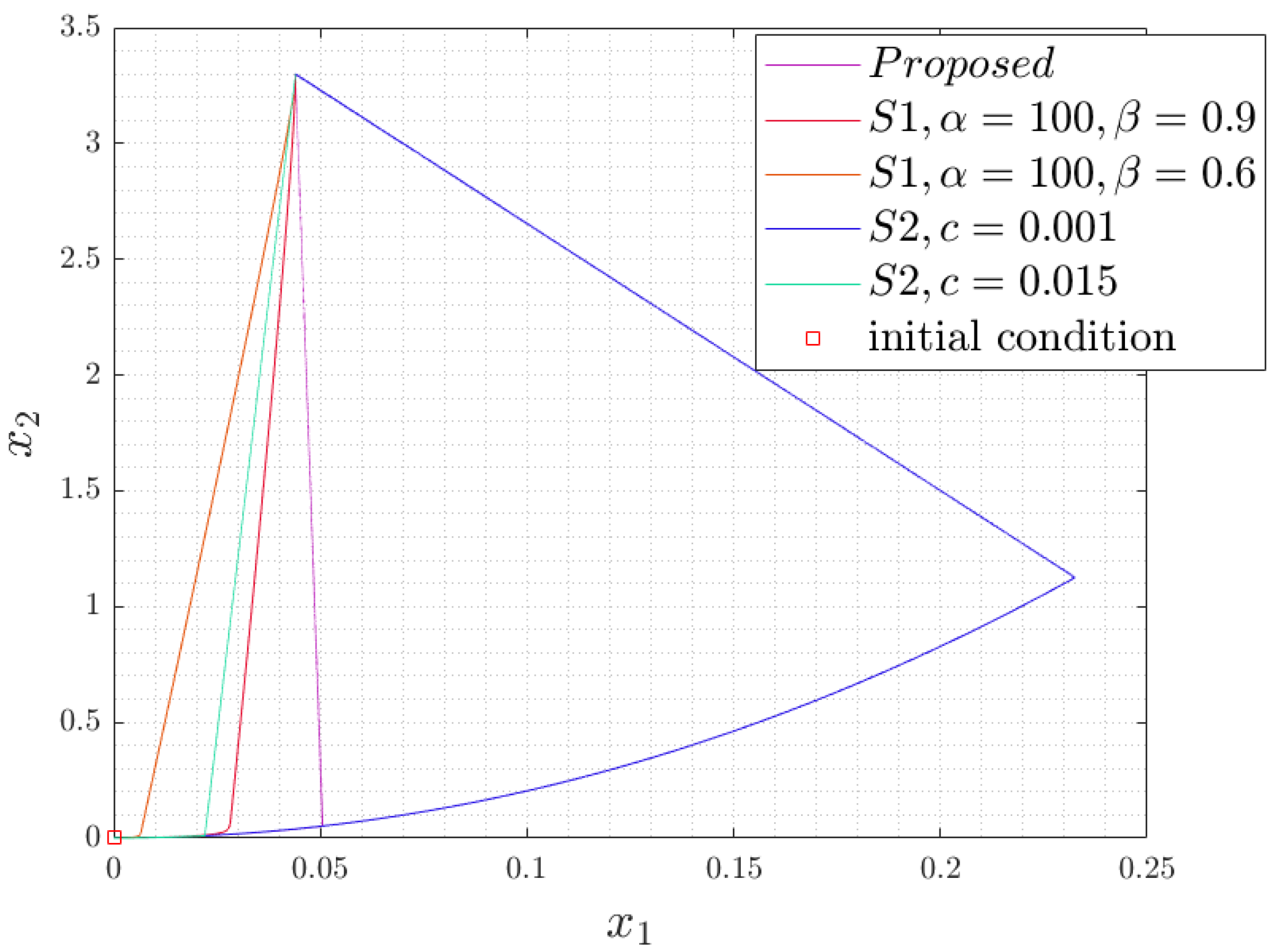
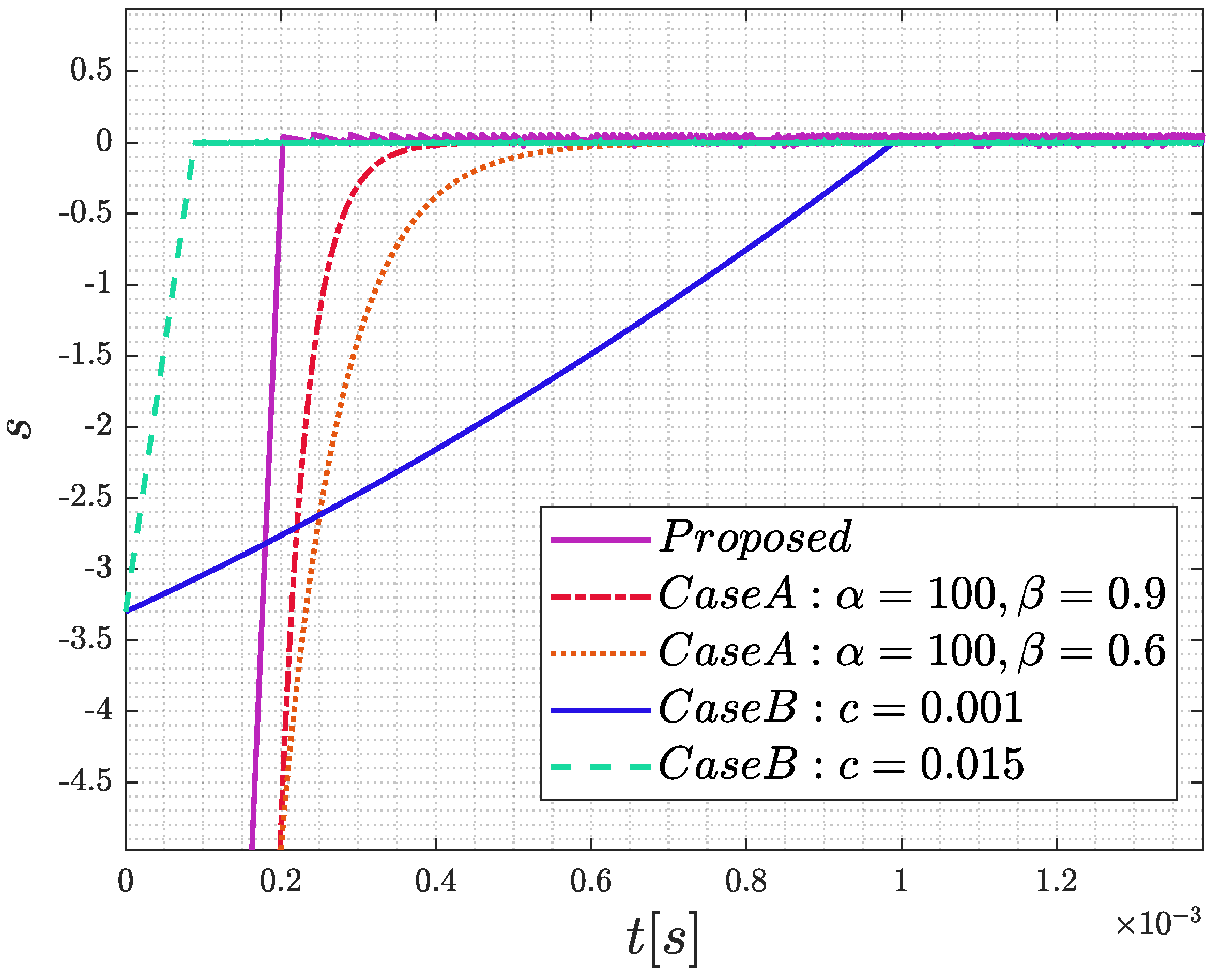
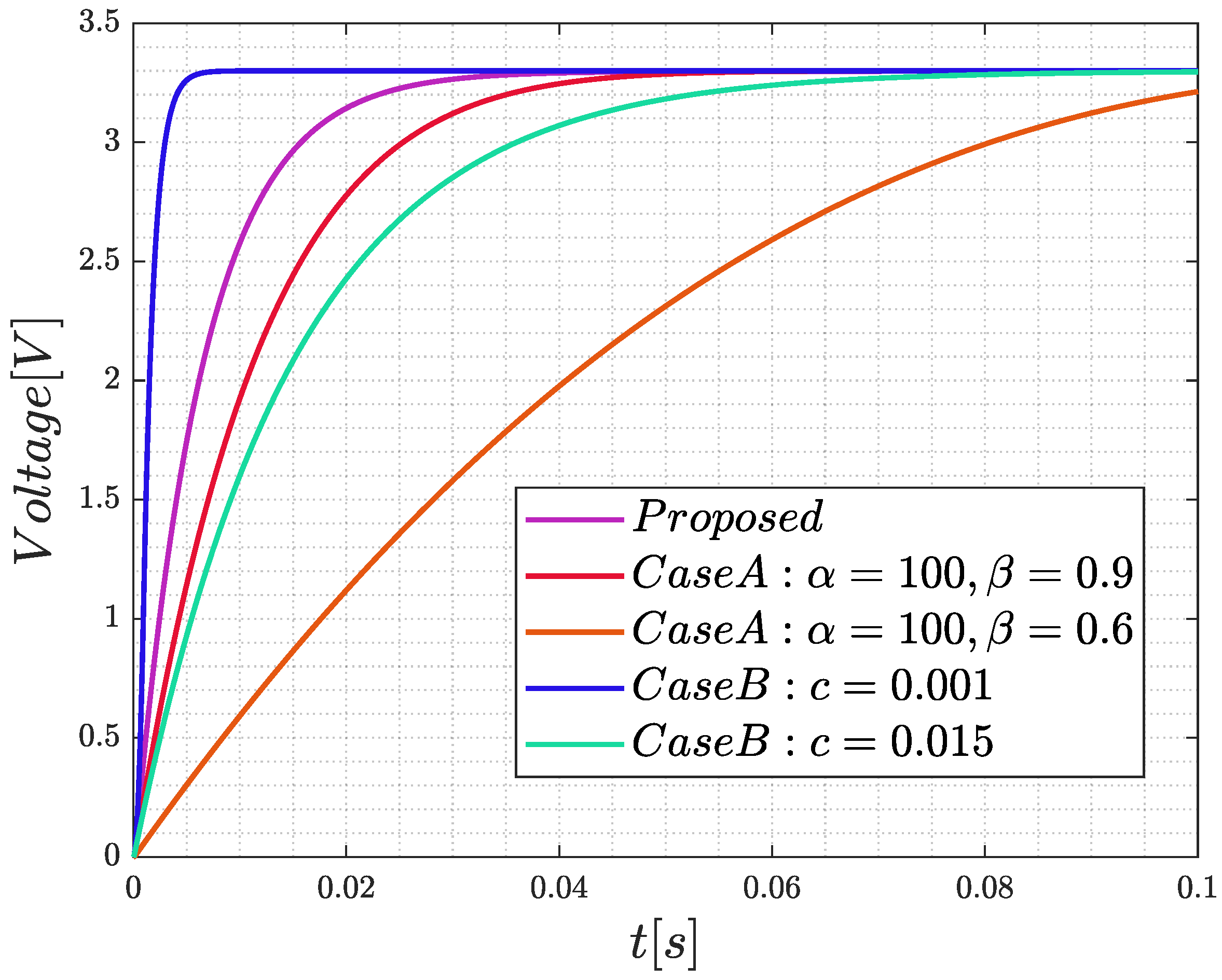
4. Simulation and Discussion of Results
4.1. Numerical Simulation
4.2. Discussion of Simulation Results
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Mumtaz, F.; Yahaya, N.Z.; Meraj, S.T.; Singh, B.; Kannan, R.; Ibrahim, O. Review on non-isolated DC-DC converters and their control techniques for renewable energy applications. Ain Shams Eng. J. 2021, 12, 3747–3763. [Google Scholar] [CrossRef]
- Warrier, P.; Shah, P. Optimal Fractional PID Controller for Buck Converter Using Cohort Intelligent Algorithm. Appl. Syst. Innov. 2021, 4, 50. [Google Scholar] [CrossRef]
- Ullah, N. Fractional order sliding mode control design for a buck converter feeding resistive power loads. Math. Model. Eng. Probl. 2020, 7, 649–658. [Google Scholar] [CrossRef]
- Lin, X.; Liu, J.; Liu, F.; Liu, Z.; Gao, Y.; Sun, G. Fractional-order sliding mode approach of buck converters with mismatched disturbances. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 3890–3900. [Google Scholar] [CrossRef]
- Sánchez, A.G.S.; Soto-Vega, J.; Tlelo-Cuautle, E.; Rodríguez-Licea, M.A. Fractional-Order Approximation of PID Controller for Buck–Boost Converters. Micromachines 2021, 12, 591. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, O.; Bodur, F. Second-order sliding mode controller design of buck converter with constant power load. Int. J. Control 2022, 1–17. [Google Scholar] [CrossRef]
- Amin, A.A.; Abdullah, M. A Comparative Study of DC-DC Buck, Boost, and Buck-boost Converters with Proportional-integral, Sliding Mode, and Fuzzy Logic Controllers. Recent Adv. Electr. Electron. Eng. 2022, 15, 75–91. [Google Scholar] [CrossRef]
- Belkhier, Y.; Achour, A.; Hamoudi, F.; Ullah, N.; Mendil, B. Robust energy-based nonlinear observer and voltage control for grid-connected permanent magnet synchronous generator in the tidal energy conversion system. Int. J. Energy Res. 2021, 45, 13250–13268. [Google Scholar] [CrossRef]
- Al Alahmadi, A.A.; Belkhier, Y.; Ullah, N.; Abeida, H.; Soliman, M.S.; Khraisat, Y.S.H.; Alharbi, Y.M. Hybrid wind/PV/battery energy management-based intelligent non-integer control for smart DC-microgrid of smart university. IEEE Access 2021, 9, 98948–98961. [Google Scholar] [CrossRef]
- Kaleem, A.; Khalil, I.U.; Aslam, S.; Ullah, N.; Al Otaibi, S.; Algethami, M. Feedback PID Controller-Based Closed-Loop Fast Charging of Lithium-Ion Batteries Using Constant-Temperature–Constant-Voltage Method. Electronics 2021, 10, 2872. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Ali, Z.; Ullah, N.; Ro, J.S. A super twisting fractional order terminal sliding mode control for DFIG-based wind energy conversion system. Energies 2020, 13, 2158. [Google Scholar] [CrossRef]
- Belkhier, Y.; Achour, A.; Shaw, R.N.; Ullah, N.; Chowdhury, M.S.; Techato, K. Energy-based combined nonlinear observer and voltage controller for a PMSG using fuzzy supervisor high order sliding mode in a marine current power system. Sustainability 2021, 13, 3737. [Google Scholar] [CrossRef]
- Chafekar, N.; Mate, U.; Kurode, S.; Vyawahare, V. Design and implementation of fractional order sliding mode controller for DC-DC Buck Converter. In Proceedings of the 2019 Fifth Indian Control Conference (ICC), New Delhi, India, 9–11 January 2019; pp. 201–206. [Google Scholar]
- Yang, N.; Wu, C.; Jia, R.; Liu, C. Fractional-order terminal sliding-mode control for buck DC/DC converter. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Xie, L.; Liu, Z.; Ning, K.; Qin, R. Fractional-Order Adaptive Sliding Mode Control for Fractional-Order Buck-Boost Converters. J. Electr. Eng. Technol. 2022, 17, 1693–1704. [Google Scholar] [CrossRef]
- Taheri, B.; Sedaghat, M.; Bagherpour, M.A.; Farhadi, P. A New Controller for DC-DC Converters Based on Sliding Mode Control Techniques. J. Control Autom. Electr. Syst. 2019, 30, 63–74. [Google Scholar] [CrossRef]
- Ali, S.; Raza, M.T.; Abbas, G.; Ullah, N.; Al Otaibi, S.; Luo, H. Sliding Mode Observer-Based Fault Detection in Continuous Time Linear Switched Systems. Energies 2022, 15, 1090. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Khalil, H.K. Nonlinear Control; Pearson: New York, NY, USA, 2015; Volume 406. [Google Scholar]
- Labbadi, M.; Cherkaoui, M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances. ISA Trans. 2020, 99, 290–304. [Google Scholar] [CrossRef] [PubMed]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Berlin/Heidelberg, Germany, 2014; Volume 10. [Google Scholar]
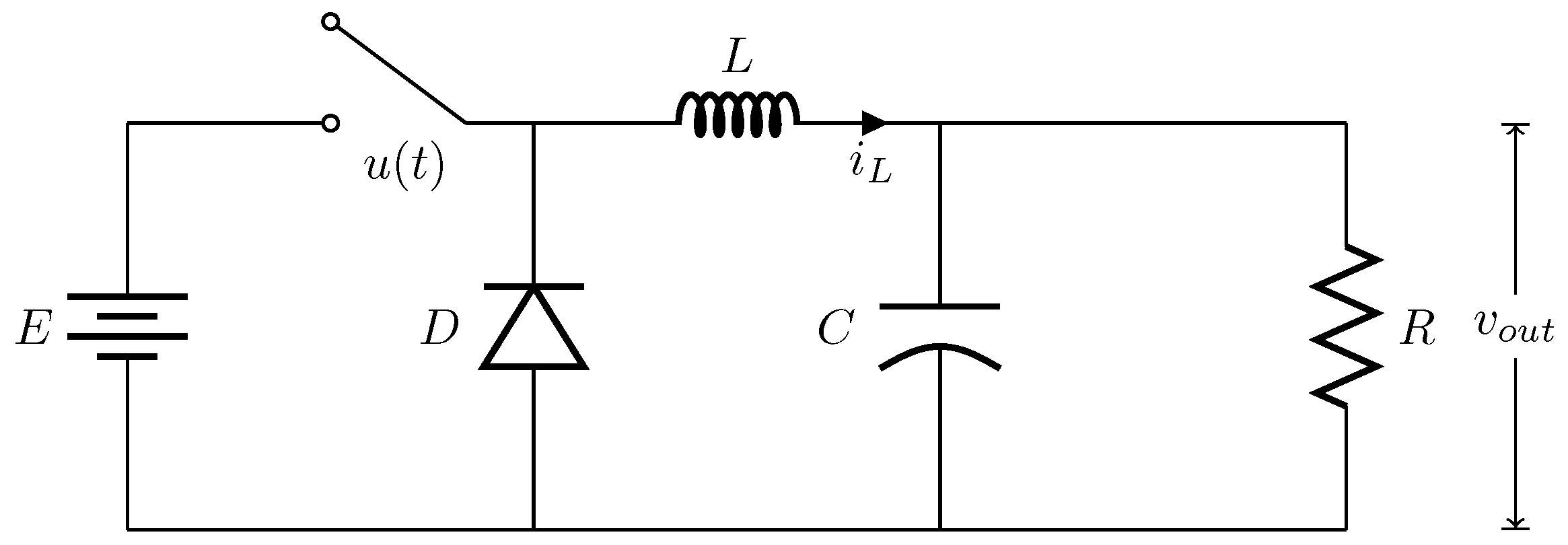

| Description | Parameter | Value | Units |
|---|---|---|---|
| Inductor | L | 0.02 | H |
| Capacitor | C | 10 | F |
| Load resistance | R | 75 | |
| Input voltage | E | 5 | V |
| Reference voltage | V_d | 3.3 | V |
| Surface | Gain |
|---|---|
| case A | , , K = 1 |
| case A | , , K = 1 |
| case B | c = 0.001, K = 1 |
| case B | c = 0.015, K = 1 |
| case C (Proposed) | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huerta-Moro, S.; Martínez-Fuentes, O.; Gonzalez-Diaz, V.R.; Tlelo-Cuautle, E. On the Sliding Mode Control Applied to a DC-DC Buck Converter. Technologies 2023, 11, 33. https://doi.org/10.3390/technologies11020033
Huerta-Moro S, Martínez-Fuentes O, Gonzalez-Diaz VR, Tlelo-Cuautle E. On the Sliding Mode Control Applied to a DC-DC Buck Converter. Technologies. 2023; 11(2):33. https://doi.org/10.3390/technologies11020033
Chicago/Turabian StyleHuerta-Moro, Sandra, Oscar Martínez-Fuentes, Victor Rodolfo Gonzalez-Diaz, and Esteban Tlelo-Cuautle. 2023. "On the Sliding Mode Control Applied to a DC-DC Buck Converter" Technologies 11, no. 2: 33. https://doi.org/10.3390/technologies11020033
APA StyleHuerta-Moro, S., Martínez-Fuentes, O., Gonzalez-Diaz, V. R., & Tlelo-Cuautle, E. (2023). On the Sliding Mode Control Applied to a DC-DC Buck Converter. Technologies, 11(2), 33. https://doi.org/10.3390/technologies11020033








