Efficiency of the Brazilian Bitcoin: A DFA Approach
Abstract
1. Introduction and Literature Review
2. Methods and Data
2.1. Detrended Fluctuation Analysis
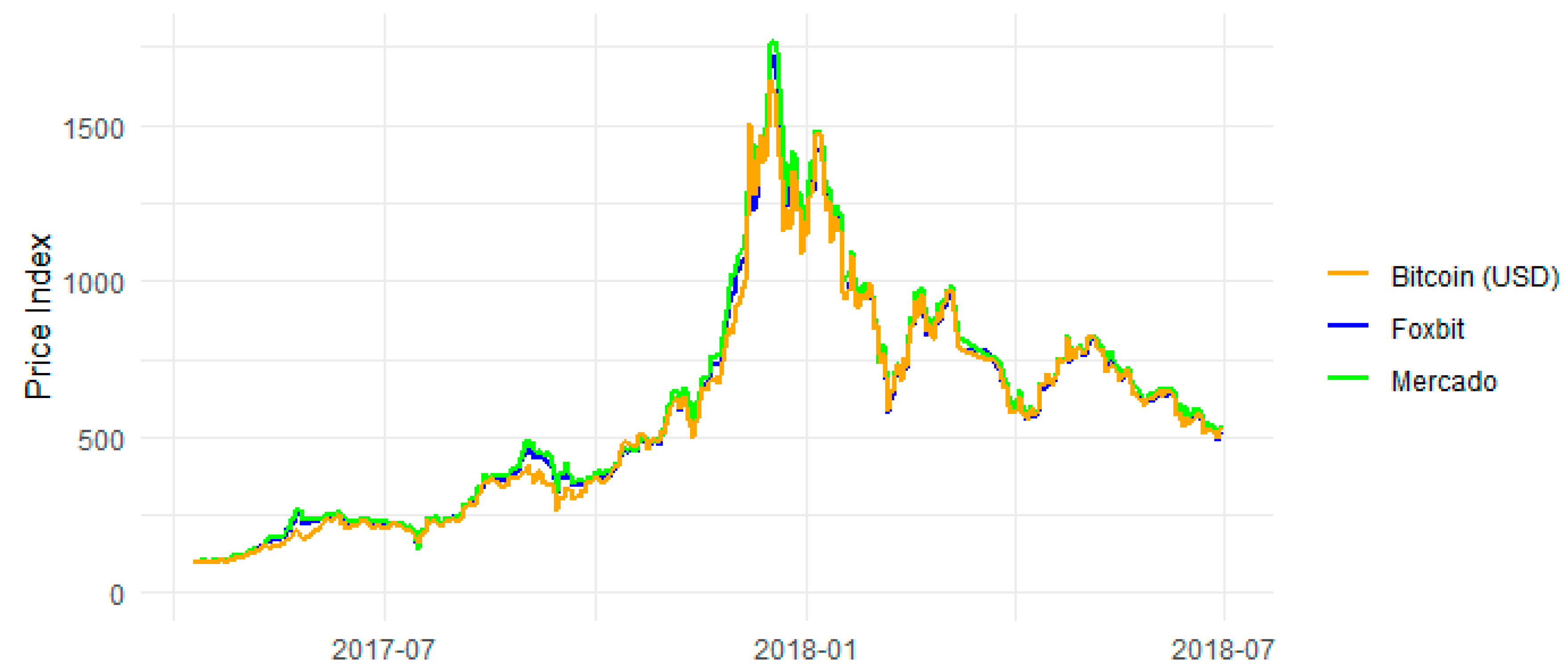
2.2. Data
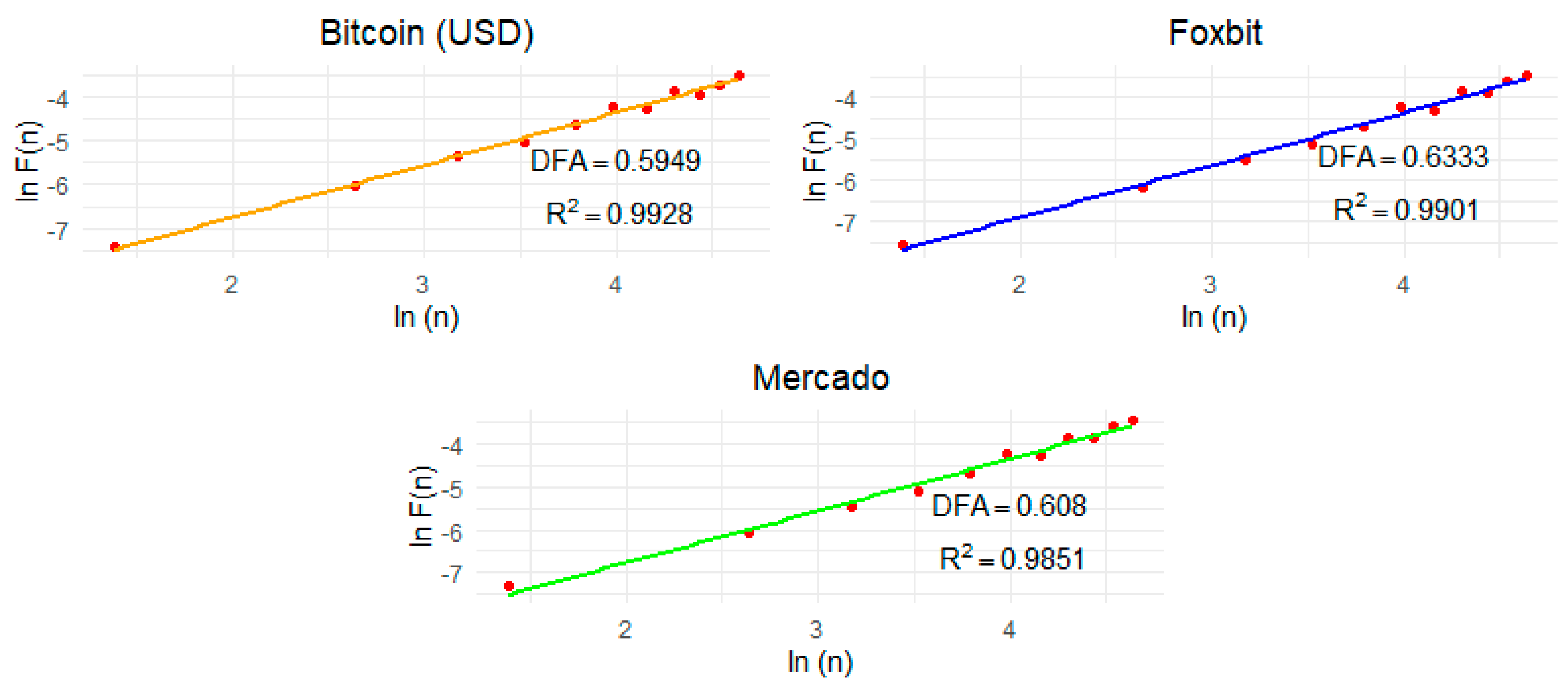
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alaoui, Marwane, Elie Bouri, and David Roubaud. 2019. Bitcoin price–volume: A multifractal cross-correlation approach. Finance Research Letters 31. [Google Scholar] [CrossRef]
- Alvarez-Ramirez, José, Eduardo Rodriguez, and Carlos Ibarra-Valdez. 2018. Long-range correlations and asymmetry in the Bitcoin market. Physica A 492: 948–55. [Google Scholar] [CrossRef]
- Al-Yahyaee, Khamis, Walid Mensi, and Seong-Min Yoon. 2018. Efficiency, multifractality, and the long-memory property of the bitcoin market: A comparative analysis with stock, currency, and gold markets. Finance Research Letters 27: 228–34. [Google Scholar] [CrossRef]
- Ausloos, Marcel. 2000. Statistical physics in foreign exchange currency and stock markets. Physica A 285: 48–65. [Google Scholar] [CrossRef]
- Ausloos, Marcel, and Kristinka Ivanova. 1999. Application of the detrended fluctuation analysis (DFA) method for describing cloud breaking. Physica A 274: 349–54. [Google Scholar]
- Ausloos, Marcel, and Kristinka Ivanova. 2003. Dynamical model and non-extensive statistical mechanics of a market index on large time windows. Physical Review E 68: 046122. [Google Scholar] [CrossRef]
- Ausloos, Marcel, Nicolas Vandewalle, Ph Boveroux, Albert Minguet, and Kristinka Ivanova. 1999. Applications of statistical physics to economic and financial topics. Physica A 274: 229–40. [Google Scholar] [CrossRef]
- Bariviera, Aurelio. 2017. The inefficiency of Bitcoin revisited: A dynamic approach. Economics Letters 161: 1–4. [Google Scholar] [CrossRef]
- Bariviera, Aurelio, María José Basgall, Waldo Hasperué, and Marcelo Naiouf. 2017. Some stylized facts of the Bitcoin market. Physica A 484: 82–90. [Google Scholar] [CrossRef]
- Brauneis, Alexander, and Roland Mestel. 2018. Price discovery of cryptocurrencies: Bitcoin and beyond. Economics Letters 165: 58–61. [Google Scholar] [CrossRef]
- Brock, William, Josef Lakonishok, and Blake LeBaron. 1992. Simple technical trading rules and the stochastic properties of stock returns. The Journal of Finance 47: 1731–64. [Google Scholar] [CrossRef]
- Caporale, Guglielmo, Luis Gil-Alana, and Alex Plastun. 2018. Persistence in the cryptocurrency market. Research in International Business and Finance 46: 141–48. [Google Scholar]
- Charfeddine, Lanouar, and Youcef Maouchi. 2019. Are shocks on the returns and volatility of cryptocurrencies really persistent? Finance Research Letters 28: 423–30. [Google Scholar] [CrossRef]
- Costa, Natália, Carlos Silva, and Paulo Ferreira. 2019. Long-range behaviour and correlation in DFA and DCCA analysis of cryptocurrencies. International Journal of Financial Studies 7: 12. [Google Scholar] [CrossRef]
- Fama, Eugene. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fama, Eugene, and Kenneth French. 1988. Permanent and temporary components of stock prices. Journal of Political Economy 96: 246–73. [Google Scholar] [CrossRef]
- Forbes. 2018. More People Opening Crypto Trading Accounts in Brazil than Traditional Securities. Available online: https://www.forbes.com/sites/kenrapoza/2018/05/30/more-people-opening-crypto-trading-accounts-in-brazil-than-traditional-securities/#63bde32c7e21 (accessed on 4 April 2020).
- Garnier, Josselin, and Knut Solna. 2019. Chaos and order in the bitcoin market. Physica A 524: 708–21. [Google Scholar] [CrossRef]
- Grech, Dariusz, and Zygmunt Mazur. 2013. On the scaling ranges of detrended fluctuation analysis for long-term memory correlated short series of data. Physica A 392: 2384–97. [Google Scholar] [CrossRef][Green Version]
- Jiang, Yonghong, He Nie, and Weihua Ruan. 2018. Time-varying long-term memory in Bitcoin market. Finance Research Letters 25: 280–84. [Google Scholar] [CrossRef]
- Kaplanov, Nikolei. 2012. Nerdy money: Bitcoin, the private digital currency, and the case against its regulation. Loyola Consumer Law Review 25: 111–74. [Google Scholar] [CrossRef]
- Köchling, Gerrit, Janis Müller, and Peter Posch. 2019. Price delay and market frictions in cryptocurrency markets. Economics Letters 174: 39–41. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav. 2018. On bitcoin markets (in)efficiency and its evolution. PhysicaA 503: 257–62. [Google Scholar] [CrossRef]
- Kyriazis, Nikolaos. 2019. A Survey on Efficiency and Profitable Trading Opportunities in Cryptocurrency Markets. Journal of Risk and Financial Management 12: 67. [Google Scholar] [CrossRef]
- Lahmiri, Salim, and Stelios Bekiros. 2018. Chaos, randomness and multi-fractality in bitcoin market. Chaos, Solitons & Fractals 106: 28–34. [Google Scholar]
- Lahmiri, Salim, Stelios Bekiros, and Antonio Salvi. 2018. Long-range memory, distributional variation and randomness of bitcoin volatility. Chaos, Solitons & Fractals 107: 43–48. [Google Scholar]
- Liu, Yanhui, Pierre Cizeau, Martin Meyer, Chung-Kang Peng, and Harry Stanley. 1997. Correlations in economic time series. Physica A 245: 437–40. [Google Scholar] [CrossRef]
- Machado, Aloísio, Marcus Silva, and Gilney Zebende. 2014. Autocorrelation and cross-correlation in time series of homicide and attempted homicide. Physica A 400: 12–19. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit. 1971. When can price be arbitraged efficiently? A limit to the validity of the random walk and martingale models. The Review of Economics and Statistics 53: 225–36. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2018. Bitcoin: A Peer-to-Peer Electronic Cash System. Non-Publihed Work. Available online: https://nakamotoinstitute.org/bitcoin/ (accessed on 4 April 2020).
- Panagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2019. The effects of markets, uncertainty and search intensity on bitcoin returns. International Review of Financial Analysis 63: 220–42. [Google Scholar] [CrossRef]
- Peng, Chung-Kang, Sergey Buldyrev, Shlomo Havlin, Michael Simons, Harry Eugene Stanley, and Ary Goldberger. 1994. Mosaic organization of DNA nucleotides. Physical Review E 49: 1685–89. [Google Scholar] [CrossRef]
- Ponsford, Matthew. 2015. A comparative analysis of bitcoin and other decentralised virtual currencies: Legal regulation in the People’s Republic of China, Canada, and the United States. Hong Kong Journal of Legal Studies 9: 29–50. [Google Scholar]
- Sensoy, Ahmet. 2019. The inefficiency of bitcoin revisited: A high-frequency analysis with alternative currencies. Finance Research Letters 28: 68–73. [Google Scholar] [CrossRef]
- Staiger, Robert, and Alan Sykes. 2010. “Currency manipulation” and world trade. World Trade Review 9: 583–627. [Google Scholar] [CrossRef]
- Sukpitak, Jessada, and Varagorn Hengpunya. 2016. Efficiency of Thai stock markets: Detrended Fluctuation analysis. Physica A 458: 204–9. [Google Scholar] [CrossRef]
- Takaishi, Tetsuya. 2018. Statistical properties and multifractality of bitcoin. Physica A 506: 507–19. [Google Scholar] [CrossRef]
- Tiwari, Aviral, Rabin Jana, Debojyoti Das, and David Roubaud. 2018. Informational efficiency of bitcoin—An extension. Economics Letters 163: 106–9. [Google Scholar] [CrossRef]
- Trautman, Lawrence. 2014. Virtual currencies; bitcoin & what now after liberty reserve, silk road, and mt.gox? Richmond Journal of Law and Technology 20: 1–108. [Google Scholar]
- Urquhart, Andrew. 2016. The inefficiency of Bitcoin. Economics Letters 148: 80–82. [Google Scholar] [CrossRef]
- Velde, François. 2013. Bitcoin: A primer. Chicago Fed Letter. 317. Available online: https://www.chicagofed.org/publications/chicago-fed-letter/2013/december-317 (accessed on 4 April 2020).
- Wang, Wei. 2018. Liquidity and market efficiency in cryptocurrencies. Economics Letters 168: 21–24. [Google Scholar]
- Zhang, Wei, Pengfei Wang, Xiao Li, and Dehua Shen. 2018. The inefficiency of cryptocurrency and its cross-correlation with Dow Jones Industrial Average. Physica A 510: 658–70. [Google Scholar] [CrossRef]
- Zhang, Yuanyuan, Stephen Chan, Jeffrey Chu, and Saralees Nadarajah. 2019. Stylised facts for high frequency cryptocurrency data. Physica A 513: 598–612. [Google Scholar] [CrossRef]
| Variable | Bitcoin (USD) | Foxbit | Mercado |
|---|---|---|---|
| Mean | 0.0039 | 0.0039 | 0.0040 |
| Median | 0.0062 | 0.0037 | 0.0041 |
| Maximum | 0.2251 | 0.2685 | 0.3599 |
| Minimum | −0.2075 | −0.1800 | −0.1982 |
| Std. Dev. | 0.0527 | 0.0479 | 0.0511 |
| Skewness | 0.1548 | 0.1391 | 0.2829 |
| Kurtosis | 5.5502 | 6.3738 | 10.3257 |
| Exchange | DFA Estimation |
|---|---|
| Bitcoin (USD) | 0.5949 ± 0.0160 |
| Foxbit | 0.6333 ± 0.0201 |
| Mercado | 0.6080 ± 0.0236 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintino, D.; Campoli, J.; Burnquist, H.; Ferreira, P. Efficiency of the Brazilian Bitcoin: A DFA Approach. Int. J. Financial Stud. 2020, 8, 25. https://doi.org/10.3390/ijfs8020025
Quintino D, Campoli J, Burnquist H, Ferreira P. Efficiency of the Brazilian Bitcoin: A DFA Approach. International Journal of Financial Studies. 2020; 8(2):25. https://doi.org/10.3390/ijfs8020025
Chicago/Turabian StyleQuintino, Derick, Jessica Campoli, Heloisa Burnquist, and Paulo Ferreira. 2020. "Efficiency of the Brazilian Bitcoin: A DFA Approach" International Journal of Financial Studies 8, no. 2: 25. https://doi.org/10.3390/ijfs8020025
APA StyleQuintino, D., Campoli, J., Burnquist, H., & Ferreira, P. (2020). Efficiency of the Brazilian Bitcoin: A DFA Approach. International Journal of Financial Studies, 8(2), 25. https://doi.org/10.3390/ijfs8020025






