Data Envelopment Analysis and Multifactor Asset Pricing Models
Abstract
1. Introduction
2. Data and Efficiency Analysis
3. Multifactor Asset Pricing Models Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Panel A | ||||||
| αi | βiRMRF | βiSMB | βiHML | βiDEA | R2 | |
| P1 | 0.00001 | 0.72500 | −0.03498 | −0.13344 | −0.00672 | 0.699 |
| 0.008 | 18.462 * | −0.362 | −1.559 | −0.904 | ||
| P2 | −0.00015 | 0.68950 | 0.03730 | −0.10205 | −0.00577 | 0.709 |
| −0.082 | 18.969 * | 0.417 | −1.288 | −0.840 | ||
| P3 | −0.00068 | 0.73318 | −0.00146 | −0.23141 | −0.01505 | 0.729 |
| −0.366 | 19.667 * | −0.015 | −2.849 * | −2.136 | ||
| P4 | −0.00027 | 0.66036 | 0.02814 | −0.07859 | −0.01493 | 0.730 |
| −0.159 | 19.370 * | 0.335 | −1.058 | −2.316 * | ||
| P5 | −0.00028 | 0.69663 | −0.01145 | −0.09888 | −0.01045 | 0.720 |
| −0.155 | 19.157 * | −0.128 | −1.248 | −1.520 | ||
| P6 | −0.00018 | 0.70371 | −0.04959 | −0.11263 | −0.01544 | 0.748 |
| −0.104 | 20.318 * | −0.582 | −1.492 | −2.359 * | ||
| P7 | 0.00001 | 0.69221 | −0.02033 | −0.11473 | −0.01373 | 0.743 |
| 0.003 | 20.205 * | −0.241 | −1.537 | −2.119 * | ||
| P8 | −0.00029 | 0.69893 | −0.05205 | −0.11688 | −0.01911 | 0.757 |
| −0.169 | 20.608 * | −0.623 | −1.581 | −2.981 * | ||
| P9 | 0.00009 | 0.68879 | −0.08391 | −0.08150 | −0.01565 | 0.742 |
| 0.054 | 19.869 * | −0.983 | −1.079 | −2.388 * | ||
| P10 | −0.00036 | 0.72169 | −0.12809 | −0.11672 | −0.01475 | 0.749 |
| −0.203 | 20.339 * | −1.467 | −1.509 | −2.199 * | ||
| P11 | −0.00016 | 0.72227 | −0.10462 | −0.09785 | −0.01301 | 0.745 |
| −0.091 | 20.181 * | −1.188 | −1.255 | −1.922 ** | ||
| P12 | −0.00012 | 0.71936 | −0.03390 | −0.14850 | −0.02247 | 0.763 |
| −0.067 | 20.862 | −0.399 | −1.976 * | −3.448 * | ||
| P13 | −0.00052 | 0.72088 | −0.04617 | −0.21277 | −0.02463 | 0.755 |
| −0.295 | 20.351 * | −0.529 | −2.757 * | −3.678 * | ||
| P14 | −0.00005 | 0.71099 | −0.05945 | −0.14467 | −0.01921 | 0.745 |
| −0.025 | 20.019 * | −0.680 | −1.869 ** | −2.861 * | ||
| P15 | 0.00022 | 0.68800 | −0.08782 | −0.07565 | −0.01133 | 0.745 |
| 0.127 | 19.733 * | −1.023 | −0.995 | −1.719 ** | ||
| P16 | −0.00001 | 0.71240 | −0.00394 | −0.11358 | −0.01885 | 0.735 |
| −0.004 | 20.874 * | −0.047 | −1.527 | −2.922 * | ||
| P17 | −0.00010 | 0.70986 | −0.14161 | −0.10103 | −0.01922 | 0.760 |
| −0.057 | 20.603 * | −1.670 ** | −1.345 | −2.951 * | ||
| P18 | −0.00068 | 0.72072 | −0.15536 | −0.15191 | −0.01856 | 0.760 |
| −0.383 | 20.382 * | −1.785 ** | −1.971 | −2.777 * | ||
| P19 | −0.00026 | 0.69972 | −0.16780 | −0.14017 | −0.01822 | 0.753 |
| −0.152 | 20.940 * | −2.0410 * | −1.925 ** | −2.885 * | ||
| P20 | −0.00034 | 0.71460 | −0.20556 | −0.16629 | −0.01597 | 0.764 |
| −0.210 | 22.295 * | −2.606 * | −2.381 * | −2.636 * | ||
| Panel B | ||||||
| RMRF | SMB | HML | DEA | |||
| RM−RF | 1 | −0.098 | 0.288 | −0.294 | ||
| SMB | 1.000 | 0.048 | −0.071 | |||
| HML | 1.000 | 0.114 | ||||
| DEA | 1 |
| αi | βiRMRF | βiSMB | βiHML | R2 | |
|---|---|---|---|---|---|
| P1 | 0.00013 | 0.73767 | −0.02400 | −0.15109 | 0.698 |
| 0.064 | 20.1171 * | −0.250 | −1.814 ** | ||
| P2 | −0.00005 | 0.70039 | 0.04674 | −0.11722 | 0.708 |
| −0.030 | 20.6417 * | 0.527 | −1.521 | ||
| P3 | −0.00044 | 0.76157 | 0.02316 | −0.27095 | 0.722 |
| −0.232 | 21.6597 * | 0.252 | −3.3939 * | ||
| P4 | −0.00003 | 0.68852 | 0.05255 | −0.11780 | 0.722 |
| −0.016 | 21.3683 * | 0.624 | −1.610 | ||
| P5 | −0.00011 | 0.71635 | 0.00564 | −0.12634 | 0.716 |
| −0.061 | 21.0124 * | 0.063 | −1.632 | ||
| P6 | 0.00007 | 0.73284 | −0.02434 | −0.15320 | 0.740 |
| 0.041 | 22.3759 * | −0.284 | −2.0601 * | ||
| P7 | 0.00023 | 0.71810 | 0.00212 | −0.15079 | 0.737 |
| 0.134 | 22.2287 * | 0.025 | −2.0557 * | ||
| P8 | 0.00003 | 0.73499 | −0.02080 | −0.16710 | 0.745 |
| 0.015 | 22.7194 * | −0.246 | −2.2748 * | ||
| P9 | 0.00035 | 0.71832 | −0.05832 | −0.12262 | 0.734 |
| 0.200 | 21.9044 * | −0.681 | −1.647 | ||
| P10 | −0.00012 | 0.74952 | −0.10397 | −0.15548 | 0.743 |
| −0.066 | 22.3809 * | −1.188 | −2.0447 * | ||
| P11 | 0.00005 | 0.74680 | −0.08335 | −0.13202 | 0.740 |
| 0.028 | 22.1758 * | −0.947 | −1.7265 ** | ||
| P12 | 0.00025 | 0.76175 | 0.00285 | −0.20753 | 0.748 |
| 0.142 | 22.9835 * | 0.033 | −2.7578 * | ||
| P13 | −0.00012 | 0.76735 | −0.00590 | −0.27747 | 0.737 |
| −0.066 | 22.4433 * | −0.066 | −3.5742 * | ||
| P14 | 0.00027 | 0.74723 | −0.02803 | −0.19514 | 0.734 |
| 0.149 | 22.0979 * | −0.317 | −2.5416 * | ||
| P15 | 0.00041 | 0.70938 | −0.06928 | −0.10543 | 0.731 |
| 0.234 | 21.6647 * | −0.810 | −1.418 | ||
| P16 | 0.00030 | 0.74796 | 0.02689 | −0.16310 | 0.749 |
| 0.174 | 22.9976 * | 0.316 | −2.2087 * | ||
| P17 | 0.00022 | 0.74611 | −0.11018 | −0.15152 | 0.749 |
| 0.123 | 22.7135 * | −1.284 | −2.0314 * | ||
| P18 | −0.00037 | 0.75574 | −0.12501 | −0.20067 | 0.743 |
| −0.208 | 22.4747 * | −1.423 | −2.6282 * | ||
| P19 | 0.00004 | 0.73410 | −0.13801 | −0.18804 | 0.754 |
| 0.025 | 23.0654 * | −1.6590 ** | −2.6021 * | ||
| P20 | −0.00008 | 0.74473 | −0.17945 | −0.20825 | 0.776 |
| −0.047 | 24.4820 * | −2.2578 * | −3.0151 * |
References
- Abdelsalam, Omneya, Meryem Duygun Fethi, Juan Carlos Matallín, and Emili Tortosa-Ausina. 2014. On the Comparative Performance of Socially Responsible and Islamic Mutual Funds. Journal of Economic Behavior and Organization 7: 108–28. [Google Scholar] [CrossRef]
- Adler, Nicole, and Boaz Golany. 2002. Including Principal Component Weights to Improve Discrimination in Data Envelopment Analysis. Journal of the Operational Research Society 53: 985–91. [Google Scholar] [CrossRef]
- Ammann, Manuel, Sandro Odoni, and David Oesch. 2012. An Alternative Three-factor Model for International Markets: Evidence from the European Monetary Union. Journal of Banking and Finance 36: 1857–64. [Google Scholar] [CrossRef]
- Andreu, Laura, Miguel Serrano, and Luis Vicente. 2018. Efficiency of mutual fund managers: A slacks-based manager efficiency index. European Journal of Operational Research 273: 1180–93. [Google Scholar] [CrossRef]
- Babalos, Vassilios, Michael Doumpos, Nikolaos Philippas, and Constantin Zopounidis. 2015. Towards a Holistic Approach for Mutual Fund Performance Appraisal. Computational Economics 46: 35–53. [Google Scholar] [CrossRef]
- Banker, Rajiv D., Abraham Charnes, and William W. Cooper. 1984. Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Management Science 30: 1078–92. [Google Scholar] [CrossRef]
- Basso, Antonella, and Stefania Funari. 2001. A Data Envelopment Analysis Approach to Measure the Mutual Fund Performance. European Journal of Operational Research 135: 477–92. [Google Scholar] [CrossRef]
- Basso, Antonella, and Stefania Funari. 2003. Measuring the Performance of Ethical Mutual Funds: A DEA Approach. Journal of the Operational Research Society 54: 521–31. [Google Scholar] [CrossRef]
- Basso, Antonella, and Stefania Funari. 2005. A Generalized Performance Attribution Technique for Mutual Funds. Central European Journal of Operations Research 13: 65–84. [Google Scholar]
- Basso, Antonella, and Stefania Funari. 2007. DEA Models for Ethical and non Ethical Mutual Funds with Negative Data. Mathematics and Methods in Economics Finance 2: 21–40. [Google Scholar]
- Basso, Antonella, and Stefania Funari. 2016. DEA Performance Assessment of Mutual Funds in Data Envelopment Analysis. In A Handbook of Empirical Studies and Applications. Edited by Joe Zhu. New York: Springer, pp. 229–88. [Google Scholar]
- Berk, Jonathan B., and Richard C. Green. 2004. Mutual Fund Flows and Performance in Rational Markets. Journal of Political Economy 112: 1269–95. [Google Scholar] [CrossRef]
- Breeden, Douglas T. 1979. An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities. Journal of Financial Economics 7: 265–96. [Google Scholar] [CrossRef]
- Campbell, John Y., and Robert J. Shiller. 1988. The Dividend-Price Ratio and Expectations of Future Dividends and Discount Factors. Review of Financial Studies 1: 195–227. [Google Scholar] [CrossRef]
- Cao, Zhiguang, Stephen Satchell, P. Joakim Westerholm, and Hui Henry Zhang. 2018. The Idiosyncratic Volatility Anomaly and the Resale Option in Chinese Stock Markets. Available online: https://ssrn.com/abstract=3274652 (accessed on 3 April 2020).
- Carhart, Mark. M. 1997. On Persistence in Mutual Fund Performance. Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Charnes, Abraham, William W. Cooper, and Edward Rhodes. 1981. Evaluating Program and Managerial Efficiency: An Application of Data Envelopment Analysis to Program Follow Through. Managerial Science 27: 668–97. [Google Scholar] [CrossRef]
- Chen, Long, Robert Novy-Marx, and Lu Zhang. 2011. An Alternative Three-Factor Model. Available online: https://ssrn.com/abstract=1418117 (accessed on 28 June 2019).
- Chordia, Tarun, Avanidhar Subrahmanyam, and Qing Tong. 2014. Have capital market anomalies attenuated in the recent era of high liquidity and trading activity? Journal of Accounting and Economics 58: 41–58. [Google Scholar] [CrossRef]
- Chordia, Tarun, Richard Roll, and Avanidhar Subrahmanyam. 2011. Recent trends in trading activity and market quality. Journal of Financial Economics 101: 243–63. [Google Scholar] [CrossRef]
- Clarke, Charles. 2014. The Level, Slope and Curve Factor Model for Stocks. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2526435 (accessed on 17 November 2018).
- Cochrane, John H. 2011. Presidential Address: Discount Rates. Journal of Finance 66: 1047–1108. [Google Scholar] [CrossRef]
- Cochrane, John. H. 2005. Asset Pricing, Revised ed. Princeton: Princeton University Press. [Google Scholar]
- Cornish, Edmund A., and Ronald A. Fisher. 1937. Moments and Cumulants in the Specification of Distributions. Review of the International Statistical Institute 4: 307–20. [Google Scholar] [CrossRef]
- Durán-Santomil, Pablo, Luis Otero-González, Renato Heitor Correia-Domingues, and Juan Carlos Reboredo. 2019. Does Sustainability Score Impact Mutual Fund Performance? Sustainability 11: 2972. [Google Scholar] [CrossRef]
- Eling, Martin. 2006. Performance Measurement of Hedge Funds using Data Envelopment Analysis. Financial Markets and Porfolio Management 20: 442–71. [Google Scholar] [CrossRef]
- Favre, Laurent, and José-Antonio Galeano. 2002. Mean-Modified Value-at-Risk Optimization with Hedge Funds. Journal of Alternative Investments 5: 21–25. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A Five-Factor Asset Pricing Model. Journal of Financial Economics 116: 1–22. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2016. Dissecting Anomalies with a Five-Factor Model. Review of Financial Studies 29: 69–103. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fecher, Fabienne, D. Kessler, Sergio Perelman, and Pierre Pestieau. 1993. Productive performance of the French insurance industry. Journal of Productivity Analysis 4: 77–93. [Google Scholar] [CrossRef]
- Feng, Guanhao, Stefano Giglio, and Dacheng Xiu. 2019. Taming the Factor Zoo A Test of New Factors. Fama-Miller Working Paper. Chicago Booth Research Paper No. 17(4). Chicago, IL, USA: Chicago Booth School of Business, pp. 1–56. [Google Scholar]
- Galagedera, Don Upatissa Asoka, and Param Silvapulle. 2002. Australian Mutual Fund Performance Appraisal using Data Envelopment Analysis. Managerial Finance 28: 60–73. [Google Scholar] [CrossRef]
- Gibbons, Michael. R., Stephen A. Ross, and Jay Shanken. 1989. A Test of the Efficiency of a Given Portfolio. Econometrica 57: 1121–52. [Google Scholar] [CrossRef]
- Glawischnig, Markus, and Margit Sommersguter-Reichmann. 2010. Assessing the Performance of Alternative Investments using Non-parametric Efficiency Measurement Approaches: Is it convincing? Journal of Banking and Finance 34: 295–303. [Google Scholar] [CrossRef]
- Gökgöz, Fazil, and Duygu Çandarli. 2011. Data Envelopment Analysis: A Comparative Efficiency Measurement for Turkish Pension and Mutual Funds. International Journal of Economic Perspectives 5: 261–81. [Google Scholar]
- Gregoriou, Greg N., and Jean Pierre Gueyie. 2003. Risk-Adjusted Performance of Funds of Hedge Funds using a Modified Sharpe Ratio. Journal of Wealth Management 6: 77–83. [Google Scholar] [CrossRef]
- Gregoriou, Greg. N., Komlan Sedzro, and Joe Zhu. 2005. Hedge Fund Performance Appraisal using Data Envelopment Analysis. European Journal of Operational Research 164: 555–71. [Google Scholar] [CrossRef]
- Guillén, Jorge. 2011. Latin American Private Pension Funds’ Vulnerabilities. Economía Mexicana 20: 357–78. [Google Scholar]
- Harvey, Campbell. R., Yan Liu, and Heqing Zhu. 2016. …and the Cross-Section of Expected Returns. Review of Financial Studies 29: 5–68. [Google Scholar] [CrossRef]
- Kapur, Sandeep, and Allan Timmermann. 2005. Relative Performance Evaluation Contracts and Asset Market Equilibrium. Economic Journal 115: 1077–102. [Google Scholar] [CrossRef][Green Version]
- Lettau, Martin, and Sydney Ludvigson. 2001a. Consumption, Aggregate Wealth, and Expected Stock Returns. Journal of Finance 56: 815–49. [Google Scholar] [CrossRef]
- Lettau, Martin, and Sydney Ludvigson. 2001b. Resurrecting the (C)CAPM: A Cross-Sectional Test When Risk Premia Are Time-Varying. Journal of Political Economy 109: 1238–87. [Google Scholar] [CrossRef]
- Lewellen, Jonathan, Stefan Nagel, and Jay Shanken. 2010. A Skeptical Appraisal of Asset-Pricing Tests. Journal of Financial Economics 96: 175–94. [Google Scholar] [CrossRef]
- Lovell, C. A. Knox. 1993. Production Frontiers and Productive Efficiency. In Measurement of Productive Efficiency: Techniques and Applications. Edited by Harold O. Fried, C. A. Knox Lovell and Shelton S. Schmidt. New York: Oxford University Press, pp. 3–67. [Google Scholar]
- McLean, R. David, and Jeffrey Pontiff. 2016. Does academic research destroy stock return predictability? Journal of Finance 71: 5–32. [Google Scholar] [CrossRef]
- McMullen, Patrick, and Robert Strong. 1998. Selection of Mutual Funds using Data Envelopment Analysis. Journal of Business and Economics Studies 4: 1–12. [Google Scholar]
- Morey, Mattew R., and Richard C. Morey. 1999. Mutual Fund Performance Appraisals: A Multi-horizon Perspective with Endogenous Benchmarking. Omega 27: 241–58. [Google Scholar] [CrossRef]
- Murthi, B. P. S., Yoon K. Choi, and Preyas Desai. 1997. Efficiency of Mutual Funds and Portfolio Performance Measurement: A Non-parametric Approach. European Journal of Operational Research 98: 408–18. [Google Scholar] [CrossRef]
- Parkan, Celik. 1991. The Calculation of Operational Performance Ratings. International Journal of Production Economics 24: 165–73. [Google Scholar] [CrossRef]
- Pätäri, Eero, Timo Leivo, and Samuli Honkapuro. 2012. Enhancement of Equity Portfolio Performance Using Data Envelopment Analysis. European Journal of Operational Research 220: 786–97. [Google Scholar] [CrossRef]
- Pérez-Gladish, Blanca, Paz Méndez Rodríguez, Bouchra M’zali, and Pascal Lang. 2013. Mutual Funds Efficiency Measurement under Financial and Social Responsibility Criteria. Journal of Multi-Criteria Decision Analysis 20: 109–25. [Google Scholar] [CrossRef]
- Premachandra, I. M. 2001. A Note on DEA vs Principal Component Analysis: An Improvement to Joe Zhu’s Approach. European Journal of Operational Research 132: 553–60. [Google Scholar] [CrossRef]
- Premachandra, I. M., Joe Zhu, John Watson, and Don Upatissa Asoka Galagedera. 2016. Mutual Fund Industry Performance: A Network Data Envelopment Analysis Approach. In Data Envelopment Analysis. International Series in Operations Research & Management Science. Edited by Joe Zhu. Boston: Springer, vol. 238, pp. 165–228. [Google Scholar]
- Premachandra, I. M., Joe Zhu, John Watson, and Don Upatissa Asoka Galagedera. 2012. Best-performing US Mutual Fund Families from 1993 to 2008: Evidence from a Novel two-stage DEA model for Efficiency Decomposition. Journal of Banking and Finance 36: 3302–17. [Google Scholar] [CrossRef]
- Roll, Richard. 1977. A Critique of the Asset Pricing Theory’s Tests Part I: On Past and Potential Testability of the Theory. Journal of Financial Economics 4: 129–76. [Google Scholar] [CrossRef]
- Rubio, J. Francisco, Neal Maroney, and M. Kabir Hassan. 2018. Can Efficiency of Returns Be Considered As a Pricing Factor? Computational Economics 52: 25–54. [Google Scholar] [CrossRef]
- Serrano Cinca, Carlos, and Cecilio Mar Molinero. 2004. Selecting DEA Specifications and Ranking Units Via PCA. Journal of the Operational Research Society 55: 521–28. [Google Scholar] [CrossRef]
- Sherman, H. David, and Franklin Gold. 1985. Bank branch operating efficiency: Evaluation with Data Envelopment Analysis. Journal of Banking & Finance 9: 297–315. [Google Scholar]
- Vidal-Garcia, Javier, Marta Vidal, Sabri Boubaker, and Majdi Hassan. 2018. The Efficiency of Mutal Funds. Annals of Operation Research 267: 555–84. [Google Scholar] [CrossRef]
- Wilkens, Kathryn, and Joe Zhu. 2001. Portfolio Evaluation and Benchmark Selection: A Mathematical Programming Approach. Journal of Alternative Investments 4: 9–19. [Google Scholar] [CrossRef]
- Zhao, Xiujuan, and Wuyi Yue. 2010. A Multi-subsystem Fuzzy DEA Model with its Application in Mutual Funds Management Companies’ Competence Evaluation. In International Conference on Computer Science. Amsterdam: Elsevier, pp. 2479–88. [Google Scholar]
- Zhao, Xiujuan, Shouyang Wang, and King Keung Lai. 2011. Mutual Funds Performance Evaluation based on Endogenous Benchmarks. Expert Systems with Applications 38: 3663–70. [Google Scholar] [CrossRef]
- Zhu, Joe. 1998. Data Envelopment Analysis vs. Principal Component Analysis: An Illustrative Study of Economic Performance of Chinese Cities. European Journal of Operational Research 111: 50–61. [Google Scholar] [CrossRef]
| 1 | All data is publicly available at dx.doi.org/10.17632/2xh658swv4.2. |
| 2 | All data is publicly available at dx.doi.org/10.17632/2xh658swv4.2. |
| 3 | All results are publicly available at dx.doi.org/10.17632/2xh658swv4.2. |
| 4 | All data is publicly available at dx.doi.org/10.17632/2xh658swv4.2. |
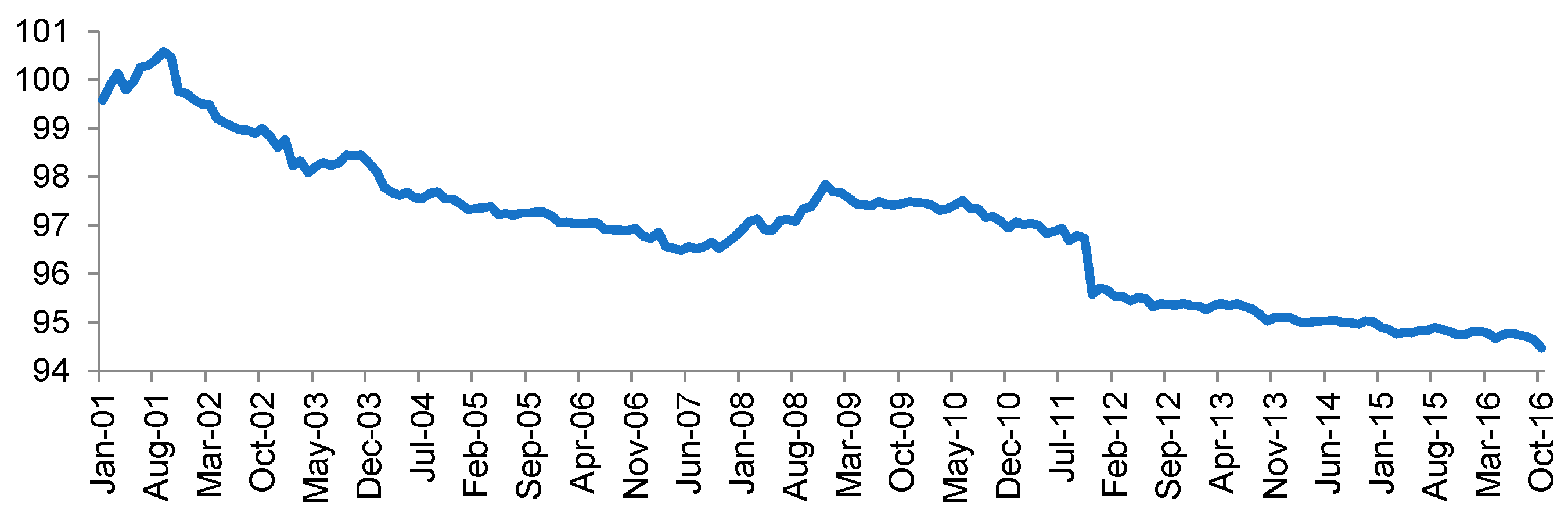
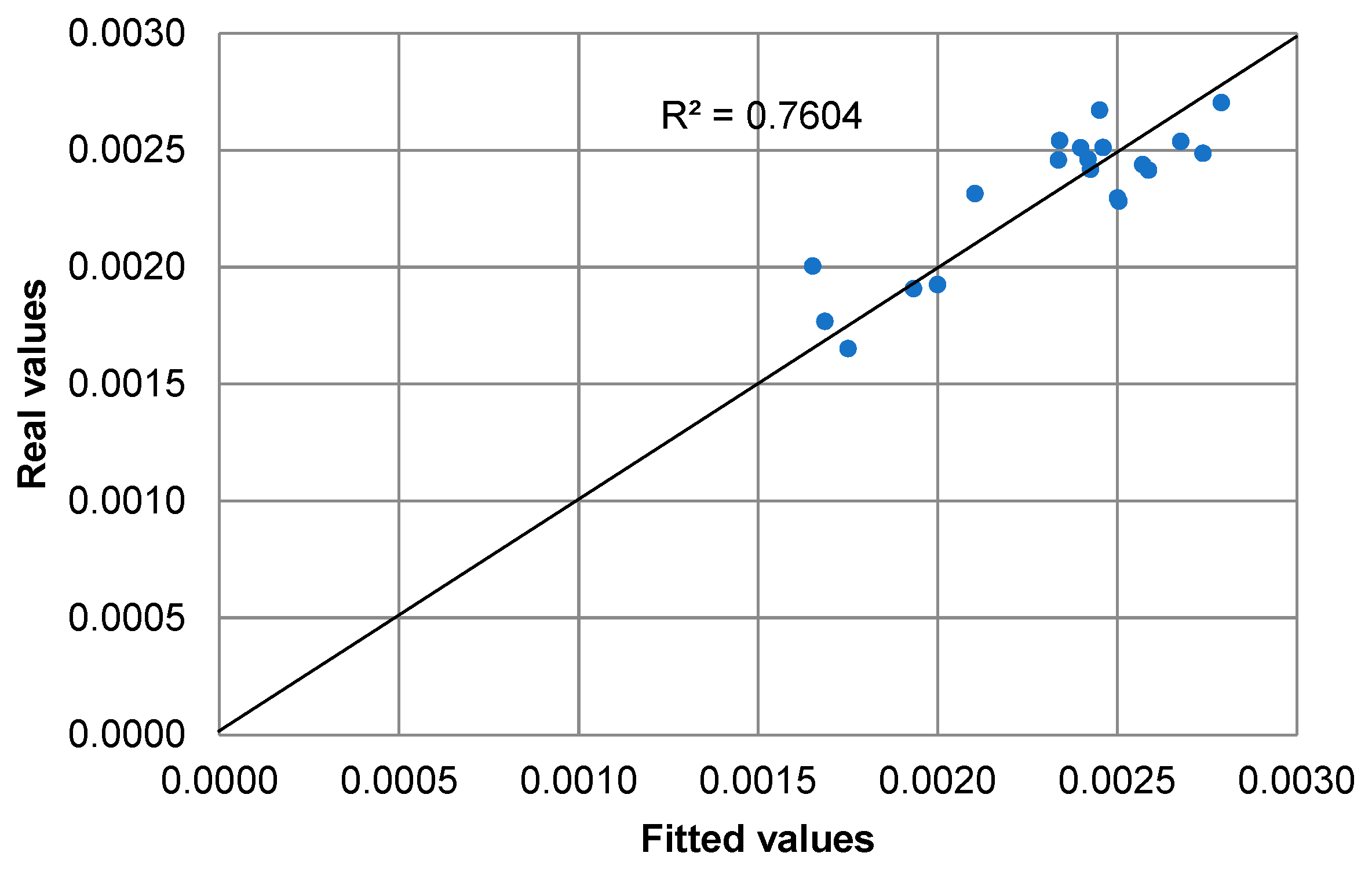
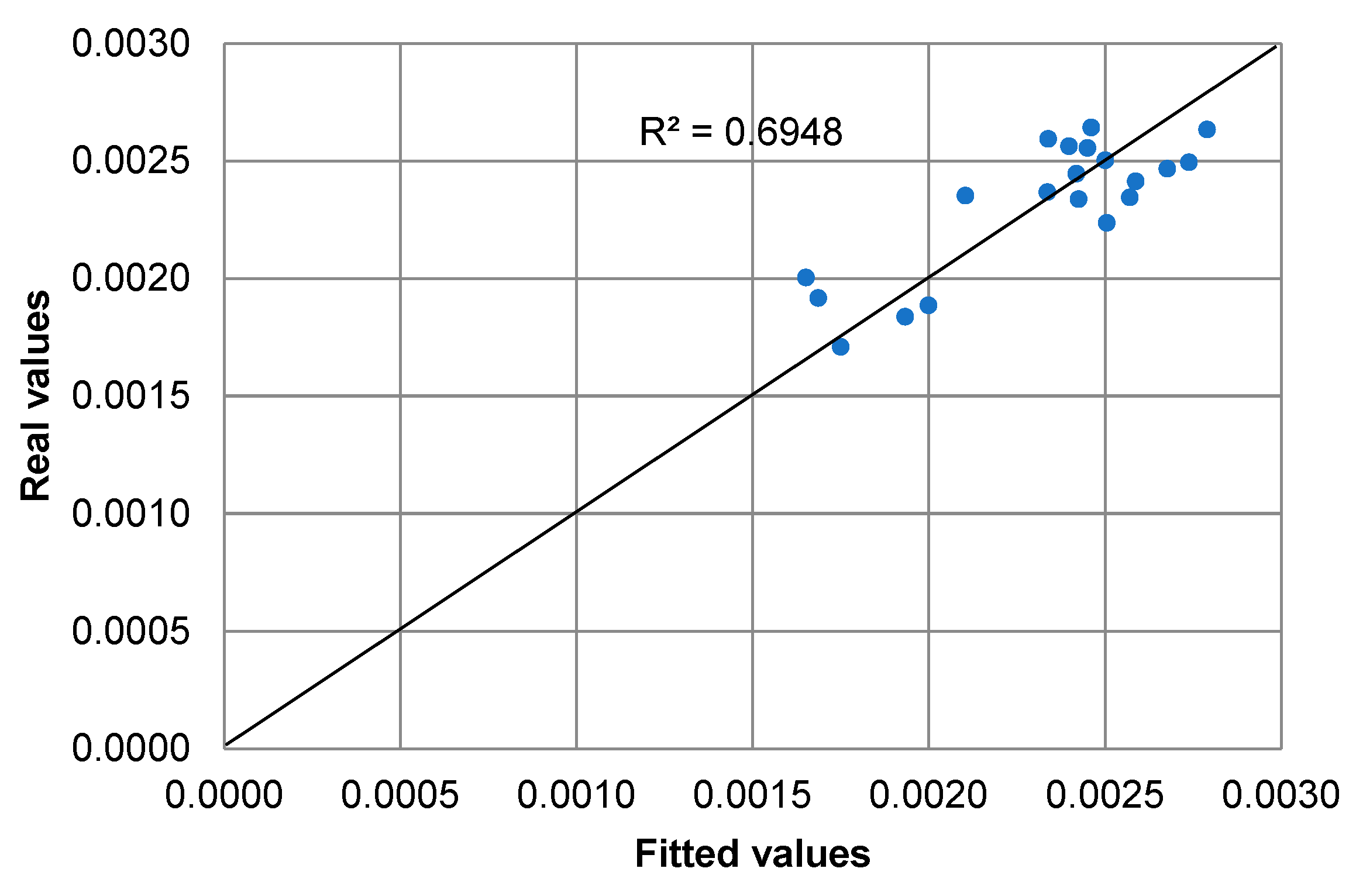
| Panel A: | Returns | |||||
| Average | SD | Max | Min | Skewness | Kurtosis | |
| 0.363 | 4.814 | 44.284 | −44.543 | −0.633 | 2.156 | |
| Panel B: | Volume (€ Mill.) | |||||
| Average | STD | |||||
| 547,100 | 689,962 |
| Inputs | |
| Risk measures | Standard deviation (SD) |
| Lower partial moments order 1 (LPM1) | |
| Lower partial moments order 2 (LPM2) | |
| Lower partial moments order 3 (LPM3) | |
| Value at risk (VaR) | |
| Conditional value at risk (CVaR) | |
| Modified value at risk (MVaR) | |
| Kurtosis (K) | |
| Outputs | |
| Return measures | Average return (Rme) |
| Maximum return (Rmax) | |
| Minimum return (Rmin) | |
| Higher partial moments order 1 (HPM2) | |
| Higher partial moments order 2 (HPM3) | |
| Higher partial moments order 3 (HPM4) | |
| Skewness (S) |
| Input | Component 1 | Component 2 | Output | Component 1 | Component 2 |
|---|---|---|---|---|---|
| SD | 0.9689 | 0.0338 | Average Return | 0.5481 | −0.0210 |
| VaR 95% | 0.8787 | 0.0568 | Rmax | 0.6882 | 0.4594 |
| CVaR 95% | 0.9866 | 0.0223 | Rmin | −0.7217 | 0.3729 |
| MVaR 95% | 0.0152 | 0.9970 | Skewness | −0.0225 | 0.9818 |
| LPM 1 | 0.9813 | 0.0267 | HPM 1 | 0.9807 | 0.0536 |
| LPM 2 | 0.9930 | 0.0359 | HPM 2 | 0.9782 | 0.0531 |
| LPM 3 | 0.9892 | 0.0384 | HPM 3 | 0.9767 | 0.0529 |
| Kurtosis | 0.4210 | −0.0594 | |||
| Explained variance | 72.47% | 84.94% | Explained variance | 59.65% | 78.41% |
| Portfolio | Mean Return | SD | Skewness | Kurtosis | Jarque–Bera |
|---|---|---|---|---|---|
| P1 (Small) | 0.251 | 4.781 | −0.719 | 1.462 | 35.400 |
| P2 | 0.247 | 4.504 | −0.832 | 1.519 | 42.707 |
| P3 | 0.170 | 4.783 | −0.845 | 1.491 | 42.744 |
| P4 | 0.246 | 4.782 | −0.831 | 1.404 | 39.867 |
| P5 | 0.235 | 4.587 | −0.800 | 1.298 | 35.712 |
| P6 | 0.243 | 4.609 | −0.760 | 1.204 | 31.652 |
| P7 | 0.260 | 4.518 | −0.783 | 1.079 | 30.467 |
| P8 | 0.235 | 4.598 | −0.698 | 1.223 | 28.999 |
| P9 | 0.269 | 4.562 | −0.715 | 1.275 | 30.867 |
| P10 | 0.211 | 4.733 | −0.692 | 1.321 | 30.801 |
| P11 | 0.241 | 4.731 | −0.697 | 1.274 | 30.023 |
| P12 | 0.258 | 4.733 | −0.669 | 1.133 | 25.882 |
| P13 | 0.194 | 4.600 | −0.733 | 1.109 | 28.431 |
| P14 | 0.252 | 4.700 | −0.732 | 1.051 | 27.323 |
| P15 | 0.275 | 4.528 | −0.744 | 1.260 | 31.983 |
| P16 | 0.280 | 4.659 | −0.717 | 1.425 | 34.373 |
| P17 | 0.244 | 4.697 | −0.695 | 1.034 | 25.235 |
| P18 | 0.166 | 4.555 | −0.693 | 1.092 | 26.201 |
| P19 | 0.201 | 4.397 | −0.664 | 1.142 | 25.821 |
| P20 (Big) | 0.176 | 4.605 | −0.687 | 1.039 | 24.961 |
| Portfolios | Average Score | Mean Return |
|---|---|---|
| P1 (Small) | 1.000 | 0.251 |
| P2 | 0.964 | 0.247 |
| P3 | 0.963 | 0.170 |
| P4 | 0.934 | 0.246 |
| P5 | 0.917 | 0.235 |
| P6 | 0.917 | 0.243 |
| P7 | 0.913 | 0.260 |
| P8 | 0.900 | 0.235 |
| P9 | 0.924 | 0.269 |
| P10 | 0.887 | 0.211 |
| P11 | 0.875 | 0.241 |
| P12 | 0.876 | 0.258 |
| P13 | 0.888 | 0.194 |
| P14 | 0.895 | 0.252 |
| P15 | 0.874 | 0.275 |
| P16 | 0.891 | 0.280 |
| P17 | 0.884 | 0.244 |
| P18 | 0.947 | 0.166 |
| P19 | 0.884 | 0.201 |
| P20 (Big) | 0.808 | 0.176 |
| Average | 0.907 | 0.233 |
| P1-P20 spread | 0.192 | 0.075 |
| Panel A | ||||||||||
| γ0 | γ1 | γ2 | γ3 | γ4 | GRS | J-test | R2 | R2Adj | ||
| Estimate | −0.0014 | 0.0066 | 0.0028 | 0.0085 | −0.0194 | 7.222 | 6.698 | OLS | 0.761 | 0.682 |
| (0.0037) | (0.0069) | (0.0028) | (0.0041) | (0.0362) | (0.031) | (0.035) | GLS | 0.708 | 0.611 | |
| t-statistic | −0.3804 | 0.9595 | 1.0010 | 2.0916 | −0.5366 | |||||
| Panel B | ||||||||||
| Estimate | −0.0024 | 0.0083 | 0.0027 | 0.0076 | 7.980 | 7.057 | OLS | 0.695 | 0.619 | |
| (0.0040) | (0.0068) | (0.0029) | (0.0033) | (0.033) | (0.028) | GLS | 0.594 | 0.493 | ||
| t-statistic | −0.6299 | 1.2241 | 0.9459 | 2.3253 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solórzano-Taborga, P.; Alonso-Conde, A.B.; Rojo-Suárez, J. Data Envelopment Analysis and Multifactor Asset Pricing Models. Int. J. Financial Stud. 2020, 8, 24. https://doi.org/10.3390/ijfs8020024
Solórzano-Taborga P, Alonso-Conde AB, Rojo-Suárez J. Data Envelopment Analysis and Multifactor Asset Pricing Models. International Journal of Financial Studies. 2020; 8(2):24. https://doi.org/10.3390/ijfs8020024
Chicago/Turabian StyleSolórzano-Taborga, Pablo, Ana Belén Alonso-Conde, and Javier Rojo-Suárez. 2020. "Data Envelopment Analysis and Multifactor Asset Pricing Models" International Journal of Financial Studies 8, no. 2: 24. https://doi.org/10.3390/ijfs8020024
APA StyleSolórzano-Taborga, P., Alonso-Conde, A. B., & Rojo-Suárez, J. (2020). Data Envelopment Analysis and Multifactor Asset Pricing Models. International Journal of Financial Studies, 8(2), 24. https://doi.org/10.3390/ijfs8020024






